地球物理学报  2019, Vol. 62 Issue (7): 2394-2404   PDF    
引用本文
黄谟涛, 刘敏, 邓凯亮, 等. 2019. 海域流动点外部扰动引力无奇异计算模型. 地球物理学报, 62(7): 2394-2404, doi: 10.6038/cjg2019L0739.  
Huang M T, Liu M, Deng K L, et al. 2019. A nonsingular model for computing the external gravity field at a mobile point in a sea area. Chinese J. Geophys. (in Chinese), 62(7): 2394-2404, doi: 10.6038/cjg2019L0739.  
海域流动点外部扰动引力无奇异计算模型
黄谟涛1, 刘敏2, 邓凯亮1,3, 欧阳永忠1,4, 陆秀平1, 翟国君1, 吴太旗1, 陈欣1     
1. 海军海洋测绘研究所, 天津 300061;
2. 信息工程大学, 郑州 450001;
3. 国防科学技术大学, 长沙 410073;
4. 南京信息工程大学, 南京 210044
收稿日期 2018-06-12, 2019-04-16 收修定稿
基金项目: 国家自然科学基金项目(41804011;41706111;41774021), 国家重点研发计划(2016YFC0303007;2016YFB0501704), 国家重大科学仪器设备开发专项资助项目(2011YQ12004503), 国家973计划资助项目(613219)共同资助
第一作者简介: 黄谟涛, 男, 1961年生, 博士生导师, 研究方向为海洋重力场测定理论方法.E-mail:Ouyangyz@sohu.com
通讯作者: 邓凯亮, 男, 1983年生, 博士, 研究方向为海空重力测量理论及应用技术.E-mail:dengkailiang036@163.com
摘要：针对海域重力场变化特征和远程飞行器机动发射保障应用需求，本文分析研究了地球外部空间扰动引力三类传统计算模型的技术特点及其适用性，指出了采用表层法作为海域流动点扰动引力计算模型的合理性及需要解决的关键问题，分析论证了空中扰动引力计算对地面观测数据的分辨率和精度要求，提出通过引入局部积分域恒等式变换、局域泰勒级数展开和非网格点内插方法，消除表层法计算模型积分奇异性固有缺陷的研究思路，进而推出了适合于海域流动点应用的扰动引力无奇异计算模型，较好地满足了全海域和全高度段对局部扰动重力场快速赋值的实际需求.以超高阶全球位模型EGM2008作为标准场，通过数值计算验证了无奇异计算模型的可行性和有效性，在重力场变化比较剧烈的海沟区，该模型的计算精度优于2×10-5m·s-2.
关键词: 外部扰动引力      表层法      奇异性      局部积分域恒等式变换      局域泰勒级数展开      非网格点内插方法     
A nonsingular model for computing the external gravity field at a mobile point in a sea area
HUANG MoTao1, LIU Min2, DENG KaiLiang1,3, OUYANG YongZhong1,4, LU XiuPing1, ZHAI GuoJun1, WU TaiQi1, CHEN Xin1     
1. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China;
2. Information Engineering University, Zhengzhou 450001, China;
3. National University of Defense Technology, Changsha 410073, China;
4. Nanjing University of Information Science & Technology, Nanjing 210044, China
Abstract: In accordance with the variation characteristics of the marine gravity field and the special support requirement of launching a long range spacecraft at a mobile point, this paper presents a detail analysis on the applicability and distinguishing features of the three traditional models for computing disturbing gravity. Then the reasonability of using the surface layer method to compute the disturbing gravity in sea areas and the key problems to be resolved are pointed out. The surveying resolution and accuracy requirement of gravity anomalies on the earth' surface for calculating the external disturbing gravity field is discussed. A new study approach is suggested to modify the original surface layer model, in which a transformation of identical equation with a local integration field, Taylor series expansion in the local area and an interpolation method for non-grid point are introduced to eliminate the singularity drawback inherent in the surface layer model. And a nonsingular modified model of computing the external gravity field at a mobile point in a sea area is proposed for application, which can satisfy the practical needs of determining the local gravity field quickly in all sea areas and full height. A numerical test using a synthetic gravity data set from the ultra-high-degree geopotential model EGM2008 proves the feasibility and validity of the suggested model. The approximation accuracy of the modified model is superior to 2×10-5m·s-2 in rugged oceanic trench areas with intense variations of the gravity field.
Keywords: External disturbing gravity    Surface layer method    Singularity    Transformation of identical equation with a local integration field    Taylor series expansion in local area    Interpolation method for non-grid point    
0 引言

地球外部扰动引力场计算在大地测量和空间科学技术研究、人造卫星及各类航天器飞行保障中具有非常重要的应用价值(Moritz, 1966；Heiskanen and Moritz, 1967；黄谟涛等，2005).目前常用于计算外部扰动引力场的数学模型主要有三类：一类是基于全球重力位模型的球谐展开式，主要作为移去恢复算法的基础模型，用于扰动引力场的低频段计算(陆仲连，1996；黄谟涛等，2005).另一类是基于经典Stokes边值理论的直接积分模型、基于质体引力位等值层原理的表层法模型和基于Poisson积分的向上延拓模型(Heiskanen and Moritz, 1967；陆仲连，1996)，此类模型的主要特点是，采用的输入量均为地球表面重力场的直接观测参量，不需要作进一步的转换处理，对数据预处理的技术要求比较简单.但由于此类模型都源于重力测量边值问题的球面解，故它们自身都无法顾及地形效应的影响，同时还普遍存在积分奇异性干扰问题.第三类是基于现代Bjerhammar换置边值理论的等效源模型(Bjerhammar，1964)，包括等效重力异常模型(Heiskanen and Moritz, 1967；李建成等，2003)、虚拟点质量模型(Sunkel, 1983; 吴晓平，1984；黄金水和朱灼文，1995；黄谟涛等，2005；王建强等，2010)及虚拟单层密度模型(许厚泽和朱灼文，1984；操华胜等，1985).此类模型的主要优势是，它们能以简单的方式顾及地形效应的影响，而且不存在数值积分奇异性问题.但在数据预处理阶段，需要完成地面重力观测量到地球内部等效场源的转换，等同于地面观测数据的向下延拓，其中所涉及的积分方程迭代或矩阵求逆过程很容易受到观测噪声的干扰，使解算结果偏离正确的数值解(Bjerhammar，1987；束蝉方等，2011).当计算范围和地面起伏较大时，地面场元向下延拓过程引起的欠适定性问题会更加突出，这是此类等效源模型固有的“先天性”弱点.

显然，应当针对不同的应用需求，选择合适的扰动引力计算模型.就远程飞行器发射保障应用而言，由陈国强(1982)和陆仲连等(1993)得知，考虑到计算精度和速度两个方面的要求，人们通常采用全球模型(即球谐展开式)和局部模型(即前面的第二或第三类模型)的组合，作为远程飞行器主动段飞行轨迹的扰动引力计算模型，单独采用全球位模型作为被动段飞行轨迹的计算模型.可见，球谐展开式是地球外部扰动引力场计算模型不可或缺的组成部分，如何在诸多的直接积分模型和等效源模型中，挑选并构造出符合海域发射阵位保障需求的局部重力场快速计算模型，是本文拟研究解决的核心问题.相比于陆地固定点发射阵位的传统保障模式，海域外部空间扰动引力场保障需求具有鲜明的特点：一是海上发射阵位是非固定的流动点，具有较大的灵活机动性，实时性保障要求更高；二是保障范围几乎涵盖全球海域，需要大面积的基础数据作保障，数据转换阶段的连续性和光滑度要求更高；三是发射阵位周边附近区域是变化平缓的海平面，计算时不必顾及远区陆地地形效应的影响，数值计算的复杂性和难度相对降低.根据上述保障需求，结合前面针对各类计算模型技术特点的分析，我们认为，具有简单核函数结构的表层法模型更适合于海域流动点扰动引力的快速计算.其理由是：与其他同类的积分模型相比，表层法模型核函数的数学结构更为简单，输入数据保障要求更容易得到满足；与等效源模型相比，表层法不需要对地面观测数据做等效转换处理，不存在向下延拓解算引起的数值不稳定性问题，而等效源模型能够自动顾及地形效应影响的技术优势在海域却无法得到体现.很显然，就海域保障应用而言，表层法存在的唯一缺陷(也是同类积分模型的共同缺陷)是超低空计算的积分奇异性问题.关于重力场数值积分奇异性问题的研究，国内外学者已经提出了许多富有成效的解决方案(Heiskanen and Moritz, 1967；Bian，1997；Hwang，1998；郭东美和许厚泽，2011；刘长弘，2016；陈欣，2016)，其核心思想是：对数据中央区块效应做分离处理，通过非奇异变换，建立相对应的球冠域或矩形域中央区效应无奇异计算模型.但上述研究的重点主要聚焦于大地水准面、垂线偏差、地形改正等几类常用参数的计算，关于扰动引力计算积分奇异性的研究成果鲜有公开文献报导，已有的相关研究还显不够充分，采用的处理方法还不够完善(刘长弘，2016).针对表层法积分奇异性问题，本文通过引入基于局部积分域的恒等式变换、局域泰勒级数展开和非网格点内插方法，将表层法原始计算模型转换为具有稳定数值解的连续函数模型，进而推出了适合于海域应用的扰动引力无奇异计算模型.

1 传统表层法计算模型及精度分析 1.1 表层法计算模型

由Heiskanen和Moritz(1967)知，利用表层法计算地球外部扰动引力三分量的积分式为

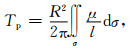
(1)

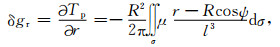
(2)

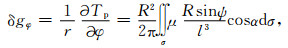
(3)

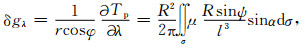
(4)

其中，

式中，Tp为外部空间计算点P处的扰动位；(r, φ, λ)和(R, φ′, λ′)分别代表计算点和球面流动点的地心向径、地心纬度和地心经度；ψ为计算点和流动点之间的球面角距；l为计算点和流动点之间的空间距离；Δg为地面(包括海面，下同)观测重力异常；T为地面点扰动位；ζ为地面高程异常；γ为地面平均重力；μ称为广义面密度；R为地球椭球平均半径；h为计算高度(大地高)；dσ为单位球积分面积元.

1.2 计算精度与数据需求分析

利用式(2)—(4)计算扰动引力三分量的精度主要取决于数据质量和建模误差两个方面的因素(Heiskanen and Moritz, 1967；Zhang et al., 1998；黄谟涛等，2005)，前者指由于使用移去恢复技术引入的位系数误差和由观测噪声引入的数据传播误差；后者包括积分离散化误差、远区截断误差和数据截断误差.为了突出主要影响因素，同时考虑到次要因素的可控性，这里重点讨论数据观测和数据截断两项误差对扰动引力计算精度的影响.

实际计算扰动引力时，必须对式(2)—(4)做离散化处理，假设已知的重力异常和高程异常均以网格化形式给出，且为相互独立的等精度观测量，则根据误差传播律可得扰动引力的数据传播误差估计式为

(5)

(6)

(7)

其中，

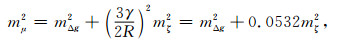
(8)

式中，mΔg和mζ分别代表地面网格平均重力异常和高程异常的中误差，包含数据观测误差和代表误差两个部分.目前海域高程异常的确定精度已经远高于1 m，故由式(8)知，广义面密度的计算几乎不受高程异常数据误差的影响，可近似取mμ=mΔg.

这里参照黄谟涛等(2016)，以P(φ=40°, λ=120°)为计算点，以40°×40°为数据覆盖范围(此范围足以忽略积分远区影响)(吴晓平，1992；Zhang et al., 1998)，分别采用5′×5′、2′×2′和1′×1′三种格网数据，同时分别取mΔg=3, 5, 7 mGal(10-5m·s-2)，依次计算mδgr、mδgφ、mδgλ，具体见表 1.

表 1 扰动引力数据传播误差估计(单位：10-5m·s-2) Table 1 Estimation of errors in propagation of disturbing gravity data (unit:10-5m·s-2)

对比本文表 1和黄谟涛等(2016)中的表4计算结果可以看出，数据误差对由Pizzetti公式导出的直接积分模型(Heiskanen and Moritz, 1967)和表层法计算模型的影响规律是一致的，即数据误差越大，引起扰动引力的计算误差也越大，积分元大小对数据误差传播几乎不产生影响；但同样的误差量对两种模型的影响量值却有较大的差异，对前者的影响明显大于后者.这个结果说明，相比直接积分模型，表层法计算模型的核函数具有更加优良的数学特性(收敛更快速)，选择表层法作为扰动引力三分量计算模型更有利于减弱数据误差的影响.黄谟涛等(2016)研究认为，为满足远程飞行器飞行轨道控制保障需求，地球外部扰动引力的计算精度应优于4 mGal.如果以这样的精度要求为依据，那么在同时考虑计算模型误差、数据截断误差等其他因素综合影响的情况下，采用表层法作为计算模型，可将数据误差指标限定为7 mGal，比采用直接积分模型时的5 mGal指标降低了2 mGal.反过来，如果数据误差特性保持不变，那么采用表层法模型计算扰动引力三分量将取得比直接积分模型高出1~2 mGal的精度.

利用扰动引力三分量的球谐展开式，可推出垂直和水平分量在不同频段的能量谱计算模型，并根据国际上推出的重力异常阶方差拟合模型，计算得到扰动引力在相应频段的能量谱.这里直接引用黄谟涛等(2016)的计算结果，如表 2所示.

表 2 扰动引力能量谱分布(单位：10-5m·s-2) Table 2 Distributions of disturbing gravity power spectra (unit:10-5m·s-2)

由表 2看出，扰动引力计算精度随数据分辨率的提高而提升，当使用的数据分辨率截断到5′时，截断误差影响量超过3 mGal；数据截断到2′时，截断误差影响量可控制在1 mGal以内.可见，如果仍然以扰动引力优于4 mGal计算精度要求为限定指标，那么至少应当采用精细到2′分辨率的地面观测数据.

2 无奇异的表层法计算模型 2.1 垂直分量无奇异计算模型

前面对表层法计算模型所作的精度分析，都是建立在该模型具有稳定的数值解基础之上的，但由式(2)—(4)得知，当计算高度h→0和球面角距ψ→0，即计算点接近数据点或与数据点重合时，公式(2)—(4)的数值积分都将出现不同程度的奇异性问题.另外，由Heiskanen和Moritz(1967)得知，在以Poisson积分为基础的同类参量向上延拓计算模型中，都会涉及由三维空间Dirac核函数引起的数值不连续性问题，即当计算点由外部空间趋于球面时，计算参量在边界面会出现不合理的数值跳变.不难看出，本文的公式(2)就属于此类特殊的计算模型.因为当r→R时，由式(2)确定的扰动引力径向分量δgr(r, φ, λ)并不收敛于球面上的参数值δgr(R, φ, λ)，显然不符合数值逼近理论最基本的连续性要求.这也是引起表 1计算结果中扰动引力径向分量的数据传播误差相比两个水平分量要小几个数量级的主要原因.

为了解决公式(2)的积分奇异性问题，同时消除由三维空间Dirac函数引起的数值矛盾，这里参照Heiskanen和Moritz(1967)的研究思路，通过引入合适的恒等式变换，将原计算模型转换为具有稳定数值解的连续函数模型.首先，不难推证：

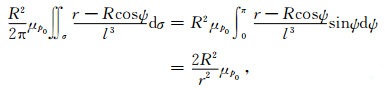
(9)

式中，μp0为地面计算点处的广义面密度.将式(2)和式(9)相减，并略加整理得：

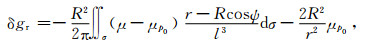
(10)

不难看出，经上述恒等式变换后，式(10)不再存在积分奇异性问题.同时，理论上，当r→R时，由式(10)确定的扰动引力径向分量δgr(r, φ, λ)收敛于球面上的参数值δgr(R, φ, λ)，推证如下：

当r→R时，式(10)右端积分第一项为

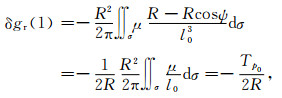
(11)

式中，；Tp0为地面计算点处的扰动位.式(10)右端积分第二项为

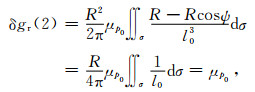
(12)

式(10)右端第三项为

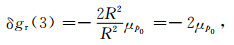
(13)

将式(11)、(12)和(13)三项相加得：

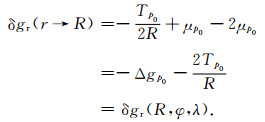
(14)

可见，经改化后的计算式(10)在边界面不再出现数值跳跃现象.至此就从理论上解决了公式(2)存在的积分奇异和数值不连续性问题.但需要指出的是，在实际应用中，受观测数据覆盖范围的限制，一般将计算模型的全球积分划分为近区和远区，通过引入一定阶次的全球位模型和移去恢复技术，在近区采用实测数据(减去全球位模型)进行计算，远区则只顾及到全球位模型的作用.在近区计算部分，为了提高计算效率，通常以计算点为中心，将整个数据覆盖区按流动点到计算点由近至远划分成若干个环带，距离计算点越近的环带，数据网格间隔越小，即数据分辨率越高.目前常用的数据网格组合依次为：2′×2′、5′×5′、20′×20′和1°×1°(黄谟涛等, 2005, 2016).

由前面的推证过程得知，式(10)是从恒等式(9)变换过来的，它们都建立在全球积分基础之上.很显然，实际应用中的有限区域积分并不满足恒等式(9)的理论假设，这就意味着，当采用有限的积分区域时，计算公式(10)是不严密的.试算结果表明，由此引起的扰动引力计算误差随计算高度的增大而增大，最大可达几十毫伽.为了消除该项误差影响，本文对式(9)和(10)做进一步的改化处理.因计算公式(2)的奇异性和数值不连续性问题都只出现在计算点附近小区域，故我们只需要对计算点所在的最高分辨率数据区块(比如2′×2′网格数据覆盖的2°×2°数据区块)做特殊处理.假设该数据区块的积分半径为ψ0，则不难推得：

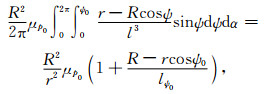
(15)

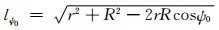
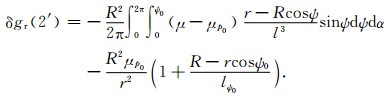
式中，.单独对该数据区块做类似于式(10)的恒等变换，即得：

(16)

本文称上述变换为局部积分域恒等式变换.不难看出，式(16)已经不再存在积分奇异性和数值不连续性问题.可见，在实际应用中，我们只需要把数据覆盖域划分为内区(对应2′×2′网格数据域)和外区(含5′×5′、20′×20′和1°×1°数据域)，内区采用式(16)进行计算，外区仍保持原计算式(2)不变，这样就完成了扰动引力垂直分量无奇异计算模型的构建，用公式形式表示为

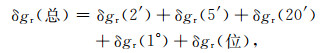
(17)

式中，δgr(2′)由式(16)计算，δgr(5′)、δgr(20′)和δgr(1°)统一由式(2)计算，δgr(位)代表全球位模型的贡献量，其计算式为

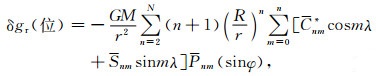
(18)

式中，GM为地球引力常数；Cnm*和Snm为完全正常化位系数；Pnm(sinφ)为完全正常化勒让德函数；N为球谐展开式的最高阶次，在实际应用中，受计算时间的限制，N值不宜取得太高，一般取为N=36.需要补充说明的是，因为采用了移去恢复技术，故此时积分式(2)和(16)中的观测量(μ和μp0)都应当是扣除了全球位模型后的残差值(下同).

2.2 水平分量无奇异计算模型

由式(3)和(4)得知，当计算点与数据点重合时，计算点所在的数据块对扰动引力水平分量不起作用，实际计算时可将该数据块从积分域中剔除，以避免出现积分奇异性问题.当计算点与数据点不重合但两点相距很近时，由于积分核函数在计算高度h→0和球面角距ψ→0的邻域内变化极为剧烈，致使公式(3)和(4)的数值积分在计算点周围超低空高度段仍将受到不同程度的奇异性干扰，其影响量可达几个毫伽甚至更大.为了消除此项影响，通常也是将计算点所在的数据块从积分域中剔除，具体做法是将式(3)和(4)对2′×2′网格数据的内区积分改写为

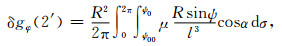
(19)

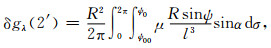
(20)

式中，ψ00代表计算点所在的2′×2′网格数据块半径，即表示该数据块已经从上述数值积分中分离出来.但需要指出的是，当计算点周围的重力场变化比较剧烈时，上述两种情形(即计算点与数据点重合和不重合)下忽略计算点所在数据块影响的做法都可能带来几个毫伽的计算误差.显然，相对于扰动引力优于4 mGal的计算精度要求，这一数据块的影响是不能被忽略的.下面单独给出计算该数据块影响的解析式.

首先采用极坐标系(s, α)对积分核函数在小范围内作平面近似处理：

此时，与计算点重合数据块的积分式可写为(这里以纬度方向分量为例)：

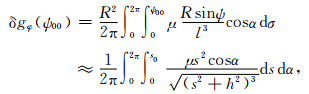
(21)

其次，在计算点P的地面投影点P0处，采用平面坐标系将广义面密度μ按泰勒级数展开为

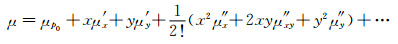
(22)

式中，x轴指向正北，y轴向东；μ′x代表μ对x的偏导数，其他符号意义类同；并有：x=scosα，y=ssinα.将式(22)代入(21)，不难推得：

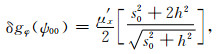
(23)

同理可得：

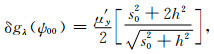
(24)

式中，s0代表数据网格大小的一半，当网格数据为2′×2′时，s0=1′.假设与计算点重合的数据格网为(i, j)，则有：

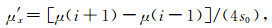
(25)

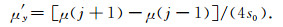
(26)

当计算高度h=0时，式(23)和(24)简化为

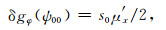
(27)

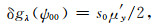
(28)

将式(25)和(26)代入得

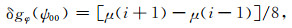
(29)

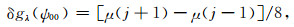
(30)

由式(29)和(30)可以看出，当计算点周围的重力场变化比较剧烈，比如一个网格间距的重力异常变化超过10 mGal时，计算点所在数据块对扰动引力水平分量的影响是相当可观的，可达2~3 mGal甚至更大.至此，我们也就完成了扰动引力水平分量无奇异计算模型的构建，用公式形式表示为

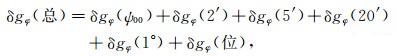
(31)

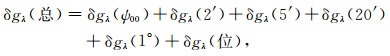
(32)

式中，δgφ(ψ00)和δgλ(ψ00)由式(23)和(24)计算；δgφ(2′)和δgλ(2′)由式(19)和(20)计算；δgφ(5′)、δgφ(20′)和δgφ(1°)统一由式(3)计算；δgλ(5′)、δgλ(20′)和δgλ(1°)统一由式(4)计算；全球位模型贡献量δgφ(位)和δgλ(位)的计算式为

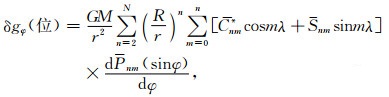
(33)

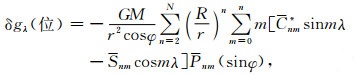
(34)

式中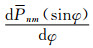，为Pnm(sinφ)对φ的导数，其他符号意义同前.

2.3 非网格点扰动引力计算模型

由前面为避免积分奇异问题而设计的变换计算策略得知，式(16)、(23)和(24)都是以数据网格点作为计算点为前提条件建立起来的.当计算点为非网格点时，上述各个恒等式要求的积分区域对称性假设不再严格成立，故它们不能直接用于非数据网格点的计算.此时，可利用计算点(非网格点)周围的4个网格点计算结果内插出计算点上的扰动引力.设计算点距4个网格点的距离分别为s1, s2, s3和s4，由式(16)、(23)和(24)计算得到4个网格点扰动引力分量的内区(即2′×2′网格数据覆盖域)影响量分别为δg1, δg2, δg3和δg4，则可由下式内插得到计算点扰动引力分量的对应部分：

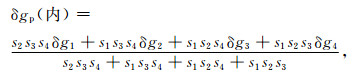
(35)

式中，δgp(内)只代表非网格点扰动引力分量的内区影响部分，剩下的外区(即2′×2′网格数据覆盖域以外部分)影响仍直接采用传统的数值积分公式进行计算.

如前所述，与陆地固定发射阵位相比较，海域发射阵位的主要特点是高度机动性和覆盖范围全球性(至少需要覆盖整个太平洋和印度洋).这样的特性一方面要求重力场保障必须有超大范围的基础数据作保证，另一方面要求必须具备实时或准实时化的保障能力，具体体现为诸元数据准备和扰动引力计算两个阶段的快速保障能力.诸元数据准备阶段是指从确认发射阵位到飞行器轨道计算(含扰动引力计算)开始之前的一段时间，这个阶段如果用时过长，那么势必影响后端诸元参数的计算、分析及飞行器发射时间的决策.选用表层法作为扰动引力计算模型，其最大的优势就体现为：可在极短的时间内完成扰动引力计算所需的数据准备工作，因为该模型只需要依据发射点坐标即可迅速从不同分辨率的基础数据文件中选定所需的局部网格数据，不需要作任何的转换或处理.这是点质量等其他等效源方法无法相比的，因为后者在数据准备阶段都需要完成多层等效源参数(点质量或虚拟单层密度)的解算，这对于机动性要求很强、实时性保障要求很高的海域发射阵位来说，时间上的负担往往是无法接受的.

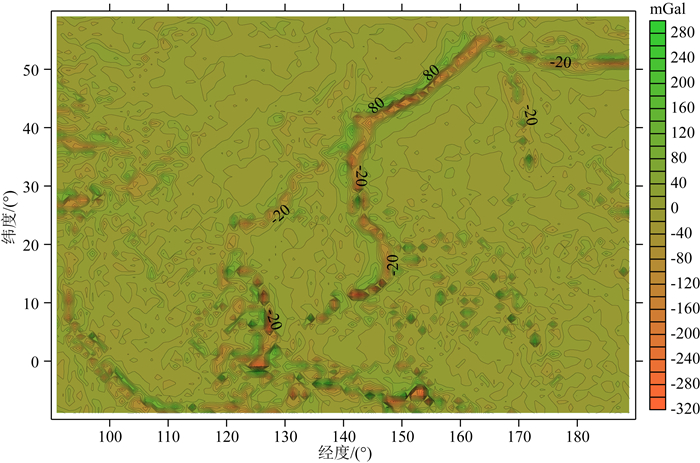
3 模型精度数值检验与分析

扰动引力计算精度主要取决于模型逼近误差和数据传播误差两个方面的因素(Zhang et al., 1998；黄谟涛等，2005)，数值离散化误差、远区截断误差和数据截断误差都属于模型逼近误差的范畴.为了定量估计模型逼近误差的大小，本文采用2160阶次的全球位模型EGM2008作为标准场开展数值计算检验，由其模拟产生外部扰动引力三分量的基准值，同时计算1°×1°、20′×20′、5′×5′和2′×2′四组地面重力异常和高程异常的伪观测量，作为确定外部空间扰动引力场的基础数据.试验区涵盖了重力场变化比较剧烈的马里亚纳海沟，区域范围为：φ:10°S~60°N；λ:90°E—190°E，计算某一点扰动引力采用的四种分辨率基础数据覆盖范围为1°×1°→30°×30°；20′×20′→10°×10°；5′×5′→4°×4°；2′×2′→2°×2°；参考场的阶次取为N=36.表 3列出了四组地面重力异常和高程异常计算量(已扣除36阶参考场)的统计结果，图 1为20′×20′网格重力异常分布的等值线图.

表 3 位模型地面重力异常和高程异常统计结果 Table 3 Statistic of ground gravity and elevation anomalies from potential model EGM2008
图 1 EGM2008位模型重力异常等值线图 Fig. 1 Contours of gravity anomalies from potential model EGM2008

为了考察本文提出的无奇异表层法计算模型对超低空扰动引力场的逼近效果，这里特别选取位于马里亚纳海沟的两个点作为计算点，分别采用不同的改化模型计算不同高度的扰动引力三分量，并将其与相对应的位模型计算基准值作对比分析.其中，一个计算点选取与2′×2′数据网格点重合，具体位置为P1(φ=27°01′N, λ=143°01′E)；另一个计算点选取为非数据网格点，具体位置为P2(φ=27°00′10″N, λ=143°00′15″E).这里把原始的表层法计算模型(即公式(2)—(4))称为模型一，把由公式(10)、(19)和(20)组成的阶段改化模型称为模型二，把由公式(16)、(19)、(20)、(23)和(24)组成的阶段改化模型称为模型三，把由模型三加上公式(35)组成的最终改化模型称为模型四.表 4和表 5分别列出了两个计算点在不同高度上的扰动引力三分量位模型计算基准值，同时列出了不同赋值模型计算结果与对应基准值的互比结果.

表 4 P1点不同赋值模型计算结果与对应基准值的互比结果(单位：10-5m·s-2) Table 4 Comparison of different models and EGM2008 at point P1 (unit:10-5m·s-2)
表 5 P2点不同赋值模型计算结果与对应基准值的互比结果(单位：10-5m·s-2) Table 5 Comparison of different models and EGM2008 at point P2 (unit:10-5m·s-2)

由前面的模型改化过程和误差源分析得知，原始模型(模型一)的计算误差主要来自积分核函数在超低空高度段的奇异性，改化模型二的计算误差主要来自：①径向分量有限区域积分不满足恒等变换式(9)要求全球积分的理论假设；②扰动引力水平分量计算式忽略了与计算点重合数据块的影响.改化模型三的计算误差主要来自：当计算点为非数据网格点时，改化模型采用的积分区域不满足各个恒等变换式要求的对称性假设.从表 4试验结果首先可以看出，由核函数奇异性引起的计算误差在10 km以下高度段都是不可忽略的；积分区域不能覆盖全球引起的径向分量计算误差在整个高度段都远远超出预定精度指标；当计算点为数据网格点时，改化模型三已经基本消除了核函数奇异性的影响，同时也大大减弱了模型二的两个主要误差源的干扰，其计算精度优于2 mGal.从表 5互比结果进一步可以看出，当计算点为非数据网格点时，虽然积分核函数在径向分量上的奇异性影响有所减弱，但在3 km以下的超低空高度仍然不可忽略；积分奇异性对水平分量的影响反而大于忽略与计算点重合数据块带来的影响，包括积分区域非对称性在内的其他影响因素引起的计算误差也远远超出限定指标要求，只有模型四较好地解决了前面指出的影响模型一至模型三计算精度的各类误差干扰问题，就本试验而言，模型四的计算精度同样优于2 mGal.考虑到海上流动计算点不是事先人为选定的，而是依据发射阵位的特殊要求实时确定的，计算点与数据网格点不重合是常态化事件，故实际应用中自然应当优先选择模型四作为海域外部空间扰动引力的计算模型.

为了进一步说明表层法改化模型的优越性，本文使用与上述试验完全一致的数据组合，开展局部点质量模型解算(黄金水和朱灼文，1995；王建强等，2010)，然后在两个相同的试验点上进行扰动引力计算.其中，1°×1°、20′×20′、5′×5′和2′×2′四层点质量的埋藏深度依次取为：H(1°)=60 km；H(20′)=20 km；H(5′)=5 km；H(2′)=2 km.两个计算点在不同高度上的扰动引力计算值与基准值的比较结果如表 6所示.

表 6 P1, P2点质量模型计算结果与对应基准值的互比结果(单位：10-5m·s-2) Table 6 Comparison of point mass model and EGM2008 at point P1 and P2 (unit:10-5m·s-2)

对比表 6和表 4、表 5计算结果可以看出，无论是在数据网格点P1，还是在非数据网格点P2，利用点质量模型计算扰动引力的整体精度都不如最终的表层法改化模型(即前面的模型四)，前者在1 km以下高度段的计算误差已经超出扰动引力计算精度指标要求.这说明在重力场变化比较剧烈的海沟区，点质量模型对超低空重力场的逼近能力远不如综合利用重力异常和高程异常信息的表层法模型.实际上，在海底地形变化相对平缓的广阔海域，点质量模型与表层法模型计算结果的差异一般都不超过1 mGal，受篇幅所限，这里不再列出这些普通计算点的比对结果.海沟区是重力场变化特征比较明显的一类特殊区域，无论是在水平方向还是在垂直方向，重力场参数变化都相当剧烈，以本文试验区为例，包围计算点P2的四个2′×2′网格重力异常分别为：左上角点Δg1=-91.37 mGal；右上角点Δg2=-110.53 mGal；左下角点Δg3=-93.05 mGal；右下角点Δg4=-112.46 mGal.这就意味着，在大约2′球面距离内，重力异常变化超过20 mGal，每公里变化超过5 mGal，其变化剧烈程度相当于陆地上的特大山区(陆仲连，1996).由此可见，本文试验针对的是一类海底地形变化非常特殊的区域，表层法模型能够在这样的区域获得优于2 mGal的计算精度，足以说明该模型具有良好的适应能力.

4 结论

针对海域流动点外部重力场快速赋值需求，本文提出了基于表层法的无奇异计算改进模型，通过理论分析论证和数值计算检验，得出以下几点结论：

(1) 表层法计算模型不需要对重力异常和高程异常基础数据作进一步的转换处理，积分核函数结构更为简单，同时海域外部扰动引力计算可不顾及地面不规则地形效应的影响，故表层法模型更适合于海域外部重力场的快速赋值.

(2) 通过引入局部积分域恒等式变换、局域泰勒级数展开和非网格点内插方法，推出了基于表层法的扰动引力三分量无奇异计算模型，有效克服了传统表层法积分模型固有的奇异性问题，较好地满足了全海域和全高度段对局部扰动引力场快速赋值的实际需求，具有良好的应用前景；

(3) 相比较而言，本文推出的表层法改进模型比点质量模型具有更高的计算精度，在重力场变化比较平缓的广阔海域，该改进模型的逼近误差(不包括数据传播误差)一般不超过1 mGal；在重力场变化比较剧烈的海沟区，该模型的计算误差不超过2 mGal.

References
Bian S. 1997. Some cubature formulas for singular integrals in physical geodesy. Journal of Geodesy, 71(8): 443-453. DOI:10.1007/s001900050112
Bjerhammar A. 1964. A New Theory of Geodetic Gravity. Stockholm: Tekniska Hogskolan.
Bjerhammar A. 1987. Discrete Physical Geodesy. Dept. of Geodetic Science and Surveying. Report 380. Columbus, Ohio: The Ohio State University.
Cao H S, Zhu Z W, Wang X L. 1985. Digital realization of the theory of repre-senting the Earth's gravity field by fictitious single-layer density. Acta Geodaetica et Cartographica Sinica (in Chinese), 14(4): 262-273.
Chen G Q. 1982. Spacecraft Dynamics in Gravity Anomaly Field (in Chinese). Changsha: National University of Defense Technology Press.
Chen X. 2016. Research on refined processing of marine gravity measurement data[Ph.D.thesis] (in Chinese). Dalian: Dalian Naval Academy.
Guo D M, Xu H Z. 2011. Research on the singular integral of local terrain correction computation. Chinese Journal of Geophysics (in Chinese), 54(4): 977-983. DOI:10.3969/j.issn.0001-5733.2011.04.012
Heiskanen W A, Moritz H. 1967. Physical Geodesy. San Francisco: Freeman and Company.
Huang J S, Zhu Z W. 1995. Frequency response point masses model of exterior disturbing gravity field. Acta Geophysica Sinica (in Chinese), 38(2): 182-188.
Huang M T, Zhai G J, Guan Z, et al. 2005. Determination and Application of Marine Gravity Field (in Chinese). Beijing: Surveying and Mapping Press.
Huang M T, Liu M, Ouyang Y Z, et al. 2016. Effect of external disturbing gravity field on spacecraft guidance and surveying line layout for marine gravity survey. Acta Geodaetica et Cartographica Sinica (in Chinese), 45(11): 1261-1269.
Hwang C. 1998. Inverse Vening Meinesz formula and deflection-geoid formula:applications to the predictions of gravity and geoid over the South China Sea. Journal of Geodesy, 72(5): 304-312. DOI:10.1007/s001900050169
Li J C, Chen J Y, Ning J S, et al. 2003. Theory of the Earth's Gravity Field Approximation and Determination of China Quasi-Geoid 2000 (in Chinese). Wuhan: Wuhan University Press.
Liu C H. 2016. Improved Direct Integral Methods Calculating Exterior Disturbing Gravity in Low-altitude Airspace[Ph. M. Thesis] (in Chinese). Zhengzhou: PLA Information Engineering University.
Lu Z L, Wu X P, Ding X B, et al. 1993. Gravimetry in Ballistic Missile (in Chinese). Beijing: Bayi Press.
Lu Z L. 1996. Theory and Method of the Earth's Gravity Field (in Chinese). Beijing: PLA Publishing House.
Moritz H. 1966. The computation of the external gravity field and the geodetic boundary-value problem.//Orlin H ed. Gravity Anomalies: Unsurveyed Areas. Washington D C: American Geophysical Union, 9: 127-136.
Shu C F, Li F, Li M F, et al. 2011. Determination of GPS/gravity quasi-geoid using the Bjerhammar method. Chinese Journal of Geophysics (in Chinese), 54(10): 2503-2509. DOI:10.3969/j.issn.0001-5733.2011.10.008
Sunkel H. 1983. The generation of a mass point model from surface gravity data. Columbus, Ohio: Ohio State University.
Wang J Q, Li J C, Zhao G Q, et al. 2010. The construction and analysis for three-tier point mass model of gravity. Acta Geodaetica et Cartographica Sinica (in Chinese), 39(5): 503-507, 515.
Wu X P. 1984. Point-mass model of local gravity field. Acta Geodaetica et Cartographica Sinica (in Chinese), 13(4): 249-258.
Wu X P. 1992. Applications of data in the determination of the external disturbing gravity field outside the earth. Journal of PLA Institute of Surveying and Mapping (in Chinese), (4): 1-10.
Xu H Z, Zhu Z W. 1984. Representation of gravity field outside the earth using fictitious single layer density. Scientia Sinica (Series B), 27(9): 985-992.
Zhang C D, Lu Z L, Wu X P. 1998. Truncation error formulae for the disturbing gravity vector. Journal of Geodesy, 72(3): 119-123. DOI:10.1007/s001900050153
操华胜, 朱灼文, 王晓岚. 1985. 地球重力场的虚拟单层密度表示理论的数字实现. 测绘学报, 14(4): 262-273. DOI:10.3321/j.issn:1001-1595.1985.04.003
陈国强. 1982. 异常重力场中飞行器动力学. 长沙: 国防科技大学出版社.
陈欣. 2016.海域重力测量数据的精化处理研究[博士论文].大连: 海军大连舰艇学院.
郭东美, 许厚泽. 2011. 局部地形改正的奇异积分研究. 地球物理学报, 54(4): 977-983. DOI:10.3969/j.issn.0001-5733.2011.04.012
黄金水, 朱灼文. 1995. 外部扰动重力场的频谱响应质点模型. 地球物理学报, 38(2): 182-188. DOI:10.3321/j.issn:0001-5733.1995.02.006
黄谟涛, 翟国君, 管铮, 等. 2005. 海洋重力场测定及其应用. 北京: 测绘出版社.
黄谟涛, 刘敏, 欧阳永忠, 等. 2016. 重力场对飞行器制导的影响及海洋重力测线布设. 测绘学报, 45(11): 1261-1269. DOI:10.11947/j.AGCS.2016.20160175
李建成, 陈俊勇, 宁津生, 等. 2003. 地球重力场逼近理论与中国2000似大地水准面的确定. 武汉: 武汉大学出版社.
刘长弘. 2016. 改进的直接积分方法计算低空扰动引力. 郑州: 解放军信息工程大学.
陆仲连, 吴晓平, 丁行斌, 等. 1993. 弹道导弹重力学. 北京: 八一出版社.
陆仲连. 1996. 地球重力场理论与方法. 北京: 解放军出版社.
束蝉方, 李斐, 李明峰, 等. 2011. 应用Bjerhammar方法确定GPS重力似大地水准面. 地球物理学报, 54(10): 2503-2509. DOI:10.3969/j.issn.0001-5733.2011.10.008
王建强, 李建成, 赵国强, 等. 2010. 重力三层点质量模型的构造与分析. 测绘学报, 39(5): 503-507, 515.
吴晓平. 1984. 局部重力场的点质量模型. 测绘学报, 13(4): 249-258. DOI:10.3321/j.issn:1001-1595.1984.04.002
吴晓平. 1992. 在推求地球外部扰动重力场中数据的采用. 解放军测绘学院学报, (4): 1-10.
许厚泽, 朱灼文. 1984. 地球外部重力场的虚拟单层密度表示. 中国科学(B辑), 17(6): 575-580.