2. 中国科学院大学, 北京 100049;
3. 高铁地震学联合研究组, 北京 100029
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. The Joint Research Group of High-Speed Rail Seismology, Beijing 100029, China
自19世纪末,随着弹性力学的发展,波在介质中的传播问题逐步得到了解决.Lamb (1904)详细地研究了作用在弹性半无限空间表面或内部的单点力源冲击下的弹性波传播解析解,之后这一类问题被统称为Lamb问题.而单点力源是对地震勘探中人工震源的一个恰当合理的数学表述,因此,Lamb问题就成了近现代勘探地震学的正反演理论基础.而如今,随着交通需求量的骤增,高铁已经成为了人们快速出行的一个主要的选择.而行进中的高铁,由于其接近匀速的运行速度、确定的长度和荷载使其能够成为一个可以重复的人工震源,并且纵横交错的高铁铁路系统拓宽了这一人工震源的分布范围,从而使得它具有探测地球内部结构和物性参数的巨大潜力.
行进中的高铁可以高度抽象为一个快速移动的线源来进行研究,因此移动线源的Green函数可能会成为高铁地震学的理论基础.本文以固定位置和激发时刻的单点力源的Green函数为基础,通过线积分关系,先分别给出了移动线源冲击作用下的弹性半空间和全空间中的Green函数;再对问题进行简化,重点分析了全空间中的远场Green函数,以突出移动线源Green函数的频谱特征和空间能量分布的方向性特点;最后考虑了更接近实际观测条件的半空间情况.由于半空间中的Green函数表达式相对复杂,理论分析存在一定难度,因此我们采用有限差分数值模拟的方式来合成地震记录并与在高铁线路附近地表处采集的实际地震记录进行对比.
1 移动线源的Green函数固定点源的Green函数是移动线源Green函数的基础.Johnson(1974)系统地阐述了弹性半空间中,作用在空间位置ξ,时刻τ(τ=0),沿n方向的单位集中脉冲力
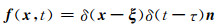
|
(1) |
下的Green函数推导过程,其中f=[fx, fy, fz],δ为狄拉克delta函数,并给出了自由表面位置处Green函数的积分表达公式,即

|
(2) |
式中p为积分变量,H为阶跃函数,F=[0 0 1]T,代表单点垂直力,μ为剪切模量,α为P波速度,β为S波速度,r为力源位置ξ与观测点位置x之间的距离,即
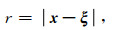
|
(3) |
其余变量的表达形式请参考附录.行进中的高铁可以被抽象为弹性半空间自由表面处的一个移动线源,它可以被看作为多个移动的单力源,并以一定的时间间隔逐次激发.基于以上思想,我们可以将Luo(2018)1)提出的高铁震源函数
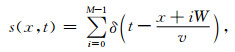
|
(4) |
表示为以下的积分形式:
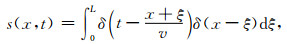
|
(5) |
其中v为高铁的运行速度,W为车厢的长度,M为车厢的总数,L=MW为列车的长度.类似地,通过叠加原理(Lay and Wallace, 1995),我们可以将式(5)中多个单点力源所对应的半空间Green函数进行叠加,进而得到移动线源的半空间Green函数GL,即
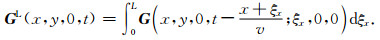
|
(6) |
正如式(2)所示,单点力源下的半空间Green函数为半解析形式,计算较为复杂,因而使得式(6)的积分计算与理论分析存在一定难度.
为了简化数学问题,我们先忽略掉自由表面边界条件引起的面波、P波和S波的反射和转化等复杂的近地表波现象,采用相对较为简单的无限均匀完全弹性空间中的Green函数(Aki and Richards, 2002),即
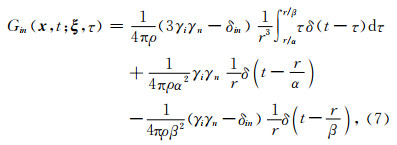
|
(7) |
式中的三项分别为近场项、远场P波项和远场S波项,其中γi和γn分别为与矢量x和单位集中脉冲力有关的方向余弦,ρ是介质密度.当只考虑远场P波时,其Green函数为
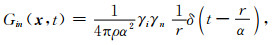
|
(8) |
式中的γiγn为P波的辐射花样,可以记为Rp进行简化表示.通过将式(6)中线积分内的半空间Green函数替换为式(8),我们可以得到移动线源的远场P波Green函数的表达形式:
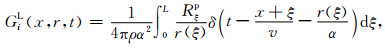
|
(9) |
而位移函数可以通过Green函数与震源时间函数的卷积得到,即
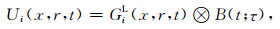
|
(10) |
其中的震源时间函数可以为任意形式的地震子波,这里我们将B(t; τ)设定为一个箱型函数,用来描述移动线源中每一个点在不同时刻的振动,τ为振动的持续时间.式(9)中的积分表达是无法通过解析的方法计算得到的,但我们可以在某些特定的情况下对其进行简化处理.
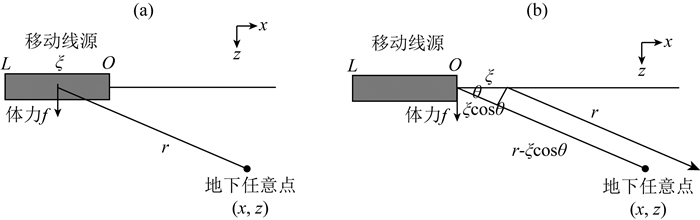
先来假设一种最简单的情况.如图 1a所示,由于是在远场位置处接收,移动线源的长度L相比于线源中各个点到接收位置的距离r来说非常的小,可以近似为一个点源进行处理,从而可以使用移动线源中心点的物理量来表示整个线源,即
|
图 1 移动线源到接收位置处路径的几何结构 (a) L < < r;(b)考虑逐次挤压. Fig. 1 Geometry of a moving line source and its path to a remote receiver (a) L < < r; (b) Considering the successive compression. |
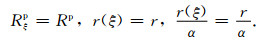
|
(11) |
因此,可以将式(9)中线积分内的Rp, r和r/α提出,得到
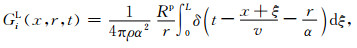
|
(12) |
经积分运算后得
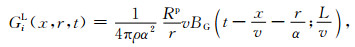
|
(13) |
其中BG是一个箱型函数,即
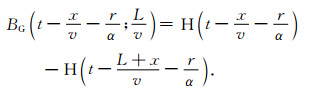
|
(14) |
定义持续时间τG=L/v.简单地讲,移动线源的远场Green函数是由一个与线源的长度和移动速度有关的箱型函数进行表示的.
然而,以上的推导中未体现出移动线源在行进过程中是通过逐次挤压铁轨来产生振动的.因此,如图 1b所示,振动的传播距离为
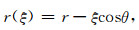
|
(15) |
代入式(9),并根据远场情况下L < < r得
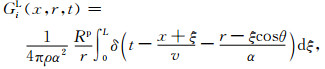
|
(16) |
进而可以得到与式(13)相似的结果
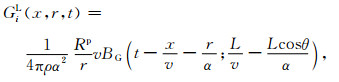
|
(17) |
这里持续时间τG不再是一个常数,它与接收位置相对于线源行进方向的夹角有关.相比于式(13),在Green函数中引入了线源行进方向的影响.类似地,使用如下点源的S波Green函数:
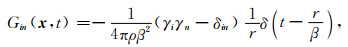
|
(18) |
我们也可以获得移动线源远场S波的Green函数.
2 远场Green函数的频谱和空间能量分布特征第1节中,我们通过两种不同的简化处理方式,分别获得了式(13)和式(17)中的移动线源远场Green函数.本节,我们将通过数值计算的方式讨论这两个Green函数的频谱和空间能量分布特征.式(13)和(17)可以统一表示为以下的形式:
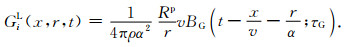
|
(19) |
通过傅里叶变换,可以将式(19)中的Green函数变换到频率域,之后再忽略其中的相位并取模值得
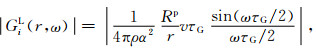
|
(20) |
用于计算Green函数的频率响应和辐射能量分布.
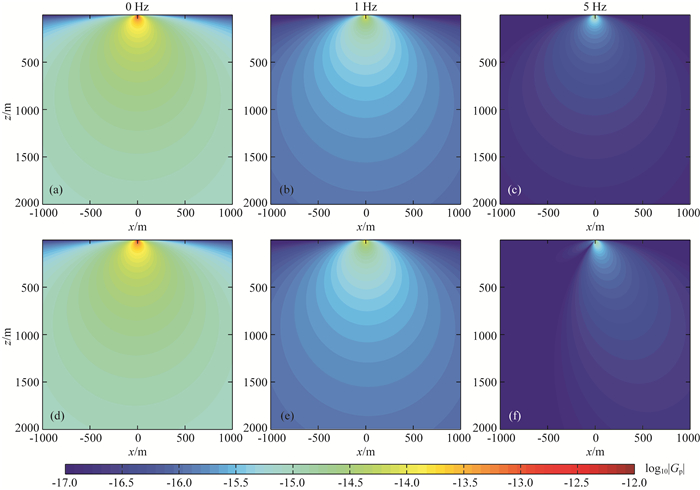
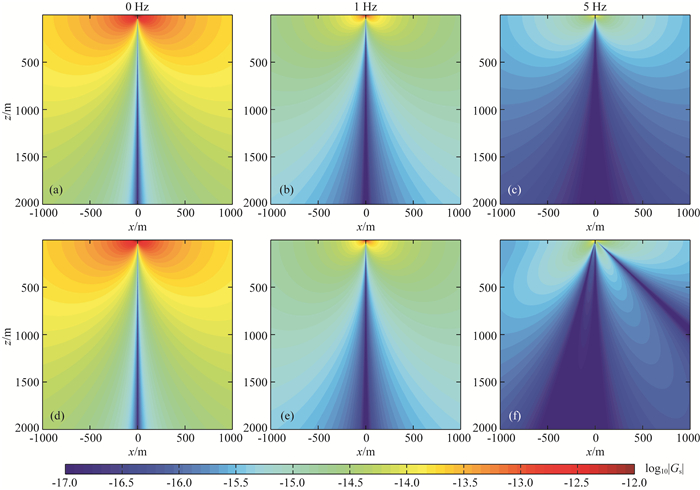
在数值计算中,我们将移动线源与高铁相对应,设定它的总长度L=26.6×8 m,即8节车厢的长度,运行速度v=300 km·h-1,沿x正方向行进,并假定线源中各个质点对铁轨的作用力沿z正方向.对于地下介质参数,P波和S波速度分别设定为3000 m·s-1和1000 m·s-1,密度为1000 kg·m-3.移动线源作用下的弹性波场辐射能量可以用式(20)中的频率域Green函数的模值来进行表示.图 2和图 3中分别展示了不同频率下的远场P波Green函数模值|Gp|和远场S波Green函数模值|Gs|.从中可以看出,在τG=L/v时,即τG是独立于观测位置的常数,波场能量的辐射情况与点源一致(如图 2a, b, c和图 3a, b, c),完全是由P波或S波的辐射花样来决定的.这是由于在推导公式的过程中,为了简化积分运算,忽略了线源长度,用其中点来等效处理造成的.当考虑了移动线源的长度以及在行进过程中对铁轨的逐次挤压时,即τG=L/v -Lcosθ/α,波场的辐射能量呈现出明显的方向性特征(如图 2d, e, f和图 3d, e, f),在移动线源前后接收到的能量不再相同.因此,移动线源的波场辐射能量是由辐射花样和线源的行进方向共同决定的.
|
图 2 不同频率下的远场P波辐射能量|Gp|的空间分布 (a)、(b)和(c)为τG=L/v时的计算结果;(d)、(e)和(f)为τG=L/v-Lcosθ/α时的计算结果.横坐标正数表示观测位置在高铁前方,负数表示观测位置在高铁后方. Fig. 2 The radiation energy represented by |Gp| for P-wave in the far field at different frequency (a), (b) and (c) is calculated when τG=L/v; (d), (e) and (f) is calculated when τG=L/v-Lcosθ/α. Numbers in the positive axis indicate that the observation position is in front of the high-speed train, while numbers in the negative axis indicate that the observation position is behind the high-speed train. |
|
图 3 不同频率下的远场S波辐射能量|Gs|的空间分布 (a)、(b)和(c)为τG=L/v时的计算结果;(d)、(e)和(f)为τG=L/v-Lcosθ/α时的计算结果.横坐标正数表示观测位置在高铁前方,负数表示观测位置在高铁后方. Fig. 3 The radiation energy represented by |Gs| for S-wave in the far field at different frequency (a), (b) and (c) is calculated when τG=L/v; (d), (e) and (f) is calculated when τG=L/v-Lcosθ/α. Numbers in the positive axis indicate that the observation position is in front of the high-speed train, while numbers in the negative axis indicate that the observation position is behind the high-speed train. |
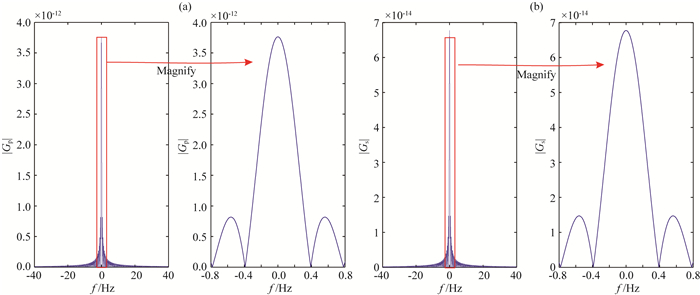
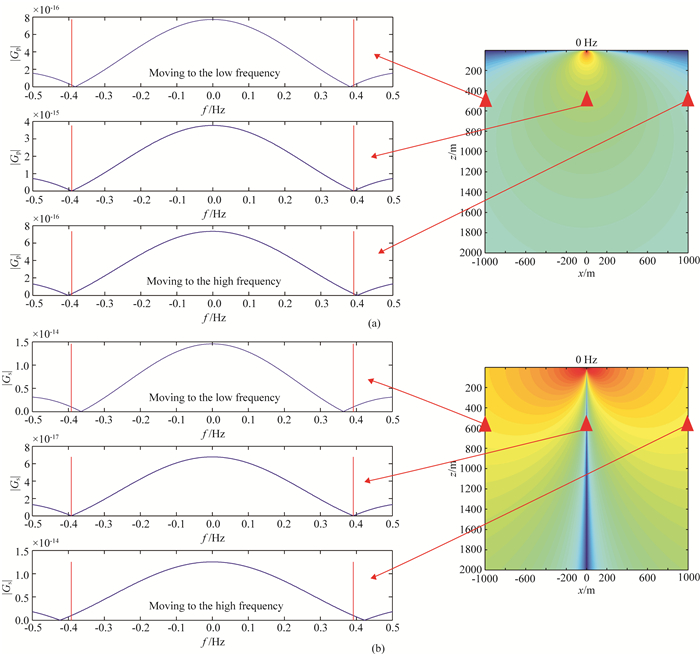
此外,根据式(20),我们还可以分析空间中某一点处Green函数的振幅谱.图 4分别给出了接近移动线源正下方(空间坐标为x=1 m, z=500 m)位置处的远场P波和S波的振幅谱.从中可以看出,无论是远场P波还是S波,波场能量都是以小于0.39 Hz的低频为主,这一特征频率是由线源的长度和移动速度决定的,即f=v/L.但由于线源是移动的,对于空间中不同位置处的观测点,接收到的波的频率会发生改变,这也就是所谓的多普勒效应.如图 5所示,当观测点位于移动线源前方时,观测到的频率相对于特征频率变大;而当观测点位于移动线源后方时,观测到的频率相对于特征频率变小.相比于P波速度,S波速度较小,更为接近线源的移动速度,因此这一频率移动的特点在S波的波场中显示的更为明显(如图 5b).
|
图 4 地下x=1 m, z=500 m处Green函数的振幅谱 (a)远场P波的|Gp|振幅谱;(b)远场S波的|Gs|振幅谱. Fig. 4 Amplitude spectra of Green function at the location x=1 m, z=500 m (a) |Gp| for far-field P-wave; (b) |Gs| for far-field S-wave. |
|
图 5 移动线源波场中的多普勒效应 (a)远场P波;(b)远场S波. Fig. 5 Doppler effect of the wavefields for the moving line source (a) P-wave received in the far field; (b) S-wave received in the far field. |
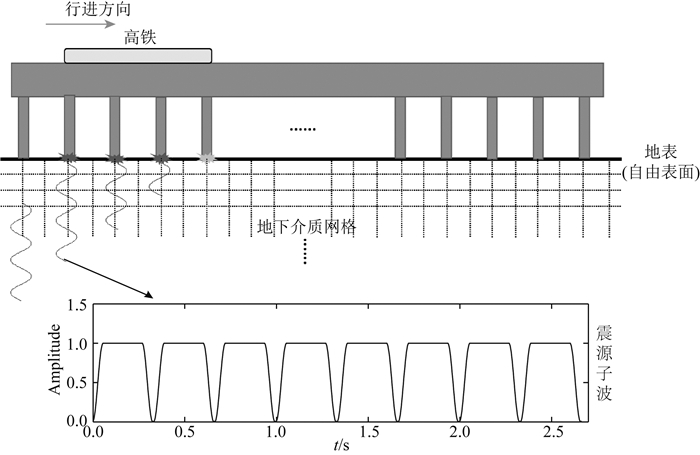
在实际情况中,高铁是在地表(自由表面)的铁轨上运行的,而野外的地震数据采集也主要是在地表或近地表进行,因此,地表这一强阻抗突变界面必然会对高铁振动信号的产生和传播带来影响.正如第1节中式(2)和(6)所示,半空间中移动线源的Green函数表达式是半解析的,直接计算和理论分析难度较大,因而在本节中我们采用数值模拟的方法来正演半空间中的高铁地震记录.如图 6所示,地下介质是以规则网格的形式进行离散化的.为了模拟半空间环境,离散模型顶部的自由表面边界条件是通过自适应自由表面表达(Cao et al., 2018)来实现的,而模型的其余边界采用PML吸收边界条件.对于模型内部满足的弹性波方程是通过三维速度-应力交错网格有限差分格式(Virieux, 1986; Kristek et al., 2002)来进行求解的.
|
图 6 高铁地震信号数值模拟中的桥墩震源模型和震源子波 Fig. 6 Bridge-based source model and wavelet for numerical modeling of seismic waves induced by the high-speed train |
由于正演问题的离散化表达,这里需要将线源(高铁震源)离散化表示为一系列位置不同但以相同速度移动的点源组合,即采用式(4)中的求和形式,而不是式(5)的积分形式.此外,为了合成地震记录,需给定地震子波,这里我们采用图 6所示的方波形震源子波,而各个点源之间的地震子波存在着一定的时间延迟,其大小为高铁依次经过两个点源位置处的时间差.对于这一离散的移动线源表达方式,我们可以采用图 6所示的桥墩震源模型来进行理解,组成线源的一个个以一定间隔排列的点源可以被看作是连接高铁与地面之间高架桥的桥墩,当高铁从上面经过时,高铁本身和其所在位置处的铁轨、桥梁和桥墩耦合在一起,它们整体产生的振动通过桥墩传至地表,并在地表处以点震源的方式释放能量.而这里的方波形震源子波是一种最简单的耦合描述方式,即不同车厢经过时对桥墩的持续压力,每个方波的持续长度为高铁经过一节车厢的距离时所需要的时间,例如图 6中表示的是8节车厢,每节车厢长27 m,高铁运行速度为300 km·h-1.
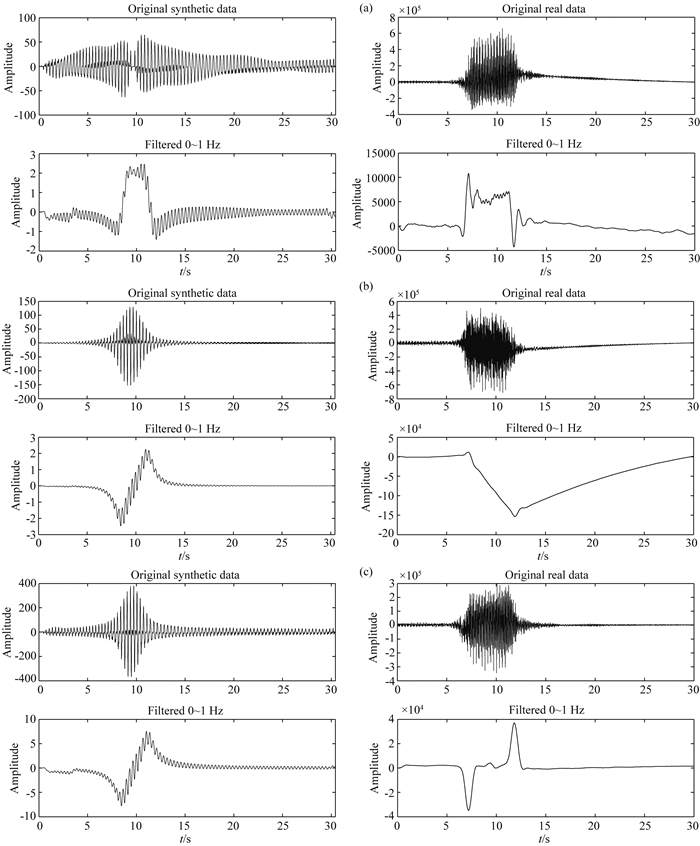
图 7中展示了在近场情况下,基于桥墩震源模型的合成地震信号和在野外使用宽频带地震记录仪观测到的高铁地震信号的对比结果.这里,我们设定高铁线路的延伸方向为x方向,与其相垂直的方向为y方向.因此,观测点的坐标可以表示为x=648 m,y=54 m.当以高铁车头当前所在位置为坐标原点开始计时,并假定其以300 km·h-1的速度行进,大约7.8 s左右高铁开始通过观测点.如图 7中的对比结果所示,尽管二者在原始记录上差别较大,但经过1 Hz低通滤波后,在低频情况下具有一定的相似性.将高铁震源抽象为移动线源正是为了简化或者忽略掉高铁机车本身以及路基耦合方面的细节,从宏观角度来分析并理解这一震源形式(其对应于地震信号的低频成分).因而证实了以移动线源来建模高铁震源具有一定的适用性.而对于实际数据中高频成分的理解,还需要进一步的研究与讨论.
|
图 7 高铁地震的数值模拟信号与野外宽频带地震仪观测信号对比 (a)质点振动速度的x分量;(b)质点振动速度的y分量;(c)质点振动速度的z分量. Fig. 7 A comparison of the synthetic seismic data and the real data acquired by broadband seismograph when a high-speed train arrives (a) The x-component of particle velocity; (b) The y-component of particle velocity; (c) The z-component of particle velocity. |
本文将行进中的高铁抽象为移动线源来进行研究,以弹性半空间和全空间中固定位置处单力源作用下的Green函数为基础,通过线积分关系,将单力源的Green函数在不同位置和时间延迟下进行组合,分别获得了移动线源冲击作用下的弹性半空间和全空间中的Green函数.为了便于理论分析,文中以一定的假设条件为基础,将全空间中移动线源的Green函数进行了简化,所得到的远场P波和S波Green函数均显示出以下两个基本特征:1)激发的地震波场以低频能量为主,但由于震源的移动性,会产生多普勒效应,因而不同位置处接收到的波场频率范围与高铁运行速度、行进方向和车长相关;2)激发的地震波场在空间上的能量分布情况呈现出一定的方向性,是由辐射花样和高铁行进方向共同决定的.而对于理论分析和简化处理较为困难的半空间中移动线源的Green函数,采用了有限差分数值模拟的方式来替代,以进行合成地震记录与在高铁线路附近地表处采集的实际地震记录的对比,初步验证了基于移动线源来进行高铁震源建模的可行性.基于以上结论,我们希望对高铁震源激发的地震波场加以利用,其激发出的低频能量易于穿透地球深部,因此,地表接收到的地震信号中有可能存在来自地下深部的信息;而其辐射能量的空间分布情况有利于指导地震信号采集中的观测系统设计.
附录单力源作用下的半空间Green函数(式(2))中所涉及到的变量的表达形式为
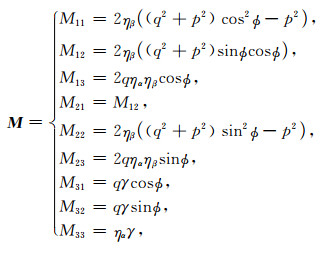
|

|
其中p为积分变量,θ为倾角,Φ为方位角.在计算式(2)中等号右边第一项时,
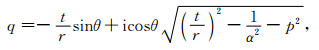
|
第二项时,
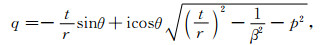
|
其中i为复数单位.在计算第三项和第四项时,
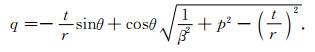
|
Aki K, Richards P G. 2002. Quantitative Seismology. Sausalito, California: University Science Books.
|
Cao J, Chen J B, Dai M X. 2018. An adaptive free-surface expression for three-dimensional finite-difference frequency-domain modelling of elastic wave. Geophysical Prospecting, 66(4): 707-725. DOI:10.1111/gpr.2018.66.issue-4 |
Johnson L R. 1974. Green's function for Lamb's problem. Geophysical Journal International, 37(1): 99-131. DOI:10.1111/j.1365-246X.1974.tb02446.x |
Kristek J, Moczo P, Archuleta R. 2002. Efficient methods to simulate planar free surface in the 3D 4th-order staggered-grid finite-difference schemes. Studia Geophysica et Geodaetica, 46(2): 355-381. DOI:10.1023/A:1019866422821 |
Lamb H. 1904. On the propagation of tremors over the surface of an elastic solid. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 203: 1-42. DOI:10.1098/rsta.1904.0013 |
Lay T, Wallace T C. 1995. Modern Global Seismology. San Diego: Academic Press, Inc.
|
Virieux J. 1986. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. DOI:10.1190/1.1442147 |
 2019, Vol. 62
2019, Vol. 62

