2. 科隆大学地球物理与气象研究所, 德国科隆 50923;
3. 地球内部多尺度成像湖北省重点实验室, 武汉 430074
2. Institute of Geophysics and Meteorology, University of Cologne, Cologne 50923, Germany;
3. Hubei Subsurface Multi-scale Imaging Key Laboratory, Wuhan 430074, China
作为地球物理电磁法勘探的重要分支,瞬变电磁法(Transient Electromagnetic Method,TEM)已广泛应用于煤炭矿产资源勘探、水文地质调查与环境工程勘察等领域(薛国强等, 2008; Haroon et al., 2015; 李海等, 2016; 李建慧等, 2016a; Yogeshwar and Tezkan, 2017).该方法利用不接地回线或接地线源向地下发射一次脉冲磁场(薛国强等, 2013),并通过观测地下介质感应产生的纯二次场来探测介质电导率分布.
反演是瞬变电磁数据处理与定量解释中极其重要的步骤,而正演计算是反演的核心.目前TEM三维正演主要基于两种策略:其一为时间域转频率域算法,该方法首先根据模型尺寸以及TEM采样时间确定频点分布范围,然后求解频率域Maxwell方程组获得对应频率的电磁场响应,再通过Gaver-Stehfest(GS)算法或正余弦算法将频率域响应转换到时间域从而获得所需的瞬变电磁响应(Newman et al., 1986; Sugeng, 1998; Li et al., 2011; 李建慧等, 2013).另一种为直接时域算法,该方法直接从时域Maxwell方程组出发,采用显式或隐式差分格式进行时间域离散,利用解析或数值算法求得t=0时刻的初始电磁场后,根据一定的时间步长规则逐步迭代求取各个时间点上的时域电磁场(Wang and Hohmann, 1993; Haber et al., 2004; Um et al., 2010; 邱稚鹏等, 2013; 孙怀凤等, 2013; Li et al., 2018; 周建美等, 2018).其中,显式差分格式中时间步长需满足Courant-Friedrichs-Lewy(CFL)稳定性条件,致使晚期时间步长需要较为密集,影响计算效率,但每次迭代无需求解大型线性方程组.隐式差分格式不需满足CFL条件,即晚期步长可相对较大,但需要在每个迭代步长求解大型线性方程组,为该方法最耗时部分.
从数值模拟方法的角度来讲,目前TEM三维正演模拟采用的数值方法包括积分方程法(Newman et al., 1986; Swidinsky and Edwards, 2009)、有限差分法(Wang and Hohmann, 1993; Commer and Newman, 2004; 许洋铖等, 2012; 孙怀凤等, 2013; 李展辉和黄清华, 2014)、有限体积法(Haber et al., 2004; 张烨等, 2012; Oldenburg et al., 2013; 周建美等, 2018)和有限单元法(Sugeng, 1998; Um et al., 2010, 2015; Fu et al., 2015; Li et al., 2016a, 2018; 李建慧等, 2016b).这些数值方法的广泛应用极大地推动了瞬变电磁三维正演研究的发展.总体而言,提高求解精度及计算效率仍是当前瞬变电磁三维正演算法研究重点.
随着电磁勘探技术的发展,地下介质的宏观电各向异性现象逐渐引起了研究者的广泛关注,不同类型电磁勘探方法的电各向异性正反演及分析均得到了大量研究,并证明了地下电各向异性结构对电磁法数据处理与解释存在较大影响,刘云鹤等(2018)对地球物理电磁法各向异性的研究现状与发展趋势进行了较好的综述.
瞬变电磁法作为主流的电磁勘探方法,对其各向异性的认识和研究也较为深入.Yu等(1997)针对海底三轴各向异性介质进行了瞬变电磁响应模拟.Um等(2010)采用时域有限单元法对电偶极子在三维任意各向异性介质中激发的瞬变电磁场进行了模拟,但并未进行相关各向异性分析.Dennis等(2012)提出可通过TEM勘探过程中的涡流系统的扩散速率对水平方向上电导率的各向异性进行判断.Yin等(2016)采用时域有限单元法对时间域航空电磁法的三维各向异性进行了模拟,并对典型的各向异性模型进行了模拟分析.周建美等(2018)采用有限体积法对双轴各向异性介质地层中的中心回线瞬变电磁响应进行了三维正演与分析,并认为影响瞬变电磁信号的主要是水平方向电导率.大回线源瞬变电磁法作为瞬变电磁勘探的主要方式之一,目前关于其任意各向异性介质的影响研究相对较少.
为探讨电各向异性对大回线瞬变电磁信号的影响方式与程度,本文采用拟态有限体积法对时域Maxwell方程组进行空间域离散,利用隐式差分格式的后退欧拉算法进行时间域离散,实现了任意各向异性介质中的TEM三维正演.考虑到时域隐式差分格式下,每个时刻对应的大型线性方程组的系数矩阵只与网格剖分、介质电导率分布以及时间步长相关,而与相应时刻电磁场无关,本文将时间分段等步长算法与方程直接求解法相结合来提高计算效率与精度.最后,通过对主轴各向异性、倾斜各向异性以及水平各向异性介质中大回线源瞬变电磁信号响应的模拟,对比分析了不同电各向异性类型对TEM电磁信号的影响模式.
1 方法理论 1.1 控制方程首先从时域扩散方程出发,在任意各向异性介质中,对于给定的计算区域Ω×[0, tf],时域Maxwell方程组可表示为(Haber et al., 2007; 薛国强等; 2014)
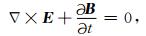
|
(1) |
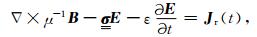
|
(2) |
式中,E为电场强度(V·m-1),B为磁感应强度(T).μ为磁导率(H·m-1),通常取为真空中磁导率即μ=μ0.Jr(t)表示外部激发电流源的电流密度(A·m-2). ε为真空中介电常数.Ω表示空间计算区域,[0, tf]表示为时间计算范围.

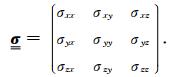
|
(3) |
对于任意的各向异性电导率张量
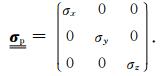
|
(4) |
经过如图 1所示三次坐标旋转而得到.首先绕z轴逆时针旋转角度αs,得到新坐标系(x1,y1,z1),再将其绕x1轴逆时针旋转角度αd得到新坐标(x2,y2,z2).最后,绕z2轴逆时针旋转角度αl得到坐标系(x3,y3,z3).整个坐标旋转过程称为欧拉旋转,αs、αd和αl分别称为各向异性走向角、各向异性倾角和各向异性偏角(Pek and Santos, 2006).每次旋转可得到与角度相对应的旋转矩形
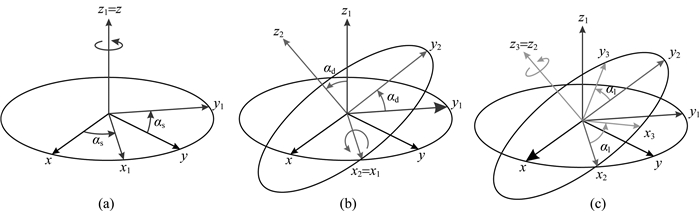
|
图 1 任意各向异性电导率张量欧拉旋转示意图 Fig. 1 Arbitrarily anisotropic tensor conductivity Euler rotation |

|
(5) |
总体坐标转换矩阵R可通过这三个旋转矩阵的乘积表示,R=R1R2R3,任意各向异性电导率张量
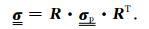
|
(6) |
本文采用后退欧拉法对时间域连续的Maxwell方程组在时间域进行离散(Haber et al., 2004; Oldenburg et al., 2013),考虑离散步长为δt时,在每个离散时间点上,时域Maxwell方程组将离散为以下形式
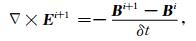
|
(7) |
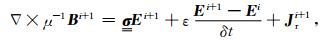
|
(8) |
其中,i与i+1表示前后两个时刻.
为求解(7)、(8)方程组,本研究采用拟态有限体积法对上述方程组在空间域进行离散.首先考虑方程(7)和(8)的离散弱解形式(Hyman and Shashkov, 1999; 彭荣华等, 2016)
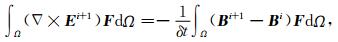
|
(9) |
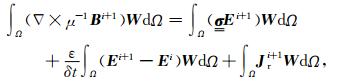
|
(10) |
其中W与F分别为与电场E与磁场B属于相同希尔伯特空间的任意网格函数.对(10)式左端进行分部积分可得
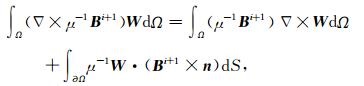
|
(11) |
其中n为计算边界∂Ω外法线方向的单位向量.假设计算区域Ω足够大,则场源所激发的电磁场在计算区域边界上可忽略不计,此时可将计算区域边界上的切向电场分量取为零,即采用理想导体边界条件(PEC)
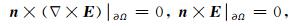
|
(12) |
将(11)与(12)式代入到(10)式中,可得
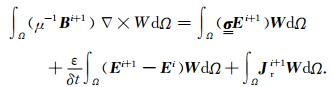
|
(13) |
本文采用基于Yee交错网格(Yee, 1966)对(9)式以及(12)式进行离散.其中,交错网格剖分形式,电场和磁场分量采样方式如图 2所示
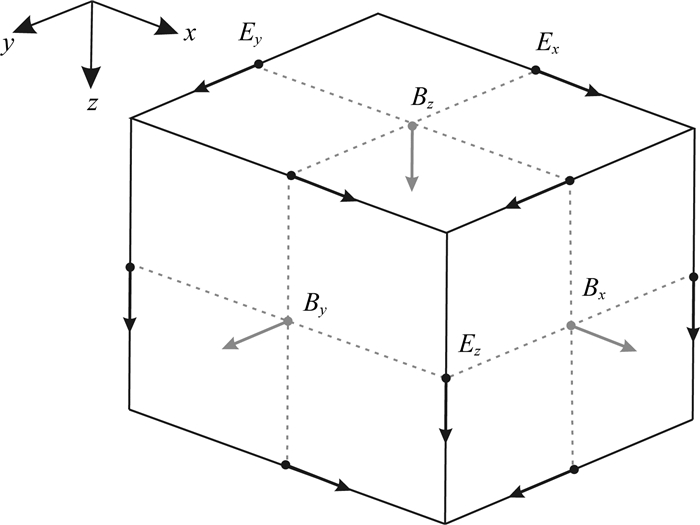
|
图 2 空间交错网格离散 电场E定义在棱边中心,磁场B定义在面心.电导率张量、磁导率定义在单元体心. Fig. 2 The staggered grid used for spatial discretization Electric fields E are sampled on cell edges and magnetic field B on cell faces. The conductivity tensor and magnetic permitivity are placed on cell center and assumed to be constant over the cell. |
通过对离散化的(9)式与(13)式在其控制体积内近似积分,并考虑F和W为希尔伯特空间的任意网格测试函数,可得到其简化后的矩阵形式
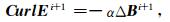
|
(14) |
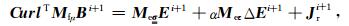
|
(15) |
其中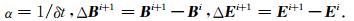
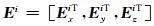
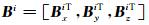
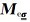
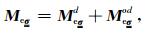
|
(16) |
其中
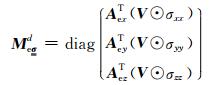
|
(17) |
与电导率张量的对角元素对应,与各向同性情况下的电导率平均矩阵相似. 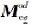
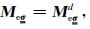
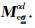
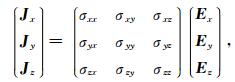
|
(18) |
但对于交错网格采样方式,不同方向上的电场分量的采样位置相互正交,即单一电场采样点只能定义一个方向的电场分量,因此需要采用插值近似方法.本文采用(Weiss and Newman, 2002)提出的近似插值方法,即对电流密度进行体积分近似,而不仅仅是单个采样点上的电流密度.例如x方向棱边上的电流密度Jx需由该棱边上的电场Ex,与其相邻的四个y方向棱边上的电场Ey以及四个z方向棱边上的电场Ez在其控制体积内的积分获得,同理可获得Jy与Jz的体积分近似.在整个计算区域采用此种近似插值方式,便可获得矩阵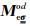
将(14)式代入(15)式中,消去i+1时刻的磁感应强度Bi+1,可得到关于i+1时刻电场强度Ei+1的二阶线性方程组
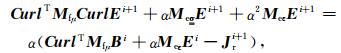
|
(19) |
通过求解(19)式,便可得到i+1时刻的电场Ei+1,然后通过(20)式可求得i+1时刻的磁感应强度Bi+1
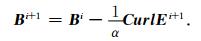
|
(20) |
为求解(19)式而得到每个时刻的时域电磁场,首先需要获得初始时刻(t=0)的电磁场分布.若场源采用上升沿激发,则初始时刻电场和磁场均为零.若采用下降沿激发,则需要对初始电磁场进行求解,且不同的发射源形式,初始场分布不同.
回线源情况下,回线内存在稳定的直流电流,将会在全空间产生稳定磁场.通过(14)与(15)式消去i+1时刻的电场Ei+1,并假定α=0,可得到初始时刻磁场B0的线性方程组
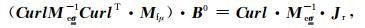
|
(21) |
该方程具有奇异性,可通过添加磁场无散条件(∇·B=0)使其稳定.交错网格采样形式下, 散度算子离散形式可以表示为梯度算子的离散形式的负转置,即无散条件的离散式可表示为
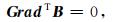
|
(22) |
对上式两端乘以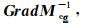
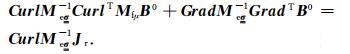
|
(23) |
通过求解(23)式二阶线性方程组便可求得导线中稳定电流产生的磁场,即为回线源情况下的初始磁场.
接地导线源情况下,将会有电流注入到地下介质中.因此初始场不仅需要考虑导线中稳定电流产生的磁场,还需包括注入到地下介质中稳定电流场,此时可通过求解(24)式任意各向异性介质直流问题来获取(Li and Spitzer, 2005).
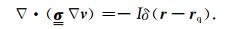
|
(24) |
本文将只考虑回线源的情况,对于接地线源的各向异性正演本文不做讨论.
1.4 时间域迭代策略随时间推移求解方程(19)是本文算法最耗时的部分,因此合理选择时间域迭代方式和方程求解方法对于提高正演效率及精度至关重要.方程(19)可简化为
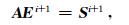
|
(25) |
其中A为系数矩阵,Si+1为右端项.由A与Si+1具体表达形式可知,该系数矩阵只与模型网格剖分、介质电导率性质以及时间步长相关,而右端项将与第i个时刻的电场和磁场相关.对于给定正演问题,在不修改网格剖分的情况下,时间步长不变,系数矩阵A将不发生改变.本文采用直接求解法对方程(25)进行求解,选择基于多波前分解算法的MUMPS直接求解器(Amestoy et al., 2001, 2006).对于相同时间步长δt,系数矩阵A相同,仅需对其进行一次LU分解,而与该δt相对应时刻的电磁场进行一次回代即可求得.为提高计算效率,时间步长δt将每隔Nδt步进行加倍,整个模拟时间采用P个不同时间步长.假设MUMPS对系数矩阵进行一次分解的时间为tfs,单次回代时间为tb,则正演过程中方程求解总时间为(Oldenburg et al., 2013)
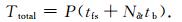
|
(26) |
时间步长与TEM模拟的精度和效率相关,一般来说时间步长越小精度越高,但总体模拟时间就会越长.因此需要选择恰当的时间步长策略,在保证模拟精度情况下,尽量选择较大的时间步长.经过多个不同类型模型的测试与分析,本文选择的初始时间步长δt=10-7s,初始计算时刻为10-7s,且每间隔Nδt=50步对时间步长进行加倍.
2 算法验证本节将通过一维各向异性模型和三维各向同性模型正演数值结果的对比分析验证本算法对回线源瞬变电磁模拟的有效性及精度.
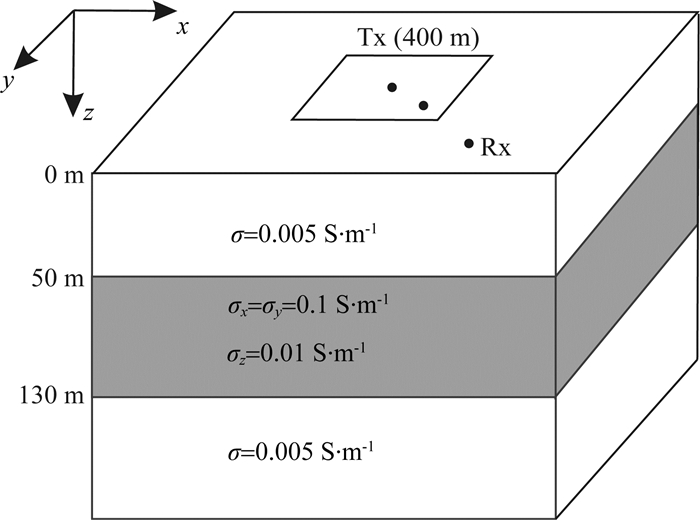
2.1 一维层状各向异性模型为验证本文所开发的算法对于各向异性介质瞬变电磁正演的准确性及精度,首先考虑具有准解析解的一维横向各向同性(VTI)模型.如图 3所示为一维VTI模型,在电导率为0.005 S·m-1的均匀半空间中存在一个各向异性低阻层,该层水平电导率为σh=0.1 S·m-1(σx=σy=0.1 S·m-1),垂直电导率σv=0.01 S·m-1(σz=0.01 S·m-1),厚度为80 m,顶部距地面50 m.发射源为边长400 m的矩形回线框,发射电流为1 A.所有模型的空气电导率均设置为10-8S·m-1.时间迭代步长策略依据1.4节设置,初始计算时间点为10-7s,初始时间步长δt为10-7s,等步长时间数目Nδt为50,最晚模拟时间点为0.03 s,总体模拟时间剖分段数P为14.计算区域尺寸为10 km×10 km×10 km,网格剖分总数为62×62×60.本文所有计算均在一台小型并行工作站上进行,该工作站包含2个4核的Intel-Xeon-E5410型号CPU,CPU主频为2.6 GHz,计算机总内存为128G,操作系统为Ubuntu 16.04.该一维各向异性模型时间域响应的准解析解采用正余弦变换算法(Key, 2012; Li et al., 2016b)由频率域转换而来,一维频率域各向异性响应采用由Hünziker等(2015)开发的软件EMmod计算.
|
图 3 一维VTI模型示意图 Fig. 3 1D VTI model |
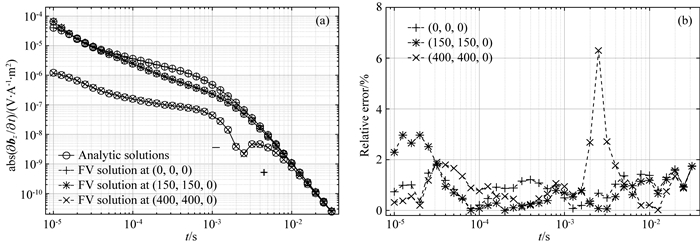
图 4给出了三个不同测点处模型的脉冲响应∂bz/∂t的三维数值解与一维准解析解的对比.从图中可知,在回线中心(0,0,0)m、靠近回线(150,150,0)m以及回线外(400,400,0)m三个测点处,0.01 ms到30 ms整个观测时间范围内,三维数值解与一维准解析解吻合良好,相对误差基本都在2%以内,符合TEM正演精度要求.回线外测点在观测时间2 ms附近处,脉冲响应发生了一次变号,相对误差出现局部变大的现象,这在TEM正演模拟过程中难以避免.
|
图 4 一维层状VTI模型数值解与解析解对比 (a)三个测点处的脉冲响应值; (b)相对误差值. Fig. 4 The comparison of numerical and analytic solutions for 1D VTI model (a)The responses of three observation locations; (b) Relative error. |
在一维各向异性层状模型的精度对比基础上,本论文进一步对三维复杂各向同性模型进行了正演测试,模型正演结果将与已发表的文章结果和成熟的软件结果进行对比验证.
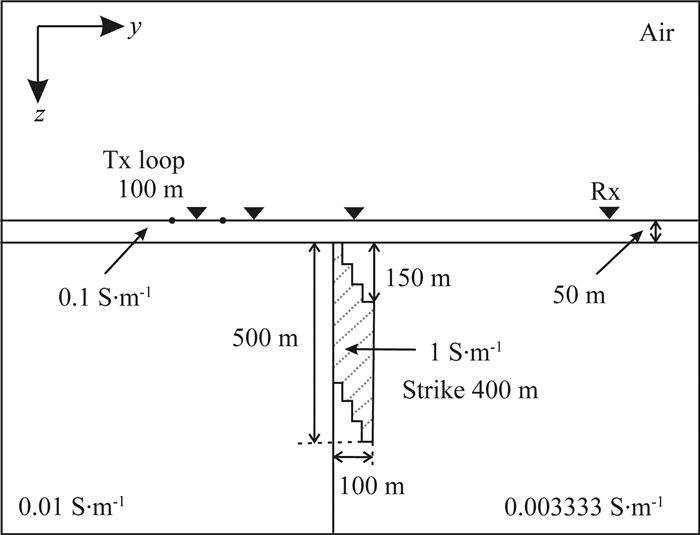
如图 5所示为三维复杂各向同性垂直接触带模型,该模型首次由Commer和Newman(2004)设计并应用于接地线源瞬变电磁算法的验证,Li(2016a)采用该模型对其开发的回线源瞬变电磁算法进行了验证.该模型上覆厚度为50 m电导率为0.1 S·m-1的高导层,此层下介质由一垂直接触面剖分为电导率分别为0.01 S·m-1和0.003333 S·m-1的左右两部分,在垂直接触面上部存在一个电导率为1 S·m-1的复杂高导异常体,其沿接触面伸展方向为400 m,厚度为100 m,垂直深度约为500 m.本文采用与Li(2016a)相同的发射源布置,发射回线边长为100 m,中心位置位于(0,50,0)m.接收站沿x=0方向布置,坐标分别为(0,50,0)、(0,150,0)、(0,450,0)以及(0,1050,0)m.
|
图 5 三维复杂垂直接触带模型垂直切面图 Fig. 5 The model of a complex conductor at a vertical contact |
图 6给出了该复杂三维模型的脉冲响应∂bz/∂t与Li(2016a)有限元算法以及SLDM(Druskin and Knizhnerman, 1994)软件的结果对比.由对比结果可知,本算法结果与另外两种算法的结果吻合非常好,仅在回线外测点出现响应变号的位置与SLDM结果存在细微偏差.

|
图 6 回线源三维复杂模型数值结果对比(包括Li(2016a)的有限元解、SLDM软件的解以及本算法的解) Fig. 6 The comparison of the numerical solutions for 3D complex model, which include FE, SLDM and FV solutions |
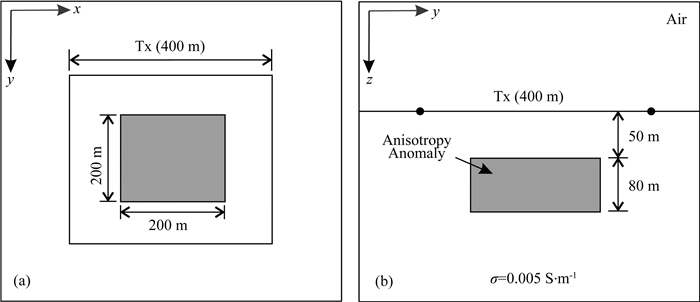
为充分了解各向异性介质结构对大回线瞬变电磁响应的影响,并分析从响应出发识别介质各向异性结构的可能性,本文设计了图 7所示各向异性模型.如图 7所示,在电导率为0.005 S·m-1的均匀各向同性介质半空间中,存在一个顶部埋深为50 m,尺寸为200 m×200 m×80 m的低阻各向异性异常体,其中心位置为(0,0,90)m.发射回线边长为400 m,中心位置为(0,0,0)m,此时发射回线与异常体存在对称关系.
|
图 7 三维各向异性模型示意图 (a)水平切片图z=0;(b)垂直剖面图x=0. Fig. 7 3D anisotropic model (a) Horizontal slice at z=0; (b) Vertical slice at x=0. |
首先,为分析各向异性情况下不同方向电导率对TEM信号的影响,本文通过对图 7所示模型异常体的各方向电导率进行变化设置成不同类型各向异性.考虑各向异性主轴方向与模型坐标方向(x,y,z)一致,按表 1对低阻异常体的电导率进行设置,Model 1设置异常体为各向同性,三个方向电导率均为0.1 S·m-1;Model 2在Model 1的基础上将z方向电导率设置为1 S·m-1;Model 3修改x方向电阻率为1 S·m-1;Model 4将x、y方向电导率均修改为1 S·m-1.
|
|
表 1 三维模型各向异性低阻异常体电导率设置(单位:S·m-1) Table 1 Anisotropy anomaly conductivity setting of 3D model (unit: S·m-1) |
图 8给出了Model 1至Model 4模型在(0,0,0)、(100,100,0)、(300,300,0)m三个接收点处的脉冲响应∂bz/∂t的绝对值,以及各向异性模型Model 2至Model 4的响应对各向同性模型Model 1的响应的归一化场值.从图中可知,三个测点处各向异性模型Model 2的响应均与各向同性模型Model 1的响应基本相同,而Model 3与Model 4的模型响应相对Model 1的响应差别较大,其中Model 4的响应差异最大.

|
图 8 各向同性与各向异性模型TEM脉冲响应∂bz/∂t与归一化场值图 Fig. 8 TEM impulse responses ∂bz/∂t and the normalized field for isotropic and anisotropic models |
同时,为探讨异常体各向异性影响范围,沿x=0方向布置测线,并选取早期0.28 ms和中晚期1.25 ms两个时间道,对比各向异性情况下不同偏移距处的TEM信号响应.如图 9所示,(a)、(c)分别为0.28 ms与1.25 ms两个时间道,TEM脉冲响应∂bz/∂t的分布图,(b)、(d)为对各向同性模型Model 1的响应进行归一化之后的场值分布.从图中可知,早期时间道0.28 ms,由于涡流场没有完全到达异常体,故低阻异常体的各向异性影响程度较低,但影响范围较广.中晚期时间道1.25 ms,涡流场通过低阻异常体且被其束缚于周围,故各向异性相对影响较大,影响范围主要集中于异常体附近.同时,在整个测线范围内,垂直方向电导率的影响都非常小,归一化的场值几乎全为1.

|
图 9 各向同性与各向异性模型TEM脉冲响应∂bz/∂t沿测线x=0分布及归一化场值图 Fig. 9 TEM impulse responses ∂bz/∂t and the normalized field for isotropic and anisotropic models along x=0 |
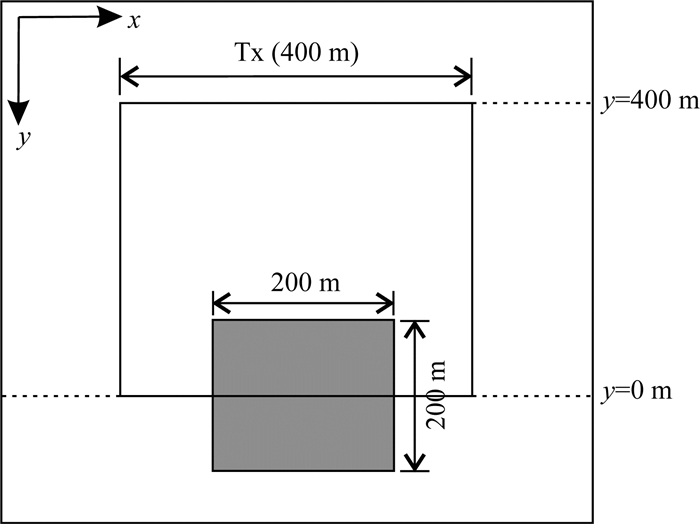
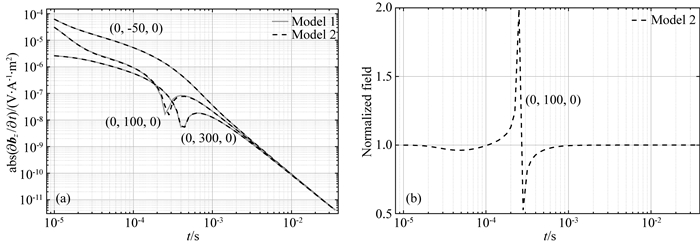
为进一步探讨垂直方向电导率对大回线瞬变电磁信号的影响,本文将发射回线与异常体的对称关系进行改变.如图 10所示,在图 7模型的基础上将发射回线沿y轴负方向偏移200m,并计算表 1所示Model 1与Model 2的TEM响应.如图 11所示为三个不同测点处的响应,其中(0,-50,0)测点位于回线内异常体上方,(0,100,0)测点位于回线外异常体边界处,(0,300,0)测点位于回线外远离异常体处.从图 11a可知,Model 1与Model 2在(0,-50,0)与(0,300,0)测点处的响应在整个测量时间段几乎完全重合,而(0,100,0)点处两模型的响应在变号附近出现差异.同理,为量化该差异大小,将模型Model 2的响应对模型Model 1的响应归一化,从图 11b可知归一化场值在响应差异处约为0.8~1.2.
|
图 10 三维各向异性模型水平切片图z=0 Fig. 10 3D anisotropic model horizontal slice at z=0 |
|
图 11 各向同性与各向异性模型TEM脉冲响应∂bz/∂t及归一化场值图 (a)测点处的脉冲响应;(b)测点(0, 100, 0)处归一化场值图. Fig. 11 TEM impulse responses ∂bz/∂t and the normalized field for isotropic and anisotropic models (a) The responses for observation locations; (b) Normalized field at (0, 100, 0). |
由此可知,在大回线源激励情况下,TEM响应主要受水平方向电导率影响,而垂直方向电导率对信号的影响很小(周建美等,2018),尤其当各向异性异常体与发射回线对称时,垂直方向电导率对TEM信号几乎完全无影响.发射回线与各向异性异常体之间不存在对称关系时,由于异常体的边界影响,垂直方向电导率将影响异常体边界附近的TEM响应,但影响程度远小于水平方向电导率.
3.2 各向异性倾角影响分析
考虑到各向异性的一般性,本节将分析倾斜各向异性对TEM信号的影响.首先,设定图 7模型的低阻异常体的各向异性电导率主轴方向与模型坐标方向一致,电阻率张量为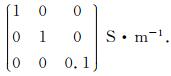
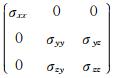
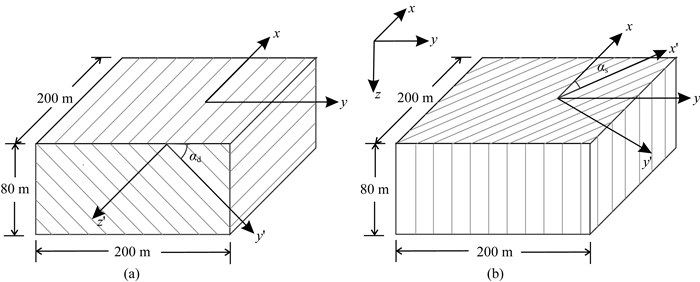
|
图 12 异常体主轴各向异性电导率旋转示意图 (a)关于x 轴旋转; (b)关于z轴旋转. Fig. 12 Rotation of the principal conductivity of anomaly (a) Rotation around x axis; (b) Rotation around z axis. |
为更好理解倾斜各向异性在整个测量区域内对TEM信号的影响程度与机制,这里采用TEM脉冲响应∂bz/∂t在地面上的二维等值线进行展示.如图 13所示,展示了涵盖早中晚期的0.05 ms、0.63 ms以及1.58 ms三个观测时间点,绕x轴旋转倾角αd为0°、30°、60°、90°时的响应分布.根据“烟圈”理论可知,当回线中发射电流关断瞬间在地下介质中将产生一个感应涡流系统(Li et al., 2016a),随着观测时间向后推移,涡流系统不断向下和向外扩散.观测时间为0.05 ms时,该涡流系统刚扩散到低阻异常体,响应受异常体影响较小,当各向异性倾角变化时,图 13(a—d)响应的分布和幅值差异性较小.当观测时间推移到0.63 ms,涡流系统经过异常体,从图 13(e—h)响应可见当倾角由0°逐渐增加到90°时,响应分布出现较大变化,异常体中心区域幅值降低,体现出阻值增大效应.从图 13f与13g可见响应关于x轴出现不对称情形,且该不对称主要分布于异常体边界位置,体现出倾斜各向异性的边界效应.观测时间为1.58 ms时,从图 13(i—l)可知,相对于0.63 ms,此时倾角的变化对响应的幅值和分布影响更大,当倾角为30°、60°时在y=100 m的异常体边界附近更是出现了响应变号的现象.

|
图 13 倾斜各向异性模型TEM脉冲响应∂bz/∂t的等值线图 (a)-(d)观测时间为0.05 ms;(e)-(h)观测时间为0.63 ms; (i)-(h)观测时间为1.58 ms.白色虚线表示响应的正负值分界线,中心黑色线框表示发射回线. Fig. 13 The contour maps of TEM impulse responses ∂bz/∂t for dipping anisotropic model (a)-(d) are for observation time 0.05 ms; (e)-(h) are for observation time 0.63 ms; (i)-(l) are for observation time 1.58 ms; the dotted white line indicates the boundary between the domains of positive and negative impulse responses, and the black square indicates the transmitting loop. |
为进一步分析各向异性的影响,本节将讨论水平各向异性情况下走向角的影响,即主轴各向异性电导率绕z轴旋转.同理,设定图 7模型的低阻异常体的各向异性电导率主轴方向与模型坐标方向一致,电导率张量为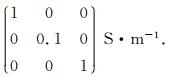
如图 14所示,与3.2节相同,展示了0.05 ms、0.63 ms以及1.58 ms三个观测时间点,主轴各向异性电导率绕z轴旋转角度为0°、30°、60°、90°时的响应分布.对比图 14与图 13可知,总体上图 13中的响应受角度的影响远大于图 14,说明绕x轴旋转主轴各向异性电导率较绕z轴旋转主轴各向异性电导率对TEM信号影响更大.图 14(a—d)为0.05 ms时刻的响应,由于在早期涡流刚到达异常体,此时受偏转角度αs影响较小.从0.63 ms和1.58 ms的响应图可见,通过脉冲响应∂bz/∂t的分布可清晰判断出各向异性的主轴方向.并且从1.58 ms的响应图可见,此时响应的幅值也将随旋转角度αs变化.

|
图 14 主轴各向异性绕z轴旋转模型TEM脉冲响应∂bz/∂t的等值线图 (a)-(d)观测时间为0.05 ms;(e)-(h)观测时间为0.63 ms; (i)-(h)观测时间为1.58 ms.中心黑色线框表示发射回线. Fig. 14 The contour maps of TEM impulse responses ∂bz/∂t for principal conductivity rotated around z axis (a)-(d) are for observation time 0.05 ms; (e)-(h) are for observation time 0.63 ms; (i)-(l) are for observation time 1.58 ms; the black square indicates the transmitting loop. |
本文采用拟态有限体积法对时域Maxwell方程组进行空间离散,并结合后退欧拉法进行时间域离散,实现了任意各向异性介质的大回线源瞬变电磁三维正演.通过一维各向异性模型、三维各向同性模型验证了该算法精度与有效性.
通过对三维主轴各向异性模型响应的计算与分析可知,当各向异性异常体与回线源存在对称关系时,TEM信号主要受水平方向电导率影响,而垂直方向电导率几乎无影响.当异常体与回线源不存在对称关系时,垂直方向电导率将对异常体边界附近的响应产生影响,但影响程度远低于水平电导率.
本文进一步分析了一般各向异性对TEM信号的影响,模拟计算结果表明各向异性倾角对信号的幅值与分布产生较大影响,并由于异常体的边界影响将会导致信号失去对称性.各向异性的走向角对信号的幅值影响较小,但会影响信号分布,从信号的分布能较容易判断出水平电导率主轴方向.
致谢 感谢德国科隆大学Bülent Tezkan教授的指导及其组内同学的有益讨论,感谢中国地质大学(武汉)李建慧老师提供的一维正余弦转换代码和中国海洋大学韩波博士在各向异性推导方面的指导,感谢两位审稿专家对本文的完善提供的宝贵建议.
Amestoy P R, Duff I S, L′Excellent J Y, et al. 2001. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM Journal on Matrix Analysis and Applications, 23(1): 15-41.
|
Amestoy P R, Guermouche A, L′Excellent J Y, et al. 2006. Hybrid scheduling for the parallel solution of linear systems. Parallel Computing, 32(2): 136-156. DOI:10.1016/j.parco.2005.07.004 |
Commer M, Newman G. 2004. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics, 69(5): 1192-1202. DOI:10.1190/1.1801936 |
Dennis Z R, Cull J P. 2012. Transient electromagnetic surveys for the measurement of near-surface electrical anisotropy. Journal of Applied Geophysics, 76: 64-73. DOI:10.1016/j.jappgeo.2011.10.014 |
Druskin V, Knizhnerman L. 1994. Spectral approach to solving three-dimensional Maxwell′s diffusion equations in the time and frequency domains. Radio Science, 29(4): 937-953. DOI:10.1029/94RS00747 |
Fu H H, Wang Y Q, Um E S, et al. 2015. A parallel finite-element time-domain method for transient electromagnetic simulation. Geophysics, 80(4): E213-E224. DOI:10.1190/geo2014-0067.1 |
Hünziker J, Thorbecke J, Slob E. 2015. The electromagnetic response in a layered vertical transverse isotropic medium: A new look at an old problem. Geophysics, 80(1): F1-F18. |
Haber E, Ascher U M, Oldenburg D W. 2004. Inversion of 3D electromagnetic data in frequency and time domain using an inexact all-at-once approach. Geophysics, 69(5): 1216-1228. DOI:10.1190/1.1801938 |
Haber E, Oldenburg D W, Shekhtman R. 2007. Inversion of time domain three-dimensional electromagnetic data. Geophysical Journal International, 171(2): 550-564. DOI:10.1111/gji.2007.171.issue-2 |
Haber E, Ruthotto L. 2014. A multiscale finite volume method for Maxwell′s equations at low frequencies. Geophysical Journal International, 199(2): 1268-1277. DOI:10.1093/gji/ggu268 |
Han B, Li Y G, Li G. 2018. 3D forward modeling of magnetotelluric fields in general anisotropic media and its numerical implementation in Julia. Geophysics, 83(4): F29-F40. DOI:10.1190/geo2017-0515.1 |
Haroon A, Adrian J, Bergers R, et al. 2015. Joint inversion of long-offset and central-loop transient electromagnetic data: Application to a mud volcano exploration in Perekishkul, Azerbaijan. Geophysical Prospecting, 63(2): 478-494. DOI:10.1111/gpr.2015.63.issue-2 |
Hyman J M, Shashkov M. 1999. Mimetic discretizations for Maxwell′s equations. Journal of Computational Physics, 151(2): 881-909. DOI:10.1006/jcph.1999.6225 |
Key K. 2012. Is the fast Hankel transform faster than quadrature?. Geophysics, 77(3): F21-F30. DOI:10.1190/geo2011-0237.1 |
Li H, Xue G Q, Zhong H S, et al. 2016. Joint inversion of CMP gathers of multi-channel transient electromagnetic data. Chinese Journal of Geophysics (in Chinese), 59(12): 4439-4447. DOI:10.6038/cjg20161206 |
Li J H, Zhu Z Q, Liu S C, et al. 2011. 3D numerical simulation for the transient electromagnetic field excited by the central loop based on the vector finite-element method. Journal of Geophysics and Engineering, 8(4): 560-567. DOI:10.1088/1742-2132/8/4/008 |
Li J H, Hu X Y, Zeng S H, et al. 2013. Three-dimensional forward calculation for loop source transient electromagnetic method based on electric field Helmholtz equation. Chinese Journal of Geophysics (in Chinese), 56(12): 4256-4267. DOI:10.6038/cjg20131228 |
Li J H, Cao X F, Ling C P, et al. 2016a. Geoelectric models and their corresponding successful cases for transient electromagnetic prospecting. Progress in Geophysics (in Chinese), 31(1): 232-250. DOI:10.6038/pg20160127 |
Li J H, Farquharson C G, Hu X Y, et al. 2016b. A vector finite element solver of three-dimensional modelling for a long grounded wire source based on total electric field. Chinese Journal of Geophysics (in Chinese), 59(4): 1521-1534. DOI:10.6038/cjg20160432 |
Li J H, Farquharson C G, Hu X Y. 2016a. 3D vector finite-element electromagnetic forward modeling for large loop sources using a total-field algorithm and unstructured tetrahedral grids. Geophysics, 82(1): E1-E16. |
Li J H, Farquharson C G, Hu X Y. 2016b. Three effective inverse Laplace transform algorithms for computing time-domain electromagnetic responses. Geophysics, 81(2): E113-E128. DOI:10.1190/geo2015-0174.1 |
Li J H, Lu X S, Farquharson C G, et al. 2018. A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources. Geophysics, 83(3): E117-E132. DOI:10.1190/geo2017-0216.1 |
Li Y G, Spitzer K. 2005. Finite element resistivity modelling for three-dimensional structures with arbitrary anisotropy. Physics of the Earth and Planetary Interiors, 150(1-3): 15-27. DOI:10.1016/j.pepi.2004.08.014 |
Li Z H, Huang Q H. 2014. Application of the complex frequency shifted perfectly matched layer absorbing boundary conditions in transient electromagnetic method modeling. Chinese Journal of Geophysics (in Chinese), 57(4): 1292-1299. DOI:10.6038/cjg20140426 |
Liu Y H, Yin C C, Cai J, et al. 2018. Review on research of electrical anisotropy in electromagnetic prospecting. Chinese Journal of Geophysics (in Chinese), 61(8): 3468-3487. |
Newman G A, Hohmann G W, Anderson W L. 1986. Transient electromagnetic response of a three-dimensional body in a layered earth. Geophysics, 51(8): 1608-1627. DOI:10.1190/1.1442212 |
Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics, 78(1): E47-E57. DOI:10.1190/geo2012-0131.1 |
Pek J, Santos F A M. 2006. Magnetotelluric inversion for anisotropic conductivities in layered media. Physics of the Earth and Planetary Interiors, 158(2-4): 139-158. DOI:10.1016/j.pepi.2006.03.023 |
Peng R H, Hu X Y, Han B, et al. 2016. 3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method. Chinese Journal of Geophysics (in Chinese), 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
Qiu Z P, Li Z H, Li D Z, et al. 2013. Non-orthogonal-Grid-based three dimensional modeling of transient electromagnetic field with topography. Chinese Journal of Geophysics (in Chinese), 56(12): 4245-4255. DOI:10.6038/cjg20131227 |
Sugeng F. 1998. Modeling the 3D TDEM response using the 3D full-domain finite-element method based on the hexahedral edge-element technique. Exploration Geophysics, 29(4): 615-619. |
Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time. Chinese Journal of Geophysics (in Chinese), 56(3): 1049-1064. DOI:10.6038/cjg20130333 |
Swidinsky A, Edwards R N. 2009. The transient electromagnetic response of a resistive sheet: straightforward but not trivial. Geophysical Journal International, 179(3): 1488-1498. DOI:10.1111/gji.2009.179.issue-3 |
Um E S, Harris J M, Alumbaugh D L. 2010. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach. Geophysics, 75(4): F115-F126. DOI:10.1190/1.3473694 |
Um E S, Commer M, Newman G A, et al. 2015. Finite element modelling of transient electromagnetic fields near steel-cased wells. Geophysical Journal International, 202(2): 901-913. DOI:10.1093/gji/ggv193 |
Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling. Geophysics, 58(6): 797-809. DOI:10.1190/1.1443465 |
Weiss C J, Newman G A. 2002. Electromagnetic induction in a fully 3-D anisotropic earth. Geophysics, 67(4): 1104-1114. DOI:10.1190/1.1500371 |
Xu Y C, Lin J, Li S Y, et al. 2012. Calculation of full-waveform airborne electromagnetic response with three-dimension finite-difference solution in time-domain. Chinese Journal of Geophysics (in Chinese), 55(6): 2105-2114. DOI:10.6038/j.issn.0001-5733.2012.06.032 |
Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation. Progress in Geophysics (in Chinese), 23(4): 1165-1172. |
Xue G Q, Chen W Y, Zhou N N, et al. 2013. Short-offset TEM technique with a grounded wire source for deep sounding. Chinese Journal of Geophysics (in Chinese), 56(1): 255-261. DOI:10.6038/cjg20130126 |
Xue G Q, Wang H Y, Yan S, et al. 2014. Time-domain Green function solution for transient electromagnetic field. Chinese Journal of Geophysics (in Chinese), 57(2): 671-678. DOI:10.6038/cjg20140230 |
Yee K S. 1966. Numerical solution of initial boundary value problems involving maxwell′s equations in isotropic media. IEEE Transactions on Antennas and Propagation, 14(3): 302-307. DOI:10.1109/TAP.1966.1138693 |
Yin C C, Qi Y F, Liu Y H. 2016. 3D time-domain airborne EM modeling for an arbitrarily anisotropic earth. Journal of Applied Geophysics, 131: 163-178. DOI:10.1016/j.jappgeo.2016.05.013 |
Yogeshwar P, Tezkan B. 2017. Two-dimensional basement modeling of central loop transient electromagnetic data from the central Azraq basin area, Jordan. Journal of Applied Geophysics, 136: 198-210. DOI:10.1016/j.jappgeo.2016.11.001 |
Yu L, Evans R L, Edwards R N. 1997. Transient electromagnetic responses in seafloor with triaxial anisotropy. Geophysical Journal International, 129(2): 292-304. DOI:10.1111/gji.1997.129.issue-2 |
Zhang Y, Wang H N, Tao H G, et al. 2012. Finite volume algorithm to simulate 3D responses of multi-component induction tools in inhomogeneous anisotropic formation based on coupled scalar-vector potentials. Chinese Journal of Geophysics (in Chinese), 55(6): 2141-2152. DOI:10.6038/j.issn.0001-5733.2012.06.036 |
Zhou J M, Liu W T, Li X, et al. 2018. Research on the 3D mimetic finite volume method for loop-source TEM response in biaxial anisotropic formation. Chinese Journal of Geophysics (in Chinese), 61(1): 368-378. DOI:10.6038/cjg2018K0598 |
李海, 薛国强, 钟华森, 等. 2016. 多道瞬变电磁法共中心点道集数据联合反演. 地球物理学报, 59(12): 4439-4447. DOI:10.6038/cjg20161206 |
李建慧, 胡祥云, 曾思红, 等. 2013. 基于电场Helmholtz方程的回线源瞬变电磁法三维正演. 地球物理学报, 56(12): 4256-4267. DOI:10.6038/cjg20131228 |
李建慧, 曹晓峰, 凌成鹏, 等. 2016a. 瞬变电磁法勘探的地电模型及其成功案例分析. 地球物理学进展, 31(1): 232-250. DOI:10.6038/pg20160127 |
李建慧, Farquharson C G, 胡祥云, 等. 2016b. 基于电场总场矢量有限元法的接地长导线源三维正演. 地球物理学报, 59(4): 1521-1534. DOI:10.6038/cjg20160432 |
李展辉, 黄清华. 2014. 复频率参数完全匹配层吸收边界在瞬变电磁法正演中的应用. 地球物理学报, 57(4): 1292-1299. DOI:10.6038/cjg20140426 |
刘云鹤, 殷长春, 蔡晶, 等. 2018. 电磁勘探中各向异性研究现状和展望. 地球物理学报, 61(8): 3468-3487. |
彭荣华, 胡祥云, 韩波, 等. 2016. 基于拟态有限体积法的频率域可控源三维正演计算. 地球物理学报, 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
邱稚鹏, 李展辉, 李墩柱, 等. 2013. 基于非正交网格的带地形三维瞬变电磁场模拟. 地球物理学报, 56(12): 4245-4255. DOI:10.6038/cjg20131227 |
孙怀凤, 李貅, 李术才, 等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049-1064. DOI:10.6038/cjg20130333 |
许洋铖, 林君, 李肃义, 等. 2012. 全波形时间域航空电磁响应三维有限差分数值计算. 地球物理学报, 55(6): 2105-2114. DOI:10.6038/j.issn.0001-5733.2012.06.032 |
薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展. 地球物理学进展, 23(4): 1165-1172. |
薛国强, 陈卫营, 周楠楠, 等. 2013. 接地源瞬变电磁短偏移深部探测技术. 地球物理学报, 56(1): 255-261. DOI:10.6038/cjg20130126 |
薛国强, 王贺元, 闫述, 等. 2014. 瞬变电磁场时域格林函数解. 地球物理学报, 57(2): 671-678. DOI:10.6038/cjg20140230 |
张烨, 汪宏年, 陶宏根, 等. 2012. 基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应. 地球物理学报, 55(6): 2141-2152. DOI:10.6038/j.issn.0001-5733.2012.06.036 |
周建美, 刘文韬, 李貅, 等. 2018. 双轴各向异性介质中回线源瞬变电磁三维拟态有限体积正演算法. 地球物理学报, 61(1): 368-378. DOI:10.6038/cjg2018K0598 |
 2019, Vol. 62
2019, Vol. 62


