地磁场是反映地球演变、地质构造演变(Novik et al., 2016)等过程的重要物理量.磁偶极子模型在很多领域得到了应用,因为自然界的磁现象均可等效为若干个磁偶极子磁场的叠加,在特定情况下也可以等效为一个磁偶极子(刘光鼎, 1997; 刘立波和万卫星, 2014; 温珍河等, 2014; 殷长春等, 2015).在利用磁异常探测舰船及潜艇等目标时,就将目标磁场近似为一个磁偶极子的磁场(翁行泰等, 1994; 王光辉等, 2008; 孙烨等, 2012; 徐如刚等, 2014; 姚振宁等, 2014).一般情况下,船磁由软磁材料在地磁场中感生磁场和硬磁材料磁场组成.船磁就是这两种磁场共同作用的结果.在目标磁隐身的要求下,舰船出海时都要消磁,但在长期航行后,其软磁材料的感生磁场重新建立占据了船磁主要成分.此时船磁磁矩方向与地磁矢量方向相同.这种实际情况会简化定位算法设计.
地磁场是矢量场,目前主要的矢量磁传感器包括磁通门磁传感器和MEMS磁传感器,安装时三轴需要严格校正(Wu and Shi, 2015),使用时需要实时测量传感器姿态信息.总场光泵磁力仪分辨率和精度高,对磁目标探测距离远.工作姿态方面只要避开死区角度即可.因此利用地磁总场测量目标位置具有定位精度高、定位距离远,方便可靠的优点.
由于地磁场是随时间变化的,在空间分布上并不均匀,存在异常点(徐文耀等, 2005; 冯彦等, 2010; 陈斌等, 2011; 郑玉航等, 2013; 翁爱华等, 2017),文中通过设计地磁场二重梯度的算法消除地磁场随时间变化的影响和空间异常场的影响(高金田等, 2005; Zalfvsky et al., 2012; Pang et al., 2014).因此基于地磁总场定位方法具备了实用性,对于目标磁探测(Yang et al., 2010; Beiki et al., 2012; Iacca et al., 2014; Wahlström and Gustafsson, 2014)及目标磁隐身(目标磁矩测量及消磁)都具有参考意义.
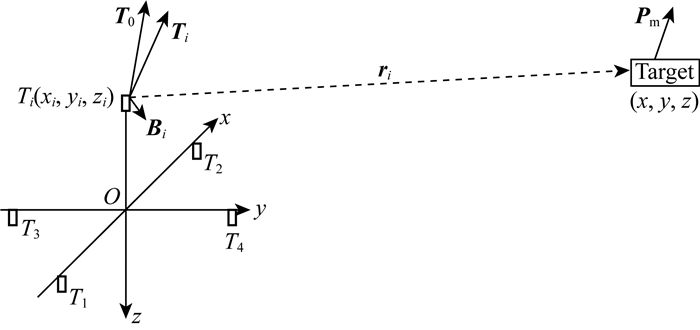
1 用地磁总场对目标定位原理 1.1 地磁总场测量阵列的构成当目标距传感器超过自身尺度2~3倍及以上时, 满足远场条件,目标磁场就可以认为是偶极子磁场.用多个地磁总场传感器构成如图 1所示的阵列.
|
图 1 磁定位阵列方案示意图 Fig. 1 Diagram of magnetic-locating arrays |
T0是无目标时地磁场矢量,T0是其大小.Ti是有目标时磁传感器i所在位置(xi, yi, zi)的磁场测量值,i=1, 2, 3, ….当地地磁倾角和磁偏角分别为θ, φ.设目标在(x, y, z)点,Pm是目标磁矩矢量,传感器i到目标的位移矢量ri=(x-xi)i+(y-yi)j+(z-zi)k.目标磁矩Pm在传感器i处产生的磁场矢量Bi,
则

|
(1) |
其中Pm的方向倾角和偏角分别为α, β,则Pm=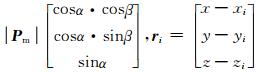
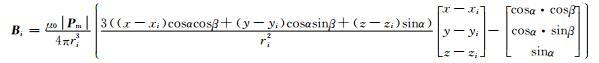
|
地磁场单位方向矢量e=[cosθ·cosφ cosθ·sinφ sinθ].在远场测量条件下,传感器所在位置的Bi值远小于T0值,因此传感器测量值Ti≈T0+e·Bi.其中
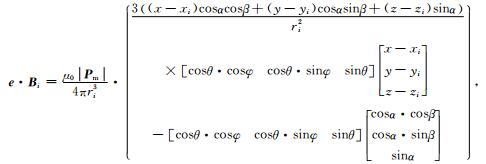
|
(2) |
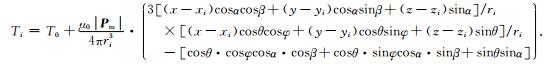
|
(3) |
这是一般情况下传感阵列测量的远场标量方程组.通过这个方程组,可以计算出目标位置及磁矩的大小及方向,方程组未知数7个,分别是(T0, x, y, z, |Pm|, α, β),因此传感器数量i至少7个才有可能完全求解.当目标硬磁磁场很小,软磁材料的感生磁场为主要成分时,目标磁矩方向与地磁矢量方向相同.令V是目标铁磁质体积,χm是铁磁质材料磁化率,μ0是真空磁导率.目标的磁矩矢量Pm与地磁场矢量T0满足如下的关系:

|
(4) |
于是式(3)简化为
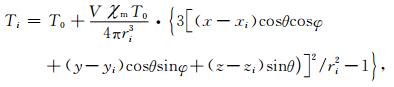
|
(5) |
方程组(5)未知数5个,分别是(T0, x, y, z, |Pm|),因此传感器数量i至少5个才有可能完全求解.求解(x, y, z)可以实现目标定位,求解|Pm|能初步估计目标的体积质量,为目标识别提供依据.
1.2 消除地磁场中变化成份的影响公式(3)中地磁场T0是随时间变化的,随空间分布不均匀,T0是时间t和空间坐标(xi, yi, zi)的函数,即T0=T0(t0, i)+ΔT(t-t0).其中T0(t0, i)是t0时刻(xi, yi, zi)处的地磁场值,ΔT(t-t0)为t-t0时段内地磁值随时间增量,在局部空间内仅是时间的函数,这对目标定位会产生影响.在测量结果中必须消除这种随时间和空间变化的影响.位于(xi, yi, zi)的传感器i在t时刻测量值Ti(t, xi, yi, zi)由以下三项组成
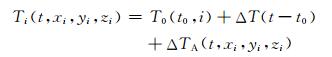
|
ΔTA(t, xi, yi, zi)为t时刻位于(x, y, z)的目标引起位于(xi, yi, zi)的传感器i测量值增量,由公式(2)和(3),ΔTA(t, xi, yi, zi)等同于e·Bi(t).同理位于(xj, yj, zj)的传感器j在t时刻测量值为
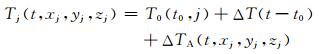
|
在t0时刻传感器i和j的测量值分别为
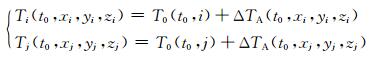
|
令ΔTij|Theory=ΔTA(t, xi, yi, zi)-ΔTA(t, xj, yj, zj)-ΔTA(t0, xi, yi, zi)-[ΔTA(t0, xj, yj, zj)]
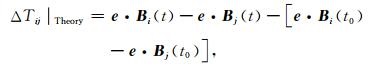
|
(6) |
令

|
(7) |
可得
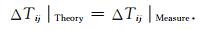
|
(8) |
为方便令ΔTij|Theory=ΔTij T,ΔTij|Measure=ΔTij M,i,j=1, 2, 3…, i≠j.式(6)中的e·Bi(t)表达式由(2)式给出,式(7)中Ti(t, xi, yi, zi)是传感器i在t时刻的测量值.因此根据多个传感器i测量值得到二重梯度构成(8)式方程组,消除了地磁场随时间变化ΔT(t-t0)和空间分布T0(t0, i)的影响.依据(8)式计算目标位置(x, y, z)及磁矩Pm,其结果与地磁场随时间变化无关,也与地磁场空间分布无关.
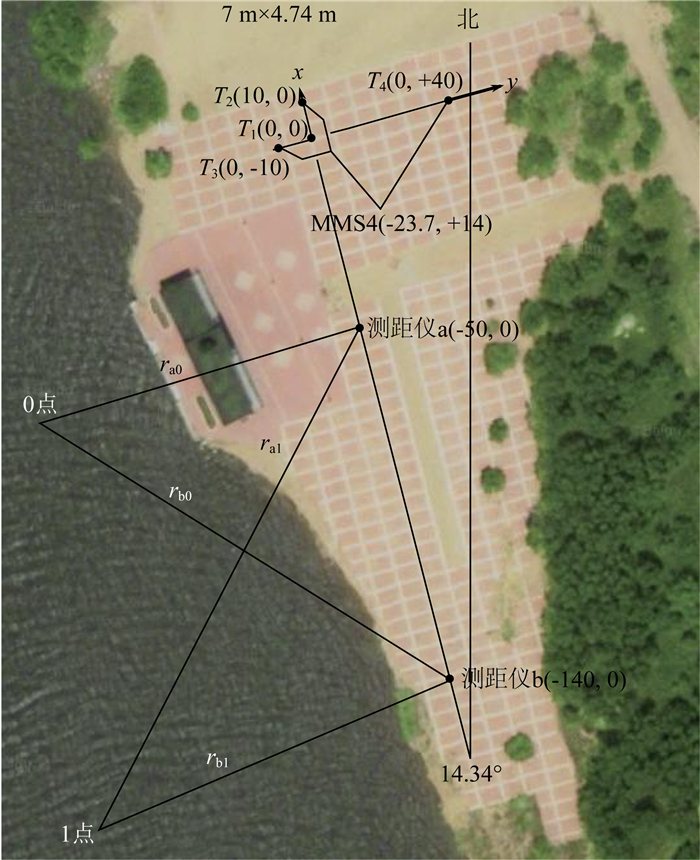
2 目标定位实验研究及数据处理 2.1 测量阵列构成如图 2是实验区域的卫星地图照片,实验地点在松花江沿岸某地,地面长方格尺寸是7 m×4.74 m.直角坐标系x轴正向沿北偏西14.34°,y轴正向沿东偏北14.34°,z轴正向垂直水平面向下.四台地磁总场光泵磁传感器水平面坐标T1(0,0)、T2(10,0)、T3(0,-10)、T4(0,40),所有坐标单位m,构成如图阵列,光泵磁传感器灵敏度为0.6 pT.目标船航行至坐标点(141,-225.3)起开始测量,目标船沿直线航行至(-107,-190.3).光泵磁传感器布设于铝制的三脚架上,传感器距地面1.43 m.当地地磁倾角θ=63.3°,偏角φ=-10.34°,转换到测量坐标系中,θ=63.3°,φ=4°;t0选取船航至(141,-225.3)的时刻.目标船实际位置坐标由两台激光测距仪实时测量,并结合测量现场照片进行了几何修正.
|
图 2 实验区域卫星照片 Fig. 2 Satellite photos of the experiment area |
图 3是四台光泵磁传感器测量的地磁总场值随传感器采样序号变化的曲线,横轴为采样点序号,传感器最高采样率10 Hz,图 3中选择传感器每秒输出5个磁场数据.纵轴是磁场测量值,单位nT.图 3中黑、蓝、绿、红线是T1, T2, T3, T4测量值,其中既有地磁场自身随时间的变化,也有目标船航行产生的磁场变化.因地磁场自身变化幅度较大,混乱复杂,目标信号淹没在地磁变化中,很难观察船磁信号的变化规律.
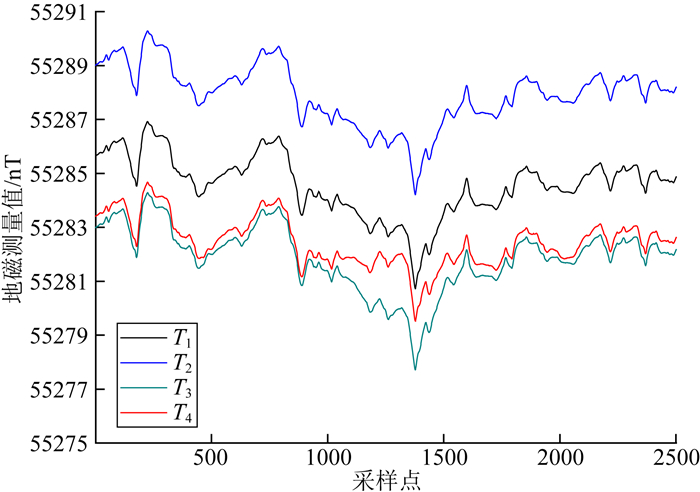
|
图 3 四台磁传感器测量值曲线 Fig. 3 Measuring curves of four magnetic sensors |
图 4是传感器梯度ΔT14M、ΔT24M、ΔT34M、ΔT12M、ΔT13M随采样序号变化的曲线,横轴采样点序号,纵轴是两个传感器测量值之差,单位是nT.图 4曲线中地磁场随时间的变化被滤除了,剩下目标船舶航行引起的磁场变化,曲线规律性明显.而依据公式(7)二重梯度数据处理,可消除变化磁场和分布不均匀磁场对目标定位的影响,提高计算精度.

|
图 4 磁传感器测量梯度值曲线 Fig. 4 Measured gradient curves of magnetic sensor |
为了求解公式(8)令
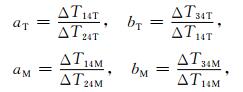
|
(9) |
ΔT14, ΔT24, ΔT34由公式(6)和公式(7)定义,再由(2)式,aT和bT表达式中已经消除了|Pm|,aT和bT仅是目标位置坐标(x, y, z)的函数.由2.1节所述,实验中目标船在水平面直线航行,因此目标船坐标z是常数.求解方程组(10)可以得到由地磁数据定位的目标坐标(xn, yn) (n=0, 1, 2, …, m).目标船舶的实际坐标(xn, yn)由两台激光测距仪测定.

|
(10) |
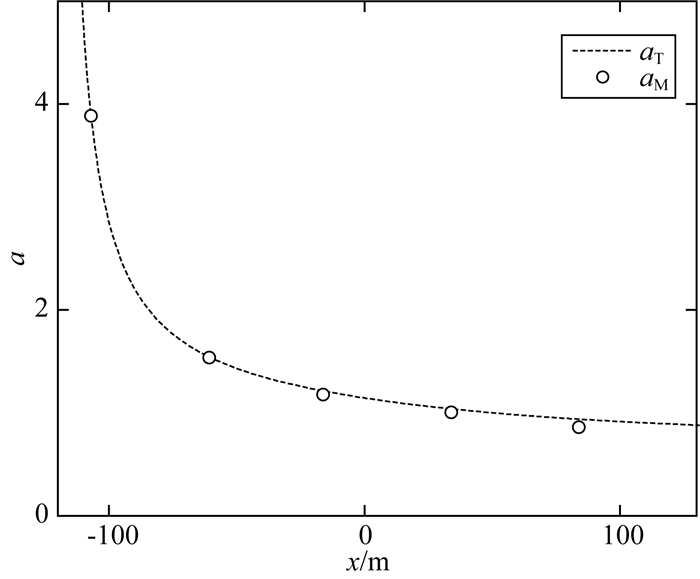
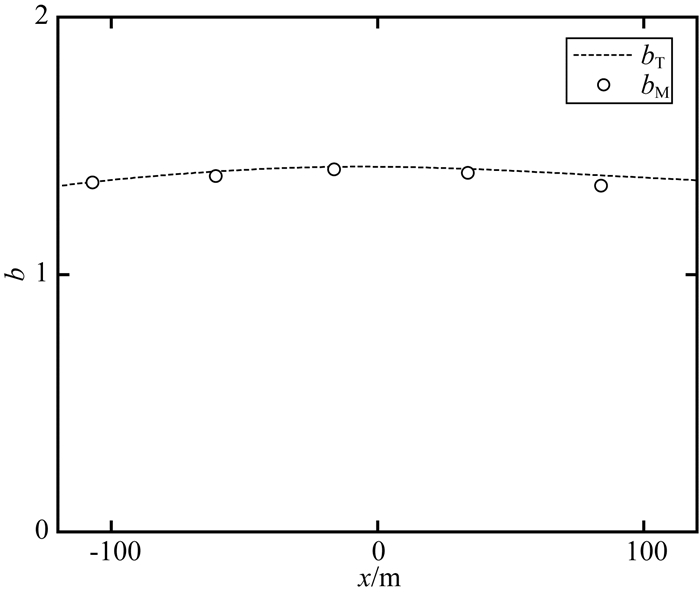
2.1节所述目标船从(141, -225.3)行驶至(-107, -190.3),在6个位置点(xn, yn) n=0, 1, 2, …, 5,用4台光泵磁传感器测量船行至每个位置点(xn, yn)时各传感器所在位置的磁场值Ti, i=1, 2, 3, 4.根据公式(7)和(9)计算出ΔT14M、ΔT24M、ΔT34M、aM、bM的值,数据如表 1所示.ΔT14M、ΔT24M、ΔT34M与位置xn的关系曲线如图 5、图 6、图 7中的o点所示.aM, bM与位置xn的关系曲线如图 8,图 9中的o点所示.将(xn, yn)代入公式(6)和(9),得到ΔT14T、ΔT24T、ΔT34T、aT、bT分别与xn的理论关系曲线,如图 5至图 9中的虚线所示.可见,理论曲线与测量值吻合得非常好.因为目标沿直线运动,yn是xn的线性函数,目标在水面运动zn是常数,因此图 5至图 9中没有表达yn、zn与磁场的变化关系.
|
|
表 1 目标定位实验数据表 Table 1 Experimental data of object-locating |
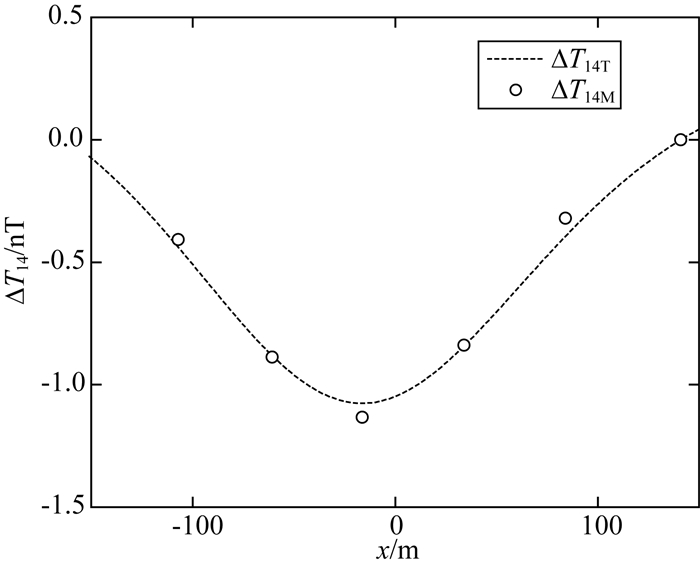
|
图 5 ΔT14与位置xn的理论曲线与实验测量数据 Fig. 5 Theoretical curve and experimental data of ΔT14 and position xn |
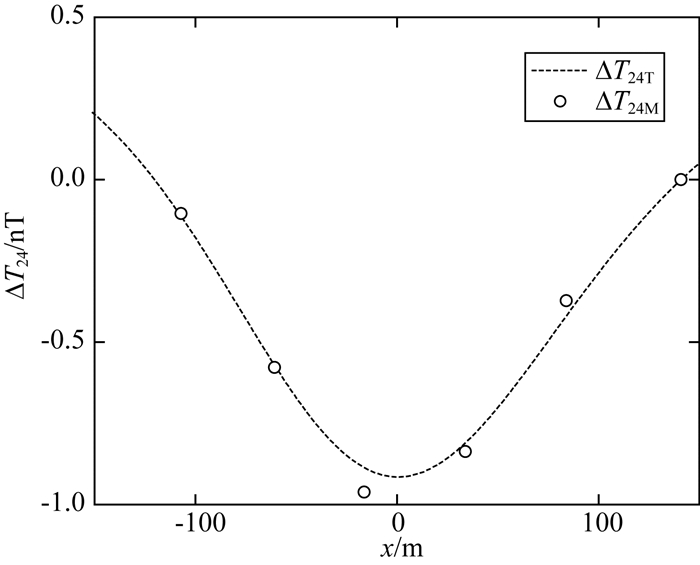
|
图 6 ΔT24与位置xn的理论曲线与实验测量数据 Fig. 6 Theoretical curve and experimental data of ΔT24 and position xn |

|
图 7 ΔT34与位置xn的理论曲线与实验测量数据 Fig. 7 Theoretical curve and experimental data of ΔT34 and position xn |
|
图 8 a与位置xn的理论曲线与实验测量数据 Fig. 8 Theoretical curve and experimental data of a and position xn |
|
图 9 b与位置xn的理论曲线与实验测量数据 Fig. 9 Theoretical curve and experimental data of b and position xn |
表 2是按照公式(10)依据磁场数据用LINGO软件计算的目标船定位结果.对于t0时刻,n=0,目标船位于(141,-225.3),两传感器测量的二重梯度均为零,公式(9)中的a、b无数学意义,因此不能定位,其临近点计算误差也比较大.其余点的定位结果见表 2中数据.
|
|
表 2 目标磁场定位实验结果 Table 2 Experimental result of magnetic object-locating |
如果对于t0时刻,两传感器测量的二重梯度人为加入一个已知偏置项,这样在t0时刻附近的点都脱离了零比零型无数学意义的情况,因此t0时刻附近点的定位误差显著减小.例如,在公式(6)和(7)等号右侧加入2 nT的直流偏置,即令
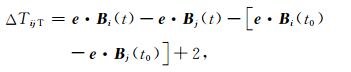
|
(11) |
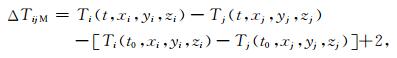
|
(12) |
用式(11)和(12)计算a、b,然后用LINGO软件求解公式(10),得到目标船位置(xn, yn),其结果如表 3.相比表 2结果,n=0、1、2、3、4时,目标船定位误差明显减小.
|
|
表 3 目标磁场定位的梯度偏置算法实验结果 Table 3 Experimental result of magnetic object-locating with bias magnetic gradient algorithm |
将表 2中的磁场定位结果和表 3中的偏置算法的磁场定位结果绘制于图 10中,可见偏置算法的定位精度要高于普通磁场定位精度.对于偏置量的大小可以人为设置,原则只要使t0时刻两传感器的梯度偏移1~2 nT即可,但也不宜过大,否则将使定位灵敏度降低.
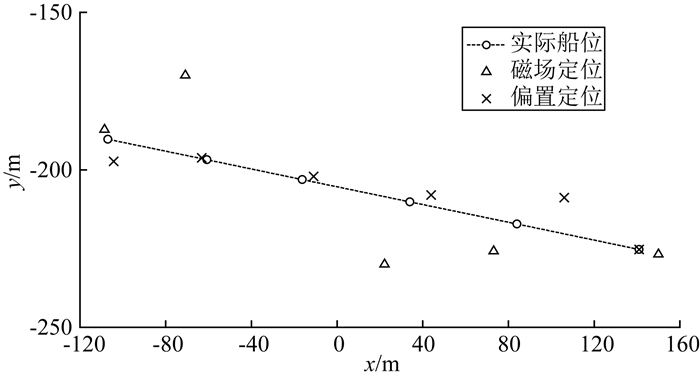
|
图 10 磁场定位与偏置算法定位的实验结果 Fig. 10 Experimental results of the magnetic-locating and the bias algorithm |
把定位结果(xn, yn)代入公式(8)计算目标船的平均磁矩大小2.98×105 A·m2.目标船由驳船和拖船组成,依据卫星照片和现场照片估算驳船长63 m,宽9 m,高4 m,据此估算驳船排水量2300 t,自重270 t.拖船长27 m,宽6 m,拖船自重按100 t计.因此目标船铁磁材料体积约47.4 m3,设船铁磁材料磁化率150(张安明等, 2014),代入公式(4)估算目标船的磁矩大小3.13×105 A·m2,与公式(8)计算结果基本吻合.测量出磁矩的大小反过来可以大致估计目标自重及排水量等指标,对目标识别有一定的参考意义.
3 结论以远场磁偶极子模型为依据,提出了地磁总场阵列对目标定位的算法,利用MATHCAD对算法中的非线性方程组进行了仿真,用LINGO软件求解了算法方程组.在松花江沿岸某地开展了目标定位实验.以航行中船舶为测量目标,采用四台光泵磁传感器构成阵列,布设于铝制的三脚架上,距地面1.43 m,光泵磁传感器对地磁总场的灵敏度为0.6 pT.从坐标点(141,-225.3)起,目标船沿直线航行至(-107,-190.3),测量得到各传感器地磁梯度数据与理论曲线完全吻合,定位结果比较准确.实验证明了这种利用地磁总场对目标定位方法是可行的,并可以排除地磁场随时间变化和空间分布不均匀的影响.
致谢 感谢天津海之星水下机器人有限公司哈尔滨分公司桑恩方教授团队提供的帮助,使实验得以顺利完成.同时感谢评阅人和编辑部提出的修改意见,使本文更加完善.
Beiki M, Clark D A, Austin J R, et al. 2012. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data. Geophysics, 77(6): J23-J37. DOI:10.1190/geo2011-0437.1 |
Chen B, Gu Z W, Gao J T, et al. 2011. Analyses of geomagnetic field and its secular variation over China for 2005.0 epoch using Spherical Cap Harmonic method. Chinese Journal of Geophysics (in Chinese), 54(3): 771-779. DOI:10.3969/j.issn.0001-5733.2011.03.017 |
Feng Y, Pan J J, An Z C, et al. 2010. Calculation and analysis of geomagnetic field horizontal gradients in China. Chinese Journal of Geophysics (in Chinese), 53(12): 2899-2906. DOI:10.3969/j.issn.0001-5733.2010.12.013 |
Gao J T, An Z C, Gu Z W, et al. 2005. Selections of the geomagnetic normal field and calculations of the geomagnetic anomalous field. Chinese Journal of Geophysics (in Chinese), 48(1): 56-62. DOI:10.3321/j.issn:0001-5733.2005.01.010 |
Iacca G, Bakker F L, Wörtche B H. 2014. Real-time magnetic dipole detection with single particle optimization. Applied Soft Computing, 23(5): 460-473. DOI:10.1016/j.asoc.2014.06.026 |
Liu G D. 1997. Progress of marine geophysics in China. Acta Geophysica Sinica (in Chinese), 40(S1): 46-49. |
Liu L B, Wan W X. 2014. A brief overview on the issue on space physics and space weather. Chinese Journal of Geophysics (in Chinese), 57(11): 3493-3501. DOI:10.6038/cjg20141101 |
Novik O B, Ershov S V, Volgin M N, et al. 2016. Magnetic location of a possible earthquake epicentre area: A mathematical model. Geomatics, Natural Hazards and Risk, 7(1): 113-126. DOI:10.1080/19475705.2013.878398 |
Pang H F, Pan M C, Wan C B, et al. 2014. Integrated compensation of magnetometer array magnetic distortion field and improvement of magnetic object localization. IEEE Transactions on Geoscience and Remote Sensing, 52(9): 5670-5676. DOI:10.1109/TGRS.2013.2291839 |
Sun Y, Xiao C H, Zhou G H. 2012. An active method and its analytical formulas of magnetic sensor positioning using the magnetic source. Hydrographic Surveying and Charting (in Chinese), 32(4): 25-28. DOI:10.3969/j.issn.1671-3044.2012.04.008 |
Wahlström N, Gustafsson F. 2014. Magnetometer modeling and validation for tracking metallic targets. IEEE Transactions on Signal Processing, 62(3): 545-556. DOI:10.1109/TSP.2013.2274639 |
Wang G H, Zhu H, Guo Z D. 2008. Analysis of magnetic dipole approximate range for a submarine. Journal of Naval University of Engineering (in Chinese), 20(5): 60-63. DOI:10.7495/j.issn.1009-3486.2008.05.014 |
Wen Z H, Zhang X H, Hao T Y, et al. 2014. Progress in compilation of geoscience map series for China seas and adjacent regions. Chinese Journal of Geophysics (in Chinese), 57(12): 3907-3919. DOI:10.6038/cjg20141205 |
Weng A H, Li S W, Li J P, et al. 2017. Progress in deep electromagnetic induction studies. Progress in Geophysics (in Chinese), 32(4): 1679-1692. DOI:10.6038/pg20170436 |
Weng X T, Cao M F. 1994. A research on the calculation of the induced magnetic field of a submarine. Journal of Shanghai Jiaotong University (in Chinese), 28(5): 69-76. |
Wu Y, Shi W. 2015. On calibration of three-axis magnetometer. IEEE Sensors Journal, 15(11): 6424-6431. DOI:10.1109/JSEN.2015.2459767 |
Xu R G, Gu Z W, Li Z J, et al. 2014. Application of Chinese geomagnetic survey and geomagnetic model for 2005-2010. Progress in Geophysics (in Chinese), 29(5): 2092-2099. DOI:10.6038/pg20140515 |
Xu W Y, Wei Z G, Xia G H. 2005. Regional features of the secular variation of the geomagnetic field in China for 2000. Chinese Journal of Geophysics (in Chinese), 48(3): 551-560. DOI:10.3321/j.issn:0001-5733.2005.03.012 |
Yang W A, Hu C, Li M, et al. 2010. A new tracking system for three magnetic objectives. IEEE Transactions on Magnetics, 46(12): 4023-4029. DOI:10.1109/TMAG.2010.2076823 |
Yao Z N, Liu D M, Liu D S, et al. 2014. A real-time magnetic localization method of underwater non-cooperative magnetic targets based on unscented particle filter. Acta Physica Sinica (in Chinese), 63(22): 309-314. DOI:10.7498/aps.63.227502 |
Yin C C, Zhang B, Liu Y H, et al. 2015. Review on airborne EM technology and developments. Chinese Journal of Geophysics (in Chinese), 58(8): 2637-2653. DOI:10.6038/cjg20150804 |
Zalfvsky Z, Bregman Y, Salomonski N, et al. 2012. Resolution enhanced magnetic sensing system for wide coverage real time UXO detection. Journal of Applied Geophysics, 84(4): 70-76. DOI:10.1016/j.jappgeo.2012.06.003 |
Zhang A M, Chen W T, Yu W Q, et al. 2014. The equivalent calculation for the induced magnetic fields of a ship hull module. Chinese Journal of Ship Research (in Chinese), 9(3): 109-112. DOI:10.3969/j.issn.1673-3185.2014.03.017 |
Zheng Y H, Liu Y Y, Zhang J S, et al. 2013. Modeling of magnetic anomaly and Analysis about performance of geomagnetic matching of MF7. Progress in Geophysics (in Chinese), 28(5): 2256-2263. DOI:10.6038/pg20130507 |
陈斌, 顾左文, 高金田, 等. 2011. 2005.0年代中国地区地磁场及其长期变化球冠谐和分析. 地球物理学报, 54(3): 771-779. DOI:10.3969/j.issn.0001-5733.2011.03.017 |
冯彦, 潘剑君, 安振昌, 等. 2010. 中国地区地磁场水平梯度的计算与分析. 地球物理学报, 53(12): 2899-2906. DOI:10.3969/j.issn.0001-5733.2010.12.013 |
高金田, 安振昌, 顾左文, 等. 2005. 地磁正常场的选取与地磁异常场的计算. 地球物理学报, 48(1): 56-62. DOI:10.3321/j.issn:0001-5733.2005.01.010 |
刘光鼎. 1997. 中国海洋地球物理进展. 地球物理学报, 40(S1): 46-49. |
刘立波, 万卫星. 2014. 我国空间物理研究进展. 地球物理学报, 57(11): 3493-3501. DOI:10.6038/cjg20141101 |
孙烨, 肖昌汉, 周国华. 2012. 磁主动式海底磁传感器定位方法及其解析公式. 海洋测绘, 32(4): 25-28. DOI:10.3969/j.issn.1671-3044.2012.04.008 |
王光辉, 朱海, 郭正东. 2008. 潜艇磁偶极子近似距离条件分析. 海军工程大学学报, 20(5): 60-63. DOI:10.7495/j.issn.1009-3486.2008.05.014 |
温珍河, 张训华, 郝天珧, 等. 2014. 我国海洋地学编图现状、计划与主要进展. 地球物理学报, 57(12): 3907-3919. DOI:10.6038/cjg20141205 |
翁爱华, 李世文, 李建平, 等. 2017. 深部电磁感应研究进展. 地球物理学进展, 32(4): 1679-1692. DOI:10.6038/pg20170436 |
翁行泰, 曹梅芬. 1994. 潜艇感应磁场的三维有限元法计算研究. 上海交通大学学报, 28(5): 69-76. |
徐如刚, 顾左文, 黎哲君, 等. 2014. 2005—2010年中国地磁测量与地磁场模型的应用. 地球物理学进展, 29(5): 2092-2099. DOI:10.6038/pg20140515 |
徐文耀, 魏自刚, 夏国辉. 2005. 2000年中国地区地磁场长期变化的区域特征. 地球物理学报, 48(3): 551-560. DOI:10.3321/j.issn:0001-5733.2005.03.012 |
姚振宁, 刘大明, 刘胜道, 等. 2014. 基于不敏粒子滤波的水中非合作磁性目标实时磁定位方法. 物理学报, 63(22): 309-314. DOI:10.7498/aps.63.227502 |
殷长春, 张博, 刘云鹤, 等. 2015. 航空电磁勘查技术发展现状及展望. 地球物理学报, 58(8): 2637-2653. DOI:10.6038/cjg20150804 |
张安明, 陈文涛, 虞伟乔, 等. 2014. 舰船壳体模块感应磁场的等效计算. 中国舰船研究, 9(3): 109-112. DOI:10.3969/j.issn.1673-3185.2014.03.017 |
郑玉航, 刘元元, 张金生, 等. 2013. MF7磁异常场模型的建模与匹配性能分析. 地球物理学进展, 28(5): 2256-2263. DOI:10.6038/pg20130507 |
 2019, Vol. 62
2019, Vol. 62


