2. 东方地球物理公司, 河北涿州 072750;
3. 中交铁道设计研究总院有限公司, 北京 100088
2. Bureau of Geophysical Prospecting Inc., Zhuozhou Hebei 072750, China;
3. CCCC Railway Consultants Group Co., LTD, Beijing 100088, China
岩石储层受到应力场作用会产生具有一定主方向排列的断裂、裂缝和裂隙.对于裂缝的尺度、裂缝相互作用和连通性等的研究在天然地震及能源勘探中具有重要的意义.裂缝会诱导产生地震各向异性效应,当地震波长远大于裂缝尺度时,裂缝介质可以看成等效的各向异性介质(Hudson, 1981; Hudson, 1986;Schoenberg and Sayers, 1995).介质的裂缝裂隙面通常与介质所受到的应力最大方向一致,对于实际介质各向异性特征研究可以提供介质裂隙面方位和裂缝密度等属性特征(高原和吴晶,2008;郝重涛和姚陈,2014).石油地震研究中,忽略各向异性会导致地震偏移成像模糊、反射点位置和深度错误及振幅解释不准确等问题(Jenner, 2011).由于岩层在不同的地质历史时期会遭受不同强度和方向的构造应力场作用,并且由于应力场的局部变化和岩性变化,储层中裂缝排列常具有多个优选方位(王赟等, 2017).与占主导裂缝的方位有一定夹角的强度较弱的裂缝一起形成介质的裂缝模型,也就是多组多尺度裂缝模型(Zhang et al., 2013).常用的研究及应用方法一般是将介质看成单组裂缝的HTI介质模型,为了更真实反映各向异性介质地震波场特征,必须考虑介质裂缝的多组性.
相对于HTI和正交各向异性介质,具有较低对称性的单斜各向异性可以描述更为复杂的地震裂缝模型.多组裂缝引起的各向异性可以由在各向同性背景岩石中引入多组互相平行排列的裂缝产生的(Winterstein, 1990),地下裂缝可能与地面成任意角度,当单组裂缝不平行也不垂直于VTI各向异性介质对称轴面时,其等效介质也是单斜各向异性(Sayer, 1998).对于多组裂缝的研究主要集中在裂缝弹性参数正演计算、属性特征分析及反演方面(Liu et al., 1993;刘恩儒等, 2006;Sayers, 1998;Far et al., 2013, 2014).Hudson裂缝模型(Hudson, 1981; Hudson, 1986)及线性滑移模型(Schoenberg and Sayers, 1995;Sayers and Kachanov, 1995)是两种常用的裂隙岩石等效各向异性计算方法.Liu等(2000)给出了裂缝岩石中计算等效介质多种方法的比较与讨论,这些计算方法同样可以计算多组裂缝各向异性特征.由于地质结构的复杂性,实际介质各向异性特征一般都是具有低阶对称性特征,为了分析复杂各向异性介质的特征,对于实际表现为低阶对称性的各向异性介质,很多研究者提出求解其高阶对称性各向异性参数近似的概念和方法(Fedorov, 1968;Arts et al., 1991;Dellinger, 2005;Den Boer, 2014),李磊和郝重涛(2012)对此方法进行了应用研究.
为了研究附加裂缝对于介质总体各向异性特征的影响,本文基于线性滑移模型方法(Schoenberg and Sayer, 1995)进行多组垂直裂缝的等效各向异性求取,得到多组裂缝的等效单斜各向异性弹性参数.通过与单斜介质最为接近的等效HTI介质空间搜索(Dellinger, 2005),分析多组垂直裂缝的单斜介质在多大程度上接近于HTI介质,并研究两者的地震属性特征和差异,如纵波速度、快慢横波速度和快横波极化方向的变化等以量化分析附加裂缝引起的各向异性介质弹性强度及介质对称性主轴变化.本文结果和方法对于地震数据分析和解释中通常将高阶各向异性对称性替代低阶对称性介质的适用精度和可行性研究具有重要的意义,并为在地震方法研究中将高阶对称性各向异性介质中已有的正反演计算方法推广到低阶各向异性情况下提供研究基础.
1 多组裂缝各向异性等效介质弹性参数计算方法主裂缝以外附加裂缝的综合效应都是降低介质的刚度,改变介质对称性主轴方位.根据线性滑移理论,岩石的总柔度是背景岩石的柔度加上由于裂缝存在导致的附加柔度,本文利用线性滑移模型方法计算多组裂缝模型弹性常数.
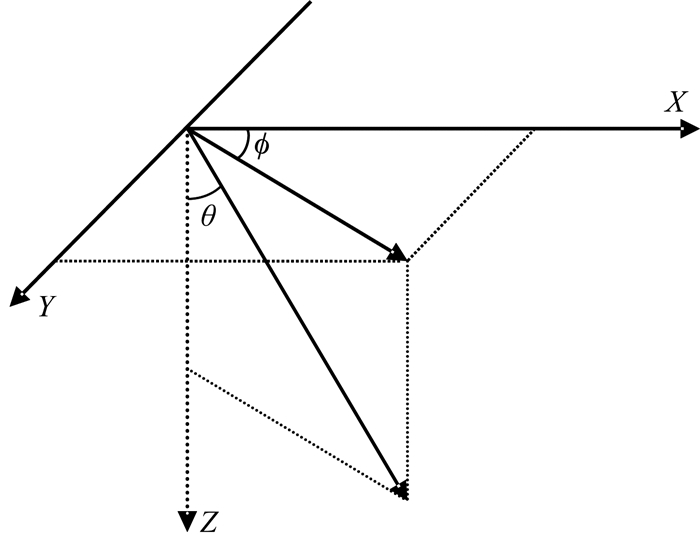
图 1是一组裂缝示意图,其中裂缝介质对称主轴与x轴夹角为ϕ,倾角为θ.裂缝介质的柔度S可以由背景介质柔度S0加上扰动介质柔度ΔSijkl构成,如公式(1)所示(Sayers and Kachanov, 1995; Far et al., 2013)
|
图 1 裂隙介质对称主轴与X轴夹角为ϕ,倾角为θ的一组裂缝示意图 Fig. 1 Sketch map of one set of fracture, the angle between the principal symmetry axis and X axis is ϕ and the dip angle is θ |
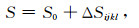
|
(1) |
弹性刚度常数可以由关系式C=S-1得到,ΔSijkl由(2)式计算

|
(2) |
其中δik是Kronecker符号,αij和βijkl由与裂缝相关参数如裂缝方位、裂缝面积及裂缝正向和切向柔量等给出.它们与常用的弱度张量ZN及ZT(Schoenberg and Sayers, 1995; 王赟等, 2008)关系是二阶张量αij正比于ZN,四阶张量βijkl正比于ZN-ZT.
当存在多组裂缝时,忽略裂缝之间相互作用,可以对每组裂缝引起的扰动柔度参数进行累积求和就可以得出多组裂缝的柔度.

|
(3) |
其中Sb是背景介质柔量,Sf(r)是附加第r组裂缝的柔度张量,N为裂缝组数.
2 低阶对称性各向异性介质及其等效高阶对称性常数计算实际岩石储层都是较为复杂的各向异性介质,VSP和岩石物理测量等方法可以提供具有较低对称性的各向异性参数(宋连腾等, 2015).但由于地表地震等观测排列的局限性,利用常规地表地震资料估算低阶各向异性弹性参数难度较大,只能用较高对称性的各向异性介质模型对称.
在局部坐标系内,简单常用的各向异性类型可以由各向异性参数直观地进行判断,根据各向异性弹性参数识别介质对称性可以减少参数矩阵非对角线元素非零数.但当全局坐标系与局部坐标系不一致时,哪怕是简单的各向异性类型参数特征也不易识别.特征值分解方法是一种根据各向异性弹性参数求取介质对称轴的方向从而研究其对称性的方法(Cowin and Mehrabadi, 1987; Helbig, 1994; Zheng, 2007; Browaeys and Chevrot, 2004).为了研究主裂缝以外的裂缝系统对于岩石总体各向异性弹性参数影响,本文利用Dellinger(2005)给出的方法求解最接近于单斜各向异性的HTI等效介质,计算由多组垂直裂缝诱导单斜各向异性的等效HTI近似.
各向异性常数C与参考介质常数R的距离如公式(4)所示(Den Boer, 2014; Dellinger, 2005).
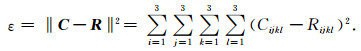
|
(4) |
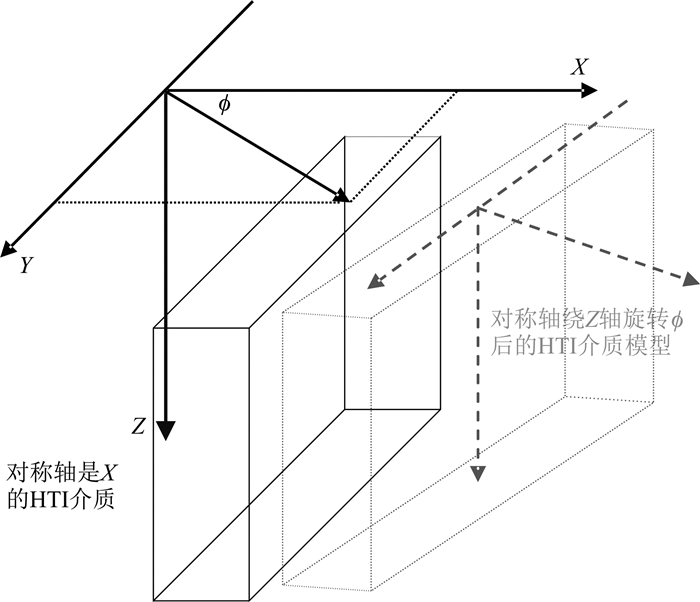
对于具有水平对称轴的HTI各向异性介质,其中裂缝走向与Y轴平行的模型是对称轴为X的HTI介质(如图 2),其HTI弹性参数如公式(5)形式
|
图 2 将HTI介质的对称轴在Z等于常数的平面内进行旋转,搜索最接近于低阶各向异性介质的等效HTI模型 Fig. 2 The equivalent HTI model which closest to the low-order anisotropic media is found by rotating the symmetry axis of the HTI media in the plane of constant Z |

|
(5) |
其中c44=(c33-c23)/2.
通过Voigt表示形式,利用公式(5),公式(4)变为式(6)所示
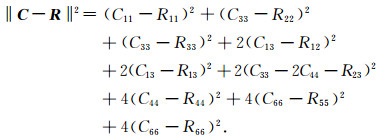
|
(6) |
将(6)式求对C11, C66, C13, C33, C44的偏导数并取零求解得到
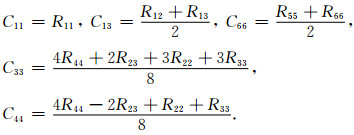
|
(7) |
与Dellinger(2005)等在全半空间内搜索方法不同,本研究仅搜索对称轴在水平平面内,也就是固定对称轴倾角为90°时进行方位角搜索.图 2是搜索等效介质方法示意图,将对称轴在水平面内进行旋转,根据与参考HTI介质空间距离的最小准则求取最接近于单斜各向异性介质的等效HTI介质.
3 多组垂直裂缝模型研究图 3给出了在坐标系内两组垂直裂缝示意图,两组裂缝走向与X轴分别成夹角ϕ1和ϕ2,当介质中具有不同方向多套裂缝时,介质就是多组裂缝.当两组不同强度的裂缝非垂直相交时介质是单斜各向异性,而当夹角成90°时介质退化为正交各向异性介质.

|
图 3 坐标系内两组垂直裂缝示意图,两组垂直裂缝走向与X轴分别成夹角ϕ1和ϕ2 Fig. 3 Sketch of two sets of vertical fractures, the angles between the fractures and X axis are ϕ1and ϕ2, respectively |
这里利用本文第一节所述的线性滑移理论计算等效介质的裂缝弹性常数.对于旋转不变各向异性介质,裂缝法线柔度BN和切向柔度BT是计算中的重要参数.根据Sayers和Kachanov(1995)及Sayers等(2009)等的研究,由杨氏模量E、泊松比ν及硬币形裂缝体半径a可以得到BN和BT.实验(Lubbe et al., 2008)及数值计算表明BN/BT比值在0~2之间;当BN/BT=1时是椭圆各向异性;对于砂岩,裂缝垂向与剪切向柔度相等.这里给出背景介质模型参数VP=6.0 km·s-1,VS=2.6 km·s-1, ρ=2.5 g·cm-3,这样背景介质对应的泊松比是0.38.
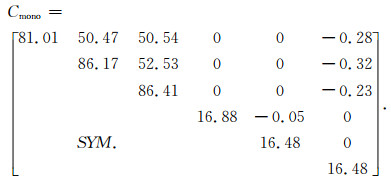
为了研究两组裂缝的总体裂缝密度及介质对称主轴方位并便于与传统方法比较以验证所用计算方法的正确性,这里使用弱各向异性裂缝模型.在上述背景介质中存在两组裂缝,其中裂缝1与X轴成90°,裂缝2与X轴夹角在0到90°之间变化,表 1给出了两组裂缝模型参数.基于空间距离最小准则,给定对称轴倾角90°即对称轴位于水平平面内,只对方位进行搜索寻找最接近于HTI介质的模型.当裂缝2与X轴夹角为70°即两组裂缝夹角20°时,单斜各向异性介质参数如等式(8)所示,相应的等效HTI各向异性参数如表 2所示.
|
|
表 1 两组裂缝参数 Table 1 Media parameters for the two sets of fractures |
|
|
表 2 等效HTI介质各向异性参数 Table 2 Anisotropic parameters for the equivalent HTI media |
|
(8) |
图 4表示了两组裂缝介质等效裂隙面方位角、裂缝密度及拟合误差随着两组裂缝夹角的变化,其中图 4a是裂缝介质等效裂隙面方位随夹角变化,星形是使用本文搜索方法得到的结果,方形是由Sayers(1998)得到的解析结果,直线表示Liu等(1993)的经验结果.由图可见,空间搜索结果与解析结果一致,而Liu等(1993)较早提出的经验公式仅在夹角小于30°时与解析及搜索结果吻合较好.根据HTI介质弹性常数由Bakulin等(2000)可以求解得到介质的裂缝密度,图 4b三角形显示了介质总体裂缝密度随着两组裂缝夹角的变化结果,由图可见Liu等(1993)的经验公式只是简单的两组裂缝密度的和,也就是一个常数,这两者只有在夹角角度很小时(小于20°)才能一致(如图 4b).图 4c表示了弹性常数拟合误差百分比,它展示了搜索得到的HTI介质的弹性参数与单斜介质的弹性参数接近程度,由图可见两组裂缝夹角越大,等效HTI介质偏离单斜各向异性越远.但由于这里所用的各向异性强度较弱,拟合误差百分比较小,两者较为接近.

|
图 4 两组裂缝等效裂隙面方位角及裂缝密度随两者夹角的变化(主裂缝与X轴成90°,横坐标是裂缝2与裂缝1的夹角) (a)介质对称主轴方位角随夹角变化,星形表示搜索结果,方形表示由Sayers(1998)得到的解析结果,蓝线表示(Liu et al., 1993)的经验结果;(b)介质总体裂缝密度随着两组裂缝夹角的变化; (c)弹性常数拟合误差百分比随裂缝夹角变化. Fig. 4 The azimuths and crack densities of the principal stress for the two set cracks vary with the angle between them(The main crack azimuth is 90° to the X-axis and the abscissa is the angle between the crack 1 and the crack 2) (a) Shows that the overall principal stress azimuth varies with angle between the crack 1 and the crack 2, the star represents the search result, the square represents the analytical result from (Sayers, 1998) and the blue line represents the empirical result from Liu et al. (1993); (b) Overall crack density changes with the angle between the two cracks and the percentage of elastic constant fitting is shown in Fig. 4c. |
这里的背景介质和3.1节中一致,在此背景介质中存在两组裂缝,其中裂缝1走向与X轴成90°,裂缝2与X轴夹角30°,多组裂缝模型参数如表 3所示.得到的单斜各向异性介质参数如等式(9)所示.
|
|
表 3 两组裂缝介质参数 Table 3 Media parameters for the two sets of fractures |

|
(9) |
为了显示各向异性介质中地震属性特征,本文利用数值方法精确计算各向异性介质中纵横波相速度以及横波极化方位随倾角和方位角变化,并使用等面积投影方法显示相关属性(Mainprice, 1990; Walker and Wookey, 2012).在下列相关极图中X轴正向向右,Y轴正向向上,Z轴符合右手螺旋坐标系法则.
图 5给出了单斜各向异性介质P波相速度VP(图 5a)、快慢S波相速度VS1(图 5b)和VS2(图 5c)及快S波极化方向随传播方向的变化(图 5d),其中图(5d)中的背景等值线图是VS1和VS2的差值百分比,图上短线条是所在点快横波极化方向.由图 5可见介质等效裂隙面方位,强度较弱的裂缝2的存在对介质总体效应是改变了裂缝的强度和方向.相对于各向同性背景介质,单斜介质弹性参数强度降低,总体裂缝走向相对于主裂缝方向1的90°有所改变,介质主轴走向位于裂缝1与裂缝2之间,更偏向于裂缝1.图 5a、5b和5c中左下角分别给出了计算所得单斜各向异性体中相速度的最大值和最小值及随方位角和倾角变化的最大百分比.

|
图 5 单斜各向异性介质相速度随传播方向变化 (a) P波VP; (b)快S波VS1; (c)慢S波VS2; (d)快S波极化方向,其中图(d)背景等值线图是VS1和VS2差值的百分比,短线条表示所在点快横波极化方向. Fig. 5 Phase velocities and the direction of fast S wave polarization vary with the propagation direction for the monoclinic anisotropic medium (a) P wave VP, (b) fast S wave VS1, (c) slow S wave VS2 and (d) is for fast S wave polarization direction and the contour of background is the difference percent between fast and slow S wave. |
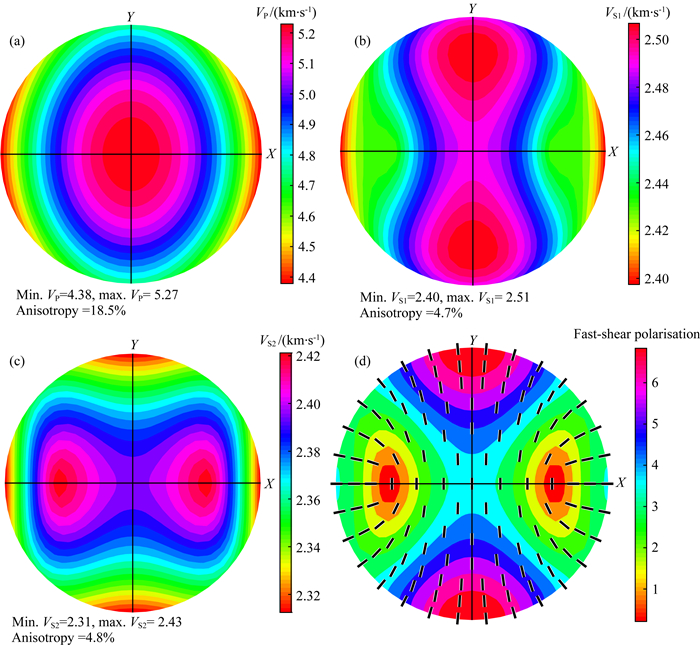
当裂缝2方位角取为零时,也就是裂缝2垂直于裂缝1时,介质是正交各向异性介质.图 6给出了正交各向异性介质中P波相速度VP(图 6a)、快慢S波相速度VS1(图 6b)和VS2(图 6c)及快S波极化方向随传播方向变化(图 6d).
|
图 6 同图 5,但是对应的是正交各向异性介质情况 Fig. 6 The figure are the same as Fig. 5, but corresponding to the case of orthotropic media |
当两组裂缝正交时,介质是正交各向异性,Tsvankin(1997)给出描述正交各向异性介质参数的9个参数表达式.当介质中只有一组垂直裂缝且裂缝的对称轴平行于坐标轴X轴时,各向异性介质的参数ε(1)=0, δ(1)=0, γ(1)=0.表 4是各向异性弹性参数值,其中表 4的第一行给出了当表 1中裂缝2走向与X轴夹角为0时情况,也就是两组裂缝正交时正交各向异性介质的弹性参数值(图 5).表 4的第二行是当各向同性背景介质基础上只有表 1中一组裂缝1时的HTI介质Tsvankin参数.
|
|
表 4 正交各向异性和HTI介质的Tsvankin参数 Table 4 Tsvankin parameters for orthotropic and HTI media |
在计算得到单斜各向异性介质弹性参数(图 5)之后,下一步研究所得到的弹性参数特征.Cowin和Mehrabadi(1987)给出和一个对称平面相垂直矢量的充分必要条件,也就是这个矢量是涨缩弹性张量D(dij=cijkk; i, j, k=1, 2, 3)和Voigt弹性张量V(vik=cijkj; i, j, k=1, 2, 3)的特征矢量的相等量.对于单斜介质,D和V中有一个相同的特征矢量垂直于唯一对称面.这里对于两组垂直裂缝构成的单斜各向异性介质,二次对称轴是两组裂缝相交的交线,对称面是XY平面.
对单斜各向异性介质(表 3及等式(9)),搜索得到的等效HTI介质参数如表 5所示,裂缝对称轴与X轴夹角是165.47°,也就是裂缝方位角是75.47°.与解析方法得到的结果(75°)接近,搜索所得弹性参数与原单斜介质差值正则化后的百分比是5.0%(公式(6)).
|
|
表 5 等效HTI介质各向异性参数 Table 5 Anisotropic parameters for the equivalent HTI media |
在此等效HTI各向异性介质中,P波相速度VP、快慢S波相速度VS1和VS2及快S波极化方向随传播方向变化如图 7所示.

|
图 7 HTI各向异性介质P波速度VP、快慢S波速度VS1和VS2及快S波极化方向随传播方向变化 (a) VP;(b) VS1;(c) VS2;(d)快S波极化方向. Fig. 7 The phase velocities of P wave, the fast and slow S wave, and the direction of fast S wave polarization vary with the propagation direction for the equivalent HTI anisotropic medium (a) VP; (b) VS1; (c) VS2; (d) Fast S wave polarization direction. |
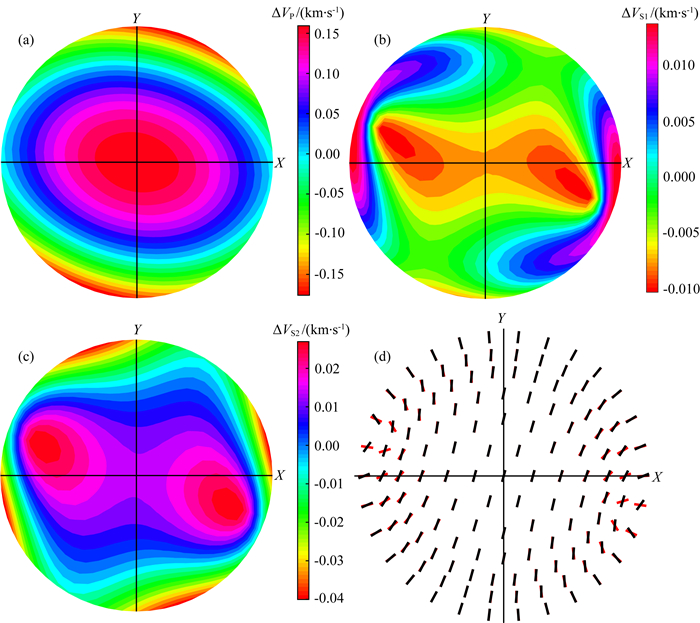
为了研究计算得到的等效HTI介质特征及相对应多组裂缝,这里求取了单斜介质和HTI介质中相速度之差,并叠合显示了两种介质中快S波极化方向.图 8a、8b和8c是单斜各向异性介质相速度与等效HTI介质相速度的差值随传播方向变化,其中图 8a是P波相速度差ΔVP,8b是快剪切波速度差ΔVS1,8c是慢剪切波速度差ΔVS2.图 8d是单斜各向异性及其等效HTI介质剪切快波极化方向叠合显示,其中红色对应的是单斜介质,黑色是等效HTI介质.由图 8可见P和S波相速度差在各个方向上都较小,而极化方向在与等效裂隙面方向垂向方向相关区域差别较大.利用宽方位数据的极化特征在方位上的差异有望研究主裂缝以外其他附加裂缝特征.
|
图 8 单斜各向异性介质相速度与等效HTI介质相速度随传播方向的差异 (a)表示P波相速度差ΔVP; (b)表示快剪切波波速VS1差ΔVS1; (c)慢剪切波波速度差ΔVS2; (d)单斜各向异性及其等效HTI介质快波极化方向叠合显示,其中红色的是单斜介质,黑色是等效HTI介质. Fig. 8 (a), (b) and (c) show the difference between the phase velocities of the monoclinic anisotropic media and the phase velocities of the equivalent HTI media as a function of the propagation direction (a) The velocity difference of the P wave velocity; (b) The difference of fast wave for S wave velocity; (c) The difference of slow wave for S wave velocity; (d) Overlapping display for the polarization directions of the monoclinic anisotropy and its equivalent HTI medium wave, wherein red is a monoclinic medium and black is its equivalent HTI medium. |
在裂缝性介质中常存在明显的属性方位各向异性特征,如地震波的振幅、波阻抗、速度和走时等随观测方位的变化而变化.在研究和生产应用中一般通过椭圆拟合属性随方位角的变化来预测裂缝的发育密度强度、走向和方位等方位各向异性特征(Contreras et al., 1999; Grechka et al., 2000).这里模型计算单斜及其等效的HTI介质各向异性体中反射波P波和快慢S波走时随方位变化,研究两者之间的差别,分析通常地震数据处理解释中以HTI模型逼近单斜介质的精度.
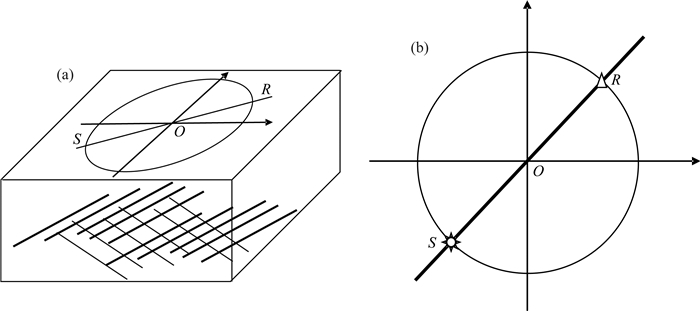
这里给出单层介质模型,层厚度1 km,层内各向异性介质分别是单斜各向异性及其对应的等效HTI弹性参数两种情况(等式(9)和表 5).为了方便得到共中心点道集,使用的观测排列如图 9所示,在沿着中心点为O,半径1 km的圆圈上等方位角放置炮点S,接收点R也位于此圆上并与炮点及圆心在同一条直线上,模拟接收来自第一层底的反射,每次一炮激发一个检波点接收,这样共中心点在圆心位置O.
|
图 9
介质模型及观测系统示意图
炮点沿着以O为圆心的圆等方位间隔布置,接收点也位于此圆上并与炮点及圆心在同一条直线上. (a)表示了裂缝模型及观测系统设置示意图,裂缝模型是单斜各向异性和HTI介质两种情况; (b)观测系统平面显示. Fig. 9 The model and observation configuration The shots locate along the circle centered at O at equal azimuth intervals, and the detection points are located on the circle and the source, the detector and the circle center are on the same straight line. (a) is the sketch of fracture model and observation configuration, and (b) is the plane view of observation configuration. |
根据给定的模型、层内弹性参数及炮检点位置,利用初至各向异性射线追踪计算射线路径,通过优化方法进行两点射线追踪计算P波和快慢S波走时(Gajewski and Pšençik, 1987).图 10显示了射线追踪计算的各向异性介质的走时结果,其中图 10a是两种介质中P波走时对比,图 10b是相应的VS1和VS2波走时对比.根据计算结果,纵波VP走时最大差别是0.306%,快横波VS1走时最大差别是0.105%,慢横波VS2走时的最大差别是0.313%.结果表明,在两种各向异性介质的各个方位上走时差别较小,利用走时差异难以识别较HTI更为复杂的各向异性特征以及主裂缝以外附加裂缝的特征.

|
图 10 利用射线追踪得到的在两种各向异性介质中走时 (a) P波走时对比; (b)快横波VS1和慢横波VS2波走时. Fig. 10 Travel time from ray tracing in two types of anisotropic media (a) Comparison of P wave travel time; (b) VS1 and VS2 of S wave travel time. |
这里计算三组裂缝并分析其特征,图 11是三组裂缝示意图,分别由位于X、Y轴的裂缝和与X正方向夹角为45°的裂缝组成.每组裂缝的强度等同于表 1中裂缝2的强度.使用本文之前用到的同样方法对这三组裂缝计算,得到的单斜各向异性介质参数如等式(10)所示.

|
图 11 三组裂缝,分别位于X、Y轴和与X正方向夹角为45°的裂缝 Fig. 11 Three sets of fractures, among which two located in the X and Y axis and the other one located at an angle of 45 degrees with the positive X-direction cracks |
|
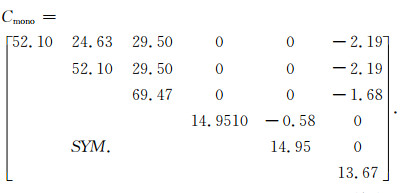
(10) |
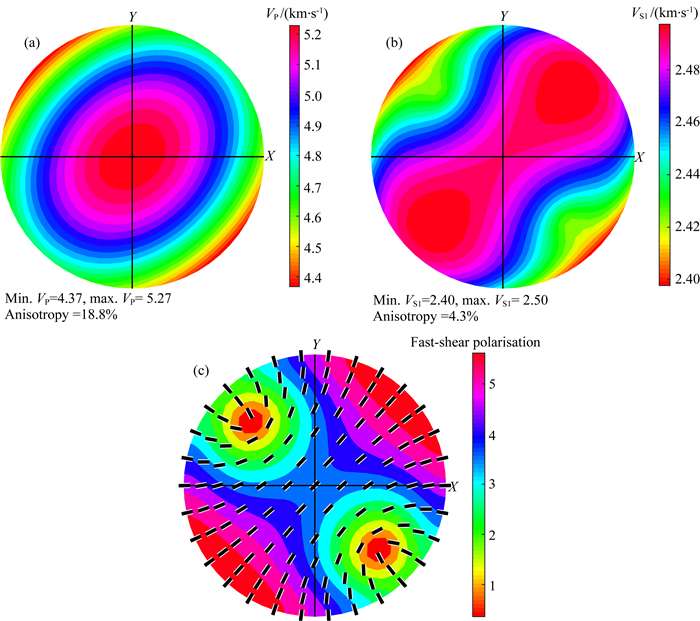
图 12是三组裂缝引起的单斜各向异性介质P波相速度VP(图 12a)、快S波相速度VS1(图 12b)及快S波极化方向随传播方向变化关系(图 12c).其中图 12c的背景等值线图是快慢剪切波VS1和VS2的差值百分比,图上短线条是所在点快横波极化方向.使用最小空间距离准则进行搜索,空间距离上最接近于单斜介质的等效HTI介质裂缝走向与图 11中的裂缝2方位一致.搜索得到的等效HTI介质弹性参数结果如表 6所示,它与原单斜介质弹性参数差值百分比是7.4%(公式(6)).
|
图 12 三组裂缝形成的单斜各向异性介质P波相速度VP、快S波相速度VS1及快S波极化方向随传播方向变化 图(a)VP、图(b)VS1和图(c)快S波极化方向,其中图(c)中背景等值线图是快慢横波VS1和VS2的差值百分比,短线条是所在点快横波极化方向. Fig. 12 The phase velocities of P wave, the fast S wave, and the direction of fast S wave polarization vary with the propagation direction for the monoclinic anisotropic medium from three sets of fractures (a) VP, (b) VS1, and (c) fast S wave polarization direction. For (c) the contour of background is the difference percent between fast and slow S wave. |
|
|
表 6 等效HTI介质各向异性参数 Table 6 Anisotropic parameters for the equivalent HTI media |
图 13显示了上述单斜各向异性介质与等效HTI介质地震属性差异,其中图 13a是单斜各向异性介质与HTI介质纵波VP差值在不同方向上的变化,图 13b是两者快横波VS1差值.图 13c表示了单斜各向异性及其等效HTI介质快波极化方向叠合显示,其中红色的是单斜介质,黑色是等效HTI介质.纵横波在各个方向上差异较小,而快波极化方向在垂直于介质等效裂隙面方向上差别较明显.

|
图 13 单斜各向异性介质与等效HTI介质属性差异 (a)单斜各向异性介质与HTI介质纵波VP差值随方位变化; (b)两者快横波VS1差值; (c)表示了单斜各向异性及其等效HTI介质快波极化方向叠合显示,其中红色的是单斜介质,黑色是等效HTI介质. Fig. 13 The difference of phase velocities of P wave, the fast S wave between monoclinic anisotropy and its equivalent HTI medium, and the direction of fast S wave polarization vary with the propagation direction (a) ΔVP; (b) ΔVS1, and (c) the overlap display of the polarization directions for the monoclinic anisotropy (red) and its equivalent HTI medium (black). |
由于地质作用及地质过程的复杂性,多组裂缝普遍存在于地壳中.为了研究主裂缝以外裂缝对于介质总体特征的影响,本文针对多组裂缝利用线性滑移模型计算得到单斜各向异性介质,通过低阶对称各向异性介质的等效近似得到具有高阶对称性的等效各向异性常数,研究主裂缝以外的裂缝对于地震各向异性特征和地震属性的影响.
本研究首先在弱各向异性情况下,给定了两组垂直裂缝模型,计算等效单斜介质弹性常数,并利用空间最小距离准则搜索得到最接近的HTI介质.并将本文计算方法得到的结果与已有的研究结果进行对比,验证了所用的各向异性参数正演计算方法及其等效HTI求解的正确性.其次对于一般强度各向异性介质,将上述两种的各向异性介质特征进行比较,通过分析P波相速度、快慢横波相速度、快横波极化特征及其差异的空间变化进行各向异性属性研究.另外计算了三组裂缝及其等效HTI介质,讨论了两种各向异性情况下相速度差异以及极化特征.一般来说裂缝单斜介质与其等效HTI介质的相速度在各个方位上各向异性差别很小,而在垂直于等效裂隙面方向上的极化特征差别较大.
在通常存在明显的方位各向异性特征的裂缝性储层中,基于纵横波方位各向异性的预测方法一般通过分析地震属性随方位角/入射角的变化特征,并通过椭圆拟合来预测裂缝的发育密度强度和走向方位等属性.这里给出了一个单层单斜各向异性介质及其等效的HTI介质模型,分别研究了反射P波和快慢S波走时随方位的变化,由结果可以看出在各个方位上走时差别较小,单独依靠走时难以研究多组裂缝特征.
随着现代观测技术的发展以及地震资料多属性的利用,在天然地震与石油地震勘探中越来越多地进行更为复杂的各向异性研究.石油地震资料OVT(Offset Vector Tile, 偏移距矢量片)宽方位地震资料处理是一种保留方位角信息的资料处理方法,包括P波方法和PS波方法(段文胜等, 2013; Vinje et al., 2015).在OVT数据基础上综合利用随方位角变化的时差、振幅及极化特征进行各向异性反演,可望得到具有较低对称性的介质各向异性弹性参数.本文研究结果与方法为反演得到低阶各向异性和精度分析供了方法和工具,并为研究将已有的适合于高阶对称性的各向异性介质计算方法推广到低阶各向异性情况下提供基础.
致谢 感谢郑需要老师在地震各向异性理论方面的指导,特别感谢两位匿名评审专家的宝贵修改意见.
Arts R J, Helbig K, Rasolofosaon P N J. 1991. General anisotropic elastic tensor in rocks, approximation, invariants, and particular directions.//61st Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1534-1537.
|
Bakulin A V, Grechka V, Tsvankin I. 2000. Estimation of fracture parameters from reflection seismic data-Part :HTI models due to a single fracture set. Geophysics, 65(6): 1788-1802. DOI:10.1190/1.1444863 |
Browaeys J T, Chevrot S. 2004. Decomposition of the elastic tensor and geophysical applications. Geophysical Journal International, 159(2): 667-678. DOI:10.1111/gji.2004.159.issue-2 |
Contreras P, Grechka V, Tsvankin I. 1999. Moveout inversion of P-wave data for horizontal transverse isotropy. Geophysics, 64(4): 1219-1229. DOI:10.1190/1.1444628 |
Cowin S C, Mehrabadi M M. 1987. On the identification of material symmetry for anisotropic elastic materials. The Quarterly Journal of Mechanics and Applied Mathematics, 40(4): 451-476. DOI:10.1093/qjmam/40.4.451 |
Dellinger J. 2005. Computing the optimal transversely isotropic approximation of a general elastic tensor. Geophysics, 70(5): I1-I10. DOI:10.1190/1.2073890 |
Den Boer L D. 2014. An efficient algorithm for computing nearest medium approximations to an arbitrary anisotropic stiffness tensor. Geophysics, 79(3): C81-C90. DOI:10.1190/geo2013-0388.1 |
Duan W S, Li F, Wang Y C, et al. 2013. Offset vector tile for wide azimuth seismic processing. Oil Geophysical Prospecting (in Chinese), 48(2): 206-213. |
Far M E, Sayers C M, Thomsen L, et al. 2013. Seismic characterization of naturally fractured reservoirs using amplitude versus offset and azimuth analysis. Geophysical Prospecting, 61(2): 427-447. DOI:10.1111/gpr.2013.61.issue-2 |
Far M E, Hardage B, Wagner D. 2014. Fracture parameter inversion for Marcellus shale. Geophysics, 79(3): C55-C63. DOI:10.1190/geo2013-0236.1 |
Fedorov F I. 1968. Theory of Elastic Waves in Crystals. New York: Springer.
|
Gajewski D, Pšençik I. 1987. Computation of high-frequency seismic wavefields in 3-D laterally inhomogeneous anisotropic media. Geophysical Journal International, 91(2): 383-411. DOI:10.1111/j.1365-246X.1987.tb05234.x |
Gao Y, Wu J. 2008. Compressive stress field in the crust deduced from shear-wave anisotropy:an example in capital area of China. Chinese Science Bulletin, 53(18): 2840-2848. |
Grechka V, Contreras P, Tsvankin I. 2000. Inversion of normal moveout for monoclinic media. Geophysical Prospecting, 48(3): 577-602. DOI:10.1046/j.1365-2478.2000.00200.x |
Hao C T, Yao C. 2014. Tele-seismic PS-wave splitting from the basement in the Capital area of China. Chinese Journal of Geophysics (in Chinese), 57(8): 2573-2583. DOI:10.6038/cjg20140817 |
Helbig K. 1994. Foundations of Anisotropy for Exploration Seismics. Oxford: Elsevier Science Ltd.
|
Hudson J A. 1981. Overall properties of a cracked solid. Mathematical Proceedings of the Cambridge Philosophical Society, 88(2): 371-384. |
Hudson J A. 1986. A higher order approximation to the wave propagation constants for a cracked solid. Geophysical Journal International, 87(1): 265-274. DOI:10.1111/gji.1986.87.issue-1 |
Jenner E. 2011. Combining VTI and HTI anisotropy in prestack time migration:Workflow and data examples. The Leading Edge, 30(7): 732-739. DOI:10.1190/1.3609087 |
Li L, Hao C T. 2012. Feasibility to neglect the tilt of the symmetry axis of a TTI medium. Chinese Journal of Geophysics (in Chinese), 55(6): 2004-2013. DOI:10.6038/j.issn.0001-5733.2012.06.022 |
Liu E, Crampin S, Queen J H, et al. 1993. Behaviour of shear waves in rocks with two sets of parallel cracks. Geophysical Journal International, 113(2): 509-517. DOI:10.1111/gji.1993.113.issue-2 |
Liu E R, Hudson J A, Pointer T. 2000. Equivalent medium representation of fractured rock. Journal of Geophysical Research:Solid Earth, 105(B2): 2981-3000. DOI:10.1029/1999JB900306 |
Liu E R, Yue J H, Pan D M. 2006. Frequency-dependent anisotropy:Effects of multiple fracture sets on shear-wave polarisations. Chinese Journal of Geophysics (in Chinese), 49(5): 1401-1409. DOI:10.1002/cjg2.v49.5 |
Lubbe R, Sothcott J, Worthington M H, et al. 2008. Laboratory estimates of normal and shear fracture compliance. Geophysical Prospecting, 56(2): 239-247. DOI:10.1111/gpr.2008.56.issue-2 |
Mainprice D. 1990. A FORTRAN program to calculate seismic anisotropy from the lattice preferred orientation of minerals. Computers & Geosciences, 16(3): 385-393. |
Sayers C M, Kachanov M. 1995. Microcrack-induced elastic wave anisotropy of brittle rocks. Journal of Geophysical Research:Solid Earth, 100(B3): 4149-4156. DOI:10.1029/94JB03134 |
Sayers C M. 1998. Misalignment of the orientation of fractures and the principal axes for P and S waves in rocks containing multiple non-orthogonal fracture sets. Geophysical Journal International, 133(2): 459-466. DOI:10.1046/j.1365-246X.1998.00507.x |
Sayers C M, Taleghani A D, Adachi J. 2009. The effect of mineralization on the ratio of normal to tangential compliance of fractures. Geophysical Prospecting, 57(3): 439-446. DOI:10.1111/gpr.2009.57.issue-3 |
Schoenberg M, Sayers C M. 1995. Seismic anisotropy of fractured rock. Geophysics, 60(1): 204-211. DOI:10.1190/1.1443748 |
Song L T, Wang Y, Liu Z H, et al. 2015. Elastic anisotropy characteristics of tight sands under different confining pressures and fluid saturation states. Chinese Journal of Geophysics (in Chinese), 58(9): 3401-3411. DOI:10.6038/cjg20150932 |
Tsvankin I. 1997. Anisotropic parameters and P-wave velocity for orthorhombic media. Geophysics, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
Vinje V, Zhao P, Gaiser J. 2015. Offset vector tile gather extension and weighting to reduce footprint in dual-datum and converted-wave migration.//85th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1534-1537.
|
Walker A M, Wookey J. 2012. MSAT-A new toolkit for the analysis of elastic and seismic anisotropy. Computers & Geosciences, 49: 81-90. |
Wang Y, Shi Y, Yang D Y. 2008. Application of the weakness ratio in fracture medium fluid detection. Chinese Journal of Geophysics (in Chinese), 51(4): 1152-1155. |
Wang Y, Liu Y Y, Zhang M G. 2017. Seismic Equivalent Medium Theory for Fractured Anisotropy. Beijing: Science Press.
|
Winterstein D F. 1990. Velocity anisotropy terminology for geophysicists. Geophysics, 55(8): 1070-1088. DOI:10.1190/1.1442919 |
Zhang J L, Wang Y, Lu J. 2013. A new algorithm for frequency-dependent shear-wave splitting parameters extraction. Journal of Geophysics and Engineering, 10(5): 055005. DOI:10.1088/1742-2132/10/5/055005 |
Zheng X Y. 2007. Identification of symmetry planes in weakly anisotropic elastic media. Geophysical Journal International, 170(1): 468-478. DOI:10.1111/gji.2007.170.issue-1 |
段文胜, 李飞, 王彦春, 等. 2013. 面向宽方位地震处理的炮检距向量片技术. 石油地球物理勘探, 48(2): 206-213. |
高原, 吴晶. 2008. 利用剪切波各向异性推断地壳主压应力场:以首都圈地区为例. 科学通报, 53(23): 2933-2939. DOI:10.3321/j.issn:0023-074X.2008.23.015 |
郝重涛, 姚陈. 2014. 首都圈地区远震基底波PS波分裂研究. 地球物理学报, 57(8): 2573-2583. DOI:10.6038/cjg20140817 |
李磊, 郝重涛. 2012. 忽略TTI介质对称轴倾角的可行性. 地球物理学报, 55(6): 2004-2013. DOI:10.6038/j.issn.0001-5733.2012.06.022 |
刘恩儒, 岳建华, 潘冬明. 2006. 地震各向异性——多组裂隙对横波偏振的影响. 地球物理学报, 49(5): 1401-1409. DOI:10.3321/j.issn:0001-5733.2006.05.020 |
宋连腾, 王赟, 刘忠华, 等. 2015. 不同围压和流体饱和状态下致密砂岩弹性各向异性特征. 地球物理学报, 58(9): 3401-3411. DOI:10.6038/cjg20150932 |
王赟, 石瑛, 杨德义. 2008. 弱度比在裂隙含流体检测中的应用. 地球物理学报, 51(4): 1152-1155. DOI:10.3321/j.issn:0001-5733.2008.04.024 |
王赟, 刘媛媛, 张美根. 2017. 裂缝各向异性地震等效介质理论. 北京: 科学出版社.
|
 2019, Vol. 62
2019, Vol. 62


