2. 南京大学地球科学与工程学院, 南京 210046;
3. Department of Geology, University of Illinois, Urbana, IL 61801;
4. 武汉大学测绘学院, 武汉 430079;
5. 中国地震局地震预测研究所, 北京 100036;
6. 福建省地震局, 福州 350003
2. School of Earth Sciences and Engineering, Nanjing University, Nanjing 210046, China;
3. Department of Geology, University of Illinois, Urbana, IL 61801, USA;
4. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
5. Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China;
6. Earthquake Administration of Fujian Province, Fuzhou 350003, China
准确的地震定位是开展地震学研究的基础,高精度定位的地震时空分布为研究区域构造活动性、深部介质的物性、地震成像,以及研究孕震构造和地震孕育发生过程都十分重要(Li et al., 2018).高精度定位地震需要准确的定位技术及其误差的可信度分析来支撑,定位的准确性及其不确定性主要依赖以下三个因素:地震到时的测量误差、计算走时所用的模型误差和地震定位的非线性问题,定位反演中需要考虑到非线性问题(Pavlis, 1986), 三个因素中由速度模型所引起的误差影响最大.自从开始进行定位研究,研究人员就在为改进速度模型而努力.标准的常规定位方法使用的是一维速度模型,如HYPO71(Lee and Lahr, 1975)、Hypoellipse(Lahr,1999)、Hypo2000(Klein,2002)、Hyposat(Schweitzer, 2001)等,其中福建台网主要使用Hypo2000和Hyposat两种相互验证的综合定位方法.
早期传统利用天然地震获取一维速度模型的方法主要有Herglotz-Wiechert方法、Gutenberg反演方法、τ(p)方法等(Cai et al., 2015),这些方法主要是利用台站走时资料来反演速度结构,前提是震源位置较为准确.现在有很多种方法能同时反演速度结构和震源参数(Kissling et al., 1994),但是同时反演震源位置和速度结构取决于地震的定位误差和速度的扰动足够小时才能使包括震源和速度未知数的联合方程是线性的,否则定位的误差将会直接影响速度结构的准确性,从而造成速度结构的不准确,这是进行震源和速度同时联合反演的前提条件.速度模型误差给定位精度带来最大的影响是来自于近震,主要是来自地震的射线经过高度横向非均一性的地壳和上地幔.
准确的速度模型是诸如地震定位、大尺度构造应力场研究、地球动力学等研究的基础性资料,各种三维地震成像结构也依赖于研究地区较好的一维速度结构模型.福建地区一维速度模型的研究较为丰富,通过分析深地震测深剖面,廖其林等(1988)利用走时反演获得福建沿海一条二维速度结构剖面,同时构建了在地壳内划分出三层结构的简单一维模型.陈祥熊等(2005)通过对比人工爆破剖面模型和华南模型并结合福建地质构造分布情况,同样提出了一种三层结构的一维速度模型.依靠最新的密集爆破数据,使用不同的拾取震相(如Pg, Pc, Pm, Pn),Cai等(2015)反演构建了最新的福建地区一维速度模型,并讨论了一维速度模型构建过程和该模型与其他一维速度模型的残差比较,但没有讨论将该模型运用在地震定位.目前福建地区日常定位使用的一维速度模型是华南模型(范玉兰等,1990),该模型具有分层简单,能追踪到多种震相等特点,但该模型是建立在整个华南爆破和天然地震资料的基础上,对于具体地区地震定位能否满足其定位需求,还需要更深入的研究.
本文利用福建一系列人工爆破在固定地震台站记录的独特波形数据,拾取初至和续至波到时,利用初至和续至波走时联合反演方法,构建福建地区一维速度模型,并对几种模型定位进行评价.由于人工爆破地震数据具有准确的震源位置与深度信息,对构建一维速度模型以及对不同一维速度模型在定位中的分析比较研究具有独特优势.我们认为本研究新构建的福建地区一维P波速度模型(称为福建爆破模型, 英文缩写FJEM)对现有模型有一定的改进,建议地震部门日常地震定位使用,而且,由于本地区地壳结构相对简单,本模型也可为福建及临近省份有关工作提供参考.
1 数据与方法本文使用福建18个爆破地震(Cai et al., 2015)在区域地震台网记录到的地震波形资料(图 1).所有爆破地震是在2010年8月到2012年8月期间进行的(蔡辉腾等,2016),具体时间及位置信息见表 1.这些波形数据中仅使用了垂直分量数据,手工拾取出初至P波(first arrival)和续至P波(secondary arrival);其中初至P波震相十分清晰,拾取较为容易.对于续至P波的拾取则采用波形相关的方法来拾取走时,主要分为两步,首先将离震源较近、震相清晰的初至Pg波截取下来并将要拾取的续至波大概位置标出(图 2a, 2c);然后根据手工拾取的续至P波截取下来与近距离的初至Pg波形进行互相关(图 2b, 2d),得到了二者的延迟走时,再加上该初至P波走时得到续至波走时.总共拾取出800条有效P波走时数据(图 2e),其中Pg震相526条,分布在5~340 km的范围内;Pn震相274条,主要分布在140~350 km的范围内;续至波震相169条,分布在150 km到340 km的范围内.各个爆破地震被记录到的台站数目在27~84之间,平均单个爆破地震被55个台站记录到.从记录到的台站数目可以看出,这些爆破地震具有较强的能量,能被较远的台站记录到;所有这些拾取的走时,最小的震中距为5 km,最远为近400 km(图 2e, 2f).此外, 考虑到同时建立P波与S波速度模型对地震源深度有较好约束,我们对爆破事件的S波震相进行了检测.但是,尽管S波震相有的时候发育较好,但因受P波尾波等噪声的影响,拾取初至非常困难.而且,不同台站的记录中S波波形一致性较差,无法准确获取互相关时差.因此,文中没有开展S波走时测量和速度模型研究.
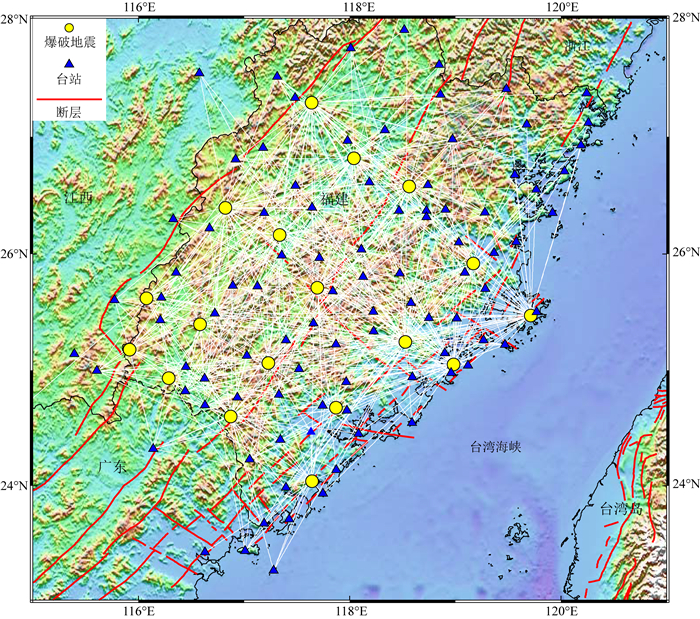
|
图 1 福建地区爆破地震、台站及断层分布 黄实心圆代表爆破点,蓝色三角代表台站,红线代表断层. Fig. 1 Locations of explosions, regional seismic-network stations and faults in Fujian area The yellow circles show explosions, the blue triangles show stations, and the red lines show faults. |
|
|
表 1 使用的爆破地震 Table 1 Explosions used in this study |
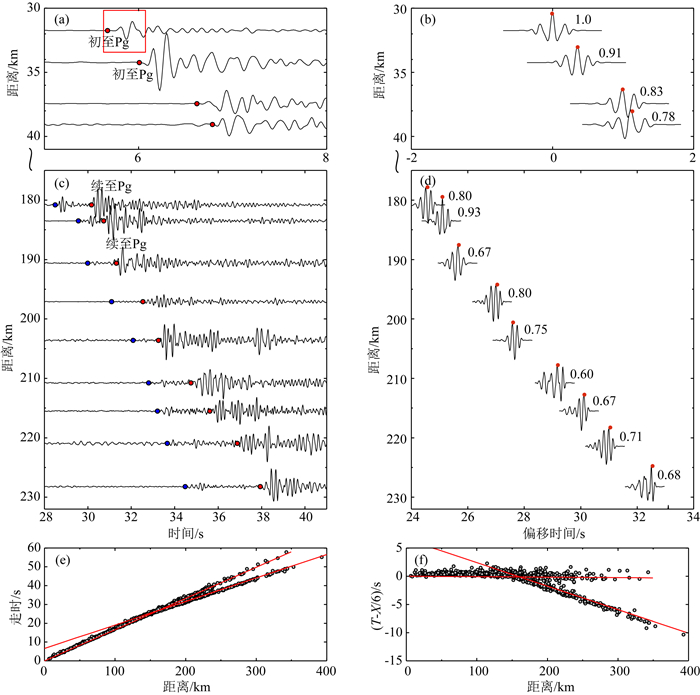
|
图 2 运用手工和波形相关方法拾取典型爆破地震记录的震相和走时分布 (a)和(c)中红圈代表Pg震相,蓝圈代表Pn震相.(a)和(b)为小距离下地震记录及其与典型Pg波形互相关波形,红色方框为典型Pg波形,右侧数字为互相关系数值;(c)和(d)为远距离下的地震记录及其与典型Pg震相的互相关波形,右侧数字为互相关系数值;(e)和(f)分别为所有爆破震相的时距曲线与折合走时曲线,其中红色曲线为初始模型理论走时. Fig. 2 Typical examples of an explosion Pg and Pn travel-time picks from vertical-component seismograms of Fujian seismic network by handpicked and waveform correlation method The red circle represents Pg arrival and the blue circle represents Pn arrival in (a) and (c). (a) and (b) panels show the seismograms and cross-correlation results at small distances; (c) and (d) panels show the seismograms and cross-correlation results in large distances; (e) panel shows travel-time distance plot from all picks; (f) panel shows the reduced time plot, the red lines in (e) and (f) show theoretical traveltimes by initial model for Pg and Pn phases. |
本文采用Xu和Song(2010)的联合Pg/Pn反演方法,该方法可用于初至Pg波、续至Pg波及Pn波走时多次迭代联合反演地壳及上地幔顶部三维速度结构,本文只反演一维地壳及上地幔顶部的速度模型.该方法对地壳Pg波和莫霍面Pn波走时计算采用不同方法,前者追踪Pg波采用了直接利用球面坐标系下伪弯曲射线追踪方法(Koketsu and Sekine, 1998),追踪Pg波时不考虑Moho和地幔而把地壳结构向深部延深, 这样续至波可以同样追踪;追踪Pn波时对走时进行分段计算;然后再判断是哪个震相(初Pg、续至Pg、还是Pn)(详见Xu and Song, 2010).
考虑到爆破地震位置已知,本文对该方法进行了适当修改,对Pg和Pn走时计算均包括代表台站下方速度结构非均一性的台站校正项,但都不考虑事件延迟项.在走时层析成像中,台站校正项常常代表由台站高程,台站下方浅层复杂速度结构引起的走时异常(Lin et al., 2011).
对于地壳Pg波射线,从第j个震源到第k个台站的走时残差表示为方程:
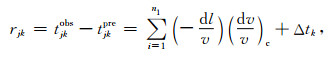
|
(1) |
其中tjkobs是观测走时,tprejk是理论走时,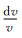
对于Pn波射线,走时可以分为三部分:从震源到莫霍面的走时、沿莫霍面滑行的走时以及莫霍面到台站的走时.
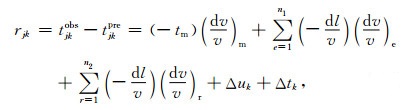
|
(2) |
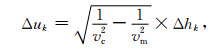
|
(3) |
Δtk与方程(1)一样代表的是台站校正项;Δhk代表莫霍面深度的变化量,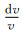
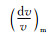
初始模型选用的是拟合小距离(100 km内)Pg和大距离(250 km外)Pn波的时距曲线得到的粗略模型,包括初始地壳平均速度5.79 km·s-1、上地幔顶部速度8.18 km·s-1和Moho深度28.8 km.地壳速度为连续模型,由节点组成,节点间为线性差值.考虑到福建区域地表普遍存在约3 km厚度的低速层(陈祥熊等,2005;蔡辉腾等,2014),因此设置了地表和3 km的节点,以便更加接近实际情况,其它节点以约5 km为间隔分布(图 4).在进行走时计算时,采用了一种多次迭代识别初至、续至Pg和Pn震相的方法(Xu and Song, 2010),可以区分不同震相并去除拾取错误的震相.福建地区的莫霍面深度在35 km范围内,因此设置初始距离为0.8°,当震中距小于该值时,只考虑方程(1)的计算(属于初至Pg波).由于爆破走时的震中距小于5°,因此当震中距大于0.8°时,分别利用方程(1)和方程(2)计算走时,当单个走时残差大于2 s时,不考虑该走时,另外Pg和Pn的走时残差的差值如果小于0.5 s,也不考虑该走时;最后根据各自走时残差的大小来确定该走时属于哪种震相(初至Pg、续至Pg或Pn).
反演方法采用带阻尼最小平方法(LSQR)(Paige and Saunders, 1982a;1982b),对方程(1)和方程(2)进行联合求解,使方程(4)达到最小.由于联合反演中各参数的量纲不同,因此将方程(1)和(2)中系数矩阵A进行列范数下归一化预处理,然后利用LSQR进行参数反演.另外,为了克服方程求解的不稳定性,加入了阻尼因子λ和平滑因子μ;经过多次试算,最终选取λ值为0.8,μ值为10.
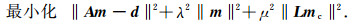
|
(4) |
式(4)中,第一项是方程的最小平方残差,第二项代表是阻尼项,用于控制整个解的稳定性,第三项代表的是地壳速度平滑项,用于控制相邻节点解的平滑性.
2 结果 2.1 构建一维速度模型及与其他模型比较从初始模型开始反演,之后对反演得到的数据残差进行筛选,剔除所有走时残差的1.5倍标准差外的走时数据,根据筛选后的数据再重新进行反演.反演中每次迭代都对速度和莫霍面深度进行了更新,反演一共迭代了6次得到最终反演模型,即本文的福建爆破模型(FJEM模型).最终射线数目为600条.表 2给出模型的深度和速度及莫霍面深度.
|
|
表 2 福建爆破模型(FJEM)参数及误差 Table 2 Parameters of Fujian explosion model (FJEM) and their errors |
|
图 3 爆破数据反演前后残差数据分布 (a)和(c)显示反演前后残差与震中距的分布情况;(b)反演前后数据残差直方图分布(rms为残差均方根值);(d)反演后Pg和Pn震相与距离的分布. Fig. 3 Distributions of traveltime residuals before and after the inversion from explosion data (a) and (c) Maps show the residual times versus distance after initial iteration and last iteration, respectively; (b) Histogram showing the ray numbers versus residual times distributions before and after joint inversion; (d) Map show a very clear Pg and Pn phase from travel time versus distance after inversion. |
走时残差的均方根从反演前0.42 s减小为反演后0.22 s(图 3b, 3c),方差减小幅度达到了72%.这个大的方差改进在很大程度上反映初始模型很粗糙,如从小距离得到的地壳速度代表的是上地壳,对大距离和续至Pg有系统的偏差(图 2e, 2f).但也反映我们的迭代收敛过程不受差的初始模型的影响.由于所用方法(Xu and Song, 2010)对震相区分的精细考虑,反演后初至Pg、Pn、续至Pg震相明显区分开来(图 3d).
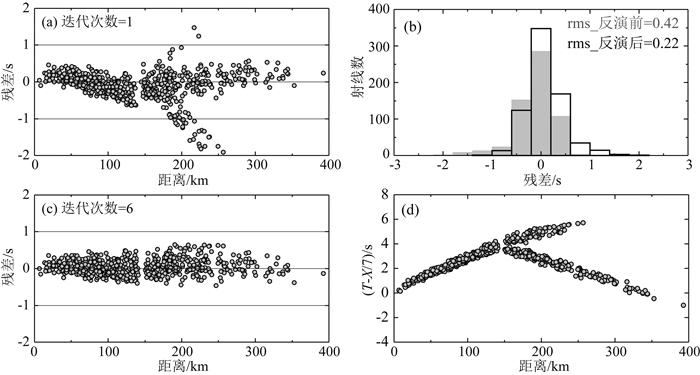
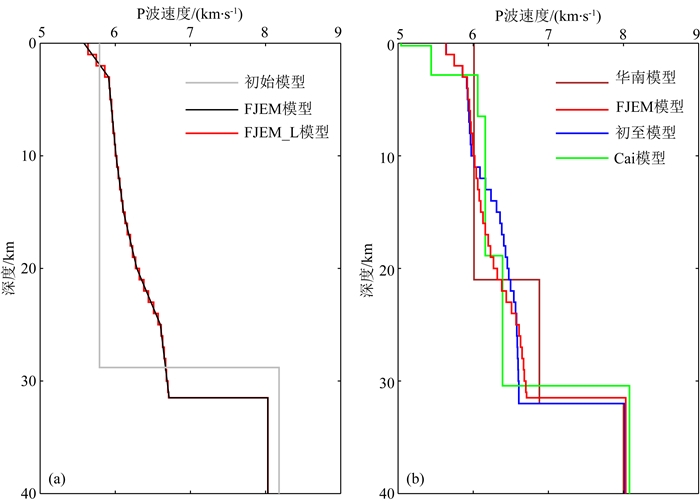
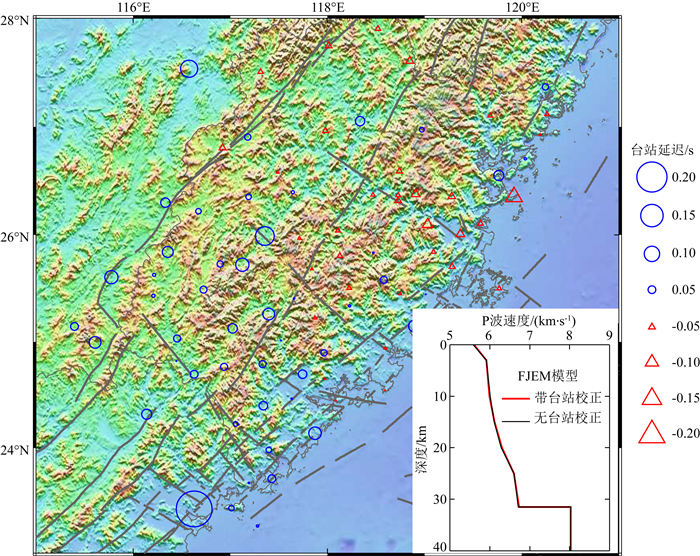
图 4比较FJEM模型和其他模型.FJEM模型上地幔顶部速度为8.03 km·s-1,地壳厚度为31.5 km,地壳速度在5.58~6.72 km·s-1之间变化(图 4a).第一层的速度为5.58 km·s-1显示了与其他研究相一致的低速特征(蔡辉腾等,2014).在0~20 km范围的上地壳速度在5.58~6.29 km·s-1之间,显示上地壳的速度较低.在25 km以下,下地壳的速度在6.6~6.7 km·s-1之间,明显高于上地壳的速度值,整个地壳有较强梯度.FJEM模型的平均速度跟华南模型地壳平均速度(6.3 km·s-1)相近(低0.07 km·s-1),但华南模型为两层均匀模型,而FJEM模型整个地壳有较强梯度.莫霍面的深度为31.5 km,与其他模型类似,也与黄晖等(2010)用接收函数得到莫霍面深度(28~33 km)相接近.本次反演得到的台站校正范围在-0.1 s到0.19 s之间(图 5),台站校正项分布显示福建东北区域以负值为主,而南部则以正值为主.另外,为了与华南模型等其他模型做比较,利用相同爆破地震数据也构建了不考虑台站校正项的一维速度模型,结果显示二者差异很小(图 5).
|
图 4 几种一维速度模型比较 (a)初始模型(灰线)和所有爆破走时获得的福建爆破模型(FJEM模型),连续一维速度模型(黑线)和转换后的层状速度模型(红线);(b)表示4种一维速度模型,分别为利用爆破初至数据(蓝线)和所有爆破数据(FJEM模型, 红线)构建的一维速度模型,由爆破剖面获取的速度模型(绿线,来自Cai et al., 2015)和华南模型(棕色线). Fig. 4 Comparison of various 1-D P-wave velocity models (a) Panel shows initial model and inversion model (FJEM model) from joint inversion with explosion dataset, gray line shows initial model, black line is continued model (FJEM model) and red line is layered model (FJEM_L model) transformed from continued model; (b) Panel shows four different 1-D models, FJEM model with all explosion data (red line), inversion model with first arrivals of explosion data (blue line), Cai model (green line, from Cai et al., 2015), South China model (brown line). |
|
图 5 利用爆破数据反演得到的台站校正项 蓝圈代表正的校正项,红三角代表负的校正项,右下角是带台站校正和无台站校正FJEM模型对比. Fig. 5 Station corrections from the joint inversion of the explosion data Blue circles represent positive station correction times, while red triangles represent negative station correction times. Right-lower panel shows FJEM model with station corrections (red line) and without station corrections (black line). |
使用的反演方法(Xu and Song, 2010)考虑了续至Pg波的作用,能增加中下地壳的有效覆盖,进而有效约束整个模型的构建.实际上,许多近震层析成像方法没有考虑引入续至波,只是利用了初至波走时进行速度结构反演(Kissling, 1988, Evans et al., 1994).为了研究续至Pg波在反演中的作用,仅利用初至Pg波,采用相同迭代反演方法构建了基于初至Pg波走时的一维速度模型.从二者速度模型的比较来看,在0~10 km的范围内,速度变化很小;而在10~25 km的中下地壳范围具有明显的不同(图 4b),利用初至波走时反演的速度要比所有P波走时反演的速度值偏高,显示续至Pg波走时在反演中发挥了一定作用,可以通过增加中下地壳结构的射线约束中下地壳的速度结构.Cai模型为沿各个爆破地震剖面获取的平均一维速度模型(Cai et al., 2015),与FJEM模型相比,3 km以内的浅部速度值较小,在15 km以内速度值略微增加,但是中下地壳速度值则明显偏低,而上地幔顶部速度值达到8.08 km·s-1,是这几种模型中最高的(图 4b).
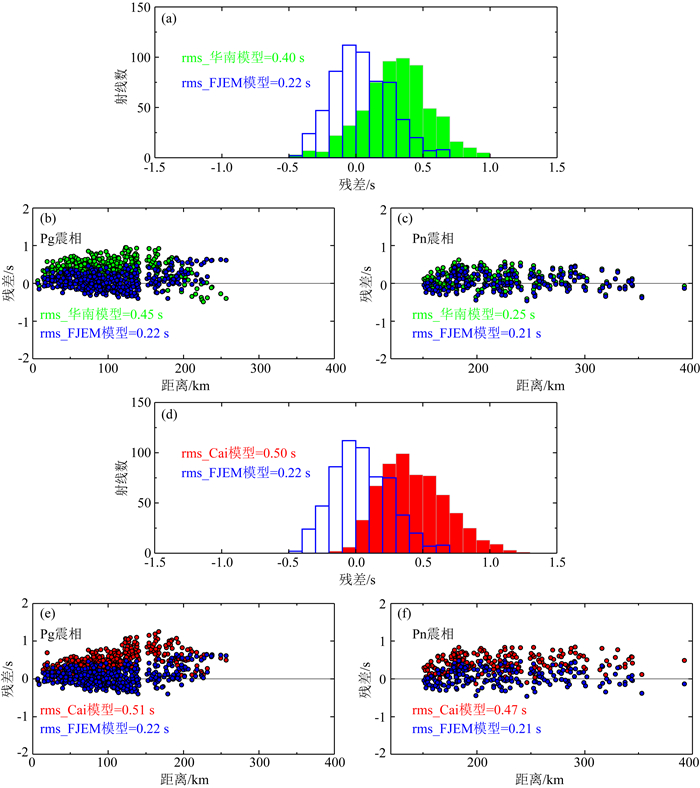
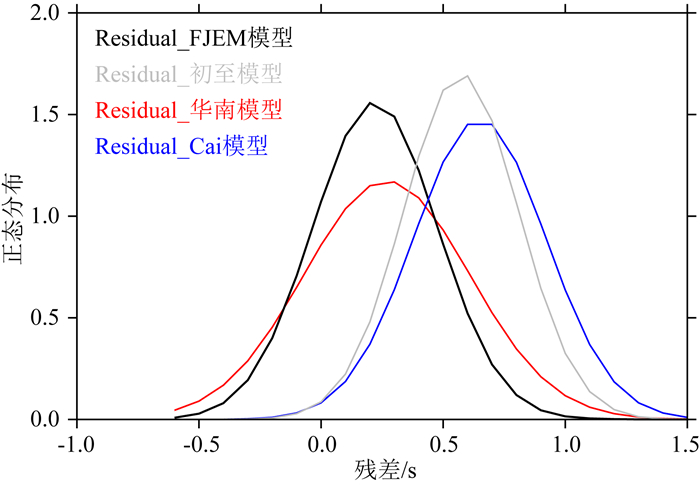
与此同时,利用手工拾取具有较高精度的爆破地震走时,可以检验不同模型的残差分布情况.从图 6中看出,FJEM模型、华南模型、Cai模型的残差均方根依次增加,分别为0.22 s,0.40 s,0.50 s,并且Cai模型和华南模型的残差都系统性偏向正残差值, 显示本次FJEM模型具有更高的走时计算精度.基于这些模型中下地壳速度结构差别较大,因此比较了几种模型下的续至Pg的残差分布情况(图 7).Cai模型和初至波模型残差明显系统性偏向正值,同时华南模型在不同震中距下的残差也大于FJEM模型,说明本文基于爆破地震到时的FJEM模型在一定程度上对地壳各个深度的约束要比以前模型更好.
|
图 6 爆破拾取走时在不同模型下残差统计分布 (a)和(d)分别为FJEM模型与华南模型、Cai模型残差直方图分布,显示华南模型和Cai模型以正残差为主;(b), (c), (e), (f)为不同模型下Pg和Pn震相残差分布比较. Fig. 6 Statistics of traveltime residuals of the explosions relative to different models (a) and (d) show residual time histogram distributions for South China model, FJEM model, Cai model, respectively; (b) and (c) present residuals distribution of Pg and Pn phases between South China model and FJEM model; (e) and (f) present residuals distribution of Pg and Pn phases between FJEM model and Cai model. |
|
图 7 四种模型下的续至P波残差分布 黑线为FJEM模型,灰线为初至模型,红线为华南模型,蓝线为Cai模型. Fig. 7 Distributions of secondary P-wave residuals from four models Black line represents FJEM model, gray line represents first arrival model, red line represents South China model, blue line represents Cai model. |
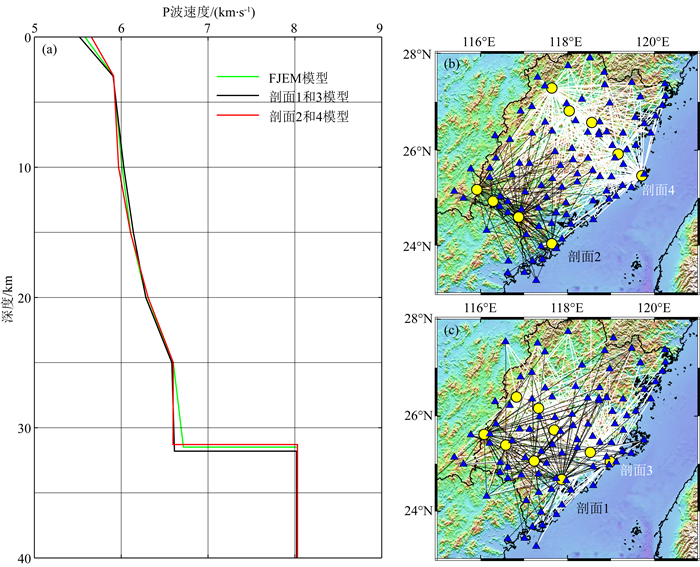
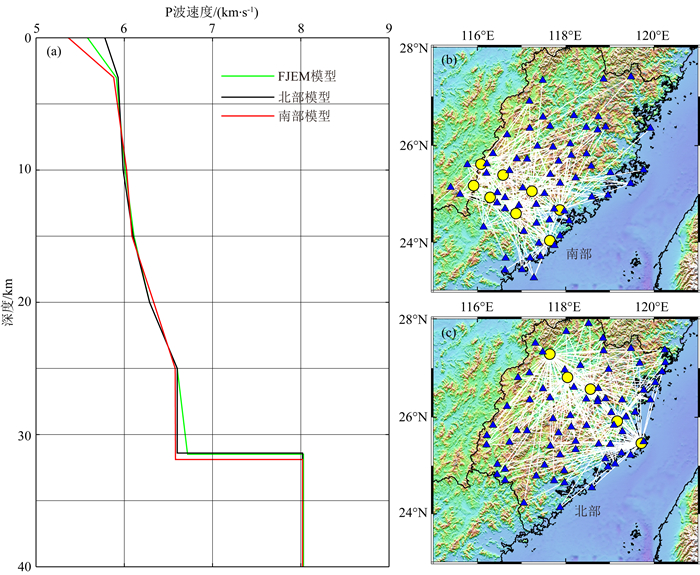
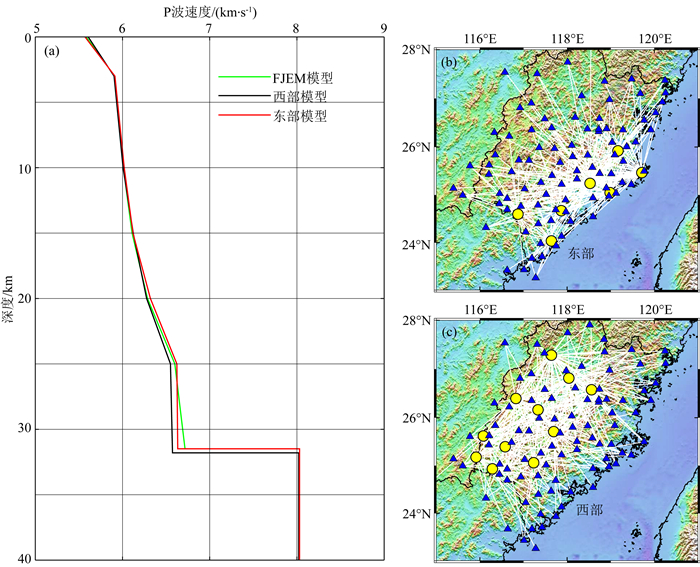
本次爆破地震在福建地区分布较广且相对均匀(图 1),对这些拾取的爆破走时数据进行不同位置组合并反演速度模型可以为研究福建不同区域的速度结构提供参考.利用剖面1和3的爆破地震走时和剖面2和4的爆破地震走时分别构建各自的一维速度模型,其中剖面1和3的走时数目为354,剖面2和4的走时数目为328个,二者数目相近.如图 8a所示,反演的两种模型差别较小,与所有数据反演的模型结果较为接近,体现了当数据覆盖福建大部分地区时,所反演的速度结构是相似的,这在一定程度上说明了反演结果的稳定性.为了检验福建不同区域的速度结构,基于射线数量与分布情况,分别组合不同位置爆破地震构建了福建南北部和东西部的一维速度结构模型.图 9a显示福建地区0~3 km的浅表层南北部速度差异明显,但深部地壳速度变化较小,北部地壳厚度稍薄于南部地壳厚度.图 10a显示福建地区东部沿海的一维速度结构在深度大于20 km下地壳部分稍高于福建西部的速度结构,而在中上地壳差异性较小.以上不同爆破地震走时数据反演的一维速度结构变化较小,显示福建地区存在相对简单的速度结构.虽然这种组合不同爆破地震反演没有考虑台站分布,但从图 9和图 10中射线分布来看,台站分布对反演结果影响较小.
|
图 8 不同剖面组合和所有爆破数据反演的速度模型 (a)中绿线代表所有爆破数据FJEM模型,黑线代表剖面1和3组合的爆破数据反演模型,红线代表剖面2和4组合的爆破数据反演模型;(b)和(c)为组合数据的射线分布. Fig. 8 Velocity models inverted from different explosion profiles Green line represents FJEM model, black line shows result from profile 1 and 3, red line shows result from profile 2 and 4. |
|
图 9 福建南北部剖面组合和所有爆破数据反演得到的速度模型 (a)中绿线代表所有爆破数据FJEM模型,黑线代表北部的爆破数据反演模型,红线代表南部的爆破数据反演模型;(b)和(c)为组合数据的射线分布. Fig. 9 Velocity models inverted from south and north Fujian profiles Green line represents FJEM model, black line shows result for north Fujian, and red line shows result for south Fujian. |
|
图 10 福建东西部剖面组合和所有爆破数据反演得到的速度模型 (a)中绿线代表所有爆破数据FJEM模型,黑线代表西部的爆破数据反演模型,红线代表东部的爆破数据反演模型;(b)和(c)为组合数据的射线分布. Fig. 10 Velocity models inverted from east and west Fujian profiles Green line represents FJEM model, black line shows result for west Fujian, red line shows result for east Fujian. |
反演采用的最小平方迭代法对反演结果不能进行误差分析估计,本文采用常用的bootstrap方法,通过对所有射线进行随机采样,保持各反演参数不变,进行相同迭代次数的反演,从而估计出各个反演参数的误差估计值.总共进行了100次随机采样,获得了各个反演参数的误差估计值(表 2).从表 2中可以看出,浅部的误差最大为0.052 km·s-1,下地壳的误差最大为0.044 km·s-1,莫霍面深度误差为0.18 km,地幔顶部Pn波速度基本为0,显示出各参数误差估计值很小,具有很好稳定性和可靠性.
3 讨论 3.1 利用爆破地震精确位置检验一维速度模型华南模型主要包括上地壳21.4 km和下地壳11 km两层,速度值分别为6.01 km·s-1,6.88 km·s-1,对应的莫霍面深度为32.4 km,上地幔顶部速度为7.98 km·s-1(范玉兰等,1990).但是这种仅将地壳划分为两层且在地壳有大的速度跳跃的结构是对华南地区一种高度的简化和近似,与实际爆破资料得到的剖面结构还具有很大不同.根据准确的爆破地震位置,利用拾取的爆破走时,对包括华南模型在内的上述模型进行定位质量评价是检验这些一维速度模型定位质量的直接和有效方法.由于FJEM模型是层状连续一维速度模型,Hypo2000定位所用模型需要层状均匀一维速度模型,需要将连续模型转换成定位所需的层状均匀模型.为减小因模型变化带来的误差,采取将FJEM模型逐一差值得到每公里节点的速度值,然后取上下相邻节点的平均速度作为该层的均匀速度值,可以看出连续模型与层状模型在层数较多情况下相互吻合(图 4a).
首先利用Hypo2000软件对FJEM模型和华南模型进行定位比较,华南模型在Hypo2000定位时不包括台站校正,为了减小对比条件的不同,保证一定相似性,使用不带台站校正项的FJEM模型.从18个爆破地震筛选出来512条初至P波走时进行定位对比分析研究,定位质量判别参数使用定位残差均方根(RMS),以及与实际水平、垂直位置和起点时刻的差值,分别对应为ErrH,ErrZ,ErrT.表 3和表 4显示FJEM模型和华南模型都表现出了较高的定位精度.采用华南模型的爆破地震定位结果表 4显示该一维速度模型具有很高的定位精度,其水平位置差值(ErrH)在0.184~2.126 km之间,均值为0.524 km;对浅表层的爆破地震,其定位的震源深度差值在2.85~6.71 km范围, 在深度上有一定差别.采用FJEM模型的定位结果表 3显示定位残差均方根在0.07~0.15 s之间,均值为0.10 s;与真实位置相比,水平位置差值(ErrH)在0.065~1.972 km之间,均值为0.508 km,定位的震源深度差值在0.24~4.01 km范围内.
|
|
表 3 利用FJEM模型(没有考虑台站项)对爆破地震的定位 Table 3 Parameters of 18 explosions relocated using FJEM model (no station correction) |
|
|
表 4 利用华南模型对爆破地震的定位 Table 4 Parameters of 18 explosions relocated using South China model |
台站相对于地震的方位角覆盖程度反映在方位空隙角(Gap),即两个相邻台站之间最大的方位角差别.整个爆破地震定位的空隙角(Gap)在36°~157°之间,显示这些爆破地震都具有很好的台站方位覆盖.根据Wu等(2013)的研究表明,地震定位的空隙角(Gap)与定位误差呈正的线性相关,相关系数能达到0.82,尽管台站对地震的覆盖较好,福建地区18个爆破地震的定位结果显示相关系数为0.48,表明两者相关性较弱, 这可能是由于这些爆破都具有很好的台站方位覆盖,水平误差已经很小(见下更多讨论).为了检验FJEM模型对华南模型是否有所改进,对比了所有爆破地震定位的残差均方根、水平位置与震源深度的差值.FJEM模型和华南模型的残差均方根均值(0.109s,0.111 s)和水平差值均值(0.508 km, 0.524 km)都没有显著的差别.然而,在震源深度差值方面,FJEM模型在0.24~4.01 km之间,华南模型在2.85~6.67 km之间,前者的震源深度差值均值(1.27±1.12 km)是后者深度差值均值(4.67±1.16 km)的近四分之一.
此外,将爆破剖面获取的Cai模型(Cai et al., 2015)和爆破初至P波数据获取的模型的定位结果放在表 5中一起做比较.利用爆破地震检验来源于不同数据反演获得模型可以检验这些模型的定位效果.表 5显示仅利用爆破数据初至波反演的模型要比同时采用初至和续至波反演得到的FJEM模型在定位爆破地震时水平位置精度要低一些,但总体相差不大,说明地震定位对地球速度模型有一定的容错度.与同样是由爆破剖面获取的Cai模型相比,来自台网记录的爆破走时获取的FJEM模型在水平位置、发震时间及定位质量方面具有明显优势,这可能与台网射线的分布更加均匀有关.
|
|
表 5 不同模型对爆破地震定位误差统计表 Table 5 Statistics of relocation of 18 explosions with various models |
基于爆破数据获取的FJEM模型在一定程度上代表了福建地区的速度结构,前面讨论了华南模型对爆破地震的定位分析情况,而日常工作中主要以天然地震定位为主,研究华南模型对天然地震定位的误差分析更加具有实际意义.本文根据真实分布地震目录数据,计算FJEM模型模拟天然地震的合成走时并加入随机噪声,然后采用日常使用的华南模型和Hypo2000软件(只用初动数据)进行定位,评估华南模型对福建区域发生地震的定位情况.
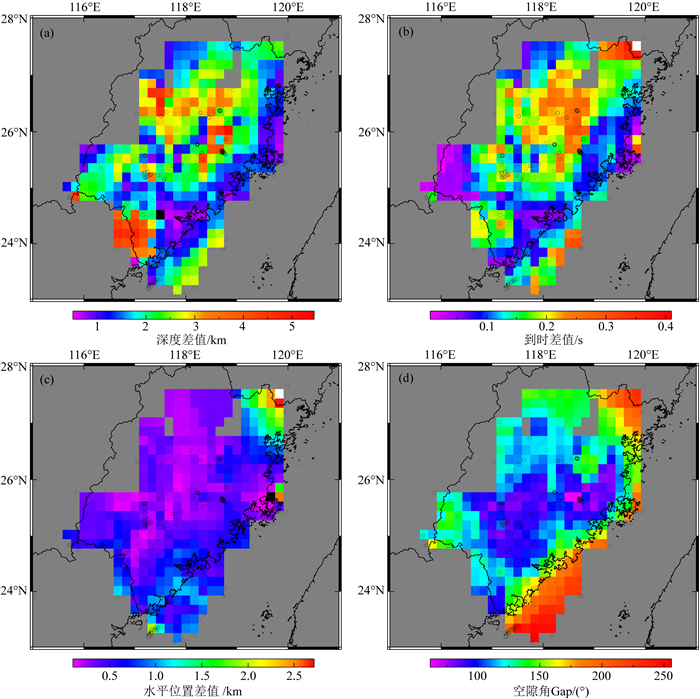
选取了2008—2012年间天然地震进行筛选,筛选出接收台站至少8个的地震共563个(图 11d),接收台站数在4~7之间覆盖较差的地震共1374个(图 12d),然后产生合成走时并加入随机噪声(标准差为0.05 s),同样利用Hypo2000软件使用华南模型对这两组合成地震进行重新定位分析.图 11为华南模型对台站覆盖较好的563个基于FJEM模型的理论地震定位结果分析,可以看出在福建边缘的地震空隙角要大于福建中部,其中福建北部沿海以及台湾海峡的地震空隙角较大,这主要与记录地震的台站分布有关.一般认为地震空隙角越大,台站分布越不均匀,对地震的定位能力越差.563个理论地震中,所有地震水平位置差值的均值为0.5 km,这些水平位置差值与方位空隙角分布具有较好的对应性,在方位覆盖较好的中部(空隙角Gap < 120°),95%的水平位置差值在0.7 km以内,其定位结果与地震目录结果相差小,在边缘等区域(Gap>180°)时,95%的水平位置差值在5.4 km以内,水平位置差值显著偏大.震源深度差值的表现则有所不同(图 11a),在具有较小空隙角分布的中南部区域,尽管具有较好的水平定位能力,但震源深度差值变化却较大,显示震源深度误差与水平位置差值没有明显的对应关系,震源深度差值最小是沿着海岸线分布,与空隙角分布也没有必然联系,主要与到时差值的关系较为密切,当Gap < 120°时相关系数能达到0.74,Gap>180°时相关系数能达到0.79.所有震源深度差值的均值为2.4 km,标准差为1.9 km(95%的深度差值在6.4 km以内).
|
图 11 台站记录数量大于7时华南模型定位误差分布 利用2008—2012年间筛选的563地震和FJEM模型得到理论到时,然后用华南模型重定位. (a)深度差值分布;(b)到时差值分布;(c)水平位置差值分布;(d)所有地震的空隙角分布. Fig. 11 Distributions of mislocations from South China Model with number of stations greater than 7 Synthetic travels times were calculated for 563 earthquakes in 2008—2012 using FJEM model, which were then used to relocate the earthquakes. (a) Presents depth difference; (b) Presents origin time difference; (c) Presents horizontal difference; (d) Presents azimuthal Gap of the events. |
|
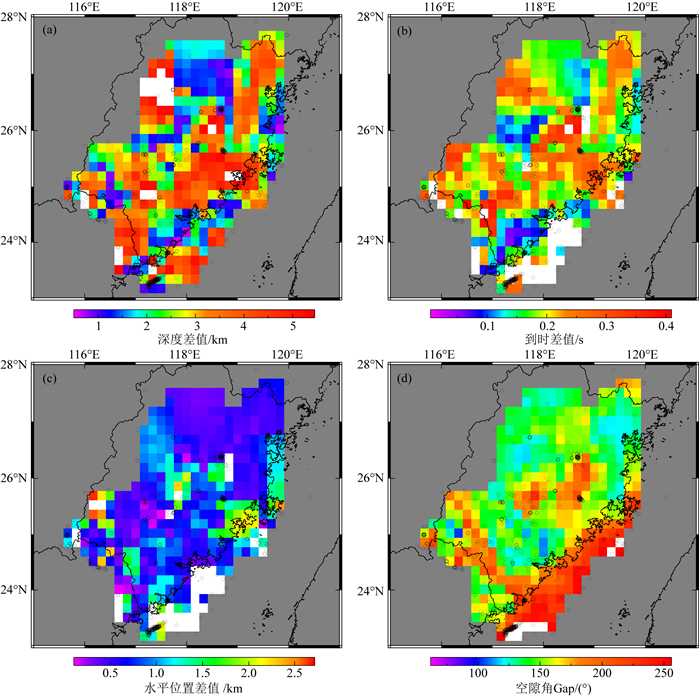
图 12 台站记录数量4~7时华南模型定位误差分布 2008—2012年,总共有1374个地震,图中白色部分为超出色标值范围. Fig. 12 Distributions of mislocations from South China Model with number of stations of 4 to 7 The total number of events is 1374 in 2008—2012, the white color indicates outside the range of the color pallets. |
图 12为台站覆盖较差的1374个地震定位结果分布.与图 11相比,地震定位空隙角显著增加,所有地震水平位置差值的均值为1.3 km,水平位置差值在福建中部偏小(Gap < 120°),95%的水平位置差值在3.4 km以内,但在沿海区域差距较大(Gap>180°)时,95%的水平位置差值在18.4 km以内.而震源深度差值分布则较为复杂,其均值为2.2 km,标准差为2.0 km(95%的深度差值在5.9 km以内).
从华南模型对基于爆破数据的FJEM模型模拟地震目录进行重新定位的结果来看,华南模型和FJEM模型在定位上存在一定的差别,这种差别在某种程度上代表了这两个模型的定位误差.水平误差跟台站分布(主要是方位分布)有极大关系.在台站较多、方位覆盖较好时,水平定位误差大都(95%)小于1 km,方位覆盖较差时,一些(5%)可能大于5 km.在台站较少、方位覆盖较好时,水平误差也大都小于3~4 km,方位覆盖较差,一些可能大于18 km.震源深度的误差则跟台站数目、方位覆盖没有明显的关系,主要跟发震时间有互易关系(trade-off),平均深度误差约为2 km,一些可大于5~6 km.因而,正如爆破数据测试所显示(见上),在只用初动的数据的情况下,改进的一维模型对减小深度误差有较大作用.
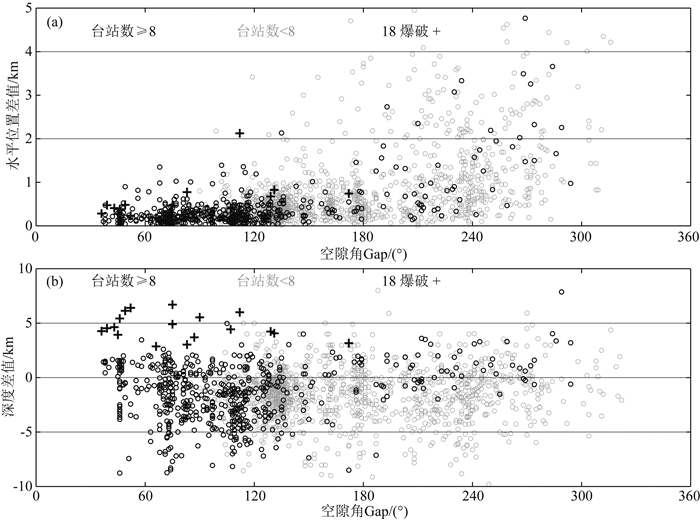
3.3 参考模型对地震定位的影响进一步分析以上合成地震测试结果跟爆破事件重新定位结果相吻合(图 13).图 13显示各种测试定位误差结果相对于Gap的分布.对任何合理的参考模型,水平定位基本取决于台站方位角的覆盖.当Gap小于180°时,绝大部分水平误差小于2 km;当Gap从180°时增加时,水平定位误差很快增大(图 13a).震源深度则不然(图 13b),对Gap大或小、台站多或少,深度误差无多大差别, 即使方位角分布很好、台站很多时,华南模型定位的深度误差也常常可达几公里.
|
图 13 华南模型的定位误差与空隙角分布 根据实际地震目录(2008—2012),由FJEM模型得到理论合成到时,然后用华南模型重新定位.对于18个爆破,则是用实际观测和华南模型定位与实际位置得到的误差.图中画出水平位置误差(a)和深度误差(b)与空隙角(Gap)分布.其中黑色十字表示18个爆破地震,黑色圆圈表示台站数至少8的理论地震,灰色圆圈表示台站数小于8的理论地震. Fig. 13 Distribution of mislocations and Gap for South China Model Synthetic arrival times were generated using the FJEM model and real earthquake locations from earthquake bulletins (2008—2012), which were then used to relocate the earthquakes. For the 18 explosions, mislocations are the difference between the relocation using real observations and South China Model and the real location. The plot shows the distributions of horizontal mislocation (a) and depth mislocation (b) with respect to azimuthal gap (Gap). Black crosses represent 18 explosions, black circles represent earthquakes with number of stations at least 8, and gray circles represent earthquakes with number of stations less than 8. |
这是因为利用华南模型时,深度误差与发震时间存在互易效应.如爆破重定位检验所示,FJEM模型能改进深度的根本原因是它减小了这种互易效应.原因是华南模型为高度近似模型,分两层,层内速度为常数不随深度变化,而FJEM模型地壳速度有较强的速度梯度,使得走时随震源深度变化(垂向慢度,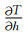
以下方程中符号包括:T为走时,X为水平距离,p为水平慢度(射线参数),η为垂向慢度,h为震源深度,v0为震源区速度,H为地壳厚度,vm为地幔速度.
地壳上行Pg波:
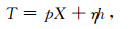
|
(5) |
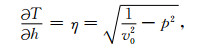
|
(6) |
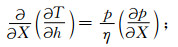
|
(7) |
地壳下行Pg波:
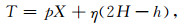
|
(8) |
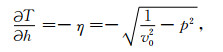
|
(9) |
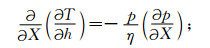
|
(10) |
Pn波:
由于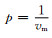
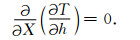
|
(11) |
如果地壳为一层均匀模型,速度为常数,射线为直线,在平面地球(flat earth)中只有上行Pg波,无下行Pg波.通常h«X, 那么Pg走时曲线T-X约为一条直线,其斜率(也就是p)约为常数,所以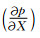
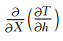
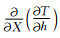
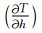
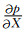
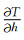
本文利用爆破数据和多震相联合反演的方法,得到福建爆破一维速度模型(FJEM),分析了模型可靠性,比较了不同模型.同时由于爆破震源的精确性,本文检验了各种一维速度模型定位效果.另外,本文利用新的模型和合成走时,分析了日常所用华南模型的可能定位误差.本文主要结论如下:
(1) 利用地震台网记录的爆破地震走时数据,采用联合初至和续至波反演福建地区一维地壳及上地幔顶部速度结构,得到福建爆破模型FJEM.相对于华南模型,FJEM模型得到的走时残差有显著减少(均方根从0.40到0.22 s).从续至Pg的拟合来看,FJEM模型对地壳各个深度的约束要比以前模型都更好.
(2) 不同爆破地震数据组合反演得到了较为稳定的一维速度模型,说明整个福建地区存在较为简单的一维速度结构.
(3) 通过对爆破地震进行重新定位测试,显示华南模型对爆破地震具有较高水平位置定位能力,平均差值为0.52±0.45 km,但对这些位于浅表层的爆破地震震源深度定位有较大误差,平均为4.7±1.2 km.而本文福建爆破模型(FJEM)与华南模型相似的水平定位能力,但是用FJEM模型震源深度误差小很多(1.3±1.1 km).
(4) 根据华南模型对基于FJEM模型的合成地震目录定位结果分析,显示地震方位(空隙角)分布与地震水平定位误差密切相关,在福建中部地区水平定位误差较小、福建边缘及海峡区域水平定位误差较大.震源深度的误差则跟台站数目及分布没有明显的关系,而是与发震时间误差有互易关系,在日常只用初动的数据的情况下,改进的一维模型对减小深度误差有较大作用.
(5) 从中可以看出,地震水平定位误差基本上受台站方位覆盖影响,而受参考速度模型影响较小;而在深度方面,本文改进的FJEM模型不仅更加接近真实的速度结构(拟合走时更好)而且也减小了深度误差.因此建议在福建及其邻近区域的日常定位中用FJEM模型替代华南模型.
致谢 感谢福建省地震局提供爆破的波形数据和地震目录数据,感谢两位匿名审稿专家提出的宝贵修改意见,文中所用图件使用GMT(Wessel and Smith, 1998)制作生成.
Cai H T, Jin X, Wang S X. 2014. The research progress of velocity structure of crust and upper mantle in Fujian area. Progress in Geophysics (in Chinese), 29(4): 1485-1490. DOI:10.6038/pg20140401 |
Cai H T, Jin X, Wang S X. 2015. One-dimensional velocity structure of the crust in Fujian, Southeast China. Terrestrial, Atmospheric and Oceanic Sciences, 26(5): 493-502. DOI:10.3319/TAO.2015.04.08.01(T) |
Cai H T, Jin X, Wang S X, et al. 2016. The crust structure and velocity structure characteristics beneath Ninghua-Datian-Hui'an. Chinese Journal of Geophysics (in Chinese), 59(1): 157-168. DOI:10.6038/cjg20160113 |
Chen X X, Lin S, Li Z N, et al. 2005. Preliminary 1-D model of crust velocity structure in Fujian-Taiwan region. Earthquake (in Chinese), 25(2): 61-68. |
Evans J R, Eberhart-Phillips D, Thurber C H. 1994. User's manual for SIMULPS12 for imaging VP and VP/VS:A derivative of the "Thurber" tomographic inversion SIMUL3 for local earthquakes and explosions. Open-File Rep. Denver, Colo:U.S. Geological Survey: 94-431. |
Fan Y L, Lin J Z, Hu R H, et al. 1990. The development of travel timetable for near earthquake in South China. South China Seismological Journal (in Chinese), 10(2): 1-16. |
Huang H, Mi N, Xu M J, et al. 2010. S-wave velocity structures of the crust and uppermost mantle, and Poisson's ratios in Fujian province. Geological Journal of China Universities (in Chinese), 16(4): 465-474. |
Kissling E. 1988. Geotomography with local earthquake data. Review of Geophysics, 26(4): 659-598. DOI:10.1029/RG026i004p00659 |
Kissling E, Ellsworth W L, Eberhart-Phillips D, et al. 1994. Initial reference models in local earthquake tomography. Journal of Geophysical Research:Solid Earth, 99(B10): 19635-19646. DOI:10.1029/93JB03138 |
Klein F W. 2002. User's Guide to HYPOINVERSE-2000, A Fortran program to solve earthquake locations and magnitudes. Open-File Rep. Denver, Colo:U.S. Geological Survey, 123. |
Koketsu K, Sekine S. 1998. Pseudo-bending method for three-dimensional seismic ray tracing in a spherical earth with discontinuities. Geophysical Journal International, 132(2): 339-346. DOI:10.1046/j.1365-246x.1998.00427.x |
Li Y L, Wang B S, He R Z, et al. 2018. Fine relocation, mechanism, and tectonic indications of middle-small earthquakes in the Central Tibetan Plateau. Earth and Planetary Physics, 2(5): 406-419. DOI:10.26464/epp2018038 |
Lahr J C. 1999. HYPOELLIPSE:A computer program for determining local earthquake hypocentral parameters, magnitude, and first-motion pattern (Y2K compliant version). Open-File Rep. Denver, Colo:U.S. Geological Survey, 92. |
Lee W H K, Lahr J C. 1975. HYPO71 (revised):A computer program for determining hypocenter, magnitude and first motion pattern of local earthquakes. Open-File Rep. Denver, Colo:U.S. Geological Survey, 64. |
Liao Q L, Wang Z M, Wang P L, et al. 1988. Explosion seismic study of the crustal structure in Fuzhou-Quanzhou-Shantou region. Acta Geophysica Sinica (in Chinese), 31(3): 270-280. |
Lin YP, Zhao L, Hung S H. 2011. Assessment of tomography models of Taiwan using first-arrival times from the TAIGER active-source experiment. Bulletin of the Seismological Society of America, 101(2): 866-880. DOI:10.1785/0120100244 |
Paige C C, Saunders M A. 1982a. LSQR:sparse linear equations and least squares problems. ACM Transactions on Mathematical Software, 8(2): 195-209. DOI:10.1145/355993.356000 |
Paige C C, Saunders M A. 1982b. LSQR:an algorithm for sparse linear equations and sparse least squares. ACM Transactions on Mathematical Software, 8(1): 43-71. DOI:10.1145/355984.355989 |
Pavlis G L. 1986. Appraising earthquake hypocenter location errors:a complete, practical approach for single-event locations. Bulletin of the Seismological Society of America, 76(6): 1699-1717. |
Schweitzer J. 2001. HYPOSAT-an enhanced routine to locate seismic events. Pure and Applied Geophysics, 158(1-2): 277-289. |
Wessel P, Smith W H F. 1998. New, improved version of generic mapping tools released. Eos, Transactions American Geophysical Union, 79(47): 579. DOI:10.1029/98EO00426 |
Wu Y M, Chang C H, Hao K C, et al. 2013. On the use of explosion records for examining earthquake location uncertainty in Taiwan. Terrestrial, Atmospheric and Oceanic Sciences, 24(4): 685-694. |
Xu Z J, Song X D. 2010. Joint inversion for crustal and Pn velocities and Moho depth in eastern margin of the Tibetan plateau. Tectonophysics, 491(1-4): 185-193. DOI:10.1016/j.tecto.2009.11.022 |
蔡辉腾, 金星, 王善雄. 2014. 福建地区地壳上地幔速度结构研究进展. 地球物理学进展, 29(4): 1485-1490. DOI:10.6038/pg20140401 |
蔡辉腾, 金星, 王善雄, 等. 2016. 宁化-大田-惠安地壳构造与速度结构特征. 地球物理学报, 59(1): 157-168. DOI:10.6038/cjg20160113 |
陈祥熊, 林树, 李祖宁, 等. 2005. 福建-台湾地区一维地壳速度结构的初始模型. 地震, 25(2): 61-68. |
范玉兰, 林纪曾, 胡瑞贺, 等. 1990. 华南地区近震走时表的研制. 华南地震, 10(2): 1-16. |
黄晖, 米宁, 徐鸣洁, 等. 2010. 福建地区地壳上地幔S波速度结构与泊松比. 高校地质学报, 16(4): 465-474. DOI:10.3969/j.issn.1006-7493.2010.04.006 |
廖其林, 王振明, 王屏路, 等. 1988. 福州-泉州-汕头地区地壳结构的爆炸地震研究. 地球物理学报, 31(3): 270-280. DOI:10.3321/j.issn:0001-5733.1988.03.004 |
 2019, Vol. 62
2019, Vol. 62


