2. 吉林大学应用地球物理实验教学中心, 长春 130026;
3. 吉林大学地质资源立体探测虚拟仿真实验教学示范中心, 长春 130026;
4. 国土资源部应用地球物理重点实验室, 长春 130026;
5. 油页岩地下原位转化与钻采技术国家地方联合工程实验室, 长春 130026
2. Central Lab of Applied Geophysics, Changchun 130026, China;
3. Virtual Simulation Experiment Teaching Center for Stereoscopic Exploration of Geological Resources, Changchun 130026, China;
4. Key Laboratory of Applied Geophysics, Ministry of Land and Resources, Changchun 130026, China;
5. National-Local Joint Engineering Laboratory of In-situ Conversion, Drilling and Exploitation Technology for Oil Shale, Changchun 130026, China
随机地震反演,以地质统计学为基础,是地震反演算法与随机序贯模拟算法的结合,在解决储层的预测和表征等科学问题中发挥着重要作用.较之传统的确定性反演,随机地震反演不再将其结果限制于数值为定值的物性参数模型,而是以大量的高分辨率等概率随机实现作为备选模型,再从中挑选出“最佳”的模型作为反演结果.因此,随机地震反演具有一定的随机性,其反演结果更加接近于真实地质模型.
虽然随机地震反演具有明显的优势,但是它存在两个主要问题难以解决.其一,随机序贯模拟为每个随机实现(stochastic realizations)都带来了随机噪声,并且这些噪声几乎无法消除和利用;其二,从大量的随机实现中挖掘有用信息是非常困难的,通常人们只能从这些随机实现中选出一个较为合理的阻抗结果(Rowbotham et al., 2003;Sabeti et al., 2017).因此,如何将随机实现所含有的噪声适当压制或利用,并提取大量随机实现中携带的有用信息,在随机地震反演问题的研究中具有重要的意义.
基于上述两方面问题考虑,对随机地震反演理论的深入探究一直是学者们关注的焦点.Deustch等(Deutsch and Cockerham, 1994;Deutsch and Journel, 1994)和孙思敏等(孙思敏和彭仕宓,2007)应用模拟退火算法,对随机实现中的模型参数值进行了重新组合和调整.Sabeti等(Sabeti et al., 2017)将遗传算法应用于随机地震反演,得到了较好的声波阻抗反演结果.Liu等(Liu et al., 2016)将模拟退火算法和遗传算法混合,相比于只应用遗传算法,这一结果的耗时稍多,准确性更好.以上工作都在一定程度上解决了随机地震反演中存在的两个问题,但是这些算法大多是以随机搜索为基础的智能优化算法,其依赖于经验而确定的参数较多,如模拟退火法中的降温方式,遗传算法中的初始种群的给定,交叉概率和变异概率等;另外,这些算法中都存在比较繁琐的中间步骤,如模拟退火法中需要给定步长函数或嵌入其他最优化算法,遗传算法中在每个迭代步都需要编码和解码两个步骤.
神经网络是一种重要的最优化算法,其拓扑结构清晰,易于计算机实现.本文将随机地震反演与神经网络相结合,利用大量的随机实现建立训练集,并充分挖掘有用信息.神经网络的学习过程分为有监督和无监督两类.无监督神经网络较早的应用于求解地震反演问题.1988年,Zhao和Mendel(1988)提出了实现地震信号反褶积的Hopfield神经网络算法.随后,由于无监督神经网络解决问题的局限性,人们逐渐对有监督神经网络更加关注.Baddari等将RBF神经网络用于声波阻抗的反演,并指出经过BP算法训练的RBF网络可以有效避免反演结果陷入局部极小点(Baddari et al., 2009).吴媚和符力耘等应用Caianicllo神经网络解决了地震反演中子波提取和提升反演结果抗噪能力等多个问题(吴媚等,2008;Fu,2004).Leite和Vidal(2011)利用由三维叠后地震数据反演得到的声波阻抗数据,应用前馈神经网络算法实现了,得到了三维孔隙度模型.
有监督神经网络算法可以建立观测数据与模型参数之间的非线性关系.网络的训练过程需要充足的“输入-输出”数据体,作为训练集、验证集和测试集.对于具体的地球物理反问题,这种数据体的确定主要有两种方式.一种是以“软数据”为基础,建立一些与待反演模型具有类似或相关结构的合成模型,将这些模型的正演结果作为输入,模型参数作为输出,如文献(Baddari et al., 2009)选用了含噪理论模型作为训练集的输出;另一种是以“硬数据”为基础,将测井中的物性参数作为输出,将井位对应的地震观测数据(或其反演结果,如阻抗)作为输入,从而预测井位附近或井中缺失的物性参数(Leite and Vidal, 2011).
一般来说,第二种方法的结果更可信,因为它建立了观测数据与介质模型的真实物性参数之间的非线性关系.但是在地学研究中,“硬数据”的获取是非常昂贵的,因此这种方法很难有效实施.这使得寻找相关的“软数据”合成模型成为利用神经网络算法解决地震反演问题的关键.随机地震反演可以由测井数据生成大量的随机实现模型,并且在变差函数和克里金插值的作用下,这些模型具有相似的空间统计学特征和随机性,这就使得大量的随机实现为神经网络提供了同时具有空间相关性和多样性的学习样本.源于这种思想,本文希望将神经网络算法和随机地震反演算法有机的结合,提出一种新的随机地震反演算法.通过神经网络的训练和拟合,随机地震反演的两个主要问题在一定程度上得到了解决.包括含噪声的随机实现并没有直接作为反演结果,而是用于组成训练集,这使得学习样本的多样性得以保证;以及反演结果大多优于传统方法的结果.
1 随机地震反演方法随机地震反演是地质统计学反演的重要组成部分.地质统计学反演由Haas和Dubrule等提出和发展(Haas and Dubrule, 1994;Dubrule et al., 1998;Yang and Zhu, 2017),以地质统计学理论和随机函数理论为基础,利用地质信息,在每一个地震道上,生成多个可供选择的等概率随机实现,再结合地震反演方法,计算得到最终的反演结果(Robinson,2001).由于等概率随机实现由随机模拟算法计算生成,后续的地震反演工作以这些等概率随机实现为基础,所以这个过程也称为随机地震反演.
随机地震反演一般包括随机模拟和地震反演两个部分.随机模拟一般以测井数据为基础,应用序贯随机模拟方法,生成同一个位置储层参数的多个等概率随机实现.
等概率随机实现的获取是随机地震反演的基础,其主要步骤为:
(1) 将反问题的待求解区域网格化;
(2) 随机的选择一个待模拟的网格点;
(3) 估计该点的局部条件概率分布(local conditional probability distribution,简称LCPD);
(4) 从LCPD中随机的抽取一个值,作为该网格点的估计值;
(5) 将该值添加到条件数据集中;
(6) 返回步骤(2),计算新的待模拟点,直至网格上的所有点都被模拟.
以上流程也是序贯随机模拟的一般过程.常用于随机地震反演的序贯随机模拟算法,一般包括序贯高斯模拟(SGS)和序贯指示模拟(SIS)等.其区别在于LCPD的估计方法.另外,序贯高斯模拟适用于一些中间值比较连续,且极端值比较分散的物性参数,如孔隙度、波阻抗等;序贯指示模拟可用于模拟离散化的变量,如储层类型等.本文将主要应用序贯高斯模拟算法来模拟波阻抗模型的随机实现.序贯高斯模拟的计算过程比较繁琐,包括条件累积概率分布函数(CCDF)的计算和正态得分变换等步骤,其中CCDF的计算还涉及到变差函数的估计和克里金方程组的求解等过程(吴胜和,2010).
随机地震反演过程是对随机实现进行逐一优选的过程.所谓优选,主要包含两层含义,一是从大量随机实现中选出与真实介质参数模型匹配最好的,这一般通过比较地震观测数据与随机实现的相应正演结果之间的相关系数来确定;二是利用反演算法,从随机实现中通过重新组合或搜索等方式确定最终的反演结果(潘新朋等,2018).
本文利用随机实现组成的学习样本来训练神经网络,建立地震数据和阻抗模型之间的非线性关系,并得到较好的反演结果.
2 基于神经网络的随机地震反演思路 2.1 BP神经网络的实现神经网络可以以任意精度逼近一个非线性连续函数,即以自变量为输入,以因变量为输出,以任意高的精度来替代这个函数(Van Der Baan and Jutten, 2000).在地球物理领域,人们应用神经网络来确定地球物理数据与介质参数模型之间的数学关系(Poulton,2002).在反问题的研究中,神经网络是一种将数据转化为信息的有效工具.最常用的神经网络是前馈神经网络(feedforward neural network,简称FNN).这是因为FNN适用于很多数据到信息的转化问题,结构简单且易于计算机实现.FNN至少包括三部分结构,即输入层、隐层和输出层,这种结构也称为多层感知机(multilayer perceptron,简称MLP)(Manoj and Nagarajan, 2003).
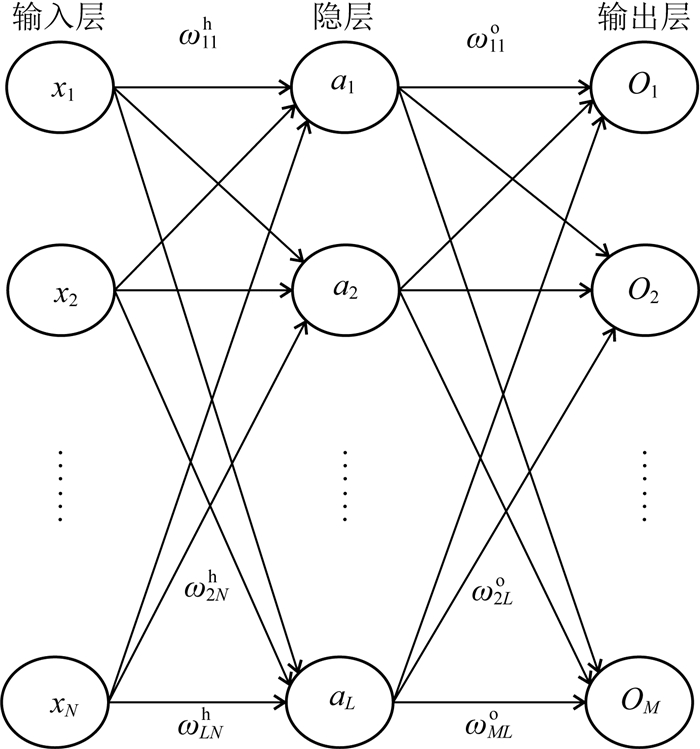
MLP中的基本处理单元是神经元.MLP运行的机制是数据由输入层进入神经网络,然后在权系数的作用下,将加权后的数据传递到隐层,再由隐层的激活函数作用后,再次加权运算并输出结果到输出层,详见图 1.
|
图 1 多层感知机 Fig. 1 Multilayer perceptron |
假设已知Q个向量对(x1,y1),(x2,y2),…,(xQ,yQ)具有某种非线性关系.令x和y为分别含有N和M个元素的向量,以x为输入,y为输出,应用神经网络描述这种关系,即输入层具有N个神经元,输出层具有M个神经元.假定神经只具有一个隐层,且隐层神经元的个数为L.当神经网络为全连接的,则输入层的每个神经元都与隐层中的任一神经元连接.这种连接以加权求和的数学方式表达,并经隐层神经元中激活函数作用,记为该神经元向输出层传递的数值.
以输入向量xn为例,其对应于隐层的第m个神经元的数学表达amn为
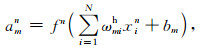
|
(1) |
其中f表示激活函数,m=1,2,…,L,上角标h表示隐层,ωmih表示输入层的第i个神经元对隐层第m个神经元的加权系数,xin表示输入向量xn的第i个分量,bm表示隐层第m个神经元的偏置项.
激活函数f是一个有界非线性函数,有很多选择,其中比较常用的是Sigmoid函数:
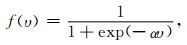
|
(2) |
其中α控制函数值趋于0.5的速率.激活函数赋予神经网络高度的非线性表现能力,使神经网络能够适用于求解非线性问题.
与公式(1)类似,输出层的第k个神经元Okn可表示为
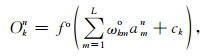
|
(3) |
其中k=1,2,…,M,上角标o表示输出层,ωkmo表示隐层的第m个神经元对输出层的第k个神经元的加权系数,ck表示输出层的第k个神经元的偏置项.
实际上,向量y是神经网络的期望输出,它与神经网络的实际输出之间存在误差,
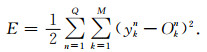
|
(4) |
神经网络的训练是一个以E为目标函数的最优化过程.常用的训练算法是误差回传算法,简称BP算法.由公式(4)可知,误差函数E是由输出层的各神经元决定的,因此误差回传的第一步是调整隐层到输出层神经元的加权系数.以隐层第m个神经元到输出层第k个神经元的加权系数ωkmo为例,其从第l个取值到第l+1个取值的更新方式为
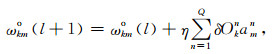
|
(5) |
其中ωkmo(l)为第l个训练步得到的权系数,η为学习率,通常在范围(0,0.05]内取值,δOkn的具体形式由最优化算法决定,常用的算法有Levenberg-Marquardt算法(L-M法)、共轭梯度法、模拟退火法和遗传算法等.当采用梯度类最优化算法时,δOkn为误差函数(4)式的负梯度分量;当采用蒙特卡罗类最优化算法时,δOkn是一个随机变量.梯度类算法运算较快,但容易陷入局部极小点;蒙特卡罗类算法运算较慢,但不易陷入局部极小点.我们可以针对具体问题,选择适当的方法.
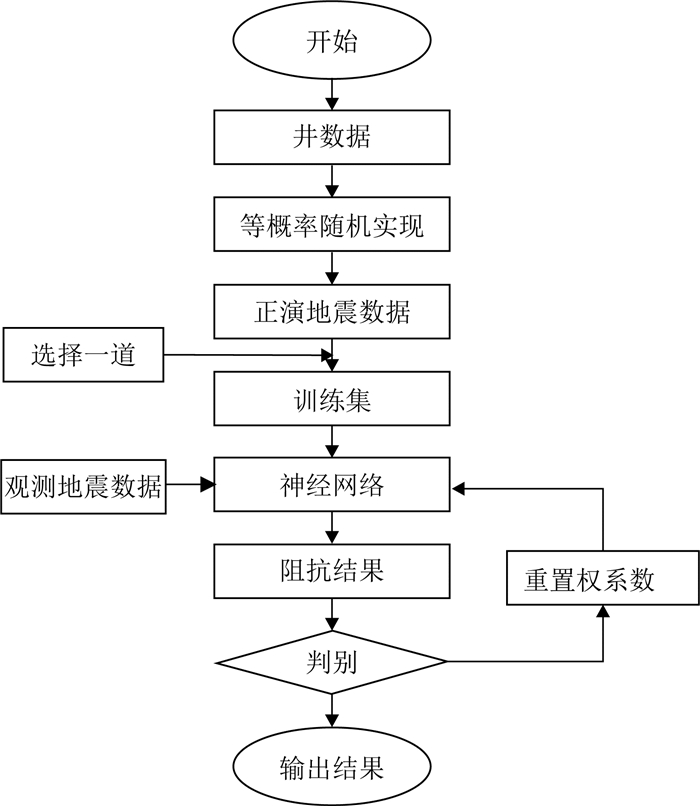
2.2 基于神经网络的随机地震反演流程本文提出了一种基于神经网络的随机地震反演算法.我们将通过序贯随机模拟得到的等概率随机阻抗实现作为训练集的输出,将这些阻抗分别对应的地震正演结果作为输入,由此逐个地震道的训练神经网络.待训练完毕后,再将各道的观测地震数据逐一的输入相应的神经网络模型,从而输出最终的波阻抗反演结果.我们采用重置权系数的方式,来避免神经网络陷入局部极小点.当神经网络输出的阻抗结果所对应的正演地震数据与实际地震数据之间的相关系数达到或超过某一阈值时,我们将该结果记为该道的最终反演结果,然后再选择另一道,依次进行神经网络的训练、阻抗结果的计算、判别等步骤,直至所有地震道位置对应的反演工作都完成,如图 2.
|
图 2 基于神经网络的随机地震反演的流程图 Fig. 2 Flowchart of stochastic seismic inversion based on neural network |
序贯随机模拟提供了大量的等概率阻抗模型,这些模型中有的比较接近真实的待反演阻抗模型,有的与待反演结果存在较大差异.传统的方法大多是在大量的等概率随机实现中,选取一个地震正演结果与观测地震数据相关性较好的实现作为最终的反演结果.这只是从大量的随机性结果中被动的选取一个相对合理的结果,此外随机实现还携带着噪声.这种方法显然忽视了其他等概率模型的作用.实际上,无论等概率模型是否足够接近待反演结果,它们都为反演过程提供了多样性的参考.在下一部分,我们将展示利用神经网络可以从大量的随机实现中充分的挖掘有用信息,甚至得到更优的反演结果.
使用自激自收的地震波场作为正演数据,其描述为子波与反射系数的褶积,
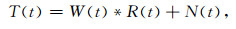
|
(6) |
其中,符号“*”表示褶积算子,T(t)表示合成地震记录,W(t)表示地震子波,R(t)表示反射系数序列,N(t)表示随机噪声.褶积模型在关于地震反演的工作中被大量的使用(Baddari et al., 2009;Cheng et al., 1996;Lines and Treitel, 1984;Tarantola,1984;Zhang and Castagna, 2011).
3 基于合成模型的数值模拟在已有工作中,人们大多以多个隐层或多个神经元的神经网络为工具(Baddari et al., 2009;Liu and Liu, 1998),进行地球物理反问题的研究.这主要是因为用于拟合神经网络的有效训练集是不易确定的.
本文中由于神经网络的训练集具有的特殊性,即同一道的等概率随机阻抗实现同时具有一定的“空间相关性”和“多样性”.这使得我们用结构较简单的神经网络就可以较准确的描述阻抗与地震数据之间的非线性关系.我们提出仅利用包含5个神经元的单隐层前馈神经网络即可实现对50个输出的神经网络的有效拟合.
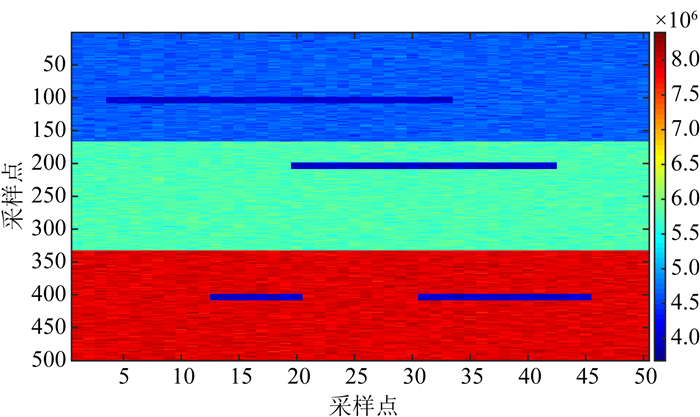
首先令阻抗Z的单位为kg·m-2·s-1,建立一个具有三层结构的阻抗模型.该目标模型受随机因素微扰,由浅至深速度和密度总体递减,三层的纵波速度分别约为1500,1800,2400 m·s-1,密度分别约为3100,3200,3300 kg·m-3,设置低波阻抗带的阻抗为4×106 kg·m-2·s-1,如图 3所示.为了便于讨论,横轴和纵轴只表示采样点,其中横轴道间距为100 m,纵轴采样间隔为4 ms.
|
图 3 阻抗模型 Fig. 3 Impedance model |
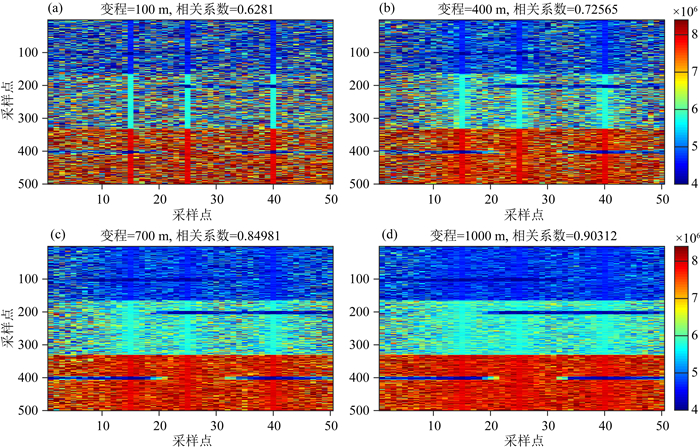
令模型中的第15,25和40道为已知数据(井数据),利用序贯高斯模拟方法,在不同空间相关性距离(即变程)影响下,生成多组随机实现.其中,井数据不是精细尺度下的数据,而是从阻抗模型中提取的阻抗数据,受噪声干扰小,比较稳定可靠,不需要调整尺度.本文主要考虑了横向变程的影响.同时,计算了每个随机实现与阻抗模型的相关系数.如图 4a,变程为100 m的随机实现模型与阻抗模型的相关系数为0.6281,其层状结构并不明显,并且低波阻抗带的显示也不连续.当变程逐渐增大时,已知数据对待估点数值的影响逐渐增强.变程达到400 m(图 4b)时,相关系数为0.72565,已经可以观测到较明显的层状结构,但横向连续性仍然较差;变程达到700 m(图 4c)时,相关系数为0.84981,横向连续性增强;变程达到1000 m(图 4d)时,相关系数为0.90312,层状结构非常明显,横向连续性继续增强.图 4c和4d已经与待反演的阻抗模型具有较高的相关性,但其第二层和第三层的低波阻抗带的横向范围明显大于图 3中的阻抗模型.
|
图 4 四组等概率随机实现 Fig. 4 Four pictures of equi-probability realizations |
因此,我们把变程较大和较小的等概率随机实现同时纳入神经网络的训练集,变程较大的实现可以为反演结果提供具有较强空间相关性,变程较小的实现可以为反演结果提供多样性的参考.这有别于传统的基于神经网络的波阻抗反演.传统方法中,对井数据进行染噪处理,把它们作为训练集的输出,把对应的地震正演数据作为训练集的输入.以第5道和第27道为例,为两种方法各选50组阻抗模型.传统方法的训练集输出是由第15,25和40道数据的加噪结果组成的;本文的训练集输出是变程为10+(i-1)×25,i=1,2,…,50,的50个随机实现组成.
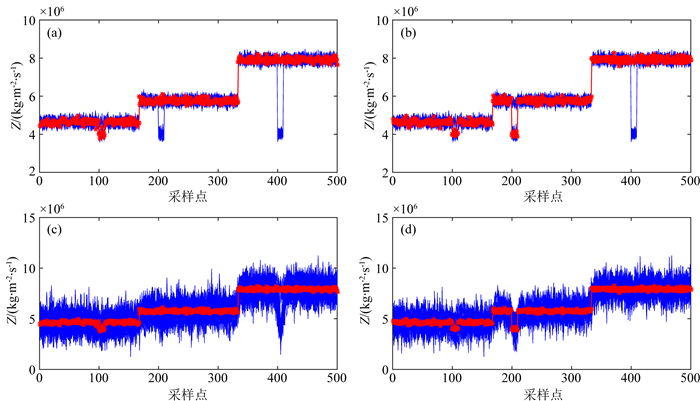
如图 5所示,NN表示传统的神经网络反演方法,NN+SGS表示应用随机模拟生成的等概率随机实现.其中红色的曲线表示该道的待反演阻抗曲线,蓝色表示训练集中的阻抗样本.由图 5a和图 5b可见,训练集中含有一些待反演阻抗曲线不具备的低阻特征,这将对反演结果产生不良影响.等概率随机实现的分布要比染噪测井数据分散得多,但大多在待反演阻抗曲线附近上下波动,如图 5c和图 5d.
|
图 5 传统神经网络反演和本文方法的训练集对比 (a)第5道的训练集(NN); (b)第27道的训练集(NN); (c)第5道的训练集(NN+SGS); (d)第27道的训练集(NN+SGS). Fig. 5 Comparison between training sets of traditional neural network inversion and our method |
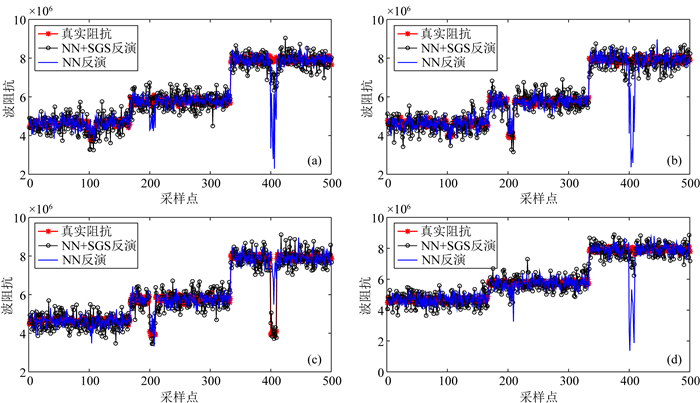
从反演的效果来看,本文方法的效果在有些地震道位置上明显优于传统的神经网络算法,如图 6a、图 6b和图 6d;在有些道,两种方法的效果都很好,如图 6c.因此,从计算结果来看,本文提出的新算法的反演效果优于传统的神经网络算法.
|
图 6 单道反演结果的对比(一) (a)第5道的结果; (b)第27道的结果; (c)第37道的结果; (d)第47道的结果. Fig. 6 Comparison of inversion results for single traces:Ⅰ |
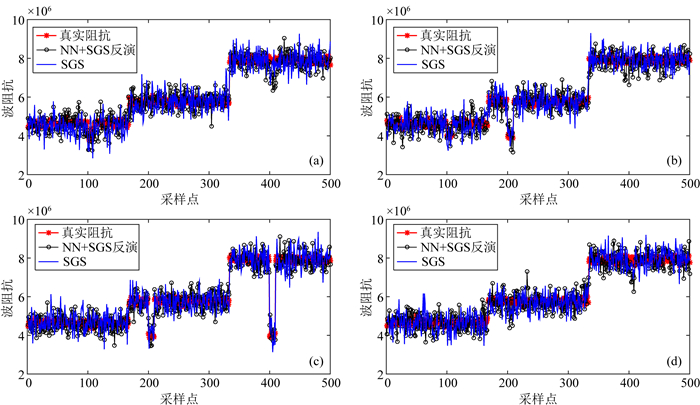
如图 7,我们选用正演地震数据与观测地震数据相关系数最大的阻抗模型,与应用本文方法得到的反演结果进行对比.随机实现和反演结果都非常接近待反演的阻抗曲线,但很容易看出“最佳”随机实现的波动性更强,特别是第5道和第47道的情况.因此,如果把神经网络的反演过程当作数据的去噪过程,反演结果相比于随机实现,其所含有的噪声更低一些.
|
图 7 单道反演结果的对比(二) (a)第5道的结果; (b)第27道的结果; (c)第37道的结果; (d)第47道的结果. Fig. 7 Comparison of inversion results for single traces:Ⅱ |
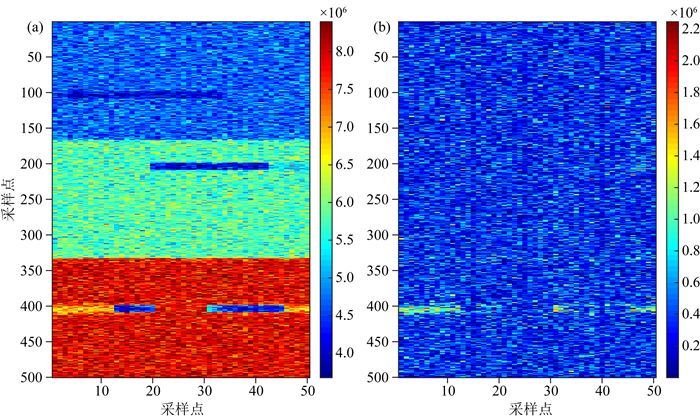
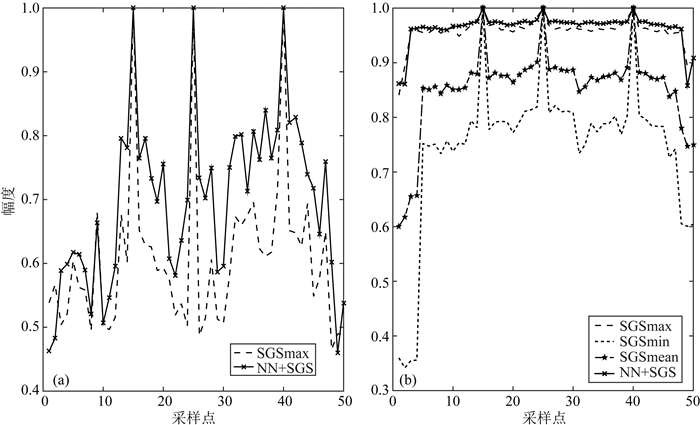
我们应用基于神经网络的随机地震反演算法,求解了全部50道数据,其反演结果如图 8.在图 9a中,实线表示反演结果对应的正演地震数据与实际地震数据之间的相关系数,虚线表示等概率随机实现中对应正演数据与实际地震数据之间的相关系数的最大值.在图 9b中,SGSmax,SGSmin和SGSmean分别表示等概率随机实现中与实际阻抗模型之间的相关系数的最大值、最小值和平均值.可见,绝大部分反演结果优于等概率随机实现中的最佳结果.这说明本文算法实现了对大量等概率随机实现中有用信息的充分挖掘.
|
图 8 反演结果及绝对误差 (a)基于NN+SGS算法的反演结果; (b)反演结果的绝对误差. Fig. 8 Inversion results and absolute errors |
|
图 9 相关系数曲线 (a)地震数据的相关系数; (b)阻抗数据的相关系数. Fig. 9 Curves for correlation coefficients |
本文建立了一种新型的随机地震反演算法.一方面,神经网络的应用,使得从大量的等概率随机实现中充分挖掘到有效信息,并得到较之传统神经网络算法和通过相关系数优选等概率模型方法更好的结果;另一方面,地质统计学方法的引入,丰富了建立训练集的研究方法,不同变程的等概率随机实现,同时保证了训练集中元素的空间相关性和多样性.该方法不仅提高了随机地震反演的计算精度,还简化了神经网络的结构.数值模拟结果表明,只通过单隐层前馈神经网络就可以有效的解决一个500个阻抗参数的反演问题.
地震勘探中的噪声大多是加性噪声,由于本文方法采用随机模拟算法为神经网络提供了大量的可参考的训练集,因此可以比较有效的解决这类问题.但对于其他类型的噪声或噪声强度更大的情况,我们的研究仍有待完善.在克服神经网络的容易陷入局部极小点的情况,仍需要进行更深入的研究.另外,针对更复杂的物性参数模型,特别是真实勘探数据和真实地质模型,本文方法仍需要进一步提升,其适用性仍需检验.其中包括记录长度增长时,需要通过增加隐层节点数量或调整网络结构(谢远涛,2007)来进行反演的深入研究.由图 8可见,在连续性、背景和底层低波阻抗带等方面,反演结果还不够理想.这是因为反演的参数较多,由具有简单结构的神经网络得到的计算结果仍然具有一定误差.另外,相比于反演参数的数量,训练集的样本数量和质量仍需要提高.
致谢 感谢吉林大学杨宝俊教授的讨论和建议.感谢匿名审稿专家提出的宝贵意见.
Baddari K, Aïfa T, Djarfour N, et al. 2009. Application of a radial basis function artificial neural network to seismic data inversion. Computers & Geosciences, 35(12): 2338-2344. DOI:10.1016/j.cageo.2009.03.006 |
Cheng Q S, Chen R, Li T H. 1996. Simultaneous wavelet estimation and deconvolution of reflection seismic signals. IEEE Transactions on Geoscience and Remote Sensing, 34(2): 377-384. DOI:10.1109/36.485115 |
Deutsch C V, Cockerham P W. 1994. Practical considerations in the application of simulated annealing to stochastic simulation. Mathematical Geology, 26(1): 67-82. DOI:10.1007/BF02065876 |
Deutsch C V, Journel A G. 1994. The application of simulated annealing to stochastic reservoir modeling. SPE Advanced Technology Series, 2(2): 222-227. DOI:10.2118/24754-PA |
Dubrule O, Thibaut M, Lamy P, et al. 1998. Geostatistical reservoir characterization constrained by 3D seismic data. Petroleum Geoscience, 4(2): 121-128. DOI:10.1144/petgeo.4.2.121 |
Fu L Y. 2004. Joint inversion of seismic data for acoustic impedance. Geophysics, 69(4): 994-1004. DOI:10.1190/1.1778242 |
Haas A, Dubrule O. 1994. Geostatistical inversion-a sequential method of stochastic reservoir modelling constrained by seismic data. First Break, 12(11): 561-569. DOI:10.3997/1365-2397.1994034 |
Leite E P, Vidal A C. 2011. 3D porosity prediction from seismic inversion and neural networks. Computers & Geosciences, 37(8): 1174-1180. DOI:10.1016/j.cageo.2010.08.001 |
Lines L R, Treitel S. 1984. A review of least-squares inversion and its application to geophysical problems. Geophysical Prospecting, 32(2): 159-186. DOI:10.1111/j.1365-2478.1984.tb00726.x |
Liu C J, Yin X Y, Wang B L. 2016. Seismic stochastic inversion based on hybrid genetic algorithm.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, doi: 10.1190/IGCBeijing2016-114.
|
Liu Z P, Liu J Q. 1998. Seismic-controlled nonlinear extrapolation of well parameters using neural networks. Geophysics, 63(6): 2035-2041. DOI:10.1190/1.1444496 |
Manoj C, Nagarajan N. 2003. The application of artificial neural networks to magnetotelluric time-series analysis. Geophysical Journal International, 153(2): 409-423. DOI:10.1046/j.1365-246X.2003.01902.x |
Pan X P, Zhang G Z, Yin X Y. 2018. Probabilistic seismic inversion for reservoir fracture and petrophysical parameters driven by rock-physics models. Chinese Journal of Geophysics (in Chinese), 61(2): 683-696. DOI:10.6038/cjg2018K0759 |
Poulton M M. 2002. Neural networks as an intelligence amplification tool:A review of applications. Geophysics, 67(3): 979-993. DOI:10.1190/1.1484539 |
Robinson G. 2001. Stochastic seismic inversion applied to reservoir characterization. CSEG Recorder, 26(1): 38-40. |
Rowbotham P S, Marion D, Lamy P, et al. 2003. Multidisciplinary stochastic impedance inversion:integrating geological understanding and capturing reservoir uncertainty. Petroleum Geoscience, 9(4): 287-294. DOI:10.1144/1354-079302-490 |
Sabeti H, Moradzadeh A, Ardejani F D, et al. 2017. A new stochastic 3D seismic inversion using direct sequential simulation and co-simulation in a genetic algorithm framework. Journal of Mining and Environment, 8(3): 321-335. DOI:10.22044/jme.2016.628 |
Sun S M, Peng S M. 2007. Inversion of geostatistics based on simulated annealing algorithm. Oil Geophysical Prospecting (in Chinese), 42(1): 38-43. |
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
Van Der Baan M, Jutten C. 2000. Neural networks in geophysical applications. Geophysics, 65(4): 1032-1047. DOI:10.1190/1.1444797 |
Wu M, Fu L Y, Li W X. 2008. A high-resolution nonlinear inversion method of reservoir parameters and its application to oil/gas exploration. Chinese Journal of Geophysics (in Chinese), 51(2): 546-557. |
Wu S H. 2010. Reservoir Characterization & Modeling (in Chinese). Beijing: Petroleum Industry Press.
|
Xie Y T. 2007. The determination of the number of the hidden cells and the variable selection of the neural network. Statistics & Information Forum (in Chinese), 22(6): 9-15. |
Yang X W, Zhu P M. 2017. Stochastic seismic inversion based on an improved local gradual deformation method. Computers & Geosciences, 109: 75-86. |
Zhang R, Castagna J. 2011. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition. Geophysics, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
Zhao X F, Mendel J M. 1988. Minimum-variance deconvolution using artificial neural networks.//58th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 738-741, doi: 10.1190/1.1892433.
|
潘新朋, 张广智, 印兴耀. 2018. 岩石物理驱动的储层裂缝参数与物性参数概率地震反演方法. 地球物理学报, 61(2): 683-696. DOI:10.6038/cjg2018K0759 |
孙思敏, 彭仕宓. 2007. 基于模拟退火算法的地质统计学反演方法. 石油地球物理勘探, 42(1): 38-43. DOI:10.3321/j.issn:1000-7210.2007.01.009 |
吴媚, 符力耘, 李维新. 2008. 高分辨率非线性储层物性参数反演方法和应用. 地球物理学报, 51(2): 546-557. DOI:10.3321/j.issn:0001-5733.2008.02.027 |
吴胜和. 2010. 储层表征与建模. 北京: 石油工业出版社.
|
谢远涛. 2007. 人工神经网络变量选取与隐藏单元数的确定. 统计与信息论坛, 22(6): 9-15. DOI:10.3969/j.issn.1007-3116.2007.06.002 |
 2019, Vol. 62
2019, Vol. 62


