2. 中石化石油工程地球物理有限公司胜利分公司, 山东东营 257088;
3. 中原油田分公司物探研究院, 河南濮阳 457001
2. SGC Shengli, Shandong Dongying 257088, China;
3. Geophysical Exploration Research Institute of Zhongyuan Oilfield Company, Henan Puyang 457001, China
随着石油地质理论与地震处理解释技术的进步、地震与钻探设备的发展,现阶段石油工业为保持稳产或提高产量,地震勘探目标逐渐转向深层、复杂构造、地层和岩性圈闭油气藏(印兴耀等,2013;林承焰等,2013;程冰洁等,2012),因此对后期的叠前偏移成像等处理技术提出更高要求.而这些处理技术均要求地震勘探数据均匀、对称和波场连续无假频采样,物理属性规则分布,不完整、不规则数据的规则化在地震数据处理中也就显得尤为重要.
基于数学变换的地震数据规则化重构方法是目前应用最为广泛的一种重构方法(熊翥,2012),其基本思想是把地震数据变换到各种不同的数据域,如Radon域(Hampson,1986)、Fourier域(Duijndam et al., 1999;孟小红等,2008)、Wavelet域(崔兴福等,2003)、Curvelet域(Hennenfent and Herrmann, 2005;曹静杰和王本锋,2015)等,进行数据插值和规则化处理,然后通过反变换得到理想规则的地震数据,其优势是基于稀疏变换,不需要各种地质、地球物理等先验信息,对于有限带宽的采样数据,能够获得很好的重建结果.但由于需要满足线性同相轴假设条件,在处理非规则地震数据时该类方法抗假频性能较差.
压缩感知理论(Donoho,2006;Candès et al., 2006)打破了香农采样定理的制约,可用较少的数据实现高精度的完整信号重构.地震数据可以通过数学变换进行稀疏表示,满足压缩感知应用于数据重建的前提条件,因此,近年来发展了一系列结合傅里叶变换(Zhang et al., 2013)、小波变换(郭念民等,2014)、曲波变换(Herrmann and Hennenfent, 2008;Ma,2011;白兰淑等,2014)、Contourlet变换(张良等,2017b)和Shearlet变换(张良等,2017a)等数学变换的地震数据重建方法.形态成分分析(Morphological Component Analysis,MCA)方法是Starck等(2004)提出的一种类似于混叠信号盲分离的信号分解方法,将信号分解为几种形态特征区别明显的分量来有效地逼近数据的内部结构,国内外学者先后将其应用在不完整地震数据恢复中(Herrmann and Hennenfent, 2006;李海山等,2012;Du and Wu, 2015;Yang and Fomel, 2015),该方法采用多种字典分别稀疏表示信号的不同特征,提高了对地震数据的重构效果.近年来,压缩感知与形态成分分析联合方法被应用于数据分离(Donoho and Kutyniok, 2013;Kutyniok,2013)、地震数据噪声衰减(Chen et al., 2016)及图像修复(Candès et al., 2011;Studer et al., 2012)中,通过不同字典的线性组合对信号的不同特征分别进行稀疏表示,再结合各种稀疏恢复算法即可去除信号中存在的随机噪声或恢复丢失的图像信息.但是线性结合会取各类字典单独使用时的平衡,而不是综合最优.
对于深反射地震剖面来说,大都布置在地质构造比较复杂的区段,复杂的地质构造使深反射地震剖面上的波组特征复杂,这些采用单一、固定基函数或者各种基函数简单的线性组合不能最有效地表征数据的内部结构特征.为了提高对图像精细信息的识别能力,Aharon等(2006)提出自适应字典学习方法对图像进行自适应的稀疏表示方法,能够较好的保留精细信息.为了快速得到字典,同时控制字典的自由度,Cai等(2014)提出了基于数据驱动紧框架理论(Data Driven Tight Frame,DDTF),Liang等(2014)和Yu等(2015, 2016)将紧框架字典作为稀疏表示基,再通过凸集映射算法(Projection Onto Convex Sets,POCS)重构地震数据,实现了复杂结构信息的精确恢复.该字典学习适用于数据局部具有复杂结构的情形,与全局信息的关联较差(于四伟,2017).
综上所述,结合MCA和压缩感知的优势,本文提出了一种改进的形态成分分析方法.通过不同的字典稀疏描述复杂构造的局部特征和全局信息,同时对各稀疏字典进行加权,结合压缩感知理论,在迭代过程中根据数据自身特点不断调整各稀疏变换字典在稀疏描述中的权重,实现对复杂构造地震数据的最佳稀疏描述,使得地震数据的各种特征都可以被精确的重构出来,从而实现对复杂缺失地震数据的高精度恢复.
1 基于MCA理论的重构思想MCA理论的核心形态多样性(Morphological Diversity)引入了一个新的数学建模框架,既可以得到信号的最稀疏表示,也可以得到利用字典结构的快速算法(Starck et al., 2010).其基本思想是利用大型字典中对信号显著特征的先验知识表示,大型字典由许多子字典联合,每个子字典都能稀疏描述某种类型的结构,即每个分量对应的字典仅能稀疏表示该分量,而对其他分量不能稀疏表示.例如,通过傅里叶和小波字典组合,可以很好的描述同时包含平稳和局部化特征的信号,然后引入缺失算子,通过构建并求解约束最优化问题实现对缺失数据的重建.
假设信号f∈RN可以建模为P个形态不同的成分fi之和:
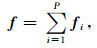
|
(1) |
式中每个fi称为形态成分.观测到的不完整信号为:
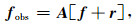
|
(2) |
其中:r~N(0, σr2)为噪声残差;f为式(1)所示的不同形态成分的组合;A∈RN×N为缺失算子.矩阵A由0、1元素构成,对应fobs中采集到的数据位置为1,缺失数据位置为0.如果各个形态成分分别在给定的P个字典Ψi下稀疏,令Ψ=[Ψ1,Ψ2,…,ΨP]为合并后的字典,则
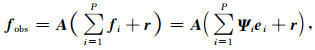
|
(3) |
式中,ei为分量fi在字典Ψi下的稀疏表示.
通过求解约束最优化问题即可实现对缺失数据的重建(Fadili et al., 2009):
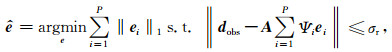
|
(4) |
式中σr为噪声均方差,ê为估计的稀疏域系数,通过该估计值可以得到的完整信号.
基于MCA理论的重构方法使用不同字典的线性组合描述信号,每个字典偏向于其对应的特征,这样就可以使信号的各种特征都能得到最精确的表示,从而实现对不完整地震数据的高效重构.但是该方法效果取决于各种字典单独使用时的平衡,对于地质构造复杂的地震信号,每种字典由于其表示的信号特征不同,简单的线性组合无法对复杂地震数据进行最有效的描述,因此重构效果并不理想.
2 基于压缩感知的加权MCA重构方法Donoho等(2004)提出的压缩感知理论指出,当信号具有稀疏性或者可以由某个稀疏域稀疏表示时,通过设计一个与稀疏变换基不相关的模型矩阵观测该信号,将高维信号投影到低维空间上,得到少量观测值,再通过稀疏促进算法求解最优问题实现信号的高概率重构.因此基于该理论的缺失地震数据重构模型不需要满足常规重构方法的那些假设条件,但需符合2个条件,信号具有稀疏性和采样矩阵的“有限等距特性”.
2.1 单一字典稀疏表示对于一个离散数据d∈RN,假设变换域集合Ψ可以对其进行稀疏表示,矩阵形式表示如下:
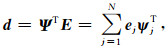
|
(5) |
其中,Ψ=[ψ1, …, ψN]∈RN为变换域的基函数向量,ΨT为Ψ的逆变换;N为基函数总个数,向量e=[e1, e2, …, eN],ej=〈d,ψj〉(j=1,…,N)为变换域系数.
根据压缩感知理论,若信号具有稀疏性,即使信号缺失的数据较多,也可由合适的测量矩阵和稀疏促进算法重构出完整信号.因此,选择合适的稀疏变换域是压缩感知理论实现准确重构的关键部分.
从严格意义上讲地震记录属于非平稳信号(Trifunac,1971).因此,学者们提出并发展了众多以小波变换和曲波变换为基础的稀疏表示方法.小波变换具有多分辨分析的特点,在时频域都具有表征信号局部特征的能力;非抽样小波变换(UWT)克服了离散小波变换在重构时产生的大量假象,可以提供丰富的时域特征信息和精确的频率局部化信息;曲波变换由于其对具有光滑奇异性的目标函数进行高效、稳定和近乎最优的表达,被认为是目前对地震信号最稀疏的表达方式之一;Contourlet变换具有良好的多分辨率特性和时频局部化特性以及良好的各向奇异性特征;Shearlet变换也是一种多尺度变换(Kittipoom et al., 2012),能够对曲线特征进行最佳的描述.但是,Contourlet变换和Shearlet变换在对地震数据进行多尺度分解时效率比较低.
表 1总结了不同的稀疏字典适用的数据特征,根据待处理数据特点可以选择最优的字典对地震数据进行稀疏表示.
|
|
表 1 不同稀疏表示方法特点对比 Table 1 Comparison of features of various sparsity transform methods |
对于地质构造简单的缺失地震数据在单一的稀疏域(Fourier、Radon、Curvelet等)即可以得到较稀疏的表示.但对于复杂地质构造的信号,单一字典的稀疏描述方式无法将信号的内部复杂结构特征全部有效的表示出来,MCA方法使用不同字典对信号内部的不同结构特征分别进行有效逼近,但是其简单的线性组合是取各类字典单独使用时的平衡,没有考虑各字典在重构过程中发挥的作用,仍然无法对复杂构造信号进行最稀疏描述.
因此本文对MCA方法进行改进,发展了基于加权MCA的稀疏表示方法,其矩阵形式表示为:
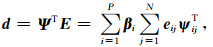
|
(6) |
其中,稀疏变换域基函数集合Ψ=[β1Ψ1, …, βPΨP],Ψi∈RN为第i个变换域基函数向量,ΨT为Ψ的逆变换,向量ei=[ei1, ei2, …, eiN],eij=〈d,ψij〉(i=1,…,P,j=1,…,N)为第i个变换域系数,N为第i个字典的基函数总个数,βi为第i个字典的权值系数,用于调整字典对信号的贡献,其变化规律与信号本身的复杂程度和选择的稀疏字典有关,一般可以选择按指数或线性规律变换.
由式(6)可以看出,基于加权MCA的稀疏表示方法是对信号的不同特征选择最佳字典组合,采用不同的稀疏域进行表示,根据信号的内部特征对各个稀疏表示方法进行加权,从而对信号进行更稀疏的描述,通过选择合适的测量矩阵和稀疏促进算法,在迭代过程中根据数据自身特点不断调整各稀疏变换字典在稀疏描述中的权重,实现对复杂信号的最优稀疏表示,最后重构出完整信号.值得一提的是,对于一个可以将信号进行最稀疏描述的庞大的最佳字典,还要面临稀疏域系数计算时间过高的问题,因此需要根据信号特点在字典大小和计算时间之间取得平衡.
2.3 模型矩阵模型矩阵由测量矩阵、约束矩阵和稀疏表示矩阵组成,其中测量矩阵和约束矩阵的乘积又称为采样矩阵.不完整信号dobs∈Rn可以看作由完整信号d通过采样矩阵Ф∈Rn×N映射得到:
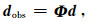
|
(7) |
式中,n为采集的信号个数,且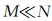
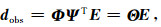
|
(8) |
式中,Θ=[Θ1, …, ΘP]为模型矩阵,其中Θi:=RMΨiT∈Rn×N.根据压缩感知理论,Θi同样需要满足有限等距性质(RIP)(Candès,2008;Baraniuk,2007),才能将N维信号第i个特征的Ki个最大值稳定地重构出来.
任何满足RIP性质(Kirachaiwanich and Liang, 2011)的矩阵均可作为采样矩阵并取得很好的重构效果,理论上该性质近乎完美,具有丰富内涵,是压缩感知采样矩阵需要满足的充分条件,但实际上很难判断一个矩阵是否满足RIP性质,也很难用该性质指导采样矩阵的设计.
压缩感知理论通常将采样矩阵分为两种:第一种为随机采样矩阵,已有学者证明了高斯随机矩阵、伯努利随机矩阵及部分傅里叶矩阵等满足RIP的性质(Baraniuk et al., 2008;Candès and Tao, 2006).从某种意义上讲,选择随机采样对于稀疏矩阵是一种最佳策略,仅需要最少的K个采样即可恢复稀疏度为v≤K×log(N/K)的信号,且分析时需要的常量都很小.第二种为非相关采样矩阵,即采样矩阵与变换基Ψ是不相关的,其不相关性可以通过计算它们之间的相关系数,μ=N1/2maxi, j(|〈Фi, Ψj〉|),μ越小,Ф与Ψ之间的相关性越小,采样所需要的数量也越少.
在实际数据采集时,大量的地震数据在连续波场中由检波器获得,高精度的仪器设备保障了时间方向的无假频密集规则采样,因此Hennenfent将测量过程看作是在Dirac基中完成的,即M:=I(I为单位矩阵),且Dirac基与傅里叶基、曲波基等有最大的不相关度(Starck et al., 2010).
2.4 稀疏促进算法及其实现压缩感知理论区别于奈奎斯特理论的线性感知问题,由于采集数据量n要小于信号长度N,重构时需要求解欠定方程组.当信号d是稀疏或可压缩的,基于加权MCA稀疏表示的不完整信号的最稀疏解描述为如下问题的解:
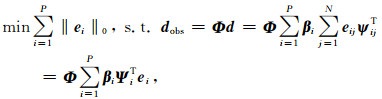
|
(9) |
式(9)为经典的NP-hard非凸优化问题,借鉴Donoho等(2006)、Elad等(2005)对非凸优化问题的处理方法,将该问题表示为约束优化问题:
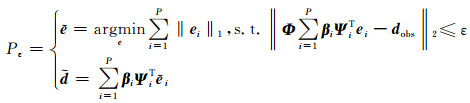
|
(10) |
进一步将式(10)所示问题转化为简单的非约束优化问题:
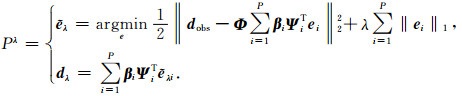
|
(11) |
式(11)描述的问题求解同样依赖于拉格朗日乘子λ,它决定了l2数据误差与l1范数在求解过程中所占权重,这样求解Pε问题就转化为通过不断降低λε调整λ解决Pλ问题,其中
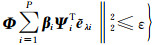
本文通过梯度下降法(Figueiredo and Nowak, 2003;Vogel,2002)求解上述问题,在迭代过程中不断减小各稀疏变换字典的阈值参数λi,最终得到近似解.具体算法如下:
输入:缺失地震数据dobs,采样矩阵Ф;
初始化:各稀疏变换字典的权重系数βi、阈值参数
迭代开始:
外循环:判断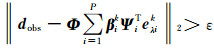
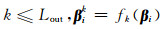
内循环:j=0 to Lin-1,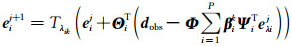
执行:k=k+1;eik=eij+1;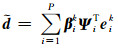
输出: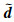
上述算法中,βik为第i个稀疏变换在第k次迭代中的权值系数,根据该稀疏变换在迭代中所起的作用逐渐递增或降低,从而改变第i个稀疏变换在逼近解中的权重;λik为第i个稀疏变换在第k次迭代的阈值,随着迭代次数的增加逐渐减小,逐渐逼近精确解,Tλik(ei):=sgn(ei)·max(0, ei-|λik|)为软阈值函数.
3 理论模型实验及方法对比针对简单构造模型数据和复杂构造模型数据,本文分别采用单一非抽样小波变换、曲波变换作为稀疏表示字典的方法、MCA作为稀疏表示方法以及本文提出的加权MCA作为稀疏表示方法结合压缩感知理论对缺失数据进行重构.
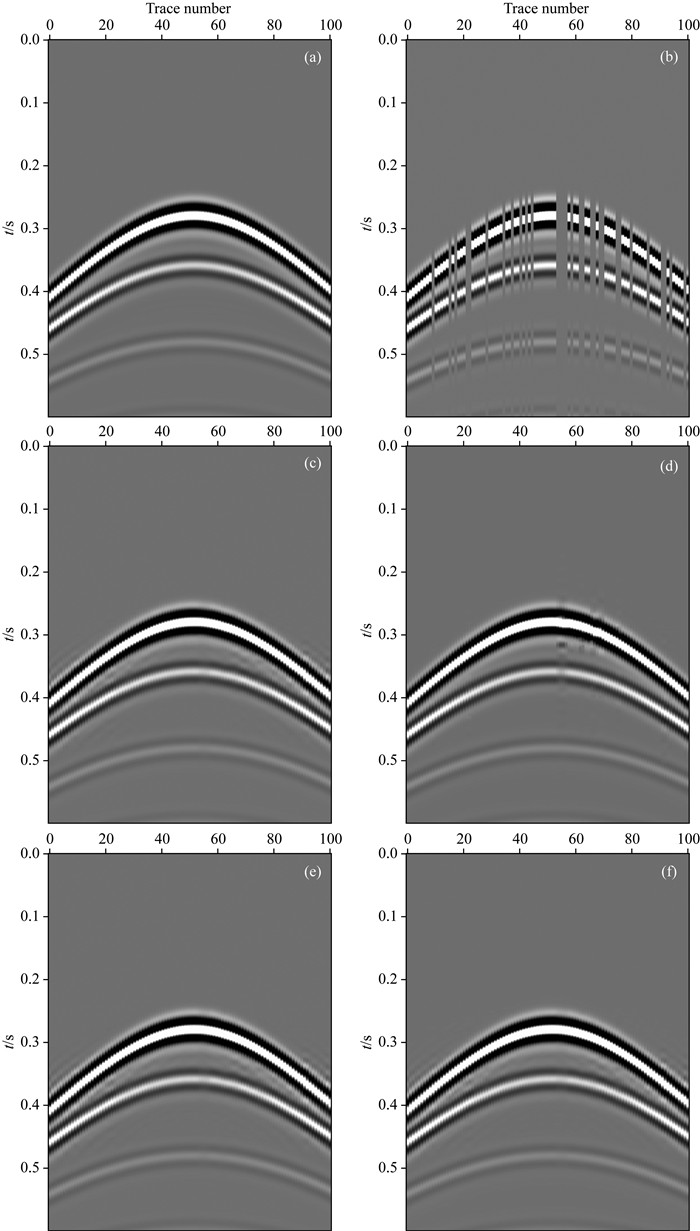
3.1 简单构造模型本文所用的简单地质构造模型如图 1a,为有限差分法模拟的单炮记录,共101道接收,道间距为25 m,时间采样个数为600,时间采样率为1 ms.图 1b为随机缺失30%的数据,图 1c-1f分别为采用单一非抽样小波变换、曲波变换作为稀疏表示字典的方法、MCA作为稀疏表示方法以及本文提出的加权MCA作为稀疏表示方法结合压缩感知理论对缺失数据进行重构的结果.
|
图 1 简单构造地震数据 (a)原始模拟数据;(b)随机采样模拟数据;(c)、(d)、(e)、(f)分别为非抽样小波变换、曲波变换、MCA方法及本文方法的重构结果. Fig. 1 Seismic data of simple structure (a) Original data to be simulated; (b) Simulation data sampled randomly; (c)-(f) Reconstructed seismic data by UWT, Curvelet, MCA and the method of this paper, respectively. |
从图中可以看出,本文提出的方法与其余三种方法均能够很好的将缺失的地震数据重构出来.本文还对四种方法对缺失数据恢复的效果进行了定量的对比,重构的质量(Hennenfent and Herrmann, 2006;Naghizadeh and Sacchi, 2010)定义如下:
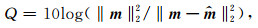
|
(12) |
其中的m为完整地震数据,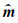
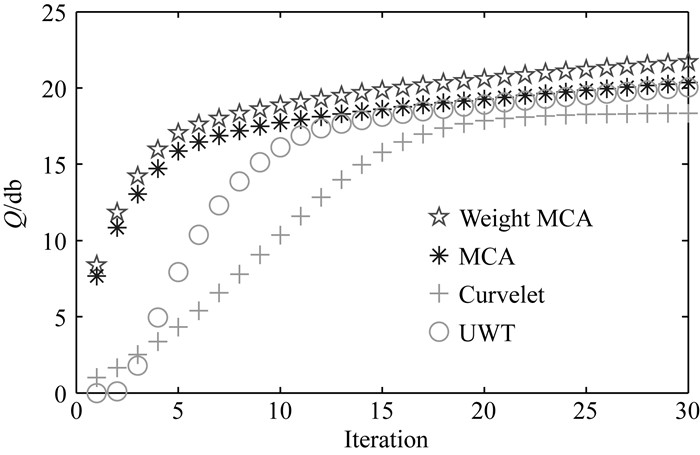
|
图 2 非抽样小波变换、曲波变换、MCA方法和本文方法对简单构造模型的重构质量及收敛速度对比图 Fig. 2 Comparison of reconstruction quality and convergence velocity of simple construction model by UWT, Curvelet, MCA and the method of this paper |
为了进一步说明本文方法在高丢失地震数据重构中的优势,我们对不同程度缺失道的重构结果进行了对比.对图 1a所示的单炮记录分别随机缺失40%、50%、60%和70%,重构效果如图 3a-3d所示.由图可见,对于缺失40%、50%及60%的地震数据本文提出的方法都能够很好的将其重构出来;而对于缺失70%的地震数据,曲波在重构时会出现严重的边界效应,因此其两侧的数据恢复的效果较差.图 4给出本文方法对不同采样率地震数据的重构质量及其收敛速度,可以看出缺失数据在40%和50%时收敛速度较慢,需要迭代25次左右,随着缺失数据的增多,迭代的收敛速度提高,8次左右就可以达到最大值,但是其重构质量降低.
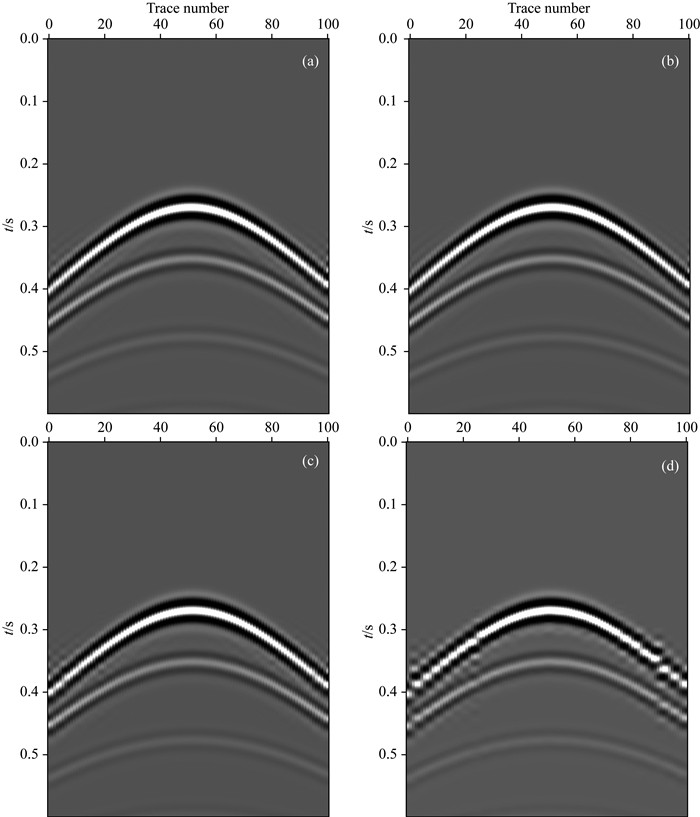
|
图 3 简单构造地震数据(a)缺失40%重构结果,(b)缺失50%重构结果,(c)缺失60%重构结果,(d)缺失70%重构结果 Fig. 3 Reconstructed seismic data of simple structure. (a)-(d) Missing 40%, 50%, 60%, and 70% of data, respectively |
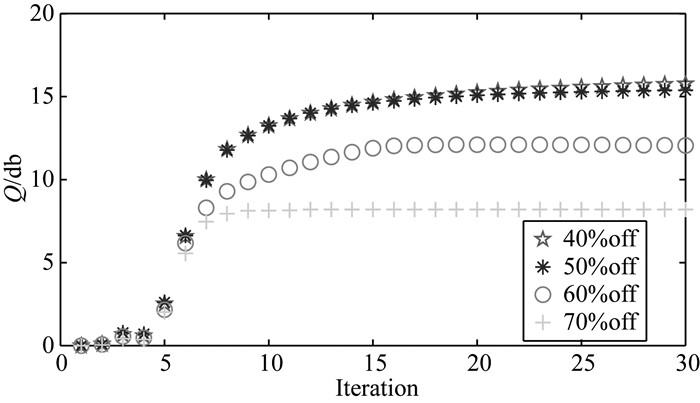
|
图 4 本文方法对简单构造模型随机采样60%、50%、40%及30%的重构质量及收敛速度对比图 Fig. 4 Comparison of reconstruction quality and convergence velocity with random sub-sampling 60%, 50%, 40%, and 30% for simple structural model using the method of this paper |
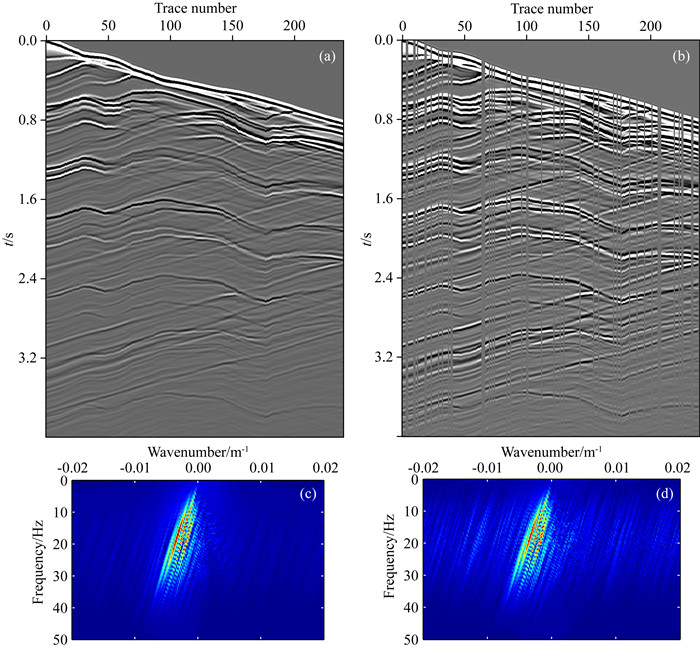
本文所用的复杂地质构造模型如图 5a,该模型为采用有限差分法模拟的单炮记录,共240道接收,道间距为25 m,时间采样个数为1000,时间采样率为4 ms.图 5b为随机缺失30%的数据,图 5c和图 5d分别为其对应的频谱图.从图中可以看出,完整的地震数据在波数域是稀疏的,其能量主要集中在少量波数成分上,而缺失地震数据的频谱能量则向各个波数进行分散,出现了明显的空间假频.
|
图 5 复杂构造地震数据 (a)原始模拟数据;(b)随机采样模拟数据;(c)、(d)分别为(a)、(b)对应的频谱图. Fig. 5 Seismic data of complex structure (a) Original data to be simulated; (b) Simulated data by random sampling; (c) and (d) Spectra corresponding to (a) and (b), respectively. |
对信号进行稀疏表示既是MCA方法重构的核心,也是压缩感知重构的重要前提之一.图 5a所示的地震剖面,由于地质构造复杂,含有的信号特征丰富,不仅含有弯曲的同相轴,还存在局部奇异点,采用单一变换不能最有效表示剖面中所包含的这些特征,需要选择特定的变换对其进行最优表示.
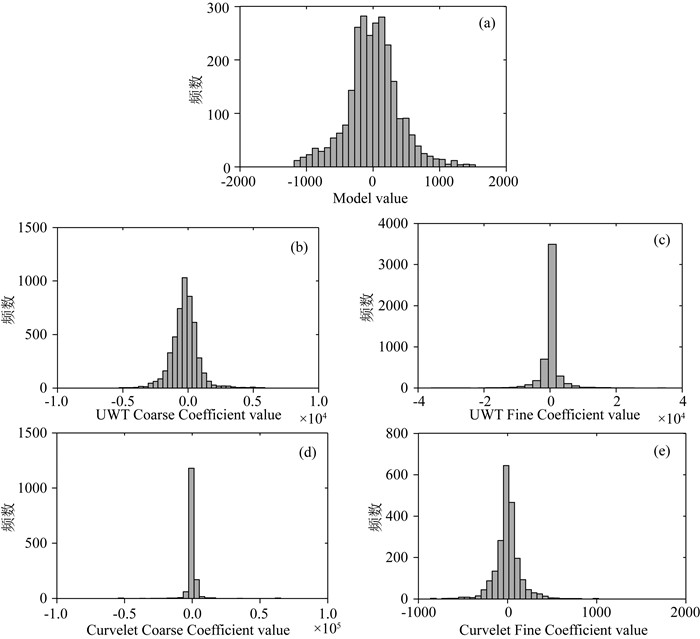
综合考虑复杂地震数据的自身特点和计算复杂度,本文选择两种字典对地震信号进行稀疏表示,非抽样小波变换和曲波变换.图 6a为模型数据在时间域中的统计分布直方图,可以看出数据值分布较分散,只有一小部分数值为零,因此模型数据在时间域是不稀疏的;图 6b和图 6c分别为模型数据在非抽样小波域中粗尺度和细尺度下系数的统计分布直方图,该变换粗尺度系数的非零值较多、细尺度系数的零值较多,因此其对模型数据的粗尺度特征稀疏性描述较差,而对细尺度特征的稀疏性描述较好,即对局部奇异特征能够进行较好的稀疏表示;图 6d和图 6e分别为模型数据在曲波域中粗尺度和细尺度下系数的统计分布直方图,与非抽样小波域系数的特征相反,曲波域粗尺度系数基本分布在零值附近,且以零值居多,而细尺度系数的非零值相对较多一点,可见该变换域对模型数据的粗尺度特征稀疏性描述较好,对细尺度特征的稀疏性描述较差.因此,本文用非抽样小波变换字典稀疏表示地震记录的局部奇异点,用曲波变换字典稀疏表示地震记录的弯曲同相轴等多方向的线状变化特征.
|
图 6 统计直方图 (a)模型数据时域;(b)、(c)模型数据分别在非抽样小波域粗尺度和细尺度下;(d)、(e)模型数据分别在曲波域粗尺度和细尺度下. Fig. 6 Statistical histograms (a) Synthetic data in time domain; (b) Coarse scale in UWT domain; (c) Fine scale in UWT domain; (d) Coarse scale in Curvelet domain; (e) Fine scale in Curvelet domain. |
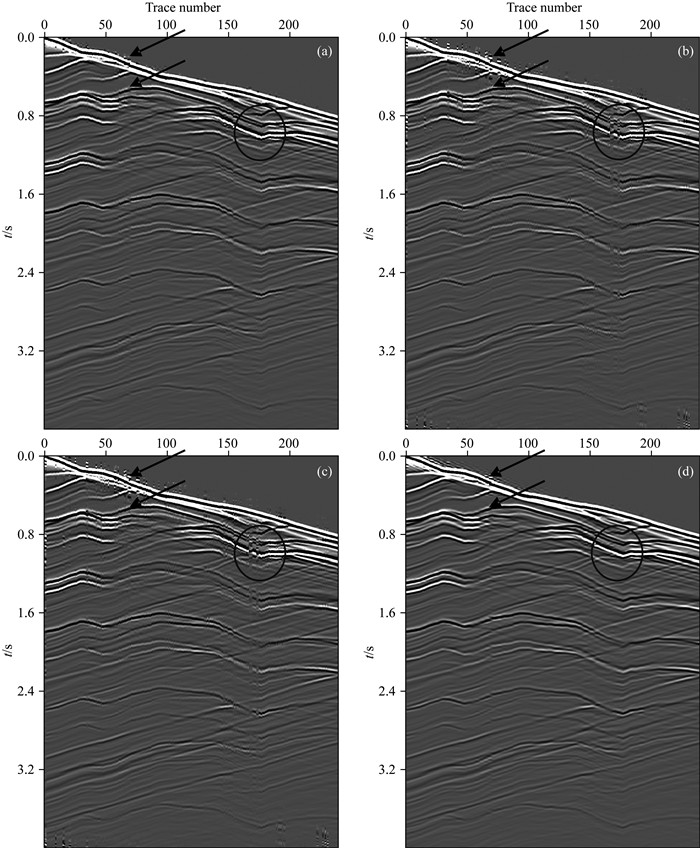
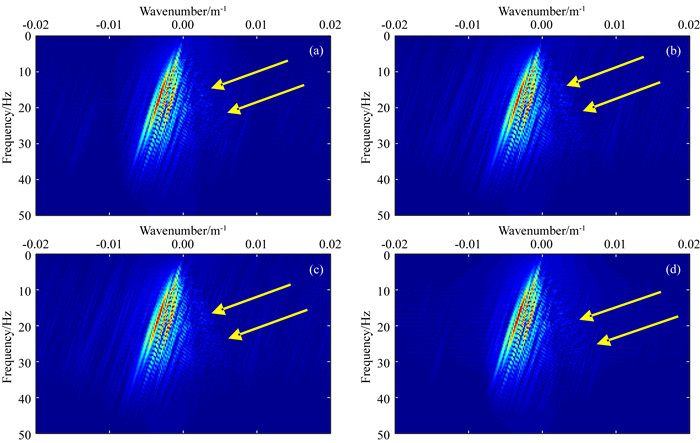
分别用单一非抽样小波变换、曲波变换作为稀疏表示字典的方法、MCA作为稀疏表示方法以及本文提出的加权MCA作为稀疏表示方法结合压缩感知理论对缺失数据进行重构,图 7为得到的数据重建结果,图 8为四种重构结果对应的频谱图.
|
图 7 模型测试结果 (a)非抽样小波变换作为稀疏字典迭代恢复结果;(b)曲波变换作为稀疏字典迭代恢复结果;(c) MCA方法迭代恢复结果;(d)加权MCA方法迭代恢复结果. Fig. 7 Reconstruction results of synthetic data by four methods (a) UWT; (b) Curvelet; (c) MCA; (d) Method of this paper. |
|
图 8 模型数据恢复结果的频谱图 (a)非抽样小波变换;(b)曲波变换;(c) MCA方法;(d)本文方法. Fig. 8 Spectra of reconstruction results for synthetic data by four methods (a) UWT; (b) Curvelet; (c) MCA; (d) Method of this paper. |
图 7a为用非抽样小波做稀疏字典重构的地震数据,可以看出浅层的强能量轴和地质构造较复杂的数据都得到了较好的恢复,但是对构造较简单、缺失道数较多位置的数据恢复的效果较差,由图 8a的频谱图可以看出,由于数据缺失分散的能量被很好的集中到了低波数部分,但是分散在高波数的一些较低的能量被当作噪声切掉.
图 7b为用曲波做稀疏字典重构的地震数据,可以看出对于构造较简单的信号,即使缺失的道数较多也可以被较好的恢复出来,但是由于变换无法稀疏表示局部的细节特征,使得缺失的地震数据中结构较复杂的信号无法得到恢复,由图 8b的频谱图可以看出,部分能量得到了一定的恢复,但是还是有一部分能量分散在不同的波数成分中.
图 7c为使用MCA方法对缺失数据进行重构的结果,即曲波变换与非抽样小波变换的线性组合对缺失的模型数据进行稀疏描述,通过与图 7a和图 7b对比可以看出,恢复的效果介于前两种方法之间,对浅层的强能量轴的恢复效果略好于曲波做稀疏字典的方法,地质构造复杂的缺失数据也部分得到了恢复,从图 8c的频谱图中也可以看出,该方法恢复的能量较前两种方法集中.
图 7d为应用本文提出的加权MCA方法对缺失数据进行稀疏表示得到的重构结果.如2.4节所述,在恢复过程中迭代初期主要是恢复描述其结构特征的稀疏近似解,且由3.2.1节的分析和上述分别用两种字典对模型数据的恢复结果的分析可知,曲波变换能够更稀疏的描述该特征,因此在迭代初期以曲波字典为主,然后逐渐减小曲波字典的作用,增加非抽样小波字典的作用,即增加数据中描述复杂构造的能量信息,不断迭代得到真实的逼近解.本文对两种字典的权重调整如下:
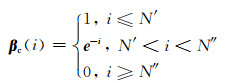
|
(13a) |
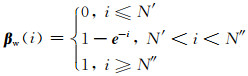
|
(13b) |
式中,βc(i)、βw(i)分别为曲波变换和非抽样小波变换的第i次权重,N′ < N″分别为小于Lout的某次迭代.需要说明的是,“稀疏字典的选择”对加权参数具有一定的影响,选择的字典不同,加权参数的变换规律也受到一定的影响,重构效果也会有所不同.本文β按指数规律变化,是由经验选取的.
相比前三种方法,本文提出的方法重构的同相轴的连续性和光滑性都得到了很大的提高,对缺失道数较多的位置也能够准确恢复缺失的数据.尤其是对浅层的强能量轴和构造变化复杂的位置,都能较好的恢复.从图 8d的频谱图中也可以看出,由于数据缺失造成的空间假频得到了很好的压制,对于部分能量较弱的频谱也得到了一定的提高.
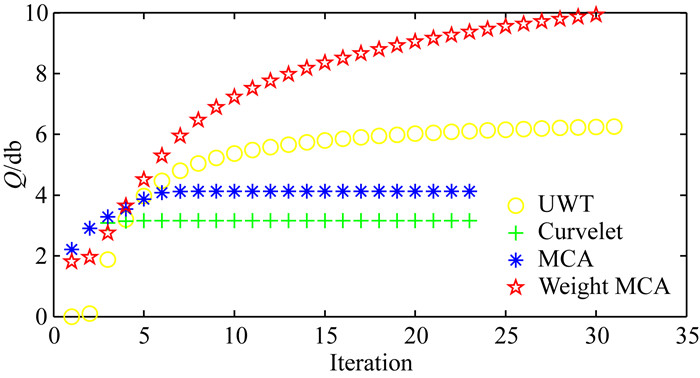
图 9为四种方法的重构质量和收敛速度对比,可以看出曲波变换能够对粗尺度的信息进行稀疏描述,因此在迭代初期对数据重构的质量要高一些,但是由于其对细尺度的信息稀疏描述限制,导致在后期的迭代过程中无法将更多的细节信息加入到迭代数据中,最终的恢复效果很差;非抽样小波变换的处理效果恰恰相反,在迭代初期由于不能对粗尺度的信息稀疏表示,迭代质量因子很小,在后来的迭代过程中逐渐加入细节信息,使迭代的效果逐渐变好;MCA方法是前两种方法的线性组合,迭代初期的效果要好于前两种方法,但是随着迭代次数的增加,由于粗尺度信息的能量偏强,非抽样小波变换没有发挥太多作用,对于构造复杂的缺失数据该组合并没有发挥两种稀疏字典各自的优势;本文提出的方法在迭代后期减小了曲波变换对重构的作用,使得最后的重构效果得到了大幅的提高.正演模型数据试验验证了本文提出的方法对恢复复杂构造随机缺失地震数据的有效性.
|
图 9 非抽样小波变换、曲波变换、MCA方法和本文方法复杂构造模型的重构质量及收敛速度对比图 Fig. 9 Comparison of reconstruction quality and convergence velocity for complex structural model by UWT, Curvelet, MCA and method of this paper |
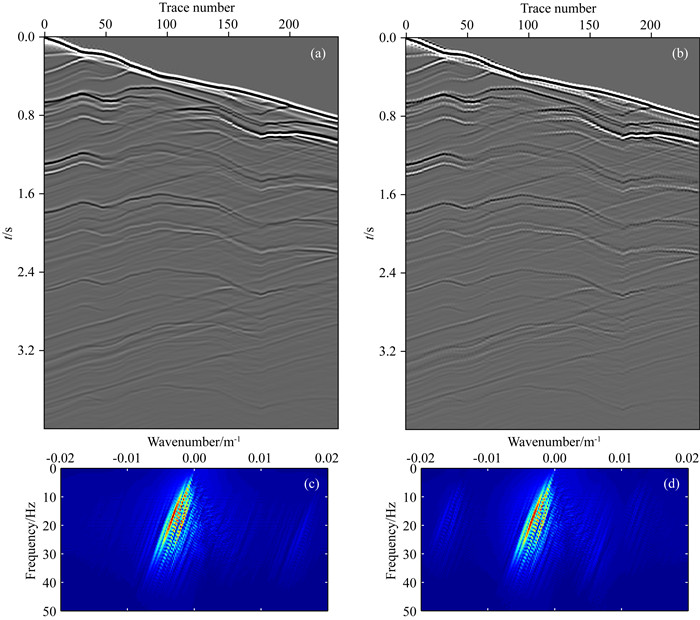
为了进一步凸显本文方法对复杂构造情况下地震数据重构的适应性,对规则采样下不同程度缺失的数据进行了测试,并对其抗假频重构的效果进行了分析对比.图 10展示了图 5a所示的单炮记录高缺失情况下的数据重构结果及频谱结果.对于采样50%地震数据本文提出的方法都能够很好的将局部复杂构造信息和线状特征信息精确的重构出来,空间假频也得到了很好的抑制;对于采样30%的地震数据,连续性较好的线状特征信息也可以恢复出来,空间假频得到部分抑制,但是由于构造复杂且缺失的数据过多,有一部分能量分散在高波数中,如图 10d所示.由此可见,本文方法对于复杂构造情况下的高缺失数据重构具有较强的适应性.
|
图 10 本文方法对复杂模型规则采样50%及30%的重构结果及频谱图 (a)规则采样50%;(b)规则采样30%;(c)、(d)为(a)、(b)对应的频谱图. Fig. 10 Reconstruction results of complex model by the method of this paper (a) Regular sampling 50%; (b) Regular sampling 30%; (c) and (d) Spectra corresponding to (a) and (b), respectively. |
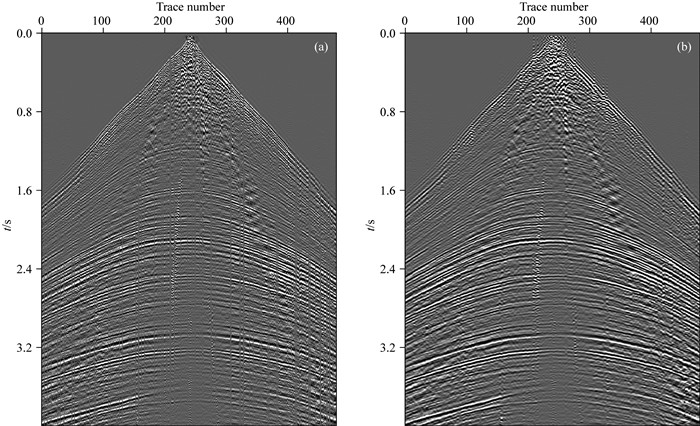
为了验证本方法的有效性和实用性,我们对某地区的实际资料进行了试处理.实际数据比模型数据要复杂,且不同的数据的复杂程度也不一样.本文选择的是某单炮记录,共480道,每道1000个时间采样点,采样间隔为4 ms,如图 11a所示,在局部地段存在坏道,缺失地震道较多,且既有强能量、连续性好的同相轴,也有能力弱、连续性差的信号,如不较好地重构地震道,将对储层研究产生严重影响.应用本文提出的方法对该数据进行处理,得到如图 11b所示的地震剖面.可以看出经恢复后,各缺失道和坏道均得到了很好的恢复,地震同相轴光滑、连续,其中深层弱信号的同相轴恢复效果最为明显.
|
图 11 实际资料测试效果 (a)原始地震记录;(b)重构后地震数据. Fig. 11 Test results of real data (a) Original seismic record; (b) Reconstructed seismic data. |
本文提出了面向复杂地质构造的缺失地震数据重构方法,即在MCA理论与压缩感知理论的基础上,针对数据自身特点选择合适的稀疏变换字典,通过设置各种稀疏变换字典在其稀疏描述中的权重,实现对复杂构造的地震数据的最稀疏描述,在迭代过程中也不断调整各稀疏表示方法的权值系数,使得地震数据的各种特征都可以被精确的重构出来.文章详细比较了基于非抽样小波变换、曲波变换以及MCA理论的压缩感知重构方法与本文提出的方法在缺失的合成数据中的重建效果,结果表明相比前三种方法,本文提出的方法重构质量高、反演结果稳定可靠,抗假频性能好,最后的实际地震数据重建结果验证了本文方法在实际资料重建中的准确性和有效性.
Aharon M, Elad M, Bruckstein A. 2006. rmK-SVD:An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
Bai L S, Liu Y K, Lu H Y, et al. 2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing. Chinese Journal of Geophysics (in Chinese), 57(9): 2937-2945. DOI:10.6038/cjg20140919 |
Baraniuk R. 2007. A lecture on compressive sensing. IEEE Signal Processing Magazine, 24(4): 118-121. DOI:10.1109/MSP.2007.4286571 |
Baraniuk R, Davenport M, DeVore R, et al. 2008. A simple proof of the restricted isometry property for random matrices. Constructive Approximation, 28(3): 253-263. DOI:10.1007/s00365-007-9003-x |
Cai J F, Ji H, Shen Z W, et al. 2014. Data-driven tight frame construction and image denoising. Applied and Computational Harmonic Analysis, 37(1): 89-105. DOI:10.1016/j.acha.2013.10.001 |
Candès E J, Romberg J, Tao T. 2006. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
Candès E J, Tao T. 2006. Near-optimal signal recovery from random projections:Universal encoding strategies?. IEEE Transactions on Information Theory, 52(12): 5406-5425. DOI:10.1109/TIT.2006.885507 |
Candès E J. 2008. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Mathematique, 346(9-10): 589-592. DOI:10.1016/j.crma.2008.03.014 |
Candès E J, Eldar Y C, Needell D, et al. 2011. Compressed sensing with coherent and redundant dictionaries. Applied and Computational Harmonic Analysis, 31(1): 59-73. DOI:10.1016/j.acha.2010.10.002 |
Cao J J, Wang B F. 2015. An improved projection onto convex sets method for simultaneous interpolation and denoising. Chinese Journal of Geophysics (in Chinese), 58(8): 2936-2947. DOI:10.6038/cjg20150826 |
Chen Y K, Ma J W, Fomel S. 2016. Double-sparsity dictionary for seismic noise attenuation. Geophysics, 81(2): V193-V206. DOI:10.1190/GEO2014-0525.1 |
Cheng B J, Xu T J, Li S G. 2012. Research and application of frequency dependent AVO analysis for gas recognition. Chinese Journal of Geophysics (in Chinese), 55(2): 608-613. DOI:10.6038/j.issn.0001-5733.2012.02.023 |
Cui X F, Liu D Q, Zhang G Q. 2003. Wavelet transform to achieve seismic trace interpolation. Oil Geophysical Prospecting (in Chinese), 38(S1): 93-97. DOI:10.13810/j.cnki.issn.1000-7210.2003.s1.019 |
Donoho D L. 2006. Compressed sensing. IEEE Transactions on Information Theory, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
Donoho D L, Kutyniok G. 2013. Microlocal analysis of the geometric separation problem. Communication on Pure and Applied Mathematics, 66(1): 1-47. DOI:10.1002/cpa.21418 |
Du Z Y, Wu G C. 2015. Theory and application of irregular seismic data reconstruction based on MCA.//85th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts 3880-3884, doi: 10.1190/segam2015-5854455.1.
|
Duijndam A J W, Schonewille M A, Hindriks C O H. 1999. Reconstruction of band-limited signals, irregularly sampled along one spatial direction. Geophysics, 64(2): 524-538. DOI:10.1190/1.1444559 |
Elad M, Starck J L, Querre P, et al. 2005. Simultaneous cartoon and texture image inpainting using morphological component analysis (MCA). Applied and Computational Harmonic Analysis, 19(3): 340-358. DOI:10.1016/j.acha.2005.03.005 |
Fadili M J, Starck J L, Murtagh F. 2009. Inpainting and zooming using sparse representations. Computer Journal, 52(1): 64-79. DOI:10.1093/comjnl/bxm055 |
Figueiredo M A T, Nowak R D. 2003. An EM algorithm for wavelet-based image restoration. IEEE Transactions on Image Processing, 12(8): 906-916. DOI:10.1109/TIP.2003.814255 |
Guo N M, Li H S, Feng X M, et al. 2014. Pre-stack seismic data reconstruction based on the undecimated wavelet transform. Oil Geophysical Prospecting (in Chinese), 49(3): 508-516. DOI:10.13810/j.cnki.issn.1000-7210.2014.03.014 |
Hampson D. 1986. Inverse velocity stacking for multiple elimination.//56th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, doi: 10.1190/1.1893060.
|
Hennenfent G, Herrmann F. 2005. Sparseness-constrained data continuation with frames: applications to missing traces and aliased signals in 2/3-D.//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 24: 2162-2165, doi: 10.1190/1.2148142.
|
Hennenfent G, Herrmann F J. 2006. Seismic denoising with nonuniformly sampled curvelets. Computing in Science & Engineering, 8(3): 16-25. DOI:10.1109/MCSE.2006.49 |
Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
Kirachaiwanich D, Liang Q L. 2011. Compressive sensing: to compress or not to compress.//Proceedings of 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA: IEEE, 809-813, doi: 10.1109/ACSSC.2011.6190119.
|
Kittipoom P, Kutyniok G, Lim W Q. 2012. Construction of compactly supported shearlet frames. Construction Approximation, 35(1): 21-72. DOI:10.1007/s00365-011-9142-y |
Kutyniok G. 2013. Theory and applications of compressed sensing. GAMM-Mitteilungen, 36(1): 79-101. DOI:10.1002/gamm.201310005 |
Li H S, Wu G C, Yin X Y. 2012. Morphological component analysis in seismic data reconstruction. Oil Geophysical Prospecting (in Chinese), 47(2): 236-243. DOI:10.13810/j.cnki.issn.1000-7210.2012.02.020 |
Liang J W, Ma J W, Zhang X Q. 2014. Seismic data restoration via data-driven tight frame. Geophysics, 79(3): V65-V74. DOI:10.1190/geo2013-0252.1 |
Lin C Y, Dong C M, Ren L H, et al. 2013. Development of reservoir characterization and its stimulation. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 37(5): 22-27. DOI:10.3969/j.issn.1673-5005.2013.05.004 |
Ma J W. 2011. Improved iterative Curvelet thresholding for compressed sensing and measurement. IEEE Transactions on Instrumentation and Measurement, 60(1): 126-136. DOI:10.1109/TIM.2010.2049221 |
Meng X H, Guo L H, Zhang Z F, et al. 2008. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform. Chinese Journal of Geophysics (in Chinese), 51(1): 235-241. DOI:10.3321/j.issn:0001-5733.2008.01.029 |
Naghizadeh M, Sacchi M D. 2010. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data. Geophysics, 75(6): WB189-WB202,. DOI:10.1190/1.3509468 |
Starck J L, Elad M, Donoho D. 2004. Redundant multiscale transforms and their application for morphological component separation. Advances in Imaging and Electron Physics, 132: 287-348. DOI:10.1016/S1076-5670(04)32006-9 |
Starck J L, Murtagh F, Fadili J M. 2010. Sparse Image and Signal Processing:Wavelets, Curvelets, Morphological Diversity. Cambridge: Cambridge University Press.
|
Studer C, Kuppinger P, Pope G, et al. 2012. Recovery of sparsely corrupted signals. IEEE Transactions on Information Theory, 58(5): 3115-3130. DOI:10.1109/TIT.2011.2179701 |
Trifunac M D. 1971. Response envelope spectrum and interpretation of strong earthquake ground motion. Bulletin of the Seismological Society of America, 61(2): 343-356. |
Vogel C R. 2002. Computational Methods for Inverse Problems. Philadelphia: Society for Industrial and Applied Mathematics.
|
Xiong Z. 2012. Seismic exploration for strati-lithologic reservoirs. Oil Geophysical Prospecting (in Chinese), 47(1): 1-18. DOI:10.13810/j.cnki.issn.1000-7210.2012.01.009 |
Yang P L, Fomel S. 2015. Seislet-based morphological component analysis using scale-dependent exponential shrinkage. Journal of Applied Geophysics, 118: 66-74. DOI:10.1016/j.jappgeo.2015.04.003 |
Yin X Y, Zhang S X, Zhang F. 2013. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification. Chinese Journal of Geophysics (in Chinese), 56(7): 2378-2390. DOI:10.6038/cjg20130724 |
Yu S W, Ma J W, Zhang X Q, et al. 2015. Interpolation and denoising of high-dimensional seismic data by learning a tight frame. Geophysics, 80(5): V119-V132. DOI:10.1190/geo2014-0396.1 |
Yu S W, Ma J W, Osher S. 2016. Monte Carlo data-driven tight frame for seismic data recovery. Geophysics, 81(4): V327-V340. DOI:10.1190/geo2015-0343.1 |
Yu S W. 2017. Seismic data reconstruction based on adaptive sparse inversion[Ph. D. thesis] (in Chinese). Harbin: Harbin Institute of Technology.
|
Zhang H, Chen X H, Wu X M. 2013. Seismic data reconstruction based on CS and Fourier theory. Applied Geophysics, 10(2): 170-180. DOI:10.1007/s11770-013-0375-3 |
Zhang L, Han L G, Xu D X, et al. 2017a. Seismic data reconstruction with Shearlet transform based on compressed sensing technology. Oil Geophysical Prospecting (in Chinese), 52(2): 220-225. DOI:10.13810/j.cnki.issn.1000-7210.2017.02.004 |
Zhang L, Han L G, Liu Z G, et al. 2017b. Seismic data reconstruction based on compressed sensing and Contourlet transform. Geophysical Prospecting for Petroleum (in Chinese), 56(6): 804-811. DOI:10.3969/j.issn.1000-1441.2017.06.005 |
白兰淑, 刘伊克, 卢回忆, 等. 2014. 基于压缩感知的Curvelet域联合迭代地震数据重建. 地球物理学报, 57(9): 2937-2945. DOI:10.6038/cjg20140919 |
曹静杰, 王本锋. 2015. 基于一种改进凸集投影方法的地震数据同时插值和去噪. 地球物理学报, 58(8): 2936-2947. DOI:10.6038/cjg20150826 |
程冰洁, 徐天吉, 李曙光. 2012. 频变AVO含气性识别技术研究与应用. 地球物理学报, 55(2): 608-613. DOI:10.6038/j.issn.0001-5733.2012.02.023 |
崔兴福, 刘东奇, 张关泉. 2003. 小波变换实现地震道内插. 石油地球物理勘探, 38(S1): 93-97. DOI:10.13810/j.cnki.issn.1000-7210.2003.s1.019 |
郭念民, 李海山, 冯雪梅, 等. 2014. 非抽样离散小波变换叠前地震数据重建方法. 石油地球物理勘探, 49(3): 508-516. DOI:10.13810/j.cnki.issn.1000-7210.2014.03.014 |
李海山, 吴国忱, 印兴耀. 2012. 形态分量分析在地震数据重建中的应用. 石油地球物理勘探, 47(2): 236-243. DOI:10.13810/j.cnki.issn.1000-7210.2012.02.020 |
林承焰, 董春梅, 任丽华, 等. 2013. 油藏描述技术发展及启示. 中国石油大学学报(自然科学版), 37(5): 22-27. DOI:10.3969/j.issn.1673-5005.2013.05.004 |
孟小红, 郭良辉, 张致付, 等. 2008. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建. 地球物理学报, 51(1): 235-241. DOI:10.3321/j.issn:0001-5733.2008.01.029 |
熊翥. 2012. 地层、岩性油气藏地震勘探方法与技术. 石油地球物理勘探, 47(1): 1-18. DOI:10.13810/j.cnki.issn.1000-7210.2012.01.009 |
印兴耀, 张世鑫, 张峰. 2013. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究. 地球物理学报, 56(7): 2378-2390. DOI:10.6038/cjg20130724 |
于四伟. 2017.基于自适应稀疏反演的地震数据重构[博士论文].哈尔滨: 哈尔滨工业大学.
|
张良, 韩立国, 许德鑫, 等. 2017a. 基于压缩感知技术的Shearlet变换重建地震数据. 石油地球物理勘探, 52(2): 220-225. DOI:10.13810/j.cnki.issn.1000-7210.2017.02.004 |
张良, 韩立国, 刘争光, 等. 2017b. 基于压缩感知和Contourlet变换的地震数据重建方法. 石油物探, 56(6): 804-811. DOI:10.3969/j.issn.1000-1441.2017.06.005 |
 2019, Vol. 62
2019, Vol. 62


