0 引言

在大地电磁(MT)观测资料中，阻抗张量是2×2复数矩阵形式一般情况下阻抗张量非对角元Z_xy和Z_yx的相位位于一、三或二、四象限内，但在少数情况中非对角元Z_xy和Z_yx的相位会超出正常象限范围，这种现象称为相位超象限现象.在资料处理中，基于各向同性的MT二维反演技术无法拟合低频段的相位超象限数据，这不仅在一定程度上降低了所获取的地下电性结构的可靠性，而且也无法合理解释相位超象限现象.随着MT正、反演技术的发展，阻抗相位出现超象限现象也被越来越多的报道和关注.但是这些研究主要基于各向同性介质模型，并提出三维结构引起的电流沟道效应(Current Channelling)可以用来解释观测数据中的相位超象限现象(Jones et al., 1988；Livelybrooks et al., 1996；Chouteau and Tournerie, 2000；Lezaeta and Haak, 2003；Weckmann et al., 2003；Kumar and Manglik, 2012；Vaittinen et al., 2012；Ichihara et al., 2013；de Lugoet al., 2013；Xiao et al., 2013, 2015, 2016；Kühn et al., 2014；Cherevatova et al., 2015；邵贵航和肖骑彬，2016).地球介质中电阻率各向异性是一种非常普遍的现象(Jones，2012).在考虑各向异性的情况下，即使结构比较简单的模型都会引起类似于复杂各向同性结构的大地电磁响应.因此，为了能够更全面地分析地下介质性质，有必要针对相位超象限这种特殊的大地电磁观测数据开展各向异性模型研究.

Pek和Verner(1997)在各向同性介质中植入一个各向异性块体和一个各向异性层，其中各向异性块体出露地表，各向异性层位于块体之下，二者上下接触；通过二维有限差分正演计算，发现当块体的宽度有限并且各向异性走向与层的各向异性走向接近垂直时，沿异常块体上方的Z_yx相位出现超象限.Heise和Pous(2003)在Pek和Verner的模型基础上，比较系统的研究了影响阻抗相位的几个参数，提出在块体和层的各向异性走向差异较大、具有较大的各向异性比、背景电阻率明显高于各向异性块体的最大电阻率时，会出现相位超象限现象.Chen等(2009)则进一步改变上下结构中两个各向异性体的规模及埋深，研究认为除了块体的各向异性比很大、深浅块体的各向异性走向角差异较大外，当深部块体的横向尺度大于浅部块体、深部各向异性块体埋深较大时，会在浅部各向异性块体上方产生相位超象限现象.

以上研究中，Heise和Pous(2003)试图建立起各向异性模型参数与电场响应之间的近似关系式，进而分析阻抗相位发生超象限时各向异性模型参数需要具备的条件.但是以上研究都是基于二维各向异性模型，为了进一步探讨引起相位超象限现象的各向异性模型更本质的特征，本文基于已实现的三维任意各向异性介质模型的大地电磁正演算法，通过构建更加普通的三维各向异性模型，来分析这种具有上下结构关系的模型在三维空间上的相位响应以及引起相位超象限现象的参数组合特征.

1 算法基础

Reddy和Rankin(1975)首次应用有限元法实现了大地电磁二维任意各向异性模型的数值计算，但是此后对各向异性模型的研究发展非常缓慢.Pek和Verner(1997)使用有限差分法提出了针对二维任意各向异性模型计算的算法.Li (2002)通过有限元法也实现了二维任意各向异性模型的数值计算.Qin等(2013)通过傅里叶变换求解了二维大地电磁中轴向各向异性无限延伸断层的准解析解.胡祥云等(2013)将MT各向异性二维模拟应用在实测数据分析中.霍光谱等(2015)研究了带地形的MT各向异性二维正演并进行了实例的对比分析.Martinelli和Osella(1997)通过Rayleigh\|Fourier技术计算了三维垂直各向异性模型的MT响应.Weidelt(1999)基于交错网格有限差分法求解了三维各向异性MT问题.最近，Junge(2016)尝试通过三维任意各向异性的模拟结果来概括不同各向异性参数对传输函数的影响.Xu和Li(2016)报道了使用有限元法计算三维电各向异性模型响应的算法.

1.1 基本理论

考虑时谐因子e^-iωt，大地电磁似稳场方程微分形式如下：

(1)

(2)

其中E和H分别为电场和磁场，μ₀为真空磁导率，ω代表角频率，代表电导率张量，它是一个3×3对称、正定矩阵(Pek and Verner, 1997；Martí，2014).在笛卡尔右旋坐标系下(X和Y轴为水平方向，Z轴正方向垂直向下)，麦克斯韦方程可以写为不同分量组合的微分形式，比如在二维各向异性情况下，可以组合成只包含与电性走向平行的E_x和H_x分量微分形式(Reddy and Rankin, 1975; Pek and Verner, 1997).但是这种形式无法拓展至三维情况.在三维各向同性有限差分近似中，可以采用只求解电场方程(FDE)或者磁场方程(FDH).Siripunvaraporn等(2002)提出与FDH相比，FDE方法对网格剖分大小没有那么敏感.本文对三维任意各向异性的处理则是采用类似的电场方程.

(3)

方程(3)的微分展开形式如下：

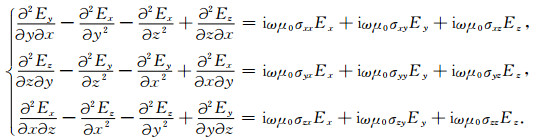
(4)

其中σ_ij(i, j=x, y, z)为电导率张量元素；在计算三维模型的电、磁响应时，通过对方程组(4)数值计算得到主场电场，然后通过方程(5)求得辅助磁场.

(5)

当地下介质为一维时，电场只随深度(Z)变化，方程组(4)简化为：

(6)

当地下介质为二维时，电场沿电性结构走向方向变化为0，即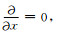方程组(4)简化为：

(7)

1.2 数值计算

图 1a表示的是三维模型的离散网格，对场的定义采用了经典的交错网格形式(Yee, 1966).如图 1b所示，本文中电场定义在网格体棱边中心，磁场定义在垂直网格体的各个表面.

对方程组(4)的数值近似中，等号左端项的差分与各向同性情况相似，而右端电流密度项因为各向异性的原因，每个电流密度分量都需要考虑三个分量电场值，处理方式与各向同性情况不同.我们采用Weiss和Newman (2002)提到的方法来进行右端项近似.

除了离散地下介质，在地表以上添加了空气层(在本算法中取12层，空气层电导率为10^-10 S·m^-1).顶层边界条件取统一值.在实现三维数值模拟的工作之前，我们先实现了一维和二维各向异性正演计算，因此这里的三维模型四周边界直接按二维模型处理，谭捍东等(2003)在模拟三维各向同性介质的大地电磁响应时就采用了这种侧边界处理方式.底边界以下设置为均匀半空间.

为了对方程组(4)中的各方程作统一的处理，我们对不同分量E_x，E_y和E_z都设置了相同数量的未知量.N_z，N_y和N_x分别表示沿Z, Y和X方向离散的网格数量，则未知量个数一共为3×(N_z)×(N_y-2)×(N_x-2)，在将近似项和边界条件代入方程组(4)后便可得到一个形如AX = B的线性方程组，其中A, X和B分别表示系数矩阵、未知向量和右端向量.在向量X中，未知量按E_x、E_y、E_z的顺序排列，相应的系数矩阵呈现出一种结构对称的形态.非零元素在系数矩阵A分布非常稀疏，因此采用行压缩存储格式(CRS)进行保存，求解方程则用PARDISO直接法进行(Schenk and Grtner, 2004; Kuzmin et al., 2013).其中关于算法实现的细节，已另外撰写成文(Yu et al., 2018)，因此这里不做过多赘述.

我们设置两组正交初始电场(E_x0⁽¹⁾=1.0，E_y0⁽¹⁾=0和E_z0⁽¹⁾=0以及E_x0⁽²⁾=0，E_y0⁽²⁾=1.0和E_z0⁽²⁾=0)来对应两组非线性相关的极化模式：X″极化和Y″极化.在求得地表相应的场值E_x⁽¹⁾、E_y⁽¹⁾、H_x⁽¹⁾、H_y⁽¹⁾、H_z⁽¹⁾和E_x⁽²⁾、E_y⁽²⁾、H_x⁽²⁾、H_y⁽²⁾、H_z⁽²⁾后便通过(8)式求得到阻抗张量.

(8)

2 理论模型分析

Heise和Pous (2003)在文中详细描述了一个具有上下结构关系的二维各向异性模型引起相位超象限的特征.基于此模型的结构特征，我们构建了不同的三维理论模型来进一步讨论各向异性块体水平长度变化、各向异性走向角变化以及各向异性体电导率的变化对阻抗相位的影响.在下文中，所有模型的网格剖分均为46×46×39(X×Y×Z)，外加12层空气层.

2.1 各向异性块体水平长度变化对相位的影响

在图 2中，我们构建了3个具有上下结构关系的各向异性模型.从Md1到Md3，把模型中上部的各向异性块体沿X轴方向的长度不断加大.在Md1中，上部各向异性块体的水平长度相等，对应的阻抗相位没有出现超象限现象；当上部块体沿X方向的长度增加时，与之对应的地表投影区域的相位值明显偏离于背景相位值(如图 2中的Md2及其相位yx分量的平面切片)；当X方向长度显著大于Y方向长度时(如图 2中的Md3模型中，上部块体沿X方向长度是Y方向长度的4.4倍)，在112.47 s的Z_yx相位切片中异常区域的相位接近-90°，并且在长周期1325 s的Z_yx相位切片中出现明显的相位超象限区域.此时的三维各向异性块体由于沿一个水平方向的延伸明显大于另一个水平方向，我们把它称作为准二维体.在Md3模型的相位切片中，Z_yx相位响应的超象限区域明显具有方向性，这一方向与上部块体的各向异性走向吻合.

2.2 准二维体各向异性走向角对相位的影响

图 3则表示在上下各向异性体的结构和规模不变的情况下，保持它们之间的各向异性走向相互垂直，使各向异性走向角α按15°间隔变化，并分别计算模型响应.取周期为1325 s时相应的Z_yx相位切片(Z_xy相位均未出现超象限现象，这里没有列出).在异常体投影范围内的超象限区域呈现出明显随各向异性走向角的变化，其中各向异性走向与水平坐标轴平行时，不产生相位超象限现象.从超象限范围上观察，当α=±45°时，相比于其他角度，超象限范围在沿Y轴方向上大部分达到上部异常体的地表投影区的边界，且面积明显大于其他角度对应的超象限区域；从超象限区域的形态上来看，它沿X轴方向的两端边界展布方向与各向异性走向非常接近.在[-90°，0°]的走向角范围内超象限区域形态与[0°，90°]内相对称.图 3中α取±15°或±75°即各向异性走向与结构走向夹角较小或各向异性走向与结构走向正交方向夹角较小时，并未出现相位超象限现象，可见，相位超象限现象需要各向异性走向与准二维体结构走向夹角在一定范围才能产生.

从穿过准二维中心剖面上的电场分布来看(图 3c，3e)，对于X″极化模式，在α=±15°和±30°情况中平行于走向的电场E_x⁽¹⁾穿过上部异常体的地表投影区时，模值会明显变小，在其他走向角下，E_x⁽¹⁾模值几乎没有变化，而且E_x⁽¹⁾相位都无明显变化.对于Y″极化模式，E_y⁽²⁾在穿过异常体时模值明显变小，在α=±30°、±45°和±60°时E_y⁽²⁾在异常体范围内相位发生了明显的变化，对应位置处变化最明显的发生在α=±45°时.

2.3 各向异性块体主轴电导率差异对相位的影响

图 4中Md4在Md3基础上，增加下伏各向异性层的埋深至23 km后相位不再出现超象限现象，这也说明两者在相同的各向异性参数情况下，这种规模的上覆各向异性体与下伏各向异性层非接触结构比接触的结构更难产生相位超象限.Chen等(2009)通过构建类似的非接触的上下二维结构，对上下异常体设置更高的主轴电导率之比(图中表示为电阻率形式)，产生了较强烈的相位超象限现象.参考Chen等(2009)构建模型的各向异性参数，增加主轴电导率的差异，Md5也产生了相位超象限现象.在这种非接触不利于产生超象限现象的情况下，Md5明显比Md3产生的超象限现象要强烈.这说明了各向异性体主轴电导率差异增大相比于上下接触关系的变化更易引起阻抗相位超象限现象.

在上部异常体沿两个水平方向尺度相同的情况下，我们把水平方向长度不断加大，如图 5中的Md1-Md6-Md7，当Md7中水平边长达到Md1的4倍以上时，虽然在112.47 s周期的Z_xy和Z_yx相位切片出现相位增大或减小的异常条带，但仍没有出现相位超象限.对比图 2中的Md3和图 5中的Md7可以发现，在相同的背景及各向异性参数的情况下，上部各向异性体表现出准二维特征比这种水平尺度相同的规则三维体更容易产生相位超象限现象.

但是，当我们在Md7的基础上增加异常体的各向异性比构成Md8(图 6)，此时模型的响应中阻抗分量Z_xy相位产生超象限现象.从相位超象限区域内的Site 1和Site 2两个点的MT响应曲线也可以看出，Z_xy相位在100 s左右就已经超出象限.周期1325 s相位切片中的超象限区域形态呈现非常规则的倾斜条带，而且越靠近与X轴平行的两个边界，超象限程度越高(对应图中蓝色区域).这表现出主轴电导率差异的增加相比于改变上部各向异性体形态更易产生阻抗相位超象限现象.

2.4 规则各向异性块体各向异性走向角对相位的影响

以Md8模型为基础，计算了不同各向异性走向角下的1325 s相位切片(图 7).与图 3中准二维构造相位切片类似的是，图 7中超象限区域的形态也具有明显的与各向异性走向一致的条带趋势.与图 3不同的是，α=±45°时，不再产生相位超象限现象.当各向异性走向与X轴或者X″极化方向夹角锐角小于45°时，阻抗分量Z_xy的相位发生超象限；反之，当各向异性走向与Y轴或者Y″极化方向夹角锐角小于45°时，阻抗分量Z_yx的相位发生超象限.在产生超象限现象的情况中，当各向异性走向角与水平坐标轴或对应极化方向夹角不断变小时，相位超象限的区域面积增加，但是超象限程度明显减弱，如图 7中α从30°变到15°时，相位异常区域明显增大，但异常程度也相应减弱，当α继续变小接近0°时，异常程度继续减弱直至消失.

对图 7中出现相位超象限的情况进一步分析，可以得出这样的认识：当构成上部各向异性块体的平行两边沿各向异性走向角方向发生重叠时，如果两边的方向与X″极化方向正交，则相位超象限发生在Z_xy分量上；如果两边的方向与Y″极化方向正交，则相位超象限发生在Z_yx分量上.重叠的范围越大，那么产生超象限区域的范围也会更大，但超象限程度会相应减弱，如图 7中α=15°和α=30°所示.如果没有发生重叠，则不会出现相位超象限现象.

3 近似解析分析 3.1 基本假设

我们在计算三维结构的电、磁场响应时，在空气层顶给定两组正交的极化电场.在X″极化时，电场初值取为：E_x0⁽¹⁾=1, E_y0⁽¹⁾=0，E_z0⁽¹⁾=0；在Y″极化时，电场初值取为：E_x0⁽²⁾=0, E_y0⁽²⁾=1，E_z0⁽²⁾=0.最后分别求解在这两组正交极化模式下的电、磁场，为了方便后面的分析，我们把在上述两种极化模式下求得的地表电、磁场分别记为E_x⁽¹⁾、E_y⁽¹⁾、E_z⁽¹⁾、H_x⁽¹⁾、H_y⁽¹⁾、H_z⁽¹⁾和E_x⁽²⁾、E_y⁽²⁾、E_z⁽²⁾、H_x⁽²⁾、H_y⁽²⁾、H_z⁽²⁾.Pek和Verner (1997)在求解二维各向异性问题时，使用的是电、磁场分量耦合在一起的待求方程组，他们给定E极化模式和H极化模式的初始值时，考虑了地表磁场在空间上表现出稳定的特点.Heise和Pous(2003)在分析二维各向异性结构对地表电场的影响时，充分利用了H极化模式中地表磁场初始值取值的特殊性，经过简化并建立阻抗与电场以及电场与模型电导率参数之间的近似解析关系式，从而解释引起相位超象限的各向异性模型的电导率特征.本文与Heise和Pous(2003)对初始场的处理不同，但对于我们所研究的模型类型，不同极化模式中所感应的地表场都有以下性质：①与主极化电场方向正交的地表感应磁场非常稳定，在固定频率下几乎为常数(模值与相位均非常稳定)，如X″极化模式下的H_y⁽¹⁾和Y″极化模式下的H_x⁽²⁾，我们把它们称为主磁场；②与主磁场正交的地表感应磁场H_x⁽¹⁾和H_y⁽²⁾，我们称之为次磁场，它们与对应的主感应磁场H_y⁽¹⁾和H_x⁽²⁾相比至少小一个数量级.在这种情况下，地表阻抗分量Z_yx有表达式：

(9)

根据性质②，分母H_x⁽¹⁾H_y⁽²⁾-H_y⁽¹⁾H_x⁽²⁾中可以忽略前一项.这里根据地表水平磁场所表现的性质所进行的近似与Heise和Pous(2003)文中通过以主磁场作为极化场所进行的近似也是类似的，同样对于我们研究的模型，这一项也会变得非常小，可以忽略且不失一般性.根据前面提到的性质①，H_x⁽²⁾在固定的频率下几乎为常数，从而得到阻抗分量Z_yx的近似表达式(9)，其相位特征几乎只随E_y⁽²⁾变化而变化.进行类似的近似，也可知Z_xy的相位特征几乎只随E_x⁽¹⁾变化而变化.如图 3c和3e中横穿准二维体中心剖面的地表电场分布，在穿过异常区域时，E_x⁽¹⁾相位几乎不发生变化，因此Z_xy没有发生超象限现象，而当各向异性角在一定范围时，E_y⁽²⁾发生了明显的相位变化，从而导致Z_yx相位产生超象限现象.

Heise和Pous(2003)在分析二维各向异性模型时，提到平行于走向的电场在Y″极化模式下几乎不受各向异性影响，但是横切走向的电场却因各向异性产生强烈的扭曲.根据边界电流密度连续性条件和欧姆定律可以得到式子σ^hE_y^h=σ_xy^bE_x+σ_yy^bE_y^b，可得

(10)

其中b表示各向异性块体，h表示背景的各向同性介质，E_y^h表示在背景介质中沿Y轴方向的电场，E_y^b表示在各向异性块体中沿Y轴方向的电场，E_x表示平行于边界并在边界两边连续的沿X轴方向的电场.当存在各向异性时，(10)式右边第二项有可能变得很大并超过第一项甚至使得横向电场在各向异性块体内反向.

3.2 相位超象限指标 3.2.1 水平电场的影响

对前文三维情况中准二维结构中心部位超象限区域的分析也可当作二维处理，这里进一步对(10)式中不同部分进行探讨，表示各向异性体电导率张量，σ_x，σ_y和σ_z表示各向异性体三个主轴电导率，α，β和γ表示各向异性角，当β=0，γ=0时，

(11)

将(11)式代入(10)式中，

(12)

其中为各向异性水平轴向电导率比，为围岩电导率对主轴电导率σ_x之比.

进一步，在Y″极化模式下，上部各向异性块体中的电场E_y^b相对E_y^h的变化可以表示为相变函数

(13)

(13) 式最右端表达式第一项为实数，第二项包含复数项因此如果要产生显著的相位差Δφ，复数项一定不能为零.Heise和Pous(2003)指出单独的存在于各向同性背景中的各向异性体(不含各向异性层)在H极化模式中感应的E_x比E_y^h至少小两个数量级可以被忽略，而无法产生相位超象限现象.这种情况同样适用于解释在三维情况下，单独的准二维体或规则三维各向异性体也不能产生相位超象限.

3.2.2 背景场的影响

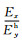
将这种上下结构中的电场表述为(E)=(E)_host+(E)_second，(E)_host表示背景电导率结构感应部分，(E)_second表示以(E)_host为场源产生各向异性体感应部分，参考Newman和Alumbaugh(2002)以及秦策等(2017)的处理方式，(E)_second满足的方程：

(14)

其中背景电导率结构和异常体电导率结构均用张量形式从而不失一般性.分量E_x=(E_x)_host+(E_x)_second，前面提到的单独各向异性体的结构中，背景可以视为各向同性半空间结构，故在Y″极化模式下，(E_x)_host为零，(E_x)_second太小足以被忽略，从而E_x也可以被忽略，导致(13)式中复数项几乎为零，则Δφ几乎为零，解释了单独的各向异性体无法产生相位超象限现象.更进一步分析，背景为一维各向同性结构或二维各向同性结构时，因为这两种结构情况下Y″极化模式是无法感应出(E_x)_host的，而单独各向异性体感应的(E_x)_second相对太小，故这种背景中单独各向异性体边界上函数F_y虚部也几乎为零，也不能使E_y产生剧烈的相变从而产生相位超象限现象.对于我们研究的典型上下结构模型Md3和Md8，背景可以视为一个含各向异性层的一维各向异性结构，在这个背景下，Y″极化模式中会感应(E_x)_host，当E_x不为零时，E_y才有可能产生剧烈的相变.

为了对上面的分析进行验证，把图 4中Md3、Md4和Md5的上部各向异性体去掉，形成图 8a中对应的层状各向异性模型.三个模型在Y″极化模式下感应出的地表电场E_x⁽²⁾的模值(E_x⁽²⁾_Module)在短周期时接近0，随着周期的增加，模值逐渐增加，在10⁴s前后达到峰值后模值减小.在周期为10²~10⁵s的范围内，模型B_Md5感应的E_x⁽²⁾的模值要明显大于模型B_Md3和B_Md4所感应的E_x⁽²⁾模值；模型B_Md3感应的E_x⁽²⁾的模值略高于B_Md4感应出的E_x⁽²⁾模值.这三个背景模型在Y″极化模式中感应的E_x⁽²⁾相对大小关系与图 4中超象限现象程度表现出正相关性.图 8b中水平背景电场比的模值(E_x⁽²⁾/E_y⁽²⁾_Module)曲线表现出与E_x⁽²⁾_Module曲线相似的随周期而变化的特征，这里E_x⁽²⁾/E_y⁽²⁾可以近似地描述(13)式中的项.同样，模型对应曲线的极大值都出现在10²~10⁴s范围内，B_Md5模型对应的极大值要明显大于模型B_Md3和B_Md4对应的极值；模型B_Md4对应的极值最小.三个模型的E_x⁽²⁾/E_y⁽²⁾_Module变化程度也与图 4中模型表现出的超象限现象程度相吻合.

总之，对于具有上下结构关系的二维、准二维或三维各向异性模型，使Z_yx产生相位超象限现象的前提是需要背景场能感应出与X轴平行的电场E_x，其次是的大小不可忽略.

3.2.3 相位超象限指标函数

当(13)式中复数项不为零，我们进一步讨论系数和对函数值F_y的影响，为了使F_y的幅角足够大，需要增加(13)式最右端表达式中复数项的比重，构建(13)式中关于复数项比重绝对值的函数

(15)

所以当函数f_y(κ, λ, α)越大时，F_y中的复数项比例越大，越可能产生相位超象限现象.取

则(15)式可写为

(16)

在上下结构二维或准二维模型的中心，f_y可以作为判别相位超象限的指标.

分别对不同各向异性参数进行分析，其他参数不变时，若时，随κ的增大f_y1(κ)递增，当时，值基本只受主轴电导率σ_x的影响；若时，随κ的减小f_y1(κ)递增，当 1时，值基本只受主轴电导率σ_y的影响.因此，当水平主轴电导率差异足够大时，较大的主轴电导率的值越高，越易于产生相位超象限现象.

f_y2(λ)则表示其他参数不变时，当围岩电导率相对于主轴电导率越小时，越易于产生相位超象限现象.

f_y3(α)则表明当其他参数不变，上部各向异性体的各向异性走向角达到45°时，相位超象限程度最高，当α为0或者90°的整数倍时，此项为零.

总结以上分析，对于具有上下结构关系的准二维(以及二维)各向异性模型，发生相位超象限现象需要使穿过上部异常体边界的电场相位发生剧烈变化，以图 3中南北走向的准二维构造为例，相位超象限产生的条件：①Y″极化模式中可以感应出沿X轴平行的背景场(E_x)_host，从而能产生足够大小的E_x.②水平主轴电导率差异足够大，并且较大的水平主轴电导率值要足够高.③围岩电导率相对于主轴电导率足够低.④各向异性走向不与X轴或Y轴平行.

4 结论

本文将经典的二维上下结构各向异性模型拓展到三维情况中，并对引起的相位超象限现象进行了系统模型研究，得到以下认识：

(1) 在上下结构各向异性模型中，当各向异性参数保持相同时，上部各向异性体形态为准二维体比上部为规则三维体更容易产生相位超象限现象；上部各向异性体与下部各向异性单元呈接触状态时相比于非接触状态更利于相位超象限的产生；

(2) 相比于改变上部各向异性体形态以及上下各向异性单元的接触关系，增大各向异性主轴电导率差异更容易产生相位超象限现象；

(3) 在三维上下结构模型中，上部各向异性体的各向异性走向角对相位超象限产生的程度以及分布范围具有明显影响.当上部为规则三维各向异性体时，发生超象限区域沿各向异性走向方向呈条带状，并且超象限程度最高的区域都出现在与相应极化方向正交的边界附近.

对于产生相位超象限现象的准二维结构两端的区域，存在未超象限的部分，它们和超象限区域之间的边界明显与各向异性走向方向相关.同样，对于上部规则三维各向异性体对应的相位超象限条带，它的展布方向也几乎与各向异性走向相符.由于在准二维结构两端，以及三维规则异常体边界附近，电、磁场响应的三维特征明显，难以作进一步的简化分析.

通过进一步的近似解析分析，提出了相位超象限指标函数可以直观地解释在二维或准二维上下结构模型中产生相位超象限需要具备的条件：

(1) 与上部各向异性体结构走向正交的电场极化模式中，背景模型可以感应出足够大的与结构走向平行的水平电场；

(2) 水平各向异性主轴电导率差异足够大，并且较大的主轴电导率值要足够高；

(3) 围岩电导率相对于各向异性主轴电导率足够低；

(4) 各向异性走向不与水平坐标轴方向平行.

致谢  感谢两位审稿人提出的非常有意义的修改意见，使文章得到进一步改善.