前苏联学者Tikhonov(1950)和法国学者Cagniard (1953)提出了通过观测天然电磁场来研究地下结构的方法,并在进一步完善了理论之后形成了大地电磁测深方法.大地电磁测深法以天然交变电磁场为场源(频率范围在10-4~104Hz),目前已普遍用于矿产普查、地热田调查、油气勘探、水文环境等诸多领域(Belyavskii and Sukhoi, 2004;吕英,2012;Zhang et al., 2015),同时也是深部地球探测必不可少的方法.
大地电磁法一二维反演已很成熟,前人已做了很多工作.Constable等(1987)提出求解光滑模型实现了Occam反演;陈小斌等(2005)分析了难以选择正则化因子的原因,实现了自适应正则化反演;DeGroot-Hedlin和Constable(2004)基于Occam算法通过新的粗糙度矩阵实现了尖锐边界的二维反演;Smith和Booker(1991)提出了基于近似雅克比矩阵的快速松弛反演方法.
随着计算机性能的不断提升,大地电磁三维反演方法也得到了迅速发展.Mackie和mackie(1989)使用共轭梯度法对大地电磁三维数据进行反演;Smith和Booker(1991)利用前一次迭代计算得到的场值来近似代替水平微分项实现三维快速松弛反演;Spichak等(1995)将贝叶斯统计方法应用到大地电磁三维反演中;Newman和Alumbaugh(2000)在Mackie的基础上将非线性共轭梯度法用于大地电磁三维反演;谭捍东等(2003)在深入分析三维张量阻抗表达式的基础上,提出了快速计算灵敏度矩阵的方案,实现了大地电磁法三维快速松弛反演;胡祖志等(2006)在计算灵敏度时用一维灵敏度代替三维灵敏度,实现了大地电磁拟三维反演;Siripunvaraporn和Egbert(2009)基于Occam反演将模型转换到数据空间再进行反演,大大减少了数据存储需求和计算量,并于2009年发布了大地电磁三维反演程序WSINV3DMT;Egbert等(2014)基于NLCG算法实现了适用于多种电磁反问题的并行反演程序ModEM.近年来,为了更好的拟合复杂地形,基于非结构网格的大地电磁三维正反演成为研究热点,例如Mitsuhata和Uchida(2004)提出了一种通过计算三维电导率NIT响应的有限元算法.
以上大地电磁三维反演技术之间的差异主要在于模型剖分、正演技术和最优化方法,模型粗糙度约束项均采用光滑算子和L2范数进行计算.L2范数能够得到稳定的反演过程和较为准确的反演结果,但有时会因为光滑过度损失细节.多尺度反演能够在不同尺度上对模型进行约束,可提高反演分辨率,是地球物理领域一个热门研究方向.由于空间域模型在小波域中具有不同尺度的特征,我们可以通过小波变换实现多尺度反演.通常在空间域中具有分块连续结构的模型在小波域中具有非常稀疏的表示,即空间域的模型在小波域中被压缩.如果在小波域中能够恢复压缩的稀疏系数,那么在空间域中我们就能够恢复其准确结构.在地震层析成像领域,基于小波变换的多尺度反演早有应用,例如Chiao和Kuo(2001)、Chiao和Liang(2003)及Hung等(2011).在电磁勘探领域多尺度反演研究相对较少,目前只有徐义贤和王家映(1998)实现了波数域大地电磁一维反演,Nittinger和Becken(2016)基于双树复小波变换实现了大地电磁的二维反演,以及Liu等(2018)实现了基于小波变换的频率域航空电磁三维反演.
鉴于大地电磁三维反演目前尚无人进行多尺度反演研究,本文在总结前人的工作基础上,开展模型空间压缩的大地电磁三维反演方法研究.我们首先详细介绍反演方法的原理和实施方案,进而通过理论算例和实测数据反演分析其相对于传统方法的有效性.
1 模型空间压缩反演理论本文反演方法是将空间域模型转换到小波域进行压缩,并在小波域中利用不同尺度的稀疏系数对模型进行描述.通过反演迭代对小波域中的稀疏系数进行更新后通过逆小波变换得到空间域模型.与其他反演方法类似,首先定义一个目标函数,其中对数据拟合项我们使用L2范数.然而,为保持小波域系数的稀疏特性,对模型约束项我们使用L1范数.目标函数具体形式为
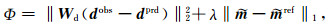
|
(1) |
其中,dobs是观测数据,dprd是模型正演响应,Wd是一个由数据噪声标准差的倒数构成的对角矩阵,λ是权衡数据和模型复杂度的正则化因子,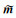
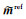
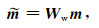
|
(2) |
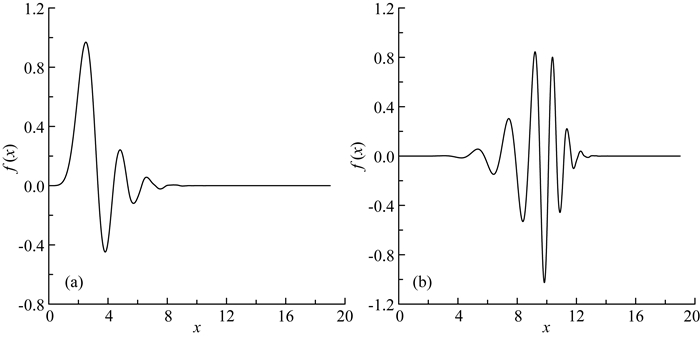
其中,Ww是小波变换矩阵,m是空间域模型.小波变换可通过滤波算法完成.本文使用db10变换,其小波变换函数如图 1所示.
|
图 1 小波变换函数db10 (a)近似函数;(b)细节函数. Fig. 1 Wavelet transform functions db10 (a) Scaling/approx. function; (b) Wavelet/detail function. |
为最小化公式(1)中的目标函数, 我们可使用不同的最优化方法,例如非线性共轭梯度法(NLCG)、拟牛顿法及使用近似二阶导数的高斯-牛顿法(GN).本文使用收敛速度较快的高斯-牛顿法,则由(2)式可得:
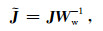
|
(3) |
其中,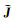
由(1)和(2)式可得GN反演控制方程为
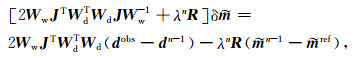
|
(4) |
其中,Ww-1= WwT,dn-1是上一个模型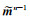
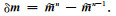
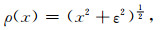
|
(5) |
其中,ε是绝对值小于1的常数.由(5)式可推导出(4)式中R的形式为
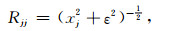
|
(6) |
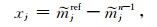
|
(7) |
其中,j是向量x中元素的索引,ε用于保证在x=0时导数的存在.矩阵R和灵敏度矩阵J都依赖于模型,并且每次迭代都会更新.因此,本文使用迭代重新加权最小二乘方法(IRLS)求解公式(4)逆问题(Farquharson,2008).在每次迭代中,我们使用预条件处理共轭梯度(PCG)方法求解方程(4).在小波域获得模型更新后,空间域模型更新公式为
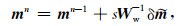
|
(8) |
其中,s为比例因子(Haber,2014).公式(4)中的正则化因子λ通过“冷却方法”选择.
由于R矩阵的存在会导致方程(4)具有较大的条件数,为加速方程的求解速度需对共轭梯度使用预条件处理技术.通常预条件处理是在共轭梯度计算中生成一个矩阵V,在利用显式灵敏度矩阵计算方式时,可利用LU分解等技术由2WwJ TWdTWdJWw-1+λnR计算V.然而,本文中近似Hessian矩阵的前半部分WwJTWdTWdJWw-1是隐式方法计算的,无法找到类似于LU分解方法求解V,因此无法对它们进行修改.为简单起见,本文只对R进行修正.其预条件处理方法是用已知的残差r和一个矩阵V,并使其满足:
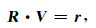
|
(9) |
考虑到R是一个非奇异对角矩阵,由公式(9)可得:
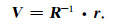
|
(10) |
为测试本文提出反演方法的有效性,我们以国际上常用的“棋盘”模型为例进行三维反演测试.模型如图 2a所示,异常体总共分三层,每层有九个电阻率高低不同的异常体,绿色背景电阻率为100 Ωm,红色高阻异常体电阻率为1000 Ωm,蓝色低阻异常体电阻率为10 Ωm.所有异常体的长度均为32 km,宽度都为16 km.在垂向方向上第一层异常体厚度为10 km,第二层异常体厚度为32 km,第三层异常体厚度为48 km.第一层和第二层之间及第二层和第三层之间的间隔均为8 km.本文使用全阻抗(Zxx,Zxy,Zyx,Zyy)和倾子作为反演数据,数据采样为在10~10000 s区间内对数等间隔12个周期上获得.对于阻抗张量,所有数据均加入3%的高斯噪声.本算例中我们使用66×66×59个网格进行正反演.测点位于计算区域中部560 km×1120 km区域,15×15分布,共计225个测点,在x方向的测点间距是40 km,y方向测点间距是80 km.反演结果如图 2b—d所示.为简单起见,高斯牛顿法简写为GN,基于小波变换的高斯牛顿法简写为WT-GN.预条件处理后基于小波变换的高斯牛顿法简写为PWT-GN.

|
图 2 三维大地电磁理论模型及反演结果 (a)真实模型;(b) GN反演结果;(c) WT-GN反演结果;(d) PWT-GN反演结果. Fig. 2 Synthetic model and 3D MT inversions (a) True model; (b) GN inversion; (c) WT-GN inversion; (d) PWT-GN inversion. |
从图 2给出的反演结果可以看出,三种反演方法均能较好地恢复异常体的位置和电阻率.GN方法和ModEM3D(Egbert et al., 2012)程序中NLCG方法的反演结果一致.GN方法反演结果中深部低阻体中心区域的电阻率较低,外围呈光滑过度形态,符合光滑约束反演的特征.深部高阻体没有被反演出来是由于电磁法对高阻不敏感的缘故.相比之下,深部低阻体的异常比高阻大得多,因此容易被反演出来.与GN方法相比,WT-GN反演(图 2c)对浅部和深部低阻异常体的形态和分布范围均能较好恢复,但浅部异常体呈现条带状.产生这种条带状分布的主要原因是两个方向的网格尺度不一致,并且CG求解收敛不充分造成的.和前两种方法相比,PWT-GN反演结果效果非常好.各异常体的形态、位置和电阻率均得到了准确地恢复.特别需要注意的是,PWT-GN反演将深部高阻异常体很好地反演出来.然而,我们认为这并不代表PWT-GN方法可以恢复高阻异常体.由于高阻异常体引起的异常小,因此高阻体电阻率值过高过低均不会对数据拟合产生太大影响.对于常规光滑模型反演,高阻体不被反演出来会产生较小的模型粗糙度,因此高阻异常体电阻率值接近背景电阻率值;而对于小波域反演,对于数据不敏感的区域,模型的变化规律符合小波变换规律时会产生更小的模型粗糙度,进而导致与传统方法(图 2b)深部高阻体不同的反演结果.PWT-GN方法使得高阻异常电阻率略高于真实模型.这种现象会造成在无数据区域(例如扩边区域)或对数据影响很小的区域(垂直方向较深的区域)产生虚假异常,因此在反演中应使这部分区域不参与模型更新.低阻异常体对数据影响较大,可以克服这种虚假异常,得到较为真实的电阻率分布.
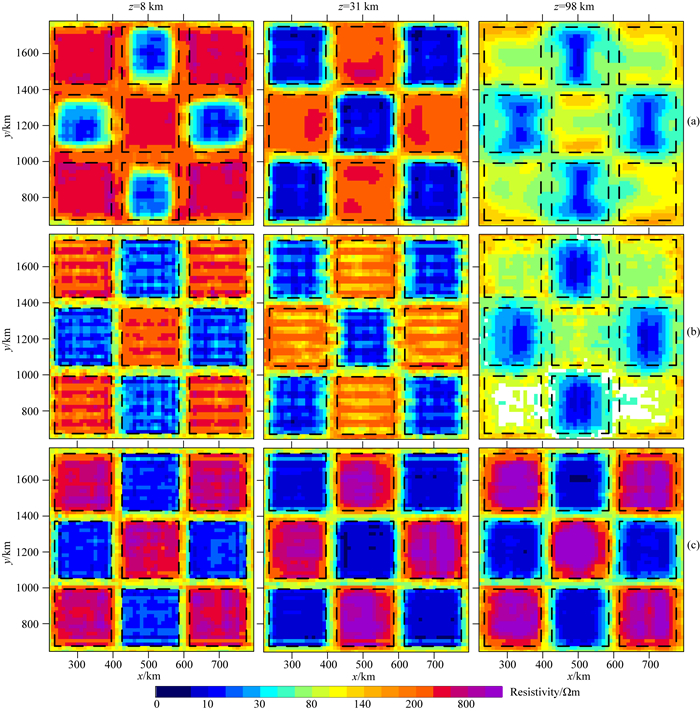
为进一步分析三种反演结果的差异,我们对图 2中给出的反演结果进行水平切片,如图 3a、b、c所示.水平切片位置分别位于反演模型纵向网格上第14、24、34层(深度分别为8 km、31 km和98 km).从图 3中可以看出,在浅部无论是GN、WT-GN还是PWT-GN方法均能较好地恢复异常体的位置和电阻率,但由于光滑约束的影响传统GN方法的反演结果与其他两种算法的结果相比边界不够清晰.随着深度增加,GN方法对中间层异常体的电阻率和形态恢复效果较好,但对第三层低阻异常体的形态恢复不好,高阻异常体难以识别.对于WT-GN方法,虽然由于CG求解收敛的不够充分导致浅层异常在大尺度网格方向连续性较差,但是深部低阻异常体形态的恢复略好于GN方法.PWT-GN方法反演结果无论是在浅部还是在中深部,对于异常体边界均刻画的很好.
|
图 3 理论模型反演水平切片图 (a) GN反演结果;(b) WT-GN反演结果;(c) PWT-GN反演结果. Fig. 3 Horizontal slices of inversions on synthetic model Black dashed lines indicate abnormal bodies. (a) GN inversion; (b) WT-GN inversion; (c) PWT-GN inversion. |
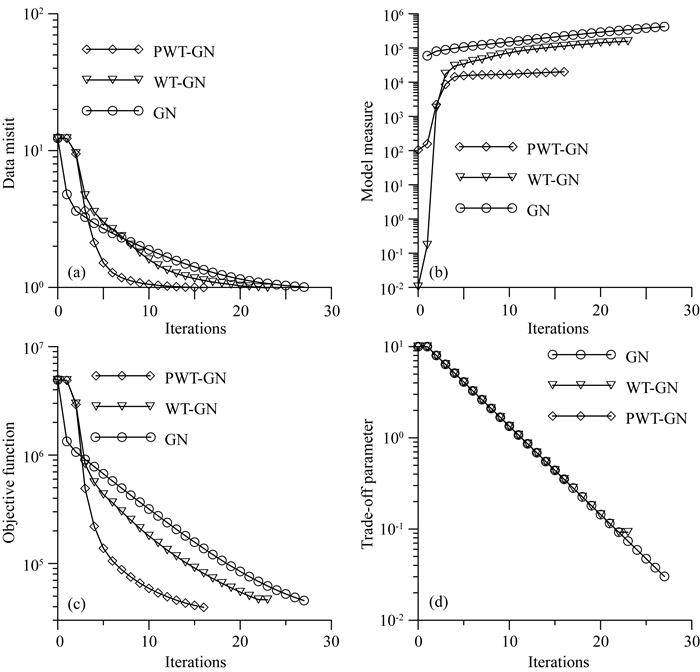
图 4a给出三种反演方法的RMS下降曲线.由图可以看出,迭代早期WT-GN方法的RMS下降速度比GN稍慢,但经过几次迭代后,下降速度很快超过GN方法.图 4b给出模型改变量随迭代次数的变化曲线.由图可以看出,GN方法在迭代初期就呈现模型更新的平缓变化趋势.WT-GN和PWT-GN方法,由于公式(4)中有R矩阵的影响,导致迭代早期模型改变量较小,但随着反演迭代的进行,模型改变量很快上升到较高的水平.图 4c给出目标函数随迭代次数的下降曲线.随着迭代次数的增加,PWT-GN方法很快下降到可接受的范围之内,而WT-GN和GN方法下降速度相对较慢,但WT-GN比GN方法下降速度稍快.图 4d给出正则化因子λ的下降曲线,对于三种方法正则化因子采用相同的指数衰减策略.
|
图 4 反演参数随迭代次数变化曲线 (a)数据拟合均方根误差;(b)模型改变量;(c)目标函数;(d)正则化因子. Fig. 4 Inversion parameters versus iterations (a) Data misfit; (b) Model measure; (c) Objective function; (d) Trade-off parameter. |
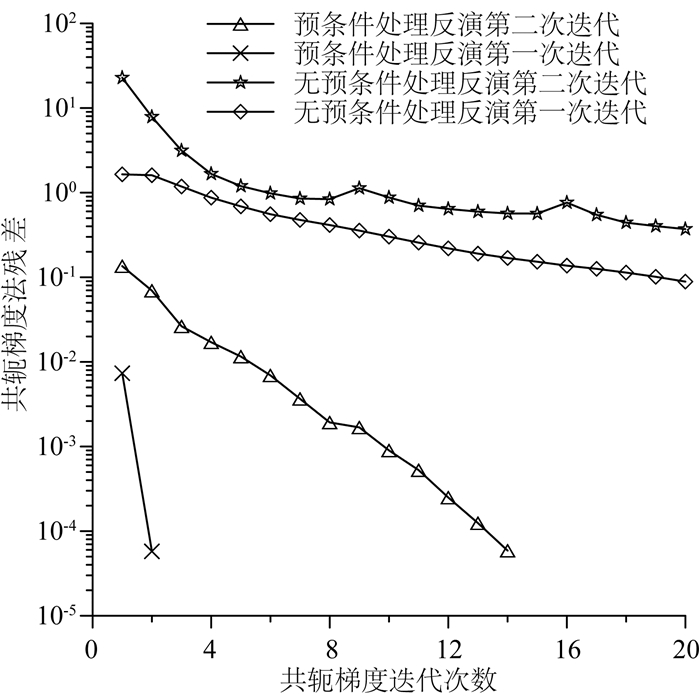
图 5是反演方程求解时,共轭梯度方法无预条件处理和有预条件处理收敛情况对比.从图 5可以看出,无论是第一次迭代还是第二次迭代,RMS下降都是预条件处理的下降速度远远大于没有经过预条件处理的数据.第一次迭代中,经过预条件处理的数据在迭代过程中只需两次迭代就能够满足精度需求,而没有经过预条件处理的数据需要经过20次的迭代.这说明本文的预条件处理方法是有效的,可较大程度上加速CG方法的收敛速度.
|
图 5 预条件处理前后共轭梯度法残差下降速率对比 Fig. 5 Comparison of residual descent rate between CG and preconditioned CG |
为进一步分析基于小波变换的GN反演效果,并说明模型空间压缩特点,本文将真实模型和三个反演结果变换到小波域, 并在图 6中进行展示.由于我们在反演过程中已通过设置阈值将部分小波系数清零,图 6中仅展示了20%较大的小波系数.从图 6a给出的真实模型在小波域的展示结果可以看出,空间域中的“棋盘”模型已经在小波域中被提取,显示为规则分布的稀疏小波系数.在小波域反演中恢复这些稀疏小波系数,即可通过逆小波变换得到空间域的反演结果.图 6b给出GN反演在小波域的展示结果.对比图 6a可以看出,GN反演结果中较大的小波系数和真实模型很接近,但在细节上有差异;图 6c给出WT-GN反演在小波域的展示结果,可以看出WT-GN反演结果产生了较多的冗余系数;图 6d给出PWT-GN反演结果在小波域的展示结果.由图可见,PWT-GN反演很好地保持了小波域系数稀疏的特点,局部系数的位置也与真实模型对应较好,因此空间域反演结果与真实模型符合很好.不足之处在于小波系数被约束的过于稀疏往往会在数据不敏感区域产生虚假异常.

|
图 6 小波域模型分布特征 (a)真实模型;(b) GN反演结果;(c) WT-GN反演结果;(d) PWT-GN反演结果. Fig. 6 Models in wavelet domain (a) True model; (b) GN inversion; (c) WT-GN inversion; (d) PWT-GN inversion. |
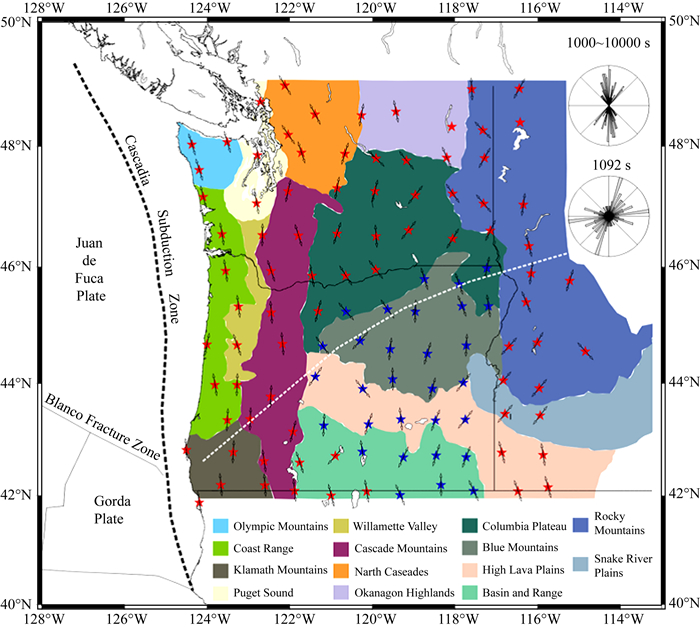
为进一步测试本文反演方法的实用性,本文对美国俄勒冈州东部和西部MT实测数据进行反演测试.图 7给出接收点的分布图,蓝色和红色星星分别代表 2006和2007年MT数据采集站点,黑色箭头代表 1000~10000 s周期内地电脉冲方向,右上角插图给出真实感应向量的玫瑰图,持续时间为1092 s.MT数据采集使用了基于磁通门磁力仪的常规长周期MT仪器系统GSY-USA.时间序列数据(持续时间通常为三周)使用标准的远程参考方法(Egbert, 1997)进行处理,因此多数情况下可在10~10000 s时间范围内获得平滑的响应曲线.尽管视电阻率存在明显的站点之间静态位移,但相位表现良好,且表现出大尺度相干特征.本文旨在测试所提出的反演算法的应用效果,因此我们对反演结果不做地质解释,详细地质解释可参考(Patro and Egbert, 2008).
|
图 7 实测数据测点分布图(参考Patro and Egbert, 2008) Fig. 7 Map of MT survey stations (modified from Patro and Egbert, 2008) |
三维反演使用的实测数据共有109个测点,每个测点包含4个复阻抗张量分量,我们选择8个周期(100~8000 s)的张量阻抗进行反演.反演模型的总尺寸为1460 km×1590 km×550 km,水平方向由48×46个网格单元组成,网格尺寸均为24 km×24 km, 垂直方向上共设有41层网格,其中包括7个空气层.
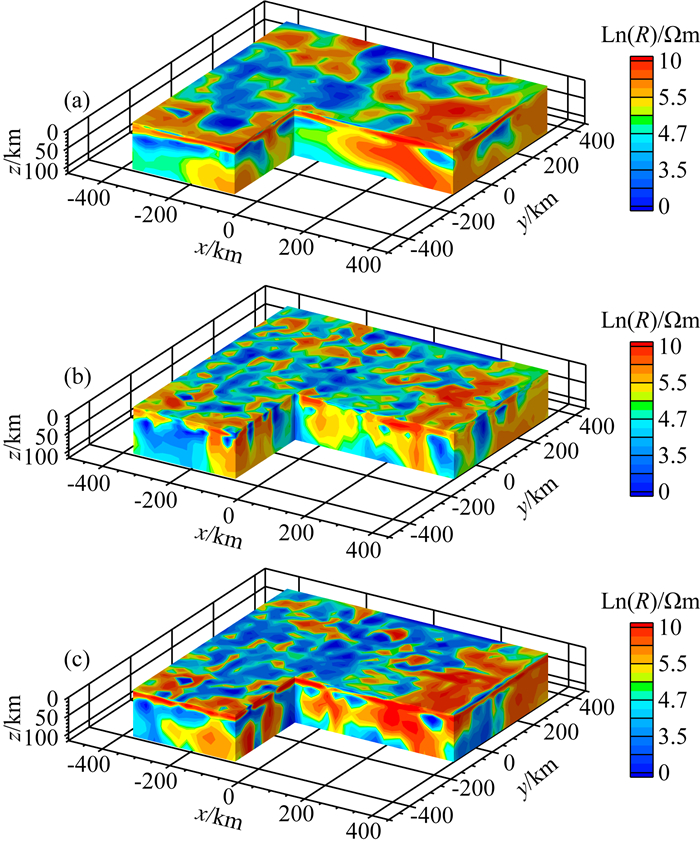
图 8a—c分别给出实测MT数据利用GN、WT-GN和PWT-GN的反演结果.分析和对比这些结果可以看出,三种方法反演的结果在大结构上基本一致.其中,GN方法与ModEM3D程序中给出的NLCG反演结果一致,反演模型整体上呈块状连续结构,高阻体结构从中心向外有明显的光滑渐变特征;基于小波变换的GN反演结果(图 8b、c)较之于传统的GN反演电阻率分布总体上差异不大,但呈现出更多细节,异常边界更加清晰.
|
图 8 实测MT数据三维反演结果 (a) GN方法;(b) WT-GN方法;(c) PWT-GN方法. Fig. 8 3D inversions of MT survey data (a) GN method; (b) WT-GN method; (c) PWT-GN method. |
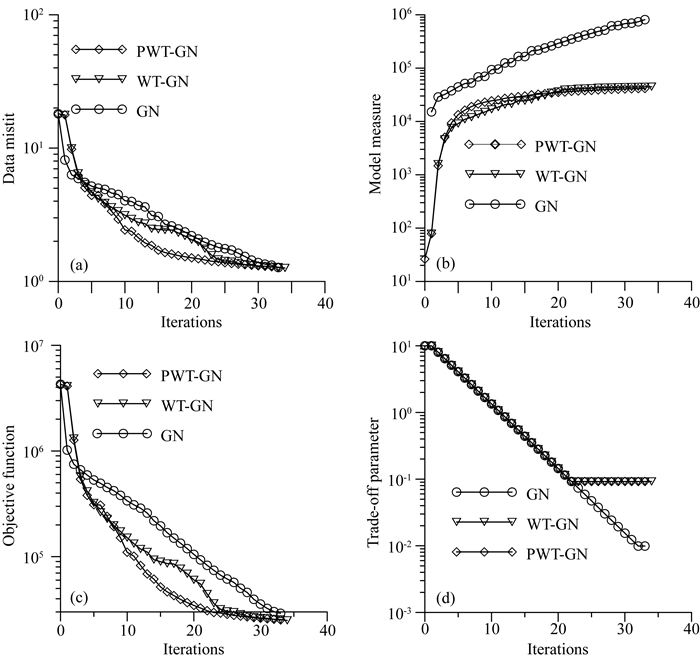
图 9a给出三种反演方法的RMS下降曲线,可以看出与理论模型算例类似的规律,即小波域反演早期迭代略快于传统的GN方法,但在晚期明显比GN方法收敛速度快.图 9b给出模型改变量随着迭代次数的变化曲线,同样可以看出GN方法模型改变量开始较大,然后变化趋于平缓,而WT-GN和PWT-GN方法开始由于R矩阵的影响变化量很小,经过几次迭代之后逐渐趋于缓慢变化.图 9c给出目标函数下降曲线,下降规律与RMS相似.图 9d给出三种方法正则化因子λ的下降策略.由于模型约束不同,针对传统GN方法的正则化因子阈值设置小于其他两种方法.
|
图 9 反演参数曲线 (a)数据拟合均方根误差;(b)模型改变量;(c)目标函数;(d)正则化因子. Fig. 9 Inversion parameters versus iterations (a) Data misfit; (b) Model measure; (c) Objective function; (d) Trade-off parameter. |
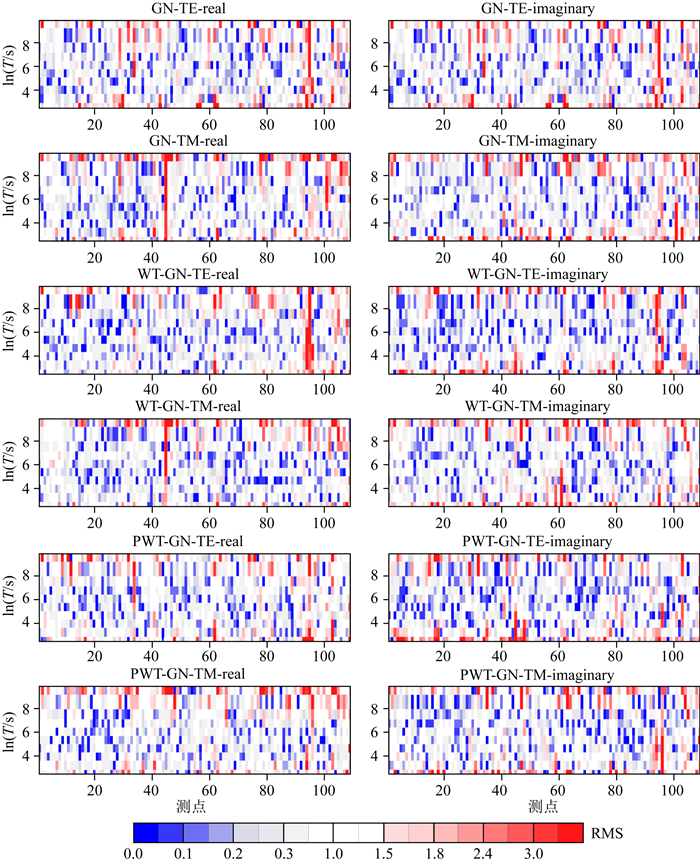
图 10给出实测数据拟合均方根误差(RMS)分布图.从图中可以看出,三种方法反演误差水平大部分均降到了可接受的误差范围之内,基于小波变换的反演数据拟合略好于传统的GN方法.
|
图 10 MT实测数据反演拟合均方根误差分布 Fig. 10 RMS distribution for MT measurement data |
本文利用小波变换成功实现了基于模型空间压缩的大地电磁三维反演方法.通过理论模型和实测数据的反演对比分析了高斯牛顿法(GN)、小波反演方法(WT-GN)、经过预条件处理后的小波反演方法(PWT-GN)的应用效果.结合小波特性,我们得出以下结论:
(1) 基于小波变换的GN反演具有小波变换多尺度特性,能够很好地反映模型的真实边界.
(2) 本文提出的基于R矩阵预条件处理方法,对提升反演方程共轭梯度CG方法的求解效率效果明显.
(3) 由于小波变换本身的特性,在对数据影响小的模型区域(例如无数据区域或模型深部区域)基于小波变换的反演会产生一些虚假异常,反演时这些区域需要进行适当控制.
(4) 基于模型空间压缩的电磁反演方法是一个较新的研究内容,本文只对其进行了基本的探索.未来我们将在变换函数选择、阈值控制和反演约束等方面进行深入研究,以期得到更好的反演效果.
致谢 感谢美国俄勒冈州立大学的Gary Egbert博士提供的ModEM3D程序和算例.
Belyavskii V V, Sukhoi V V. 2004. The method of audio-frequency magnetotelluric sounding in mineral exploration. Izvestiya Physics of the Solid Earth, 40(6): 515-533. |
Cagniard L. 1953. Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics, 18(3): 605-635. DOI:10.1190/1.1437915 |
Chen X B, Zhao G Z, Tang J, et al. 2005. An adaptive regularized inversion algorithm for magnetotelluric data. Chinese Journal of Geophysics (in Chinese) (in Chinese), 48(4): 937-946. |
Chiao L Y, Kuo B Y. 2001. Multiscale seismic tomography. Geophysical Journal International, 145(2): 517-527. DOI:10.1046/j.0956-540x.2001.01403.x |
Chiao L Y, Liang W T. 2003. Multiresolution parameterization for geophysical inverse problems. Geophysics, 68(1): 199-209. DOI:10.1190/1.1543207 |
Constable S C, Parker R L, Constable C G. 1987. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics, 52(3): 289-300. DOI:10.1190/1.1442303 |
DeGroot-Hedlin C, Constable S. 2004. Inversion of magnetotelluric data for 2D structure with sharp resistivity contrasts. Geophysics, 69(1): 78-86. DOI:10.1190/1.1649377 |
Egbert G D. 1997. Robust multiple-station magnetotelluric data processing. Geophysical Journal International, 130(2): 475-496. DOI:10.1111/gji.1997.130.issue-2 |
Egbert G D, Kelbert A. 2012. Computational recipes for electromagnetic inverse problems. Geophysical Journal International, 189(1): 251-267. DOI:10.1111/gji.2012.189.issue-1 |
Egbert G D, Kelbert A, Meqbel N, et al. 2014. ModEM:A modular system for inversion of elecgtromagnetic geophysical data. Computers & Geosciences, 66(66): 40-53. |
Ekblom H. 1987. The L1-estimate as limiting case of an Lp-or Huber-estimate.//Doge Y. Statistical Data Analysis Based on the L1-Norm and Related Methods. Yadolah Dodge, Amsterdam:Elsevier, 109-116.
|
Farquharson C G. 2008. Constructing piecewise-constant models in multidimensional minimum-structure inversions. Geophysics, 73(1): K1-K9. |
Haber E. 2014. Computational Methods in Geophysical Electromagnetics. Philadelphia, PA, USA:SIAM. |
Hu Z Z, Hu X Y, He Z X. 2006. Pseudo-three dimensional magnetotelluric inversion using nonlinear conjugate gradients. Chinese Journal of Geophysics (in Chinese) (in Chinese), 49(4): 1226-1234. |
Hung S H, Chen W P, Chiao L Y. 2011. A data-adaptive, multiscale approach of finite-frequency, traveltime tomography with special reference to P and S wave data from central Tibet. Journal of Geophysical Research:Solid Earth, 116(B6): B06307. DOI:10.1029/2010JB008190 |
Kelbert A, Meqbel N, Egbert G D, et al. 2014. ModEM:A modular system for inversion of electromagnetic geophysical data. Computers & Geosciences, 66: 40-53. |
Liu Y H, Farquharson C G, Yin C C, et al. 2018. Wavelet-based 3-D inversion for frequency-domain airborne EM data. Geophysical Journal International, 213(1): 1-15. DOI:10.1093/gji/ggx545 |
Lü Y. 2012. Application of geophysical exploration methods in geohydrological detailed investigation. Shanxi Hydrotechnics (in Chinese), (1):79-80 (in Chinese), (1): 79-80, 84. |
Madden T R, Mackie R L. 1989. Three-dimensional magnetotelluric modelling and inversion. Proceedings of the IEEE, 77(2): 318-333. DOI:10.1109/5.18628 |
Mitsuhata Y, Uchida T. 2004. 3D magnetotelluric modeling using the T-Ω finite-element method. Geophysics, 69(1): 108-119. DOI:10.1190/1.1649380 |
Newman G A, Alumbaugh D L. 2000. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophysical Journal International, 140(2): 410-424. DOI:10.1046/j.1365-246x.2000.00007.x |
Nittinger C G, Becken M. 2016. Inversion of magnetotelluric data in a sparse model domain. Geophysical Journal International, 206(2): 1398-1409. DOI:10.1093/gji/ggw222 |
Patro P K, Egbert G D. 2008. Regional conductivity structure of Cascadia:Preliminary results from 3D inversion of USArray transportable array magnetotelluric data. Geophysical Research Letters, 35(20): L20311. DOI:10.1029/2008GL035326 |
Siripunvaraporn W, Egbert G. 2009. WSINV3DMT:Vertical magnetic field transfer function inversion and parallel implementation. Physics of the Earth and Planetary Interiors, 173(3-4): 317-329. DOI:10.1016/j.pepi.2009.01.013 |
Smith J T, Booker J R. 1991. Rapid inversion of two-and there-dimensional magnetotelluric data. Journal of Geophysical Research:Solid Earth, 96(B3): 3905-3922. DOI:10.1029/90JB02416 |
Spichak V, Menvielle M, Roussignol M. 1995. Three-dimensional inversion of the MT fields using Bayesian statistics.//Oristaglio M, Spies B eds. Three-Dimensional Electromagnetics. Tulsa:SEG, 347-358.
|
Tan H D, Yu Q F, Booker J, et al. 2003. Three-dimensional rapid relaxation inversion for the magnetotelluric method. Chinese Journal of Geophysics (in Chinese) (in Chinese), 46(6): 850-854. |
Tikhonov A N. 1950. On determining electrical characteristics of the deep layers of the Earth's crust. Doklady Akademii Nauk SSSR, 73(2): 295-311. |
Xu Y X, Wang J Y. 1998. A multiresolution inversion of onedimensional magnetotelluric data. Acta Geophysica Sinica (in Chinese) (in Chinese), 41(5): 704-711. |
Zhang L L, Hao T Y, Xiao Q B, et al. 2015. Magnetotelluric investigation of the geothermal anomaly in Hailin, Mudanjiang, northeastern China. Journal of Applied Geophysics, 118: 47-65. DOI:10.1016/j.jappgeo.2015.04.006 |
陈小斌, 赵国泽, 汤吉, 等. 2005. 大地电磁自适应正则化反演算法. 地球物理学报, 48(4): 937-946. DOI:10.3321/j.issn:0001-5733.2005.04.029 |
胡祖志, 胡祥云, 何展翔. 2006. 大地电磁非线性共轭梯度拟三维反演. 地球物理学报, 49(4): 1226-1234. DOI:10.3321/j.issn:0001-5733.2006.04.039 |
吕英. 2012. 物探方法在水文地质详查中的应用. 山西水利科技, (1):79-80, 1: 79-80, 84. |
谭捍东, 余钦范, Booker J, 等. 2003. 大地电磁法三维快速松弛反演. 地球物理学报, 46(6): 850-854. DOI:10.3321/j.issn:0001-5733.2003.06.019 |
徐义贤, 王家映. 1998. 大地电磁的多尺度反演. 地球物理学报, 41(5): 704-711. DOI:10.3321/j.issn:0001-5733.1998.05.014 |
 2019, Vol. 62
2019, Vol. 62


