2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3. 北京大学地球与空间科学学院石油与天然气研究中心, 北京 100871;
4. 东华理工大学地球物理与测控技术学院, 南昌 330013
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao Shandong 266071, China;
3. Oil & Gas Reserch Center, School of Earth and Space Sciences, Peking University, Beijing 100871, China;
4. School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang 330013, China
地震反演作为地下介质弹性参数的有效预测手段,在过去的几十年里面,得到了极大的推进和发展,其中,叠前反演作为流体识别、孔隙压力预测以及各向异性参数反演等的重要工具,近年来越来越受到业界的关注.在传统的AVO反演中,将偏移数据体转换到角度域或者τ-p域,然后基于振幅随偏移的变化,利用其对地下介质属性的依赖性,实现纵波速度、横波速度以及密度三参数反演.在反演过程中,目标函数定义为观测地震数据和模拟数据之间的误差.模拟地震数据可基于精确Zoeppritz方程求得,但由于其复杂性和非线性,在实际反演过程中往往需要假设入射角较小,从而使反射系数近似为入射角正弦平方的线性函数(Aki and Richards, 1980; Shuey, 1985).线性化的AVO反演因其高效性在业界内被广泛使用(Buland et al., 1996; 陈建江和印兴耀, 2007; 杨培杰等, 2009; 宗兆云等, 2012),但是其存在较多的局限性.一方面,在传统AVO反演当中,往往假设叠前地震道集已经被仔细合理地处理过,也就是说输入地震道集仅仅由PP/PS类型的一次反射波组成,没有波模式的多次转换,也没有其他的传播效应,如几何扩散,透射损失和多次波等,而这在实际数据处理当中是很难做到的.另外一方面,线性化的反射系数都是基于小角度近似的,一般在30°以内,但目前随着宽方位高密度地震采集的发展,传统AVO反演的适用性逐渐减弱.此外,任何基于反射系数的反演结果往往都会缺乏低频信息,因为反射系数本身就是地下介质属性的一阶导数,且线性化的模型将导致反演结果不会超出地震频带.为了增强有效波,基于部分角度叠加道集的弹性波阻抗反演逐渐发展,近年来逐渐用于反演地层各向异性参数和岩石物理参数(Connolly, 1999; Cambois, 2000; 王保丽等, 2005; 印兴耀等, 2014; 陈怀震等, 2014).
考虑到地震波场比较复杂且不易分离,多种基于全波场模拟的地震反演方法得以发展,其中发展最为迅速的就是全波形反演(Virieux and Operto, 2009; 董良国等, 2013).从理论上来讲,全波形反演应该是最直接也是最精确的反演地下介质参数的方法.全波形反演的计算量非常巨大,尽管当前的计算机硬件水平和并行加速算法都取得了长足的发展(Li et al., 2012),仍然不能满足实际地震资料处理的需求,全波形反演的真正工业化仍然还有一段较长的路要走.目前业界内全波形反演往往用来获得低频速度模型,并将其作为偏移成像的背景场以获得更精确的成像效果.除全波形反演外,基于反射率法正演模拟的叠前反演方法也一直备受关注.反射率方法是基于水平层状地球介质假设的,它能计算层状地球介质当中的全波场,包括反射、透射、多次波及波模式转换等.自Thomson(1950)提出以后,反射率方法就得到广泛推广和应用,如Fuchs and Müller(1971), Kennett(1979), Kennett and Kerry(1979)和Muller(1985)等.目前讨论最多应用最广的就是Kennett(1983)提出的利用Kennett递归矩阵的反射率正演(KRM)方法.在反演方面,Zhao等(1994)描述了一种基于KRM的频率波数域反演方法.Sen和Roy(2003)用高斯-牛顿方法求解基于KRM的反演目标函数,且针对正则化因子的选取提出了不同的策略.Gouveia和Scales(1998)基于贝叶斯框架减弱叠前波形反演的不确定性.Mallick(1999)利用遗传算法寻找全局最优解,使得合成道集和观测数据在角度域达到最佳匹配.Mallick和Adhikari(2015)在顾及到计算时间成本的情况下,采用一种多尺度参数化方法执行叠前波形反演,并与传统的AVO反演结果对比,验证了其有效性和先进性.Padhi等(2015)将遗传算法和非线性最小二乘方法结合,使得反演结果更精确.Liu等(2016)对传统的KRM方法做了修改,直接在角度域合成地震道集,并基于贝叶斯反演框架,实现了储层的精细描述.刘财等(2017)基于传递矩阵理论进行了高精度地震记录合成,并实现了砂泥岩薄层结构的刻画与描述.总的来说,尽管基于全波场模拟的反演方法需要更多的计算成本,但其能获得高分辨的反演结果,这对目前的精细油气勘探发展是十分必要的.
不同于传统基于Zoeppritz方程和褶积模型的AVO反演,也不同于基于微分形式波动方程或反射率方法的全波形反演,本文基于Lippmann-Schwinger类型的波动方程积分形式,即所谓的散射积分方程(De Hoop, 1995)执行叠前地震反演.基于1.5D局部层状介质模型假设,将散射积分方程限制到数据域和目标域,分别建立数据方程和目标方程,构成反演基本方程系统.与广为使用的对比源算法(Van den Berg和Aubakar, 2001)相比,本文一方面分别求解数据方程和目标方程,交替迭代地实现地层对比度属性的反演,而不是将数据方程和目标方程融入到一个目标泛函中,采用不同正则化手段求解;另一方面,本文不直接求解积分形式的波动方程,而是以一种优化的散射级数Neumann序列建立整体场,其中,每添加一阶散射,地震数据和地下介质属性之间的非线性关系就得以进一步顾及.通过多层地质模型,分析了透射损失、多次波等对地震角道集AVA响应的影响,说明了基于全波场的地震反演的重要性.通过测井合成地震记录测试和CSEG山前带模型测试,验证了本文方法流程在高分辨率和宽带地震反演方面的优势,具有广阔的应用前景.
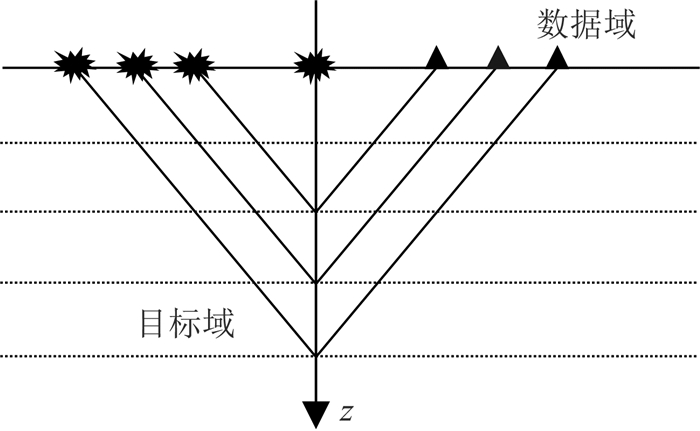
1 基本理论与技术流程 1.1 数据模型和参数变量与传统AVO反演相同,本文采用的叠前反演方法也是基于局部层状介质假设的,且输入数据也为CMP道集.如图 1所示,CMP道集被定义在观测系统平面上,也称为数据域,它照亮了地下的局部层状介质,要反演的属性被定义在垂直网格点上,也称为目标域.从图中可以看出,地层模型是1D深度模型,CMP道集数据是2D的,因此也将这种数据模型称为1.5D模型.在传统AVO反演当中,往往将CMP道集转换到角度域,而本文采用的叠前反演方法是将CMP道集转换到τ-p域,可采用线性Radon变换实现.
|
图 1 局部层状介质数据模型示意图 Fig. 1 Schematic diagram of locally layered medium data model |
在1.5D数据模型假设条件下,各向同性介质中的弹性波传播能通过应力场τzz, τxz和速度场vx, vz描述,且质点速度场和应力场通过刚度矩阵和牛顿第二定律线性地联系起来.为了获得波动方程的积分表达形式,引入柔度矩阵,即刚度矩阵的逆.柔度矩阵中基本参数包括压缩系数κ(体积模量的倒数),剪切柔度M(剪切模量的倒数)以及密度ρ.假设已知平滑的背景场κb, Mb, ρb并且将模型变量定义为对比度变量:
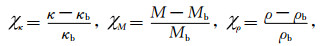
|
(1) |
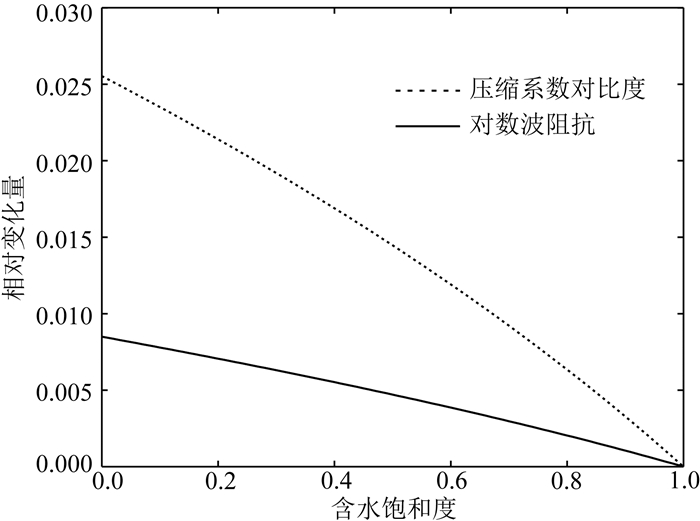
其中,χκ, χM, χρ分别为压缩系数、剪切柔度和密度的对比度.平滑背景场往往通过测井数据插值获取,用作反演的初始模型.对比度变量作为积分形式弹性波动方程中的基本变量,也是反演的目标参数,此外,对比度变量相比于传统的纵横波阻抗,对油气指示呈现出更强的敏感性.图 2展示了基于Gassmann流体替换(Mavko et al., 1998; 姚振岸和孙成禹, 2017)的纵波对数波阻抗(实线)和压缩系数对比度(虚线)相对变化量曲线,其中饱水岩石作为参考背景,岩石孔隙度为8%,饱水情况下的介质弹性参数为vpP=4747.3 m·s-1, vsS=2859 m·s-1, ρ=2511.8 kg·m-3.公式(2)和(3)给出了图 2中曲线的计算公式:

|
(2) |
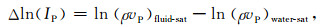
|
(3) |
|
图 2 基于Gassmann流体替换的纵波对数波阻抗和压缩系数对比度相对变量曲线 相对于水饱和背景 Fig. 2 Logarithmic P-wave impedance and compressibility contrast variation with water saturation based on Gassmann fluid substitution against a water saturated background |
其中χκfluid-sat和IP分别表示含油气岩石对比度和纵波阻抗.
从图 2可以看出,压缩系数对比度对含水饱和度的敏感性比对数纵波阻抗的3倍还高.纵横波速度和对数阻抗与压缩系数、剪切柔度存在如下解析关系:
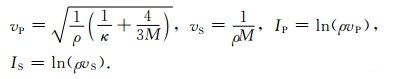
|
(4) |
从(4)式可以看出,相比于压缩系数κ,纵波速度vP对油气的敏感性被4/(3M)项稀释,而4/(3M)项与含油气饱和度没有关系,压缩系数对含油气更为敏感.在纵波阻抗中,尽管乘以密度项,但是密度对含油气的微弱依赖性质并不能对4/(3M)项的稀释做出弥补.经对多种岩石测试表明,压缩系数对比度和纵波对数阻抗对油气敏感性有大致3倍的差异具有一般性.
1.2 数据方程和目标方程与传统AVO反演不同,本文采用的叠前反演方法不是基于褶积模型,而是基于波动方程.同时,也不同于全波形反演或者逆时偏移中采用的微分形式波动方程,而是采用弹性波动方程的积分表示(Yang et al., 2008).散射积分方程(De Hoop, 1995)可以表示为
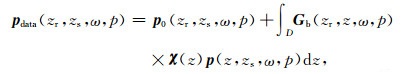
|
(5) |
其中,pdata表示弹性波场,p0为入射波场,也即背景介质中的弹性波场,Gb为背景场介质中的格林函数,χ为弹性参数对比度函数向量,p代表目标区域中的整体场,z表示目标区域D中任意一点的深度,zr和zs分别表示检波器和震源的深度,ω和p分别表示角频率和射线参数.依据散射理论,弹性波场等于入射波场和散射波场的叠加,式(5)中的第一项是入射波场,第二项即为散射波场.地震波从震源出发传播到地下每一点,形成入射波场和整体场p,整体场p考虑了地下所有散射体之间的相互作用,因而非常复杂,继而在对比度不为零的位置将产生二次震源,通过平滑背景介质中的格林函数,这些二次震源能量被传输到检波器,从而形成了地震记录.
将散射积分方程限制在观测系统平面上也即数据域,就得到所谓的数据方程:
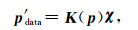
|
(6) |
其中,p′data表示切除直达波之后的反射地震记录,即将反射地震记录整体视为散射波场.算子核K是整体场p的函数,作用在对比度向量χ上.
将式(5)中沿着目标域D的积分形式记为算子核L(χ),并将其限制在目标域,则得到了所谓的目标方程:
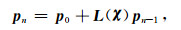
|
(7) |
其中,pn和pn-1分别表示考虑至n阶和n-1阶散射的整体场.背景介质对比度为零,入射波场p0可基于背景介质模型和地震子波估计预先予以计算,背景介质模型往往由测井资料和层位解释结果联合建立.本文采用WKBJ近似(Dingle, 1973; Gisolf and Verschuur, 2010)计算平滑背景介质中的入射波场.
联立数据方程(6)和目标方程(7)即可实现对未知变量p和χ的求解,其中,整体场p和对比度函数χ之间存在强非线性关系,在以往的求解方法当中,往往将数据方程目标泛函和目标方程目标泛函融入到同一个目标函数当中,典型的如对比源方法及其一系列推广.
1.3 正则化方法与交替迭代求解流程不同于对比源方法,本文采用一种交替迭代求解方法(王彦飞, 2007; Wang et al., 2011),即对数据方程和目标方程分别求解,迭代交替进行,直至方程系统稳定收敛(Gisolf, 2010; Haffinger et al., 2015, 2016; Beller et al., 2015).
首先,将预先计算出的入射波场p0作为整体波场的第一次估计代入到数据方程,则可实现对比度函数向量的第一次估计,继而基于目标方程可以实现整体波场的更新,伴随着更新的整体场,重新回到数据方程,开始第二次循环,如此重复就实现了整体场p和对比度函数χ的求解.
数据方程(6)的反演被视为一个线性反演,因为原本依赖于对比度函数向量χ的整体场p在反演过程中是保持不变的.因为在地震记录中存在噪声干扰,故在反演的过程中采用了乘性正则化技术(Van den Berg et al., 2003; Abubaka et al., 2004; 王彦飞等, 2011),并在共轭梯度框架下进行迭代求解.乘性正则化不同于常用的加性正则化,它采用一个全变差函数乘以l2范数意义下的成本函数形成最终的目标泛函.相比于加性正则化方法,乘性正则化方法的抗噪性更强,且趋于产生块状化的模型参数.
在目标方程(7)的计算过程中,对比度函数向量χ保持不变,则整体场p的更新也可视为一个线性的更新过程.而在整体场更新过程中,本文不是直接求解波动方程,而是采用Neumann序列迭代的方式建立起积分波动方程的精确解:
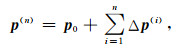
|
(8) |
其中,p(n)表示第n次交替迭代的整体波场估计,并有:
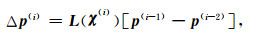
|
(9) |
研究表明,Neumann序列仅仅对低值对比度收敛,为了增强其稳定性,引入线性系数αi(n),形成优化的Neumann序列,即:
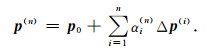
|
(10) |
上述方法也被称为“Krylov子空间方法”(Kleinman and van denBerg, 1991).式(10)中,线性系数αi(n)可以在最小二乘意义下求得.从物理含义上说,整体场的更新可解释为所有地层内部多次散射和波模式转换,也包含了真实介质和背景模型之间的地震波走时差异.
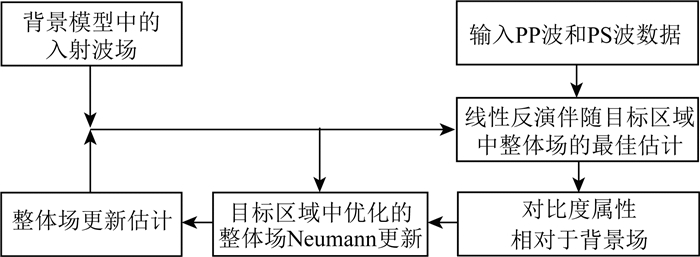
当n=1时,交替迭代反演流程就等价于反演问题的线性化(Tarantola, 1984a, 1984b),也称为Born近似.通过上述波场更新方法,越来越多阶的散射项被融入到整个交替迭代反演过程中,最终建立起地震数据与地下介质属性之间的全部非线性关系.此外,数据方程反演中采用的正则化方法本身就是一种非线性过程.综合上述过程,建立起如图 3所示的迭代非线性反演流程图.
|
图 3 交替迭代非线性反演流程图 Fig. 3 Flow-diagram of alternative iteration non-linear inversion |
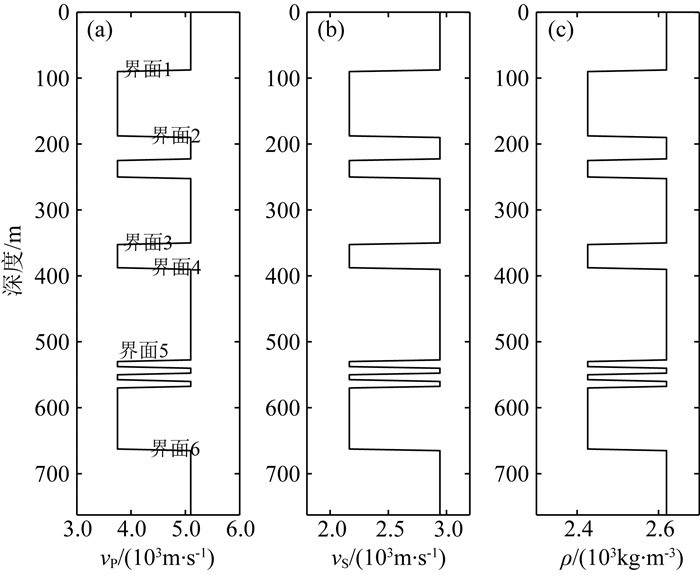
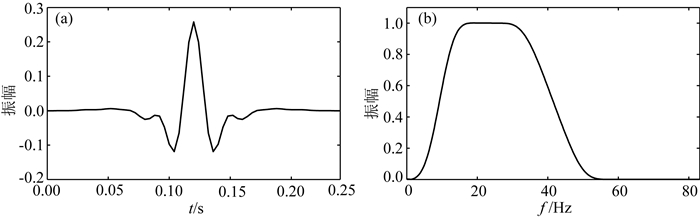
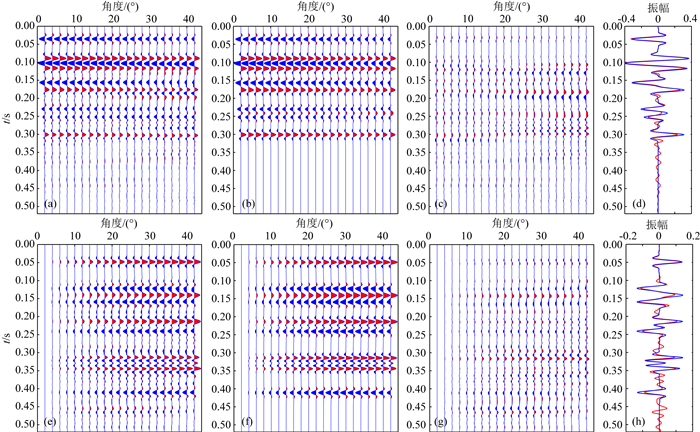
为了研究层间多次波和透射损失对地层界面AVO响应特征的影响,建立如图 4所示的多层地质模型,其中有5套地层组合结构,包括大套厚层组合、薄互层组合等,其中,薄互层组合结构为四个单层厚度为10 m的薄层的叠加.选定一个带限的零相位地震子波,其波形和频谱特征如图 5所示,且角点频率为6-12-33-50 Hz.分别采用反射率方法和褶积模型合成PP波和PS波地震角道集如图 6所示.反射率方法考虑的是整个多层地质模型的综合响应,属于一种半解析解方法,它考虑了层间多次波、波模式转换以及透射损失等多种动力学因素的影响,而褶积模型基于的仅仅是单弹性界面的反射系数,且在目前AVO反演过程中往往只用到其小角度近似.尽管本节在褶积合成角道集的过程中采用了精确Zoeppritz方程,但其和反射率合成地震记录仍然存在较大的差异,从两者的差异剖面当中可以看出,随着深度的增加,透射损失越来越严重,且随着入射角度的增加,受到层间多次波的影响越来越严重.就薄层的调谐特征来说,采用两种方法合成的地震记录存在较大的差异,尤其是在大角度处,调谐波形形态已出现严重偏差,因此,在目前的地震反演中,薄互层仍然不能得到有效的识别.从图 6d和图 6h中的波形对比也可以看出,层间多次波夹杂在整道地震记录当中,并且和透射损失效应一起影响着地层界面的振幅响应.
|
图 4 多层地层模型 (a)纵波速度; (b)横波速度; (c)密度. Fig. 4 A multilayer stratigraphic model (a) P-wave velocity; (b) S-wave velocity; (c) Density velocity. |
|
图 5 零相位地震子波(a)及其地震子波振幅谱(b) Fig. 5 The zero-phase wavelet together with its amplitude spectrum used in the forward modelling, with trapezium corner frequencies of 6-12-33-50 Hz |
|
图 6 多层地质模型合成地震角道集 (a)反射率法合成PP波角道集; (b)基于Zoeppritz方程合成PP波角道集; (c) PP波差异角道集; (d) 10°PP波地震道波形对比; (e)反射率法合成PS波角道集; (f)基于Zoeppritz方程合成PS波角道集; (g) PS波差异角道集; (h) 10°PS波地震道波形对比. Fig. 6 Synthetic angle gathers for multilayer model in Fig. 1 (a) PP-wave angle gather by reflectivity method; (b) PP-wave angle gather based on Zoeppritz equation; (c) Difference between angle gathers in Fig. 2a and Fig. 2b; (d) Waveform comparison of 10°seismic record; (e) PS-wave angle gather by reflectivity method; (f) PS-wave angle gather based on Zoeppritz equation; (g) Difference between angle gathers in Fig. 2e and Fig. 2f; (h) waveform comparison of 10°seismic record. |
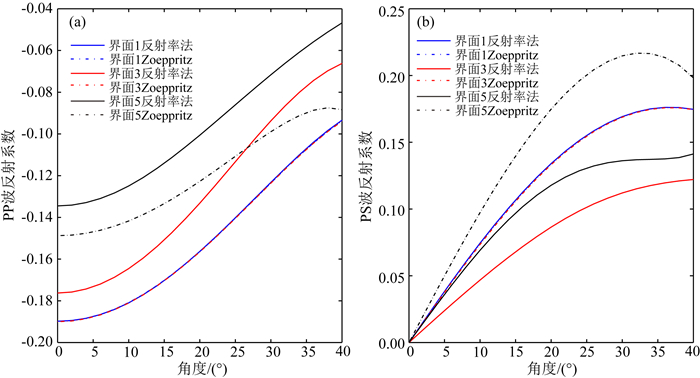
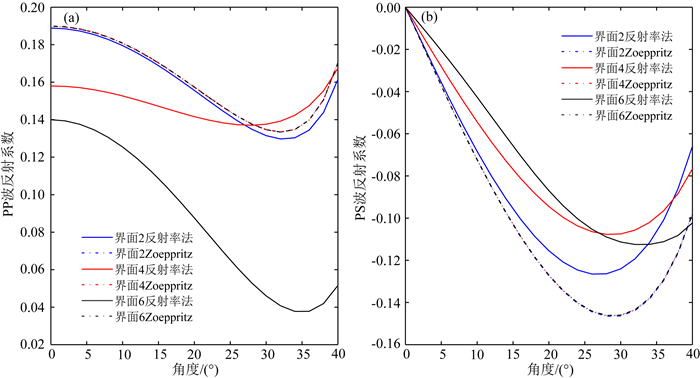
从图 4选定6个考察界面,分别从图 6a,6b和图 6e,6f中拾取其对应的AVA曲线如图 7和8所示,研究其响应特征规律,其中界面1,3,5对应负反射系数,而界面2,4,6对应正反射系数.在图 7和图 8当中,虚线代表利用Zoeppritz方程计算合成地震记录的AVA曲线,实线表示利用反射率法计算合成地震记录的AVA曲线.对于界面1和3来说,界面上下介质性质相同,利用Zoeppritz方程计算的PP波和PS波反射系数是一致的,但在反射率方法的计算结果中,对于界面1来说,没有透射损失和层间多次波的影响,和利用Zoeppritz方程计算的结果基本保持一致,而界面3的反射波受到层间多次波和透射损失的影响,相比于利用Zoeppritz方程计算的结果反射系数有所降低.尽管界面5性质和界面1,3相同,但由于薄互层的调谐作用,其反射系数已不再遵循Zoeppritz方程.总的来说,由于透射损失的影响,利用反射率方法计算出的反射系数依然相对较低.就界面2,4,6而言,界面性质相同,由Zoeppritz方程计算出的反射系数完全一致,而利用反射率法计算出结果已严重偏离Zoeppritz方程计算结果,不再是简单的递减,这可归结为透射损失和层间多次波的综合影响,如图 8所呈现出的暗点特征会出现在不同的角度道上.因此在实际地震数据当中,层间多次波和透射效应等与一次反射波混叠在一起,可能会误导反演和解释结果.
|
图 7 基于反射率法和Zoeppritz方程的AVA曲线 (a) PP波; (b) PS波. Fig. 7 Amplitude variation with incident angles based on reflectivity modelling and Zoeppritz equation (a) PP-wave; (b) PS-wave. |
|
图 8 基于反射率法和Zoeppritz方程的AVA曲线 (a) PP波; (b) PS波. Fig. 8 Amplitude variation with incident angles based on reflectivity modelling and Zoeppritz equation (a) PP-wave; (b) PS-wave. |
从上面的分析中可以看出,即便是采用精确Zoeppritz方程获取的地层AVA或AVO响应曲线,也与真实地层反射系数存在一定差距,且入射角度越大,误差越大,因此传统的AVO反演已经不能满足目前宽方位精细地震勘探的需求,开展基于全波场信息的叠前反演愈发重要.本文基于波动方程开展叠前地震反演,将透射损失、层间多次波、极化方式转换等都包含进来,是一种较为精确的全波场反演方法,能获得高分辨率的地震介质属性.
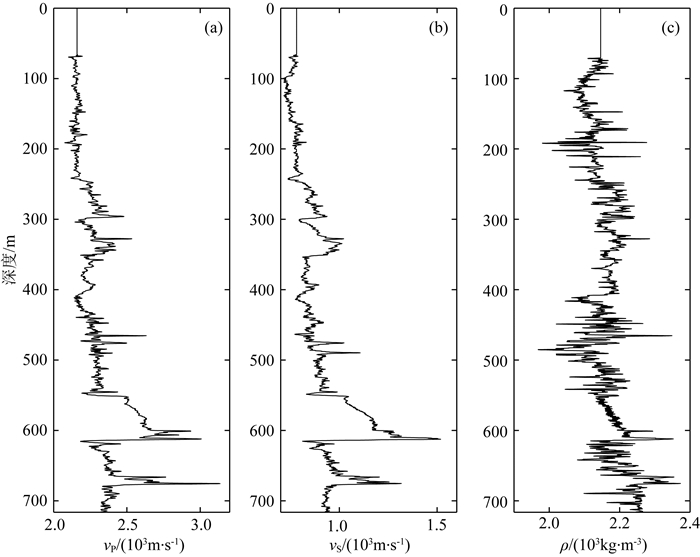
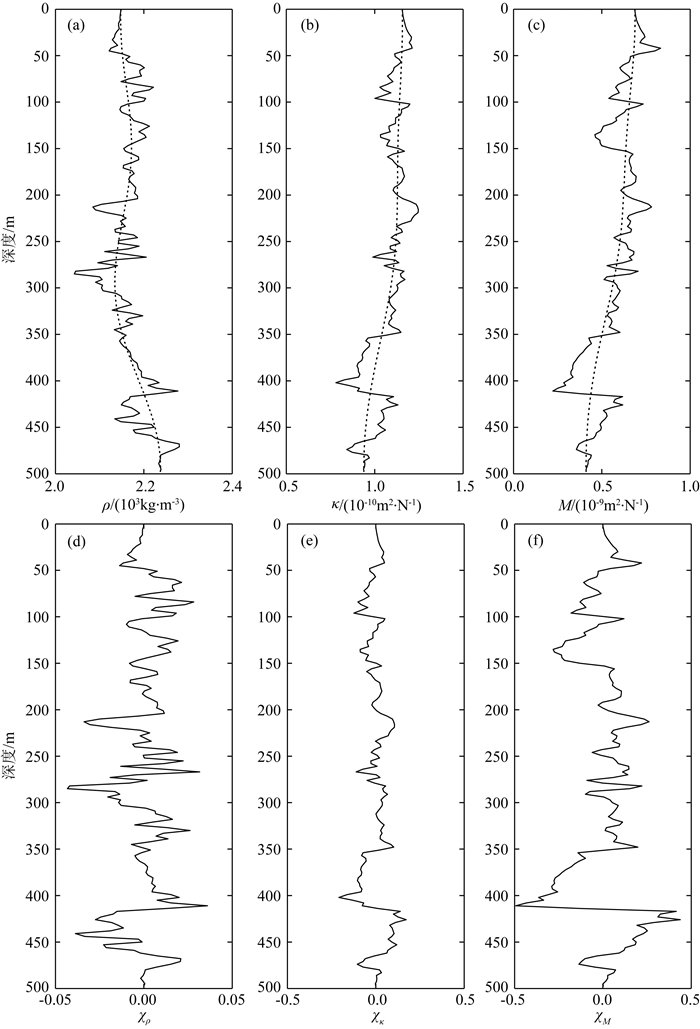
3 测井合成地震记录反演测试将本文所述的基于波动方程的交替迭代反演方法应用于测井地震记录中,验证其反演效果.图 9给出了纵波速度,横波速度以及密度测井曲线.依据反演方法的参数变量需求,由Backus平均(曹丹平, 2015)测井曲线计算出压缩系数、剪切柔度和密度三参数及其对比度曲线如图 10所示,其中虚线表示背景信息,其采用低通滤波的方法获得,本文采用对应时间频带为0~4 Hz的波数域滤波器予以计算,参考速度为测井曲线平均速度.从对比度曲线可以看出,密度对比度取值范围约为压缩系数对比度和剪切柔度对比度的1/10,也就意味着随着深度增加,密度相对变化较弱,这也就是在目前的地震反演当中密度参数难以稳定准确反演的原因之一.
|
图 9 测井曲线 (a)纵波速度; (b)横波速度; (c)密度. Fig. 9 Well logs (a) P-wave velocity; (b) S-wave velocity; (c) density velocity. |
|
图 10 由Backus平均测井曲线计算出的压缩系数、剪切柔度和密度三参数及其对比度曲线 (a)密度及其背景曲线; (b)压缩系数及其背景曲线; (c)剪切柔度及其背景曲线; (d)密度对比度曲线; (e)压缩系数对比度曲线; (f)剪切柔度对比度曲线.其中,虚线表示背景. Fig. 10 Compressibility, shear compliance, density three parameters and their contrast curves calculated from Backus averaged well logs (a) Density and its background curve; (b) Compressibility and its background curve; (c) Shear compliance and its background curve; (e) Density contrast curve; (f) Compressibility contrast curve; (g) Shear compliance contrast curve. In which, dot line represent background. |
依旧是采用图 5所示的零相位地震子波,采用反射率方法合成地震记录,并添加随机噪声使合成地震记录能量信噪比为30 dB,其中合成地震记录为τ-p域地震记录,最大射线参数对应最大地层纵波速度的P波入射角度为40°.
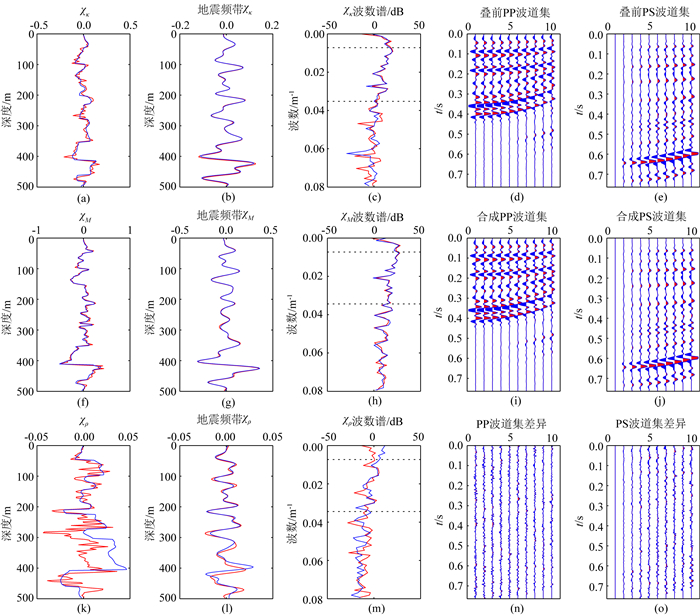
图 11给出了反演结果,其中红色曲线代表真实值,蓝色曲线表示反演结果.图 11(a,f,k)分别为压缩系数对比度、剪切柔度对比度和密度对比度反演结果,压缩系数对比度和剪切柔度对比度得到了较好的反演,而在深度300~400 m范围内密度对比度的反演结果误差较大.尽管如此,在地震频带内反演结果还是能和真实值保持较高的一致性,如图 11l.压缩系数对比度、剪切柔度对比度和密度对比度的波数谱分别展示在图 11(c,h,m)中,其中虚线标明了地震频带.从中可以看出,压缩系数对比度、剪切柔度对比度反演结果的波数谱远远超出了地震频带,既朝着低波数方向,也朝着高波数方向拓展.相对于传统的线性反演,迭代交替反演流程考虑了地震数据和地下介质属性的非线性关系,基于积分波动方程,将包含层间多次波,透射损失的全波场信息融入到反演过程中,使得反演结果频带展宽,分辨率增强.密度对比度波数谱在低波数位置没有被恢复出来,也就意味着叠前地震道集中没有包含这部分信息,或者它已经被噪声淹没.图 11(d,i,n)分别给出了PP波的输入含噪合成地震记录,反演合成地震记录以及二者的差异剖面,图 11(e,j,o)为PS波地震记录.差异剖面整体为随机噪声,没有有效信息存在,这也说明了交替迭代非线性反演的准确性.
|
图 11 反演结果分析 (a)压缩系数对比度反演结果; (b)地震频带内压缩系数对比度反演结果; (c)压缩系数对比度波数谱; (d)反演输入叠前PP波道集; (e)反演输入叠前PS波道集; (f)剪切柔度对比度反演结果; (g)地震频带内剪切柔度对比度反演结果; (h)剪切柔度对比度波数谱; (i)反演预测叠前PP波道集; (j)反演预测叠前PS波道集; (k)密度对比度反演结果; (l)地震频带内密度对比度反演结果; (m)密度对比度波数谱; (n)叠前PP波道集残差; (o)叠前PS波道集残差.其中,红色曲线代表真实值,蓝色曲线表示反演结果. Fig. 11 Inversion result and analysis (a) Compressibility contrast inversion result; (b) Compressibility contrast inversion result in seismic frequency band; (c) Wavenumber spectrum of compressibility contrast; (d) Inversion input prestack PP-wave gather; (e) Inversion input prestack PS-wave gather; (f) Shear compliance contrast inversion result; (g) Shear compliance contrast inversion result in seismic frequency band; (h) Wavenumber spectrum of shear compliance contrast; (i) Inversion predicted prestack PS-wave gather; (j) Inversion predicted prestack PS-wave gather; (k) Density contrast inversion result; (l) Density contrast inversion result in seismic frequency band; (m) Wavenumber spectrum of density contrast; (n) PP-wave gather residual between inversion input and predicted gather; (o) PS-wave gather residual between inversion input and predicted gather. In which, red curves represent real value and blue curves represent inversion result. |
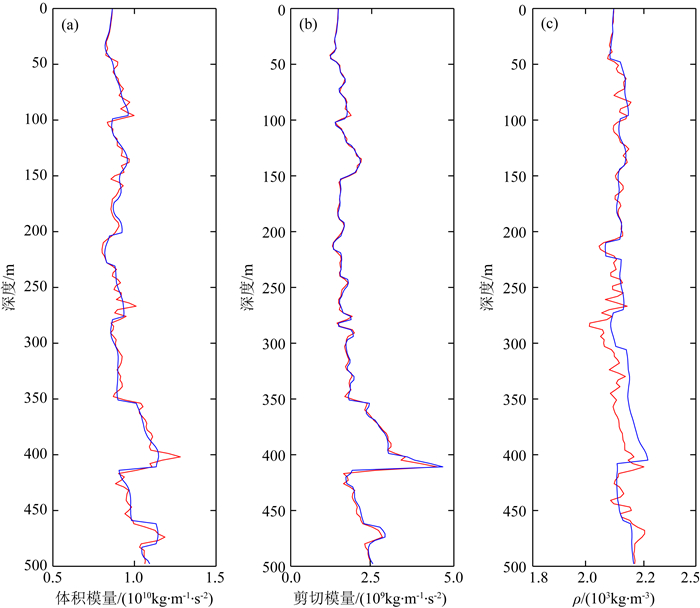
利用反演结果和背景场,计算出目前业界广泛采用的体积模量、剪切模量等流体识别因子,如图 12所示,从中可以看出,反演结果和真实值吻合度较高,尤其是对剪切模量.
|
图 12 体积模量(a)、剪切模量(b)及密度(c)三参数反演结果 (红色表示真实值,蓝色表示反演结果) Fig. 12 Inversion result of bulk modulus (a), shear modulus (b) and density (c) (Red curves represent real value and blue curves represent inversion result) |
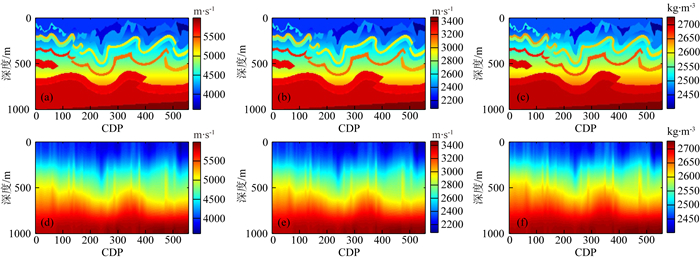
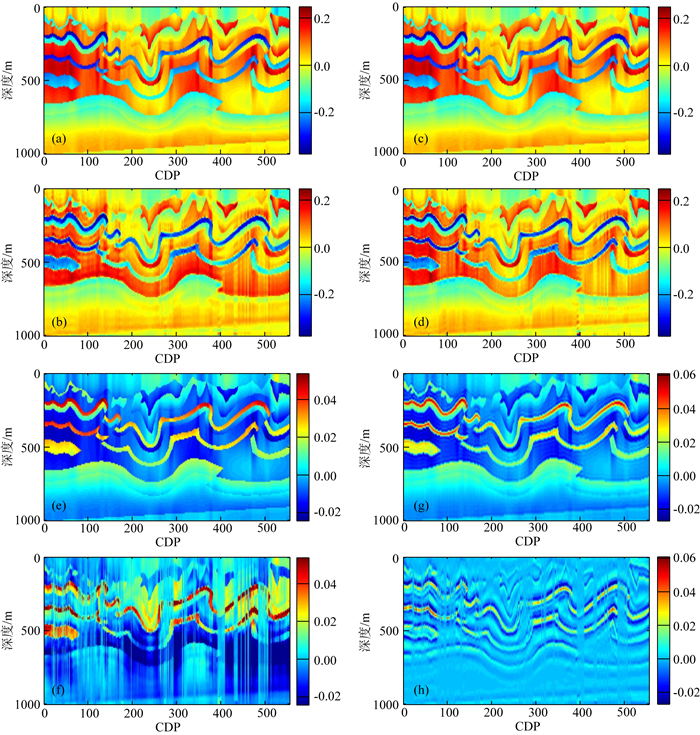
为了进一步说明文中所述交替迭代非线性反演方法的适应性,选定CSEG模型进行测试,该模型为典型的山前带模型,构造较为复杂,易于产生散射波、层间多次波等多种干扰波场,而交替迭代非线性反演方法考虑了全波场,因而更适合于该近地表模型的反演.图 13给出了CSEG模型介质弹性参数及其背景场,在背景场中,构造信息完全缺失.采用和上一节相同的参数和流程,最终得到对比度反演剖面如图 14所示,其中图 14(a,b)为真实压缩系数对比度和反演结果的对比,图 14(c,d)为真实剪切柔度对比度和反演结果的对比,从中可以看出,两个参数都以较高的分辨率得以反演.图 14(e,f)分别给出了密度对比度的真实值和反演结果,图 14(g,h)为对应的地震频带滤波结果,总的来说,密度对比度的反演结果存在一定的误差,且反演结果不稳定,二维剖面中的部分纵向道完全没有被反演出.
|
图 13 CSEG模型介质弹性参数及其背景 (a)纵波速度; (b)横波速度; (c)密度; (d)纵波速度背景; (e)横波速度背景; (f)密度背景. Fig. 13 The elastic parameters and backgrounds of CSEG model in which (a), (b) and (c) are true P-wave velocity, S-wave velocity and density, (d), (e) and (f) represent the backgrounds of P-wave velocity, S-wave velocity and density respectively |
|
图 14 真实和反演对比度剖面 (a)真实压缩系数对比度; (b)反演压缩系数对比度; (c)真实剪切柔度对比度; (d)反演剪切柔度对比度; (e)真实密度对比度; (f)反演密度对比度; (g)地震频带内真实密度对比度; (h)地震频带内反演密度对比度. Fig. 14 The true and inversion contrast profile (a), (c) and (e) are true contrast profile of compressibility, shear compliance and density, (b), (d) and (f) are inversion contrast profile of compressibility, shear compliance and density respectively, (g) and (h) show the density contrast profile in seismic frequency band |
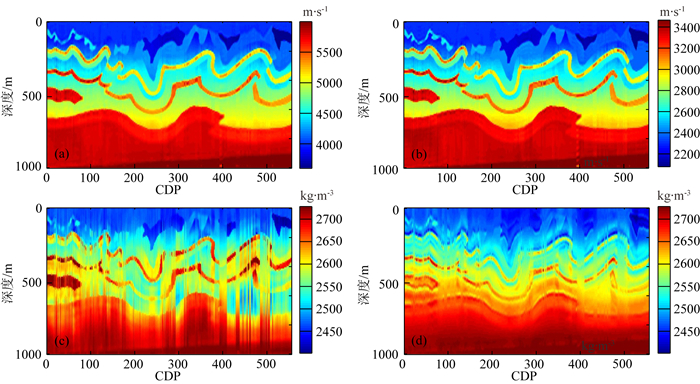
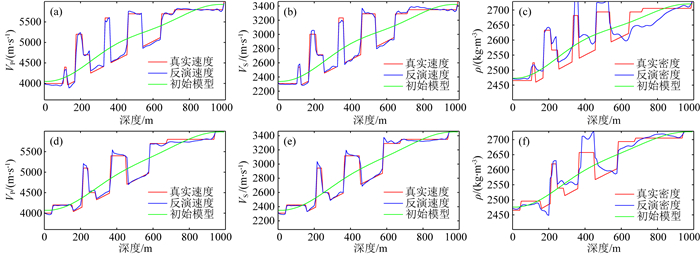
根据反演结果和背景场计算出叠前地震反演三参数:纵波速度、横波速度以及密度如图 15所示,抽取CMP50道和CMP350道如图 16所示,从中可以看出,纵波速度和横波速度都得到了较高精度的反演.
|
图 15 弹性参数反演结果 (a)纵波速度反演结果; (b)横波速度反演结果; (c)密度反演结果; (d)地震频带内密度反演结果. Fig. 15 The elastic parameters inversion results (a) P-wave velocity inversion result; (b) S-wave velocity inversion result; (c) Density inversion result; (d) Density inversion result in seismic frequency band. |
|
图 16 CSEG模型不同CMP位置介质弹性参数反演对比曲线 (a) CMP50纵波速度反演; (b) CMP50横波速度反演; (c) CMP50密度反演; (d) CMP350纵波速度反演; (e) CMP350横波速度反演; (f) CMP350密度反演,其中,红色曲线为真实数据,蓝色曲线为反演结果,绿色曲线为初始模型. Fig. 16 The elastic parameters inversion of CSEG model at different CMP location (a), (b) and (c) are P-wave velocity, S-wave velocity and density inversion of CMP 50, (d), (e) and (f) are P-wave velocity, S-wave velocity and density inversion of CMP 350, in which the red curves represent true model, blue curves represent inversion result, and green curves represent initial model. |
(1) 相比于传统的基于一次波场的AVO反演,基于全波场的地震反演方法考虑了透射损失、层间多次波、极化方式转换等因素的影响,能获得高分辨率的地下介质参数,更加适应当前精细地震勘探的需求.
(2) 定义散射积分方程的对比度弹性参数,对流体指示有更强的敏感性,因此基于散射积分方程的叠前反演能更好地服务于储层解释和流体预测.
(3) 反演流程从平滑的低频背景场出发,交替迭代求解数据方程和目标方程,在共轭梯度框架下采用乘性正则化方法求解对比度参数,采用优化的散射级数Neumann序列获得整体波场,不易陷入局部极值,能收敛到正确解.
(4) 基于散射积分方程的叠前地震反演获得的地下介质参数是处于深度域的,可以直接进行储层解释.
(5) 本文所述的反演流程考虑了地震数据和地下介质参数之间的强非线性关系,可进一步用于时移地震反演,并且可将面波数据考虑进来,用于近地表参数反演.
Abubakar A, Van den Berg P M, Habashy T M, et al. 2004. A multiplicative regularization approach for deblurring problems. IEEE Transactions on Image Processing, 13(11): 1524-1532. DOI:10.1109/TIP.2004.836172 |
Aki K, Richards P G. 1980. Quantitative Seismology:Theory and Methods. San Francisco:W. H. Freeman.
|
Beller M, Doulgeris P, Gisolf A, et al. 2015. Resolving carboniferous stacked channel sequences with a non-linear AVO technology.//77th Conference and Exhibition. EAGE.
|
Buland A, Landrø M, Andersen M, et al. 1996. AVO inversion of troll field data. Geophysics, 61(6): 1589-1602. DOI:10.1190/1.1444078 |
Cambois G. 2000. AVO inversion and elastic impedance.//2000 SEG Annual Meeting. Calgary, Alberta: SEG, 142-145.
|
Cao D P. 2015. The upscaling method of the well logging data based on Backus equivalence average method. Geophysical Prospecting for Petroleum (in Chinese), 54(1): 105-111. |
Chen H Z, Yin X Y, Zhang J Q, et al. 2014. Seismic inversion for fracture rock physics parameters using azimuthally anisotropic elastic impedance. Chinese J. Geophys (in Chinese), 57(10): 3431-3441. DOI:10.6038/cjg20141029 |
Chen J J, Yin X Y. 2007. Three-parameter AVO waveform inversion based on Bayesian theorem. Chinese J. Geophys (in Chinese), 50(4): 1251-1260. |
Connolly P. 1999. Elastic impedance. The Leading Edge, 18(4): 438-452. DOI:10.1190/1.1438307 |
De Hoop A T. 1995. Handbook of Radiation and Scattering of Waves. London: Academic Press.
|
Dingle R B. 1973. Asymptotic Expansions:Their Derivation and Interpretation. London: Academic Press.
|
Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion. Chinese J. Geophys (in Chinese), 56(10): 3445-3460. DOI:10.6038/cjg20131020 |
Fuchs K, Müller G. 1971. Computation of synthetic seismograms with the reflectivity method and comparison with observations. Geophysical Journal International, 23(4): 417-433. DOI:10.1111/j.1365-246X.1971.tb01834.x |
Gisolf D, Verschuur E. 2010. The Principles of Quantitative Acoustical Imaging. The Netherlands: EAGE Publications.
|
Gouveia W P, Scales J A. 1998. Bayesian seismic waveform inversion:Parameter estimation and uncertainty analysis. Journal of Geophysical Research, 103(B2): 2759-2779. DOI:10.1029/97JB02933 |
Haffinger P R, von Wussow P, Doulgeris P, et al. 2015. Reservoir delineation by applying a nonlinear AVO technique-A casestudy in the Nile Delta.//77th EAGE Conference and Exhibition. Spain: EAGE.
|
Haffinger P R, Jedari Eyvazi F, Steeghs T P H, et al. 2016. Quantitative prediction of injected CO2 at Sleipner using wave-equation based AVO.//78th Conference and Exhibition. Vienna, Austria: EAGE.
|
Kennett B L N. 1979. Theoretical reflection seismograms for elastic media. Geophysical Prospecting, 27(2): 301-321. DOI:10.1111/gpr.1979.27.issue-2 |
Kennett B L N, Kerry N J. 1979. Seismic waves in a stratified half space. Geophysical Journal International, 57(3): 557-583. DOI:10.1111/gji.1979.57.issue-3 |
Kennett B L N. 1983. Seismic Wave Propagation in Stratified Media. Cambridge: Cambridge University Press.
|
Kleinman R E, Van den Berg P M. 1991. Iterative methods for solving integral equations. Radio Science, 26(1): 175-181. DOI:10.1029/90RS00934 |
Li X, Aravkin A Y, van Leeuwen T, et al. 2012. Fast randomized full-waveform inversion with compressive sensing. Geophysics, 77(3): A13-A17. DOI:10.1190/geo2011-0410.1 |
Liu C, Pei S J, Guo Z Q, et al. 2017. The application of seismic amplitude inversion for the characterization of interbedded sand-shale reservoirs. Chinese J. Geophys (in Chinese), 60(5): 1893-1902. DOI:10.6038/cjg20170523 |
Liu H X, Li J Y, Chen X H, et al. 2016. Amplitude variation with offset inversion using the reflectivity method. Geophysics, 81(4): R185-R195. DOI:10.1190/geo2015-0332.1 |
Mallick S. 1999. Some practical aspects of prestack waveform inversion using a genetic algorithm:An example from the east Texas Woodbine gas sand. Geophysics, 64(2): 326-336. DOI:10.1190/1.1444538 |
Mallick S, Adhikari S. 2015. Amplitude-variation-with-offset and prestack-waveform inversion:A direct comparison using a real data example from the Rock Springs Uplift, Wyoming, USA. Geophysics, 80(2): B45-B59. DOI:10.1190/geo2014-0233.1 |
Mavko G, Mukerji T, Dvorkin J. 1998. The Rock Physics Handbook. Cambridge: Cambridge University Press.
|
Muller G. 1985. The reflectivity method:A tutorial. Journal of Geophysics, 58(3): 153-174. |
Padhi A, Mallick S, Fortin W, et al. 2015. 2-D ocean temperature and salinity images from pre-stack seismic waveform inversion methods:An example from the South China Sea. Geophysical Journal International, 202(2): 800-810. DOI:10.1093/gji/ggv188 |
Sen M K, Roy I G. 2003. Computation of differential seismograms and iteration adaptive regularization in prestack waveform inversion. Geophysics, 68(6): 2026-2039. DOI:10.1190/1.1635056 |
Shuey R T. 1985. A simplification of the Zoeppritz equations. Geophysics, 50(4): 609-614. DOI:10.1190/1.1441936 |
Tarantola A. 1984a. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
Tarantola A. 1984b. Linearized inversion of seismic reflection data. Geophysical Prospecting, 32(6): 998-1015. DOI:10.1111/gpr.1984.32.issue-6 |
Thomson W T. 1950. Transmission of elastic waves through a stratified solid medium. Journal of applied Physics, 21(2): 89-93. DOI:10.1063/1.1699629 |
Van den Berg P M, Aubakar A. 2001. Contrast source inversion method:State of art. Journal of Electromagnetic Waves and Applications, 15(11): 1503-1505. DOI:10.1163/156939301X00067 |
Van den Berg P M, Abubakar A, Fokkema J T. 2003. Multiplicative regularization for contrast profile inversion. Radio Science, 38(2): 8022. |
Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
Wang B L, Yin X Y, Zhang F C. 2005. Elastic impedance inversion and its application. Progress in Geophysics (in Chinese), 20(1): 89-92. |
Wang Y F. 2007. Computational Methods for Inverse Problems and Their Application (New Frontiers for Sciences) (in Chinese). Beijing: Higher Education Press.
|
Wang Y F, Stepanova I E, Titarink V N, et al. 2011. Inverse Problems in Geophysics and Solution Methods (Series in Global Change and Earth System Science) (in Chinese). Beijing: Higher Education Press.
|
Wang Y F, Yang C C, Yagola A G. 2011. Optimization and Regularization for Computational Inverse Problems and Applications. Berlin Heidelberg: Springer.
|
Yang J Q, Abubakar A, Van den Berg P M, et al. 2008. A CG-FFT approach to the solution of a stress-velocity formulation of three-dimensional elastic scattering problems. Journal of Computational Physics, 227(24): 10018-10039. DOI:10.1016/j.jcp.2008.07.027 |
Yang P J, Mu X, Yin X Y. 2009. Prestack three-term simultaneous inversion method and its application. Acta Petrolei Sinica (in Chinese), 30(2): 232-236. |
Yao Z A, Sun C Y. 2017. AVA/AVF characteristic analysis of fluid-containing thin-bed in time-lapse seismic. Journal of Jilin University (Earth Science Edition) (in Chinese), 47(3): 884-898. |
Yin X Y, Cao D P, Wang B L, et al. 2014. Research progress of fluid discrimination with pre-stack seismic inversion. Oil Geophysical Prospecting (in Chinese), 49(1): 22-34, 46. |
Zhao H S, Ursin B, Amundsen L. 1994. Frequency-wavenumber elastic inversion of marine seismic data. Geophysics, 59(12): 1868-1881. DOI:10.1190/1.1443574 |
Zong Z Y, Yin X Y, Wu G C. 2012. Fluid identification method based on compressional and shear modulus direct inversion. Chinese J. Geophys (in Chinese), 55(1): 284-292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
曹丹平. 2015. 基于Backus等效平均的测井资料尺度粗化方法研究. 石油物探, 54(1): 105-111. DOI:10.3969/j.issn.1000-1441.2015.01.015 |
陈怀震, 印兴耀, 张金强, 等. 2014. 基于方位各向异性弹性阻抗的裂缝岩石物理参数反演方法研究. 地球物理学报, 57(10): 3431-3441. DOI:10.6038/cjg20141029 |
陈建江, 印兴耀. 2007. 基于贝叶斯理论的AVO三参数波形反演. 地球物理学报, 50(4): 1251-1260. DOI:10.3321/j.issn:0001-5733.2007.04.035 |
董良国, 迟本鑫, 陶纪霞, 等. 2013. 声波全波形反演目标函数性态. 地球物理学报, 56(10): 3445-3460. DOI:10.6038/cjg20131020 |
刘财, 裴思嘉, 郭智奇, 等. 2017. 地震波形反演技术在砂泥岩薄互层结构表征中的应用. 地球物理学报, 60(5): 1893-1902. DOI:10.6038/cjg20170523 |
王保丽, 印兴耀, 张繁昌. 2005. 弹性阻抗反演及应用研究. 地球物理学进展, 20(1): 89-92. DOI:10.3969/j.issn.1004-2903.2005.01.017 |
王彦飞. 2007. 反演问题的计算方法及其应用[当代科学前沿论丛]. 北京: 高等教育出版社.
|
王彦飞, 斯捷潘诺娃 I E, 提塔连科 V N, 等. 2011. 地球物理数值反演问题. 北京: 高等教育出版社.
|
杨培杰, 穆星, 印兴耀. 2009. 叠前三参数同步反演方法及其应用. 石油学报, 30(2): 232-236. DOI:10.3321/j.issn:0253-2697.2009.02.012 |
姚振岸, 孙成禹. 2017. 含流体薄层时移地震AVA/AVF特征分析. 吉林大学学报(地球科学版), 47(3): 884-898. |
印兴耀, 曹丹平, 王保丽, 等. 2014. 基于叠前地震反演的流体识别方法研究进展. 石油地球物理勘探, 49(1): 22-34, 46. |
宗兆云, 印兴耀, 吴国忱. 2012. 基于叠前地震纵横波模量直接反演的流体检测方法. 地球物理学报, 55(1): 284-292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
 2019, Vol. 62
2019, Vol. 62

