2. 广西交通设计集团有限公司, 南宁 530029;
3. 山东大学 地球电磁探测研究所, 济南 250061
2. Guangxi Communications Design Group Co., Ltd., Nanning 530029, China;
3. Laboratory of Earth Electromagnetic Exploration, Shandong University, Jinan 250061, China
瞬变电磁法(TEM)以地下目标的导电性差异为物性基础,通过接地或不接地回线发射一次脉冲磁场,通过观测关断电流产生的二次场分析地下介质的导电情况.该方法具有观测纯二次场、适应性强、灵敏度和分辨率高等优点,已在工程勘察、海水入侵调查、金属矿和地下水勘探、地质调查等领域得到了广泛应用(薛国强等, 2008;朴化荣, 1990; Zhdanov, 2010).
在瞬变电磁数据处理方面,常用的方法有视电阻率成像(殷长春和朴化荣, 1991)、一维或2.5维反演(Wilson et al., 2006)、拟地震偏移成像(王家映等, 1985)等.为了获得真实的地电分布,人们常用地球物理反演的方法来处理瞬变电磁数据,目前常用的反演方法主要分为线性和非线性方法.其中,常用的最小二乘法等线性反演方法通常假定目标函数只存在一个极值,且不能很好的描述高度非线性的地球物理反演问题.Weidelt(1994)和Parker(1995)研究了基于最平缓模型的Occam反演,冯思臣等(2004)将马奎特法应用于大地电磁测深中,黄皓平和王维中(1990)使用广义逆矩阵理论和阻尼最小二乘法对时间域航空电磁数据进行了两层模型反演.这类方法虽然计算速度快,但反演结果高度依赖初始模型、易陷入局部最小(薛国强等, 2008;王家映, 2002).当给定的初始模型不合理时也可获得反演结果,并且观测数据与模拟数据的拟合差也足够小,但这些反演模型往往是不可靠的.事实上,地球物理反演问题是高度非线性的,人们很难获得接近真实地层的初始模型.为解决非线性地球物理反演难题,许多学者将完全非线性算法引入地球物理反演:Yin等(2007)研究了用于航空电磁数据反演的模拟退火方法,王若等(2011)开发了用于CSAMT反演的模拟退火算法,万玲等(2013)研究了自适应遗传算法用于MRS-TEM联合反演,程久龙等(2014)将粒子群优化算法用于矿井瞬变电磁反演.本文采用模拟退火方法开展瞬变电磁一维非线性反演.
模拟退火本质上是一种启发式的非线性反演方法,该方法使用完全随机的初始模型,在全空间范围内进行搜索,可有效避免线性反演易陷入局部最小的问题,并且最终可以获得较好的全局最优解(Kirkpatrick et al., 1983;王家映, 2002).
模拟退火最早源于统计热物理学的研究.在模拟固体物质熔融-冷却-结晶的过程中,升温导致分子运动剧烈,系统熵增大;缓慢降温,分子逐渐丧失流动性,系统熵减小;最终在常温时达到“晶体”基态,此时内能最小.后来数学家根据这一过程,建立了模拟退火算法(Kirkpatrick et al., 1983),用于解决非线性最优化问题.之后Kirkpatrick等(1983)成功将其应用于组合优化问题.模拟退火算法无需计算雅克比矩阵,在随机扰动过程中极易跳出局部最小值,已作为一种全局最优化算法在地球物理学中有着较为广泛的应用.例如:模拟退火方法在地球物理中用来解决地震资料处理的剩余静校正问题(Rothman, 1985, 1986)、一维电测深反演(Send et al., 1993)、大地电磁测深反演(师学明和王家映,1998)以及重磁资料处理(于鹏等, 2007;陈华根等, 2012)等问题.然而,模拟退火方法反演地面瞬变电磁实测数据尚未进行深入研究.
通过分析L1、L2范数的优缺点,综合考虑层状模型电阻率的突变性和非线性反演的时间成本,本文基于观测数据与模拟数据的L1范数建立目标函数,建立了随机模型更新方法,通过建立的概率评价与接收函数来确定是否接收随机产生的新模型,以确保系统优化是按照熵减小的方向发展.
1 模拟退火反演地球物理反演过程是在给定的模型空间中以某种方法不断地搜索模型参数、更新模型,最终使目标函数达到全局最小的过程(王家映, 2002).基于此过程,应用模拟退火解决回线源TEM非线性反演(李建慧等, 2011;张志厚, 2007)需要解决3个关键难题:①如何数学化表达系统状态,即构建目标函数;②如何建立合理的退温机制;③如何优化抽样方法,使系统状态随机改变.
1.1 目标函数一般情况下,地球物理反演问题的目标函数均基于观测数据与模拟数据构建目标函数.理论上,在数据拟合项中使用L1、L2范数均可,但两者各有优劣(蒋尔雄等, 2008).从概率统计来看,L1正则先验分布是Laplace分布,L2正则先验分布是Gaussian分布(费业泰, 1995).L1范数对极端值(或突变)具有更好的“容忍力”,而L2范数则具有光滑和连续的特点.当目标函数中个别数据存在较大且反常的拟合误差时,L1范数受该部分数据的影响敏感度较低,不会对目标函数值产生较大影响(Bartels and Conn, 1982).对于一维层状大地模型,不同层之间电阻率是不连续的,属于突变模型.因而在反演时使用L1范数能更有效地刻画层状边界.本文研究的模拟退火算法,一般都需要进行大量的模型计算.L2范数相对L1范数增加了平方、开方等运算,需要花费更多的计算时间,综合考虑算法的时效性和准确性,本文利用观测数据与模拟数据的L1范数最小建立目标函数,既可满足计算精度要求,也可节省计算时间.我们将模型参数的扰动等价为分子的热运动过程,将迭代过程中的步长变化等价为温度的变化.首先根据需要拟合的地层厚度和电阻率信息随机产生初始模型,然后按照给定的优化设计参数缓慢变化步长,同时模型参数以给定概率随机扰动,不断进行“模型更新→计算目标函数→接受/舍弃模型”的迭代过程.当目标函数达到阈值并不再随着迭代而降低时,即找到了反演问题的全局最优解(Kirkpatrick et al., 1983).
在回线源TEM一维模拟退火反演中,通过求解观测数据与模拟数据视电阻率的L1范数最小建立目标函数如下:
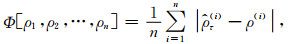
|
(1) |
式中,ρ1,ρ2, …, ρn均为观测数据n个时间道的视电阻率值,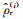
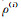
退温机制用于产生控制算法进程的迭代参数和逼近模拟退火算法的渐近收敛性,从而使算法在有限迭代次数后返回一个近似最优解.合理的退温机制可加速模型的迭代更新效率,保证算法的准确性和效率(康立山, 1994).常用退温函数有指数退温法(Vecchi & Kirkpatriek, 1983)、统计退温法(Aarts et al., 1985)、冷却时间表法(Huang et al., 1987)等.指数退温法函数形式简单,退温速度快,因此本文选用指数函数退温机制,公式如下:
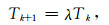
|
(2) |
其中,λ是用来控制降温速率的经验系数,一般λ取值在0.5~0.99之间,本文后续所有的计算均取λ=0.8.
1.3 抽样方法模拟退火法的初始状态、下一状态均具有随机性,因而需要通过合理的判断准则来确定是否接受新的状态(Metropolis et al., 1953).设状态空间最大值为ρmax,每个状态分量可根据如下公式确定:
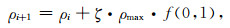
|
(3) |
其中,ρi表示第i次迭代的状态空间,ζ表示步进系数,本文取0.1,f(0, 1)表示在0~1之间产生任意随机数.
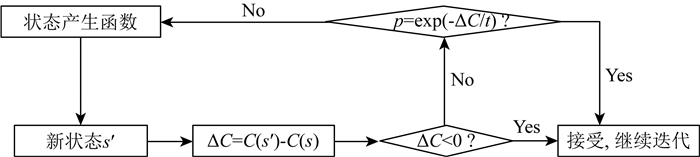
具体的抽样过程如图 1所示.即:首先,通过(3)式进行模型参数扰动并按照下式计算新旧模型的系统能量差:
|
图 1 抽样过程 Fig. 1 Sampling process |
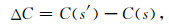
|
(4) |
其中,ΔC表示系统能量之差,C(·)表示系统能量函数,s′和s分布表示新旧两组模型.
其次,引入如下的状态接受概率函数评价新模型是否接受:
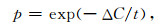
|
(5) |
其中,t为控制参数(接受温度).
最后,对于满足状态接受概率的样本继续迭代,不满足则重复该抽样步骤.
而系统的初始温度也基于公式(5)确定,即为:随机产生一定数量的1组模型,确定任意两两模型间的目标函数之差的最大绝对值|Δmax|,利用下式计算系统初温:
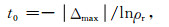
|
(6) |
其中,t0为系统初始温度,pr为初始接受概率.
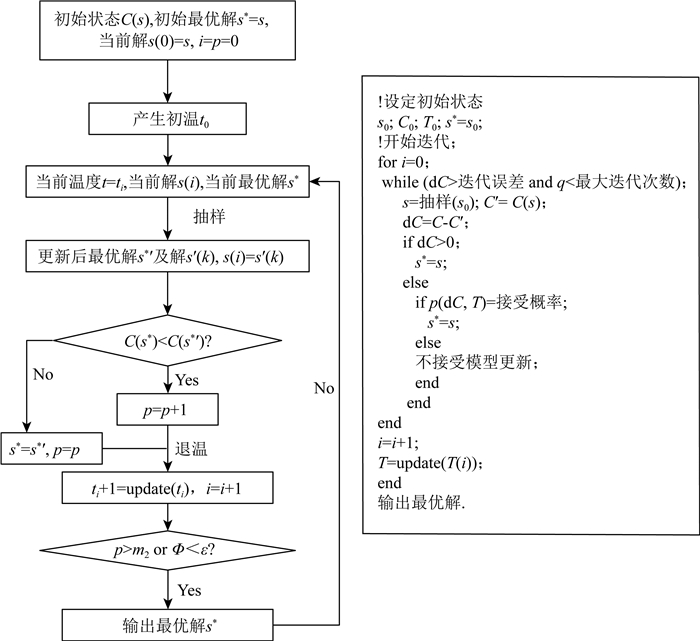
1.4 算法流程对于各向同性水平层状大地,中心回线装置瞬变电磁正演响应可通过线性数字滤波算法求解(王华军和罗延钟,2003;吴琼,2012).根据上述方法建立目标函数,并通过设计的退温机制、接收概率等实现瞬变电磁L1范数模拟退火反演的流程及伪代码如图 2所示.
|
图 2 模拟退火算法流程图及伪代码 Fig. 2 Simulated annealing algorithm flow chart and the pseudo code |
为了验证本文开发的模拟退火法算法的有效性,建立了多种层状模型进行测试.首先利用已知合成模型层数进行反演,考察单一电阻率参数下的反演优化情况,并通过对单一合成模型进行多次反演的方法考察算法的稳定性和搜索全局最优解的能力;然后,采用多层模型进行反演,其中对二层真实模型在反演初始模型中设置了5层进行对比,对三层和五层模型均设置了20层的初始模型,同时对模型的层厚和电阻率进行反演.此外,考虑了噪声对模拟退火反演的影响,测试含噪声数据反演的稳定性和准确性.本文后续合成模型的所有反演算例均在一台CPU主频为2.50 GHz的Thinkpad X1笔记本电脑上完成,为对比反演时间,所有反演计算均采用单线程模式.合成模型的所有装置参数均采用100 m×100 m方形回线,发射电流为1 A,中心点接收.
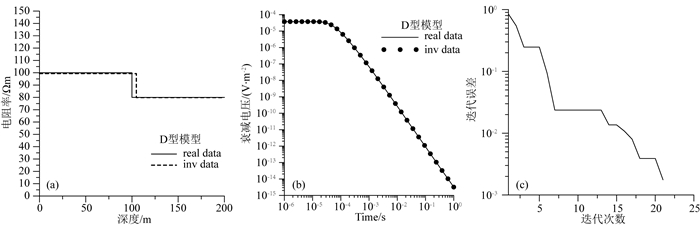
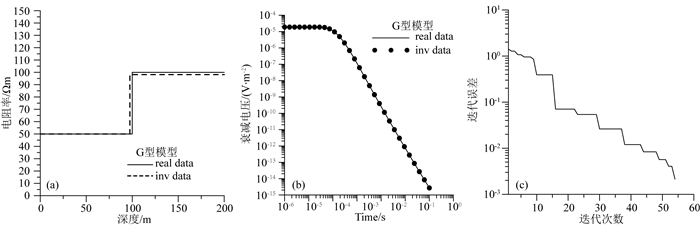
2.1 二层模型图 3和图 4分别给出了D型模型剖分为2层和5层初始模型的反演测试结果,图 5和图 6分别给出了G型模型剖分为2层和5层初始模型的反演测试结果.图 3—6中左侧为真实模型与反演模型的曲线对比,中间为正演数据与反演数据的拟合情况对比,右侧为反演的迭代误差曲线.从图中可以看出,反演模型衰减电压曲线与正演衰减电压曲线拟合效果很好.图 3和图 5所示,使用5层模型进行反演,约束反演层高在50 m以内(下同).在多次迭代过程中,最初存在极大极小值跳跃,随着迭代误差逐渐减小,迭代结果逐渐收敛于真实模型参数,且能明显看出在深度100 m左右时,上下两层的电阻率有明显差异,符合真实模型设置的情况.
|
图 3 D型模型使用2层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 3 2-layer inversion results of D-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors.(a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
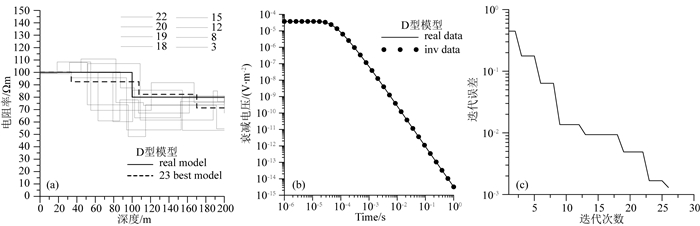
图 4 D型模型使用5层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 4 5-layer inversion results of D-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 5 G型模型使用2层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 5 2-layer inversion results of G-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
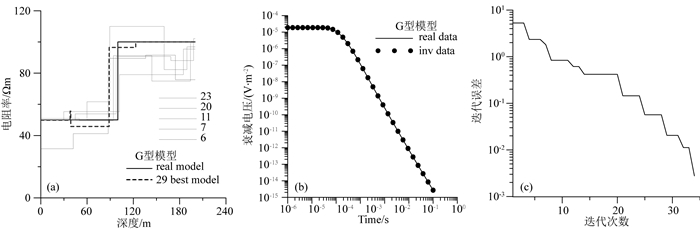
图 6 G型模型使用5层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 6 5-layer inversion results of G-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
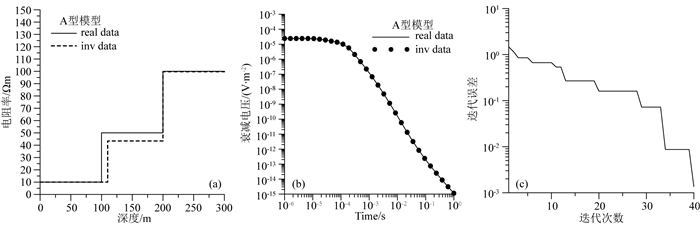
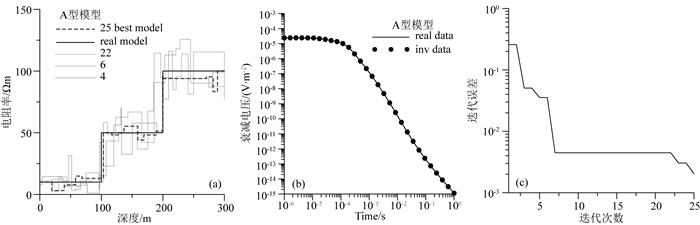
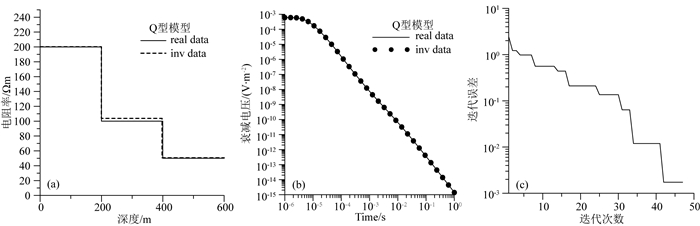
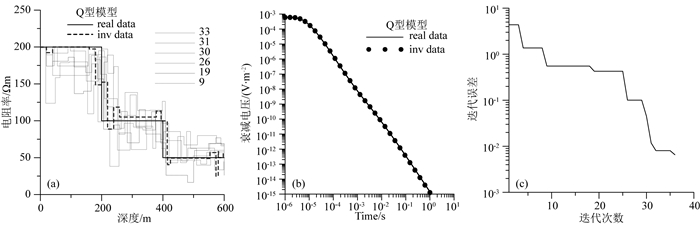
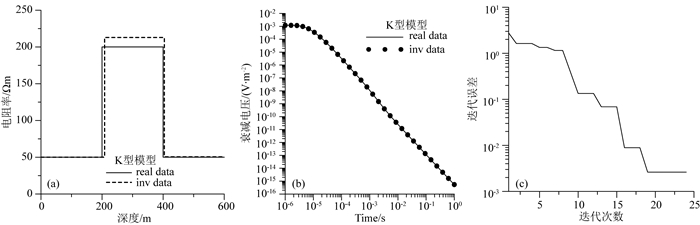
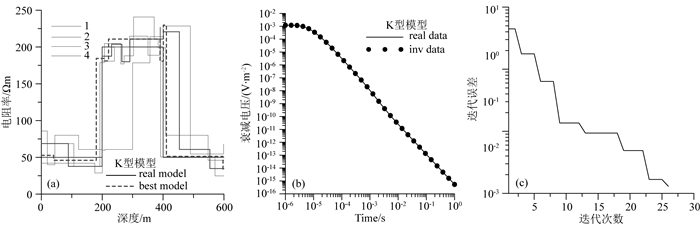
图 7—14分别给出了对A型、Q型、H型、K型模型剖分为3层和20层网格进行反演的结果对比.在图 7、图 9、图 11和图 13所示,使用3层初始模型进行反演,模型参数曲线和衰减电压曲线拟合效果良好,反演模型几乎与真实模型重合.由于实际情况往往层数未知,在图 8、图 10、图 12和图 14中,使用20层初始模型进行反演,随着计算迭代次数增加,迭代误差逐渐减小,反演结果逐渐逼近真实模型参数,最终给出的全局最优解模型基本符合真实模型的地电参数变化规律,在真实模型界面突变的位置,反演结果上下两部分地层的电阻率存在明显差异,符合真实模型设置的情况.
|
图 7 A型模型使用3层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 7 3-layer inversion results of A-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 8 A型模型使用20层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 8 20-layer inversion results of A-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 9 Q型模型使用3层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 9 3-layer inversion results of Q-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 10 Q型模型使用20层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 10 20-layer inversion results of Q-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 11 K型模型使用3层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 11 3-layer inversion results of K-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 12 K型模型使用20层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 12 20-layer inversion results of K-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
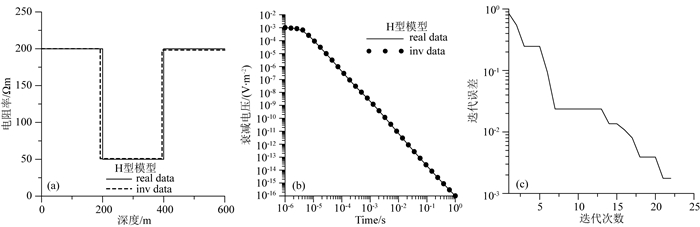
图 13 H型模型使用3层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 13 3-layer inversion results of H-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
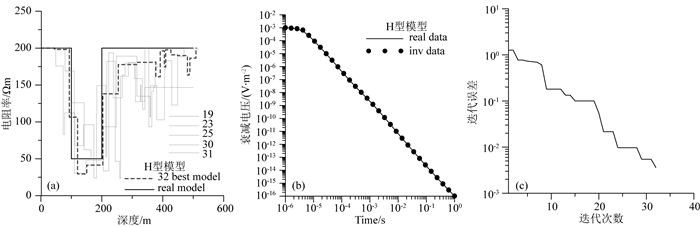
图 14 H型模型使用20层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 14 20-layer inversion results of H-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
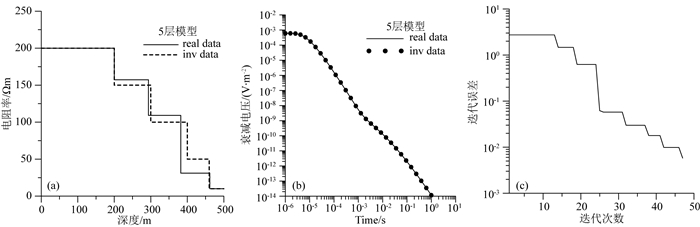
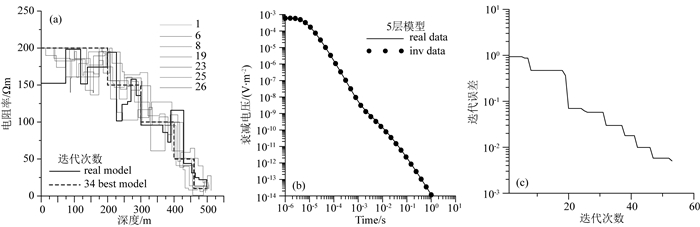
图 15和图 16给出了一组电阻率逐渐降低的5层模型使用5层和20层初始模型的反演结果对比图.如图 15所示,在模型参数反演拟合效果上,模型曲线拟合效果略差于二层、三层模型的反演结果,衰减电压曲线拟合效果较好;如图 16所示,在层数未知的情况下,使用20层模型进行反演,迭代早期,存在反演结果极大极小值跳跃的情况,随着迭代次数增加,迭代误差逐渐减小,最终反演结果收敛于实际模型参数,且能明显看出在深度200、300、400、450 m左右时,对应深度上下两部分地层的电阻率有明显差异,符合实际5层模型电阻率分布情况,衰减电压曲线拟合效果很好.
|
图 15 5层模型使用5层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 15 5-layer inversion results of five-layer-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 16 5层模型使用20层初始模型反演结果 (a)模型拟合曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 16 20-layer inversion results of five-layer-model (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
上述所有合成模型的反演迭代过程数据如表 1所示.综合上述地电模型反演结果可以看出,总体反演效果良好,反演结果能较清晰地反映设计模型的地电分布情况.由于使用多层模型反演时均采用单线程计算进行对比,可以看出,随着模型复杂程度的增加,反演时间逐渐增大,使用前述的单线程配置,反演5层模型时需要超过80 h.即使在反演时降低反演精度,计算速度也没有明显的改善,说明该方法需要进行大量的抽样才能够获得全局最优解.针对计算效率过低的问题,我们已经通过并行化和自适应正则化两种方法优化了算法效率,将另文发表.
|
|
表 1 各类模型反演时间与迭代过程数据对比 Table 1 Inversion time and iterative process of all models |
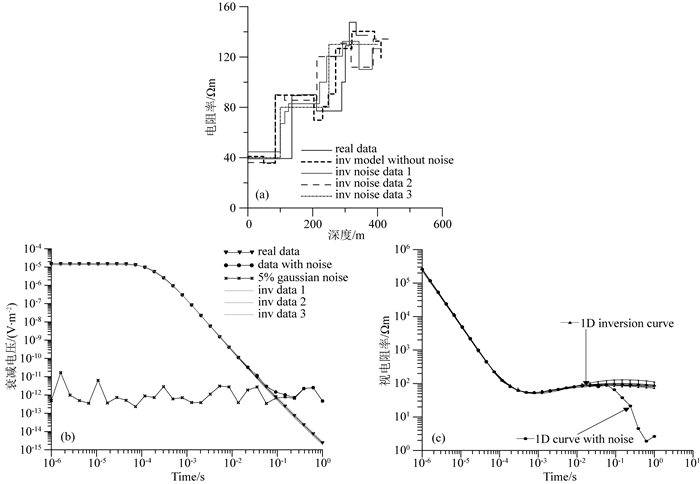
瞬变电磁野外数据观测往往伴随着或多或少的干扰,采集的数据一般都带有不同程度的噪声,为了测试本方法在反演含噪声数据时的稳定性和抗噪能力,采用Munkholm和Auken(1996)提出的瞬变电磁噪声模型,在一个A型层状模型衰减曲线上加入5%的高斯噪声,并对带噪声的数据进行反演.图 17a给出了无噪声数据以及3个不同噪声数据的反演结果,可以看出含噪声数据的反演结果与实际模型形态类似,差异不大.重复反演3次并对3次的结果进行正演计算,分别对比其衰减曲线(图 17b)和视电阻率曲线(图 17c),可以看出本方法具有较好的抗噪能力,在采集数据包含5%噪声的情况下,仍然能够获得很好的反演效果.
|
图 17 A型模型含5%高斯噪声反演结果 (a)模型拟合曲线; (b)衰减电压拟合曲线; (c)视电阻率拟合曲线. Fig. 17 A model with 5% Gaussian noise inversion results (Gray curves are noise inversion results) (a) Model fitting curves; (b) Data fitting curves; (c) Apparent resistivity fitting curves. |
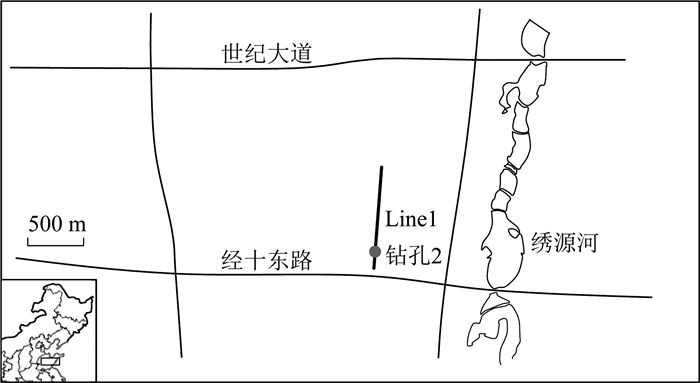
为进一步验证本方法的有效性和工程应用价值,对野外实测数据进行反演.实测数据位于山东省济南市章丘区绣源河西侧,南靠经十东路,北靠世纪大道,是拟建山东大学龙山校区的校址区(如图 18所示).该区域处在原埠村煤矿采矿范围之内,探测目的是为了探查区域内的煤田采空区.
|
图 18 工区位置图 Fig. 18 Work location |
图 18所示的瞬变电磁测线命名为Line 1,长度700 m.数据采集使用25 Hz的发射基频,发射电流等详细参数列于表 2.每点采集40道数据,每道数据对应的采集中心时间列于表 3,共25个测点,采用100 m×100 m的发射线框和3400 m2的接收线框,数据记录采用MSD-1瞬变电磁仪.在图 18中六角星的位置存在一处钻孔,相关编录信息可以为后续反演结果对比提供参考和依据.
|
|
表 2 Line 1测线的发射和接收参数表 Table 2 Transmission and reception parameters of Line 1 |
|
|
表 3 25 Hz对应的采集道数和中心时间 Table 3 25 Hz corresponding acquisition channels and center time |
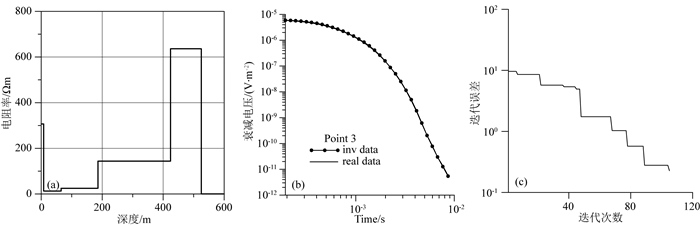
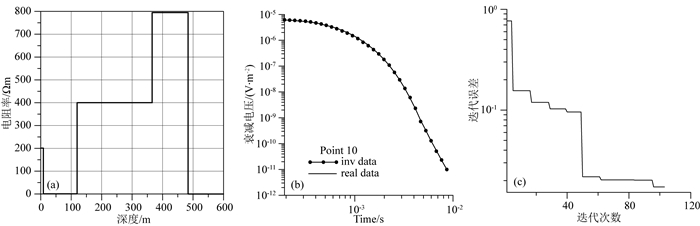
采用本文方法对测线Line 1上的所有数据进行反演,并绘成最终的反演地电断面图,判断相应地下的地质构造情况.其中,选取了第3、10、12个采样点上的反演模型、衰减电压拟合曲线、迭代误差曲线图如图 19、图 20、图 21所示.
|
图 19 点3反演结果图 (a)模型曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 19 Point 3 inversion results (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
图 20 点10反演结果图 (a)模型曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 20 Point 10 inversion results (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
|
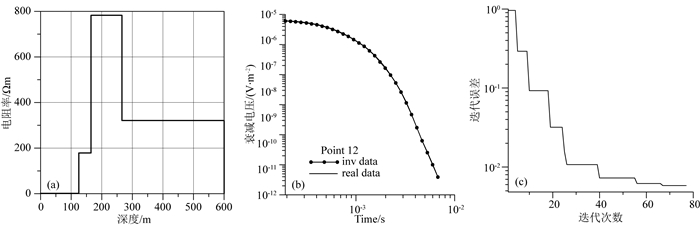
图 21 点12反演结果图 (a)模型曲线;(b)衰减电压拟合曲线;(c)迭代误差曲线. Fig. 21 Point 12 inversion results (a) Model fitting curves; (b) Data fitting curves; (c) The iteration errors. |
从反演结果可以看出,衰减电压曲线拟合效果较好,根据反演模型可初步推断在地下20~150 m左右深度存在低阻异常,在地下200~400 m左右深度存在高阻异常.
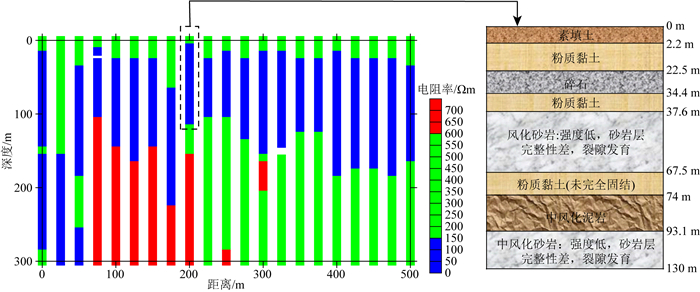
图 22为反演剖面与已知钻孔编录结果对比图.对比分析可知,由于上附地表为第四系沉积地层,含水率较低,因此0~20 m左右的地层电阻率稍高;由于22.5~130 m存在大量的裂隙发育、强度低、完整性差的风化砂岩,以及未完全固结的粉质粘土和风化泥岩,且含水率高,导致图 22中黑色虚线所夹区域呈现出明显的低阻异常;推断200~300 m左右深度为结构完整的岩矿石,根据22.5~130 m地层含水率高的判断,此处也应存在地下水,但由于此处岩层完整且密实,因此出现高阻异常.由于已知钻孔的深度为130 m,因而只对比了该深度范围的结果,更深的结果为推断,可以看出,钻探揭露的破碎、完整性差、裂隙发育的砂土层和粘土层区域基本与反演低阻区域对应.
|
图 22 反演结果(左)与钻孔结果(右)对比图 Fig. 22 Comparison of inversion results (left) and drilling results (right) |
基于L1范数建立的目标函数能有效刻画一维地电模型边界,也满足非线性反演对时效性和准确性的要求.利用单线程计算方式进行反演,随着模型层数增加,计算时间呈指数增加,而非线性递增,且该算法反演速度慢.分析造成此问题的原因如下:模拟退火法为非线性反演方法,模型更新具有随机性,需进行大量的正演模拟和反演计算,因此,计算速度较慢.但通过合成模型与实测数据反演证明了本文的模拟退火算法是一种有效的瞬变电磁非线性反演方法,可用于反演瞬变电磁模拟和实测数据.
为解决反演效率问题,可考虑在计算技术、退火机制、抽样方法、正则化因子等方面优化算法.在计算技术上,可采用CPU和GPU异构并行处理技术进行算法优化,采用GPU进行计算密集的循环计算,采用CPU进行整体程序的逻辑控制和结果输出,提升整体计算速度.在退火机制和抽样方法上,可考虑模型扰动方式与退温速率联合优化.模型扰动采用快速模拟退火(MVFSA):前期进行全局扰动,找到解的最优区间;后期进行局部扰动,找到全局最优解.既可减少退温时间的浪费,也可跳出局部最小实现全局最优,从而提升计算速度和准确性.在目标函数和正则化因子上,可在现有目标函数上构建一个正则化项,从而使模型空间合理且迅速的缩小简化并最终获得最优解.相较于L2范数正则化,L1范数在正则化过程中下降速度快,且可使权值稀疏,起到特征选择的作用.因此可采用L1范数正则化优化目标函数,实现更加精确、迅速的反演.在反演方法上,可将模拟退火法与线性方法联合实现反演.例如,反演前期通过非线性方法将模型搜索空间缩小至合理范围,后期使用阻尼最小二乘等线性方法进行梯度下降,最终快速收敛找到全局最优解,实现联合优化反演,从而达到既能搜寻全局最优又可快速收敛的目的.
说明 本文所有代码向学术研究开放,研究者可以在遵循协议的情况下从作者的git仓库下载本文所有代码和合成算例数据,请访问http://sunhuaifeng.com/code 获取代码仓库地址和下载说明.
致谢 作者感谢两位匿名审稿专家对本文提出的宝贵意见.作者感谢山东大学地球电磁探测研究所(Laboratory of Earth Electromagnetic Exploration,LEEE)团队成员在文章准备过程中提供的帮助.作者感谢山东大学数学与系统科学学院高夫征副教授在L1和L2范数分析方面给出的专业建议.
Aarts E H L, VanLaarhoken P J M. 1985. Statistica-cooling:a general approach to combinatorial optimization problems. Philips J. Res., 40(4): 193-226. |
Bartels R H, Conn A R. 1982. An approach to nonlinear l1 data fitting.//Hennart J P ed. Numerical Analysis. Berlin, Heidelberg: Springer, 48-58. doi: 10.1007/bfb0092959.
|
Chen H G, Li J X, Wu J S, et al. 2012. Study on simulated-annealing MT-gravity joint inversion. Chinese Journal of Geophysics (in Chinese), 55(2): 663-670. DOI:10.6038/j.issn.0001-5733.2012.02.030 |
Cheng J L, Li M X, Xiao Y L, et al. 2014. Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space. Chinese Journal of Geophysics (in Chinese), 57(10): 3478-3484. DOI:10.6038/cjg20141033 |
Fei Y T. 1995. Error Theory and Data Processing (in Chinese). 3rd edition. Beijing: Mechanical Industry Press.
|
Feng S C, Wang X B, Ruan S. 2004. Comparison among several inversion algorithms of 1D MT. Oil Geophysical Prospecting (in Chinese), 39(5): 594-599. DOI:10.3321/j.issn:1000-7210.2004.05.019 |
Huang M D, Romeo F, Sangiovanni-Vincentelli A. 1987. An efficient general cooling schedule for simulated annealing.//Proceedings of IEEE International Conference on Computer-Aided Design. Santa Clara: IEEE, 381-384.
|
Huang Y P, Wang W Z. 1990. Inversion of time domain aeromagnetic data. Acta Geophysica Sinica, 33(1): 87-97. |
Jiang E X, Zhao F G, Su Y F. 2008. Numerical Approximation (in Chinese). 2nd ed. Shanghai: Fudan University Press.
|
Kang L S. 1994. Non-Numerical Parallel Algorithm First Volume:Simulated Annealing Algorithm (in Chinese). Beijing: Science Press.
|
Kirkpatrick S, Gelatt C D Jr, Vecchi M P. 1983. Optimization by simulated annealing. Science, 220(4598): 671-680. DOI:10.1126/science.220.4598.671 |
Li J H, Zhu Z Q, Liu S C, et al. 2011. Calculation of apparent resistivity in large fixed loop TEM by simulated annealing algorithm. Oil Geophysical Prospecting (in Chinese), 46(1): 138-142. DOI:10.13810/j.cnki.issn.1000-7210.2011.01.029 |
Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. 1953. Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6): 1087-1092. DOI:10.1063/1.1699114 |
Munkholm M S, Auken E. 1996. Electromagnetic noise contamination on transient electromagnetic soundings in culturally disturbed environments. Journal of Environmental and Engineering Geophysics, 1(2): 119-127. DOI:10.4133/JEEG1.2.119 |
Piao H R. 1990. Principle of Electromagnetic Sounding (in Chinese). Beijing: Geological Press.
|
16.Weidelt, P. Kaikkonen. 1994. Local 1-D interpretation of magnetotelluric B-porlarization impedances. Geophys. J.Int, 117:733-748.
|
Rothman D H. 1985. Nonlinear inversion, statistical mechanics, and residual statics estimation. Geophysics, 50(12): 2784-2796. DOI:10.1190/1.1441899 |
Rothman D H. 1986. Automatic estimation of large residual statics correction. Geophysics, 51(2): 337-346. |
Sen M K, Bhattacharya B B, Stoffa P L. 1993. Nonlinear inversion of resistivity sounding data. Geophysics, 58(4): 496-507. DOI:10.1190/1.1443432 |
Shi X M, Wang J Y. 1998. One dimensional magnetotelluric sounding inversion using simulated annealing. Earth Science-Journal of China University of Geosciences (in Chinese), 23(5): 542-546. |
Stark P.B., Parker R.L. 1995. Bounded-variable least-squares:an algorithm and applications. Computational Statistics, 10: 129-41. |
Steven C. Constable, Robert L. Parker, et al. 1987. Occam's inversion; a practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics, 52 (3): 289-300. https://www.researchgate.net/publication/228077488_Occam's_inversion_A_practical_algorithm_for_generating_smooth_models_from_electromagnetic_sounding_data
|
Vecchi M P, Kirkpatriek S. 1983. Global wiring by simulated annealing. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2(4): 215-222. DOI:10.1109/TCAD.1983.1270039 |
Wan L, Lin T T, Lin J, et al. 2013. Joint inversion of MRS and TEM data based on adaptive genetic algorithm. Chinese Journal of Geophysics (in Chinese), 56(11): 3728-3740. DOI:10.6038/cjg20131114 |
Wang H J, Luo Y Z. 2003. Algorithm of a 2.5 dimensional finite element method for transient electromagnetic with a central loop. Chinese Journal of Geophysics (in Chinese), 46(6): 855-862. |
Wang J Y, Oldenburg D, Levy S. 1985. The magnetotelluric interpretation simuIating seismic method. Oil Geophysical Prospecting (in Chinese), 20(1): 66-79. DOI:10.13810/j.cnki.issn.1000-7210.1985.01.008 |
Wang J Y. 2002. Inverse Theory in Geophysics (in Chinese). 2nd ed. Beijing: Higher Education Press.
|
Wang R, Yin C C, Wang M Y, et al. 2011. Simulated annealing for controlled-source audio-frequency magnetitelluric data inversion. Geophysics, 7(2). |
Wilson G A, Raiche A P, Sugeng F. 2006. 2. 5D inversion of airborne electromagnetic data. Exploration Geophysics, 37(4): 363-371. |
Wu Q. 2012. Forward modeling of large loop transient electromagnetic field and wave-field transform theory's study[Master's thesis] (in Chinese). Xi'an: Chang'an University.
|
Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation. Progress in Geophysics (in Chinese), 23(4): 1165-1172. |
Yin C C, Piao H R. 1991. A study of the dfyinition of apparentresistivity in electromagnetic sounding. Geophysical and Geochemical Exploration (in Chinese), 15(4): 290-299. |
Yin C C, Hodges G. 2007. Simulated annealing for airborne EM inversion. Geophysics, 72(4): F189-F195. DOI:10.1190/1.2736195 |
Yu P, Wang J L, Wu J S, et al. 2007. Constrained joint inversion of gravity and seismic data using the simulated annealing algorithm. Chinese Journal of Geophysics (in Chinese), 50(2): 529-538. |
Zhang Z H. 2007. The system realization of CSAMT data inversion explanation[Master's thesis] (in Chinese). Changchun: Jilin University.
|
Zhdanov M S. 2010. Electromagnetic geophysics:Notes from the past and the road ahead. Geophysics, 75(5): 75A49-75A66. DOI:10.1190/1.3483901 |
陈华根, 李嘉虓, 吴健生, 等. 2012. MT-重力模拟退火联合反演研究. 地球物理学报, 55(2): 663-670. DOI:10.6038/j.issn.0001-5733.2012.02.030 |
程久龙, 李明星, 肖艳丽, 等. 2014. 全空间条件下矿井瞬变电磁法粒子群优化反演研究. 地球物理学报, 57(10): 3478-3484. DOI:10.6038/cjg20141033 |
费业泰. 1995. 误差理论与数据处理. 第3版. 北京: 机械工业出版社.
|
冯思臣, 王绪本, 阮帅. 2004. 一维大地电磁测深几种反演算法的比较研究. 石油地球物理勘探, 39(5): 594-599. DOI:10.3321/j.issn:1000-7210.2004.05.019 |
黄皓平, 王维中. 1990. 时间域航空电磁数据的反演. 地球物理学报, 33(1): 87-97. DOI:10.3321/j.issn:0001-5733.1990.01.010 |
蒋尔雄, 赵风光, 苏仰锋. 2008. 数值逼近. 第2版. 上海: 复旦大学出版社.
|
康立山. 1994. 非数值并行算法-第一册:模拟退火算法. 北京: 科学出版社.
|
李建慧, 朱自强, 刘树才, 等. 2011. 模拟退火法计算大定源瞬变电磁法的视电阻率. 石油地球物理勘探, 46(1): 138-142. DOI:10.13810/j.cnki.issn.1000-7210.2011.01.029 |
朴化荣. 1990. 电磁测深法原理. 北京: 地质出版社.
|
师学明, 王家映. 1998. 一维层状介质大地电磁模拟退火反演法. 地球科学-中国地质大学学报, 23(5): 542-546. |
万玲, 林婷婷, 林君, 等. 2013. 基于自适应遗传算法的MRS-TEM联合反演方法研究. 地球物理学报, 56(11): 3728-3740. DOI:10.6038/cjg20131114 |
王华军, 罗延钟. 2003. 中心回线瞬变电磁法2.5维有限单元算法. 地球物理学报, 46(6): 855-862. |
王家映, Oldenburg D, Levy S. 1985. 大地电磁测深的拟地震解释法. 石油地球物理勘探, 20(1): 66-79. DOI:10.13810/j.cnki.issn.1000-7210.1985.01.008 |
王家映. 2002. 地球物理反演理论. 第2版. 北京: 高等教育出版社.
|
吴琼. 2012. 大回线源电磁场正演与波场变换理论研究[硕士论文]. 西安: 长安大学.
|
薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展. 地球物理学进展, 23(4): 1165-1172. |
殷长春, 朴化荣. 1991. 电磁测深法视电阻率定义问题的研究. 物探与化探, 15(4): 290-299. |
于鹏, 王家林, 吴健生, 等. 2007. 重力与地震资料的模拟退火约束联合反演. 地球物理学报, 50(2): 529-538. DOI:10.3321/j.issn:0001-5733.2007.02.026 |
张志厚. 2007. CSAMT数据处理反演解释系统的实现[硕士论文]. 长春: 吉林大学.
|
 2019, Vol. 62
2019, Vol. 62


