2. 中国科学院地质与地球物理研究所, 中国科学院油气资源研究重点实验室, 北京 100049;
3. 唐山学院, 河北唐山 063020
2. Key Laboratory Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100049, China;
3. Tangshan College, Heibei Tangshan 063020, China
随着石油勘探行业的不断发展,经济对油气产量的依赖日益提高,所以如何从有限的地震资料中提取到更多精细化信息也变得愈加重要.与此同时被誉为石油勘探的最终手段的全波形反演技术(Full-waveform iversion)和逆时偏移技术(reverse time migration)也得到了迅速的发展.其中RTM技术是现在工业界应用的主流手段之一.RTM通过采用双程波波动方程,在时间上进行逆时延拓.首先对地震波场进行正向延拓并存储各时刻波场值,然后将最大时刻的检波点波场值作为边界值输入,逆时延拓到最小时刻.最后通过读取同一时刻地震波场和检波点波场值并利用成像条件提取成像值,通过多炮叠加形成RTM叠加剖面.RTM技术可以追溯到20世纪70年代,在近几十年的学者的共同努力下,RTM技术得到了迅速的发展.其大致的发展方向与Kirchhoff偏移类似,都是从叠后偏移逐渐发展到叠前偏移,由二维资料发展向三维资料,由声波逐渐发展到弹性波.McMechan(1982, 1983)首先实现了叠后地震资料的RTM成像.Dong和McMechan(1993)将各向同性RTM推广到了各向异性介质之中,迅速地推进了RTM的发展.之后,Chang和McMechan(1986, 1994)在之前的基础上又提出了三维弹性波逆时偏移方法和声波成像方法,将RTM技术推广到三维地震资料上.紧接着,Sun和McMechan(2001)详细讨论声波单分量RTM成像与弹性波RTM成像的区别,并证明了弹性波RTM较声波RTM会有更好成像质量.弹性波RTM理论上可以对复杂的地下结构、陡峭的构造进行高精度的成像.所以对弹性波RTM的研究是十分必要的.
矢量地震勘探比单一的P波勘探更能反映地下介质的弹性信息,因此多分量地震勘探已经成为一个热点问题.弹性波矢量波场的分离是逆时偏移成像中必不可少的,如果单纯对不同方向的矢量弹性波波场进行互相关成像在物理上毫无意义.故如何快速精确地将矢量弹性波场分离为纵、横波场则成了弹性波RTM中的关键性技术.Sun和McMechan(2001)提出了基于标量方程的弹性波RTM.Zhang和McMechan (2010)结合了赫姆霍兹方法和Kelvin-Christoffel方程,直接推导了矢量波场分离的算法,并取得了很好的效果.Wang等(2014)提出的一种在方程中增加应力向量的方法,保证了分离后的纵横波场振幅和相位的稳定性.
而RTM的成像结果的准确性以及计算效率很大程度上依赖于波动方程数值解的算法(Baysal et al., 1983),所以无论是对RTM还是FWI技术来说,弹性波数值模拟都是其重要环节,数值模拟的质量很大程度决定了最终反演或者偏移成像结果的优劣.现阶段常用的数值模拟方式有三种:有限差分法(finite-difference method,以下简称FDM)(Virieux, 1984)、有限元法(Komatitsch and Vilotte, 1998)、伪谱法(Kosloff, 1982).由于FDM计算花费远低于伪谱法,且易于并行计算的特点,其成为了最为常用也最简单的数值模拟方法.Alterman和Karal(1968)首次将有限差分技术运用到均匀介质的弹性波模拟.Madariaga(1976)提出了基于速度-应力方程组的交错网格有限差分方法.Igel等(1995)实现了各向异性介质的弹性波数值模拟.Liu和Sen(2009a)提出了一种基于时空频散关系的FDM,提高了波动方程数值解的精度.杜启振等(2011)采用旋转交错网格有限差分实现了2D TTI介质中波场的数值模拟.Yang等(2014)基于最小二乘优化得到了优化的交错网格有限差分算子.
数值频散是有限差分数值模拟中无法避免的一个问题,其直接影响到RTM成像效果.为了得到更高的精度以及更低的数值频散,我们需要降低子波主频或者加细网格,但其会分别导致成像分辨率降低或计算量太大的问题.所以前人在如何压制数值频散方面做了许多的研究,第一种是利用最优化算法来压制数值频散,Holberg(2010)通过最优化算法最小化频散误差得到了优化的有限差分系数.Liu(2013)基于最小二乘方法得到了全局优化的有限差分算子.Yang等(2014)基于最小二乘方法得到了全局优化的交错网格有限差分算子.Yang(2017)利用Remez算法通过最小化波数范围的最大频散误差得到了交错网格有限差分算子.
第二种方法是通过合适的窗函数截断来压制数值频散.Fornberg(1987)研究表明伪谱法可以表现为有限差分的高阶近似,换句话说有限差分法随着阶数的增加,逼近伪谱法,所以可以用时间域窗函数截断伪谱法空间褶积序列得到有限差分算子.Zhou和Greenhalgh(1992)通过广义加权的hanning窗截断得到了有限差分算子.Igel等(1995)和Chu和Stuffa(2012)则分别利用高斯窗和二项式窗函数截断伪谱法序列得到有限差分系数.而之后,因为通过截断得到的有限差分系数会因为窗函数的不同产生不同结果,简单来说就是窗函数的主瓣宽度和旁瓣衰减则控制着窗函数的性能.根据前人的研究一个窗函数拥有主瓣窄旁瓣衰减大的特性,则通过其截断得到的有限差分算子产生的数值频散小.前人们则在常规窗函数的基础上进行窗函数的优化以得到效果更好的有限差分算子系数.比如Wang等(2015)基于自褶积Chebyshev组合窗得到了优化的有限差分算子.Wang(2017)通过余弦调制二项式窗得到了优化的交错网格有限差分算子.
本文首次基于改进的余弦组合窗函数得到了优化后的有限差分算子,并将其应用于弹性波逆时偏移成像.首先我们分析了基于Taylor展开的传统有限差分算子与本文优化的基于改进余弦组合窗函数的有限差分算子.然后我们基于解耦的弹性波传播方程,对各项同性介质的弹性波场进行矢量波场分离,最大限度地保证波场分离后的纵、横波相位及振幅特性,并采用优化后的有限差分算子进行RTM成像,并与传统方法的RTM成像效果进行对比.此外我们还分析了数值频散、成像精度及成像效率等.数值实验表明,优化的RTM算法相比于传统RTM算法有相当明显的优越性.
1 理论与方法 1.1 基于解耦方程的弹性波矢量波场分离对于偏移成像来说,弹性波矢量波场的分离是关系到RTM成像精度中十分重要的一环,所以如何对矢量波场进行精确快速的分离则成了研究的重点问题.通过前人的研究我们可以得知,在各向同性介质中,应用传统的赫姆霍兹方法可以将纵横波场进行快速分离,其物理意义是通过计算原始波场的散度和旋度,利用纵横波偏振性质的不同,将原始波场分别对原始传播方向和与其正交的方向进行投影,从而实现波场分离.但是赫姆霍兹方法会增加梯度的求取,而偏移成像中的数值模拟部分会通过有限差分方法来计算,因此过多的求导会使波场误差逐渐累积,从而影响成像清晰度.此外,原始波场的振幅和相位特性会由于赫姆霍兹方法的应用而改变,从而导致PS成像准确性的降低.所以赫姆霍兹方法在现阶段各向同性介质的波场分离中应用的越来越少.
本文应用Wang等(2014)提出的一种在方程中增加应力向量的方法,其核心思想是源于声波方程,在原始方程中增加类似声波方程的应力向量,以向量的减法运算代替波场模拟后的散度和旋度的计算,通过这种方法可以保证分离后的纵横波场的振幅和相位的稳定.
二维各向同性介质下的弹性波传播方程如下:其中,τij是应力,vi是速度,λ和μ拉梅参数.
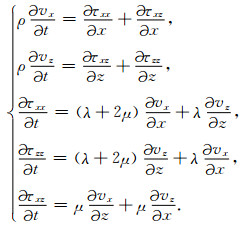
|
(1) |
常规应力的时间导数(公式(1)中的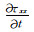
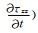
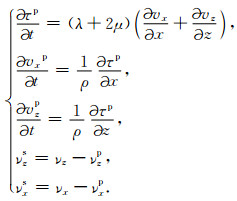
|
(2) |
应用这种方法的前提条件是假设,纵横波场是解耦的,所以这类方程又称为解耦的弹性波传播方程.但是由于在有些特殊的情况下我们需要在正演模拟前进行速度模型的平滑,因为在有些特殊的地层中比如复杂构造的薄互层中,纵横波的转化和横波分解是固有的物理现象.所以在实际应用中我们还要考虑多方面因素的影响.
因为矢量波场的解耦分离算法相比于传统的赫姆霍兹算法并不会改变原始波场的相位以及振幅信息,所以矢量波场的解耦分离算法在进行RTM时能大大提高成像的清晰度.所以本文将解耦方程分离算法引入我们的成像过程以得到更加清晰的RTM成像结果,并将下文的优化的有限差分算子应用于解耦分离的RTM成像中测试此差分算子的有效性.
1.2 利用改进余弦组合窗函数的有限差分算子优化算法通过前人的研究我们可以得知,均匀采样后的带限信号fn可以利用sinc信号来进行重构.sinc信号可以表示为
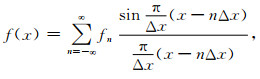
|
(3) |
其中,Δx表示空间采样间隔,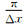
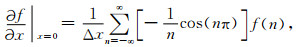
|
(4) |
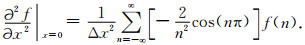
|
(5) |
通过窗函数截断以后我们可以得到
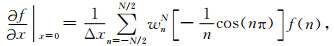
|
(6) |
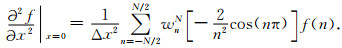
|
(7) |
由于n=0是公式(4)和(5)的一个奇异点,根据Lee和Seo(2002),公式(4)和(5)可以表示为
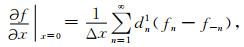
|
(8) |
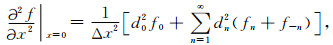
|
(9) |
其中dn2和dn1为fn的系数,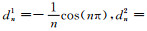
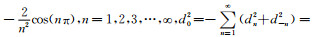
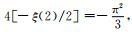
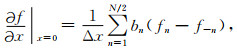
|
(10) |
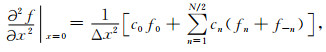
|
(11) |
其中,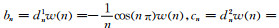
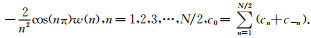
将上述两个公式(10)和(11)变换到频率域为
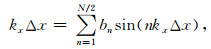
|
(12) |
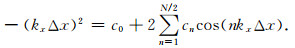
|
(13) |
对于一阶导数和二阶导数可以分别将误差函数表示为
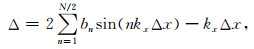
|
(14) |
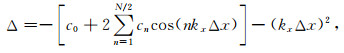
|
(15) |
余弦组合窗函数(CCWF)是一种常用于电力系统谐波分析的一种窗函数,CCWF的主要性能与该窗函数的项数与系数有关,这意味着我们可以通过调节CCWF的项数与系数而得到性能不同的窗函数(季冰,2012).许多国内外的学者研究发现,通过调节CCWF的两个参数可以得到旁瓣衰减快且主瓣较窄的窗函数.即通过此窗函数截断可以较好地抑制数值频散.
在时间域CCWF可以表示为
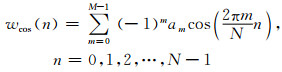
|
(16) |
其中,M窗函数的项数,am是窗函数的系数,其满足如下条件:
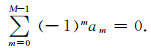
|
(17) |
CCWF的DTFT变换可以表示为如下:
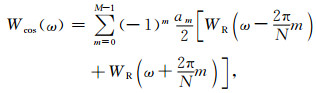
|
(18) |
其中,WR(ω)表示矩形窗的频谱函数.
CCWF的种类众多,我们选出了一些比较典型性质较好的窗函数,其系数如表 1所示.
|
|
表 1 常用CCWF系数分布 Table 1 coefficient of common cosine-combined window function |
根据前人的研究我们可以得知,不同的CCWF有不同的主瓣和旁瓣性质,根据上文的分析得知,我们需要主瓣窄且旁瓣衰减好的窗函数以抑制数值频散.主瓣越窄意味着误差函数的频谱覆盖范围会更大,而越快的旁瓣衰减则意味着误差函数的波动越小.而频谱覆盖越广,误差波动越小则抑制数值频散的能力越强.通过大量的测试我们可以发现根据精度误差的频谱覆盖范围和误差波动可以将CCWF分为两类,分别是频谱覆盖较广的窗函数和精度误差十分稳定的窗函数.
据此我们设计了一种改进的CCWF,如下:
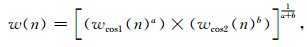
|
(19) |
其中,wcos1(n)和wcos2(n)分别指两种不同性质的CCWF,a和b分别为两种CCWF的权重参数,n=1, 2, 3…N.N为偶数,即有限差分算子的阶数.我们可以通过调节公式(19)中的四个参数wcos1(n)和wcos2(n),a和b, 以得到截断效果更好的CCWF.随着阶数N的改变,我们可以选择不同的四个参数的组合以得到更好的效果.本文通过大量数值测试得出了各阶效果较好的参数选择.具体的参数组合如表 2所示.
|
|
表 2 不同阶数下的参数选择 Table 2 Parameter selection under different orders |
接下来我们以二阶导数为例,分析改进CCWF与窗函数wcos1(n)和wcos2(n)的精度误差.
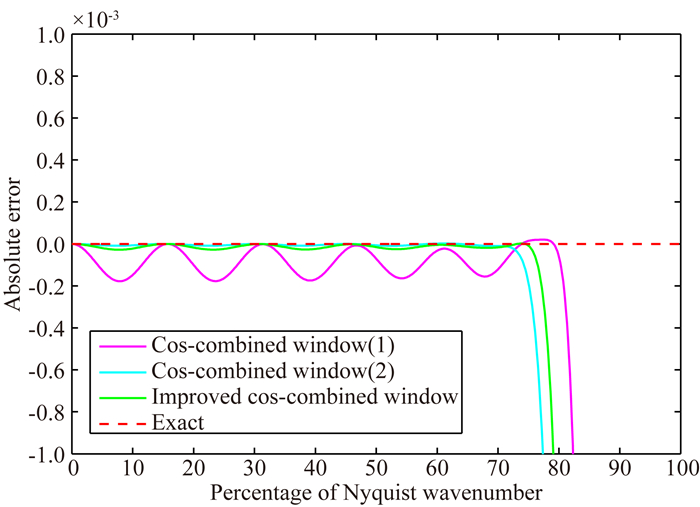
图 1、图 2表示两种CCWF和改进的CCWF的精度误差曲线的对比.其中品红色线、蓝色线、绿色线分别代表两种CCWF和改进的CCWF,由放大1000倍的误差曲线中可以发现,品红色线拥有最大的频谱覆盖范围,但其精度误差波动是三条曲线中最大的,而蓝色线的精度误差波动最小,但其频谱覆盖范围不够,而绿色线则综合了两个曲线的共同特点,不仅拥有较大的频谱覆盖范围还有较小的精度误差波动.所以说可以通过改进的CCWF截断伪谱法空间褶积序列,以得到数值频散较小的有限差分算子.
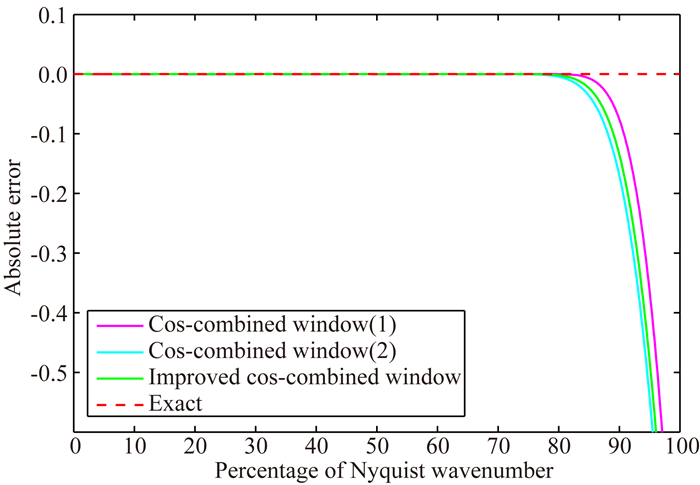
|
图 1 改进余弦组合窗函数的精度误差曲线比较(N=24) Fig. 1 Comparison of accuracy error of improved cosine-combined window for second derivative (N=24) |
|
图 2 改进余弦组合窗函数的精度误差曲线放大1000倍(N=24) Fig. 2 Comparison of accuracy error of improved cosine- combined window for second derivative (Magnified 1000 times, N=24) |
时间域二阶有限差分算子可以表示为
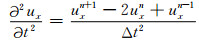
|
(20) |
和
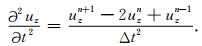
|
(21) |
常规网格下的空间与二阶有限差分算子可以表示为
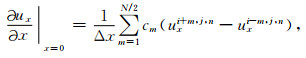
|
(22) |
和
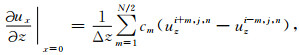
|
(23) |
其中,ux和uz表示时间域离散波场,cm表示前文所述的有限差分算子,Δx和Δz表示空间间隔.
根据上述公式最终X方向的离散方程可以表示为
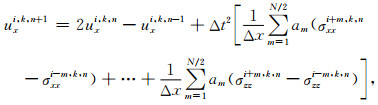
|
(24) |
其在Z方向上的方程与X方向类似.
2.1 数值频散分析在本节中,我们比较改进的CCWF和传统窗函数各阶的绝对误差(N=8, 12, 16, 20, 24).如图 3和图 4所示,图中的实线和虚线分别代表改进的CCWF和传统窗函数的精度误差.显然,改进的CCWF的频谱覆盖范围远远大于传统窗函数的频谱覆盖范围.其中,8阶的改进CCWF的频谱覆盖范围接近传统窗函数12阶的频谱覆盖范围超过了传统20阶的频谱覆盖范围接近传统方法24阶的频谱覆盖范围,而24阶改进CCWF的频谱覆盖范围则远远超过传统方法24阶的.
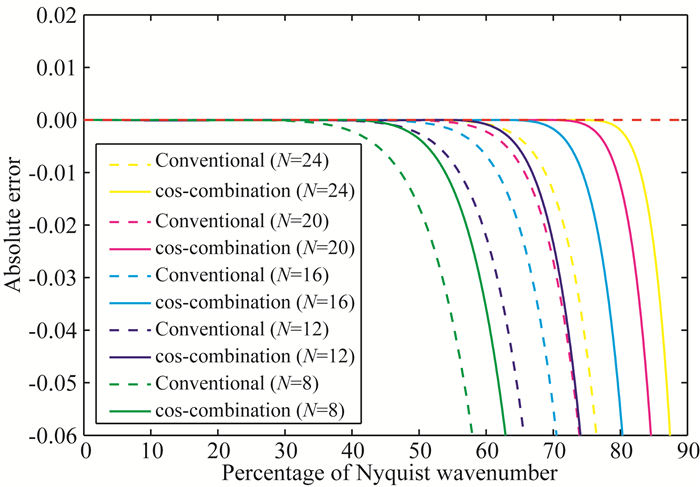
|
图 3 改进CCWF与传统窗函数精度误差比较 Fig. 3 Comparison of absolute error between improved cosine-combined window and conventional window function |
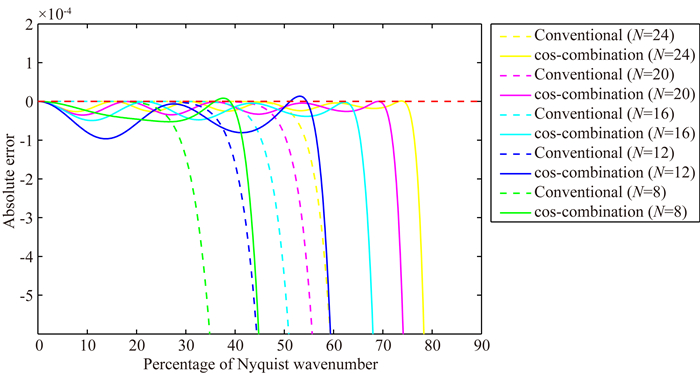
|
图 4 改进CCWF与传统窗函数精度误差的放大比较 Fig. 4 Magnification of absolute error between improved cosine-combined window and conventional window function |
图 4是图 3的精度误差曲线的放大,我们可以发现,8阶改进CCWF的频谱覆盖范围接近传统窗函数12阶,但是其精度误差波动在放大很多倍的情况下依然十分接近.同理,12阶CCWF与24阶的传统窗函数在频谱覆盖和其精度误差波动都十分接近.而改进的CCWF的20阶、24阶的有限差分算子的频谱覆盖远大于传统有限差分算子,而其精度误差波动也比传统方法稳定.这说明我们可以通过低阶的有限差分算子来代替高阶的有限差算子从而节约计算成本.
图 5是将本文的有限差分算子所得到的精度误差曲线与Wang等(2015)的基于自褶积窗函数的有限差分系数所得的精度误差曲线进行对比,可以发现在频谱覆盖略优于前人的情况下,通过我们的有限差分系数能够明显降低精度误差的波动,即使精度误差波动更稳定,从而压制数值频散.
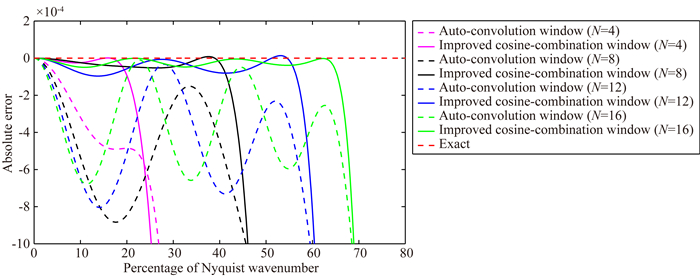
|
图 5 改进CCWF与自褶积窗函数的精度误差放大比较 Fig. 5 Magnification of absolute error between improved cosine-combined window and auto-convolution window function |
本文中所获得的有限差分算子可以适用于大网格间距和高频子波的数值模拟,这意味着地震波场模拟会更加真实且提高计算效率.在本节中我们通过均匀的各项同性介质来测试有限差分算子压制数值频散的能力.均匀模型的P波和S波的速度分别是2000 m·s-1和1400 m·s-1,模型密度为2000 kg·m-3,50 Hz雷克子波,网格的大小为3000 m×3000 m,网格间距为5 m.
如图 6所示,(a)和(b)是8阶传统方法有限差分算子在均匀各向同性介质中的波场快照,我们可以发现明显的数值频散,(c)和(d),(e)和(f)分别为新方法8阶和传统方法16阶的波场快照.我们可以发现新方法8阶有限差分算子的压制数值频散的能力远远好于8阶的传统方法,且略微好于传统方法16阶.这说明了我们的新方法能用低阶的有限差分算子代替高阶,节约计算成本.RTM技术的基础是正演的数值模拟,数值模拟的好坏,直接影响到成像结果的精度.也就是说我们通过改进的CCWF优化了有限差分算子,大大提高了其压制数值频散的能力,也为接下来的RTM成像打下良好的基础.

|
图 6 均匀各向同性模型测试 (a) 8阶传统方法有限差分算子波场快照(X分量); (b) 8阶传统方法有限差分算子波场快照(Z分量); (c) 8阶新方法有限差分算子波场快照(X分量); (d) 8阶新方法有限差分算子波场快照(Z分量); (e) 16阶传统方法有限差分算子波场快照(X分量); (f) 16阶传统方法有限差分算子波场快照(Z分量). Fig. 6 The test of homogeneous ISO medium (a) The snapshot of 8th order traditional method (X component); (b) The snapshot of 8th order traditional method (Z component); (c) The snapshot of 8th order improved cosine combined window (X component); (d) The snapshot of 8th order improved cosine combined window (Z component); (e) The snapshot of 16th order traditional method (X component); (f) The snapshot of 16th order traditional method (Z component). |
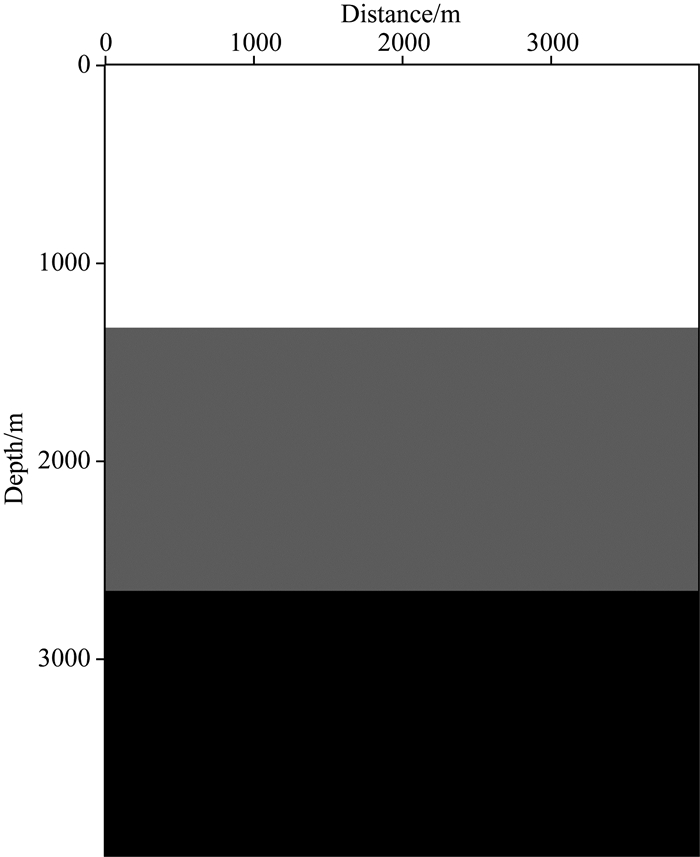
在本节中,我们应用简单三层模型来测试弹性波RTM的成像效果及精度.模型大小是401×401个网格点,网格间距是10 m,其中上层、中层和下层的P波速度为2000 m·s-1,2400 m·s-1,2800 m·s-1,S波速度为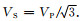
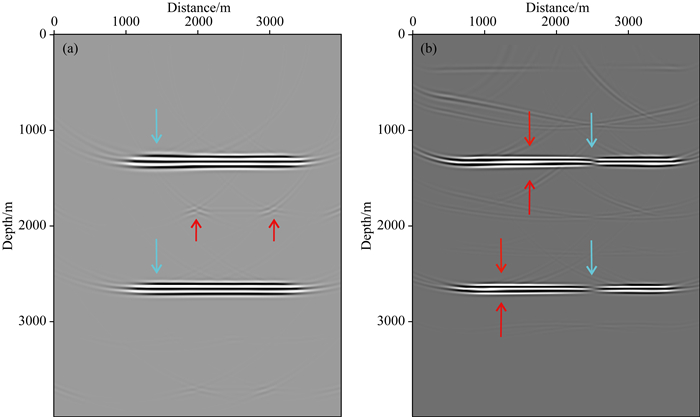
我们分别应用12阶改进的CCWF有限差分算子、24阶传统有限差分算子,以及改进的矢量波场解耦方程分离算法来进行RTM成像.图 8中,(a)和(b)分别为应用12阶改进CCWF有限差分算子和传统的赫姆霍兹波场分离算法进行RTM成像得到的PP波和PS波成像结果.图 9中(a)和(b)分别为应用12阶改进的CCWF有限差分算子和解耦方程波场分离算法进行RTM成像得到的PP波和PS波成像结果.图 10中(a)和(b)分别为应用24阶传统有限差分算子和传统波场分离算法进行偏移成像得到的PP波和PS波成像结果.
|
图 7 简单三层速度模型 Fig. 7 The velocity model of simple three-layers |
|
图 8 基于12阶优化有限差分算子的赫姆霍兹分离RTM成像结果 (a) PP波; (b) PS波. Fig. 8 Helmholtz separation RTM Imaging results based on 12th order optimized finite difference operators (a) PP Waves; (b) PS Waves. |
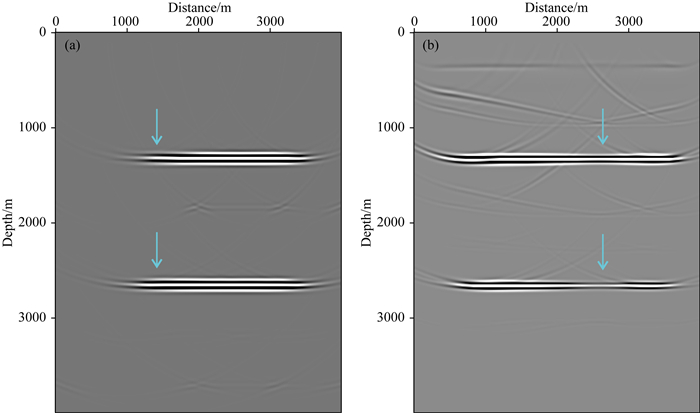
|
图 9 基于12阶优化有限差分算子的解耦方程分离RTM成像结果 (a) PP波; (b) PS波. Fig. 9 Decoupling separation RTM imaging results based on 12th order optimized finite difference operators (a) PP wave; (b) PS wave. |
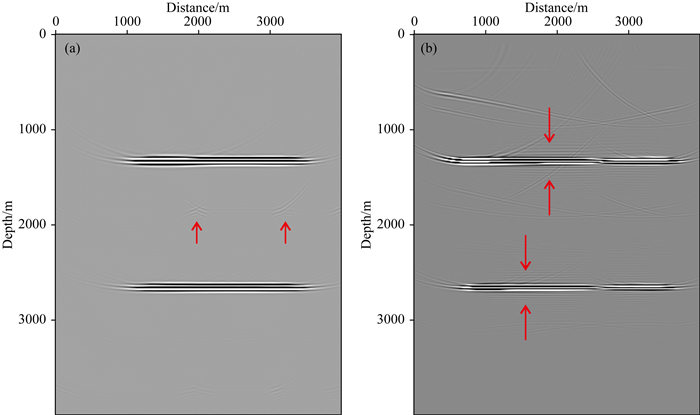
|
图 10 基于24阶传统有限差分算子的赫姆霍兹分离RTM成像结果 (a) PP波; (b) PS波. Fig. 10 Helmholtz separation RTM imaging results based on 24th order traditional finite difference operators (a) PP Waves; (b) PS Waves. |
通过对比图 8和图 10可以发现,图 8中应用12阶优化的有限差分算子的成像结果在反射界面处的数值频散好于24阶传统有限差分算子的,尤其对于PS波其压制数值频散的效果更明显.由图 8和图 10中的红色箭头所指处我们观察到,应用了优化的有限差分算子可以明显压制数值频散,我们通过观察图 11中(a)和(b)的局部放大可以发现,数值频散被压制后的成像效果得到明显的提升.这说明了应用我们的有限差分算子进行RTM成像可以有效地压制数值频散从而提高成像精度.

|
图 11 RTM成像结果局部放大 (a), (b)分别为图 7和图 9的PS波成像的局部放大; (c), (d)分别为图 8和图 7的PP波成像的局部放大; (e), (f)分别为图 8和图 7的PS波成像的局部放大. Fig. 11 The partial magnification results of RTM imaging (a) and (b) are the partial magnification results of the PS wave imaging of Figs. 7 and 9, respectively; (c) and (d) are the partial magnifications of the PP wave imaging of Figs. 8 and 7, respectively; (e) and (f) are partial magnifications results of the PS wave imaging of Fig. 8 and 7, respectively. |
通过对比图 8和图 9可以发现,图 9中应用了基于解耦方程的矢量波场分离算法,其成像清晰度好于图 8中应用传统赫姆霍兹波场分离算法的结果.PP波和PS波的成像清晰度均有很好的提升.通过观察图 8和图 9中的蓝色箭头所指处,以及图 11局部放大后的图像我们可以发现,通过解耦方程的矢量波场分离算法可以使RTM成像的能量更加集中,消除一些成像的假象,比如图 11中(c)和(d),(e)和(f)蓝色箭头所指处的成像假象被消除,整体成像效果更加清晰.证明了新方法的成像分辨率得到明显的提升.
2.4 复杂模型的RTM测试针对各向同性介质,我们分别采用优化后的常规网格CCWF有限差分算子和传统有限差分算子以进行波场的正演模拟和检波点的回传,波动方程则分别采用了原始的赫姆霍兹分离方法及解耦方程分离方法来进行RTM成像的对比.
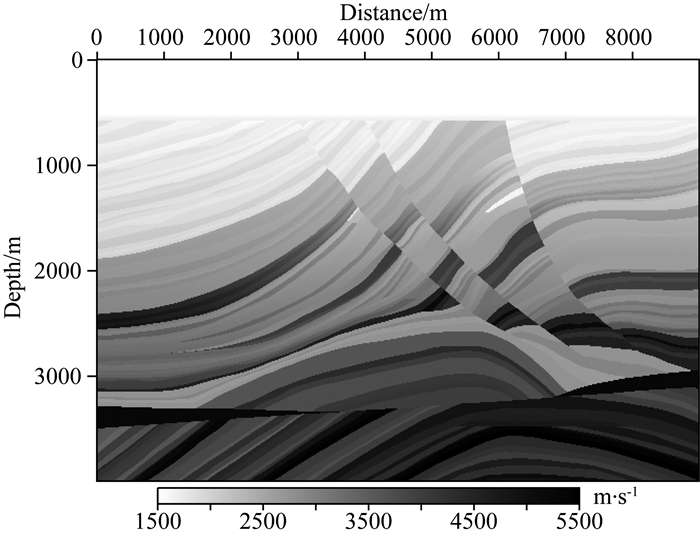
这里给出一个截取后的Marmous速度模型,如图 12所示,其中
|
图 12 Marmous速度模型 Fig. 12 Marmous velocity model |
|
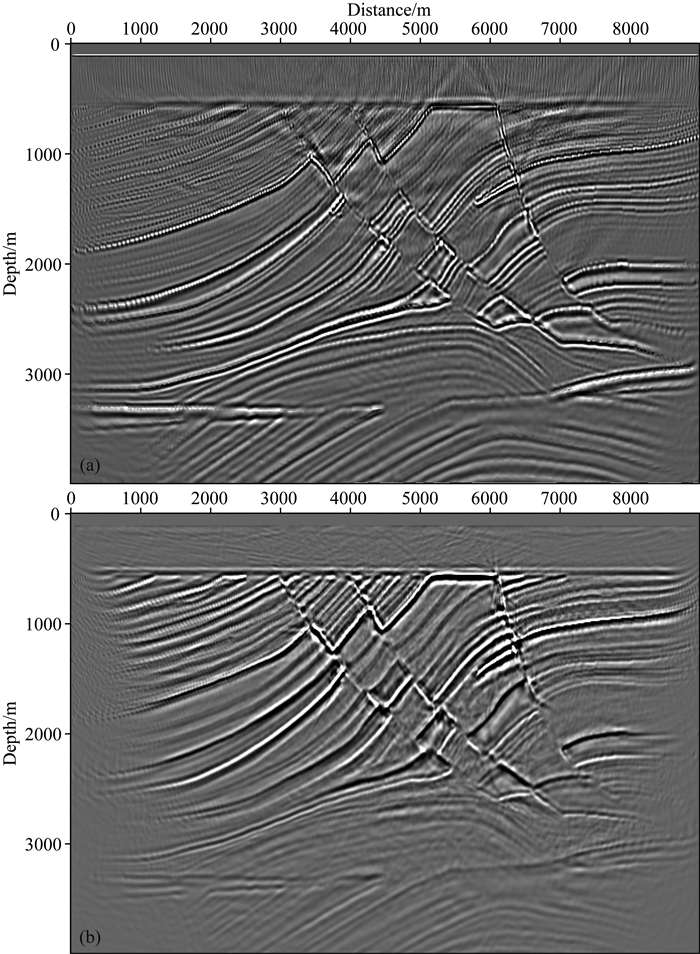
图 13 优化算法的弹性波RTM成像结果 (a) PP波; (b) PS波. Fig. 13 Elastic wave RTM imaging results of optimization algorithm (a) PP-wave; (b) PS-wave. |
|
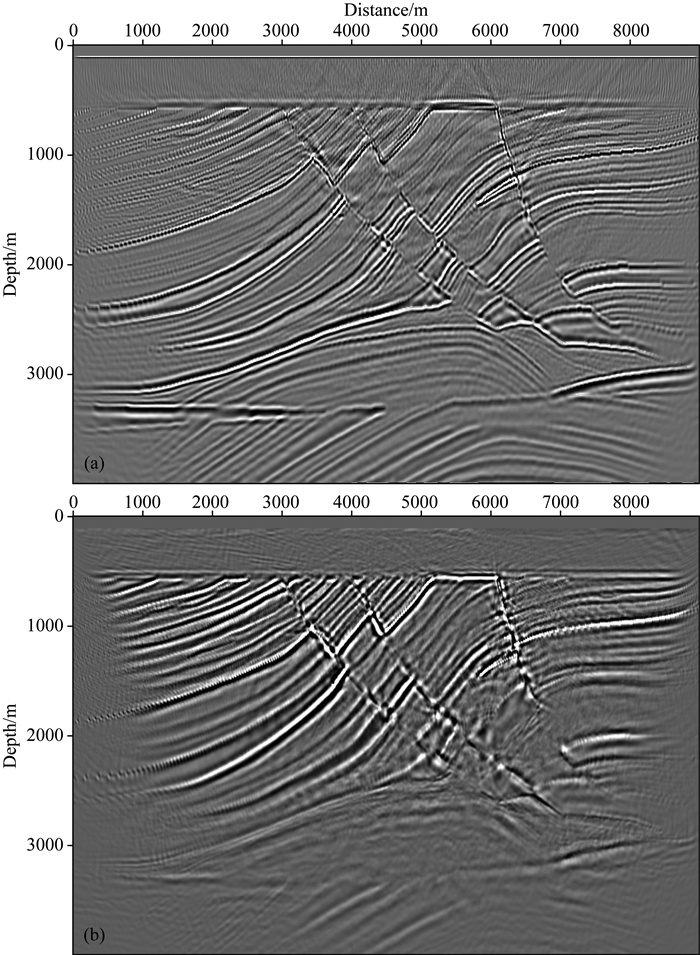
图 14 传统算法的弹性波RTM成像结果 (a) PP波; (b) PS波. Fig. 14 Elastic wave RTM imaging results of optimization algorithm (a) PP-wave; (b) PS-wave. |
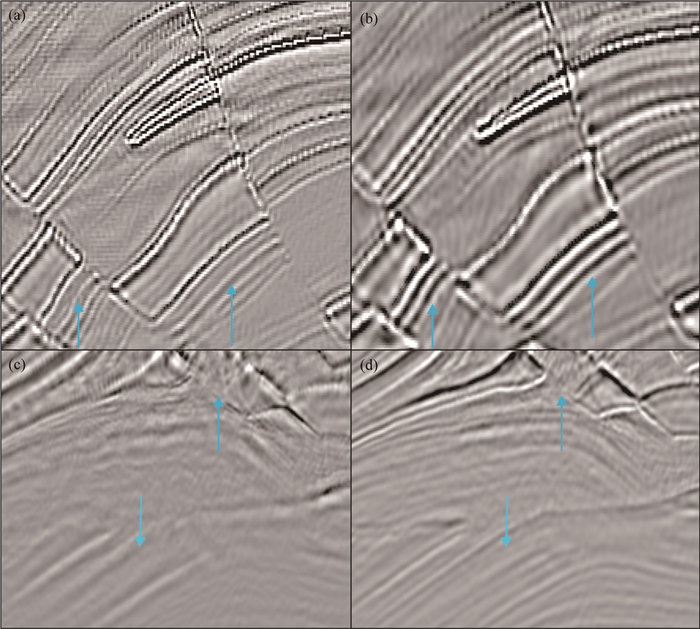
图 15为RTM成像结果的局部放大图像.图 15a为传统算法的PP波成像结果的局部放大,图 15b为优化算法的PP波成像结果的局部放大.图 15c为传统算法的PS波成像结果的局部放大,图 15d为优化算法的PS波成像结果的局部放大.观察图 15a和15b蓝色箭头所指的对应位置我们可以发现,新的成像算法由于不改变波场的相位和振幅信息,成像了传统算法无法成像的层位,明显地提升了成像精确度.观察图 15c和15d蓝色箭头所指的对应位置我们可以发现,在RTM的PS波成像结果的底层,新算法可以清晰成像,传统算法对应位置的成像结果则十分不理想.观察PS波成像结果可以发现,因为压制了数值频散以及不改变波场的相位和振幅信息,优化算法的成像清晰度及精度远远高于传统算法.
|
图 15 RTM成像结果的局部放大 (a), (b)分别为PP波放大结果;(c), (d)为PS波放大结果. Fig. 15 Partial magnification of RTM imaging results (a) and (b) are partial magnification of PP wave (c) and (d) are partial magnification of PS wave. |
本文引进了电力系统谐波中常用的窗函数CCWF,分析了CCWF窗含数的性能并对其进行了优化.通过一种新的组合加权方法得到了改进的CCWF,从而获取了对数值频散压制效果良好的有限差分算子.通过误差分析可以发现8阶的改进的有限差分算子的频谱覆盖超过了12阶的传统有限差分算子,而12阶的有限差分算子的频谱覆盖范围接近传统有限差分算子24阶.通过均匀模型的数值测试证明了改进的有限差分算子对于数值频散的压制能力得到了明显的提高.
本文还引进了一种对于弹性波矢量波场的矢量分离算法,通过与传统的赫姆霍兹算法对比得知,基于解耦方程的波场分离算法不改变原始波场的振幅和相位信息,从而在RTM成像时,可以明显地提高清晰度.
本文通过简单三层模型的RTM成像测试得到以下结论:改进的CCWF有限差分算子可以明显地压制数值频散,从而提高成像精度,新的基于解耦方程的波场分离算法可以明显提高RTM成像清晰度,并且消除成像中的假象.最后通过复杂模型的测试说明,基于优化有限差分算子的解耦方程的新算法可以明显地提高成像的精度和清晰度,得到效果更好的RTM成像结果.
附录|
|
附表 1 基于改进CCWF有限差分算子(一阶导数) Appendix Table 1 Improved cosine-combined window coefficients for the first-order |
|
|
附表 2 基于改进CCWF有限差分算子(二阶导数) Appendix Table 2 Improved cosine-combined window coefficients for the second-order |
|
|
附表 3 各阶算子计算效率 Appendix Table 3 Computational efficiency of different orders |
Alterman Z, Karal F C Jr. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of the Seismological Society of America, 58(1): 367-398. |
Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics, 48(11): 1514-1524. DOI:10.1190/1.441434 |
Chang W F, McMechan G A. 1986. Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition. Geophysics, 51(1): 67-84. DOI:10.1190/1.1442041 |
Chang W F, McMechan G A. 1994. 3-D elastic prestack, reverse-time depth migration. Geophysics, 59(4): 597-609. DOI:10.1190/1.1443620 |
Chu C L, Stoffa P L. 2012. Determination of finite-difference weights using scaled binomial windows. Geophysics, 77: W17-W26. DOI:10.1190/GEO2011-0336.1 |
Dong Z X, McMechan G A. 1993. 3-D prestack migration in anisotropic media. Geophysics, 58(1): 79-90. DOI:10.1190/1.1443353 |
Du Q Z, Sun R Y, Zhang Q. 2011. Numerical simulation of three-component elastic wavefiled in 2D TTI media in the condition of the combined boundary. OGP, 46(2): 187-195. |
Fornberg B. 1987. The pseudospectral method:Comparisons with finite differences for the elastic wave equation. Geophysics, 52: 483-501. DOI:10.1190/1.1442319 |
Holberg O. 2010. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophysical Prospecting, 35(6): 629-655. |
Igel H, Mora P, Riollet B. 1995. Anisotropic wave propagation through finite-difference grids. Geophysics, 60(4): 1203-1216. DOI:10.1190/1.1443849 |
Ji B, Liang Z R, Niu S S. 2012. FFT Harmonic Analysis Based on Nine Terms Minimum Side-lobe Cosine-sum Window. Electric Power Science and Engineering, 28(10): 16-21. |
Komatitsch D, Vilotte J P. 1998. The spectral-element method: An efficient tool to simulate the seismic response of 2D and 3D geological structures.//Peden J R, Glahe F R. The American Family and the State. San Francisco: Pacific Research Institute for Public Policy.
|
Kosloff D. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
Lee C, Seo Y. 2002. New compact spectral scheme for turbulence simulations. Journal of Computational Physics, 183(2): 438-469. DOI:10.1006/jcph.2002.7201 |
Li B, Liu G F, Liu H. 2009. A method of using GPU to accelerate seismic pre-stack time migration. Chinese Journal of Geophysics (in Chinese), 52(1): 245-252. |
Liu Y, Sen M K. 2009a. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
Liu Y, Sen M K. 2009b. Numerical modeling of wave equation by a truncated high-order finite-difference method. Earthquake Science, 22(2): 205-213. DOI:10.1007/s11589-009-0205-0 |
Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78: T113-T132. DOI:10.1190/geo2012-0480.1 |
Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. |
McMechan G A. 1982. Determination of source parameters by wavefield extrapolation. Geophysical Journal International, 71(3): 613-628. DOI:10.1111/j.1365-246X.1982.tb02788.x |
McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420. DOI:10.1111/j.1365-2478.1983.tb01060.x |
Sun R, McMechan G A. 2001. Scalar reverse-time depth migration of prestack elastic seismic data. Geophysics, 66(5): 1519-1527. DOI:10.1190/1.1487098 |
Virieux J. 1984. SH-wave propagation in heterogeneous media; Velocity-stress finite-difference method. Geophysics, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
Wang W L, McMechan G A, Zhang Q S. 2015. Comparison of twoalgorithms for isotropic elastic P and S vector decomposition. Geophysics, 80(4): T147-T160. DOI:10.1190/geo2014-0563.1 |
Wang J, Meng X H, Liu H, et al. 2017. Cosine-modulated window function-based staggered-grid finite-difference forward modeling. Applied Geophysics, 14(1): 115-124. DOI:10.1007/s11770-017-0596-y |
Wang Z Y, Liu H, Tang X D, et al. 2014. Optimized finite-difference operators based on Chebyshev auto-convolution combined window function. Chinese Journal of Geophysics (in Chinese), 58(2): 628-642. DOI:10.6038/cjg20150224 |
Yang L, Yan H, Liu H. 2014. Elastic wave modeling with staggered-grid finite-difference based on least squares.//Global Meeting. Society of Exploration Geophysicists and Chinese Petroleum Society.
|
Yang L, Yan H, Liu H. 2017. An optimal implicit staggered-grid finite-difference scheme based on the modified Taylor-series expansion with minimax approximation method for elastic modeling. Journal of Applied Geophysics, 138: 161-171. DOI:10.1016/j.jappgeo.2017.01.020 |
Zhang Q S, McMechan G A. 2010. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media. Geophysics, 75(3): D13-D16. DOI:10.1190/1.3431045 |
Zhou B Z, Greenhalgh S. 1992. Seismic scalar wave equation modeling by a convolutional differentiator. Bulletin of the Seismological Society of America, 82(1): 289-303. |
杜启振, 孙瑞艳, 张强. 2011. 组合边界条件下二维三分量TTI介质波场数值模拟. 石油地球物理勘探, 46(2): 187-195. |
季冰, 梁志瑞, 牛胜锁. 2012. 基于最小旁瓣九项余弦组合窗的FFT谐波分析. 电力科学与工程, 28(10): 16-21. |
李博, 刘国峰, 刘洪. 2009. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报, 52: 245-252. |
王之洋, 刘洪. 2015. 基于Chebyshev自褶积组合窗的有限差分算子优化方法. 地球物理学报, 58: 628-642. DOI:10.6038/cjg20150224 |
 2019, Vol. 62
2019, Vol. 62


