提高地震勘探资料信噪比是处理地震资料的关键步骤,而压制地震信号中的随机噪声是提高地震勘探资料信噪比的重要环节(Zhang et al., 2015; Thomas et al., 2002; Guitton and Claerbout, 2004), 在现阶段,常用的地震信号去噪方法包含f-x域预测去噪(Harris and White, 1997)、奇异值分解(Lu, 2006)、矢量分析法(Wang, 1989)、小波变换分频去噪方法(李亚峻等, 2007; Cao and Chen, 2005)等,这些方法在压制地震信号中的随机噪声方面发挥了巨大的作用,但是随着勘探环境的复杂化,地震信号的信噪比越来越低, 这些传统的方法对低信噪比的地震信号去噪效果并不理想.2005年,Guo和Labate (2007)等将复合小波理论和几何多尺度分析相结合,通过特殊形式的具有合成膨胀的仿射系统构造了一种接近最优的多维函数的稀疏表示法——Shearlet变换(Easley et al., 2009), 它比轮廓波和曲波方向性更加敏感而且稀疏表示特性更好,运算的速率也更快(Lim, 2010; Kittipoom et al., 2012), 更加适合对地震信号进行处理.然而,由于Shearlet变换本身缺乏平移不变性,因此在采用硬阈值Shearlet变换方法对地震数据进行去噪时,很容易产生虚假同向轴.而且这种传统的硬阈值去噪算法没有充分考虑到Shearlet变换域中信号与噪声之间的能量关系,采用相同的阈值对不同方向上的所有系数进行处理,这会造成噪声的残留和有效信号的缺失.本文结合山地地区实际数据采集情况,将递归循环平移(Recursive Cycle Spinning, RCS)与Shearlet变换相结合对地震信号进行分解变换,然后根据系数能量大小自适应变化的阈值处理变换系数,这样可以更好的压制随机噪声,同时抑制虚假同相轴的出现,从而较好地保留有效信号的幅度.
1 Shearlet变换原理及其去噪原理 1.1 Shearlet变换的原理Shearlet变换理论是基于复小波变换的(Guo et al., 2004, 2006), L2(R2)是闭区间R2的平方可积函数,当维数n=2时,函数f∈L2(R2)的连续Shearlet变换定义为
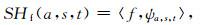
|
(1) |
式中,a∈R+为尺度参数,s∈R为剪切参数,t∈R2为平移参数,ψa, s, t是由ψ∈L2(R2)在尺度a、方向s和位置t进行扩张、剪切、平移后得到的连续Shearlet系统,表达式为(Kutyniok and Lim, 2011):
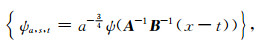
|
(2a) |
这里A、B是大小为2×2的可逆矩阵,其中A为各向异性扩张矩阵,B为剪切矩阵.他们的表达式为
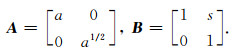
|
(2b) |
对于任意的ξ=(ξ1, ξ2)∈ 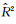
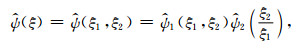
|
(3) |
式中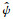
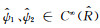
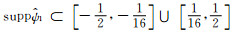
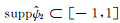
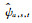
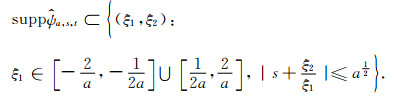
|
(4) |
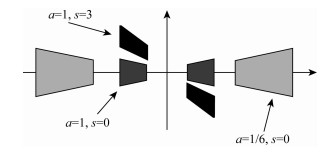
图 1给出特定情况下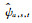
|
图 1
不同a和s时的  |
地震信号含噪模型表达式为
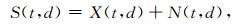
|
(5) |
其中,S(t, d)是含噪信号,X(t, d)是有效信号,N(t, d)是均值为0,方差为σ2的高斯白噪声,t表示时间,d表示道数.由于Shearlet变换是线性的(Yi et al., 2009), 因此,含噪信号s(t, d)可以进行Shearlet变换,然后用硬阈值处理Shearlet系数,保留大于阈值的系数,舍弃小于阈值的系数,含噪的地震信号在Shearlet域的表达式为
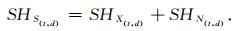
|
(6) |
硬阈值函数定义为(Donoho, 1995):
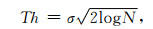
|
(7) |
式中σ为噪声的标准差,N为地震资料的大小.
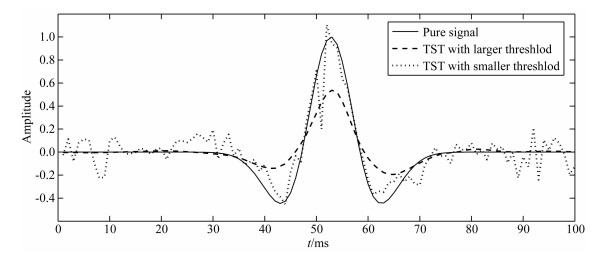
在整个去噪的过程中,阈值的选取直接影响到去噪效果的好坏, 对于不同大小的阈值,Shearlet硬阈值(Hard-Threshold Shearlet Transform Algorithm, TST)的去噪效果如图 2所示.
|
图 2 基于不同阈值的TST算法去噪结果 Fig. 2 Denoising results of the TST algorithm with different thresholds |
在低信噪比下,信号与噪声的Shearlet系数大小十分接近,如果仅通过简单的硬阈值处理会造成有效信号的丢失,导致去噪效果不理想.同时,虽然Shearlet变换比起小波变换具有一定的优势,但是类似于小波变换,Shearlet变换本身缺乏平移不变性,因而在阈值去噪的过程中,会在地震信号的不连续点邻域产生虚假同向轴,导致信号失真,影响去噪的效果.论文针对这两个问题,分别提出了两种改进方案,并对两种方案进行有效的结合,取得了良好的去噪效果.
2 基于RCSST的自适应阈值去噪 2.1 阈值的改进含噪的地震记录经Shearlet变换后,有效信号通常映射到一些特定方向的Shearlet系数上,而随机噪声分布在所有方向的Shearlet系数上.因此与信号方向对应的系数的能量要远远大于其他方向上噪声系数的能量(Zhang et al., 2013).显然,一个仅随尺度变化的阈值不能够取得理想的去噪效果.我们需要设置一个随方向不同而自适应变化的阈值.我们在硬阈值的基础上提出一个方向自适应阈值Thj, l,阈值的公式为
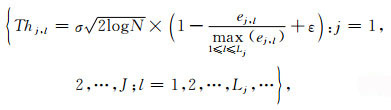
|
(8) |
式中ej, l表示尺度j方向l上的系数能量,ε表示接近于0的正整数.
本文中提出的阈值可以根据每一个方向上Shearlet系数的能量大小而自适应变化.如果某一分解方向中系数的能量较大,则该方向为信号系数主要集中的方向,对于该方向上的系数处理应该采取较小的阈值以便更好地保护有效信号.同理,当某一分解方向中系数的能量较小时,则该方向的系数主要是由噪声经Shearlet变换获得的,我们应该采取较大的阈值以便压制更多的噪声.
2.2 RCSST的基本原理Cycle Spinning(CS)算法是由Caifman和Donoho等提出的(Eslami and Radha, 2003), 首先是对地震资料的行和列进行循环平移,改变不连续点位置,然后对平移后的地震信号进行变换去噪处理,最后将去噪后的地震资料反向平移,并且叠加平均,但是取平均值通常并不能达到最优化运算,为了获得更好的去噪效果,本文采用递归循环平移(RCS),此即CS的递归形式(Fletcher et al., 2002), 其对于虚假同向轴的抑制效果要好于CS的线性平均,并且在一定的约束条件下保证收敛性, 该过程可以表示如下:
对大小为N×N的地震信号S(t, d), 定义循环平移算子Cx, y(·)为
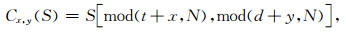
|
(9) |
循环算子是一一对应且可逆的,其逆为
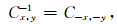
|
(10) |
下标x和y为行和列上的平移量.
对于含噪地震信号S(t, d)=X(t, d)+N(t, d), 基于循环平移Shearlet的去噪过程为
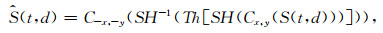
|
(11) |
式中,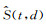
递归循环平移即在循环平移的基础上进行迭代,本文迭代规则为
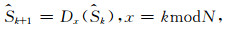
|
(12) |
式中,Dx(·)表示平移x个单位的递归操作符,即第k+1次递归的循环平移量为x, N是最大平移量,本文中N为地震信号的大小,该运算把第k次的递归运算结果作为第k+1次递归运算的输入,基本的思想是递归运算的结果收敛于一个固定点,即对于所有的x,定点(Fletcher et al., 2002):
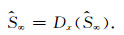
|
(13) |
基于以上内容,我们给出本文RCSST算法具体去噪流程如下:
(1) 取k=0, 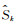
(2) 计算平移量x、y(x=y=kmodN),根据x和y的值对
(3) 对平移后的地震信号进行Shearlet变换从而获得不同尺度不同方向的系数.
(4) 对不同尺度不同方向的系数用自适应阈值进行处理.阈值函数定义为
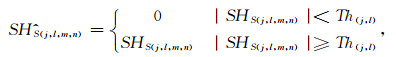
|
(14) |
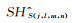
(5) 对上式得到的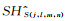
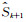
(6) 如果k=K,跳出循环并输出去噪结果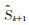
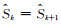
递归循环平移Shearlet算法在传统Shearlet的基础上,通过改变不连续点的位置,优化算法,有效的抑制了去噪信号的虚假同相轴,获得较好的去噪效果.
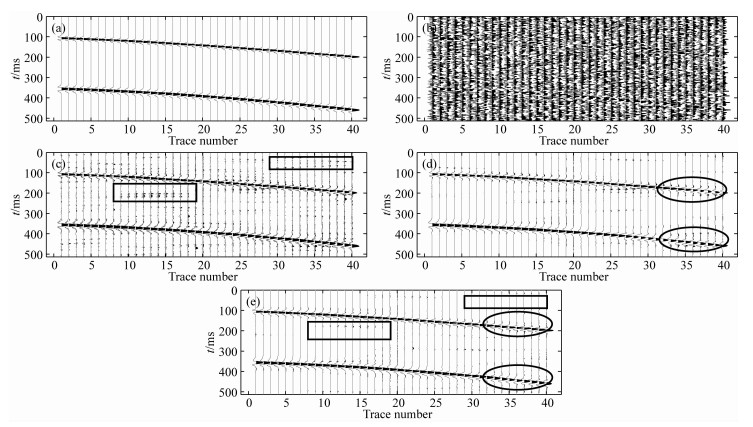
3 实验结果 3.1 地震仿真模型实验分析为了验证本文方法的可行性,首先把本文算法应用在模拟的地震信号处理中,采用Ricker子波构建模拟地震记录,该模拟地震记录包含两个同向轴,主频分别为20 Hz和30 Hz,对应的速度为4100 m·s-1, 2100 m·s-1, 采样频率为500 Hz,如图 3a所示.考虑到实际的地震信号在检波器采集的过程中引入大量的随机噪声,我们向该模拟信号中加入高斯白噪声(SNR=-13 dB),如图 3b所示.实验中我们把Shearlet硬阈值算法、循环平移Shearlet变换(Cycle Spinning Shearlet Transform, CSST)算法和本文算法进行对比,三种方法去噪结果如图 3c—e所示.从图 3c可以看出Shearlet硬阈值的去噪结果中随机噪声的去除不够彻底,而且在矩形标识的区域出现了虚假同相轴.而在图 3d的椭圆标识区域内可以看到,由于原始信号的信噪比过低,CSST算法去噪结果中的有效信号已经发生了畸变.然而在图 3e所示的本文算法去噪结果中,在没有有效信号的空白区域随机噪声被压制的十分彻底,没有产生虚假同相轴,并且有效信号的同相轴也被清晰连续的恢复了出来.
|
图 3 模拟地震资料的去噪结果对比 (a)纯净信号;(b)含噪信号;(c) TST算法去噪结果;(d) CSST算法去噪结果;(e) RCSST算法去噪结果. Fig. 3 Comparison of denoising results for synthetic seismic data using different methods (a) Pure; (b) Noisy record; (c) Denoising by TST; (d) Denoising by CSST; (e) Denoising by RCSST. |
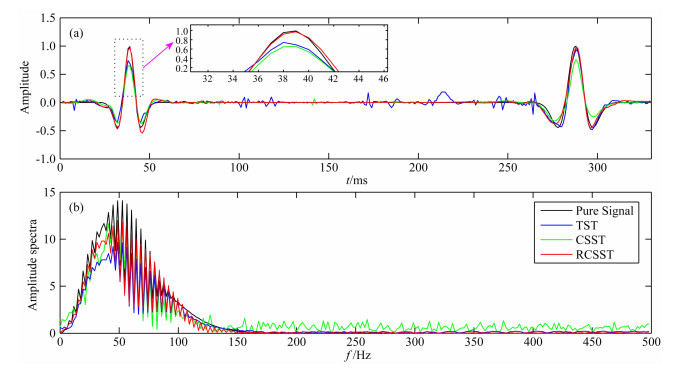
接下来通过观察单道信号的波形和频谱来进一步分析两种方法的滤波性能,从模拟信号的去噪结果中随机抽取第19道来进行波形及频谱的对比,从波形对比结果图 4a中我们可以看出,本文方法去噪后的波形更接近于原始纯净信号的波形,尤其在波峰、波谷处,且信号两侧残留的噪声幅值也远小于Shearlet硬阈值算法处理后的噪声幅值,可以看出本文方法的幅值保持的更好.再从频谱对比结果图 4b中可以看出,在频率为0~150 Hz之间本文方法去噪后的信号频谱更加接近原始纯净信号的频谱,并且150 Hz以上的高频噪声分量几乎为零,随机噪声被较好的压制.
|
图 4 随机噪声时域波形和频谱比较 (a)单道时域波形对比;(b)单道频谱对比. Fig. 4 Comparison of waveforms and frequency spectra of random noise (a) Waveforms of time-domain at single trace; (b) Frequency spectrum at single trace. |
我们在图 3a模拟的纯净地震信号中加入不同强度的高斯白噪声,通过信噪比和均方根误差(Root Mean Square Error, RMSE)两个参数从数值上来验证本文方法的有效性,其中信噪比越高,均方误差越小,去噪信号就越接近原始信号,效果就越好.它们的定义式分别为
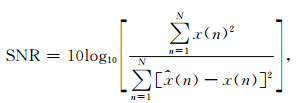
|
(15) |
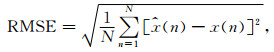
|
(16) |
这里的x(n)表示原始纯净信号,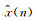
表 1和表 2分别给出了三种方法对于含有不同强度高斯白噪声地震信号去噪结果的信噪比和均方根误差,从表中我们可以看出信噪比越低,本文方法所具有的优势越明显,相较于Shearlet硬阈值算法和CSST算法的去噪结果,本文方法的去噪结果具有较高的信噪比和较小的均方根误差.通过两种方法的量化对比,不难发现,本文的方法能够更好的压制随机噪声,对原始纯净信号进行更为精准的估计.
|
|
表 1 不同噪声水平下的信噪比对比 Table 1 Comparison of SNR at different noise levels for four methods |
|
|
表 2 不同噪声水平下的RMSE对比 Table 2 Comparison of RMSE at different noise levels for four methods |
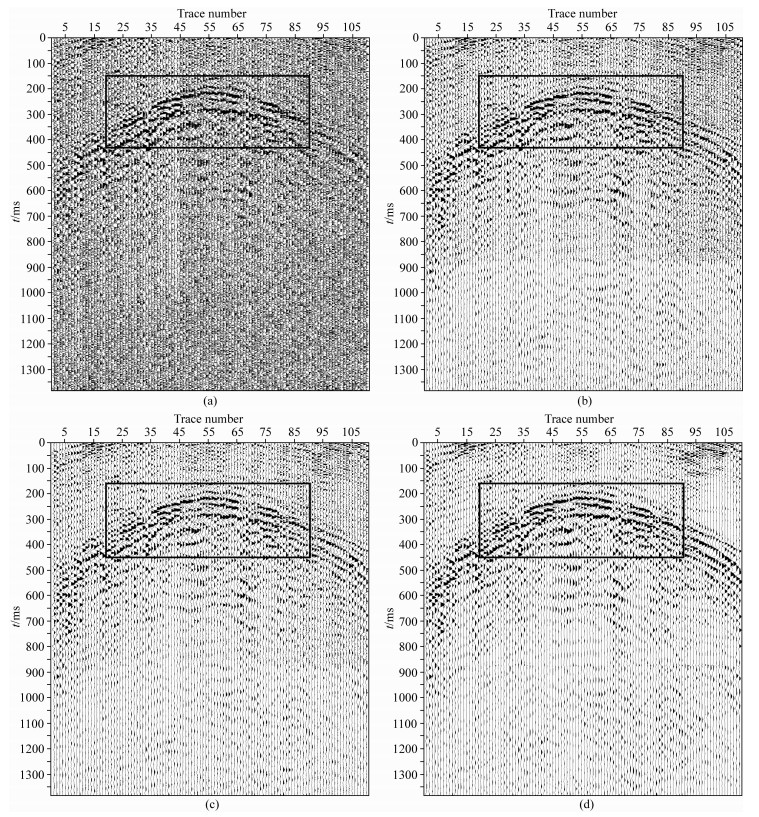
为了进一步验证本文算法在处理实际地震资料的可行性,我们将该方法应用到云南山地实际地震资料的处理当中.图 5a给出了中国云南某山地采集的部分实际地震记录,从图中可以看出随机噪声的分布较为分散,有效信号也被淹没在噪声之中.图 5b—d分别给出了传统去噪方法跟本文算法的去噪结果,对比三种算法去噪结果可以看出,RCSST算法相比于另外两种算法能够更加有效的去除随机噪声,同时也更好保护有效信号.
|
图 5 实际地震资料的去噪结果对比 (a)原始地震信号;(b) TST算法去噪结果;(c) CSST算法去噪结果;(d) RCSST算法去噪结果. Fig. 5 Denoising results of real seismic data by different methods (a) Original seismic data; (b) By TST; (c) By CSST; (d) By RCSST. |
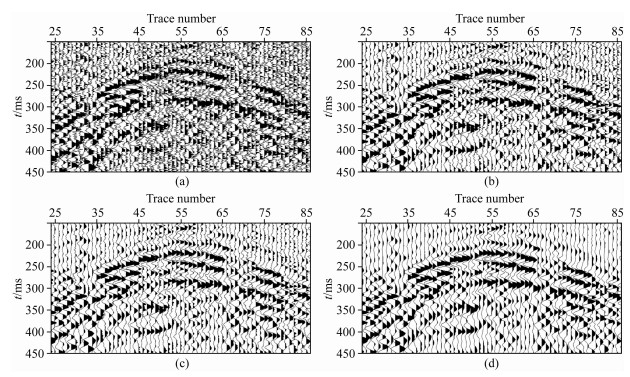
为了能够更加清晰地观察实验结果,将图 5中矩形框标识的区域放大,如图 6所示.从中可以看出,TST算法和CSST算法的处理结果中仍然含有一部分噪声,相反,本文算法的去噪结果中,噪声去除的较为彻底,而且恢复的有效信号同相轴连续性好,易于识别.
|
图 6 局部放大图 (a)原始地震信号;(b) TST算法去噪结果;(c) CSST算法去噪结果;(d) RCSST算法去噪结果. Fig. 6 Local enlarged view of denosing between traces 25-85 and travel time 150-450 ms by different methods (a) Original seismic data; (b) By TST; (c) By CSST; (d) By RCSST. |
本文针对低信噪比的地震数据资料,提出了一种基于RCSST的改进Shearlet硬阈值新算法.Shearlet变换作为一种新的时频分析技术,具有多尺度和多方向性的特点,在消噪方面具有很大的优势.但是由于Shearlet本身缺乏平移不变性,造成去噪后的地震资料容易出现虚假同向轴.本文采用递归循环平移和Shearlet变换相结合的方法抑制了虚假同相轴的出现.同时,根据Shearlet变换域系数能量大小的不同,提出了一种全新的自适应阈值,增加了噪声的压制能力和有效信号的保幅性.最后,采用模拟地震记录和实际云南山地地震记录的仿真实验对本文方法进行了验证,通过与传统的TST和CSST算法的对比,不难发现RCSST算法在有效信号的恢复上,强随机噪声的压制上,同相轴的连续性上都优于另外的两种方法.因此,本文提出的去噪算法是一种较为有效而且可以应用于实际地震资料处理的方法.
致谢 审稿专家针对本文的修改给出了建设性的意见,实验室的同学们也对本文的撰写给予了大力的帮助,特此感谢!
Cao S Y, Chen X P. 2005. The Second-generation wavelet transform and its application in denoising of seismic data. Applied Geophysics, 2(2): 70-74. DOI:10.1007/s11770-005-0034-4 |
Donoho D L. 1995. De-noising by soft-thresholding. IEEE Transactions on Information Theory, 41(3): 613-627. DOI:10.1109/18.382009 |
Easley G R, Labate D, Colonna F. 2009. Shearlet-based total variation diffusion for denoising. IEEE Transactions on Image Processing, 18(2): 260-268. DOI:10.1109/TIP.2008.2008070 |
Eslami R, Radha H. 2003. The Contourlet transform for image denoising using cycle spinning.//37th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA: IEEE, 1982-1986, doi: 10.1109/ACSSC.2003.1292328.
|
Fletcher A K, Ramchandran K, Goyal V K. 2002. Wavelet denoising by recursive cycle spinning.//IEEE International Conference on Image Processing. Rochester, NY, USA: IEEE, doi: 10.1109/ICIP.2002.1040090.
|
Guitton A, Claerbout J. 2004. Interpolation of bathymetry data from the Sea of Galilee:a noise attenuation problem. Geophysics, 69(2): 608-616. DOI:10.1190/1.1707081 |
Guo K H, Labate D. 2007. Optimally sparse multidimensional representation using shearlets. SIAM Journal on Mathematical Analysis, 39(1): 298-318. DOI:10.1117/12.613494 |
Guo K H, Labate D, Lim W Q, et al. 2004. Wavelets with composite dilations. Electronic Research Announcements of the American Mathematical Society, 10: 78-87. DOI:10.1090/S1079-6762-04-00132-5 |
Guo K H, Labate D, Lim W Q, et al. 2006. Wavelets with composite dilations and their MRA properties. Applied and Computational Harmonic Analysis, 20(2): 202-236. DOI:10.1016/j.acha.2005.07.002 |
Harris P E, White R E. 1997. Improving the performance of f-x prediction filtering at low signal-to-noise ratios. Geophysical Prospecting, 45(2): 269-302. DOI:10.1046/j.1365-2478.1997.00347.x |
Kittipoom P, Kutyniok G, Lim W Q. 2012. Construction of compactly supported shearlet frames. Constructive Approximation, 35(1): 21-72. DOI:10.1007/s00365-011-9142-y |
Kutyniok G, Lim W Q. 2011. Compactly supported shearlets are optimally sparse. Journal of Approximation Theory, 163(11): 1564-1589. DOI:10.1016/j.jat.2011.06.005 |
Li Y J, Li Y, Yang B J, et al. 2007. Suppression of surface wave and random noise by SVD and wavelet transform. Computer Engineering and Applications (in Chinese), 43(31): 182-184, 195. |
Lim W Q. 2010. The discrete Shearlet transform:A new directional transform and compactly supported Shearlet frames. IEEE Transactions on Image Processing, 19(5): 1166-1180. DOI:10.1109/TIP.2010.2041410 |
Lu W K. 2006. Adaptive noise attenuation of seismic images based on singular value decomposition and texture direction detection. Journal of Geophysics and Engineering, 3(1): 28-34. DOI:10.1088/1742-2132/3/1/004 |
Thomas R, Bram K, Fertig J, et al. 2002. Acquisition and processing of high-resolution reflection seismic data from a survey within the complex terrain of the Bavarian Folded Molasse. Geophysical Prospecting, 50(4): 411-424. DOI:10.1046/j.1365-2478.2002.00326.x |
Yi S, Labate D, Easley G R, et al. 2009. A shearlet approach to edge analysis and detection. IEEE Transactions on Image Processing, 18(5): 929-941. DOI:10.1109/TIP.2009.2013082 |
Zhang C, Lin H B, Li Y, et al. 2013. Seismic random noise attenuation by time-frequency peak filtering based on curvelet transform.//75th EAGE Conference & Exhibition Incorporating. EAGE, doi: 10.3997/2214-4609.20130660.
|
Zhang C, Li Y, Lin H B, et al. 2015. Seismic random noise attenuation and signal-preserving by multiple directional time-frequency peak filtering. Comptes Rendus Geoscience, 347(1): 2-12. DOI:10.1016/j.crte.2014.10.003 |
李亚峻, 李月, 杨宝俊, 等. 2007. SVD与小波变换相结合抑制面波与随机噪声. 计算机工程与应用, 43(31): 182-184, 195. DOI:10.3321/j.issn:1002-8331.2007.31.055 |
 2019, Vol. 62
2019, Vol. 62


