2019, Vol. 62
2. 中国地质科学院, 地球深部探测中心, 北京 100037
2. China Deep Exploration Center(SinoProbe Center), Chinese Academy of Geological Sciences, Beijing 100037, China
边界识别是位场数据解释的一项重要工作，它可以为矿产资源开发，区域构造识别等地质工作提供有用的信息.目前，应用到地质体构造边界检测中，大多数方法都属于基于异常数据的水平和垂直导数的高通滤波器，并且这些方法能够成功的用于由小而浅的地质体产生的短波长的探测中.Cordell(1979)利用总水平导数最大值圈定地质体边界，Hood和Teskey(Hood and Teskey, 1989)证明了位场垂线导数的零值线可以被用来描绘地质的线性构造.Nabighan(1984)提出解析信号振幅的极大值与磁性体的边界也存在良好的对应关系，Hsu等(1996)利用高阶解析信号使边界识别结果更加清晰，Cooper和Cowan(2004)使用不同阶的垂向导数进行增强地球物理异常的细节.但上述边界识别方法探测深源地质体边界的能力却有限，为了解决这一问题，人们开始致力于均衡滤波器的研究.第一个用于均衡深浅异常的均衡滤波方法是倾斜角法(Miller and Singh, 1994)，该方法是位场垂向导数与水平导数的绝对值的比值.随后，Verduzco等(2004)提出用倾斜角的总水平导数法均衡不同振幅地质体异常，Wijns等(2005)利用解析信号振幅均衡总水平导数，定义了新的均衡方法Theta图法，Ma(2013)利用不同阶导数的比值定义了新的边界识别器，提高了识别的地质异常体的边界分辨率.但是这些均衡边界识别方法依然会因为测量数据中同时存在正负异常而产生额外的错误边界.
目前，随着张量测量技术的进步，针对梯度张量数据的边界识别方法也在不断发展.Cooper和Cowan(2006)以及Oru
和Keskisezer(2008)对传统斜导数方法进行扩展，提出方向斜导数边界识别方法能得到较好的边界探测结果.Beiki(2010)利用方向解析信号进行边界检测，相比较于传统的解析信号方法能得到更好的结果，但是该方法也不能同时描述大振幅和小振幅异常体.Yuan和Yu(2015)对方向解析信号进行改进识别深浅地质体的边界.袁园等(2015)定义了方向总水平导数并以此作为新的均衡边界识别方法.周帅等(2016)定义了基于三维构造张量的边界识别滤波器，可清晰准确地显示不同振幅大小的地质体边界.为了在均衡深浅异常的同时，能够避免产生因为正负异常同时存在而产生的额外的假的异常边界，这些方法多是通过引入常数参数P来实现，然而常数参数的选择通常需要通过实验来确定，具有主观选择性，在很多处理位场数据情况时并不具备优势.
Marson和Klingele (1993)指出总水平导数比解析信号有更高的分辨率.因此，本文直接利用水平方向解析信号提出新的边界识别方法.将水平方向解析信号及其垂向导数分别与传统的均衡边界探测方法(倾斜角法和倾斜角的总水平导数法)进行融合.新方法在清晰准确的识别深浅地质体边界的同时能够避免产生因正负异常同时存在而产生的额外的错误边界，并且不存在主观性.
1 基于水平方向解析信号的边界识别方法重磁梯度张量为重磁位场U在x, y, z方向的二阶导数，其表达式如下：
|
(1) |
Beiki(2010)针对矩阵G的每一行定义其解析信号, 称为x, y, z方向解析信号, 其振幅表达式分别为
|
(2) |
|
(3) |
|
(4) |
Beiki(2010)利用水平方向解析信号和水平方向解析信号垂直导数进行张量数据的边界识别，其表达式分别为
|
(5) |
|
(6) |
水平方向解析信号及其垂向导数的极值对应地质体的边界，但这两种方法对较深的地质体的边界范围难以识别.为了使其能够达到均衡探测异常体的目的，本文首先利用水平方向解析信号分别与两种传统的均衡探测方法做融合，即倾斜角法及倾斜角的总水平导数法，从而形成新的边界识别方法，其定义式分别为
|
(7) |
|
(8) |
然后再利用水平方向解析信号的垂向导数分别与倾斜角法及倾斜角的总水平导数法进行融合定义新的边界识别方法，其定义式分别为
|
(9) |
|
(10) |
NTED_A和NTED_Az的极大值可圈出地质体边界，同时TED_A和TED_Az的零值线也对应着异常体的边界. NTED_A和NTED_Az分别对TED_A和TED_Az起到增强边界信息的作用.新提出的方法不仅能够同时描绘出深浅异常体的边界还能够使边界识别结果更加清晰与收敛.
方向解析信号振幅的垂向导数的直接表达式结果与通过频率域垂向导数算子计算得到的结果之间存在很大差别.为了更好地突出采集数据中的高频成分从而达到更好的边界识别效果，本文利用垂向导数算子在频率域中对水平方向解析信号进行滤波处理.因此，文中的垂向导数计算都是通过频率域垂向导数算子计算得到.
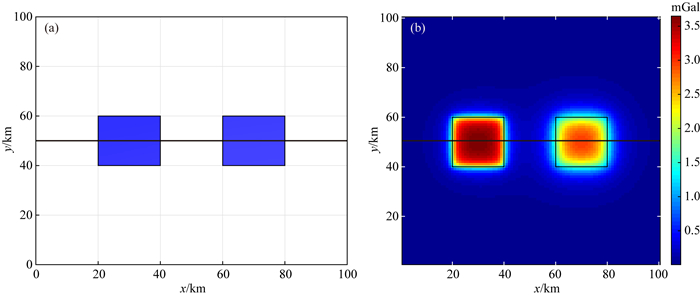
2 模型试验为了验证本文方法的可行性，将选用几种传统的边界识别方法(TDR、THDR、Theta图)与新方法进行效果对比，并在模型上进行实验说明.首先建立包含两个不同埋深的棱柱体的模型1，两个棱柱体埋深分别为1 km和3 km，剩余密度均为100 kg·m-3. 图 1a展示的是模型1的平面图，图 1b显示的是模型1的重力异常，图 1中的黑线为过模型1的剖面线，图 2为各边界识别方法在该剖面线上的剖面图.可以看出，ED_A(图 2a)的极大值能显示出异常体的边界信息，ED_Az(图 2b)的边界识别结果比ED_A的更好，在峰值两边的曲线斜率更大，因此识别的边界要更收敛.但上述两种方法在埋深较深的地质体的边界上的峰值却很小，对于深部地质体边界的识别效果不太理想.图 3c和图 3d分别表示异常的TDR和其总水平导数THDR的边界识别结果，这两种方法能够同时识别出深浅地质体的边界，但是TDR的零值线对应的边界位置与地质体的真实位置存在一定偏差，THDR均衡深浅异常的效果也并不是很好.Theta图(图 3e)能够清晰的识别出深浅地质体的边界，但识别结果也较为发散，尤其是深部地质体边界对应的峰值两侧变化的非常平缓，识别结果更加模糊.图 3f和3g分别表示TED_A和TED_Az的识别结果，同上述方法相比较，TED_A和TED_Az的识别结果在均衡深浅地质体上具有更好的效果，而且识别的边界也更加收敛.因为TED_Az是在异常的高阶导数上实现的，所以边界识别结果有着更高的分辨率, 但同时在低值部分剖面曲线有波动，证明会较易受噪声影响，不稳定.图 3h和3i分别表示NTED_A和NTED_Az的识别结果，水平导数对边界有着加强的作用，因此NTED_A和NTED_Az同TED_A和TED_Az相比，在峰值两侧的斜率更大，坡度更陡，具有更高的边界识别分辨率，对深部异常体的边界识别结果尤其清晰.
|
图 1 (a) 模型1的平面图及(b)模型1的重力异常 Fig. 1 (a) Plan view of model 1; (b) Gravity anomalies of model 1 |
|
图 2 不同方法边界识别结果的剖面图 (a)异常的ED_A结果; (b)异常的ED_Az结果; (c)异常的TDR结果; (d)异常的THDR结果; (e)异常的Theta图结果; (f)异常的TED_A结果; (g)异常的TED_Az结果; (h)异常的NTED_A结果; (i)异常的NTED_Az结果；(j)模型1的重力异常; (k)模型1的剖面图. Fig. 2 Profiles showing edge detecting results using different methods (a) ED_A of anomaly; (b) ED_Az of anomaly; (c) TDR of anomaly; (d) THDR of anomaly; (e) Theta of anomaly; (f) TED_A of anomaly; (g) TED_Az of anomaly; (h) NTED_A of anomaly; (i) NTED_Az of anomaly; (j) Gravity anomaly of model 1; (k) A depth section of model 1. |
|
图 3 (a) 模型2的平面图; (b)模型2的3D图 Fig. 3 (a) Plan view of model 2; (b) 3D view of model 2 |
为了进一步试验方法的有效性，建立一个更加复杂的地质体模型2，模型2含有四个大小不一埋深不一的棱柱体，而且模型2同时包含有正的重力异常和负的重力异常，棱柱体3的体积最大，埋深最深，顶面埋深为3 km, 棱柱体4在空间上垂直位于棱柱体3之上, 顶面埋深为1 km.棱柱体3和棱柱体4的剩余密度均为100 kg·m-3.棱柱体1和棱柱体2的顶面埋深相同，为2 km, 剩余密度均为-100 kg·m-3.图 3为模型2的平面图和3D图.其产生的重力异常如图 4a所示，图中黑色框线表示地质体的真实水平位置，分别利用上述各方法对该异常进行处理，其识别结果如图 4b-4j所示.
|
图 4 不同方法边界识别结果 (a)模型2的重力异常; (b)异常的ED_A结果; (c)异常的ED_Az结果; (d)异常的TDR结果; (e)异常的THDR结果; (f)异常的Theta图结果; (g)异常的TED_A结果; (h)异常的TED_Az结果; (i)异常的NTED_A结果; (j)异常的NTED_Az结果. Fig. 4 Edge detecting results using different methods (a) Gravity anomaly of model 2; (b) ED_A of anomaly; (c) ED_Az of anomaly; (d) TDR of anomaly; (e) THDR of anomaly; (f) Theta of anomaly; (g) TED_A of anomaly; (h) TED_Az of anomaly; (i) NTED_Aof anomaly; (j) NTED_Az of anomaly. |
图 4b和4c为分别表示异常的ED_A和ED_Az边界识别结果，从图中可以看出ED_A和ED_Az对浅部地质体依然有较好的识别效果，圈定的深部地质体边界位置则比较模糊.而三种传统的均衡边界识别方法TDR、THDR和Theta图法(分别为图 4d-4f)虽然能够均衡深浅异常, 但识别效果依然较差，识别的边界位置较为发散，而且存在的最大问题是，由于正负异常同时存在，会产生额外的错误边界, 为异常的解释带来困难.而本文新提出的几种方法的边界识别方法均取得了可靠的边界识别结果，如图 4g-4j，几种方法可清晰的显示出不同振幅异常的边界，而且没有产生假的额外的错误边界.其中，TED_Az和NTED_Az比和TED_A和NTED_A的边界识别分辨率更高.
位场实测数据中不可避免的含有噪声干扰，我们对模型2对应的重力异常加入其最大振幅的5%的高斯白噪声来测试本文对提出的新方法的抗干扰能力，图 5a为加入噪声后的重力异常，图 5b-5j为各方法的边界检测结果.通过与图 4进行比较可以看出，ED_A(图 5b)受噪声的影响相对来讲较小，而ED_Az(图 5c)受噪声的影响较大.三种传统的边界识别方法TDR、THDR和Theta图法(分别为图 5d-5f)能够大致描绘出地质体边界，而本文提出的几种新方法受噪声影响则较大，TED_A和NTED_A还能显示浅部地质体水平位置，TED_Az和NTED_Az则几乎不能识别场源边界位置，造成这一影响的主要原因是它们是基于位场及张量异常的高阶导数，而且本文中涉及到的异常的垂向导数均是在频率域中获得，因此会放大噪声的影响.
|
图 5 不同方法边界识别结果 (a)模型2加入5%高斯噪声的重力异常; (b)异常的ED_A结果; (c)异常的ED_Az结果; (d)异常的TDR结果; (e)异常的THDR结果; (f)异常的Theta图结果; (g)异常的TED_A结果; (h)异常的TED_Az结果; (i)异常的NTED_A结果; (j)异常的NTED_Az结果. Fig. 5 Edge detecting results using different methods (a) Gravity anomaly of model 2 with added 5% Gaussian noise; (b) ED_A of anomaly; (c) ED_Az of anomaly; (d) TDR of anomaly; (e) THDR of anomaly; (f) Theta of anomaly; (g) TED_A of anomaly; (h) TED_Az of anomaly; (i) NTED_A of anomaly; (j) NTED_Az of anomaly. |
为了消除对噪声的影响，在对数据应用边界识别方法之前先要对其进行滤波处理，本文采用的是向上延拓的方法，延拓的高度为3 km.延拓后的重力异常如图 6a所示，可以看出，延拓后的几种传统的边界识别方法TDR、THDR和Theta图法(分别为图 6d-6f)的边界识别分辨率均有所降低，且同图 5d-5f相比，它们均又产生了额外的错误边界.而本文所提出的方法在进行向上延拓滤波后的边界识别结果依然能获得较为清晰的深部和浅部的场源边界位置，其中TED_A和NTED_A方法的异常体边界识别效果最好，而TED_Az和NTED_Az虽然没有在正负异常之间产生假边界，但是在两个叠加地质体之间产生了假边界(图 6i-6j)，对数据的解释产生了影响.这是由于TED_Az和NTED_Az法为更高阶导数，因此对数据中的噪声更为敏感.
|
图 6 噪声数据滤波后不同方法边界识别结果 (a)模型2加入5%高斯噪声并延拓后的重力异常; (b)异常的ED_A结果; (c)异常的ED_Az结果; (d)异常的TDR结果; (e)异常的THDR结果; (f)异常的Theta图结果; (g)异常的TED_A结果; (h)异常的TED_Az结果; (i)异常的NTED_A结果; (j)异常的NTED_Az结果. Fig. 6 Edge detecting results using different methods after filtering noisy data (a) Upward-continued gravity anomaly of model2 with added 5% Gaussian noise; (b) ED_A of anomaly; (c) ED_Az of anomaly; (d) TDR of anomaly; (e) THDR of anomaly; (f) Theta of anomaly; (g) TED_A of anomaly; (h) TED_Az of anomaly; (i) NTED_A of anomaly; (j) NTED_Az of anomaly. |
为了验证本文所述方法在实际数据中的应用效果，将其应用到四川盆地的重力异常数据的处理与解释中，重力数据采自国家测绘总局编绘的1:100万的布格重力异常图, 图 7a所示即为四川盆地重力异常，该研究区域位于重力负异常区，异常由东向西逐渐降低.我们可以清晰的发现图中有一条北北东走向的重力异常带，根据相关地质资料可知，该异常带为龙门山重力梯度带，图 7a-7j中黑线标示该断裂带及其他一些已知断裂的水平位置(马国庆等，2012；颜廷杰等，2016).利用上述方法对重力异常进行处理得到的该地区的线性构造和地层之间的界限如图 7b-7j所示.
|
图 7 四川盆地重力异常边界识别结果 (a)实测重力异常; (b)异常的ED_A结果; (c)异常的ED_Az结果; (d)异常的TDR结果; (e)异常的THDR结果; (f)异常的Theta图结果; (g)异常的TED_A结果; (h)异常的TED_Az结果; (i)异常的NTED_A结果; (j)异常的NTED_Az结果. Fig. 7 Edge detecting results in Sichuan Basin, China (a) Measured gravity anomaly; (b) ED_A of anomaly; (c) ED_Az of anomaly; (d) TDR of anomaly; (e) THDR of anomaly; (f) Theta of anomaly; (g) TED_A of anomaly; (h) TED_Az of anomaly; (i) NTED_A of anomaly; (j) NTED_Az of anomaly. |
ED_A和ED_Az(图 7b-7c)识别断裂的能力较差，只能识别出四川盆地部分已知断裂的位置且识别结果较模糊，TDR、THDR和Theta图法(图 7d-7f)相比较于前两种方法效果要好很多，根据其识别结果可以很容易的识别出深大断裂的水平位置及走势且与已知的实际位置相吻合，而且相对能发现更多信息，但依然不能很好的均衡整个地区不同幅值大小的异常体边界，其主要原因是由深大断裂产生的异常幅值与其他由较浅密度界面的起伏及物性的变化引起的异常幅值相差较大.与传统的均衡边界识别方法相比，本文新提出的方法对于该地区数据的处理效果较为理想，如图 7g-7j，四种方法均能在清晰准确的圈定已知断裂的水平位置的同时显示出更多未知信息.NTED_A和NTED_Az(图 7g-7h)分别对TED_A和TED_Az(7i—7j)起到边界加强的作用, 识别的边界更加收敛，具有更高的边界识别分辨率.其中NTED_Az的识别效果最好.
4 结论本文基于水平方法解析信号与倾斜角的总水平导数法提出新的均衡边界识别方法，通过理论模型试验证明新方法相对于传统的边界识别方法具有更高的分辨率，能更加清晰准确的圈定出异常体的边界位置，而且能够适用于更加复杂的地质体.当正负异常同时存在时，能够避免产生错误的干扰边界信息.但本文方法涉及到的数据高阶垂向导数的计算增加了对测量数据中噪声的灵敏度，因此在对含噪的数据应用边界识别方法之前应对其进行滤波处理.最后将新方法应用到四川盆地重力异常的解释中，获得了区域地质构造的水平位置，并发现了更多细节信息.
Beiki M. 2010. Analytic signals of gravity gradient tensor and their application to estimate source location. Geophysics, 75(6): 159-174. DOI:10.1190/1.3493639 |
Cooper G R J, Cowan D R. 2004. Filtering using variable order vertical derivatives. Computer & Geoscience, 30(5): 455-459. |
Cooper G R J, Cowan D R. 2006. Enhancing potential field data using filters based on the local phase. Computer & Geosciences, 32(10): 1585-1591. |
Cordell L. 1979. Gravimetric expression of graben faulting in Santa Fe Country and the Espanola Basin, New Mexico. //Ingeroll R V ed. Guidebook to Santa Fe Country. Virginia, USA: New Mexico Geological Society, 59-64.
|
Hood P J, Teskey D J. 1989. Aeromagnetic gradiometer program of the geological survey of Canada. Geophysics, 54(8): 1012-1022. DOI:10.1190/1.1442726 |
Hsu S H, Si buet J C, Shyu C T. 1996. High-resolution detection of geologic boundaries from potential-field anomalies: An enhanced analytic signal technique. Geophysics, 61(2): 373-386. DOI:10.1190/1.1443966 |
Ma G Q, Huang D N, Yu P, et al. 2012. Application of improved balancing filters to edge identification of potential field data. Chinese Journal of Geophysics (in Chinese), 55(12): 4288-4295. DOI:10.6038/j.issn.0001-5733.2012.12.040 |
Ma G Q. 2013. Edge detection of potential field data using improved local phase filter. Exploration Geophysics, 44(1): 36-41. |
Marson I, Klingele E E. 1993. Advantages of using the vertical gradient of gravity for 3D interpretation. Geophysics, 58(11): 1588-1595. DOI:10.1190/1.1443374 |
Mikhailov V O, Pajot-Métivier G, Diament M, et al. 2007. Tensor deconvolution: a method to locate equivalent sources from full tensor gravity data. Geophysics, 72(5): 161-169. DOI:10.1190/1.2749317 |
Miller H G, Singh V. 1994. Potential field tilt—a new concept for location of potential field sources. Journal of Applied Geophysics, 32(2-3): 213-217. DOI:10.1016/0926-9851(94)90022-1 |
Nabighan M N. 1984. Toward a three-dimensional automatic interpretation of potential field data via generalized Hilbert transform: Fundamental relations. Geophysics, 49(6): 780-786. DOI:10.1190/1.1441706 |
Oru B, Keskinsezer A. 2008. Structural setting of the northeastern Biga Peninsula (Turkey) from tilt derivatives of gravity gradient tensors and magnitude of horizontal gravity components. Pure and Applied Geophysics, 165(9-10): 1913-1927. DOI:10.1007/s00024-008-0407-8 |
Verduzco B, Fairhead J D, Green C M, et al. 2004. New insights into magnetic derivatives for structural mapping. The Leading Edge, 23(2): 116-119. DOI:10.1190/1.1651454 |
Wijns C, Perez C, Kowalczyk P. 2005. Theta map: Edge detection in magnetic data. Geophysics, 70(4): L39-L43. DOI:10.1190/1.1988184 |
Yan T J, Wu Y G, Yuan Y, et al. 2016. Edge detection of potential field data using an enhanced analytic signal tilt angle. Chinese Journal of Geophysics (in Chinese), 59(7): 2694-2702. DOI:10.6038/cjg20160732 |
Yuan Y, Huang D N, Yu Q L. 2015. Using enhanced directional total horizontal derivatives to detect the edges of potential-field full tensor data. Chinese Journal of Geophysics (in Chinese), 58(7): 2556-2565. DOI:10.6038/cjg20150730 |
Yuan Y, Yu Q L. 2015. Edge detection in potential-field gradient tensor data by use of improved horizontal analytical signal methods. Pure and Applied Geophysics, 172(2): 461-472. DOI:10.1007/s00024-014-0880-1 |
Zhou S, Huang D N, Jiao J. 2016. A filter to detect edge of potential field data based on three-dimensional structural tensors. Chinese Journal of Geophysics (in Chinese), 59(10): 3847-3858. DOI:10.6038/cjg20161028 |
马国庆, 黄大年, 于平, 等. 2012. 改进的均衡滤波器在位场数据边界识别中的应用. 地球物理学报, 55(12): 4288-4295. DOI:10.6038/j.issn.0001-5733.2012.12.040 |
颜廷杰, 吴燕冈, 袁园, 等. 2016. 应用加强解析信号倾斜角进行位场数据的边界检测. 地球物理学报, 59(7): 2694-2702. DOI:10.6038/cjg20160732 |
袁园, 黄大年, 余青露. 2015. 利用加强水平方向总水平导数对位场全张量数据进行边界识别. 地球物理学报, 58(7): 2556-2565. DOI:10.6038/cjg20150730 |
周帅, 黄大年, 焦健. 2016. 基于三维构造张量的位场边界识别滤波器. 地球物理学报, 59(10): 3897-3858. DOI:10.6038/cjg20161028 |