2. 中国地质科学院地球物理地球化学勘查研究所, 河北廊坊 065000;
3. 青海省第三地质勘查院, 西宁 810000
2. Institute of Geophysical and Geochemical Exploration, CAGS, Langfang Hebei 065000, China;
3. No.3 Exploration Institute of Geology Resources of Qinghai Province, Xining 810000, China
我国是金属矿资源大国,铁矿等磁性金属矿床勘查仍是以航磁为基础,通过地面检查和钻探验证,转入普详查和勘探,按此方法发现的铁矿占全国已有铁矿的85%左右,但实际上有相当多的铁矿找矿问题没有解决.实践表明,一些埋藏较深、产状复杂的铁矿,依靠传统方法找矿难度加大.目前,浅部的铁矿资源已经开采殆尽,勘探目标转向矿区外围和深部.地面磁测方法受地表开采残留物、人文干扰的影响较为严重,且对深部信息敏感度不够,再加上地下矿体形态复杂,造成地面接收到的有效信号弱,有用信息难以提取.井中磁测能避开地面及浅部磁性体的干扰,实现钻孔中全方位测量,具有很高的纵向分辨率和探测精度.因此,在实际勘查过程中,针对传统方法的局限性,以井中、地面磁测资料为主体,增加信息维度,提高资料的横、纵向分辨率,结合钻孔编录、岩石物性等信息,开展三维空间联合约束反演,可以实现一定区域内地下矿体空间位置、形态及规模的“透明化”.
长期以来,磁异常反演技术一直是国内外研究热点.在磁化率成像或反演方面,前人做了很多工作.Li和Oldenburg(1996, 1998, 2000)开展了地面磁测资料、井地磁测资料联合磁化率成像研究,将深度加权函数引入模型目标函数,减小了反演结果的“趋肤效应”.Pilkington(1997),在三维磁化率成像过程中,采用预优共轭梯度算法,实现大型线性方程组的快速运算,节省了计算时间和存储空间.冯杰(2010)利用井中三分量磁测资料和地面ΔT磁测资料实现三维磁化率光滑成像,同时引入深度加权函数和预优共轭梯度算法,得到了较好的效果.张俊(2012)通过设定磁化率约束范围,实现致密约束的井地磁测联合反演,提高了聚焦效果.
考虑到强磁性体退磁和剩磁作用的影响,基于磁异常转换量的一些反演方法被提出,不仅适用于孤立场源体,也适用于磁化方向不同的多个场源体所产生的叠加磁场.Krahenbuhl和Li(2007)利用磁异常总梯度模量进行反演,得到磁化率的三维分布.欧洋(2013)采用基于矩形网格剖分的有限体积法对磁异常模量进行快速反演.通过建立静磁场的麦克斯韦方程,对每个单元内的控制方程进行积分,得到一组离散积分方程,然后用共轭梯度法求解得到磁化率的分布.刘圣博(2011)利用磁异常模量实现了三维空间的磁化率成像.李泽林等(李泽林,2014;李泽林等,2015)在前人算法的基础上,做出改进,提出了磁异常模量的数据空间三维反演方法,大大减少计算量,成像聚焦效果显著提高,促进了三维反演的实用化.刘双等(2013)利用二维磁异常模量不受磁化方向影响的特点,提出用井中磁测数据反演二维有效磁化率分布的方法,通过理论模型和实测数据计算,取得了良好的效果.
前人通过磁异常或磁异常转换量反演磁化率的方法较为成熟(陈召曦等, 2012; 郭良辉等, 2009, 2010; 姚长利等, 2003; Zhou et al, 2015; Ou and Feng, 2015),但仍存在一些问题,如:(1)利用地面数据或井中数据反演,反演数据源单一;(2)在反演过程中没有约束或约束条件不够.这些都会造成反演结果的非唯一性增强.针对上述问题,作者采用以井中三分量磁测数据和地面高精度磁测数据为主体,将钻孔编录、岩石物性等地质资料作为组合约束条件,开展三维井地磁测资料联合约束反演,减小解的非唯一性,实现磁测资料的精细反演解释.
1 三维井地磁测联合约束反演三维井地磁测联合约束反演是利用地面磁测二维平面数据(ΔT)和井中磁测X、Y、Z三个分量数据同步反演,获得地下空间磁化率的分布情况,充分利用钻孔编录、见矿情况、磁化率测井资料等先验信息,对反演过程进行约束控制.
1.1 控制方程及求解根据重磁位场理论泊松公式,推导磁化率与磁场三分量及总场的关系,建立控制方程.
设地下有一直立长方体,a, b, c分别为它的半长、半宽、半高,长方体的中心坐标为(ξc, ηc, ζc).在笛卡儿坐标系中,以观测平面上任意一点为坐标原点,Z轴向下为正,X, Y轴在水平面内,地质体走向为Y轴.设长方体的体积为ν, 剩余密度为σ,G为万有引力常量,取长方体内任一点(ξ, η, ζ),该点的体积元为dv=dξdηdζ,那么观测点P(x, y, z)处的引力位为
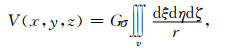
|
(1) |
式中,r表示dv到P点的距离,即
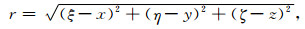
|
(2) |
这样,P点处的磁位为
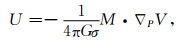
|
(3) |
P点处的磁异常为
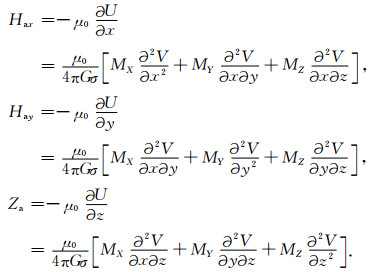
|
(4) |
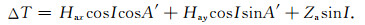
|
(5) |
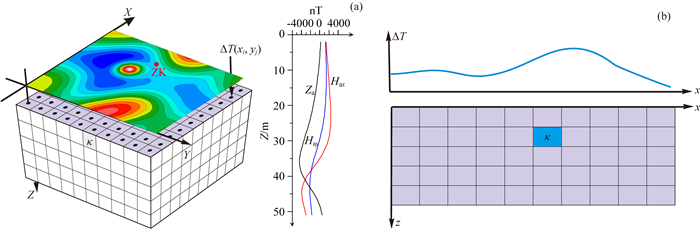
假设地下三维空间已被划分为直立长方体网格单元模型(如图 1所示),总数为M个,每个网格单元内的磁化率均匀分布;观测面和钻孔中一共有N个观测点.那么,第j个长方体在第i个观测点的磁异常可表示为
|
图 1 井地磁测联合反演模型示意图 (a) 3D空间模型示意图;(b)模型断面示意图. “·”表示地面观测点的位置,位于顶层长方体上顶面的中心,ZK表示钻孔. Fig. 1 Diagram of borehole and surface magnetic data joint inversion (a) 3D spatial model diagram; (b) Model section diagram. |
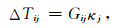
|
(6) |
式中,κj表示第j个直立长方体单元的磁化率;Gij表示单位大小磁化率的第j个直立长方体单元在第i个观测测点产生的磁异常.根据位场叠加原理,第i个观测点的磁异常ΔTi是地下全部N个直立长方体在该点处的磁异常总和,即
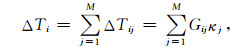
|
(7) |
写成矩阵形式:
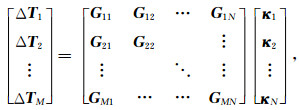
|
(8) |
即:
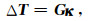
|
(9) |
式中,ΔT为M× 1维列向量,表示M个观测点上的磁异常;κ为N× 1维列向量,表示N个直立长方体单元的磁化率;G为M× N维核矩阵.
1.2 磁异常正演快速算法假如地面上有P ×Q个观测点,地下三维空间划分为L层,每一层都有M×N个长方体单元,需要完成P×Q×M×N×L个积分运算.地下三维空间经过单元划分之后,每一层长方体的大小都相等,地面上为规则网观测点,则可采用快速算法进行正演计算,既可以节省时间,又大大减少了运算量.
用长方体单元离散化地下空间,每一个长方体单元磁化率为常数,允许不同长方体单元的磁化率不同.假设长方体宽和长分别等于观测点在x轴和y轴方向上的点距.
设a, b, c分别为长方体单元在X轴、Y轴和Z轴方向上的半边长,(ξc, ηc, ζc)为直立长方体中心点的坐标,则它在观测点P(x, y, z)处所产生的磁异常为
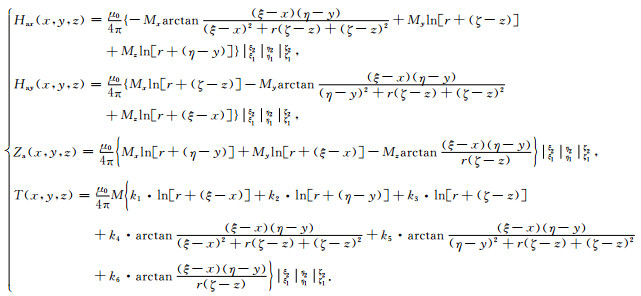
|
(10) |
令L0, M0, N0及α, β, γ分别是地磁场和总磁化强度的方向余弦,则:
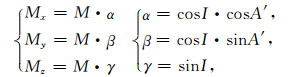
|
(11) |

|
(12) |
I0, A'0分别为地磁场的倾角和地磁场水平分量H相对X轴方向的偏角(y为地质体走向).I, A'为总磁化强度的倾角和MH相对X轴方向的偏角(y为地质体走向).其中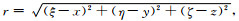
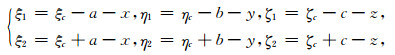
|
(13) |
令Δx=ξc-x, Δy=ηc-y, Δz=ζc-z,则
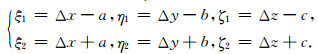
|
(14) |
在磁化率成像过程中,长方体单元的大小在地下三维空间单元划分时就已经确定,长方体半边长a, b, c为常数.因此,磁异常的幅值变化只和(Δx, Δy, Δz)有关,也就是说磁异常的幅值变化,只与长方体单元的中心坐标及观测点坐标的相对位置有关.
令观测面为水平面,观测点按规则网排列,观测点有M×N,X方向有M个观测点,点距为δx;Y方向有N个观测点,点距为δy.现将观测区域的地下三维空间划分为M×N×L个大小相等的直立长方体单元,半边长a=δx/2,b=δy/2,观测点在直立长方体单元的正上方中心,则式(14)中的Δx和Δy分别为δx和δy的整数倍,即,
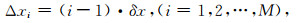
|
(15) |
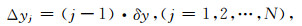
|
(16) |
那么,对于第k层的直立长方体单元,Δzk不变,在计算该层直立长方体在地面所产生的磁异常时,只需要计算M×N个不同的积分项,即:
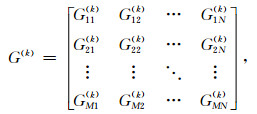
|
(17) |
式中,Gij(k)为由Δxi, Δyj和Δzk组成的积分项.则第一个观测点(x1, y1)处的磁异常为
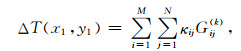
|
(18) |
沿X方向增加m个步长,则在(x1+m·δx, y1)点处的磁异常为
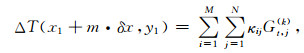
|
(19) |
其中,当m<i≤M时,t=i-m;当1<i≤m时,t=(m+2)-i.
沿Y方向增加n个步长,则在(x1, y1+n·δy)点处的磁异常为
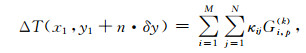
|
(20) |
其中,当n<j≤N时,p=j-n;当1<j≤n时,p=(n+2)-j.
那么,第k层的直立长方体在每一个观测点产生的磁异常为
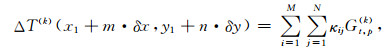
|
(21) |
式中,
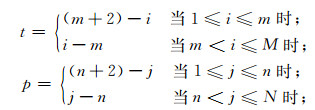
|
由此可见,我们在计算第k层直立长方体所产生的磁异常时,由于观测点数据在M×N的规则网的节点上,如果采用快速算法,仅需计算式(17)中M×N个不同的积分项即可.如果按照原来的算法,则需计算M×N×M×N个积分项,运算量是前者的M×N倍,能大大提高线性方程组中核矩阵的生成速度.
令k=1, 2, …, L,就可以计算出各层直立长方体单元产生的磁异常值,将每一个观测点上的磁异常值进行叠加,就得到地下三维空间模型所产生的总磁异常.同理,可以求得磁异常的三个分量Hax、Hay、Za.
在钻孔中,情况相对复杂.当钻孔为直孔时,测点与网格单元之间亦存在类似的几何结构关系,观测点处的异常值仅与观测点、网格单元之间的坐标有关,可以采用快速算法.但是,当钻孔为斜孔时,这种结构关系不存在,计算量大幅增加,可以采用并行加速算法等方式来缩短计算时间.
1.3 联合约束反演磁化率反演的目标函数可以写成
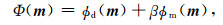
|
(22) |
其中β为正则化参数,根据期望的数据误差来选择.
ϕd(m)是数据误差函数:
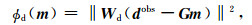
|
(23) |
G为核函数,dobs为观测数据,均包含了地面和井中的数据;Wd为加权矩阵,σj表示第j个观测数据的标准差(j=1, 2, …, N).
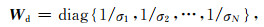
|
(24) |
ϕm(m)为模型目标函数:
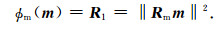
|
(25) |
模型光滑约束矩阵R1为模型向量m在X、Y、Z方向上一阶偏微分的平方和,即
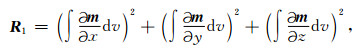
|
(26) |
写为矩阵形式为
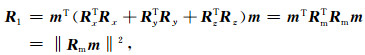
|
(27) |
Rx, Ry, Rz分别是m在X、Y、Z方向的有限差分矩阵.
Li和Oldenburg(1996, 1998)提出了深度加权函数,应用于磁化率成像和密度成像中,其具体形式如下:
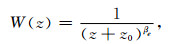
|
(28) |
式中z为单元体的中心埋深,z0是与观测点平均高度有关的常数,βe为常数,一般在反演重力异常时取2,反演磁异常时取3.
将式(23)、式(25)代入式(22),得
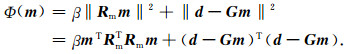
|
(29) |
此时,磁化率反演问题实际上是在观测数据拟合差最小的前提下,求目标函数的最小,同时使模型的粗糙度达到最小,达到对模型解的光滑约束.即:Φ(m)=Φmin,得到模型的改变量Δm,然后对初始模型进行修改,反复迭代至收敛为止(Mackie and Madden, 1993; Portniaguine and Zhdanov, 1999, 2002; Pilkington, 2008; 姚长利等, 2002).
1.4 正则化参数的选取正则化参数β用来权衡最佳数据拟合与最合理模型之间的权重,β值越接近于零,数据拟合越好,但β值过小,容易导致模型粗糙,使反演求解过程不稳定;β值越大,反演越稳定,得到的模型就越光滑,但得到的解接近初始模型,观测数据没有完全拟合,导致反演结果错误.
正则化参数的选取方法一般有以下几种:一是在整个反演过程中将β设为常数,这样可以节省计算时间,但不是在每次反演中都适用;二是在每次迭代后,使β依据一定的规则按比例减小,这样可以在前面的迭代过程中得到合理模型的基础上,能够较好地拟合观测数据;三是每次迭代按Tikhonov曲线来选取合适的参数,把曲线的拐点处的β值作为最佳正则化参数,这种方法效果最好,但是得到Tikhonov曲线需要很大的计算量.为了简化计算,本文采用第二种方式,按照一定的关系确定β初值,然后令β在每次迭代后按照一定比例减小,直到β小于期望.
最有效的初值β使得最优化目标函数接近于二次,这样有利于反演能够简单快速地收敛,应该选取足够大的β值,使得目标函数中的ϕd相对ϕm项可以忽略不计,使得第一次迭代就接近于二次方程的反演,因此将β(0)写成:
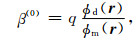
|
(30) |
其中向量r的值是任意的,q是比值的放大系数,本文中设q=10.然后在下面的迭代反演中,β按照下式变化:
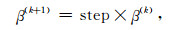
|
(31) |
setp是一个小于1的常数,一般设在0.5~0.9之间.当β值低于某一值β*时,规定β值不再随着迭代次数增加而减小.
1.5 组合约束策略经典的无地质约束反演通常是求解数据和模型目标函数的最优化问题,模型目标函数包括模型最小约束,模型各个方向导数的光滑约束等(Constable et al., 1987; Degroot-Hedlin and Constable, 1990; Mackie and Madden, 1993; Li and Oldenburg, 1996).这样求得的模型在整个研究区域内非常光滑,但是在实际中很少出现物性连续变化的情况.这样反演得到的模型结果和实际情况就会存在较大的差异,解决这些问题的一种方法是在反演中尽可能多地增加已知地质信息(Phillips, 2001; Lane et al., 2007; Farquharson et al., 2008; Williams, 2008; Lelièvre, 2009; Li and Sun, 2015, 2016;Boulanger and Chouteau, 2001; Sun and Li, 2011; Farquharson et al., 2008),例如:测量的物性参数,构造方向特征,地质统计信息,特定形态目标等.
本文中采用了如下约束策略:
(1) 通过收集试验区的岩石物性资料,获取矿体及围岩标本的磁化率参数范围,作为反演模型m的取值范围;
(2) 利用钻孔地质编录资料和磁化率测井数据对模型进行约束.对比磁化率测井曲线、井中三分量磁测曲线和钻孔编录资料,有如下两种情况:
① 井中磁测曲线有异常,对应磁化率测井曲线无异常,钻孔编录为无磁性地层,则当做旁侧异常(或井底异常)处理,程序自动反演;
② 井中磁测曲线有异常,对应磁化率测井曲线有异常,钻孔编录为磁性地层或矿(化)体.此时,需要对异常性质做出判断,若推断该异常为钻遇矿(化)体引起,则磁测数据参与反演,同时将见矿情况作为约束条件.
通过钻孔编录和磁化率测井资料,可以准确得到钻孔的见矿深度、范围,以及该深度范围内的磁化率值.假设平面坐标(x, y),深度范围z1~z2的磁化率为κ',对应位置的网格单元为mu~mv,那么应该使得

|
(32) |
将式(32)离散化后,写入模型目标函数,式(25)改写为:
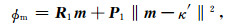
|
(33) |
其中P1为对角矩阵,已知磁化率的网格单元对应行的对角元素为1,其他元素为0.
2 模型分析地面磁测数据具有较高的横向分辨率,通常能够通过反演来确定地质体的平面位置,但不易得到其垂向分布特征.由于在钻孔中更加靠近地质体,井中磁测数据具有更高的垂向分辨率.二者结合,可以更准确地获取地质体的空间分布特征.根据这个特点,设计了组合倾斜板状体模型来验证井地磁测联合反演方法的优越性.
该模型由两个板状体构成,分别向东倾和向西倾,其中西倾板状体的倾向延伸长度大,东倾板状体的倾向延伸长度小.假设垂直磁化,将地下空间划分为25×20×10个致密排列的直立长方体,长方体单元大小为40×50×50 m,X, Y轴位于水平面内,Z轴向下,其中X方向长1000 m,Y方向长1000 m,Z方向长500 m.具体模型参数见表 1.
|
|
表 1 模型参数 Table 1 Model parameter |
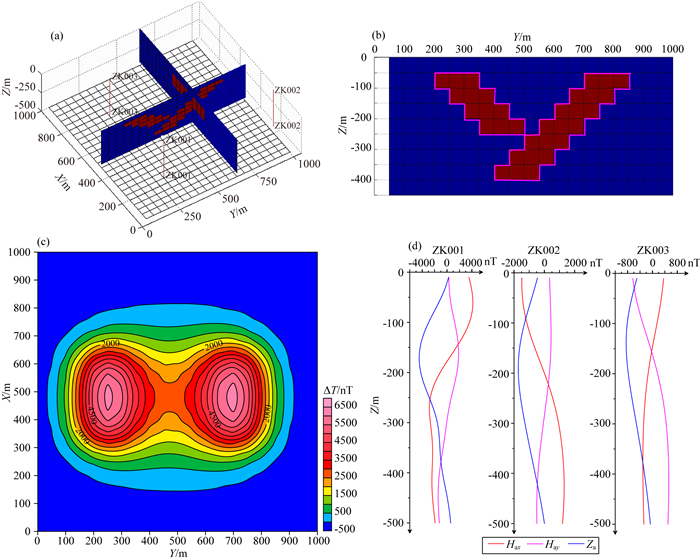
图 2是组合倾斜板状体模型及其正演磁异常.ZK001、ZK002和ZK003三个钻孔分别位于板状体的周围,图 2(c, d)是正演得到的地面ΔT磁异常和井中三分量磁异常理论值.以下将单独利用地面磁异常、井中三分量磁异常反演的结果与井地联合反演结果进行对比.
|
图 2 组合倾斜板状体模型 (a)板状体及钻孔位置;(b)模型断面图;(c)地面ΔT磁异常;(d)井中三分量磁异常. Fig. 2 Multi-inclined-prism model (a) Position of the tabular body and drillings; (b) Section map of the model; (c) Total magnetic anomaly contour map; (d) Three-component borehole magnetic anomalies. |
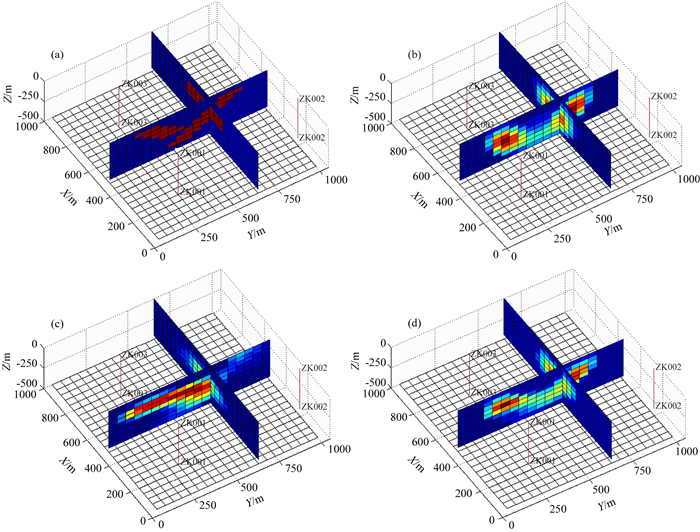
如图 3所示,通过切取三种不同反演结果X、Y方向的切片,可以直观比较不同数据反演结果的空间展布形态.
|
图 3 反演结果三维形态对比 (a)理论模型;(b)地面磁测资料反演结果;(c)井中磁测资料反演结果;(d)井地磁测资料联合反演结果. (a)中蓝色网格磁化率为0, 红色网格磁化率为1;(b、c、d)中蓝色网格磁化率为0, 其他颜色网格磁化率不等. Fig. 3 Comparison of 3D shapes of inversion results (a) Theoretical model; (b) Inversion result of surface magnetic data; (c) Inversion result of borehole magnetic data; (d) Joint inversion result of borehole and surface magnetic data. In (a), the magnetic susceptibility of the blue grid is 0, and the magnetic susceptibility of the red grid is 1;The magnetic susceptibility of blue grid in (b), (c) and(d) is 0, and the magnetic susceptibility of grid in other colors is unequal. |
图 4—图 6分别是地面磁异常、井中三分量磁异常及井地联合反演结果的断面图及数据拟合情况,图中粉色线框表示理论模型的真实位置.
|
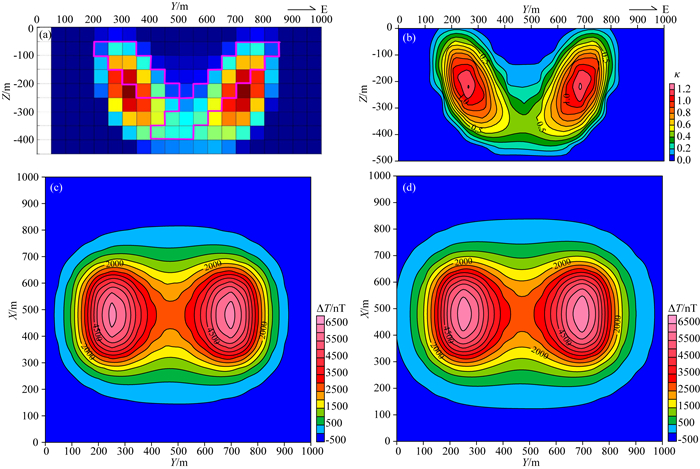
图 4 地面磁测资料反演结果 (a)反演结果断面图;(b)反演结果断面等值线图;(c)地面ΔT磁异常;(d)地面ΔT磁异常拟合结果. Fig. 4 Inversion results of surface magnetic data (a) Section map of inversion result; (b) Section contour map of inversion result; (c) Total magnetic anomaly; (d) Fitting result of total magnetic anomaly. |
|
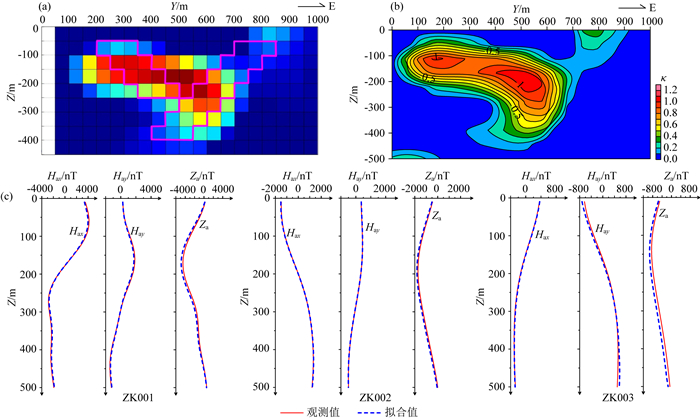
图 5 井中磁测资料反演结果 (a)反演结果断面图;(b)反演结果断面等值线图;(c)井中三分量磁异常拟合结果. Fig. 5 Inversion result of borehole magnetic data (a) Section map of inversion result; (b) Section contour map of inversion result; (c) Fitting results of three-component borehole magnetic anomalies. |
|
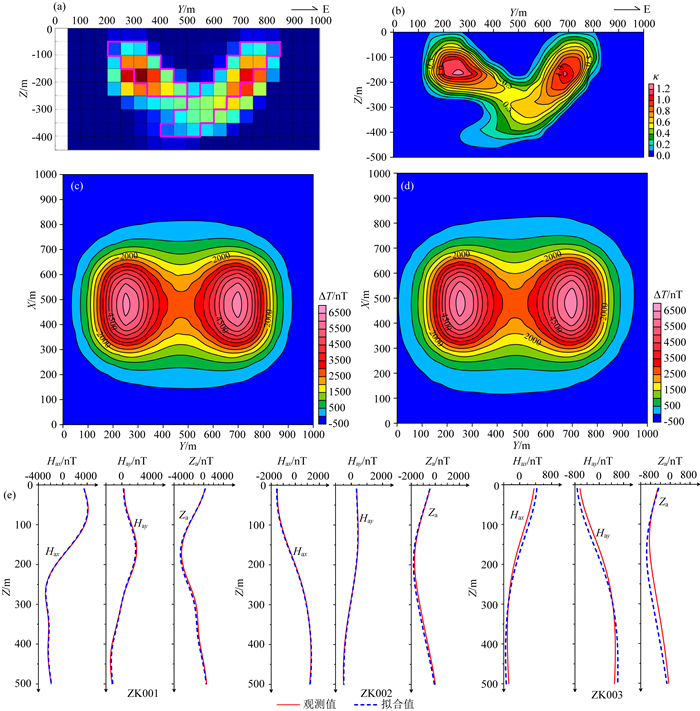
图 6 井地磁测资料联合反演结果 (a)反演结果断面图;(b)反演结果断面等值线图;(c)地面ΔT磁异常;(d)地面ΔT磁异常拟合结果;(e)井中三分量磁异常拟合结果. Fig. 6 Joint inversion results of borehole and surface magnetic data (a) Section map of inversion result; (b) Section contour map of inversion result; (c) Total magnetic anomaly; (d) Fitting result of total magnetic anomaly; (e) Fitting results of three-component borehole magnetic anomalies. |
图 4是单独用地面磁测资料反演得到的结果.从图中可以看出,反演结果为两个东、西倾向的板状体,倾向延伸长度基本一致,边界清晰,地面磁异常的形态和幅值都得到了较好地拟合,然而如图 4a中所示,理论模型的倾向延伸长度并不一致,且反演结果与模型真实的位置相差较大.
图 5是单独用井中三分量磁测资料反演的结果,可以看出,反演结果总体为一个板状体,向东倾斜,边界清晰.ZK001、ZK002、ZK003三个钻孔的井中三分量磁测曲线都拟合较好,然而如图 5a所示,理论模型为两个分别向东、西倾斜的板状体,西倾板状体的倾向延伸长度相对较大.反演结果无法从横向上区分两个板状体,其形态及空间位置与理论模型不符.
图 6是3D井地磁测资料联合反演的结果,井地联合反演与单独地面、井中数据反演所消耗的时间相当,地面磁异常的形态和幅值以及三个钻孔的井中三分量磁测曲线也都得到了较好地拟合.反演结果相对单独地面、井中资料的结果有了较大的改善,尤其突出了两个板状体的结合部位及倾向延伸情况,在横、纵方向均具有较高的分辨率,边界清晰,与理论模型基本一致.由此可见,3D井地磁测资料联合反演,充分发挥了地面数据横向分辨率高、井中数据垂向分辨率高的优势,反演结果更加接近实际,效果优于单一资料反演.
3 青海野马泉铁多金属矿区实例青海野马泉预查区位于柴达木准地台南缘(张爱奎等, 2010),隶属青海省东昆仑祁漫塔格早古生代裂陷槽.区内大面积被第四系覆盖,厚度一般在20~75 m.矿床类型属于矽卡岩型铁多金属矿床,矿体多分布于侵入体与大理岩接触变质带,受侵入接触带、岩浆岩条件、围岩岩性、断裂、裂隙及层间构造综合控制.近年来,青海省第三地质勘查院先后在野马泉及周边矿区开展了普查、详查工作,共圈出多条铁多金属矿体.矿体在剖面上呈脉状、透镜体状分布,在平面上具有膨大收缩或尖灭再现的特点,总体上形态相对简单.矿体主要为EW走向,倾向N,局部S倾,倾角38°~80°.
本区主要有第四系风成砂、大理岩、矽卡岩、角岩、磁黄铁矿化矽卡岩、磁铁矿、花岗闪长岩等.根据收集的岩石磁性资料,沉积岩基本无磁性,大理岩、花岗闪长岩具弱磁性,矽卡岩、磁黄铁矿化矽卡岩、磁铁矿等具中强磁性.
采用试验区内ZK1、ZK2、ZK3、ZK4、ZK5孔的井中三分量磁测资料与C1磁异常的地面磁测资料开展联合约束反演工作.在对测区平面磁异常数据进行区域场分离、浅表噪声去除后,得到局部异常场,作为联合反演的地面磁测数据源.表 2为钻孔见矿情况,ZK1、ZK3、ZK4、ZK5均见矿,将各钻孔的见矿位置、厚度等信息作为约束条件,代入反演过程,磁测数据参与反演.ZK2未见矿,但存在井旁异常,磁测数据参与反演.结合磁化率测井数据和矿区岩(矿)石磁性统计结果,给定磁化率的边界范围,控制模型反演结果.
|
|
表 2 试验区钻孔见矿情况统计表 Table 2 Statistical table of borehole prospecting |
图 7中C1磁异常以正值异常为主,峰值约为150 nT,为一似椭圆型.C1磁异常反演得到的结果为一透镜体状磁性体,是地下磁性矿体和磁性围岩的综合反映.磁性体中间核心部位最厚,视厚度约200 m,并向东、西两翼及南侧尖灭,北侧膨胀.走向为东西向,延伸长度约800 m.倾向为北向,延伸约400 m,反演结果与已有地质资料相符.

|
图 7 C1磁异常三维井地联合约束反演 (a) C1地面ΔT磁异常等值线图;(b)反演结果三维形态;(c) Y5600断面图;(d) X5800断面图. Fig. 7 3D joint constrained inversion of C1 magnetic anomaly by borehole and surface data (a) Total magnetic anomaly contour map of C1; (b) 3D shape of the inversion result; (c) Y5600 section map; (d) X5800 section map. |
在预查、普查矿区或者勘探程度较低的矿区开展井地联合反演工作,可快速获取全区的基本情况.对于钻孔资料较为丰富的矿区,可有针对性的对局部异常做一些联合约束反演,能更好地确定矿体走向、埋深等信息.反演过程中,作者采用20 m×20 m×20 m的网格单元,网格剖分间距越小,反演结果越精细,但随之而来的是更大的计算量,应结合地面数据和井中数据的点距来折中选择网格剖分间距.
4 结论本文针对磁性金属矿床资源勘查中存在的技术难题,利用钻孔编录、岩石物性等作为约束条件的三维井地磁测资料联合反演方法,通过组合倾斜板状体模型,验证了方法技术有效性,并在青海开展了应用试验,取得了较好的效果.同时得出以下认识:
(1) 由于磁异常随场源深度增加而迅速衰减,使得地面数据的纵向分辨率和井中数据的横向分辨率较低.模型试验表明,3D井地磁测资料联合约束反演技术,可发挥观测数据横、纵向高分辨率的优势,充分利用场源周围的数据,通过增加数据的信息量和维度,从根本上提高反演的准确性.利用钻孔编录、磁化率测井资料等先验信息约束反演模型,实现井地联合约束反演,相对单一数据源的反演结果更加准确,是一种有效抑制地球物理多解性和精细物性反演的方法.
(2) 通过将三维井地磁测联合约束反演方法应用到青海野马泉矿区,结合矿区钻孔资料,得到了该工区磁性体的基本形态和位置,推断得到的透镜体状磁性体在已有的地质资料中得到了证实.
致谢 在此,衷心感谢青海省第三地质勘查院在方法技术应用试验过程中,给予的支持和帮助.
Boulanger O, Chouteau M. 2001. Constraints in 3D gravity inversion. Geophysical Prospecting, 49(2): 265-280. DOI:10.1046/j.1365-2478.2001.00254.x |
Chen Z X, Meng X H, Guo L H. 2012. Review of 3D property inversion of gravity and magnetic data. Progress in Geophysics (in Chinese), 27(2): 503-511. |
Constable S C, Parker R L, Constable C G. 1987. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics, 52(3): 289-300. DOI:10.1190/1.1442303 |
Degroot-Hedlin C, Constable S. 1990. Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics, 55(12): 1613-1624. DOI:10.1190/1.1442813 |
Farquharson C G, Ash M R, Miller H G. 2008. Geologically constrained gravity inversion for the Voisey's Bay ovoid deposit. The Leading Edge, 27(1): 64-69. DOI:10.1190/1.2831681 |
Feng J. 2010. Joint inversion research of surface and borehole magnetic data[Ph. D. thesis] (in Chinese). Wuhan: China University of Geosciences.
|
Guo L H, Meng X H, Shi L, et al. 2009. 3D correlation imaging for gravity and gravity gradiometry data. Chinese Journal of Geophysics (in Chinese), 52(4): 1098-1106. DOI:10.3969/j.issn.0001-5733.2009.04.027 |
Guo L H, Meng X H, Shi L. 2010. 3D correlation imaging for magnetic anomaly ΔT data. Chinese Journal of Geophysics (in Chinese), 53(2): 435-441. DOI:10.3969/j.issn.0001-5733.2010.02.022 |
Krahenbuhl R A, Li Y G. 2007. Influence of self-demagnetization effect on data interpretation in strongly magnetic environments. //77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Lane R, FitzGerald D, Guillen A, et al. 2007. Lithologically constrained inversion of magnetic and gravity data sets. Preview, 129: 11-17. |
Lelièvre P G. 2009. Integrating geologic and geophysical data through advanced constrained inversions[Ph. D. thesis]. Vancouver, Canada: University of British Columbia.
|
Li Y G, Oldenburg D W. 1996. 3-D inversion of magnetic data. Geophysics, 61(2): 394-408. DOI:10.1190/1.1443968 |
Li Y G, Oldenburg D W. 1998. 3-D Inversion of gravity data. Geophysics, 63(1): 109-119. DOI:10.1190/1.1444302 |
Li Y G, Oldenburg D W. 2000. Joint inversion of surface and three-component borehole magnetic data. Geophysics, 65(2): 540-552. DOI:10.1190/1.1444749 |
Li Y G, Sun J J. 2015. Towards geology differentiation using magnetization inversions. //International Workshop on Gravity, Electrical & Magnetic Methods and their Applications. Chenghu, China, 350-353.
|
Li Y G, Sun J J. 2016. 3D magnetization inversion using fuzzy c-means clustering with application to geology differentiation. Geophysics, 81(5): J61-J78. DOI:10.1190/geo2015-0636.1 |
Li Z L. 2014. Research on 3-D inversion of magnetic data in the presence of significant remanence [Master's thesis] (in Chinese). Beijing: China University of Geosciences (Beijing).
|
Li Z L, Yao C L, Zheng Y M, et al. 2015. 3D data-space inversion of magnetic amplitude data. Chinese Journal of Geophysics (in Chinese), 58(10): 3804-3814. DOI:10.6038/cjg20151030 |
Liu S, Hu X Y, Liu T Y, et al. 2013. Magnetization vector imaging for borehole magnetic data based on magnitude magnetic anomaly. Geophysics, 78(6): D429-D444. DOI:10.1190/geo2012-0454.1 |
Liu S, Liu T Y, Feng J, et al. 2013. 2D inversion for borehole magnetic data in the presence of significant remanence and demagnetization. Chinese Journal of Geophysics (in Chinese), 56(12): 4297-4309. DOI:10.6038/cjg20131232 |
Liu S B. 2011. 3D magnetic susceptibility imaging based on the amplitude of magnetic anomalies [Master's thesis] (in Chinese). Wuhan: China University of Geosciences.
|
Mackie R L, Madden T R. 1993. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophysical Journal International, 115(1): 215-229. DOI:10.1111/j.1365-246X.1993.tb05600.x |
Ou Y. 2013. Study of magnetic inversion in the presence of demagnetization [Master's thesis] (in Chinese). Wuhan: China University of Geosciences (Wuhan).
|
Ou Y, Feng J. 2015. Joint magnetization vector inversion of surface and borehole magnetic data. International Workshop and Gravity, Electrical & amp; Magnetic Methods and Their Applications, 73-76.
|
Phillips N D. 2001. Geophysical inversion in an integrated exploration program: Examples from the San Nicolas deposit [Ph. D. thesis]. Vancouver, Canada: University of British Columbia.
|
Pilkington M. 1997. 3D magnetic imaging using conjugate gradients. Geophysics, 62(4): 1132-1142. DOI:10.1190/1.1444214 |
Pilkington M. 2008. 3D magnetic data-space inversion with sparseness constraints. Geophysics, 74(1): L7-L15. |
Portniaguine O, Zhdanov M S. 1999. Focusing geophysical inversion images. Geophysics, 64(3): 874-887. DOI:10.1190/1.1444596 |
Portniaguine O, Zhdanov M S. 2002. 3D magnetic inversion with data compression and image focusing. Geophysics, 67(5): 1532-1541. DOI:10.1190/1.1512749 |
Sun J J, Li Y G. 2011. Geophysical inversion using petrophysical constraints with application to lithology differentiation. //81st Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2644-2648.
|
Williams N C. 2008. Geologically-constrained UBC-GIF gravity and magnetic inversions with examples from the Agnew-Wiluna Greenstone Belt, Western Australia[Ph. D. thesis]. Vancouver: University of British Columbia.
|
Yao C L, Hao T Y, Guan Z N. 2002. Restrictions in gravity and magnetic inversions and technical strategy of 3D properties inversion. Geophysical and Geochemical Exploration (in Chinese), 26(4): 253-257. |
Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese Journal of Geophysics (in Chinese), 46(2): 252-258. |
Zhang A K, Mo X X, Shan G L, et al. 2010. Analysis of the feature and prospecting potential of Yemaquan deposit. Mineral Resources and Geology (in Chinese), 24(2): 97-106. |
Zhang J. 2012. Joint inversion of surface and borehole magnetic data with compact constraints [Master's thesis] (in Chinese). Fuzhou: East China Institute of Technology.
|
Zhou J J, Meng X H, Guo L H, et al. 2015. Three-dimensional cross-gradient joint inversion of gravity and normalized magnetic source strength data in the presence of remanent magnetization. Journal of Applied Geophysics, 119: 51-60. DOI:10.1016/j.jappgeo.2015.05.001 |
陈召曦, 孟小红, 郭良辉. 2012. 重磁数据三维物性反演方法进展. 地球物理学进展, 27(2): 503-511. DOI:10.6038/j.issn.1004-2903.2012.02.013 |
冯杰. 2010.井地磁测联合反演研究[博士论文].武汉: 中国地质大学(武汉). http://cdmd.cnki.com.cn/Article/CDMD-10491-2010250477.htm
|
郭良辉, 孟小红, 石磊, 等. 2009. 重力和重力梯度数据三维相关成像. 地球物理学报, 52(4): 1098-1106. DOI:10.3969/j.issn.0001-5733.2009.04.027 |
郭良辉, 孟小红, 石磊. 2010. 磁异常ΔT三维相关成像. 地球物理学报, 53(2): 435-441. DOI:10.3969/j.issn.0001-5733.2010.02.022 |
李泽林. 2014.强剩磁条件下磁数据三维反演研究[硕士论文].北京: 中国地质大学(北京). http://cdmd.cnki.com.cn/Article/CDMD-11415-1014238549.htm
|
李泽林, 姚长利, 郑元满, 等. 2015. 数据空间磁异常模量三维反演. 地球物理学报, 58(10): 3804-3814. DOI:10.6038/cjg20151030 |
刘双, 刘天佑, 冯杰, 等. 2013. 强剩磁强退磁条件下的二维井中磁测反演. 地球物理学报, 56(12): 4297-4309. DOI:10.6038/cjg20131232 |
刘圣博. 2011.基于磁异常模量的三维磁化率成像研究[硕士论文].武汉: 中国地质大学(武汉). http://cdmd.cnki.com.cn/Article/CDMD-10491-1011175386.htm
|
欧洋. 2013.考虑退磁影响的反演方法研究[硕士论文].武汉: 中国地质大学(武汉). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2436433
|
姚长利, 郝天珧, 管志宁. 2002. 重磁反演约束条件及三维物性反演技术策略. 物探与化探, 26(4): 253-257. DOI:10.3969/j.issn.1000-8918.2002.04.003 |
姚长利, 郝天珧, 管志宁, 等. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
张爱奎, 莫宣学, 刘光莲, 等. 2010. 野马泉矿床特征及找矿潜力分析. 矿产与地质, 24(2): 97-106. DOI:10.3969/j.issn.1001-5663.2010.02.001 |
张俊. 2012.致密约束井地磁测联合反演[硕士论文].抚州: 东华理工大学. http://cdmd.cnki.com.cn/Article/CDMD-10405-1012030456.htm
|
 2019, Vol. 62
2019, Vol. 62

