2. 中国石油辽河油田分公司勘探开发研究院, 辽宁盘锦 124010;
3. 中国石油大学(北京)数岩科技联合研究院, 北京 102249
2. Exploration and Development Research Institute of Liaohe Oilfield Company, Liaoning Panjin 124010, China;
3. iRock Technologies, Beijing 102249, China
随着微米-纳米CT扫描、聚焦离子束-电子束双束扫描(FIB-SEM)等成像技术在岩石物理机理和提高采收率(EOR)等领域中应用的快速发展,数字岩石受到广泛重视.通常,完整的数字岩石分析包含三个步骤,即岩石样品成像数据的采集、图像数据的处理及矿物和孔隙等信息的获取、岩石物理特性的数值模拟(Heiko et al., 2013a, 2013b; Xiong et al., 2016),其在岩石弹性、电性、核磁、渗流特性等的数值计算及理论研究中,发挥着日益重要的基础性作用(Arns et al., 2007; Zhang and Toksöz, 2012; Zhao et al., 2013; Yue and Tao, 2013; Schwartz et al., 2013; Chi and Heidari, 2015; Wang et al., 2016; 聂昕等, 2016; 郭江峰等, 2016).然而, 一方面,微纳尺度岩样图像的获取十分耗时且成本昂贵,并且对样品具有破坏性;另一方面,真实岩样扫描图像的体元大小在微米级甚至纳米级,难以刻画岩样孔隙结构的非均质性,从而对理论分析产生不利影响,形成孔隙结构、矿物及泥质分布等岩石物理特征描述的技术瓶颈.以低维成像数据为基础,通过数值方法,建立高维岩石模型,成为低成本和高效率数字岩石分析的替代方案.目前主要有两类方法.第一类,是随机重构,包括模拟退火方法(Hazlett, 1997; 莫修文等, 2016)、高斯随机场方法(Jiang et al., 2013)、多点地质统计方法(Okabe and Blunt, 2004; Zhang, 2015)、马尔科夫链蒙特卡罗(MCMC)方法(Wu et al., 2004)等,其特点是统计提取二维图像信息, 如孔隙度、孔隙形态和孔隙连通性等,将其用于约束重建过程,直到得到的三维图像与二维扫描的统计参数在误差允许范围之内.该类方法建模随机性较强,难以准确表征各向异性介质.第二类,是模拟矿物沉积及成岩过程(Øren and Bakke, 2002; Jin et al., 2003; Zhu et al., 2012; Torskaya et al., 2014),模拟矿物在重力等作用下发生自然沉降,达到稳定状态后再模拟岩石的成岩作用.其中,Øren和Bakke(2002)提出纯几何思路,针对高能和低能两种沉积环境,假设沉积颗粒只要与三个已稳定对象接触即达到稳定状态,稳定状态的搜寻采取平动或转动一个单位距离,然后逐步迭代判断;Jin等(2003)则采用离散元方法,考虑颗粒同时受到重力、浮力及颗粒间摩擦力的作用,当沉积颗粒的总体势能达到最小或阈值时便认为达到稳定状态.随机法,对颗粒稳定状态的搜寻和计算效率低,其运动方向并未考虑正在沉积的矿物颗粒与已沉积矿物颗粒产生碰撞后受到新的合力作用导致运动方向的改变.离散元法,虽然考虑了矿物颗粒在重力、内摩擦力及浮力等作用下发生沉积,对孔隙连通性和渗流特性表征更接近真实情况,但其在计算沉积矿物的总体势能时,算法复杂,计算量大,影响成岩过程复杂、孔隙尺度跨度大的岩石建模.王晨晨(2013)及刘学锋等(2013)分别提出将MCMC方法、模拟退火方法等随机建模方法与过程法相结合,提高了过程法的适用范围,但计算过程复杂.
为了克服过程法的瓶颈,本文提出一种新的矿物颗粒沉积规则和颗粒沉积过程接触检测方法,建立三维数字岩石模型,既考虑到矿物受重力及颗粒碰撞的物理作用,又改进颗粒稳态位置搜寻算法,使沉积颗粒能够快速收敛到稳定位置,针对沉积岩石的非规则特征,采取非规则化处理.文中详细讨论了建模的理论和评价准则,并成功实现了泥质砂岩、碳酸盐岩、页岩等多矿物和多尺度孔隙并存的地层数字岩石建模.
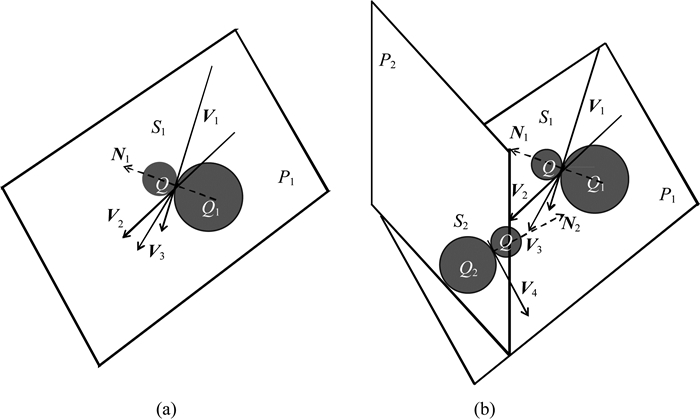
1 方法描述 1.1 矿物颗粒沉积算法首先, 确定沉积区域的边界条件, 在沉积区域底部沉积一层排列松散且互相不接触的初始矿物颗粒.随后, 在沉积区域顶部随机位置产生一个新的矿物颗粒Q, 记录下该颗粒的初始位置R, 颗粒粒径的选择可以依据岩心分析资料或指定算法确定.初始时, 颗粒受到重力作用下落, 依据其运动方向, 搜寻可能接触的已沉积颗粒, 判断颗粒最先产生接触的位置, 将Q移至新位置, 这时颗粒同时受到重力和接触颗粒的内摩擦力合力的作用.在该作用下, 颗粒Q的运动方向发生改变.为了提高接触检测效率, 引入颗粒堆积领域的一种算法(方锡武等, 2011), 设Q的运动方向为V1, 当颗粒Q第一次与已沉积矿物接触时, 按弹性碰撞理论,其新的运动方向V2应该与V1按法向量N1对称, 但为了考虑重力影响, 即颗粒运动方向必须存在向下的分量.这里采取如图 1所示的方法, 颗粒Q第一次运动接触对象为Q1, 接触点为S1, 接触平面为P1, 对应的平面法向量为N1, 新的移动方向V3的计算公式为
|
图 1 矿物颗粒运动方向示意图 (a)首次接触; (b)非首次接触. Fig. 1 The diagram of the movement direction of mineral particle (a) First contact; (b) Non-first contact. |
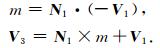
|
(1) |
V3的方向实质是V2在接触平面P1的投影方向, 该计算方法约束了新的运动方向必须有向下的分量.当颗粒Q按V3方向运动, 继续检测它新的碰撞对象, 假如下一次碰撞对象为已沉积颗粒Q2, Q与Q2的接触点为S2, 所对应的接触平面为P2, 对应的接触平面法向量为N2, 则其新的运动方向规定为两次接触平面的交线所在的方向, 其计算公式为
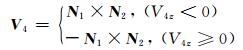
|
(2) |
如果颗粒Q运动过程中碰到底界面, 认为Q直接达到稳态位置, 如果与其他边界接触, 则按弹性碰撞处理.当颗粒最终达到稳态位置时, 记录颗粒的位置及粒径信息, 更新已沉积颗粒信息, 开始新的颗粒沉积过程.
一般来说, 颗粒至少同时与三个已沉积对象或边界接触时才算是达到稳定状态, 当颗粒寻找最终稳定状态时, 其连续多次在三个已沉积对象或边界之间运动, 例如颗粒Q的接触对象连续在Q1, Q2, Q3之间循环, 沉积过程的运动距离总体上呈逐渐变小的趋势, 并且其最终一次的移动距离d小于设定极小值ε, 我们就判定其达到稳定状态.
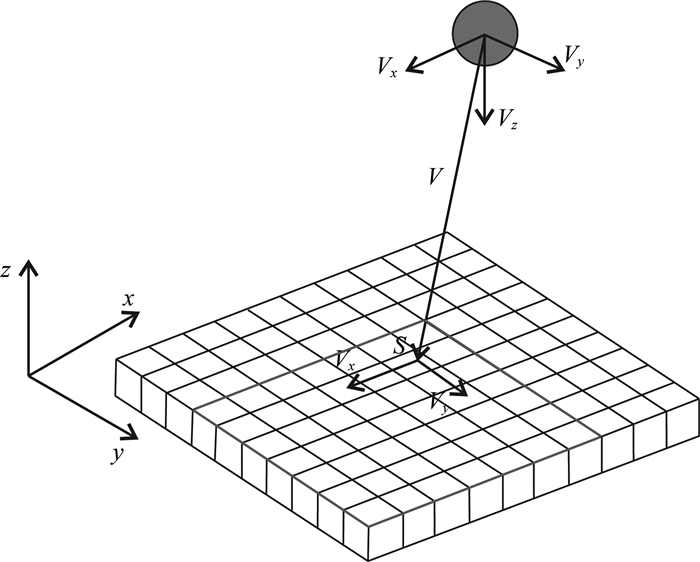
1.2 接触判断方法该算法的关键在于如何快速地判断颗粒运动过程中的接触对象.为避免冗余计算量, 采用网格化的方法将沉积区域划分为若干个小区域, 如图 2所示, 该区域被划分为一个规则的立方体网格系统, 设区域边界的长、宽、高分别为Lx、Ly、Lz, 矿物颗粒的半径最大值为rmax. z方向的网格的划分不宜太密也不宜太稀疏, 太密会导致单个颗粒同时存在于多个网格之中, 会影响接触判断方法的算法效率和稳定性, 太稀疏会导致同一个网格之内颗粒太多, 判断对象增加, 根据经验, z方向的网格大小Gz=2rmax比较合适.在x和y方向网格的大小为
|
图 2 搜寻接触颗粒示意图(方锡武等, 2011) Fig. 2 The diagram of searching contact particles (Fang et al., 2011) |
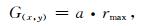
|
(3) |
其中, a的取值范围为2~6比较合适(方锡武等,2011).单个网格的大小确定后, 沿x、y、z方向的网格个数为
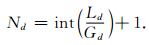
|
(4) |
这里, int表示取整.网格的规模为Nx×Ny×Nz.
网格系统记录了每个网格内所包含的矿物颗粒, 并且矿物颗粒沉积完成后同时要更新网格系统.由于在z方向的网格的高不小于最大颗粒半径值的两倍, 所以一个颗粒最多同时存在两层网格之中, 故颗粒在沉积过程的接触检测的具体算法流程为:(1)确定所有已沉积颗粒所在的最高层位置, 记为Fmax; (2)判断Fmax层的颗粒与之接触情况, 记录产生接触所需最小移动距离对应的颗粒编号T1和移动距离d1, 无接触颗粒则直接转入步骤3;(3)判断在Fmax-1层颗粒与之接触情况, 记录产生接触所需最小移动距离对应的颗粒编号T2和移动距离d2; (4)判断与边界的接触情况, 并记下移动距离d3及对应的接触边界对象B; (5)比较移动距离d1、d2和d3, 记录移动距离最小所对应的颗粒或边界, 计算颗粒Q新位置坐标, 按照公式(1)—(2)计算新的运动方向; (6)根据Q的新位置计算Q所在的层为Fnew, 令Fmax=Fnew, 重复步骤1~5直到Q达到稳定状态; (7)更新已沉积颗粒和网格系统信息, 开始新颗粒的沉积过程.为进一步地提升计算效率, 检查某一层可能接触的颗粒时, 可以将Q的运动方向考虑进来, 没有必要与该层所有的颗粒作接触判断, 设Q的运动方向为V=(Vx, Vy, Vz), 已沉积颗粒的最高层为第k层, 如图 3所示, 当Q沿着V方向运动时必然会落入第k层的点S处, 其所在网格可记为(6, 4, k), 根据上述网格的划分规则, 可知颗粒顶多同时存在于4个网格之中, 因此我们按照V沿x轴和y轴的分量Vx和Vy, 将搜寻的范围沿其反方向分别加1.按图中所示, 在该层, 我们只需搜寻位于网格(7, 3, k)与(1, 10, k)之内的颗粒, 其中沿x轴方向的步长为-1, y方向为+1, 一旦找到接触对象,便转入下一层继续搜索,最后计算最小移动距离所对应的接触对象及新的位置信息.
|
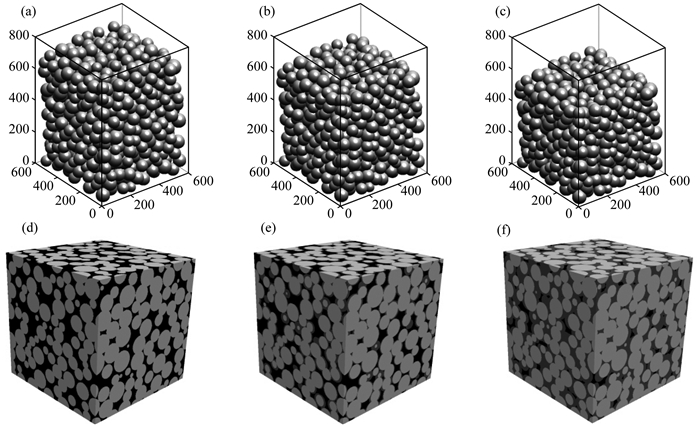
图 3 矿物成岩过程 (a)—(c)分别代表λ为0.1、0.2、0.3时的压实结果, (d)—(f)分别为未胶结、中等胶结、重度胶结的结果. Fig. 3 Diagenesis results (a)—(c) represent the results under different compaction conditions: λ is 0.1, 0.2, 0.3 respectively; (d)—(f) represent results under different cementation conditions: uncemented, moderate cemented, severe cemented respectively. |
成岩过程的数值模拟有四种方法:(1)由沉积特征沿深度的变化趋势得到的经验关系式;(2)地球化学建模;(3)基于矿物、胶结物、化学反应率、热演化和埋藏史的定量数学建模;(4)数字岩心孔隙空间变化的几何建模(Kameda, 2005).本文采取方法(4)来模拟矿物成岩过程.该方法考虑几何结构改变,没有涉及地球化学过程.压实是指岩石在上覆压力作用下不断变得致密的过程,通过在已沉积岩石的顶部施加沿重力方向的压力实现.定义岩石压实因子为λ, 压实后, 颗粒的新纵坐标为
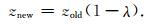
|
(5) |
岩石自生加大过程可以采用均匀增长法模拟.定义胶结因子为μ, 其取值范围为0到1.对于球形颗粒, 可以直接将颗粒的半径放大(1+μ)来实现.除此之外, 还可以通过图像处理中的膨胀算法来实现.如图 3所示, (a)—(c)是压实因子分别为0.1、0.2、0.3时的沉积情况.将压实因子设置为0.15, 分辨率为1.7 μm/voxel, 图 3中(d)—(f)分别代表未胶结、中等程度及重度胶结的结果.其孔隙度分别为33.19%、17.16%、6.13%.随着成岩程度的提高, 孔隙空间逐渐被胶结物占据, 特别是大部分喉道首先会完全被胶结物所替代, 导致岩石变得致密, 孔渗条件变差.
1.4 不规则颗粒处理在实际沉积岩石中, 矿物多呈不规则形状, 为了更加接近真实的沉积结果, 采用Pilotti(1998)提出的非规则颗粒处理方法.如图 4左部分所示, 该球形颗粒被一个椭球形颗粒包围, 椭球形颗粒的中心与球形颗粒一样, 其三个半轴长在预设范围内随机取值, 但最小值要不小于对应球形颗粒的半径, 并且椭球形颗粒的倾斜方向也随机取值确定, 然后在球形颗粒表面随机取N个点, 分别得到过这N个点的球形颗粒的N个正切平面, 设位于N个正切平面组成的非规则区域内的体素点集为A, 位于椭球形颗粒内的体素点集为B, 保留体素点集C=A∩B的所有点, 即为最终的非球形颗粒, 图中深灰色区域.为了验证该方法的可行性, 本文首先对单个球形颗粒进行不规则化处理, 结果如图 4右部分所示, 随机选取球形颗粒对应的15个正切平面, 处理后该颗粒变为一个非球形多面体.
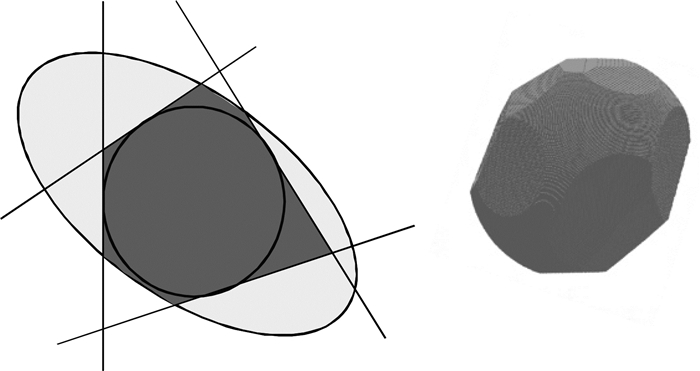
|
图 4 颗粒非球形化处理示意图 Fig. 4 The diagram of particle non-spherical algorithm |
本文将该算法用来处理初始沉积完成后的数字岩心数据体.考察不同正切平面数下的处理结果, 其沉积规模为600 μm×600 μm×800 μm, 沉积颗粒的半径上限值40 μm, 下限为20 μm, 均值30 μm, 方差为0.1, 压实因子为0.1, 如图 5所示,(a)—(c)对应正切平面数分别为5、10、15处理后的岩心,其孔隙度分别为11.36%、13.94%、14.93%.未进行非规则化处理时孔隙度为24.64%, 处理后孔隙度会减小, 随着正切平面数的增加, 不规则颗粒棱角变得不再明显, 逐渐接近球形颗粒.并且孔隙度会随着正切平面个数的增加而逐渐增加, 最终接近或达到球形颗粒的孔隙度, 其变化规律如图 6所示.

|
图 5 不同正切平面数的非球形化处理的数字岩心 Fig. 5 The digital rocks under non-spherical processing with different tangent planes |
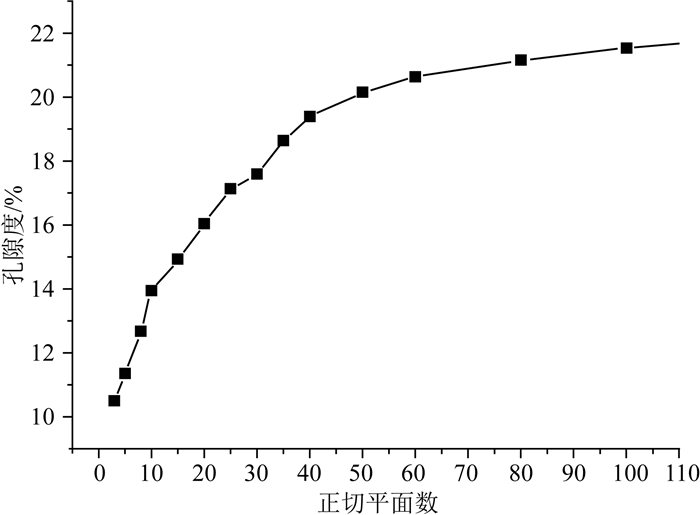
|
图 6 孔隙度与正切平面相关性 Fig. 6 The correlation between porosity and tangent planes |
为了评价建模方法的准确性, 采用英国帝国理工学院提供的人工砂岩(Sand Pack F42C)Micro-CT图像作为原始对比模型(Dong, 2007), 其网格大小为300×300×300, 分辨率为10 μm.取其中一张扫描切片作为矿物沉积初始信息, 即从该二维切片中提取矿物颗粒的粒径分布信息, 采取分水岭图像分割算法将矿物颗粒识别并提取出来, 采取等效半径方法计算粒径分布(Rabbani et al., 2014), 如图 7所示.图 7a是原始的二维切片, 图 7b是最终的矿物颗粒识别结果, 图 7c是统计得到的粒径分布, 平均粒径为149.8 μm, 对该粒径分布采取高斯函数拟合, 以该拟合结果作为初始粒径分布信息进行矿物沉积建模, 沉积范围为3500 μm×3500 μm×4200 μm.初始沉积结果如图 7d所示, 压实因子设置为0.02, 非规则化处理平面数为15, 处理后的孔隙度为32.3%, 与F42C的孔隙度33%十分接近.采用评价过程法数字岩心建模准确性常用的局部孔隙度函数及平均渗流概率函数(Biswal et al., 1999; Øren and Bakke, 2003; 赵秀才和姚军, 2007; 刘学锋等, 2009a, 2009b, 2013; 闫国亮等, 2013)来评价本文方法的准确性.
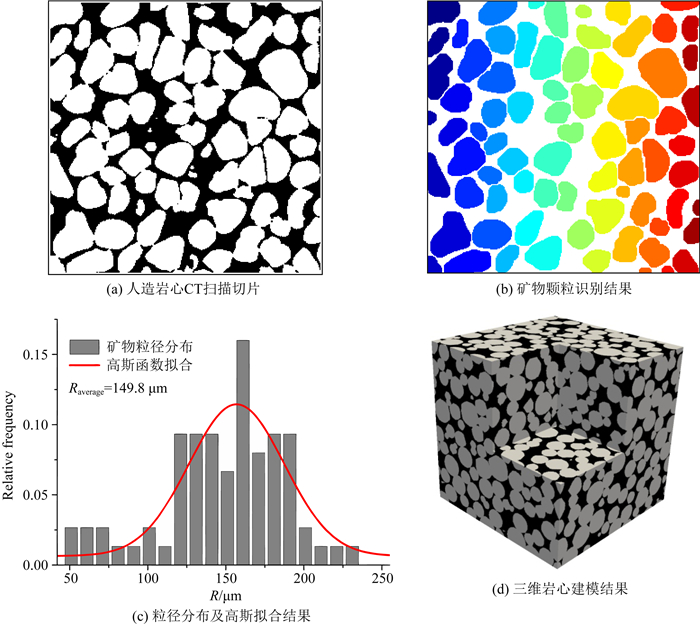
|
图 7 矿物颗粒粒径统计及高斯函数拟合结果 Fig. 7 The grain size distribution and Gauss function fitting results |
其中, 局部孔隙度函数用来表征岩心非均质性, 其基本思想是测量数字岩心数据体内足够多组边长为L的立方体单位所对应的孔隙度, 并统计分析孔隙度的分布情况, 其分布情况反映了岩心的非均质性, 一般当边长L固定时, 其孔隙度分布越集中表示均质性越好, 越分散均质性越差.局部孔隙度单元K(r, L)定义如下:
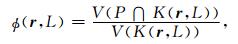
|
(6) |
局部孔隙度的分布函数为
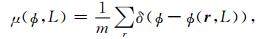
|
(7) |
其中m表示立方体边长为L时对应的测量单元体个数.
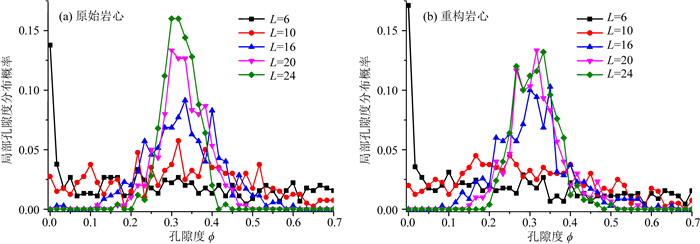
图 8分别为人工砂岩Micro-CT扫描和基于矿物沉积算法重构得到的三维数字岩心图像对应的局部孔隙度分布情况.可以看出, 当测量单元体的边长L较小时, 其对应的局部孔隙度分布较分散, 峰宽且不集中, 因为过小的测量单元体所表征的范围较小, 表现出较强的非均质性, 当边长L逐渐增加时, 其对应的孔隙度分布的峰变窄, 并且越来越接近原始尺寸的孔隙度, 表现出较好的均质性.通过对比局部孔隙度分布函数可知, 重构岩心与CT扫描岩心在相同边长L对应的测量单元体的局部孔隙度分布特征基本一致, 说明基于二维切片重构的三维数字岩心模型较好地重构出了原始岩心的非均质性信息.
|
图 8 局部孔隙度分布特征 Fig. 8 The characteristics of local porosity distributions |
局部渗流概率函数是指当测量单元体边长L一定时, 岩心在各个方向的渗透性或连通性情况, 反映了数字岩心渗流特性的各向异性.局部渗流概率函数定义如下:
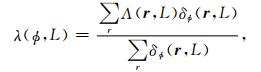
|
(8) |
其中, 当在测量方向上连通时, Λ(r, L)值为1, 否则为0.最终局部平均渗流概率分布的计算公式为
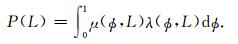
|
(9) |
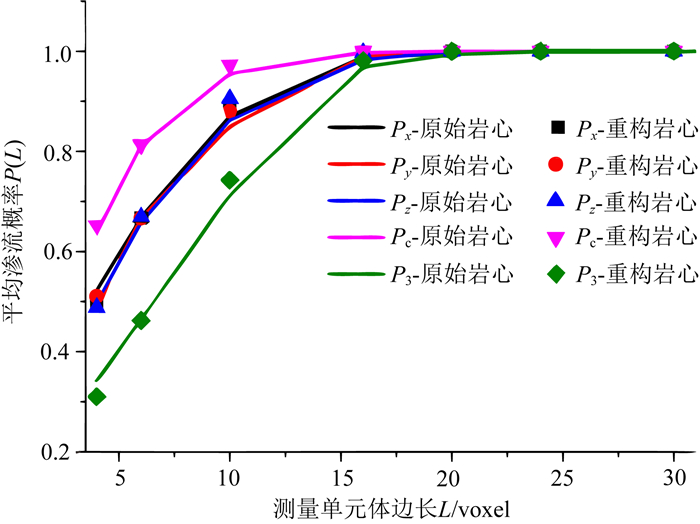
根据该方法, 分别计算了原始岩心及重构岩心的平均渗流概率分布, 如图 9所示, 其中, Px、Py、Pz分别表示x、y、z方向上具有渗透性, Pc表示至少在其中一个方向上具有渗透性, P3表示在三个方向上同时具有渗透性.
|
图 9 平均渗流概率分布特征 Fig. 9 The characteristics of average percolation probability |
可以看出, 人工砂岩在三个方向的渗透性基本一致, 表现出良好的各向同性.并且当测量单元体的边长到达15以上时, 其沿任意方向的平均渗流概率都接近于1, 表明该人工岩心连通性较好, 渗透性比较强.通过对比重构岩心的平均渗流概率分布, 重构岩心的渗流概率趋势基本与原始岩心一致, 较好地还原了岩心的渗流情况, 即其渗流方向特性与原始岩心基本一样, 且在L达到15时, 各方向的平均渗流概率达到1, 表明重构岩心与原始岩心具有基本相同的连通特性,较好地表征出原始岩心的渗流的方向特性.
3 建模实例分析 3.1 泥质砂岩泥质砂岩是指黏土颗粒和砂质颗粒分层或交替沉积的结果, 其主要结构类型分三种:分散泥质、结构泥质和层状泥质.其中, 分散泥质类似于上述粒间孔隙模型, 泥质以分散形式存在于孔隙之中, 结构泥质的泥质颗粒的作用与砂质颗粒的作用一样, 在重力作用下沉积并在岩石中起支撑作用, 层状泥质主要表现为砂泥岩互层沉积.针对层状泥质模型, 采用分层沉积模式, 即先设定每一层沉积颗粒的类型及沉积边界的范围, 然后采取基于矿物沉积的方法进行模拟.设定砂岩颗粒的半径为65 μm, 泥质颗粒的半径为25 μm, 沉积结果如图 10所示.

|
图 10 泥质砂岩数字岩石模型 (a)层状泥质;(b)结构泥质;(c)分散泥质. Fig. 10 The digital rock model of shaly sandstone (a) Laminated shale; (b) Structural shale; (c) Dispersed shale. |
图 10a中, 中间部分为砂岩层, 上、下部分为泥岩层, 该模型的总孔隙度为19.9%, 砂岩部分孔隙度为21.1%, 泥质部分的孔隙度为18.79%.针对结构泥质模型, 采取泥质颗粒和石英颗粒交替沉积, 设定矿物成分为泥质和石英颗粒, 其中泥质颗粒的半径为25 μm, 石英颗粒的粒径为80 μm, 初始沉积结果如图 10b, 其孔隙度为13.5%,泥质含量为13.6%.分散泥质的泥质分布在砂岩颗粒的表面,类似于胶结物,其体积占据粒间孔隙空间部分,因此,分散泥质的建模思路可借鉴胶结物充填的数值模拟方法,其沿原始矿物颗粒表面产生并增长占据孔隙部分, 如图 10c,为砂岩颗粒初始沉积完成后,泥质充填粒间孔隙, 附着在砂岩颗粒表面形成分散泥质的结果,压实因子取0.1,泥质充填前,其孔隙度为26%, 分散泥质形成后孔隙度为10.4%,泥质含量为15.6%.
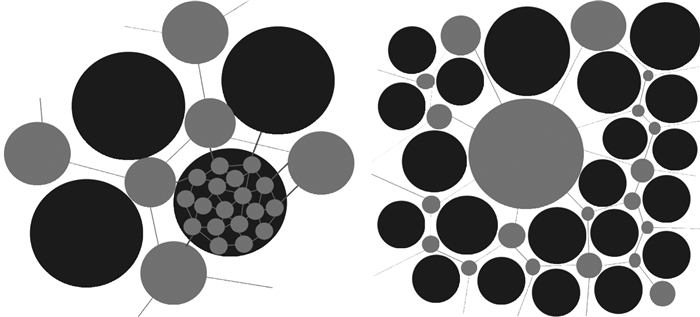
3.2 碳酸盐岩溶蚀孔洞或裂缝是碳酸盐岩储层的典型特征.针对粒内溶孔建模,由于基于矿物沉积的地层模型的颗粒的位置、粒径信息均已知, 可以指定或随机选取大粒径颗粒为待溶蚀孔隙区域, 提取其边界信息, 然后将已沉积的小颗粒微孔隙模型从其原始的沉积区域内提取出来, 根据大粒径颗粒的边界信息调整微孔隙颗粒的位置信息, 嵌入到相应的大颗粒位置中, 如果小颗粒位于大颗粒所在边界内, 则保留该颗粒, 更新沉积信息, 否则舍弃该颗粒.针对粒间填充孔隙, 原理类似, 将部分粒间孔隙空间用微小颗粒沉积模型替换, 得到粒间填充孔隙结构,针对较大的粒间溶孔,先通过矿物沉积模型建立起初始的不含孔洞的沉积地层模型, 然后随机选取若干孔隙空间作为待溶蚀区域产生溶蚀作用形成孔洞(Mehmani, 2015).图 11分别是粒内溶孔及粒间溶孔算法示意图, 其中深灰色代表大颗粒, 浅灰色代表孔隙空间.左图中,一个大颗粒发生溶蚀, 将相应的小颗粒孔隙模型尺度变换后替换原始大颗粒, 得到粒内溶蚀微孔隙空间.右部分是粒间溶孔算法示意图, 中间部分发生溶蚀或交代作用产生如图右所示的孔洞.
|
图 11 粒内溶孔及粒间溶蚀孔洞建模示意图 Fig. 11 The diagram of intragranular dissolved pore and intergranular pore network |
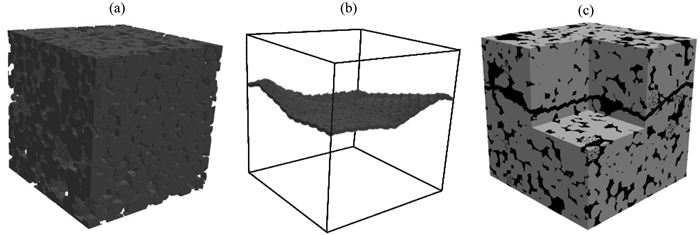
裂缝具有统计自仿射分形特征(孙洪泉和谢和平, 2008; Zhao et al., 2013),利用自仿射分形插值方法对裂缝进行数值模拟.基于该方法, 建立了含粒间溶孔、溶蚀孔洞及裂缝的碳酸盐岩数字岩石模型, 其中未溶蚀前的数字岩石的参数设置为:颗粒半径为双峰分布,半径下限为40 μm,上限为110 μm,峰值粒径分别位于55 μm和100 μm处,共沉积产生4767个颗粒.压实因子设置为0.12,分辨率为4.5 μm/voxel, 取其中300×300×300数据体, 溶蚀产生前,其孔隙度为11.3%, 当其中部分大颗粒发生溶蚀形成粒内溶孔,部分区域发生溶蚀形成粒间孔洞后,沉积结果如图 12a所示,其孔隙度为18.5%, 利用自仿射分形插值方法形成如图 12b所示裂缝,其张开度为7voxel,最终的碳酸盐岩模型如图 12c所示,孔隙度为20.8%, 其中裂缝孔隙度为2.3%.
|
图 12 碳酸盐岩数字岩石模型 Fig. 12 Digital rock model of carbonate rock |
页岩成分复杂,包括黏土矿物、黄铁矿、有机质、孔隙等部分.本文考虑有机质、黏土矿物及黄铁矿并存的数字岩石模型.页岩中有机质的赋存类型包括:(1)原生有机质或干酪根;(2)孔隙充填次生有机质;(3)充填黏土颗粒或矿物间无定型次生有机质;(4)黄铁矿晶间充填次生有机质;(5)与矿物伴生次生有机质等几类.根据其赋存形态,本文提炼出两类基于模拟沉积过程的页岩数字岩石物理模型建模方案,如图 13所示,分别是原生有机质和孔隙充填次生有机质的FIB-SEM图像及其数值建模方案,图中左下代表了原生有机质与固体骨架、黄铁矿共生的建模方案,右下代表粒间充填有机质与无机孔、固体骨架共生的建模方案,深灰色代表固体骨架,黑色代表有机质,深蓝色代表有机孔,绿色代表无机孔,黄色代表黄铁矿.

|
图 13 页岩有机质分布特征及建模方法 Fig. 13 The organic matter distribution characteristics and the modeling method of shale |
以原生有机质为例,建立如图 14所示页岩多矿物数字岩石物理模型,图中左部分为矿物颗粒三维分布,其中蓝色代表骨架, 棕色代表黄铁矿, 黑色部分代表有机质,右部分是其离散化的结果,深灰色为骨架,黑色部分为孔隙, 体积含量为8.6%,白色为有机质,体积含量为13.4%,浅灰色为黄铁矿,体积含量为1.2%.

|
图 14 页岩多矿物数字岩石模型 Fig. 14 The digital rock model of shale |
(1) 提出矿物沉积算法建立三维数字岩石模型.相比过程法和离散元法, 将沉积区域进行网格化划分, 沉积颗粒在重力作用下运动, 依据其速度方向, 只需检测若干网格层内的若干已沉积颗粒与正在沉积颗粒的接触情况即可计算得到其新的沉积位置信息, 有效地提高了微米尺度数字岩石建模效率.
(2) 对初始沉积模型进行了矿物成岩及颗粒非规则化处理.随着成岩程度的提高, 孔隙空间逐渐被胶结物占据, 导致岩石变得致密, 孔渗条件变差.并且测试发现随着处理算法中的正切平面数的提高, 其孔隙度逐渐增加, 并最终会接近球形颗粒对应的孔隙度.
(3) 采取分水岭算法提取Micro-CT扫描得到的二维切片中矿物粒径分布信息, 将其作为初始条件进行三维岩石建模.结果表明:重构三维岩石模型能够准确地表征出原始岩石的非均质性及渗流方向特性.
(4) 针对碳酸盐岩、泥质砂岩、页岩等多尺度、多矿物并存的地层类型, 利用双重孔隙介质建模思想, 建立了泥质砂岩、溶蚀孔洞、裂缝、有机质等与常规孔隙共存的地层模型, 对于多矿物和泥质含量及分布、孔隙结构等因素对岩石物理的影响提供了数值模型及理论基础.
Arns C H, Sheppard A P, Sok R M, et al. 2007. NMR petrophysical predictions on digitized core images. Petrophysics, 48(3): 202-221. |
Biswal B, Manwart C, Hilfer R, et al. 1999. Quantitative analysis of experimental and synthetic microstructures for sedimentary rock. Physica A: Statistical Mechanics and Its Applications, 273(3-4): 452-475. DOI:10.1016/S0378-4371(99)00248-4 |
Chi L, Heidari Z. 2015. Diffusional coupling between microfractures and pore structure and its impact on nuclear magnetic resonance measurements in multiple-porosity systems. Geophysics, 80(1): D31-D42. DOI:10.1190/geo2013-0467.1 |
Dong H. 2007. Micro-CT Imaging and pore network extraction [Ph. D. thesis]. London: Imperial College.
|
Fang X W, Liu Z Y, Tan J R. 2011. An algorithm for particle packing in 3D space by considering geometric and physical factors. Journal of Computer-Aided Design & Computer Graphics (in Chinese), 23(7): 1253-1262. |
Guo J F, Xie R H, Zou Y L. 2016. Simulation of NMR responses in sandstone and restricted diffusion. Chinese Journal of Geophysics (in Chinese), 59(7): 2703-2712. DOI:10.6038/cjg20160733 |
Hazlett R D. 1997. Statistical characterization and stochastic modeling of pore networks in relation to fluid flow. Mathematical Geology, 29(6): 801-822. DOI:10.1007/BF02768903 |
Jiang Z, Chen W, Burkhart C. 2013. Efficient 3D porous microstructure reconstruction via Gaussian random field and hybrid optimization. Journal of Microscopy, 252(2): 135-148. DOI:10.1111/jmi.2013.252.issue-2 |
Jin G D, Patzek T W, Silin D B. 2003. Physics-based reconstruction of sedimentary rocks. //73rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Kameda A. 2005. Permeability evolution in sandstone: digital rock approach [Ph. D. thesis]. Stanford: Stanford University. https://www.researchgate.net/publication/35166143_Permeability_evolution_in_sandstone_digital_rock_approach?ev=auth_pub
|
Liu X F, Sun J M, Wang H T. 2009a. Reconstruction of 3-D digital cores using a hybrid method. Applied Geophysics (in Chinese), 6(2): 105-112. DOI:10.1007/s11770-009-0017-y |
Liu X F, Sun J M, Wang H T, et al. 2009b. The accuracy evaluation on 3D digital cores reconstructed by sequence indicator simulation. Acta Petrolei Sinica (in Chinese), 30(3): 391-395. |
Liu X F, Zhang W W, Sun J M. 2013. Methods of constructing 3-D digital cores: a review. Progress in Geophysics (in Chinese), 28(6): 3066-3072. DOI:10.6038/pg20130630 |
Mehmani A. 2015. Investigation of the petrophysical properties of unconventional rocks using multiscale network modeling [Ph. D. thesis]. Austin: The University of Texas at Austin.
|
Mo X W, Zhang Q, Lu J A. 2016. A complement optimization scheme to establish the digital core model based on the simulated annealing method. Chinese Journal of Geophysics (in Chinese), 59(5): 1831-1838. DOI:10.6038/cjg20160526 |
Nie X, Zou C C, Meng X H, et al. 2016. 3D digital core modeling of shale gas reservoir rocks: A case study of conductivity model. Natural Gas Geoscience (in Chinese), 27(4): 706-715. |
Okabe H, Blunt M J. 2004. Prediction of permeability for porous media reconstructed using multiple-point statistics. Physical Review E, 70(6): 066135. DOI:10.1103/PhysRevE.70.066135 |
Øren P E, Bakke S. 2002. Process based reconstruction of sandstones and prediction of transport properties. Transport in Porous Media, 46(2-3): 311-343. |
Øren P E, Bakke S. 2003. Reconstruction of Berea sandstone and pore-scale modelling of wettability effects. Journal of Petroleum Science and Engineering, 39(3-4): 177-199. DOI:10.1016/S0920-4105(03)00062-7 |
Pilotti M. 1998. Generation of realistic porous media by grains sedimentation. Transport in Porous Media, 33(3): 257-278. DOI:10.1023/A:1006598029153 |
Rabbani A, Jamshidi S, Salehi S. 2014. An automated simple algorithm for realistic pore network extraction from micro-tomography images. Journal of Petroleum Science and Engineering, 123: 164-171. DOI:10.1016/j.petrol.2014.08.020 |
Schwartz L M, Johnson D L, Mitchell J, et al. 2013. Modeling two-dimensional magnetic resonance measurements in coupled pore systems. Physical Review E, 88(3): 032813. DOI:10.1103/PhysRevE.88.032813 |
Sun H Q, Xie H P. 2008. Fractal simulation of rock fracture surface. Rock and Soil Mechanics (in Chinese), 29(2): 347-352. |
Torskaya T, Shabro V, Torres-Verdín C, et al. 2014. Grain shape effects on permeability, formation factor, and capillary pressure from pore-scale modeling. Transport in Porous Media, 102(1): 71-90. DOI:10.1007/s11242-013-0262-7 |
Wang C C. 2013. Construction theory and method of dual pore network model in carbonate media [Ph. D. thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Wang Y, Yue W Z, Zhang M. 2016. Numerical research on the anisotropic transport of thermal neutron in heterogeneous porous media with micron X-ray computed tomography. Scientific Reports, 6: 27488. DOI:10.1038/srep27488 |
Wu K, Nunan N, Crawford J W, et al. 2004. An efficient Markov chain model for the simulation of heterogeneous soil structure. Soil Science Society of America Journal, 68(2): 346-351. DOI:10.2136/sssaj2004.3460 |
Xiong Q R, Baychev T G, Jivkov A P. 2016. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. Journal of Contaminant Hydrology, 192: 101-117. DOI:10.1016/j.jconhyd.2016.07.002 |
Yan G L, Sun J M, Liu X F, et al. 2013. Accuracy evaluation on 3D digital cores reconstruction by process-based method. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 35(2): 71-76. |
Yue W Z, Tao G. 2013. A new non-Archie model for pore structure: numerical experiments using digital rock models. Geophysical Journal International, 195(1): 282-291. DOI:10.1093/gji/ggt231 |
Zhang T F. 2015. MPS-driven digital rock modeling and upscaling. Mathematical Geosciences, 47(8): 937-954. DOI:10.1007/s11004-015-9582-1 |
Zhang Y, Toksöz M N. 2012. Impact of the cracks lost in the imaging process on computing linear elastic properties from 3D microtomographic images of Berea sandstone. Geophysics, 77(2): R95-R104. DOI:10.1190/geo2011-0126.1 |
Zhao J P, Sun J M, Liu X F, et al. 2013. Numerical simulation of the electrical properties of fractured rock based on digital rock technology. Journal of Geophysics and Engineering, 10(5): 055009. DOI:10.1088/1742-2132/10/5/055009 |
Zhao X C, Yao J. 2007. Construction of digital core and evaluation of its quality. Journal of Xi′an Shiyou University (Natural Science Edition) (in Chinese), 22(2): 16-20. |
Zhu W, Yu W H, Chen Y. 2012. Digital core modeling from irregular grains. Journal of Applied Geophysics, 85: 37-42. DOI:10.1016/j.jappgeo.2012.06.013 |
方锡武, 刘振宇, 谭建荣. 2011. 几何与物理相结合的三维域颗粒堆积算法. 计算机辅助设计与图形学学报, 23(7): 1254-1262. |
郭江峰, 谢然红, 邹友龙. 2016. 砂岩核磁共振响应模拟及受限扩散. 地球物理学报, 59(7): 2703-2712. DOI:10.6038/cjg20160733 |
刘学锋, 孙建孟, 王海涛. 2009a. 利用混合法构建三维数字岩心(英文). 应用地球物理, 6(2): 105-112. |
刘学锋, 孙建孟, 王海涛, 等. 2009b. 顺序指示模拟重建三维数字岩心的准确性评价. 石油学报, 30(3): 391-395. |
刘学锋, 张伟伟, 孙建孟. 2013. 三维数字岩心建模方法综述. 地球物理学进展, 28(6): 3066-3072. DOI:10.6038/pg20130630 |
莫修文, 张强, 陆敬安. 2016. 模拟退火法建立数字岩心的一种补充优化方案. 地球物理学报, 59(5): 1831-1838. DOI:10.6038/cjg20160526 |
聂昕, 邹长春, 孟小红, 等. 2016. 页岩气储层岩石三维数字岩心建模——以导电性模型为例. 天然气地球科学, 27(4): 706-715. |
孙洪泉, 谢和平. 2008. 岩石断裂表面的分形模拟. 岩土力学, 29(2): 347-352. DOI:10.3969/j.issn.1000-7598.2008.02.011 |
王晨晨. 2013.碳酸盐岩介质双孔隙网络模型构建理论与方法[博士论文].青岛: 中国石油大学(华东). http://cdmd.cnki.com.cn/Article/CDMD-10425-1015024297.htm
|
闫国亮, 孙建孟, 刘学锋, 等. 2013. 过程模拟法重建三维数字岩芯的准确性评价. 西南石油大学学报(自然科学版), 35(2): 71-76. DOI:10.3863/j.issn.1674-5086.2013.02.010 |
赵秀才, 姚军. 2007. 数字岩心建模及其准确性评价. 西安石油大学学报(自然科学版), 22(2): 16-20. DOI:10.3969/j.issn.1673-064X.2007.02.004 |
 2019, Vol. 62
2019, Vol. 62


