2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
背景太阳风对于地球附近的空间环境有着重要的影响.一方面,背景太阳风中的流相互作用区(Stream Interaction Region, SIR)可以产生中小强度的地磁暴.这些地磁暴的强度虽然不及日冕物质抛射(Coronal Mass Ejection,CME)引发的地磁暴,但因其持续时间长,对高层大气的加热效果更显著,会引起神舟飞船、天宫空间站等近地轨道飞行器更明显的轨道衰减(Chen et al., 2014).另一方面,背景太阳风是CME爆发后向行星际空间传播的媒介,CME在传播过程中会因其与背景太阳风的速度差而产生加速、减速、偏转等现象(Zhou and Feng, 2013, 2017).Owens等(2017)近期的研究表明,CME在行星际演化的过程中不能视作结构不变的一个整体.CME除了会被背景太阳风加速、减速、偏转外,其本身的结构和形状也会在与背景太阳风相互作用的过程中发生改变.因此,对于CME能否到达地球、何时到达地球的预报,精确的背景太阳风结构所起到的作用,可能比之前人们认识的更加重要.
三维磁流体力学(Magnetohydrodynamics, MHD)太阳风模型是背景太阳风研究和预报的重要工具.它弥补了卫星局地数据观测的不足,可以获得大尺度背景太阳风和行星际磁场的物理参数在整个行星际空间的分布,也为空间天气预报由经验预报向数值预报发展提供了不可或缺的工具(冯学尚等, 2011, 2013; Wu and Dryer, 2015).以往的三维MHD太阳风模型假设太阳风结构在一个卡灵顿周(Carrington Rotation,CR)之内不发生明显的变化,用不随时间变化的观测输入生成定态背景太阳风(Feng et al., 2010).然而,即便在太阳活动极小期,太阳风结构在一个卡灵顿周之内也会发生明显的变化.对CME到达地球时间的集合预报研究发现,由更新磁图产生的时变背景太阳风可能能够反映更接近真实的情况,从而能更精确地预报CME到达地球的时间(Cash et al., 2015).
近年来,数据驱动的时变三维MHD太阳风模型取得了较大发展.与以往的太阳风模型相比,这些模型在内边界上采用自洽的方法,将随时间变化的观测数据输入到模型中,驱动背景太阳风演化,获得随时间变化的行星际太阳风结构.按照内边界设置位置的不同,这些模型可以分为两类.第一类模型的内边界位于日冕底部,通过MHD模拟生成日冕和行星际的磁场与太阳风结构.由于这类模型的内边界处于亚磁声速区,根据特征理论,必须自洽的将计算区域内的信息和观测输入耦合起来,才能稳定的更新边界上的物理量(Wu and Wang, 1987).Yang等(2012)通过投影特征边界条件方法,引入质量通量限制等物理条件,使用每天更新的WSO(Wilcox Solar Observatory,威尔科特斯太阳天文台)光球径向磁场概图,模拟了2007年日冕磁场和太阳风结构的演化.与日冕遥感观测和行星际局地观测的对比表明,模拟结果较好地重现了冕洞的大小和分布、冕流带的位置和形状、快慢太阳风分布和磁场极性等特征.为了弥补以往光球磁场概图中部分数据不能及时更新的缺陷,Feng等(2012)使用光球通量传输模型生成了1996年9月4日至10月29日间的光球磁场瞬时分布序列,并应用与Yang等(2012)相同的边界处理方法,使用生成的光球磁场数据驱动日冕MHD模型,模拟了该段时间内的日冕磁场和太阳风结构.与SOHO/EIT、MLSO和LASCO等观测图像的对比表明模型结果正确的产生了冕流、冕洞等大尺度结构随时间的演化过程.同时,在活动区之上,模型还产生了较为明显的非势场结构.在这些工作的基础上,Feng等(2015)将时变模拟的区域由日冕扩展到了从1Rs到1AU的整个日地空间,使用6小时更新的GONG磁图和投影特征边界条件方法驱动模型,模拟了2008年7月1日至8月11日间的太阳风演化.模拟结果不但重现了日冕的大尺度结构,还较好地重现了地球附近的局地太阳风观测.
第二类模型的内边界位于日冕顶部、行星际空间底部,一般在21.5Rs~30Rs间.在这里,太阳风的加速过程已经基本完成,超磁声速的物理特性使得边界上的所有物理量都可以直接给定,无需考虑计算区域内的信息(Odstrcil, 2003).这类模型的内边界条件一般由经验关系给出(Odstrčil and Pizzo, 1999; Riley et al., 2001; Wu et al., 2007),应用最广的是PFSS-WSA经验模型(Arge et al., 2003; McGregor et al., 2011).在PFSS-WSA模型中,日冕的磁场结构由PFSS外推计算出来,并给出模型内边界的磁场强度分布.WSA模型根据PFSS模型计算出的日冕磁场,得到膨胀因子(fs)、冕洞边界最小角距(θb)等描述日冕磁场位形的参量,再利用fs、θb计算太阳风速度在内边界的分布.密度、温度一般根据经验关系,由速度推出.Linker等(2016)利用PFSS-WSA经验模型和MAS-H三维MHD太阳风模型,建立了经验驱动的时变行星际太阳风模型.他们以模拟时间段中ADAPT模式输出的首幅光球磁场概图生成定态太阳风,再将ADAPT模式输出的其他光球磁场概图按时序输入到模型中,驱动模型内边界演化,模拟了2003年9月27日至2004年9月27日的时变太阳风结构.Merkin等(2016)使用PFSS-WSA经验模型和LFM-helio三维MHD太阳风模型,模拟了2008年1月至2008年2月的时变行星际太阳风结构,并将模拟结果与多颗卫星的局地观测做了对比.
与第一类模型相比,由于第二类模型没有覆盖包含强磁场、低β等离子体的日冕底部,因此计算的时间步长更大,到达同样物理时间所需要的计算时间更短,计算过程也更稳定.在模拟日冕时,第一类模型需要引入适当的太阳风加热加速机制来产生快、慢太阳风的分布,而这个过程的确切物理机制至今没有定论(Fletcher et al., 2015).而第二类模型将这个过程“隐藏”在了经验关系中,只需通过调整参数的方式获得理想的太阳风分布结果.使用第一类模型,自洽的模拟背景太阳风从太阳表面到行星际空间的产生和演化过程,是背景太阳风模型发展的最终目标.但第二类模型的优势,使得它们有希望更早投入到空间天气业务预报中.有对比研究表明,在一些情况下,采用经验关系驱动的太阳风模型能够更好地重现卫星局地观测(Linker, 2011).
太阳风模型模拟结果的定量评估是模型发展过程中的一个关键问题.通过与真实观测数据进行对比,给出定量的统计学评估参量,我们就能对模型重现太阳风结构的能力做出客观的评估.模型的研究者可以通过这些参量了解模型的优势与不足,明确模型进一步改进的方向.在太阳风模型被应用到实际的空间天气业务预报中时,预报员可以根据这些定量参量掌握模型的误差水平,并在使用该模型的模拟结果进行预报时加以考虑修正(Spence et al., 2004).Lee等(2009)利用ACE卫星在日地第一拉格朗日点(以下简称L1点)的观测数据,评估了WSA/ENLIL模型和MAS/ENLIL模型在2003年1月至2006年1月间的模拟结果.Gressl等(2014)利用ACE卫星在L1点的观测数据,评估了不同日冕、行星际模型组合和不同磁图数据产生的2007年太阳风模拟结果.Jian等(2015)利用OMNI数据库的L1点卫星数据,评估了美国CCMC(Community Coordinate Modeling Center,学界协同建模中心)部署的多个太阳风模型在2007年的太阳风模拟结果.
本文使用Feng等(2011)发展的CESE+HLL三维MHD太阳风模型中的HLL部分,发展了一套太阳光球磁场数据驱动的时变行星际太阳风模型.这个模型可以归入上文介绍的第二类模型的范畴.我们使用这个模型模拟了2008年全年的行星际太阳风结构,对结果进行了分析和评估,明确了模型的改进方向.第1节对经验日冕模型和行星际MHD模型的实现做了介绍,并给出了时变太阳风模拟的日冕-行星际耦合方法.第2节展示了2008年时变行星际太阳风的模拟结果,并对太阳风结构的变化特征和日冕、行星际结构间的联系做了分析.第3节利用OMNI数据库在L1点的局地观测数据,对模拟结果中连续变化的太阳风参数和行星际磁场极性反转、流相互作用区等特征现象的模拟结果进行了统计分析和定量评估.第4节总结了本文工作,分析了模型进一步的改进方向.
1 模型介绍 1.1 经验日冕模型经验日冕模型以GONG台网提供的6小时更新一次的太阳光球磁场径向概图为输入,这种概图来源于GONG台网6个台站的磁图观测(Petrie et al., 2007).相比于每27.2753天生成一次的卡灵顿周概图,这种概图能够不断根据最新的观测数据更新光球径向磁场的全球分布,提供光球磁场随时间演化的信息.
经验日冕模型的磁场由PFSS模型给出.PFSS模型假设在源表面之内,日冕磁场处于能量最低的势场状态.在源表面之外,日冕磁场只有径向分量.目前的研究一般将源表面设置于2.5Rs处.根据太阳光球磁场径向概图,PFSS模型可以得出日冕中磁场的结构与强度.尽管PFSS模型基于的假设非常简单,但以往的研究表明它能比较准确地给出冕洞分布、电流片位形及行星际磁场极性等大尺度结构.相比于更加复杂的MHD模型,其计算量较小,因此广泛应用于空间物理的研究中(Mackay and Yeates, 2012).本文采用100×180×360的网格,来覆盖1.0Rs≤r≤23.0Rs, 0.0°≤θ≤180.0°, 0.0°≤≤360.0°的区域,进行PFSS外推.
Wang和Sheeley (1990)的研究发现,太阳风在日冕中的加速过程完成后,其速度的大小与日冕磁场磁流管的超径向膨胀程度呈反比.他们引入了膨胀因子fs来定量描述磁流管的超径向膨胀,并给出了太阳风径向速度vr和fs间的关系.在此基础上,Arge等(2003)发现,太阳风速度的大小也与磁力线在光球上距离冕洞边界的最小角距θb有关.使用fs和θb共同计算太阳风速度的分布,与实际观测相符得更好.太阳风速度vr与fs、θb间的关系被称作Wang-Sheely-Arge模型(简称WSA模型).经验日冕模型的太阳风速度由WSA模型给出,其一般形式为(McGregor et al., 2011)
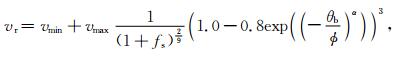
|
(1) |
fs和θb的物理意义和计算方法已有大量文献做了详尽的叙述(如Riley et al.(2015)及其中的参考文献).(1)式中的自由参数vmin,vmax,ϕ和α需要根据输入数据、模拟时期的不同进行调整,来得到与观测相符更好的太阳风分布.这里,它们的取值为vmin=240 km·s-1, vmax=560 km·s-1, ϕ=2.0, α=2.0.
1.2 行星际MHD模型为了模拟从太阳表面到行星际空间的定态太阳风结构,Feng等(2011)开发了CESE+HLL三维MHD太阳风模型.其中,靠近太阳表面的日冕部分由阴阳球形网格覆盖,使用解元-守恒元(CESE)格式求解理想MHD方程.远离太阳的部分由自适应直角坐标网格覆盖,使用二阶Harten-Lax-Leer(HLL)格式求解理想MHD方程.本文的行星际模型采用CESE+HLL模型中的HLL部分,覆盖空间范围为-250.0Rs≤x≤250.0Rs, -250.0Rs≤y≤250.0Rs, -250.0Rs≤z≤250.0Rs的三维空间.行星际模型求解日心共转坐标系中的理想MHD方程:
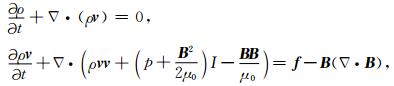
|
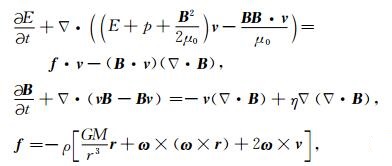
|
(2) |
其中ρ为密度,v为速度矢量,B为磁场矢量,E为等离子体能量,p为等离子体压强,r为日心距离,ω为太阳自转的角速度矢量,ω=ωez=ez2π/T, T=25.38 day.方程中各项的具体意义,模型的空间、时间差分方法和自适应网格实现等方面的内容,Feng等(2011)已经有详细的描述,这里不再重复.在HLL格式的基础上,Miyoshi和Kusano (2005)发展了MHD方程的HLLD格式.为了改进HLL格式黏性较大的问题,HLLD格式引入了更丰富的特征波结构,能够将黏性降低到与Roe格式可比的程度,但计算量较Roe格式要小很多.这里,我们使用HLLD格式替换了原模型中使用的HLL格式,以提升数值格式性能.
1.3 日冕行星际耦合
在本文的模拟中,行星际模型的内边界位于21.5Rs.在计算中,只通过MHD方程更新r>21.5Rs 
内边界上的径向速度由经验日冕模型的WSA模型,即(1)式给出.根据以往研究与我们的参数调整经验,内边界上质子的数密度由以下经验关系给出(Detman et al., 2006):
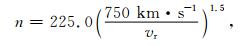
|
(3) |
式中n的单位为cm-3, vr的单位为km·s-1.边界上的温度由以下经验关系给出(Elliott et al., 2005):
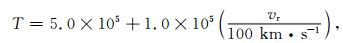
|
(4) |
式中T的单位为K,vr的单位为km·s-1.
在以往的三维MHD太阳风模拟中,绝大部分模型的模拟结果都存在行星际磁场强度被低估的现象(Jian et al., 2015).同时,尽管PFSS模型可以相对准确地给出行星际磁场的极性和电流片的位置,但其给出的行星际磁场强度存在偏弱的问题.因此,我们只利用PFSS模型在行星际模型内边界所得到的磁场极性信息,而将磁场强度重置为300 nT, 即
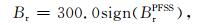
|
(5) |
式中Br的单位为nT,BrPFSS为该点由PFSS模型计算得到的径向磁场.
按照其他文献处理同样问题的一般方法(Odstrcil, 2003),我们假设惯性系中的太阳风切向速度为0,磁力线与速度方向平行,转换到模型所在的共转坐标系中后有
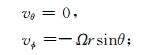
|
(6) |
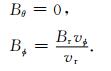
|
(7) |
通过以上的关系,对于每一幅输入的光球径向磁场概图,都可以通过经验日冕模型的计算和上文所述的经验关系,得到所有MHD变量在内边界上的值.
在进行时变模拟时,我们将不同时刻生成的磁场概图按照时序连续输入到经验日冕模型中,使边界上的各个物理量随时间变化,驱动行星际太阳风随时间演化.两幅磁场概图之间的时间间隔δt一般要比MHD数值格式的计算时间步长Δt大很多.在本文的模拟中,Δt的值一般为102s量级,而δt=6 h.对于每一个计算时间步,其内边界上的速度由前后两幅磁图生成的速度分布插值得到.假定两幅相继输入的磁场概图,对应时间分别为t1和t2,得到的速度分布分别为vr1和vr2,则时间t=nΔt(t1 < t < t2)时速度为
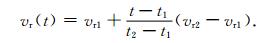
|
(8) |
当获得速度vr(t)后,可根据vr(t)的值和(3), (4)式计算边界上密度和温度在此时的值.
径向磁场Br(t)也以类似的方式得到,即
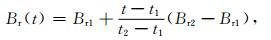
|
(9) |
其中,Br1和Br2以同样方式获得,即先由磁图和PFSS模型外推出日冕磁场,得到磁场极性信息,再由(5)式对磁场强度进行处理.通过(9)式在时间上的插值,可以获得径向磁场在t=nΔt(t1 < t < t2)时刻的值.如此,可以使径向磁场在两次输入之间平滑的变化.
在边界上,当径向磁场发生变化时,切向电场的变化必须满足方程
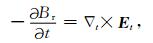
|
(10) |
才能保证在边界上不引入磁场散度误差(Yeh and Dryer, 1985).式中下标t表示在切向方向θ, ϕ上的分量.然而,单靠径向磁场Br随时间变化的信息并不能解出两个方向的切向电场.参考Yang等(2012)求解切向电场的方法,我们对切向电场Et做一Helmholtz分解
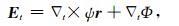
|
(11) |
其中,∇tΦ成分在代入方程(10)后因∇t×∇tΦ=0而消去,因此这部分电场信息与径向磁场变化无关,我们在此略去.即
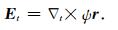
|
(12) |
将(12)式代入(10)式后,得到泊松方程
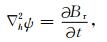
|
(13) |
求解后,可以得到切向电场
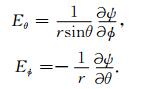
|
(14) |
按照切向电场定义,有
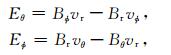
|
(15) |
由于(7)式是按照速度与磁力线平行确定的,如果按照该式给出的切向磁场计算,E=-(v×B)=0.但在模拟时变问题时,由(14)式可知Eθ≠0,Eϕ≠0.因此,需要对(6)、(7)式做修正

|
(16) |

|
(17) |
参考Merkin等(2016)的处理方法,令δvθ=0, δvϕ=0,可根据(15)、(16)式共同解得
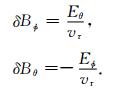
|
(18) |
我们选取了2008年作为模拟计算的时间段.在2008年,第23太阳活动周的下降期结束、极小期开始,全年的太阳活动比较平静.ACE卫星的数据分析显示(http://www-ssc.igpp.ucla.edu/~jlan/ACE/Level3/ICME_List_from_Lan_Jian.pdf),2008年全年间仅探测到了4个行星际日冕物质抛射(Interplanetary Coronal Mass Ejection,ICME)事件,其最大速度均小于500 km·s-1.因此,在2008年,日地L1点的等离子体和磁场观测数据受ICME的干扰较小,能够比较好地反映背景太阳风本身的变化趋势.在模拟过程中,我们首先采用第1节中(1)式和(3)—(7)式描述的经验关系,利用第一副磁图生成的内边界上的物理量分布,松弛200物理小时生成定态太阳风结果,将其作为时变太阳风模拟的初始条件.在松弛过程中,边界上物理量的值保持不变.之后,开始时变模拟.当模型演化到一幅磁图的观测时间t1后,读入观测时间为t2的下一幅磁图,使用1.3节中描述的进行时变模拟的方法计算更新内边界上的物理量,通过内边界的变化驱动模型计算区域内太阳风结构向t2时刻演化.通过以上过程不断读入新的磁图,即得到时变的行星际太阳风模拟结果.在计算中,计算网格依照Feng等(2011)中的判据进行动态加密、放粗,最小分辨率可达0.5Rs.
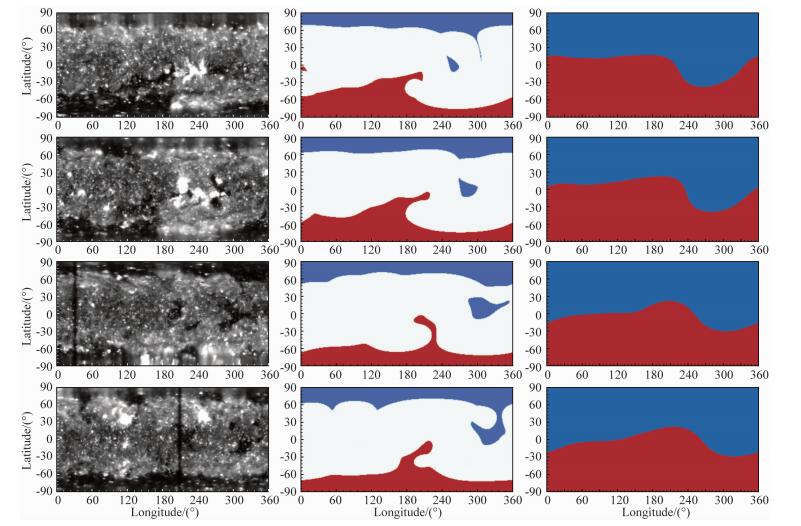
2.1 日冕结构图 1中,第一列给出了第CR2066、CR2069、CR2073、CR2076期间STEREO-A飞船EUVI仪器极紫外195Å波段的观测概图,这种概图可以反映该段时间内冕洞的分布.冕洞是日冕开放磁力线的足点区域,因其相对于同样高度的其他区域温度、密度较低而在极紫外观测中呈现较暗的颜色.第二列给出了由PFSS模型计算的冕洞结构,自上到下的计算时间分别为2008年的2月25日、5月25日、8月25日和11月25日.这四个日期均处于生成同一行的EUVI概图的卡灵顿周结束时间附近.图中的蓝色区域内径向磁场(Br)符号为负,红色区域内的Br符号为正.第三列给出了与第二列对应行时间的源表面的磁场极性结构,蓝色区域Br符号为负、红色区域Br符号为正.
|
图 1 2008年的日冕结构演化情况概图 第一列为STEREO-A飞船EUVI仪器的极紫外195 Å波段的卡灵顿周观测概图.第二列为时变模型计算的各卡灵顿周的冕洞分布,其中蓝色区域内Br < 0,红色区域内Br>0.第三列为源表面上的磁场极性,图中颜色含义与第二列相同.从上到下,EUVI概图的生成时间分别为2066、2069、2073、2076卡灵顿周,冕洞和源表面磁场结构的生成时间分别为2008年的2月25日、5月25日、8月25日和11月25日,与同一行中的EUVI概图生成时相对应. Fig. 1 Synoptic map of corona evolution for Year 2008 The first column are synoptic maps of 195 Å extreme ultraviolet observation made by EUVI instrument onboard STEREO-A spacecraft. The second column is the distribution of corona hole calculated by the model during each CR. The blue region represents corona hole whose Br < 0, while the red region represents corona hole whose Br>0. The third column is the magnetic polarity at the source surface. Color of the third column has the same mean as that of the second column. From top to bottom, the EUVI synoptic maps of the first column are generated for CR2066, CR2069, CR2073 and CR2076 respectively. Synoptic maps of the corona hole and source surface polarity are generated on Feb 25th, May 25th, Aug 25th and Nov 25th of Year 2008 respectively, which are in correspondence with the EUVI synoptic map at the same row. |
2008年所处的第23太阳周下降期和极小期的光球极区磁场强度要比21和22太阳周低.光球极区磁场强度较低时,不能提供足够的磁通量与低纬双极磁场结构连接形成闭合磁力线.因此,2008年中,极区冕洞向低纬的延伸和独立的低纬冕洞比较常见(Wang et al., 2009).在CR2066 EUVI观测的冕洞结构中,在经度0°~230°间,南极的极区冕洞向北延伸,在180°~230°间可达赤道附近.从PFSS计算的冕洞结构中可知,对应冕洞的Br>0.随着时间的变化,向低纬延伸的冕洞面积逐渐减小,使第三列中的0°~180°间的电流片逐渐向南移动.在CR2066的EUVI观测中,在经度260°附近存在一个独立的低纬冕洞,随着时间的变化这个冕洞逐渐向西移动.PFSS计算结果表明这个冕洞的Br < 0,使得电流片在经度240°至360°之间向南弯曲.当这个冕洞向西移动时,电流片向南弯曲最大的位置也随之西移.低纬冕洞的存在,使得连接相同极性冕洞的伪冕流变得更加常见,这些伪冕流使得低速流出现在了远离电流片的地方.同时,低纬冕洞也是黄道面附近快速太阳风的主要源区.
2.2 行星际太阳风结构图 2中给出了模型在r=22Rs处的太阳风结构概图,第一列为速度结构,第二列为密度结构,第三列为径向磁场结构.图 2中每行数据的生成时间与图 1中的相同.与图 1中的电流片结构对比可知,电流片附近被速度低、密度高的低速太阳风所包裹,形成了低速太阳风带.此外,在远离电流片的地方,也有低速太阳风结构.如2月25日概图中经度在240°至300°,纬度在20°至30°间的狭窄的低速太阳风结构.一般认为,这些结构与伪冕流相关.尽管伪冕流的足点连接的是相同极性的冕洞,不能形成电流片,但其足点也处在靠近冕洞边界的位置,磁流管θb的值较小,因此能够形成低速太阳风.纬度高于±60°的南极和北极地区被速度高、密度低的高速太阳风覆盖.同时,图 1中的低纬冕洞,在纬度0°的赤道附近形成了两个高速流区域.在2月25日的概图中,这两个低纬高速流区域分别位于经度80°到230°间和240°到300°间.在之后的几幅概图中,这两个低纬高速流依然存在,但位置和结构都发生了一些变化.由于(5)式对内边界磁场的设置,在22Rs处的磁场强度基本均匀,Br符号在电流片处反转.在电流片附近,存在一些Br强度稍弱的区域,如2月15日概图经度在0°至60°附近、Br < 0的区域,8月15日经度在120°至180°间、Br>0的区域.这些区域的出现是由于电流片的位置在两幅磁场概图生成的结果间发生了移动.同时,这些区域的面积不大,说明在两幅磁图间磁场结构没有发生较大的变化,磁图 6小时的时间分辨率能够比较好地描述大尺度背景太阳风结构的变化.
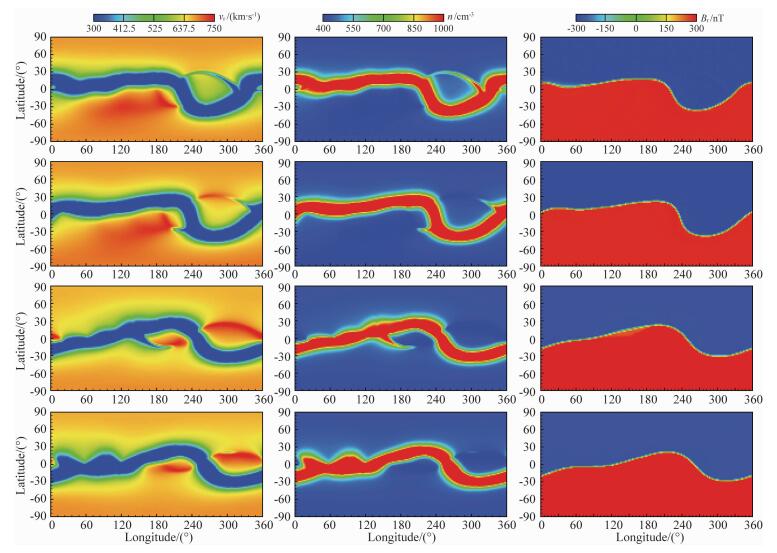
|
图 2 2008年r=22Rs处太阳风结构演化情况概图 第一列为速度结构,第二列为密度结构,第三列为径向磁场结构.第一行至第四行的时间分别为2008年的2月25日、5月25日、8月25日和11月25日. Fig. 2 Synoptic maps of solar wind structures at r=22Rs for Year 2008 The first column is velocity, the second column is density, and the third column is radial magnetic field. From the first to the forth row, the synoptic maps are generated on Feb 25th, May 25th, Aug 25th and Nov 25th of Year 2008 respectively. |
图 3中给出了与图 2相同四个时间的赤道面太阳风速度结构.由于太阳的自转,不同速度的太阳风流在子午面内形成了螺旋结构,与目前对行星际大尺度结构的结论相符.但与定态模拟结果不同的是,时变模拟结果中存在一些从内向外逐渐传播的结构.如2月25日赤道面图的右下方,一个新的快速流正在形成.在5月25日赤道面图内边界右侧,一个较小的太阳风流结构正在从内边界向外传播.在8月25日赤道面图的左上方,一个较大的快速流的结构处在变化之中.
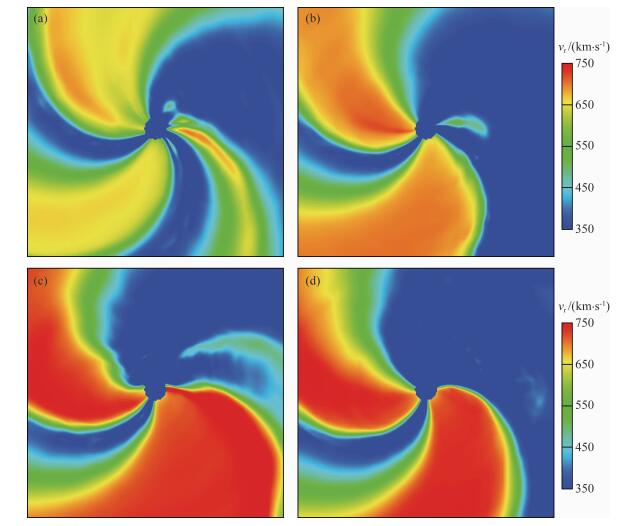
|
图 3 赤道面上的太阳风速度结构图 生成时间分别为2008年的(a)2月25日,(b)5月25日,(c)8月25日和(d)11月25日. Fig. 3 The solar wind velocity structure on the ecliptic plane The four subfigures are generated on (a) Feb 25th, (b) May 25th, (c) Aug 25th and (d) Nov 25th of Year 2008 respectively. |
图 4给出了模型在地球轨道r = 215Rs处的太阳风结构概图,时间和变量与图 2相同.通过行星际空间的演化,在高速流与低速流结构的交界面上出现了比较明显的压缩与稀疏结构.例如,在2月25日的概图中,经度240°附近的密度增强结构和经度190°附近的密度减小结构.它们形成于纬度0°、经度240°附近的高速流与各自西侧、东侧慢速流形成的压缩区与稀疏区.径向磁场结构呈现出与密度结构相似的变化,在稀疏区的强度有所降低.
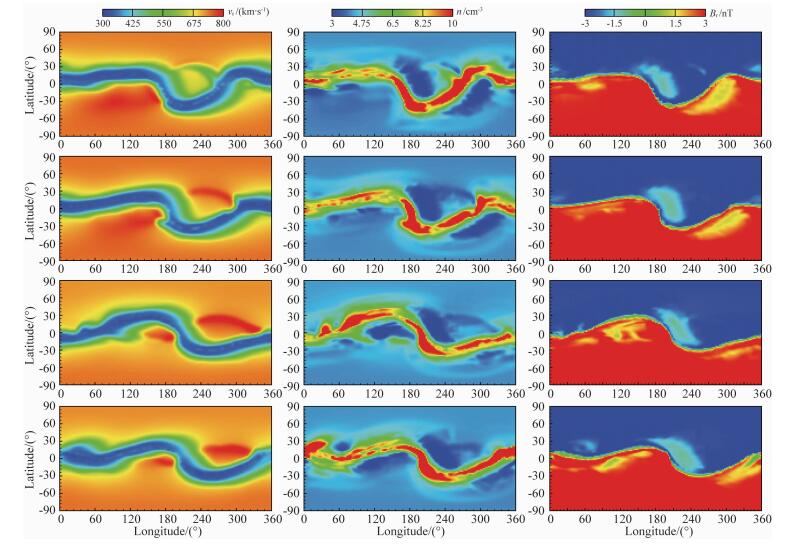
|
图 4 2008年r=215Rs处太阳风结构演化情况概图. 数据类型和生成时间与图 2相同 Fig. 4 Synoptic maps of solar wind structures at r=215Rs for Year 2008. The caption of Fig. 2 applies |
为了检验模拟结果的质量,我们对比了模型在日地L1点的模拟结果与OMNI数据库(https://omniweb.gsfc.nasa.gov/)中对应L1点局地观测的太阳风参数.太阳风的速度v、质子数密度n、磁场强度B和温度T是空间天气预报中所要给出的基本太阳风参数.因此,选取这四个连续变化的参数作为评估对象.行星际磁场极性的反转和SIR是具有明显空间天气效应的现象,因此我们对这两个现象的预报质量进行了评估.在模型计算过程中,通过GSE坐标向日心卡灵顿坐标的转换(Thompson, 2006),每隔1个物理小时计算一次L1点在模型中的位置,并通过插值得到此时该位置的太阳风参数,由此生成模型模拟结果在L1点的时间序列,与OMNI数据库中的1小时分辨率的相应数据做对比.由于目前模型中的物理机制只能反映大尺度的太阳风结构,在对比前使用高斯滤波对观测数据进行了平滑处理.
3.1 视觉对比图 5中给出了2008年v、n、B、T的模拟值和观测值的时间序列对比,其中蓝色线条为模拟结果,绿色散点为观测数据.图中用虚线分隔了这段时间内各卡灵顿周的时间范围,图上方标出了对应卡灵顿周的序号.在CR2065-CR2068的观测数据中,每个卡灵顿周中均存在两个比较明显的太阳风高速流结构,第一个高速流较窄,第二个高速流较宽,且高速流的速度在不同卡灵顿周之间变化不大.当高速流到达时,在n、B和T的结构中均有峰值与之对应,表明这两个高速流都形成了SIR结构.模拟结果较好地重现了这两个高速流.局地观测数据中的这两个高速流,来源于图 4中经度240°和经度140°附近的低纬高速流.由于L1点在CR2056-CR2068中处于赤道以南,而经度240°附近高低速流边界几乎与赤道平行,且延伸到了赤道以北,因此地球处在这个高速流区域中的时间较长,从而形成了局地数据中较宽的高速流结构.从CR2069开始,这两个高速流结构依然存在,但高速流的速度峰值在不同CR间变化较大.模拟结果依然能够重现出这些高速流,但速度峰值在CR2073-CR2077间偏高.
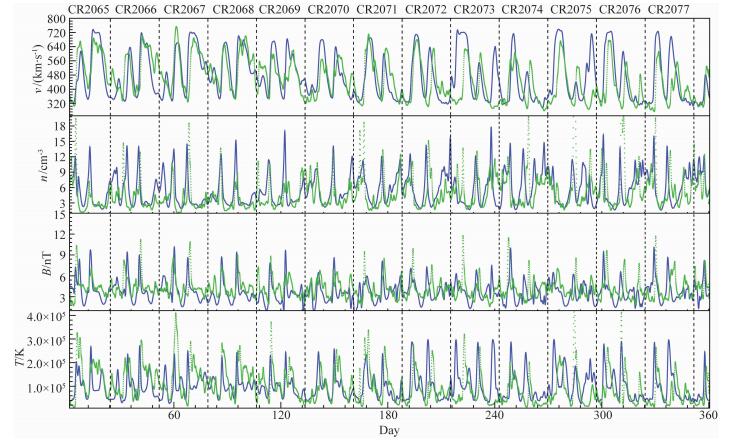
|
图 5 2008年L1点OMNI太阳风观测数据与模型模拟结果的对比图 绿色散点为OMNI观测数据,蓝色连线为模拟结果.黑色虚线为每个CR的开始和结束位置,图顶部给出了对应CR的编号. Fig. 5 Comparison between simulation results and OMNI in-situ measurements at L1 point for Year 2008 The blue lines represent the simulation results while the green scatters represent OMNI measurements. Each CR is separated by the black dashed line. The CR numbers are plotted at the top of the figure. |
密度、温度模拟结果的峰值和谷值与观测基本相符.除了磁场强度的谷值相比观测偏低外,磁场强度在大部分时间与观测符合得较好,不存在MHD太阳风模型中普遍存在的磁场强度被系统性低估的现象.在高速流到达时间存在偏差时,密度、温度、速度中的峰值会产生相同的偏差.
3.2 太阳风连续参数的统计评估在本节中,我们选取了均方误差(Mean Squared Error,MSE)和相关性系数(Correlation Coefficient,cc)这两个在太阳风模拟评估中广泛应用的统计学参量,对太阳风连续参数的模拟质量进行评估.MSE给出了模拟结果和观测值之间的总误差情况,其计算方法为:
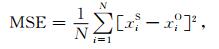
|
(19) |
其中,xiS为某一物理量的第i个模拟结果,xiO是与之对应的观测值,N为数据的总个数.
相关性系数给出了模拟结果和观测值之间的相关性程度,即模拟结果的变化趋势与观测的变化趋势是否吻合.这里使用了皮尔逊相关性系数的计算方法:
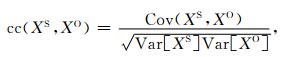
|
(20) |
其中XS、XO分别为某一物理量模拟结果和观测数据的集合,Cov(XS, XO)为模拟结果和观测数据的协方差,Var[XS]和Var[XO]分别为模拟结果和观测数据的方差.我们还计算了一定时间段内模拟结果与观测的最大值、中位数和最小值之间的比值,分别用R(max)、R(med)和R(min)表示.参考Jian等(2015)的计算方法,首先计算各个CR中的R(max)、R(med)和R(min),再将各个CR的比值进行平均,得到整个时间段内的比值.
表 1中给出了通过模型2008年模拟结果计算出来的统计学参量的值.可见,速度的相关性系数要好于密度、温度和磁场强度.2007年的太阳风特性与2008年类似,对2007年太阳风模型模拟评估的研究中同样存在这种现象(Gressl et al., 2014; Jian et al., 2015).这一方面可能由于模型目前还难以重现出密度变化中的一些小尺度结构.另一方面,密度、速度、磁场强度等结构在高速流到达时,由于高速流的压缩作用而存在一个比较窄的尖峰.当模型对高速流到达时间的预报存在偏差时,模拟结果和观测中的尖峰位置不能吻合,可能造成在一段时间内模拟结果和观测结果的变化趋势相反,从而降低了相关性系数.
|
|
表 1 2008年观测数据和模拟结果的太阳风速度、密度、磁场强度和温度的对比统计参量 Table 1 Comparison statistics of simulated and observed solar wind speed, density, magnetic field strength and temperature for Year 2008 |
图 6中给出了相关性系数随CR变化的趋势.图中的圆点表示用每个CR的数据计算的相关性系数.在此图中,CR2073前的模拟结果质量好于CR2073及之后的CR.密度、温度、磁场强度的cc变化趋势与速度的cc变化趋势基本一致.这是一个容易理解的现象.在行星际空间中,起主导作用的物理过程是快速和慢速太阳风之间的相互作用,同时,密度、温度在内边界的值是由速度导出的,因此其他量的模拟质量在很大程度上决定于速度的模拟质量.由此图可知,CR2073的速度、温度和磁场强度的cc值比其他CR都低.前文引用的ICME数据集中,2008年观测到的4个ICME均未发生在CR2073.在图 5中,模型在CR2073计算的第一个高速流,最大速度和持续时间均和观测数据有较大偏离.在CR2073末期,模型给出了一个观测中不存在的高速流.速度结构较大的偏差,使得模拟结果中高速流到达时形成的密度、磁场强度和温度的尖峰较观测存在较大的偏移.因此,密度、磁场强度和温度的偏差可能由速度偏差引起.而速度的偏差,一方面可能由于(1)式给出的WSA模型在CR2073的误差较大,需要进一步调优,另一方面也有可能来源于观测磁图质量的限制.由于观测条件的客观限制,目前所有的天基和地基太阳磁场观测设备获取的数据,都只能更新概图中太阳朝向地球那部分的磁场,因此随时间更新的光球磁场概图还不能精确的反映真实的全球磁场分布,在有些情况下可能使依赖磁场位形估计速度的(1)式出现较大误差.另外我们还计算了MSE随CR的变化趋势,与cc的变化趋势反映的信息基本一致,这里不再画出.

|
图 6 2008年L1点观测数据和模拟结果的相关性系数(cc)随CR的变化趋势 红线为速度,绿线为密度,蓝线为温度,黑线为磁场强度. Fig. 6 The variation trend of correlation coefficients (cc) between in-situ measurement data and simulated results at L1 point with the change of CR Correlation coefficients of speed, density, temperature and magnetic field strength are represented by red, green, blue and black lines respectively. |
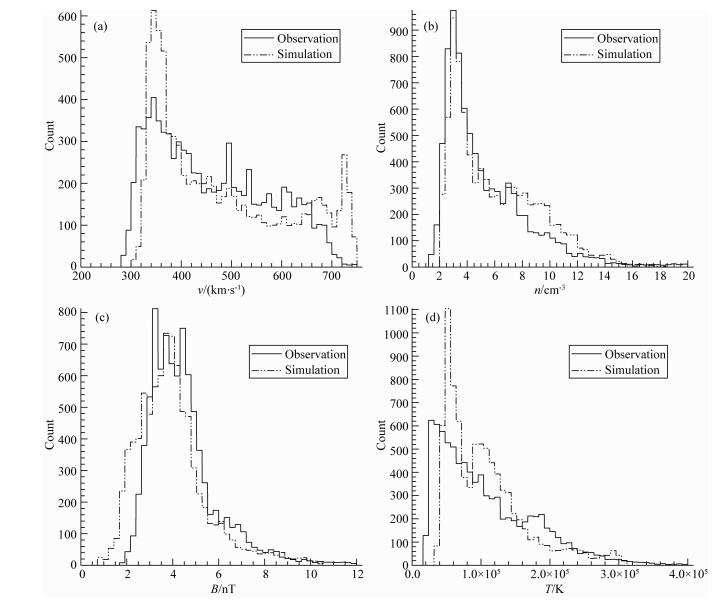
图 7中给出了观测数据和模拟结果参数在不同取值区间的出现次数统计,其中实线为OMNI观测数据的统计结果,虚线为模拟结果的统计结果.图 8以另一种形式表示了观测数据和模拟结果的分布,对于每一个观测数据及与之对应的模拟结果,我们通过观测值在横坐标中的位置和模拟值在纵坐标中的位置找到与其对应的格点,并将该点的统计次数增加1.图中连接左下角和右上角的连线所经过的区域为观测值与模拟值相等的位置.如果模拟结果精确的重现了观测,则所有的数据点都应该处于该线附近.分布在该线以上的点,模拟结果的值较观测偏大,分布在该线以下的点,模拟结果较观测偏小.图 7表明,v、n、B、T模拟结果的分布趋势与观测数据基本一致,但也存在一些偏离.在图 7的速度分布中,模拟与观测分布的峰值出现的位置相同,均在340~350 km·s-1,但模拟结果在330~370 km·s-1的出现次数要明显高于观测,在400~660 km·s-1的区间内出现的次数低于观测,在660 km·s-1以上出现的次数明显高于观测.从图 8中看,当观测数据的速度在380~500 km·s-1之间时,模拟结果对速度存在低估,大部分在这个区间中的数据点,模拟结果的速度在310~390 km·s-1间.观测数据的值在500~600 km·s-1间时,速度也被模拟结果低估.当观测数据在600~700 km·s-1之间时,模拟对速度存在高估,模拟结果的值在690~730 km·s-1间.这意味着由于模拟结果的偏差,将本该分布在400~660 km·s-1之间的一些数据点被移动到了310~390 km·s-1之间及690 km·s-1以上,从而解释了图 7中观测与模拟差异的原因.从图 5中看,对观测值在380~500 km·s-1和500~600 km·s-1间数据的低估是由于在一些高速流到达后,模拟结果比观测数据更快地下降到了慢速流中.对观测值为600~700 km·s-1的高估,是由于下半年模拟结果中快速流的峰值普遍大于观测数据.表 1中速度的R(max)和R(min)大于1,R(med)小于1,与图 7中反映的信息一致.
|
图 7 2008年L1点太阳风观测数据与模拟结果出现的频次统计 实线为观测数据统计计数,虚线为模拟结果统计计数.速度的统计范围为200~750 km·s-1,每10 km·s-1一个统计区间.密度的统计范围为0~20 cm-3,每0.4 cm-3一个统计区间.磁场强度的统计范围为0~12 nT,每0.24 nT一个统计区间.温度的统计范围为0.0~4.0×105 K,每0.8×105 K一个统计区间.对于值大于统计上限的数据,计入最后一个统计区间. Fig. 7 Distribution of observed and simulated solar wind parameters at L1 point for (a) speed, (b) density, (c) magnetic field strength and (d) temperature The solid lines represent observation data while the dashed lines represent simulation results. The ranges of speed, density, magnetic field strength and temperature are 200~750 km·s-1, 0~20 cm-3, 0~12 nT, 0.0~4.0×105 K respectively. The bin sizes of the four variables are 10 km·s-1, 0.4 cm-3, 0.24 nT and 0.8×105 K respectively. The cases with values higher than the last bin are counted in the last bin. |
图 7中密度观测数据与模拟结果出现次数的峰值相同,均在2.8~3.2 cm-3间,但模拟在1.2~2.8 cm-3间出现的次数较观测低,而在7.6~12.8 cm-3间出现的次数较观测高.在速度分布中,模型高估了低速流出现的次数,低估了高速流出现的次数.由于模型内边界的密度是由(3)式中与速度的反相关关系给出的,因此密度分布的偏离可能来自于速度分布的偏离.在图 8中,密度分布图中模拟结果偏高、偏低部分的位形分别与速度分布图中模拟结果偏低、偏高部分的位形相似.由于模拟结果相比观测在密度较小的区间中出现的较少,因此表 1中R(med)明显大于1,而观测数据中密度的取值区间比模拟结果宽,是密度R(min)>1和R(max) < 1的原因.
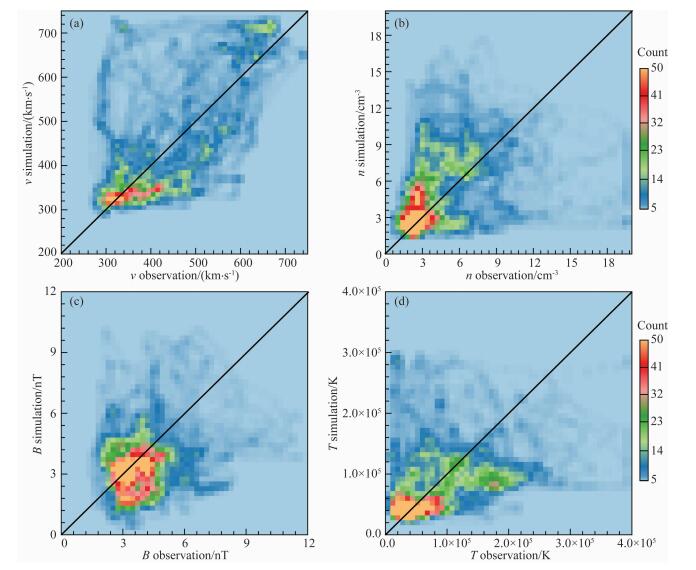
|
图 8 2008年L1点太阳风观测数据与模拟结果对应出现的频次统计 其中横轴对应观测数据,纵轴对应模拟结果,连接左下和右上的黑色实线标出了模拟与观测相等的位置.统计区间的设置与图 7相同. Fig. 8 The distributions of solar wind parameters at L1 point with respect to observation data and simulation results for (a) speed, (b) density, (c) magnetic field strength and (d) temperature The horizontal axis corresponds to observation data and the vertical axis corresponds to simulation result. The black line connecting lower left and upper right of the figure is the place where observation data and simulation result are equal. The ranges and bin sizes are same as that of Fig. 7. |
图 7的磁场强度分布中,当磁场强度处于3.12~5.52 nT间时,模拟结果的数据个数在大部分区间里明显少于观测数据.当磁场强度在0.72~2.88 nT间时,模拟结果的个数多于观测数据.在图 8的磁场强度分布图中,观测值在3.12~4.8 nT间的较多数据点的磁场强度被模拟结果低估,这些点的模拟磁场强度大都在3 nT以下.从图 5中观察可知,模拟结果中磁场强度最弱的位置是高速流到达之后、向低速流过渡的区域,即稀疏区,如CR2067的末期.从图 4的径向磁场分布图中也可看出,模拟结果磁场强度最弱的区域是高速流之后的稀疏区.在这些区域中,观测数据的磁场强度大部分在3 nT以上,而模拟结果的磁场强度则要小于3 nT.这是造成磁场强度模拟与观测间差异和磁场强度的R(min)比1小很多的原因.在CR2067中,速度和密度结构与观测符合得较好,图 6显示这个CR速度的相关性系数已经接近0.8.但磁场强度在稀疏区被低估的现象依然存在.因此,造成这种现象的原因,既有可能是稀疏区的结构存在偏差,也有可能是(5)式的磁场分布需要进一步改进.
由于内边界处的温度是由速度导出的,并与速度正相关.因此,速度在观测与模拟间差异也会反映到温度上.图 8中温度分布图的位形与速度分布图的位形存在相似之处,而图 7中,模拟结果在0.40×105~1.60×105 K间较观测数据个数多,在1.60×105~2.32×105 K间较观测数据少,可能来源前文分析的模拟结果速度分布偏差.在图 7的速度分布中,观测的最小值小于模拟值,而在温度分布中同样存在这个现象, 同时导致了温度的R(min)>2.
3.3 行星际磁场极性模拟质量的评估准确预报行星际磁场强度和行星际磁场极性的变化是在未来准确预报行星际磁场矢量的基础.在3.2节中,我们已经对行星际磁场强度的模拟结果做了评估.在本小节中,我们将对行星际磁场极性的模拟质量做评估.
在OMNI的磁场观测数据中,大尺度的行星际磁场变化上叠加了许多小尺度的扰动.为了过滤掉目前的太阳风模型无法重现的小尺度结构,我们采用了MacNeice(2009)对行星际磁场极性的处理方法,采用以下方法获得磁场极性的大尺度结构:(1)对于GSE经向角在45°~225°之间的数据,将其极性定义为负,标记为-1.对于GSE经向角为其他值的数据,将其极性定义为正,标记为+1.此处正极性指磁力线的方向指向太阳,负极性指磁力线的方向远离太阳.(2)若某点的极性与其两侧点的极性都不相同,且两侧极性的持续时间均在3 h以上,反转该点极性.(3)用极性连续的点组成极性区.(4)对于持续时间小于τ= 2 h、且任意一侧的相邻极性区持续时间大于3τ的极性区,将该极性区的极性重设成相邻区域的极性.(5)将τ设置为4, 6, …, 12 h,并依次重复(4)中的过程.(6)对于持续时间小于24 h的极性区,将其极性重置为相邻极性区的极性.
图 9第一行中标出了GSE经向角观测数据随时间变化的散点图,并用竖线分隔了各个CR的时间范围.第二行是观测数据用上一段所述步骤处理后得到的行星际磁场极性区随时间的变化,红色虚线标出了极性反转的位置,即极性区边界的位置.第一行和第二行图像的对比表明上一段所述的方法较好地反映了磁场极性大尺度变化,能够提取出观测点极性集中的区域.在CR2070前,每个CR内有两次极性反转,负极性区域的持续时间比正极性区域长.在CR2070,一个CR中发生了3次极性反转.在之后的CR中,每个CR内的极性反转次数恢复为两次,但正极性持续的时间比负极性持续的时间长.图 9第三行中标出了模拟结果的行星际磁场极性随时间的变化,蓝色虚线为模拟极性反转的位置.为了对比模拟和观测的极性反转,我们在这一行中用红色虚线标出了观测中极性反转的位置.通过与观测的对比,表明模拟结果在大部分时间中与观测相符.
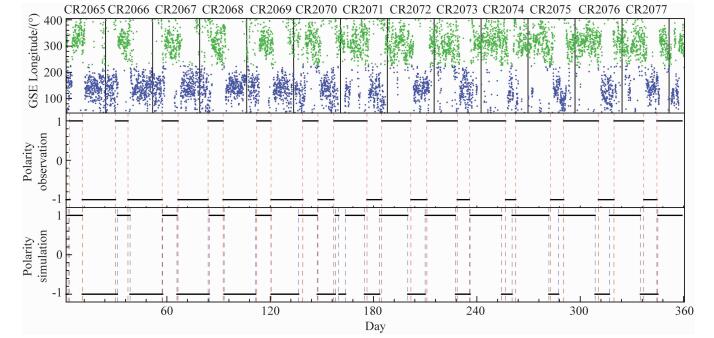
|
图 9 2008年L1点行星际磁场极性的变化图 第一行为OMNI观测数据的GSE经向角.为了便于画图识别,对于所有小于45°的数据,均对其数值增加了360°.GSE经向角在45°~225°之间的数据点标记为蓝色,其余数据点标记为绿色.数据第二行为观测数据经过处理后的极性区,其中+1为正极性,磁力线的方向指向太阳,-1为负极性,磁力线的方向远离太阳.红色虚线为极性反转发生的位置.第三行为由模拟结果生成的极性区,蓝色虚线为模拟结果极性反转的位置,红色虚线为观测数据极性反转的位置. Fig. 9 The IMF polarity variation at L1 point for Year 2008 The first row plots the GSE Longitude of the observation data. All data less than 45° are increased by 360° for convenience of plotting. Data points with GSE Longitude ranging between 45° and 225° are marked with blue while other points are marked with green. The second row is the polarity of the observation data after data processing, +1 for inward positive polarity while -1 for outward negative polarity. The red dashed line marks the polarity reverse from observation. The third row is the polarity of the simulation result. The polarity reverse of observation data and simulation result are marked by red and blue dashed lines respectively. |
磁场极性数据并非连续变化的变量,它只存在+1/-1两个值.因此,3.2节中定量评估连续参数的方法用来评估磁场极性是不合适的.这里,我们采用另外一套参数来评估磁场极性模拟的质量.我们计算了模拟结果的极性与观测相符的数据个数与总数据个数的比值,作为总体上的模拟质量参量.对于观测数据,模拟成功重现的极性反转,我们将其标记为“捕获”(Hit),未被模拟重现的极性区则标记为“遗漏”(Miss),并计算了捕获和遗漏的观测极性区个数占总极性区个数的比例.对于模拟结果,在观测中能够找到对应的极性反转,标记为“真警报” (Correct Alarm),而观测中不能找到对应极性反转的模拟极性反转,则标记为“伪警报”(False Alarm).这些参数从不同的角度反映了模型对极性这类二元值参数的预报质量.为了实现这些参数的自动计算,我们采用了以下判别准则:(1)对每个模拟结果的极性区域a,找到开始时间与其距离最小的观测极性区域b.(2)对比a与b的极性是否相同.若相同,则将b开始时的那次极性反转的属性标记为捕获.(3)如果模型在一个观测极性区覆盖的时间范围内错误的给出了多次极性反转,我们只能将其中一个极性反转记为真警报.因此,对于某一个观测极性区域b,如果在步骤(2)完成后有多个模拟极性区域与之对应,我们将寻找开始时间距离它最近的模拟极性区域,并将这个模拟极性区域开始时的那次极性反转标记为真警报.(4)对所有观测极性区域重复以上步骤后,没有被捕获的观测极性反转标记为遗漏,没有标记为真警报的模拟极性反转则被标记为伪警报.(5)对所有真警报的极性反转,我们计算了其到达时间tstartS与对应观测极性反转的到达时间tstartO的差Δt=tstartS-tstartO,并以此计算了时间差的平均值Δt及其绝对值的平均值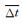
表 2中给出了由模型2008年模拟结果及对应时间观测数据计算的评估参数.在2008年,模型在89.96%的时间内给出了正确的行星际磁场极性.模型成功捕获了所有观测中的极性反转,但给出了两个不存在的极性反转.这两个不存在的极性反转出现在Day156-Day180间.在这段时间里,模型给出了一个不存在的极性区,进而给出了两个不存在的极性反转.在此期间,行星际磁场的极性结构正在发生比较大的变化,从上文描述的CR2065-CR2069的特征过渡到CR2071-CR2077的特征.虽然模型采用了时变的内边界处理方法,但由于太阳光球磁图观测数据只能随时间更新朝向地球的部分,不能很好地反映光球全球的实时变化特征,可能是造成这个偏差的原因.表中除了给出了Δt和|Δt|的平均值外,还给出了它们的均方差(±号之后).由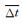
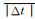
|
|
表 2 2008年行星际磁场极性模拟结果和观测数据的对比统计参数 Table 2 Comparison statistics of simulated and observed IMF for Year 2008 |
SIR是背景太阳风中空间天气效应最明显的现象.我们采用MacNeice(2009)的方法实现SIR结构的自动识别:(1)找到所有速度比1天前高50 km·s-1以上的点,并将其标记.(2)去掉所有孤立的标记点.(3)对连续出现的标记点,将它们集中的区块标记为一个高速流增强区(High Speed Enhancement, HSE),并记录每个HSE开始和结束的位置.(4)对于每个HSE,找到自其开始时间向前2天到结束间的最小速度vmin,及自开始时间到结束时间向后一天间的最大速度vmax,并将SIR开始和结束的位置标记为vmin和vmax出现的位置,进而依据开始、结束时间计算SIR的持续时间.(5)合并间隔小于0.75天的SIR.(6)消去持续时间小于0.5天的SIR.(7)对于重组之后的SIR,重新计算vmin、vmax和开始、结束时间,并将最大速度变化率最后一次出现的时间标为SIR的流界面(Stream Interface, SI).(8)消去vmin>500 km·s-1、vmax < 400 km·s-1或vmax-vmin < 150 km·s-1的SIR.需要指出的是,由于本文中的模型是连续模拟太阳风变化的时变模型,因此在不同CR间数据不存在跳跃的问题,无需其他工作中一样消去两个CR交界处的伪SIR(Jian et al., 2015).如果某一观测数据中的SIR和模拟结果中的SIR,在开始和结束时间之间存在重叠,则将观测数据中的SIR标记为捕获,将模拟结果中的SIR标记为真警报,未被标记为捕获的观测数据SIR则标记为遗漏,未被标记为真警报的模拟结果SIR则标记为伪警报.对于所有真警报的SIR,计算其SI到达时间tSIS与对应观测数据中SIR的SI到达时间tSIO的差Δt=tSIS-tSIO,并以此计算了时间差的平均值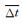
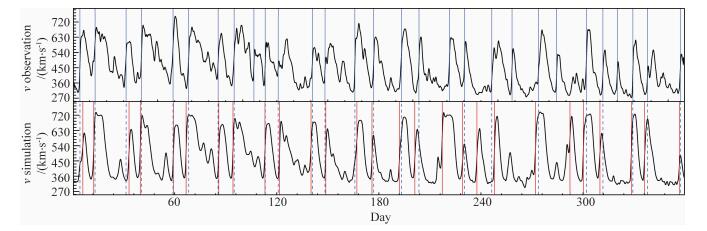
图 10中给出了应用以上步骤后识别出的SIR,其中第一行为观测数据,蓝色竖线为SI位置.第二行为模拟结果,红色竖线为模拟结果的SI位置.对于所有真警报SIR,以蓝色虚线表示对应观测SIR的SI位置.由图观察可知,以上步骤能够成功的将速度快速上升的高速流界面识别出来.模拟结果重现了观测中的大部分SIR,但也有遗漏和误报的SIR.
|
图 10 2008年观测数据与模拟结果中的SIR 第一行为观测数据速度,SI以蓝色竖线标出.第二行为模拟结果,由模拟结果得到的SI由红色竖线标出,蓝色虚线为观测数据中对应SI的位置. Fig. 10 Simulated and observed SIR for Year 2008 The first row plots the observed solar wind speed. The position of SI is marked by blue solid line. The second row plots the simulated solar wind speed. The position of simulated SI and its corresponding observed SI are marked by red solid line and blue dashed line respectively. |
表 3中给出了对SIR模拟质量的定量评估结果.模型对SIR的模拟质量要略逊于对极性反转的模拟质量,但捕获观测SIR的比例和真警报的SIR比例都超过了80%.SI到达时间的误差在1天左右,而图 10表明后半年的到达时间误差较前半年相比有增大的趋势.
|
|
表 3 2008年SIR模拟结果和观测数据的对比统计参数 Table 3 Comparison statistics of simulated and observed SIR for Year 2008 |
本文利用连续输入的太阳光球磁场数据,得到了0.1AU处的时变边界条件,驱动了CESE+HLL太阳风模型的行星际部分,模拟了2008年全年0.1~1AU的行星际太阳风结构,对其变化的特征作了分析.我们对比了模拟结果在L1点的太阳风参数与对应的OMNI观测,并建立了对模拟结果进行系统定量评估的自动化方法.对于连续变化的太阳风参数,我们计算了MSE、cc等统计学参数,并根据观测与模拟数据的分布和观测及模拟中最大值、中位数、最小值的比例,分析了模拟结果相比观测的偏离趋势,为模型的进一步调优提供了依据.对行星际磁场极性反转和流相互作用区,我们实现了一套自动识别方法,并计算了捕获/遗漏、真警报/伪警报的数量和比例,以及到达时间的误差.
2008年,第23太阳活动周由下降期转入极小期,太阳活动比较平静,CME等能够干扰背景太阳风结构的瞬变现象发生的次数较少,能够为评估背景太阳风模型提供比较好的条件.通过评估参数的计算,我们认为本文中时变经验边界条件驱动的太阳风模型能够比较好地模拟背景太阳风的大尺度特征.速度的相关性系数达到了0.6以上,磁场强度不存在数倍低估的现象,捕获了全部的行星际磁场极性反转和82.76%的流相互作用区,行星际磁场极性反转的误报率仅为6.67%,流相互作用区的误报率仅为11.11%,两种结构的到达时间误差在1天左右.
同时,通过综合分析模拟结果和观测数据的分布情况和各个评估数据,我们明确了模型在进一步改进中需要重点注意的问题.模型结果中的高速流在到达L1点后速度下降的比观测要快,在2008年下半年,高速流的速度最大值比观测要高,导致了速度和密度结构的偏差.在高速流之后的稀疏区中,磁场强度比观测低.然而,1.3节的经验关系中的自由参数较多,遍历参数空间的盲目调节是目前的计算资源所不允许的.同时,除了经验关系和自由参数外,不同观测来源的磁图同样会对模拟结果产生不小的影响(Jian et al., 2015; Riley et al., 2012).通过集合预报的方式(Riley et al., 2013),考察模型对参数和输入数据的敏感性,明确每一种调整对统计参数的影响方向,可能是一种较为有效的调优方法.
我们在0.1AU处使用的边界条件将日冕加热和太阳风加速过程“隐藏”在了经验关系中.这种相对成熟的方式,一方面为三维MHD太阳风模型尽快从实验室研究阶段转入业务应用阶段提供了可能.气象数值预报的发展经验表明,数值模型越早投入业务预报,其性能就可以在研究与应用的相互促进间越早得到提升(Siscoe, 2006).另一方面,这种经验模型也为MHD日冕模型和太阳风加速、加热机制的研究提供了限制和指引.如果0.1AU的经验关系能够通过行星际模型的演化得到与L1点局地观测相符的模拟结果,则日冕MHD模型在0.1AU给出的结果应该与其相似,才有可能进一步得到与局地观测一致的行星际太阳风.此外,在引言所述的第一类模型的发展过程中,经验模型也可以作为衡量其能力的参照(Siscoe et al., 2004),使我们可以通过相关评估参数的对比,更清晰的掌握第一类模型的适用性.
致谢 本工作使用了由全球日震台网组(GONG)项目提供的数据.GONG由AURA运行的美国国家太阳观测台及美国国家自然科学基金会通过协议共同管理.GONG数据由大熊湖天文台、高山天文台、利尔蒙斯太阳观测台、乌代布尔太阳观测台、加那利群岛天体物理研究所、托洛洛山美洲天文台的观测仪器产生.STEREO/EUVI数据由美国海军实验室网站提供.OMNI数据由网址为 http://omniweb.gsfc.nasa.gov的GSFC/SPDF OMNIWeb系统获取.本工作的计算任务于国家超级计算天津中心天河1(A)超级计算机上完成.
Arge C N, Odstrcil D, Pizzo V J, et al. 2003. Improved method for specifying solar wind speed near the sun. AIP Conference Proceedings, 679: 190-193. DOI:10.1063/1.1618574 |
Cash M D, Biesecker D A, Pizzo V, et al. 2015. Ensemble modeling of the 23 July 2012 coronal mass ejection. Space Weather, 13(10): 611-625. DOI:10.1002/2015SW001232 |
Chen G M, Xu J Y, Wang W B, et al. 2014. A comparison of the effects of CIR- and CME-induced geomagnetic activity on thermospheric densities and spacecraft orbits: Statistical studies. Journal of Geophysical Research: Space Physics, 119(9): 7928-7939. DOI:10.1002/2014JA019831 |
Detman T, Smith Z, Dryer M, et al. 2006. A hybrid heliospheric modeling system: Background solar wind. Journal of Geophysical Research: Space Physics, 111(A7): A07102. DOI:10.1029/2005JA011430 |
Elliott H A, McComas D J, Schwadron N A, et al. 2005. An improved expected temperature formula for identifying interplanetary coronal mass ejections. Journal of Geophysical Research: Space Physics, 110(A4): A04103. DOI:10.1029/2004JA010794 |
Feng X S, Yang L P, Xiang C Q, et al. 2010. Three-dimensional solar WIND modeling from the sun to earth by a SIP-CESE MHD model with a six-component grid. The Astrophysical Journal, 723(1): 300-319. DOI:10.1088/0004-637X/723/1/300 |
Feng X S, Xiang C Q, Zhong D K. 2011. The state-of-art of three-dimensional numerical study for corona-interplanetary process of solar storms. Scientia Sinica Terrae (in Chinese), 41(1): 1-28. |
Feng X S, Zhang S H, Xiang C Q, et al. 2011. A Hybrid solar wind model of the CESE+HLL method with a Yin-Yang overset grid and an AMR grid. The Astrophysical Journal, 734(1): 50. DOI:10.1088/0004-637X/734/1/50 |
Feng X S, Jiang C W, Xiang C Q, et al. 2012. A data-driven model for the global coronal evolution. The Astrophysical Journal, 758(1): 62. DOI:10.1088/0004-637X/758/1/62 |
Feng X S, Xiang C Q, Zhong D K. 2013. Numerical study of interplanetary solar storms. Scientia Sinica Terrae (in Chinese), 43(6): 912-933. |
Feng X S, Ma X P, Xiang C Q. 2015. Data-driven modeling of the solar wind from 1 Rs to 1 AU. Journal of Geophysical Research: Space Physics, 120(A9): 10159-10174. DOI:10.1002/2015JA021911 |
Fletcher L, Cargill P J, Antiochos S K, et al. 2015. Structures in the outer solar atmosphere. Space Science Reviews, 188(1-4): 211-249. DOI:10.1007/s11214-014-0111-1 |
Gressl C, Veronig A M, Temmer M, et al. 2014. Comparative study of MHD modeling of the background solar wind. Solar Physics, 289(5): 1783-1801. DOI:10.1007/s11207-013-0421-6 |
Jian L K, MacNeice P J, Taktakishvili A, et al. 2015. Validation for solar wind prediction at Earth: Comparison of coronal and heliospheric models installed at the CCMC. Space Weather, 13(5): 316-338. DOI:10.1002/2015SW001174 |
Lee C O, Luhmann J G, Odstrcil D, et al. 2009. The solar wind at 1 AU during the declining phase of solar cycle 23: Comparison of 3D numerical model results with observations. Solar Physics, 254(1): 155-183. DOI:10.1007/s11207-008-9280-y |
Linker J. 2011. A next-generation model of the corona and solar wind. Tech. Rep. AFRL-OSR-VA-TR-2012-0199, Air Force Office of AFOSR Scientific Research.
|
Linker J A, Caplan R M, Downs C, et al. 2016. An empirically driven time-dependent model of the solar wind. Journal of Physics: Conference Series, 719(1): 012013. DOI:10.1088/1742-6596/719/1/012012 |
Mackay D H, Yeates A R. 2012. The sun′s global photospheric and coronal magnetic fields: Observations and models. Living Reviews in Solar Physics, 9: 6. DOI:10.12942/lrsp-2012-6 |
MacNeice P. 2009. Validation of community models: Identifying events in space weather model timelines. Space Weather, 7(6): S06004. DOI:10.1029/2009SW000463 |
McGregor S L, Hughes W J, Arge C N, et al. 2011. The distribution of solar wind speeds during solar minimum: Calibration for numerical solar wind modeling constraints on the source of the slow solar wind. Journal of Geophysical Research: Space Physics, 116(A3): A03101. DOI:10.1029/2010JA015881 |
Merkin V G, Lyon J G, Lario D, et al. 2016. Time-dependent magnetohydrodynamic simulations of the inner heliosphere. Journal of Geophysical Research: Space Physics, 121(4): 2866-2890. DOI:10.1002/2015JA022200 |
Miyoshi T, Kusano K. 2005. A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics. Journal of Computational Physics, 208(1): 315-344. DOI:10.1016/j.jcp.2005.02.017 |
Odstrcil D. 2003. Modeling 3-D solar wind structure. Advances in Space Research, 32(4): 497-506. DOI:10.1016/S0273-1177(03)00332-6 |
Odstrčil D, Pizzo V J. 1999. Three-dimensional propagation of coronal mass ejections (CMEs) in a structured solar wind flow: 1. Journal of Geophysical Research: Space Physics, 104(A1): 483-492. DOI:10.1029/1998JA900019 |
Owens M J, Lockwood M, Barnard L A. 2017. Coronal mass ejections are not coherent magnetohydrodynamic structures. Scientific Reports, 7(1): 4152. DOI:10.1038/s41598-017-04546-3 |
Petrie G J, Bolding J, Clark R, et al. 2007. GONG synoptic magnetograms and coronal magnetic field modeling. AGU Fall Meeting Abstracts.
|
Riley P, Linker J A, Mikic′ Z. 2001. An empirically-driven global MHD model of the solar corona and inner heliosphere. Journal of Geophysical Research: Space Physics, 106(A8): 15889-15902. DOI:10.1029/2000JA000121 |
Riley P, Linker J A, Lionello R, et al. 2012. Corotating interaction regions during the recent solar minimum: The power and limitations of global MHD modeling. Journal of Atmospheric and Solar-Terrestrial Physics, 83: 1-10. DOI:10.1016/j.jastp.2011.12.013 |
Riley P, Linker J A, Mikic′ Z. 2013. On the application of ensemble modeling techniques to improve ambient solar wind models. Journal of Geophysical Research: Space Physics, 118(2): 600-607. DOI:10.1002/jgra.50156 |
Riley P, Linker J A, Arge C N. 2015. On the role played by magnetic expansion factor in the prediction of solar wind speed. Space Weather, 13(3): 154-169. DOI:10.1002/2014SW001144 |
Siscoe G, Baker D, Weigel R, et al. 2004. Roles of empirical modeling within CISM. Journal of Atmospheric and Solar-Terrestrial Physics, 66(15-16): 1481-1489. DOI:10.1016/j.jastp.2004.03.028 |
Siscoe G. 2006. A culture of improving forecasts: Lessons from meteorology. Space Weather, 4(1): 01003. DOI:10.1029/2005SW000178 |
Spence H, Baker D, Burns A, et al. 2004. Center for integrated space weather modeling metrics plan and initial model validation results. Journal of Atmospheric and Solar-Terrestrial Physics, 66(15-16): 1499-1507. DOI:10.1016/j.jastp.2004.03.029 |
Thompson W T. 2006. Coordinate systems for solar image data. Astronomy & Astrophysics, 449(2): 791-803. DOI:10.1051/0004-6361:20054262 |
Wang Y M, Sheeley N R Jr. 1990. Solar wind speed and coronal flux-tube expansion. The Astrophysical Journal, 355: 726-732. DOI:10.1086/168805 |
Wang Y M, Robbrecht E, Sheeley N R Jr. 2009. On the weakening of the polar magnetic fields during solar cycle 23. The Astrophysical Journal, 707(2): 1372-1386. DOI:10.1088/0004-637X/707/2/1372 |
Wu C C, Fry C D, Wu S T, et al. 2007. Three-dimensional global simulation of interplanetary coronal mass ejection propagation from the Sun to the heliosphere: Solar event of 12 May 1997. Journal of Geophysical Research: Space Physics, 112(A9): A09104. DOI:10.1029/2006JA012211 |
Wu S T, Wang J F. 1987. Numerical tests of a modified full implicit continuous Eulerian (FICE) scheme with projected normal characteristic boundary conditions for MHD flows. Computer Methods in Applied Mechanics and Engineering, 64(1-3): 267-282. DOI:10.1016/0045-7825(87)90043-0 |
Wu S T, Dryer M. 2015. Comparative analyses of current three-dimensional numerical solar wind models. Science China Earth Sciences, 58(6): 839-858. DOI:10.1007/s11430-015-5062-1 |
Yang L P, Feng X S, Xiang C Q, et al. 2012. Time-dependent MHD modeling of the global solar corona for year 2007: Driven by daily-updated magnetic field synoptic data. Journal of Geophysical Research: Space Physics, 117(A8): 8110. DOI:10.1029/2011JA017494 |
Yeh T, Dryer M. 1985. A constraint on boundary data for magnetic solenoidality in MHD calculations. Astrophysics and Space Science, 117(1): 165-171. DOI:10.1007/BF00660919 |
Zhou Y F, Feng X S. 2013. MHD numerical study of the latitudinal deflection of coronal mass ejection. Journal of Geophysical Research: Space Physics, 118(10): 6007-6018. DOI:10.1002/2013JA018976 |
Zhou Y F, Feng X S. 2017. Numerical study of the propagation characteristics of coronal mass ejections in a structured ambient solar wind. Journal of Geophysical Research: Space Physics, 122(2): 1451-1462. DOI:10.1002/2016JA023053 |
冯学尚, 向长青, 钟鼎坤. 2011. 太阳风暴的日冕行星际过程三维数值研究进展. 中国科学:地球科学, 41(1): 1-28. |
冯学尚, 向长青, 钟鼎坤. 2013. 行星际太阳风暴的数值模拟研究. 中国科学:地球科学, 43(6): 912-933. |
 2019, Vol. 62
2019, Vol. 62

