2. 中国地质大学(武汉)数学与物理学院, 武汉 430074
2. School of Mathematics and Physic, China University of Geosciences, Wuhan 430074, China
奇异谱分析(Singular Spectrum Analysis, SSA)是一种近年兴起的时间序列分析方法, 最早由Broomhead和King(1986)提出.自提出以来,SSA分析被广泛应用于多领域的信号处理中.
SSA分析是信号去噪和预测的一种方法.该方法从Karhumen-Loeve分解理论的基础上发展而来(Vautard and Ghil, 1989;Vautard et al., 1992).SSA分析是将原信号变换成Hankel矩阵,再对Hankel矩阵进行分解和重构,从而实现信号和噪声的分离.SSA分析能够实现信号和噪声分离的依据是它们的具有不同特征的奇异谱.
Read等(1993)在SSA的基础上提出了用于多道信号处理的MSSA方法,Oropeza和Sacchi(2011)提出基于随机奇异值分解(Randomized Singular Value Decomposition,RSVD)的MSSA方法,Huang等(2016)提出提升去噪效果的阻尼MSSA方法.在地球物理领域,Sacchi(2009)、Oropeza和Sacchi(2011)、Kreimer和Sacchi(2012)、Chiu(2013)、Gan等(2015)、Huang等(2016)利用SSA分析对一维和多维地震信号进行去噪和重建.
重磁场是由具有密度与磁性差异的不同规模、不同深度、不同形状地质体共同引起,即为不同尺度、不同幅值异常的叠加.多种异常的混叠,给目标地质体的反演和解释带来困难.如何从混叠重磁场中分离出目标地质体引起的异常,是重磁勘探的研究方向之一.
早期人们采用滑动平均和多项式拟合的方法实现不同尺度重磁异常的分离.在后来的重磁信号处理中,人们用频率域的概念描述重磁场.通过Fourier变换将重磁场由空间域变换到频率域,用振幅和相位来描述重磁场的特征.通常情况,浅部地质体产生的重磁场频率高,深部地质体产生的重磁场频率低.Spector和Grant(1970)推导了航磁异常的能谱公式,提出利用能谱分析粗略估计块状体埋深的方法,并在1975年提出匹配滤波法分离重磁场.文百红和程方道(1990)提出插值切割法分离磁异常.Mickus等(1991)首次将最小曲率法应用于美国某地区的布格重力异常分离中.随着20世纪70年代小波分析方法的提出,Fedu和Quarta(1998)提出一种基于离散小波变换的重磁位场分离方法.这些位场分离方法存在不同的问题,如窗口大小、拟合阶数、小波基的选择、区域场与局部场能谱斜率位置的确定等.
本文应用奇异谱分析分离重磁位场,通过建立理论地球物理模型,分析重磁异常的奇异谱特征.通过理论模型计算分析,总结最优参数选取方法,提出适用于位场多信号分离的分解和重构方法,并对比SSA分析和传统场源分离方法的应用效果,最后将该方法应用到鄂东南某矿区赤铁矿重力异常的识别提取中.
1 SSA和MSSA的基本原理实际工作中,剖面数据是一维的,平面数据经过网格化后可以表示成二维矩阵的形式.剖面和平面重磁数据分别采用SSA和MSSA进行分析.
1.1 SSA设有剖面重磁数据x=[x1, x2, …, xN],将该重磁数据以窗口M重新排列如下:

|
(1) |
矩阵X称为时滞矩阵(Vautard and Ghil, 1989),其自协方差矩阵表示如下:
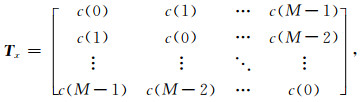
|
(2) |
Tx是Toeplitz矩阵.c是序列x的协方差:
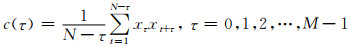
|
(3) |
计算Tx的特征值向量λ和对应的特征向量矩阵E,特征值向量表示如下:
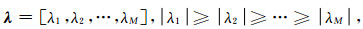
|
(4) |
特征向量矩阵表示如下:
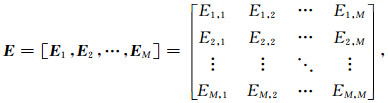
|
(5) |
其中E1, E2, …, EM是列向量,分别表示矩阵Tx的M个特征向量,并与λ1, λ2, …, λM对应.同时,矩阵Tx的奇异值向量σ可以表示如下:
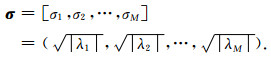
|
(6) |
通常,将奇异值向量σ称为x的奇异谱,其中明显大于0的奇异值称为有效奇异值.在实际情况中,信号奇异谱σ中的元素均大于0,其中较小的奇异值十分接近于0,而有效奇异值可以看成是非接近于0的奇异值.
通过矩阵X和特征向量矩阵E求得权矩阵A(王解先等,2013):
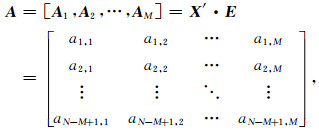
|
(7) |
权矩阵A反映了特征向量矩阵E在矩阵X中权重,那么通过权矩阵A和特征向量矩阵E可以重构出一维重磁数据x的M个不同尺度的细节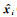
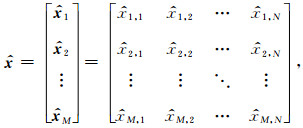
|
(8) |
(8) 式中
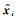
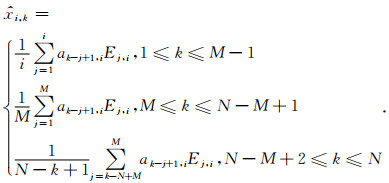
|
(9) |
不同尺度的细节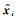
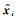
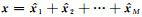
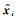
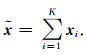
|
(10) |
设有大小为Nr×Nc平面重磁数据如下:
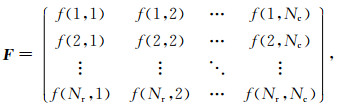
|
(11) |
通过F建立窗口大小Lr×Lc的轨迹矩阵Fi, j(Read, 1993; Oropeza and Sacchi, 2011; Huang et al., 2016):
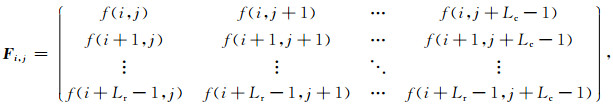
|
(12) |
令Kr=Nr-Lr+1和Kc=Nc-Lc+1,那么1≤i≤Kr,1≤j≤Kc.构建Hankel矩阵Hi,Hi表示如下:
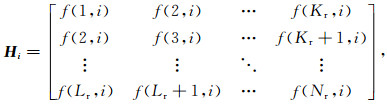
|
(13) |
然后,结合Hankel矩阵Hi,构建块Hankel矩阵W,矩阵W表示如下:
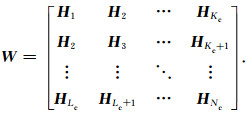
|
(14) |
矩阵W可以表示成如下形式:
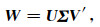
|
(15) |
其中,U和V是正交矩阵,Σ是对角矩阵.为了方便计算,令W是N×N的方矩阵,那么U和V是大小为N×N的正交矩阵,对角矩阵Σ可以表示成以下形式:
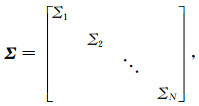
|
(16) |
其中,|Σ1|≥|Σ2|≥…≥|ΣN|.那么矩阵W的奇异值向量σ表示如下:
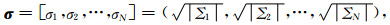
|
(17) |
令ΣK为对角矩阵Σ的截断位置,那么矩阵W的奇异值分解可以表示如下:
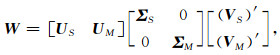
|
(18) |
其中,ΣS=diag(Σ1, Σ2, …, ΣK),ΣM=diag(ΣK+1, ΣK+2, …, ΣN),US是U的第1到K列,UM是U的第K+1到N列,VS是V的第1到K列,VM是V的第K+1到N列.那么,块矩阵W的近似可以表示如下:
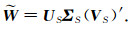
|
(19) |
最后,通过对近似矩阵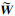
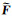
通常情况,信号的时滞矩阵是低秩的,而噪声会增加矩阵的秩.分解的过程可以看成时滞矩阵向低维子空间的投影,这些子空间的性质可以用奇异值来表征.重构的过程则是对奇异值分类,并选取特定奇异值所对应的子空间进行逆投影.分解和重构的过程实际上是矩阵降秩的过程.SSA和MSSA的实现步骤可以归纳为以下三点:
(1) 原始数据的重新排列.利用一维窗口将一维重磁数据x重新排列成时滞矩阵X,X是Hankel矩阵.二维重磁数据F则采用二维窗口重构块Hankel矩阵W.
(2) 矩阵的奇异值分解.对时滞矩阵X的自协方差矩阵或块Hankel矩阵W进行奇异值分解,得到奇异值和对应的特征向量.
(3) 重磁数据的重构.在合适位置将奇异值截断,并用截断的奇异值重构位场数据.
2 重磁场的奇异谱特征下面我们分析不同尺度(不同埋深)、不同幅值重磁异常及噪声的奇异谱特征.
(1) 幅值相同、尺度不同(埋深不同)的重磁异常的奇异谱特征
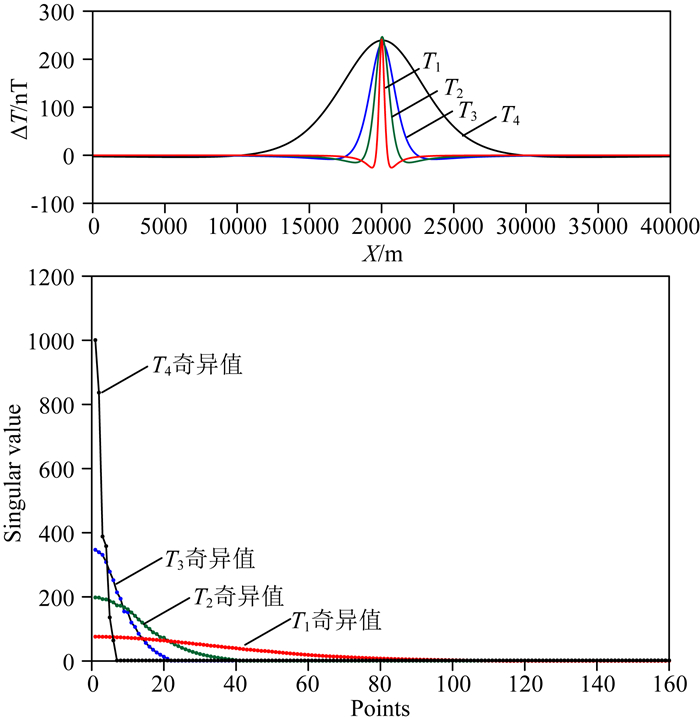
建立四个埋深不同磁化强度不同的模型,由四个模型分别产生四组幅值相同、尺度不同的磁异常如图 1所示,磁异常点数是800.分别对这四组磁异常做SSA分析,SSA分析窗口是400(采用较大窗口可以得到更多奇异值,其谱特征反映的更细致,窗口400是最大窗口,以下其他3种情况分析的点数窗口大小相同).从不同尺度磁异常的奇异谱中可以看出,随着磁异常尺度的增大,奇异值下降速度变快,有效奇异值的个数增多.这表明尺度大(埋深大)的重磁异常其奇异谱曲线陡峭,主要集中在奇异值较大的部分,尺度小(埋深小)的重磁异常其奇异谱曲线趋平缓,其特征与Fourier分析的功率谱相似.
|
图 1 幅值相同、尺度不同模型的奇异谱特征 Fig. 1 The singular spectrum features of same amplitude and different scale models |
(2) 尺度相似(埋深相同)、幅值不同的重磁异常的奇异谱特征
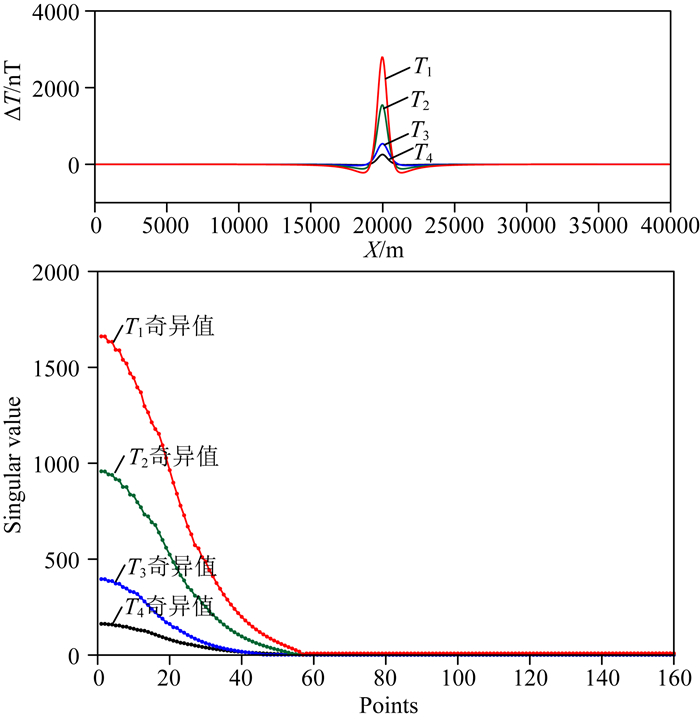
建立四个埋深相同磁化强度不同的模型,由四个模型分别产生四组尺度相似、幅值不同的磁异常如图 2所示.从不同幅值磁异常的奇异谱中可以看出,随着磁异常幅值的增大,奇异值下降速度变快,但有效奇异值的个数几乎不变.说明相同埋深的地质体奇异谱具有相似的特征,时滞矩阵的秩几乎不变.
|
图 2 幅值不同、尺度相同模型的奇异谱特征 Fig. 2 The singular spectrum features of different amplitude and same scale models |
(3) 尺度相同、幅值相同、水平位置不同的重磁异常的奇异谱特征
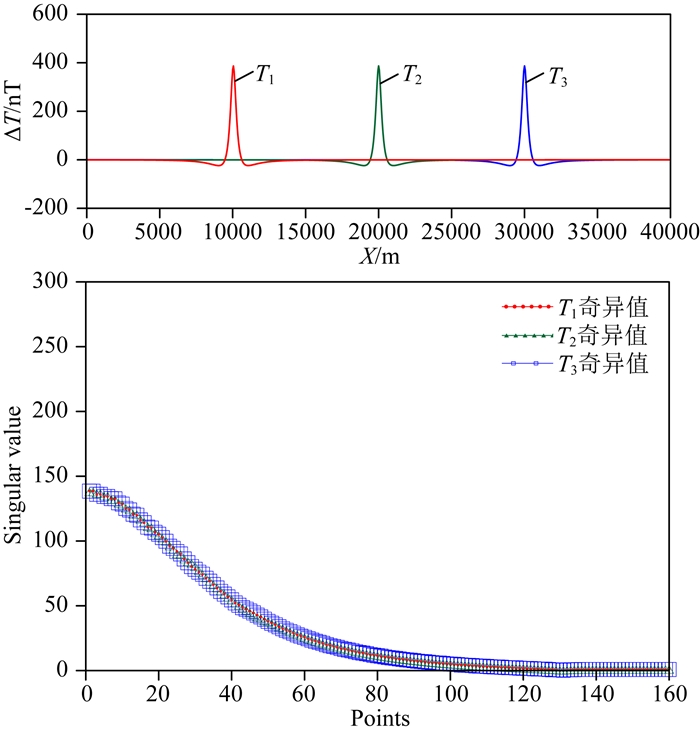
对于同一模型,水平位置不同所产生的三组尺度相同、幅值相同的磁异常如图 3所示.从图中可以看出,同一异常,分布在不同位置,其奇异谱相同.说明地质体的水平位置不影响奇异谱的分布.
|
图 3 水平位置不同模型的奇异谱特征 Fig. 3 The singular spectrum features of different horizontal position models |
(4) 高斯白噪声的奇异谱特征
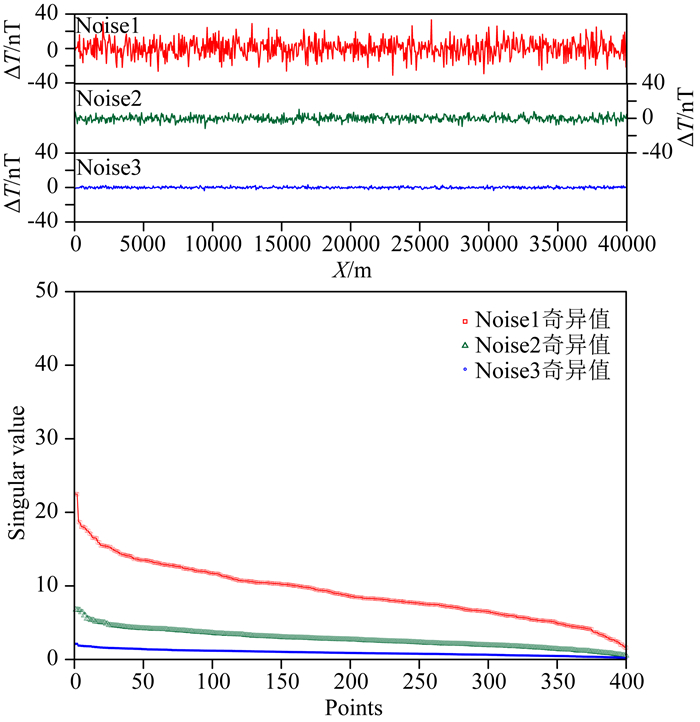
若有三组不同强度的噪声如图 4所示.从图中可以看出,三组不同强度噪声的奇异值在横坐标上都有分布.说明噪声的时滞矩阵是高秩的,噪声强度只决定奇异值的大小,而不会改变秩的大小.
|
图 4 噪声模型的奇异谱特征 Fig. 4 The singular spectrum features of noise models |
通过上面的理论模型计算分析可以知道,重磁场的奇异谱包含尺度(埋深)和幅值(物性)的信息,其中尺度决定奇异谱的下降速度和时滞矩阵的秩,幅值决定奇异谱的下降速度但不改变时滞矩阵的秩.对于重磁场,异常尺度越大,奇异谱下降速度越快,秩越低;异常幅值越高,奇异谱下降速度越快,但时滞矩阵的秩不变.噪声的奇异值在横坐标上都有分布,说明噪声的时滞矩阵是高秩的.
异常的尺度(埋深)和幅值(物性)决定了奇异谱的特征,这是利用奇异谱进行场源分离的基础.
3 参数讨论构建时滞矩阵的窗口与重构信号所选择的奇异值是SSA分析的两个参数,下面讨论在位场分离中如何选择这些参数.
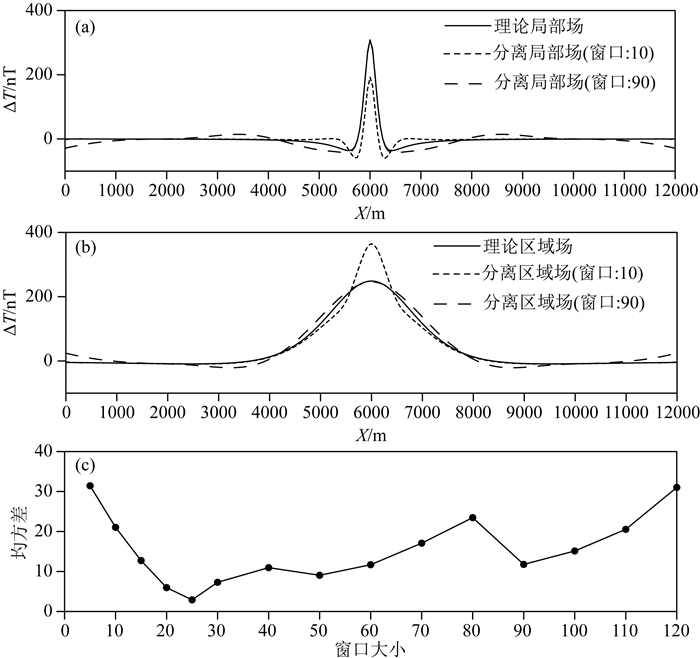
3.1 构建时滞矩阵的窗口选择时滞矩阵的自协方差矩阵Tx的大小由窗口决定,若窗口取M,矩阵Tx的奇异值个数也为M,这表示我们可以将总场分解成M个细节.因此,窗口的选择直接影响区域场和局部场的分离效果.在信号分析中,通常窗口取M/2(Golyandina et al., 2007; Chiu, 2013; Huang et al., 2016).通过理论模型计算分析发现,由于分离目标和信号特征的差异,这种窗口选择方式并不适用于解决重磁位场分离问题(图 5c给出了窗口与均方差的关系).图 5是垂向叠加模型的奇异谱分析,剖面点数是240,点距50 m,化极磁异常零值点之间宽度约1200 m,最优窗口在25个点左右,当窗口选择10个点时,区域场和局部场没有完全分离,当窗口选择90个点时,区域场过拟合,局部场出现波动.
|
图 5 过小和过大窗口的理论模型奇异谱分析 (a)分离局部场;(b)分离区域场;(c)窗口对分离结果的影响. Fig. 5 Singular spectrum analysis of synthetic model of undersize and oversize windows (a) The separated local fields; (b) The separated regional fields; (c) The effects of the windows on the results separated by SSA. |
由图 5可知,窗口选取过小会导致异常分离不完全,重构的区域场中仍包含过多局部场的信息,但是当窗口选取过大时,重构得到的区域场过拟合,导致分离得到的局部场产生波动.在重磁位场分离中,SSA分析的窗口取决于所要分离目标异常的尺度.当目标异常尺度较大时,应该选取较大的窗口进行SSA分析,当目标异常尺度较小时,则应选取较小的窗口进行SSA分析.通过理论模型计算发现,最优窗口的宽度近似等于待分离目标异常零值线的宽度.但是,窗口的改变对分离效果的影响是渐变的,因此最佳窗口可以不是某一确定的值,而是一个区间,窗口在这个区间内取值,得到的分离效果是相似的.
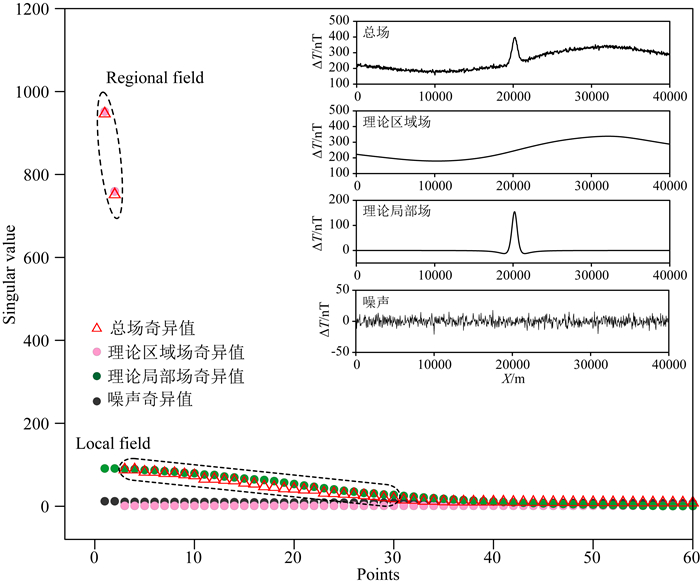
3.2 重构阶数的选择很多学者利用SSA分析去噪时,采用均值截断法、二分法等方法重构信号(Oropeza and Sacchi, 2011; 王解先, 2013),这些重构方法能否用于重磁位场分离?为了探究重磁位场分离的重构方法,建立理论叠加模型,该模型引起的磁异常如图 6右上所示,其中总场是区域场、局部场和噪声的叠加.对理论模型的总场、区域场、局部场和噪声分别做奇异谱分析.奇异谱分析窗口是400(采用较大窗口可以得到更多奇异值,其谱特征反映的更细致),截前60个奇异值如图 6所示.为了阐述方便,这里令总场、理论区域场、理论局部场和噪声的奇异值分别为σi、σiR、σiL和σiN,其中1≤i≤400.图 6中,总场的奇异谱包含了理论区域场、局部场和噪声的奇异谱特性,其中总场奇异值σ1、σ2与理论区域场奇异值σ1R、σ2R相似,总场奇异值σ3, …, σ30与理论局部场奇异值σ3L, …, σ30L相似,总场奇异值σ31, …, σ400则与噪声的奇异值σ31N, …, σ400N相似.根据上述对应关系,将总场的奇异谱分解成[σ1, σ2]、[σ3, …, σ30]、[σ31, …, σ400]三个部分,这三个部分分别是区域场、局部场和噪声的奇异谱的主要成分.可以用它们去重构区域场、局部场和噪声(采用公式(9)).
|
图 6 重构阶数的选择方法 Fig. 6 The setting of orders for reconstruction |
由上可知,总场的奇异谱包含其各成分的奇异谱特征,这为奇异值的分类提供参考.在实际问题中,我们可以根据奇异值的大小和下降趋势来进行划分(如图 6中Regional field和Local field).一般来说,奇异值大且快速下降的部分反映的是区域场的特征,奇异值较小且缓慢下降的部分反映的是局部场的特征,奇异值近似为0且分布在整个横坐标的部分反映的是噪声的特征.
4 奇异谱分析与传统方法的对比下面以不同的理论模型对比SSA分析和传统方法的分离效果,并从应用的角度讨论SSA分析在解决重磁位场分离问题中的可行性.
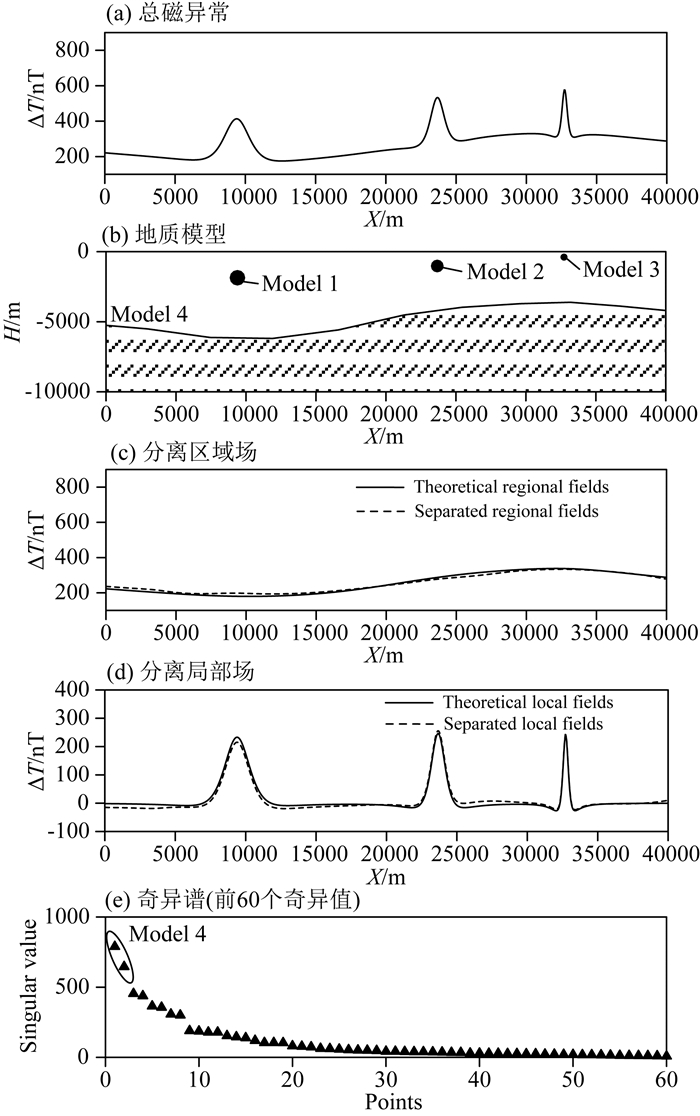
4.1 理论模型试验建立地球物理模型如图 7b、图 8b和图 9b所示.图 7b是横向叠加模型的磁异常场,共有800个数据点,点距是50 m,其中局部场由模型1(5000×10-3A·m-1)、模型2(2500×10-3A·m-1)和模型3(1500×10-3A·m-1)正演构成,区域场由模型4(2000×10-3A·m-1)正演构成.图 8b是垂向叠加模型的磁异常场,总共有241个观测点,点距是50 m,其中局部场由模型5(3000×10-3A·m-1)正演构成,区域场由模型6(5000×10-3A·m-1)正演构成.图 9b是斜向叠加模型的磁异常场,总共有241个观测点,点距是50 m,其中局部场由模型7(1000×10-3A·m-1)正演构成,区域场由模型8(4000×10-3A·m-1)正演构成.
|
图 7 横向叠加模型SSA分析 Fig. 7 Horizontal superposition model separation using SSA |
|
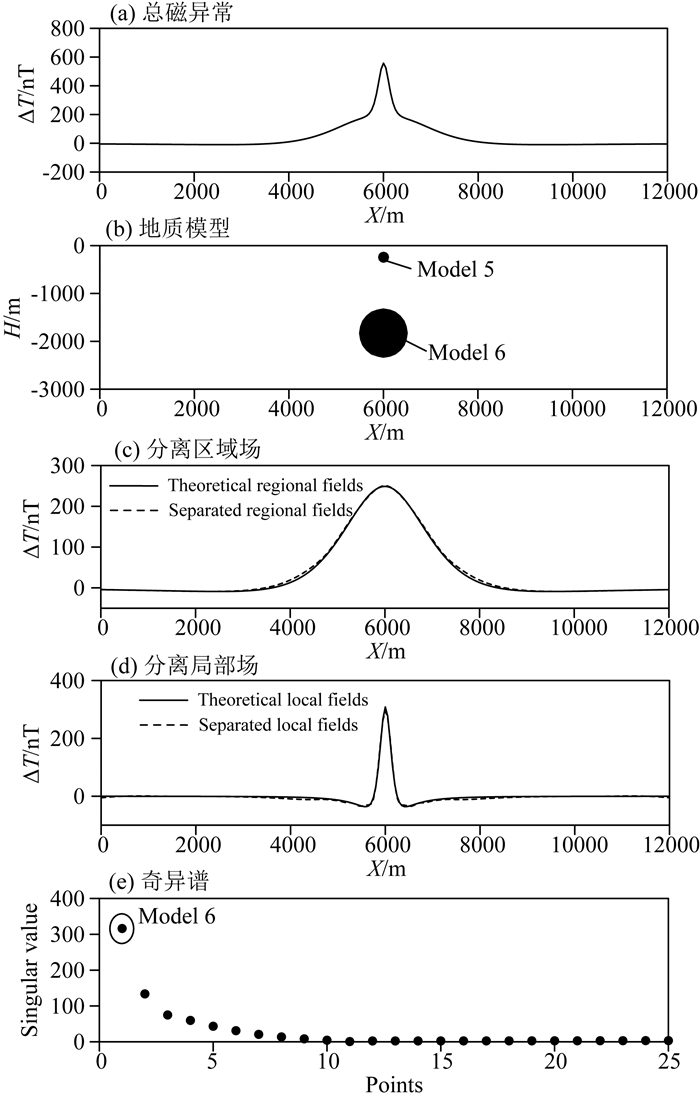
图 8 垂向叠加模型SSA分析 Fig. 8 Vertical superposition model separation using SSA |
|
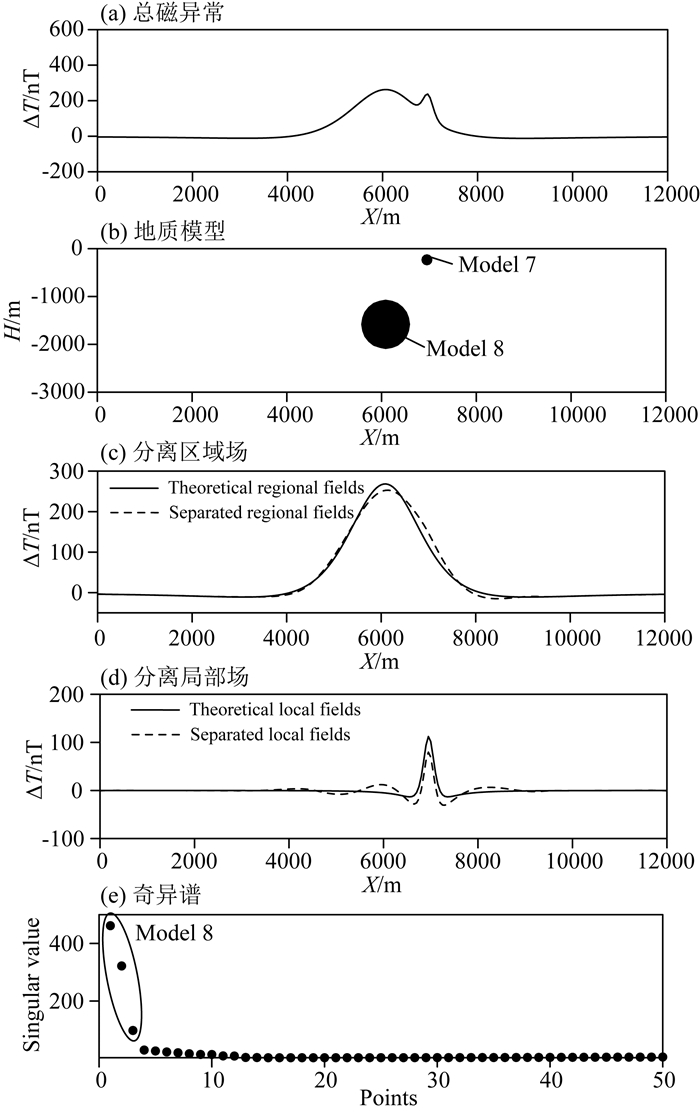
图 9 斜向叠加模型SSA分析 Fig. 9 Diagonal superposition model separation using SSA |
图 7c和7d是窗口大小为400(以Model 4为分离目标)的横向叠加模型SSA分析结果.该模型的奇异谱(图 7e)可以依据奇异值的大小和下降速度分成2个部分,第一个部分是σ1和σ2,剩余奇异值是第二个部分.这两个部分的奇异值由大到小,下降速度由快到慢.容易知道,奇异谱的第一个变化过程由区域场引起,那么采用奇异值σ1和σ2对应的细节重构信号就能够得到分离的区域场(图 7c),采用剩余奇异值对应的细节重构信号就能够得到分离的局部场(图 7d).从图中可以看出,奇异谱分析在横向叠加模型上具有良好的分离效果.
图 8c、8d是窗口大小为25(以Model 5为分离目标)的垂向模型SSA分析结果.该模型的奇异谱(图 8e)能够分成两个部分,第一个部分是σ1,剩余奇异值是第二个部分,这两个部分分别对应地质体6和地质体5产生的异常.那么,可以将奇异值σ1对应的细节作为区域场(图 8c),将剩余奇异值对应的细节重构作为局部场(图 8d).从分离结果可以看出,奇异谱分析能够实现垂向叠加模型的分离.
图 9c、9d是窗口大小为50(以Model 7为分离目标)的斜向模型SSA分析结果.该模型的奇异谱(图 9e)能够分成两个部分,第一个部分是σ1、σ2和σ3,剩余奇异值是第二个部分,这两个部分分别对应地质体8和地质体7产生的异常.那么,可以将奇异值σ1、σ2和σ3对应的细节作为区域场(图 9c),将剩余奇异值对应的细节重构作为局部场(图 8d).从分离结果可以看出,奇异谱分析能够实现斜向叠加模型的分离.
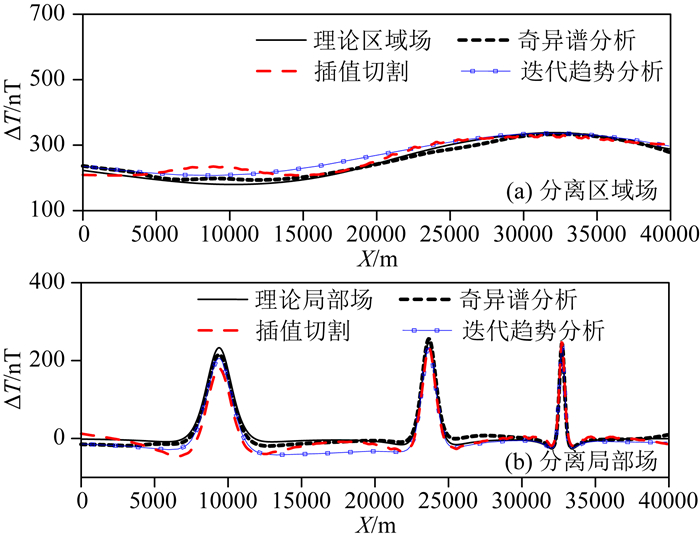
4.2 传统场源分离方法的分离本小节主要利用小波分析法(Mallat and Hwang, 1992;侯遵泽和杨文采,1997;杨文采等,2001)、匹配滤波法、插值切割法(文百红和程方道,1990)、多次迭代趋势分析法(李春芳,2011)、最小曲率法(纪晓琳等,2015;王万银等,2009)这五种传统重磁位场分离方法对4.1节中的模型进行分离.这些分离方法的参数都是在多次实验并与理论模型对比得到最好的分离效果下确定的.由于每种方法所针对的异常特点不同,每种模型采用效果最好的两种传统方法进行对比,分别见图 10、图 11和图 12.
|
图 10 横向叠加模型传统方法实验 Fig. 10 Traditional methods separation of horizontal superposition model |
|
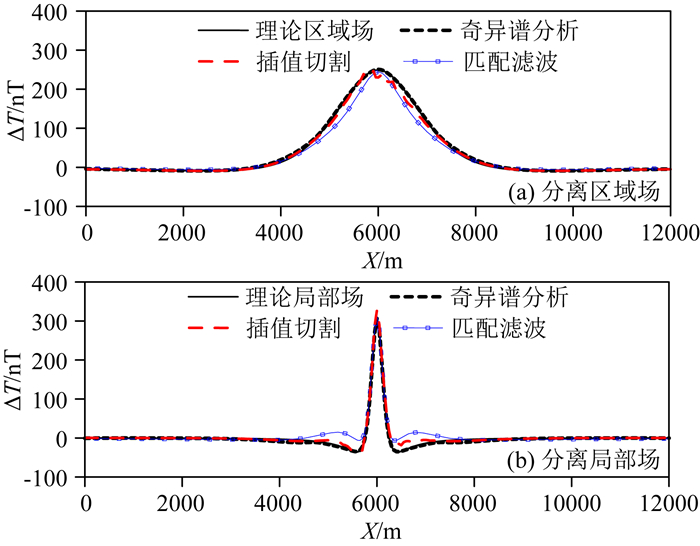
图 11 垂向叠加模型传统方法实验 Fig. 11 Traditional methods separation of vertical superposition model |
|
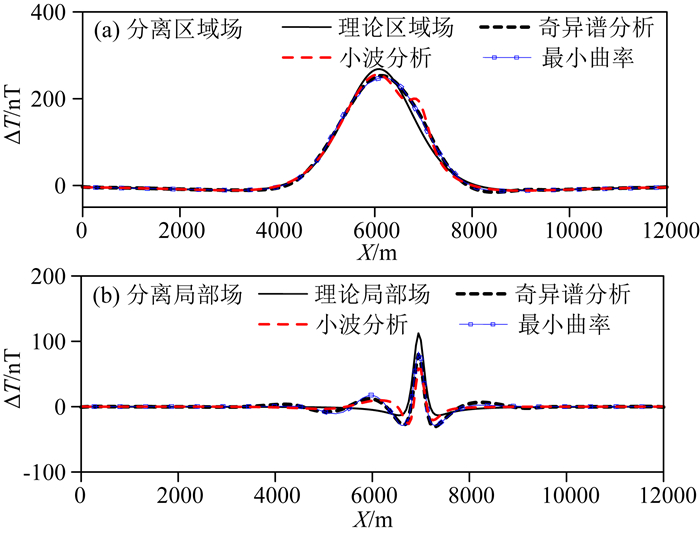
图 12 斜向叠加模型传统方法实验 Fig. 12 Traditional methods separation of diagonal superposition model |
重磁位场分离方法的优劣可以从两个方面判别,一是分离效果的好坏,二是参数选取的难易.重磁位场分离效果的好坏可以用理论场与分离场的均方差表示,均方差越小,表示分离场与理论场更接近.参数选取的难易程度又包括:1最优参数是否容易确定;2选取参数所带来的误差对分离结果的影响程度.通常,分离效果是判断方法好坏的先行标准,当方法的分离效果满足一定标准时,才有讨论参数选取难易程度的意义.
从表 1可以看出,奇异谱分析能够用于三种不同模型的异常分离,并具有很好的分离效果.小波分析、匹配滤波和插值切割均能用于三种模型的异常分离,但均方误差大于奇异谱分析.迭代趋势分析对横向叠加模型具有较好的分离效果,但是无法分离垂向和斜向叠加模型.最小曲率法对局部异常尺度较小的斜向叠加模型具有较好的分离效果,但是无法分离局部异常尺度较大的横向和垂向叠加模型.
|
|
表 1 各方法分离理论模型的均方差 Table 1 The MSE of synthetic models separated by different methods |
在参数选取的方面,小波分析存在如何根据哪一阶细节重构区域场与局部场的问题;匹配滤波存在功率谱估计场源深度误差较大的问题;插值切割需要设置插值半径和迭代次数,这两个参数对结果都有较大影响;多次迭代趋势分析参数只需设置迭代次数;最小曲率法需要设置迭代步长和迭代次数,两个参数对结果有一定影响;SSA分析需要先确定窗口大小,然后根据奇异谱分布确定重构阶数.
奇异谱分析具有适用性强,分离效果好的优点,并通过奇异谱的变化,容易选择重构阶数.但是,在二维数据的奇异谱分析中,其时滞矩阵大小是NrNc(Nr-Lr)(Nc-Lc)×NrNc(Nr-Lr)(Nc-Lc),因此在Nr和Nc较大的情况下,需要较多的计算时间.
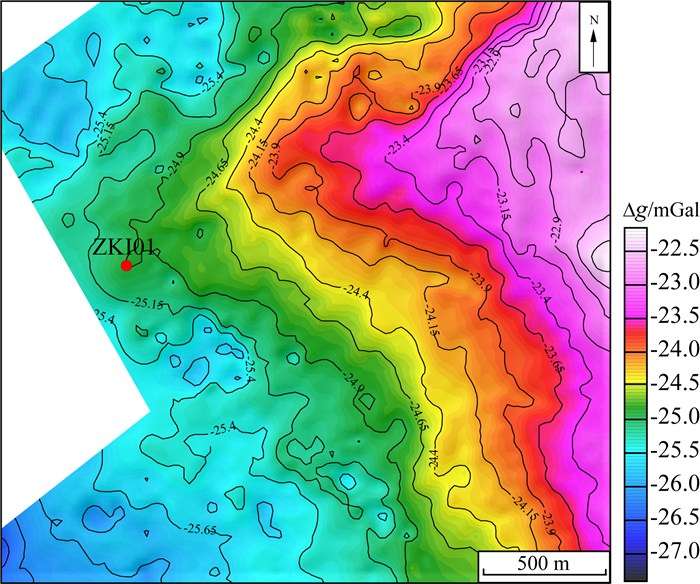
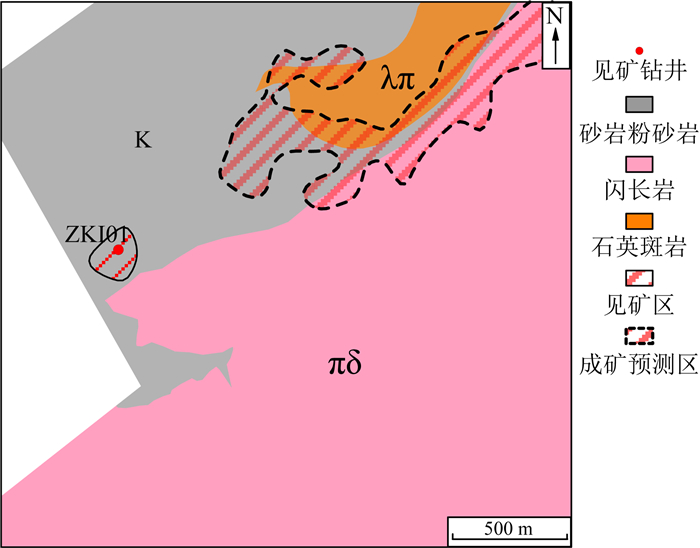
5 奇异谱分析在鄂东南某矿区的应用鄂东南矿集区以接触交代型铁矿床为主,它们主要形成于燕山期中酸性侵入岩与碳酸盐岩接触带附近.区内出露白垩纪砂岩粉砂岩和燕山期闪长岩、石英斑岩(图 13),地层北倾.区内铁矿以赤铁矿为主,伴有磁铁矿,其中赤铁矿相对围岩的剩余密度为0.55 g·cm-3,磁铁矿相对围岩的剩余密度为1.47 g·cm-3,高密度的赤铁矿和磁铁矿能够引起局部高重异常.从布格重力异常图(图 14)中可以看出,布格重力异常值在-28 mGal到-22 mGal之间,由北东高过渡到南西低.矿体产生的重力异常相对较弱,难以直接从布格重力异常图中分辨.
|
图 13 研究区地质图 Fig. 13 Geological map of study area |
|
图 14 研究区布格重力异常图 Fig. 14 The Bouguer gravity anomaly map of study area |
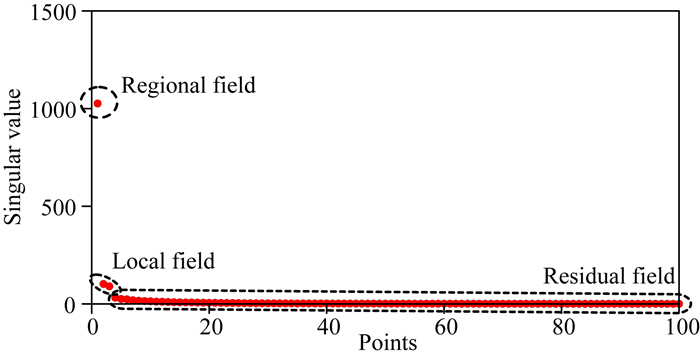
由于中浅部地质体引起的重力异常尺度较小,因此采用10×10(点线距20 m×20 m)的窗口进行多道奇异谱分析,奇异谱如图 15所示.根据奇异谱的特征分类,用奇异值σ1重构区域场(图 16a),奇异值σ2和σ3重构局部场(图 16b),其余的奇异值则视为噪声引起.
|
图 15 布格重力异常奇异谱分布图 Fig. 15 The singular spectrum of Bouguer gravity anomaly |
|
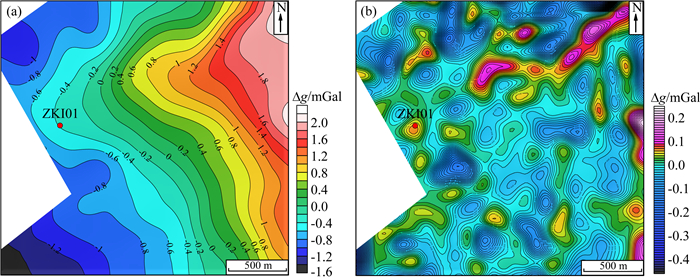
图 16 鄂东南某工区多道奇异谱分析结果 (a)区域场;(b)局部场. Fig. 16 The results processed by MSSA of work area in southeastern Hubei (a) Regional field; (b) Local field. |
区内岩体和沉积岩的接触带是成矿的有利位置,分离的局部场在接触带附近存在多个局部高重异常.西缘的局部高重异常位于闪长岩和沉积岩的接触带上,形状近圆形,极大值是0.08 mGal.东缘的局部高重异常位于石英斑岩、闪长岩和沉积岩的接触带上,该接触带具有成矿的地质条件.东缘局部高重异常形状近条带状,规模比西缘局部高重异常大,极大值是0.16 mGal.由于区内岩体和沉积岩密度低,因此推断这两个局部高重异常由中浅部的高密度地质体引起,该地质体可能是赤铁矿、磁铁矿或蚀变岩体.2014年施工的ZKI01孔位于西缘局部高重异常的中心位置,钻井见矿117 m厚,其中59 m到159 m处为赤铁矿,159 m到177 m处为磁铁矿.结合地质和钻井资料,圈定接触带东缘局部重力大于0.03 mGal的区域作为成矿远景区(见图 13).
6 结论奇异谱分析是一种近年兴起的时间序列分析方法,它利用降秩原理实现信号分离,其过程包括变换、分解和重构.分解的过程可以看成时滞矩阵向低维子空间的投影,这些子空间的性质可以用奇异值来表征.重构的过程则是对奇异值分类,并选取特定奇异值所对应的子空间进行逆投影.结合理论模型计算分析,我们发现区域场具有低秩高奇异值的特征,局部场具有低秩中低奇异值的特征,噪声具有高秩低奇异值的特征,这是利用降秩原理进行场源分离和去噪的基础.通过理论模型试验我们发现,最优窗口的宽度近似等于待分离目标异常零值线的宽度,重构阶数则根据奇异谱的特征来选择.结合理论模型和实际数据,该方法能够实现重磁位场的分离,并具有适用性强、分离效果好的优点,但相比于传统方法,其计算效率稍低.
致谢 感谢《地球物理学报》编辑部对本文的支持,以及审稿专家的宝贵意见.
Broomhead D S, King G P. 1896. Extracting qualitative dynamics from experimental data. Physica D:Nonlinear Phenomena, 20(2-3): 217-236. |
Chiu S K. 2013. Coherent and random noise attenuation via multichannel singular spectrum analysis in the randomized domain. Geophysical Prospecting, 61(1): 1-9. DOI:10.1111/gpr.2013.61.issue-1 |
Fedu M, Quarta T. 1998. Wavelet analysis for the regional-residual and local separation of potential field anomalies. Geophysical Prospecting, 46(5): 507-525. DOI:10.1046/j.1365-2478.1998.00105.x |
Gan S W, Chen Y K, Zi S H, et al. 2015. Structure-oriented singular value decomposition for random noise attenuation of seismic data. Journal of Geophysics and Engineering, 12(2): 262-272. DOI:10.1088/1742-2132/12/2/262 |
Gao J J, Sacchi M, Chen X H. 2013. A fast reduced-rank interpolation method for prestack seismic volumes that depend on four spatial dimensions. Geophysics, 78(1): V21-V30. DOI:10.1190/geo2012-0038.1 |
Golyandina N E, Usevich K D, Florinsky I V. 2007. Filtering of digital terrain models by two-dimensional singular spectrum analysis. International Journal of Ecology & Development, 8(7): 81-94. |
Hou Z Z, Yang W C. 1997. Wavelet transform and multi-scale analysis on gravity anomalies of China. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 40(1): 85-95. |
Huang W L, Wang R Q, Chen Y K, et al. 2016. Damped multichannel singular spectrum analysis for 3D random noise attenuation. Geophysics, 81(4): V261-V270. DOI:10.1190/geo2015-0264.1 |
Ji X L, Wang W Y, Qiu Z Y. 2015. The research to the minimum curvature technique for potential field data separation. Chinese Journal of Geophysics (in Chinese), 58(3): 1042-1058. DOI:10.6038/cjg20150329 |
Kreimer N, Sacchi M D. 2012. A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation. Geophysics, 77(3): V113-V122. DOI:10.1190/geo2011-0399.1 |
Li C F. 2011. The research on the separating methods for potential field in space domain[Master's thesis] (in Chinese). Xi'an: Chang'an University.
|
Mallat S, Hwang W L. 1992. Singularity detection and processing with wavelets. IEEE Transactions on Information Theory, 38(2): 617-643. DOI:10.1109/18.119727 |
Mickus K L, Aiken C L V, Kennedy W D. 1991. Regional-residual gravity anomaly separation using the minimum-curvature technique. Geophysics, 56(2): 279-283. DOI:10.1190/1.1443041 |
Oropeza V, Sacchi M. 2011. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics, 76(3): V25-V32. DOI:10.1190/1.3552706 |
Read P L. 1993. Phase portrait reconstruction using multivariate singular systems analysis. Physica D:Nonlinear Phenomena, 69(3-4): 353-365. DOI:10.1016/0167-2789(93)90099-M |
Sacchi M D. 2009. FX Singular spectrum analysis. 2009 CSPG CSEG CWLS Convention (Conference).
|
Spector A, Grant F S. 1970. Statistical models for interpreting aeromagnetic data. Geophysics, 35(2): 293-302. DOI:10.1190/1.1440092 |
Vautard R, Ghil M. 1989. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Physica D:Nonlinear Phenomena, 35(3): 395-424. DOI:10.1016/0167-2789(89)90077-8 |
Vautard R, Yiou P, Ghil M. 1992. Singular-spectrum analysis:A toolkit for short, noisy chaotic signals. Physica D:Nonlinear Phenomena, 58(1-4): 95-126. DOI:10.1016/0167-2789(92)90103-T |
Wang J X, Lian L Z, Shen Y Z. 2013. Application of singular spectral analysis to GPS station coordinate monitoring series. Journal of Tongji University (Natural Science) (in Chinese), 41(2): 282-288. |
Wang W Y, Qiu Z Y, Liu J L, et al. 2009. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing. Progress in Geophysics (in Chinese), 24(4): 1327-1338. |
Wen B H, Cheng F D. 1990. A new interpolating cut method for identifying regional and local fields of magnetic anomaly. J.Cent.-South Inst. Min. Metall. (Science and Technology) (in Chinese), 21(3): 229-235. |
Yang W C, Shi Z Q, Hou Z Z, et al. 2001. Discrete wavelet transform for multiple decomposition of gravity anomalies. Chinese Journal of Geophysics (in Chinese), 44(4): 534-541. |
侯遵泽, 杨文采. 1997. 中国重力异常的小波变换与多尺度分析. 地球物理学报, 40(1): 85-95. DOI:10.3321/j.issn:0001-5733.1997.01.010 |
纪晓琳, 王万银, 邱之云. 2015. 最小曲率位场分离方法研究. 地球物理学报, 58(3): 1042-1058. DOI:10.6038/cjg20150329 |
李春芳. 2011. 空间域位场分离方法研究[硕士论文]. 西安: 长安大学. http://cdmd.cnki.com.cn/Article/CDMD-11941-1011186171.htm
|
王解先, 连丽珍, 沈云中. 2013. 奇异谱分析在GPS站坐标监测序列分析中的应用. 同济大学学报(自然科学版), 41(2): 282-288. DOI:10.3969/j.issn.0253-374x.2013.02.022 |
王万银, 邱之云, 刘金兰, 等. 2009. 位场数据处理中的最小曲率扩边和补空方法研究. 地球物理学进展, 24(4): 1327-1338. DOI:10.3969/j.issn.1004-2903.2009.04.022 |
文百红, 程方道. 1990. 用于划分磁异常的新方法——插值切割法. 中南矿冶学院学报, 21(3): 229-235. |
杨文采, 施志群, 侯遵泽, 等. 2001. 离散小波变换与重力异常多重分解. 地球物理学报, 44(4): 534-541. DOI:10.3321/j.issn:0001-5733.2001.04.012 |
 2018, Vol. 61
2018, Vol. 61


