2. 地球信息探测仪器教育部重点实验室(吉林大学), 长春 130061;
3. 吉林大学仪器科学与电气工程学院, 长春 130061
2. Key Laboratory of Geophysical Exploration Equipment, Ministry of Education(Jilin University), Changchun 130061, China;
3. College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130061, China
地面核磁共振(surface nuclear magnetic resonance,SNMR)作为一种直接探测地下水的地球物理方法,具有测量速度快,分辨率高和定量解释等优点,近年来被广泛应用于水资源调查、水文环境监测以及地下工程水害预警等领域(Behroozmand et al., 2015;林君等,2013;肖立志等,2013).但是SNMR方法获得的信号十分微弱,通常强度只有纳伏量级(nV,10-9V),易受到各种环境噪声的干扰,导致仪器采集数据信噪比低,严重影响后续反演结果的准确性,制约了该方法在城镇、村庄以及地下工程等复杂环境中的应用(Larsen and Behroozmand, 2016).
近年来,针对SNMR信号的噪声压制方法,很多学者展开了大量研究.SNMR测量数据中主要包含三类噪声:尖峰噪声、工频谐波噪声和随机噪声(Larsen et al., 2014).尖峰噪声是由云层放电和电器点火等引起的瞬时大幅度干扰.目前比较成熟的识别和消除尖峰噪声的方法有能量运算方法(Dalgaard et al., 2012;万玲等,2016)、尖峰建模方法(Larsen and Behroozmand, 2016)和基于小波域的噪声压制方法(Costabel and Müller-Petke,2014;Strehl et al., 2006).工频谐波噪声由高压输电线、变压器和其他电气设备产生.维纳滤波(Dalgaard et al., 2012)、工频谐波建模(Larsen et al., 2014)、自适应噪声抵消(Müller-Petke and Costabel, 2014)等方法用于工频谐波噪声的抑制,均取得了较好的去噪效果.对于随机噪声,通常采用叠加的方法进行压制,主要包含直接叠加(Plata and Rubio, 2002)、针对非时稳噪声的加权叠加(Legchenko et al., 2003)和包含去尖峰噪声功能的统计叠加(Jiang et al., 2011).但是,数据叠加方法需要消耗大量的测量时间,且信号质量提高程度存在极限(Legchenko and Valla, 2002).
此外,直接从测量数据中提取SNMR信号也是目前研究的热点.Legchenko和Valla等(1998)针对单指数SNMR信号,利用非线性拟合方法,对正交检测后的SNMR信号复包络曲线进行参数提取,但该方法不适用于多弛豫SNMR信号特征参数的提取.基于经验模态分解(Ghanati et al., 2014)、奇异谱分析(Ghanati et al. 2016)和独立成分分析(田宝凤等,2015)等盲源分离理论的参数提取方法,根据观测数据提取未知源信号的主要成分,存在幅度失真和信息缺失等问题.然而,SNMR信号的指数衰减特征是已知的,充分利用其已知特征从测量数据中提取有用信号,得到的结果比盲源分离方法的可靠性更高.
稀疏表示理论以发掘信号的特征为基础(Mallat et al., 1993),力求在某个特定字典中将信号表示为少数原子的线性组合,为信号提供一种更加简洁和直接的分析方式.在地球物理数据处理中,稀疏表示在地震勘探数据面波与体波的稀疏分解(Wang et al., 2012a)以及噪声消除等(Beckouche and Ma, 2014;Zhu et al., 2015)方面得到应用.根据SNMR探测原理,多弛豫SNMR信号可等效为多个孔隙介质产生的感应信号的叠加,且能量主要集中在有限个弛豫时间T2*上,而噪声呈随机分布状态,这种稀疏先验性为稀疏表示理论应用于SNMR信号的提取提供了理论依据.
本文针对SNMR信号微弱,组成成分复杂且受噪声影响严重的问题,提出了一种基于稀疏表示的多弛豫SNMR信号提取方法.首先,建立多弛豫SNMR的稀疏分解与重构模型,并根据SNMR信号与噪声的特征区别,设计刻画SNMR信号的离散衰减余弦(discrete decay cosine,DDC)冗余字典;其次通过改进广义正交匹配追踪(generalized orthogonal matching pursuit,gOMP)算法,实现随机噪声背景下的多弛豫SNMR信号提取;再次,针对SNMR测量数据是由多次独立重复采集结果构成的特点,提出了SNMR数据流提取策略.通过仿真数据,验证多弛豫SNMR信号的提取效果,讨论了噪声对信号提取准确度的影响.最后,给出野外实测数据的SNMR信号提取及反演结果实例.
1 基于稀疏表示的SNMR信号提取方法 1.1 稀疏表示模型当多个不同孔隙介质的含水层产生的SNMR信号叠加在一起,或在同一个含水层中含有多种孔隙尺寸的介质时,SNMR信号呈现多指数衰减特性(Mohnke and Yaramanci, 2008),可表示为如下形式:

|
(1) |
其中,T2i*(i=1, 2, …, N)表示第i类孔隙介质对应的弛豫时间,e0i和φi分别为第i类孔隙介质产生信号的初始振幅和初始相位,ω为Larmor频率.
由式(1)可见,SNMR信号由少数具有不同弛豫时间的衰减余弦信号组成,该弛豫特性满足稀疏表示理论的基本要求,因此可将SNMR信号y表示为字典中m个原子的线性组合:

|
(2) |
其中D为冗余字典,α为稀疏系数向量. D中每一列Di为一个原子,αi为对应稀疏系数.原子应尽量包含信号的特征信息,才能获得较好的稀疏表示(Elad and Aharon, 2006;Protter and Elad, 2009).稀疏表示理论是在满足式(2)的条件下,利用尽可能少的原子来表示信号y,即为如下的优化问题:
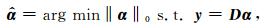
|
(3) |
其中‖‖0表示l0范数,即α中非零元素的个数.若‖α‖0=K,则称信号y的稀疏度是K.
1.2 SNMR信号提取方法设含噪SNMR信号为S=y+n,其中y为无噪SNMR信号,n为服从N(0, σ2)分布的高斯噪声(σ为噪声水平).根据噪声成分与SNMR信号特征成分弱相关的特点,含噪信号在字典D上可表示为(Deng et al., 2007)
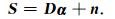
|
(4) |
因此,基于误差约束的SNMR信号提取模型可以由式(3)转化为如下优化问题(Donoho et al., 2006):
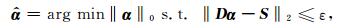
|
(5) |
其中ε为逼近残差,通常根据噪声的标准差设定.通过选择合理的字典、逼近误差及重构算法求解式(5),即可实现SNMR信号的有效提取:
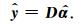
|
(6) |
字典D的选择直接影响了稀疏优化问题式(5)的求解.基于冗余字典的稀疏表示方法中,字典的组成不再要求原子间为线性独立的.只需字典中原子与信号的特征成分有较强的相关性,同时与噪声成分呈弱相关性.因此根据SNMR信号的弛豫特性,设计字典的生成函数为
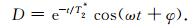
|
(7) |
根据SNMR信号的先验信息,T2*取值范围为[0.005, 1]s,用以拟合SNMR信号的衰减包络形态.ω取值范围为[ω0-10, ω0+10]Hz,用以锁定Larmor频率,其中ω0为发射频率.φ取值范围为[0, π].对参数ω,T2*,φ,t进行离散化,并分别将每个原子归一化,即得到离散衰减余弦(DDC)字典.
图 1给出了离散余弦(DCT)字典,Gabor字典(Lee,1996)及DDC字典中随机选取的两个原子,可见DDC字典中原子的衰减形态与SNMR信号的相似度最大.仿真产生SNMR信号:初始振幅为50 nV,Larmor频率为2326 Hz,T2*为0.3 s,初始相位为π/3,该信号在上述三个字典下的稀疏系数(绝对值)按照降序排列的结果(仅给出前50个较大系数)见图 1d.可以得出,SNMR信号在DCT及Gabor字典中,稀疏系数衰减过程较慢,即稀疏性较差.但是,在DDC冗余字典下SNMR信号仅有少数较大的稀疏系数,大部分系数接近于零(小于0.1),因此SNMR信号在DDC字典下稀疏性最好.

|
图 1 不同字典随机选取的两个原子的形态及SNMR信号在对应字典下的稀疏系数 (a)正交DCT字典中的原子;(b) Gabor字典中的原子;(c) DDC字典中的原子;(d) SNMR信号在不同字典下稀疏系数. Fig. 1 Two atoms selected randomly from three different dictionaries and the sparse coefficients of the SNMR signal (a) DCT dictionary; (b) Gabor dictionary; (c) DDC dictionary; (d) The sparse coefficients of different dictionary. |
实现SNMR信号提取的核心问题为对式(5)的求解,鉴于字典D的冗余性,这是一个NP-hard问题.匹配追踪(Matching Pursuit,MP)(Mallat et al., 1993)和正交匹配追踪(Orthogonal Matching Pursuit Algorithm,OMP)(Tropp et al., 2007)等贪婪类算法因为其低复杂度和较好的重建效果,得到了广泛应用.MP和OMP算法每次迭代只选择一个原子,导致重构速度较慢,且在实际应用中,当信号中混入大量噪声时,不可避免会选择错误的原子,导致重构精度降低.因此本文采用广义正交匹配追踪(gOMP)方法进行重构(Wang et al. 2012b),该算法在每一次循环中选择L个和上次迭代残差内积最大的原子,其中L≥1且L≤min(K, M/K),M为信号长度.图 2给出了对于同一仿真信号Sig1=50×(0.2×e-t/0.05+0.5×e-t/0.2+0.3×e-t/0.6)×cos(2π×2325.5×t+π/4)(单位nV),上述三种方法的重构结果及残差变化曲线,迭代次数均为20,gOMP算法中L=3.可以得出,gOMP算法在每次迭代选择多个原子加入支撑集,经过20次迭代,其重构误差较MP和OMP算法分别降低了278和68倍.

|
图 2 三种匹配追踪类算法对多弛豫SNMR信号的重构结果对比 (a)基于MP的重构结果;(b)基于OMP的重构结果;(c)基于gOMP的重构结果;(d) SNMR信号残差随迭代次数的变化. Fig. 2 Results comparison of SNMR signal reconstruction by three approaches |
gOMP算法通过在每次迭代时选取L个原子,减少了迭代次数,提高了重构精度.但针对于随机噪声环境下SNMR信号的提取,算法的迭代停止条件仍然存在问题.一方面,在实际应用中,SNMR信号的稀疏度一般无法事先确定,尤其对于野外实测SNMR信号,同一实验测区的不同测点的孔隙结构不同,其稀疏度也不相同.另一方面,残差阈值大多依靠经验选取,仅随信号的长度及信号类型的变化,自适应性较弱,严重影响含噪SNMR信号的重构精度.若阈值选取偏大,导致重构SNMR信号中含有噪声;阈值选取偏小,则导致SNMR信号部分信息丢失.本文提出了使用残差比阈值作为迭代终止条件,残差比定义如式(8):
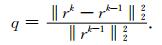
|
(8) |
其中,rk为第k次迭代的残差.在SNMR信号稀疏重构时,字典中不含有与噪声相关的原子,随着迭代次数的增加,残差分量趋于稳定,残差比在某一确定值附近波动.因此,若相邻两次迭代残差比小于设定阈值,跳出迭代,即可实现SNMR信号的有效提取,并且该方法无需根据噪声水平改变残差阈值设置.
1.3 数据流策略在SNMR野外测量中,一个脉冲矩下通常会重复采集多组独立的数据.每一组测量数据具有相同的SNMR信号成分,但是噪声成份不同.因此,本文提出一种基于数据流的SNMR信号提取策略,即将一个脉冲矩下多组测量数据首尾相连,视为一个数据流,通过整个数据流与字典的相关性进行原子的选择,并利用整个数据流参与重构系数的计算,最后提取得到唯一的一组SNMR信号.该策略不仅可以减小重构过程中受噪声的影响程度,同时保证信号提取结果的惟一性.
2 仿真结果及分析 2.1 字典参数的选择在对式(7)中参数进行离散化时,步长的选择影响着信号的重构效果和算法效率,因此本文研究了频率、T2*及相位参数离散化的优化选择方案.根据SNMR信号的特征,频率、相位采用等线性步长方案,弛豫时间采用等对数步长方案.仿真实验电脑配置为:CPU 3.4 GHz,内存16 GB.
仿真多弛豫SNMR信号(单位nV)为
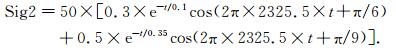
|
表 1给出了频率步长为0.5、1和2 Hz;相位步长为π/3和π/9;T2*等对数间隔离散化个数为20和50时的稀疏表示重构残差值及计算时间.重构算法采用gOMP,L=3,迭代次数为5次.由表 1可得,离散化参数越精细,字典中原子个数越多,重构效果越好,但增加了计算时间和内存消耗.因此,在满足信号提取精度的基础上,应尽量减少字典中原子数量,降低内存消耗和计算复杂度,选定合理的字典离散化方案.
|
|
表 1 字典离散化参数对SNMR信号重构结果的影响 Table 1 Performance for different dictionary parameters |
为验证本文算法的有效性,仿真生成两组单指数SNMR信号(单位nV):Sig3=50×e-t/0.05cos(2π×2325.5×t+π/6),Sig4=50×e-t/0.2cos(2π×2325.5×t+π/4),如图 3中黑色曲线所示.分别加入方差为20 nV,均值为零的同一组高斯噪声,见图 3中灰色曲线.此时,已经无法观察到明显的SNMR信号衰减趋势.利用本文提出的稀疏表示方法进行SNMR信号提取,结果见图 3中红色曲线.单指数拟合得到的SNMR信号包络如图 3中蓝色点线.基于稀疏表示的SNMR信号提取方法中,字典离散化方案为Δf=1 Hz,Δφ=π/9rad,T2*的个数为30,每次迭代选择3个相关性最大的原子,即L=3,残差比阈值q设定为0.5%(后续实验均采用此参数).由SNMR重构信号(图 3(a, d))及包络信号(图 3(c, f))可以得出,经信号提取和单指数拟合得到的SNMR信号均呈现明显衰减趋势,不存在随机噪声,且与理想SNMR信号基本重合,无明显能量损失.

|
图 3 基于稀疏表示的单指数SNMR信号提取结果 (a)单指数信号Sig3的时域图;(b) Sig3的功率谱密度;(c) Sig3的包络曲线;(d)单指数信号Sig4的时域图;(e) Sig4的功率谱密度;(f) Sig4的包络曲线. Fig. 3 Results of mono-exponential signal extraction using sparse representation method (a) T2*=0.05 s; (b) Power spectral density of Sig3; (c) Envelop of Sig3; (d) T2*=0.2 s; (e) Power spectral density of Sig4; (f) Envelop of Sig4. |
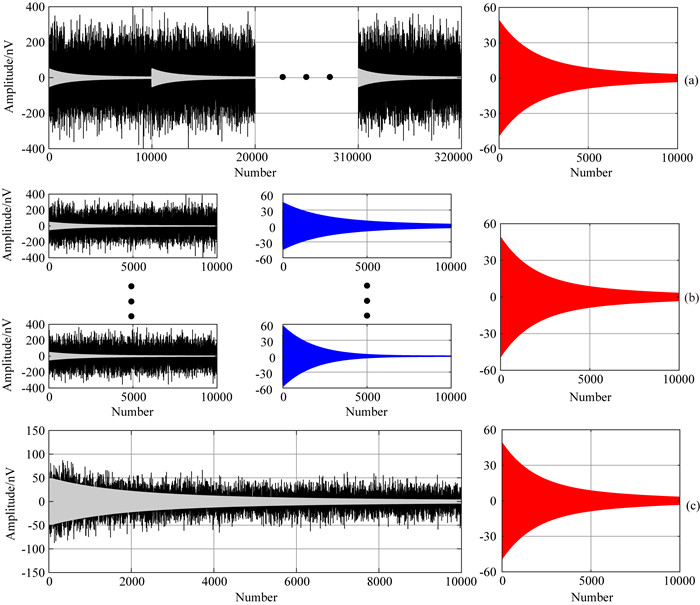
为定量评价算法性能,定义包络信号曲线的失真度为
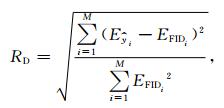
|
(9) |
其中EFIDi为SNMR信号的包络, 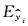
图 4给出了两组多弛豫SNMR信号的提取结果(红色曲线).其中仿真信号(单位nV)为:Sig5=50×[0.5×e-t/0.05cos(2π×2325.5×t+π/3)+0.5×e-t/0.2cos(2π×2325.5×t+π/4)]和上文给出的Sig1,加入方差为20 nV,均值为零的同一组高斯噪声.经式(9)计算,含噪信号Sig5和Sig1经稀疏表示提取得到的信号包络失真度分别为4.4%和2.6%,单指数拟合后信号包络的失真度分别为9.8%和7.7%.即对于多弛豫信号,利用文本提出的方法重构结果与无噪SNMR信号(黑线)基本一致,但利用单指数拟合方法得到的包络曲线(蓝色)误差较大.
|
图 4 基于稀疏表示的多弛豫SNMR信号提取结果 (a)多弛豫信号Sig5的时域图; (b) Sig5的功率谱密度;(c) Sig5的包络曲线;(d)单指数信号Sig1的时域图;(e) Sig1的功率谱密度;(f) Sig1的包络曲线. Fig. 4 Results of multi-exponential signal extraction using sparse representation method (a) Sig5; (b) Power spectral density of Sig5; (c) Envelop of Sig5; (d) Sig1; (e) Power spectral density of Sig1; (f) Envelop of Sig1. |
综合图 3、图 4,本文提出的基于稀疏表示的SNMR信号提取方法适用于随机噪声环境下单弛豫及多弛豫SNMR信号的提取.
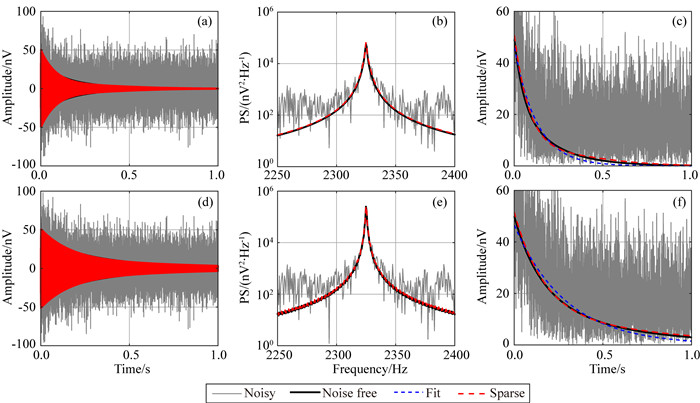
2.3 基于数据流策略的信号提取结果与对比分析本文以信号Sig1中加入方差为100 nV的高斯噪声为例进行说明,每个脉冲矩下包含32次独立采集的数据.图 5分别给出了基于稀疏表示的三种不同SNMR信号提取策略的示意图.图 5a为对长度为320000的32组数据(黑色曲线)以数据流的方式进行SNMR信号提取的过程,结果如图 5a红色曲线.图 5b中红色曲线为对32组数据分别进行SNMR信号提取的结果(蓝色曲线,只给出其中两组结果),再叠加得到的SNMR信号.由图 5b中蓝色曲线可以看出,虽然测量数据中包含相同的SNMR信号成分(灰色曲线),但是受不同随机噪声的影响,每组数据的信号提取结果存在明显差异.图 5c为对一个脉冲矩下32组数据先叠加,再对叠加后的数据进行信号提取,结果如红色曲线所示.尽管利用三种方法得到的信号质量相近,但是利用式(9)计算其信号包络失真率,结果分别为:2.1%,3.4%和2.8%.因此可以得出,基于稀疏表示的信号流提取策略优于‘先提取再叠加’和‘先叠加再提取’两种模式.
|
图 5 三种处理模式下,基于稀疏表示的信号提取 (a)基于数据流的提取策略;(b) ‘先提取,后叠加’模式,蓝色曲线为对1组含噪SNMR数据进行信号提取得到的结果;(c) ‘先叠加,后提取’模式. Fig. 5 The diagram of three different modes based on sparse representation (a) Data stream mode; (b)'extract-stack' mode; (c) 'stack-extract' mode. |
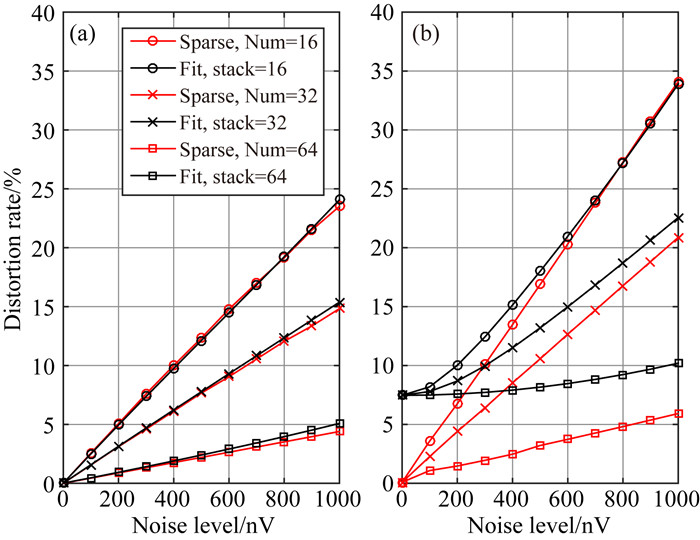
根据野外实验中仪器测量过程,仿真两组包含64次独立采集的测量数据集,其中单指数SNMR信号为Sig4,多弛豫SNMR信号为Sig5.在仿真数据中加入0~1000 nV线性增大的11组高斯噪声,分别利用稀疏表示的方法及单指数拟合方法进行SNMR信号提取,计算提取信号的包络失真度随噪声水平及测量数据叠加次数的变化曲线,如图 6所示.其中单指数方法采用先叠加,再拟合的方法,基于稀疏表示的SNMR信号提取采用2.3节中的数据流策略.
|
图 6 信号包络失真度随噪声水平及测量数据叠加次数的变化曲线 (a)单指数信号,Sig4 T2*=0.2 s;(b)多弛豫信号,Sig5. Fig. 6 The average distortion rate of reconstruction result with different noise level and the number of stack (a) Single exponential, T2*=0.2 s; (b) Multi-exponential Sig5. |
由图 6可得,单指数拟合方法和稀疏表示方法提取得到的SNMR信号的失真度均随噪声水平增大而增大SNMR,且随叠加次数的增加,信号提取失真度显著降低.对比图 6a和图 6b可得,对于单指数SNMR信号,基于稀疏表示和单指数拟合方法得到的结果基本相同;对于多弛豫SNMR信号,基于稀疏表示的信号提取结果失真度明显小于单指数拟合方法.这是由于基于gOMP的重构方法的信号稀疏表示在每次迭代中选择多个原子加入支撑集,即通过多个不同形态原子的组合实现信号逼近,而传统的单指数拟合方法仅使用单指数参数逼近SNMR信号.
由图 6b中多组失真率曲线可得,基于稀疏表示的采用数据流策略的SNMR信号提取方法,随数据组数的增多,重构性能提高水平优于传统的叠加方法,当数据组数为64时,利用本文方法得到信号失真率较传统叠加方法平均减小了3.2%.由于在信号重构过程中,采用数据流策略的SNMR信号提取方法根据多组数据的整体相关性进行原子的选择,并利用多组数据同时参与重构系数的计算,减小了信号提取过程中受噪声的影响程度.
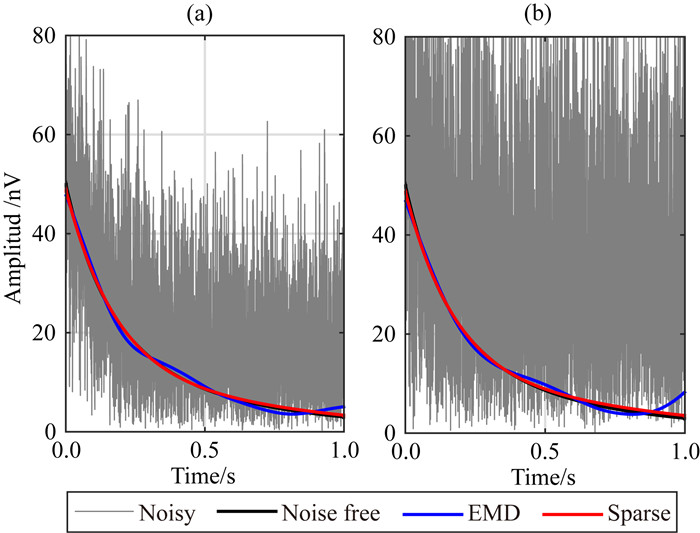
2.5 EMD方法对比为了进一步验证本文提出算法的性能,与EMD(Ghanati et al., 2016)的信号提取结果进行了对比,结果如图 7所示.仿真信号选用Sig5,分别加入方差为20 nV和40 nV,均值为零的高斯噪声.可以看出,基于EMD的信号提取结果(蓝色曲线),存在端点效应等固有缺点,且随噪声增大,模态混叠现象明显加剧(Huang et al., 1998).基于稀疏表示的信号提取结果(红色曲线)与无噪仿真信号基本重合.这是由于稀疏表示方法基于SNMR信号的弛豫特征建立冗余字典,利用具有相似特征的原子逼近信号,但是EMD属于盲源分离方法,未考虑已知的SNMR的弛豫衰减特征.图 7a及图 7b中,本文提出的基于稀疏表示的SNMR信号的失真率较EMD算法分别减小了3.3%和4.5%.
|
图 7 EMD和基于稀疏表示的方法对多弛豫SNMR信号提取结果 (a)噪声水平20 nV;(b)噪声水平40 nV. Fig. 7 Comparison between signal extraction methods based on sparse representation and EMD (a) Noise level is 20 nV; (b) Noise level is 40 nV. |
为了验证基于稀疏表示的SNMR信号提取方法的应用效果,将其应用于长春市烧锅镇获取的实测一维SNMR数据.野外实验采用单匝边长为100 m的正方形线圈,当地的地磁场为54791 nT,对应的Larmor频率为2333 Hz,变化范围小于±1 Hz,发射脉冲矩为在0.2~8.5 As间按等对数分布的20组数据,采样率为50 ksps,采集时间为0.5 s,每组脉冲矩重复采集24次.
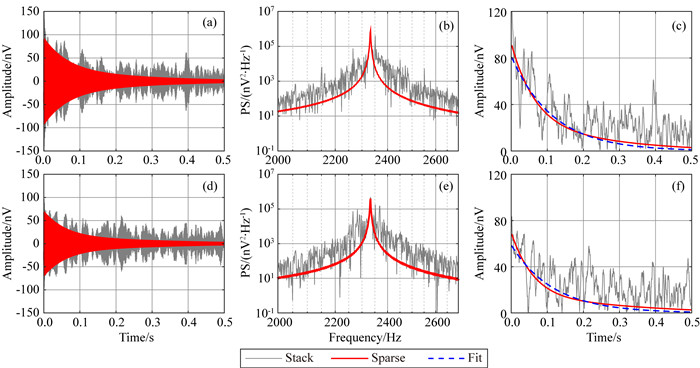
根据SNMR信号处理流程,利用MRSmatlab软件对每次采集数据分别进行了剔除尖峰噪声和谐波建模消噪(Müller-Petke et al. 2016),其中第2和第12个脉冲矩的数据处理结果、功率谱密度和信号包络如图 8中灰色曲线所示.基于稀疏表示的方法,对其进行SNMR信号提取后,结果如图 8中红色曲线所示.由图可见经信号提取后,高斯噪声显著降低且不存在能量损失.同时,图 8c和8f中单指数拟合结果(蓝色曲线),与稀疏表示方法得到的结果明显不同,证明了实测SNMR信号具有多弛豫衰减特征.
|
图 8 基于稀疏表示的实测SNMR信号提取结果 (a) Q=2,信号的时域图;(b) Q=2, 信号功率谱密度;(c) Q=2,信号包络曲线;(d) Q=12,信号的时域图;(e) Q=12,信号的功率谱密度;(f) Q=12,信号的包络曲线. Fig. 8 Results of SNMR signal extraction using sparse representation method for field data (a) Q=2, signal; (b) Q=2, power spectral density; (c) Q=2, envelop; (d) Q=12, signal; (e) Q=12, power spectral density; (f) Q=12, envelop. |
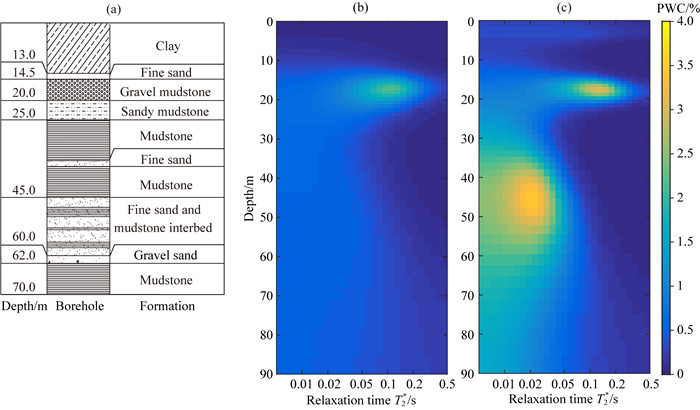
图 9a为野外实验地点的钻井资料,主要包含四个近似层状的地质结构,第一层位于地表 13 m之内,为粘土层;第二层是主要的含水层,位于地下13~25 m之间,为细砂、砂砾和粘土互层,平均含水量为12%;第三层在25~45 m之间,为粘土层;第四层在45~62 m之间,为细砂和粘土互层,平均含水量为7%.
|
图 9 实测数据一维QT反演结果 (a)钻井资料;(b)叠加后数据的反演结果;(c)经稀疏表示提取得到数据的反演结果. Fig. 9 QT inversion results of field data (a) Results of borehole logging; (b) Inversion results derived from stack data; (c) Inversion results derived from extraction signals. |
分别对24次叠加后数据和基于稀疏表示提取得到的数据进行QT反演(Müller-Petke et al., 2016),部分含水量(Partial water content,PWC)结果见图 9(b,c).可以看出,两种结果均显示位于13~25 m之间存在的主要含水层,但是叠加后数据的反演结果对于45~62 m的较深含水层,总含水量偏小,平均为3.5%,而且无法得到准确的弛豫时间.而基于稀疏表示方法提取的SNMR信号反演结果,较深水层的总含水量分别为8.6%,反演准确度均提高了2倍以上.从反演结果还能获得较深水层的弛豫时间(约为0.02 s,对应粘土层)和位置(37.98~62.35 m),因此可以证明利用提取后信号反演,分辨率明显提高,反演结果与钻井资料一致.可见,本文提出的基于稀疏表示的SNMR信号提取方法,可以有效的去除高斯噪声对反演结果的影响,提高深部含水体的识别能力.
4 结论本文针对多弛豫SNMR信号微弱、组分复杂且受噪声干扰严重等问题,首次将稀疏理论应用于地面磁共振地下水探测领域,提出了基于稀疏表示的多弛豫SNMR信号提取方法,并通过仿真和实测数据实例证明了该方法显著提高了SNMR信号质量,降低随机噪声对反演结果的影响,提高SNMR的探测和分辨能力.
基于SNMR先验特征信息,设计了刻画SNMR信号且与随机噪声不相关的离散衰减余弦冗余字典.在稀疏分解过程中,从SNMR信号的特征(而不是测量数据)角度出发,对信号进行描述,因此可以得到比在DCT和Gabor字典中更为稀疏的表示结果.
鉴于多弛豫SNMR信号组成特征,采用gOMP稀疏重构算法,每次迭代过程中通过多个原子的线性组合逼近信号.在相同的迭代次数下,可以得到比MP和OMP更精确的重构结果.改进的gOMP盲稀疏度重构算法,通过设置合理的残差比阈值控制迭代次数,无需根据噪声水平改变阈值设置,提高了算法的自适应性和普适性.
针对SNMR野外测量中一个脉冲矩下进行多次独立重复采集的特点,通过多组数据整体相关性进行原子的选择和重构系数的计算,提出了基于稀疏表示的信号流提取策略,提取效果优于‘先提取再叠加’和‘先叠加再提取’两种提取模式.该方法不仅大大减小了重构过程中受噪声的影响程度,同时保证了信号提取结果的唯一性.
Ahmed N, Natarajan T, Rao K R. 1974. Discrete cosine transform. IEEE Transactions on Computers, 100, 23(1): 90-93. |
Beckouche S, Ma J M. 2014. Simultaneous dictionary learning and denoising for seismic data. Geophysics, 79(3): A27-A31. DOI:10.1190/geo2013-0382.1 |
Behroozmand A A, Keating K, Auken E. 2015. A review of the principles and applications of the NMR technique for near-surface characterization. Surveys in Geophysics, 36(1): 27-85. DOI:10.1007/s10712-014-9304-0 |
Costabel S, Müller-Petke M. 2014. Despiking of magnetic resonance signals in time and wavelet domains. Near Surface Geophysics, 12(2): 185-197. |
Dalgaard E, Auken E, Larsen J J. 2012. Adaptive noise cancelling of multichannel magnetic resonance sounding signals. Geophysical Journal International, 191(1): 88-100. DOI:10.1111/gji.2012.191.issue-1 |
Deng G, Tay D B H, Marusic S. 2007. A signal denoising algorithm based on overcomplete wavelet representations and gaussian models. Signal Processing, 87(5): 866-876. DOI:10.1016/j.sigpro.2006.08.008 |
Donoho D L, Elad M, Temlyakov V N. 2006. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Transactions on Information Theory, 52(1): 6-18. DOI:10.1109/TIT.2005.860430 |
Elad M, Aharon M. 2006. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing, 15(12): 3736-3745. DOI:10.1109/TIP.2006.881969 |
Ghanati R, Fallahsafari M, Hafizi M K. 2014. Joint application of a statistical optimization process and Empirical Mode Decomposition to Magnetic Resonance Sounding Noise Cancelation. Journal of Applied Geophysics, 111: 110-120. DOI:10.1016/j.jappgeo.2014.09.023 |
Ghanati R, Hafizi M K, Mahmoudvand R, et al. 2016. Filtering and parameter estimation of surface-NMR data using singular spectrum analysis. Journal of Applied Geophysics, 130: 118-130. DOI:10.1016/j.jappgeo.2016.04.005 |
Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
Jiang C D, Lin J, Duan Q, Sun S M, et al. 2011. Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements. Near Surface Geophysics, 9(5): 459-468. |
Larsen J J, Dalgaard E, Auken E. 2014. Noise cancelling of MRS signals combining model-based removal of powerline harmonics and multichannel Wiener filtering. Geophysical Journal International, 196(2): 828-836. DOI:10.1093/gji/ggt422 |
Larsen J J, Behroozmand A A. 2016. Processing of surface-nuclear magnetic resonance data from sites with high noise levels. Geophysics, 81(4): WB75-WB83. DOI:10.1190/geo2015-0441.1 |
Lee T S. 1996. Image representation using 2D Gabor wavelets. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18(10): 959-971. DOI:10.1109/34.541406 |
Legchenko A, Valla P. 1998. Processing of surface proton magnetic resonance signals using non-linear fitting. Journal of Applied Geophysics, 39(2): 77-83. DOI:10.1016/S0926-9851(98)00011-1 |
Legchenko A, Valla P. 2002. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
Legchenko A, Valla P. 2003. Removal of power-line harmonics from proton magnetic resonance measurements. Journal of Applied Geophysics, 53(2-3): 103-120. DOI:10.1016/S0926-9851(03)00041-7 |
Lin J, Jiang C D, Lin T T, et al. 2013. Underground magnetic resonance sounding (UMRS) for detection of disastrous water in mining and tunneling. Chinese Journal of Geophysics (in Chinese), 56(11): 3619-3628. DOI:10.6038/cjg20131103 |
Müller-Petke M, Costabel S. 2014. Comparison and optimal parameter setting of reference-based harmonic noise cancellation in time and frequency domain for surface-NMR. Near Surf Geophys, 12(2): 199-210. |
Müller-Petke M, Braun M, Hertrich M, et al. 2016. MRSmatlab-A software tool for processing, modeling, and inversion of magnetic resonance sounding data. Geophysics, 81(4): WB9-WB21. DOI:10.1190/geo2015-0461.1 |
Mallat S, Zhang Z F. 1993. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41(12): 3397-3415. DOI:10.1109/78.258082 |
Mohnke O, Yaramanci U. 2008. Pore size distributions and hydraulic conductivities of rocks derived from magnetic resonance sounding relaxation data using multi-exponential decay time inversion. Journal of Applied Geophysics, 66(3-4): 73-81. DOI:10.1016/j.jappgeo.2008.05.002 |
Plata J, Rubio F. 2002. MRS experiments in a noisy area of a detrital aquifer in the south of Spain. Journal of Applied Geophysics, 50(1-2): 83-94. DOI:10.1016/S0926-9851(02)00131-3 |
Protter M, Elad M. 2009. Image sequence denoising via sparse and redundant representations. IEEE Transactions on Image Processing, 18(1): 27-35. |
Strehl S, Rommel I, Hertrich M, et al. 2006. New strategies for filtering and fitting of MRS signals. //Proceedings 3rd International MRS Workshop. Madrid, Spain, 65-68.
|
Tian B F, Zhou Y Y, Wang Y, et al. 2015. Noise cancellation method for full-wave magnetic resonance sounding signal based on independent component analysis. Acta Physica Sinica (in Chinese), 64(22): 0229301. |
Tropp J A, Gilbert A C. 2007. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
Wan L, Zhang Y, Lin J, et al. 2016. Spikes removal of magnetic resonance sounding data based on energy calculation. Chinese Journal of Geophysics (in Chinese), 59(6): 2290-2301. DOI:10.6038/cjg20160631 |
Wang W, Gao J H, Chen W C, et al. 2012a. Data adaptive ground-roll attenuation via sparsity promotion. Journal of Applied Geophysics, 83: 19-28. DOI:10.1016/j.jappgeo.2012.04.004 |
Wang J, Kwon S, Shim B. 2012b. Generalized orthogonal matching pursuit. IEEE Transactions on Signal Processing, 60(12): 6202-6216. DOI:10.1109/TSP.2012.2218810 |
Xiao L Z, Xie Q M, Xie R H, et al. 2013. Noise reduction for NMR logging with regularization-heursure algorithm. Chinese Journal of Geophysics (in Chinese), 56(11): 3943-3952. DOI:10.6038/cjg20131136 |
Zhu L C, Liu E T, McClellan J H. 2015. Seismic data denoising through multiscale and sparsity-promoting dictionary learning. Geophysics, 80(6): WD45-WD57. DOI:10.1190/geo2015-0047.1 |
林君, 蒋川东, 林婷婷, 等. 2013. 地下工程灾害水源的磁共振探测研究. 地球物理学报, 56(11): 3619-3628. DOI:10.6038/cjg20131103 |
田宝凤, 周媛媛, 王悦, 等. 2015. 基于独立成分分析的全波核磁共振信号噪声滤除方法研究. 物理学报, 64(22): 0229301. |
万玲, 张扬, 林君, 等. 2016. 基于能量运算的磁共振信号尖峰噪声抑制方法. 地球物理学报, 59(6): 2290-2301. DOI:10.6038/cjg20160631 |
肖立志, 谢庆明, 谢然红, 等. 2013. 核磁共振测井的正则化-启发式阈值降噪研究. 地球物理学报, 56(11): 3943-3952. DOI:10.6038/cjg20131136 |
 2018, Vol. 61
2018, Vol. 61


