对于多分量地震勘探来说，浅层的低速带常导致地震射线竖直出射地表，因此可以假设纵、横波是天然解耦的，即垂直分量主要接收纵波，水平分量主要接收横波(Gaiser，1999).但是这种假设在各向异性较强或基岩出露的地区难以成立；尤其当偏移距较大时，会产生波型泄漏现象，即水平分量与垂直分量都接收到纵波与横波的部分偏振投影(Lu and Margrave, 1999; Guevara and Cary, 1999).当地层中发育裂缝时，波型泄漏会变得更加复杂；裂缝会导致横波分裂现象的发生，使得三个分量都会接收到纵波与快慢横波(S1波与S2波)的部分能量.波型泄漏在很大程度上影响了波场的识别以及后续多分量数据的偏移成像与解释.压制波型泄漏现象，即矢量波场分离，是多分量地震数据处理的一个重要方面，也是难点所在(王赟等，2017).目前发展的算法主要有三大类：一类是利用纵波与转换横波时距曲线的差异进行波场分离，典型的方法有在f-k滤波(Dankbaar，1985)、τ-p滤波等(Stoffa et al., 1981；Donati，1996；Donati and Stewart, 1996).第二类是极化滤波方法，例如正交假设下的偏振方向滤波(Flinn，1965；Morozov and Smithson, 1996；Lu et al., 2010)、协方差矩阵特征值分析或解析信号分析极化滤波等(Samson and Olson, 1981；Benhama et al., 1988；Jurkevics, 1988；Bataille and Chiu, 1991；Cho and Spencer, 1992；Perelberg and Hornbostel, 1994；de Franco and Musacchio, 2001).近几年，在极化滤波方法体系中，仿射坐标系的旋转变换方法得到发展.仿射坐标系的坐标轴之间可以是非正交的，用不同模式波场的极化方向建立仿射坐标系，有利于波场的彻底分离.Lei (2005)基于天然地震信号，证明了不同模式的波场可以仿射坐标系的旋转变换完全分开.姚陈(2006)认为纵波与横波的震动方向是斜交的，提出了在仿射坐标系内分解矢量波场的思路.Lu等(2012)实现了地面多分量地震数据的仿射坐标系波场分离.第三类方法是基于波动方程的纵横波分离方法，在深度域速度模型比较精确的情况下，求取散度与旋度，得到纯净的纵波与横波.Sun(1999)用亥姆霍茨分解和波场延拓求取散度与旋度，以得到分离后的纵横波.Yan和Sava(2009)基于散度与旋度构建了介质中每个离散网格的波场分离算子.Wang等(2012)用波场延拓方法实现了VTI介质的纵横波波场分离.以上方法都能在一定程度上实现波场分离，但是前两类方法都是考虑压制垂直分量上的横波信息以及水平分量上的纵波信息，所以是不保幅的.对于波型泄漏较为严重的多分量地震数据，垂直分量上的横波信息以及水平分量上的纵波信息都是有用的波场.第三类方法依赖于精确的层速度模型，对于各向异性介质，还需要建立深度域各向异性参数模型.在实际应用中，尤其是针对裂缝地层，第三类方法很难付诸实施.考虑将纵波与发生分裂的横波波场从三个分量上分离并恢复矢量振幅是近几年波场分离领域研究的难点.

在本文中，我们将提出一种能够适用于实际数据的裂缝各向异性介质的纵波与分裂横波的波场分离方法，属于上述方法中的第二类.对于实际多分量地震数据，纵波与分裂横波都是矢量波场，压制波型泄露的过程实际上就是恢复矢量波场的振幅特性，其关键是波矢方向的求解与坐标系的旋转.在某一时刻，纵波与横波具有完全不同的波矢方向，理论上它们都是线性偏振的；但是为了保留储层的各向异性信息，实际的多分量地震数据采集采用了无组合的单点接收方式，多分量地震数据往往具有较低的信噪比，使得某一时窗内地震波的振动轨迹杂乱无章，导致波矢方向求解的难度(黄中玉，2005).波矢方向的求解首先在VSP(Vertical Seismic Profile，垂直地震剖面法)勘探领域得到研究.在VSP观测系统中，纵横波波矢方向常常被认为相互垂直，并可以通过将笛卡尔直角坐标系进行旋转扫描来确定.Amano(1995)在频率-深度域提出VSP纵横波矢量分离的解析解.石瑛(2005)、石瑛等(2007)基于矢端振动图分析求解了VSP波矢量方向，并通过三步坐标旋转波场分离与合成的方法，较好地分离了纵波与快、慢横波.Lu等(2012)在炮集上利用波矢叠加法实现了仿射坐标系内的波矢方向求解，并成功在叠前实现了纵横波波场分离.本文将对波型泄露现象进行理论上的阐述，将裂缝介质的波场分离分解成更容易实施的三个步骤，提高了裂缝方位角与快慢横波时差求解的精度，并通过实际数据的例子证实了该方法的有效性.

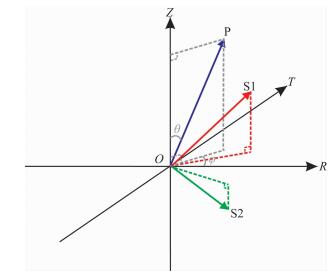
在三分量地震勘探中，检波器的原始X方向是沿着测线方向的，Y方向与之垂直，而Z分量则与地面垂直.坐标系Z-X-Y满足右手直角坐标系准则.三分量地震数据的处理首先是进行水平分量的旋转处理，使得X分量指向震源方向(即径向分量R)，Y分量与之正切(也称为切向分量T).在各向同性水平地层假设下，Z、R分量都将接收到纵、横波的偏振投影，T分量上主要为噪声.实际上的地球介质是非水平各向异性的.当地下介质发育裂缝时，横波发生分裂形成S1波与S2波.当震源相对检波器的方位与裂缝方位斜交时，P波与分裂的S波都会在检波器的三个分量上产生投影.每个单一分量上记录的波场都是纵波与分裂横波的混合波，即发生波型泄露现象.如图 1所示，笛卡尔直角坐标系Z-R-T中，用P、S1、S2分别表示P、S1、S2波的矢量，则

(1)

图 1

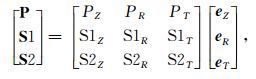
Fig. 1

图 1 Z-R-T坐标系下的波矢量示意图 Fig. 1 Schematic of wave vectors in Z-R-T coordinates

其中，e_Z、e_R、e_T分别为Z、R和T分量上的基矢量.

P_R与P_T分别表示P波在R、T分量上的波型泄露.P_Z表示P波矢量的主要偏振.在裂缝介质中P_Z、P_R与P_T是等时的.

与纵波相比，横波的波型泄露机制比较复杂.在方位各向异性介质中，沿着每一条射线路径，在与射线方向垂直的平面内，原始横波将分裂为偏振方向沿各向异性方向的快横波以及偏振方向与之垂直的慢横波.由于偏振方向不同，传播速度不同，因此到达接收点时分裂横波之间存在时延.由于检波器接收分量的极性方向与快、慢波偏振方向一般不重合，因此，快、慢横波的能量在三个接收分量上都存在，并在时延小于横波周期时复合在一起，使得波场更加复杂.对于高速或强各向异性的近地表条件，除了有快、慢横波的干涉，复合，纵、横波波场的混杂也导致了多波波场的复杂性.一般地层在形成过程中，由于在不同时期受到的地应力不同，地层从浅至深发育裂缝的裂缝密度以及方位角都有差异，震源激发的P波，产生反射转换S波，S波在穿过地层时会发生多波横波分裂，产生偏振方向不同的S1、S2波，并被地表Z、R、T检波器接收.本文假设波矢量分析的时窗包含了完整的分裂横波信息，所以S1波与S2波的波矢方位之间的夹角为90°，则

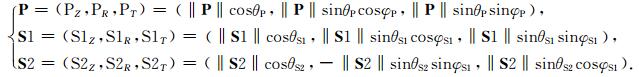
(2)

在三分量地震勘探中，我们常把R、T分量上接收到的横波分别称为SV波与SH波.实际上，这两个波场都是快慢横波形成的复合波的部分偏振：

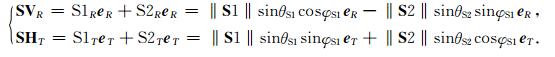
(3)

在Z分量上，横波的泄露可以描述为：

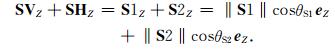
(4)

所以，在三分量地震勘探中，直接把R、T分量上的波场看成SV波与SH波是不准确的.为了获得真振幅的纵横波波场，需要将三个分量上的波场进行分解，在每个分量上拆分不同模式的波型，并将三个分量上的同模式波型进行合成，以确保获得真振幅的矢量波场.

针对方位各向异性介质，波场分离的最终目标是获得纯净的P、S1、S2波矢量波场.我们将波场分离分解成三个步骤实施：步骤1，Z、R分量仿射坐标系旋转得到ZR平面内的P波投影(用PV波矢量PV来表示，是P波波场分离过程的中间数据)与SV矢量；步骤2，将PV与T分量仿射坐标系旋转得到P与SH矢量；步骤3，将纯净的SV与SH偏移剖面通过Alford旋转得到S1剖面与S2剖面，并提取裂缝参数(Alford，1986).

步骤1：由矢量PV与SV建立坐标系PV-O-SV，则

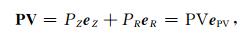
(5)

其中，PV为矢量PV的模，e_PV为PV振动方向上的基矢量.则波场分离公式：

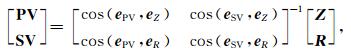
(6)

式(6)省略了时间项，则表示每个矢量可以位于任一时间样点，Z、R表示Z、R两个分量上的波矢量.公式(6)表示一种二分量仿射坐标系的旋转变换，PV与SV的夹角可以不是直角.该变换的关键是获得新旧坐标系基矢量之间的夹角，主要是e_PV与e_SV的真实矢量方向.Lu等(2012)提出了适用于二分量地震数据的波矢叠加法，可以在低信噪比条件下有效估算波矢方向.波矢叠加法可以适用于公式(6)中的波矢量方向的求解，详细过程本文不再赘述.

步骤2：将步骤1求解的波矢量PV与矢量T建立坐标系PV-O-T，并将其旋转至坐标系P-O-SH，得到

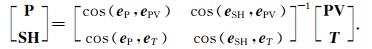
(7)

至此，我们可以在叠前获得纯净的P波、SV波与SH波矢量波场，对这些波场可以进行偏移成像.

步骤3：基于SV波与SH波剖面，我们可以利用Alford旋转来得到快慢横波剖面，并对裂缝方位与快慢横波时差进行预测.Alford旋转公式如下：

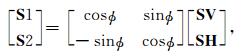
(8)

其中ϕ为裂缝方位角(即波矢量S1的方向).通过一系列角度β进行快慢横波分离：

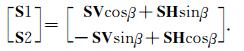
(9)

可知，当β=ϕ时，快、慢横波完全分离.同时进行时延Δt扫描：

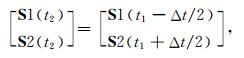
(10)

当Δt为快慢横波时差时，在t₁时刻计算快慢横波波场在t₂时刻对齐.快慢横波波场是否对齐可以采用波型互相关方法来确定，一般来说，当SV与SH剖面的地震子波匹配程度较高时，快慢横波时差正好消除，其相关系数也最高.S1波与时差消除后的S2波可以直接合成为各向同性的S波，用来后续进行结构成像或者岩心反演.S2波时移后会产生一个残差，如果残差很小，则说明S1波与S2波得到良好匹配，各向异性效应消除的更加彻底.

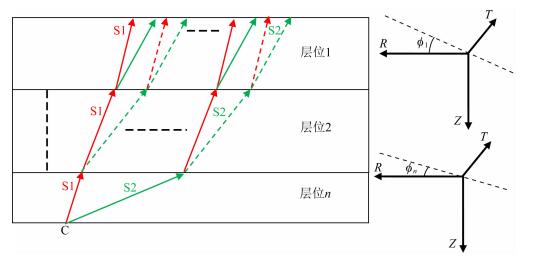
对于多套裂缝系统的地层，快慢横波的分离需要通过剥层来实现.实际地层中会有很多层位的裂隙发育程度低，接近各向同性介质或VTI介质，如图 2中的层位2，此时可以假设横波分裂也会发生，即存在虚拟的S1波与S2波.在旋转处理时，由于S2波能量为0，所以在任意角度进行波场分离时变化不大，则旋转角度为0.剥层处理时，先确定时窗长度，从浅层开始，确定旋转角第一层介质的裂缝方位角ϕ₁，进行快、慢横波分离.窗口内可能存在来自包括较深层位的多个快、慢横波同相轴，由于窗口内层位的一次反射PS波能量最强，横波分裂时差最小，所以将这两个同相轴提取出来，用互相关方法确定时差大小，同时校正快、慢横波振幅值，对慢横波数据进行时移，并压制多次分裂波型转换的波场.依次类推，最终只保留图 2所示的CS1S1S1波与CS2S2S2波.利用分离后快、慢波剖面可确定各向异性系数K_c，

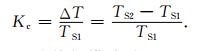
(11)

图 2

Fig. 2

图 2 多层含裂缝介质中的横波分裂 Fig. 2 Shear wave splitting in multi-layer crack-bearing strata

其中，T_S2－T_S1为快慢横波时差，可以描述地下介质的方位各向异性程度，即地下裂隙发育的程度.

在步骤2中，得到SV波与SH波的矢量波场还可以采取另一种方案做进一步处理：各向异性的叠前消除，即将SV波与SH波的矢量波场直接在叠前道集上分离快慢横波，然后将快慢横波之间的时差消除后还原成横波分裂发生之前的S波.这样各向异性波场蜕变为各向同性波场，可以用来做地层的结构成像以及各向同性弹性参数的反演.

在该数值模拟中，我们将对比本文介绍的仿射坐标系波场分离方法与特征矩阵特征值分解法波场分离效果.特征矩阵特征值分解法在Benhama等(1988)的文章中有详细的介绍，其做法是将一个给定时窗内的Z、R、T分量地震数据计算一个协方差矩阵，这个协方差矩阵的第一、第二以及第三特征值分别代表了第一、第二以及第三极化方向，可认为分别是P、SV以及SH波的极化方向；但是，该方法假设不同的波矢量是正交的，然后通过正交坐标系的旋转变换来分离不同的波矢量.抛弃T分量不考虑，特征矩阵特征值分解法也可以用来分离P与SV波.实际上，由于偏移距的存在，地震射线一般都是倾斜出射地表的，所以叠前的地震波是难以满足正交假设的.我们的方法可以认为是在特征矩阵特征值分解法的基础上存在两点改进：(1)P与SV的波矢方向是斜交的；(2)将基于正交坐标系的旋转变换改为非正交的仿射坐标系旋转变换.由于对纵横波波场做了非正交极化的假设，我们的波场分离方法将更满足实际情况.

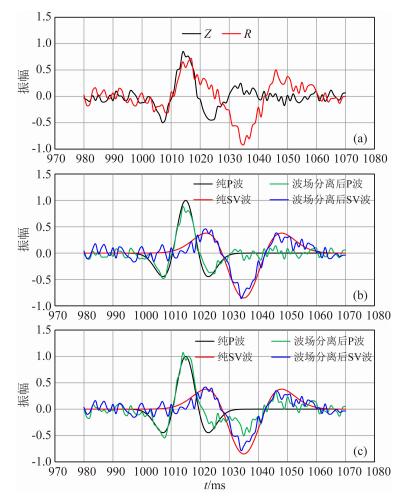
如图 3a所示的合成Z与R分量的地震记录，各自加入了10%的随机噪声；其中P波矢量振幅为1，与Z轴正方向夹角为顺时针方向30°；SV波矢量振幅为-0.85，与Z轴正方向夹角为顺时针方向100°.由于P、SV波与Z、R轴之间都是斜交的，所以存在波型泄露问题.我们分别用了特征矩阵特征值分解法(图 3b)与仿射坐标系旋转变换方法(图 3c)进行了P与SV波的分离对比.可以看出，特征矩阵特征值分解法没有能彻底分离出P、SV波场；尤其是分离后的P波分量，在1035 ms附近的横波泄露还有很强的能量.仿射坐标系旋转变换获得了很好的波场分离效果，与纯P、SV波的曲线图相比，波场分离后得到的P、SV波曲线与真实曲线吻合度很高，波型泄露问题得到很好解决.

图 3

Fig. 3

图 3 P与SV波分离对比 (a)模拟的Z、R分量记录，加入了10%的随机噪声；(b)仿射坐标系旋转法分离的P与SV波；(c)特征矩阵特征值分解法分离的P与SV波. Fig. 3 Comparison of P- and SV-wave separation (a) Synthetic Z- and R-component records added with 10% random noise; (b) P- and SV-wave separation results by the affine coordinate system rotation; (c) P- and SV-wave separation results by the eigenvector-eigenvalue decomposition.

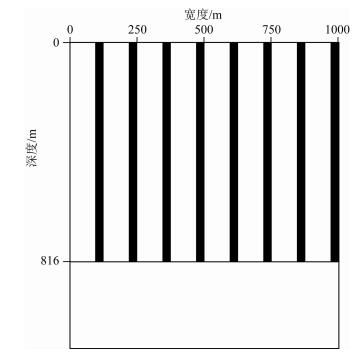
模型2采用了水平地层二维模型，如图 4所示，模型宽度1000 m，第一层发育单组裂缝，第二层为各向同性地层，炮点在模型左端点.如图 5所示，数值模拟采用了反射率法(姚陈等，1999).由于地层水平，P波泄露只在R分量上出现；但由于裂缝诱导的方位各向异性，转换横波在Z、R、T三个分量上都有较强的能量.横波发生分裂并形成复合波，R、T分量上的转换横波表现出不同的相位特征，但Z、R两分量的转换横波相位特征相同.在该模型中，PSH波泄露并没有在Z分量上出现，所以我们只实施了Z、R分量的波场分离来得到纯净的PP波与PSV波；然后直接在单炮上用PSV波与PSH波分离出PS1波与PS2波.

图 4

Fig. 4

图 4 裂缝模型示意图 第一层：纵波速度2400 m·s-1，快横波速度1200 m·s-1，密度2.0 g·cm-3，厚度800 m，裂隙密度0.1，裂缝方位角45°；第二层：纵波速度2500 m·s-1，快横波速度1300 m·s-1，密度2.1 g·cm-3，厚度300 m. Fig. 4 Sketch of crack model The first layer: P-wave velocity 2400 m·s-1, S1-wave velocity 1200 m·s-1, density 2.0 g·cm-3, thickness 800 m, crack density 0.1, crack azimuth 45 degree. The second layer: P-wave velocity 2500 m·s-1, S1-wave velocity 1300 m·s-1, density 2.1 g·cm-3, thickness 300 m.

图 5

Fig. 5

图 5 反射率法模拟的三分量记录 (a) Z分量；(b) R分量；(c) T分量. Fig. 5 Synthetic three-component records by reflectivity method (a) Z-component; (b) R-component; (c) T-component.

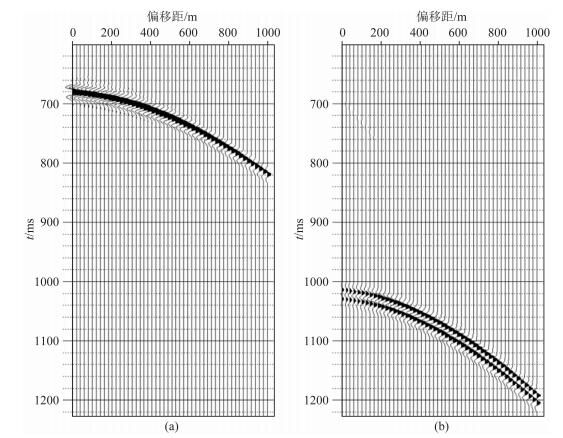
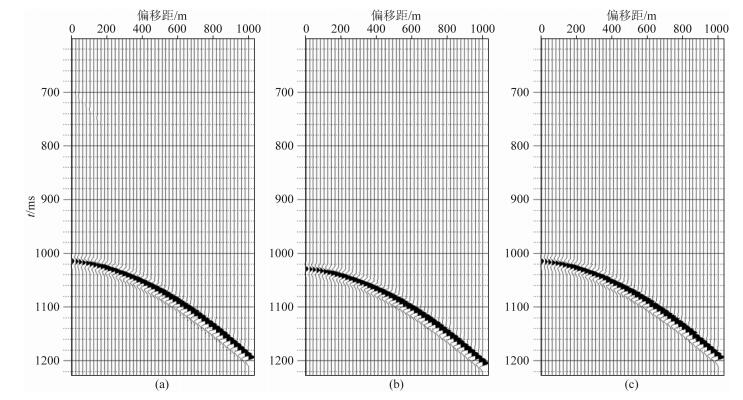
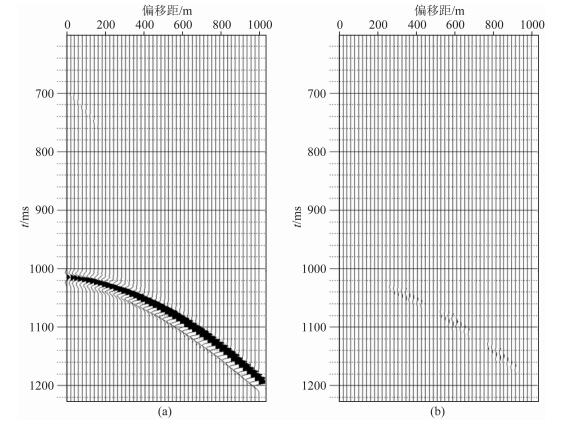
图 6为Z、R两分量进行波场分离的结果，可以看出Z分量上的PSV波泄露与R分量上PSV波偏振投影合成了真振幅的PSV波(图 6b)；同时R分量上的PP波泄露也得到压制，PP波的矢量振幅得到恢复(图 6a).图 7为PS1波与PS2波叠前分离结果，时差得到校正，振幅得到较好恢复；波场分离后，子波由之前PSV与PSH波的双相位子波恢复为PS1与PS2波的零相位子波.图 8为PS波矢量合成的结果，矢量合成后的PS2波残余能量较弱，说明PS1与PS2波波场得到很好分离.

图 6

Fig. 6

图 6 PP波与PSV波波场分离结果 (a) PP波；(b) PSV波. Fig. 6 Wave separation results of PP- and PSV-waves (a) PP-wave; (b) PSV-wave.

图 7

Fig. 7

图 7 PS1波与PS2波分离结果 (a) PS1波；(b) PS2波；(c)消除时差后的PS2波. Fig. 7 Wave separation results of PS1- and PS2-waves (a) PS1-wave; (b) PS2-wave; (c) PS2-wave after delay correction.

图 8

Fig. 8

图 8 PS1波与消除时差后的PS2波合成PS波结果 (a)合成PS波；(b) PS2波残余. Fig. 8 Composite PS-wave vector using PS1-wave and PS2-wave after delay correction (a) Composite S-wave; (b)Residual of PS2-wave.

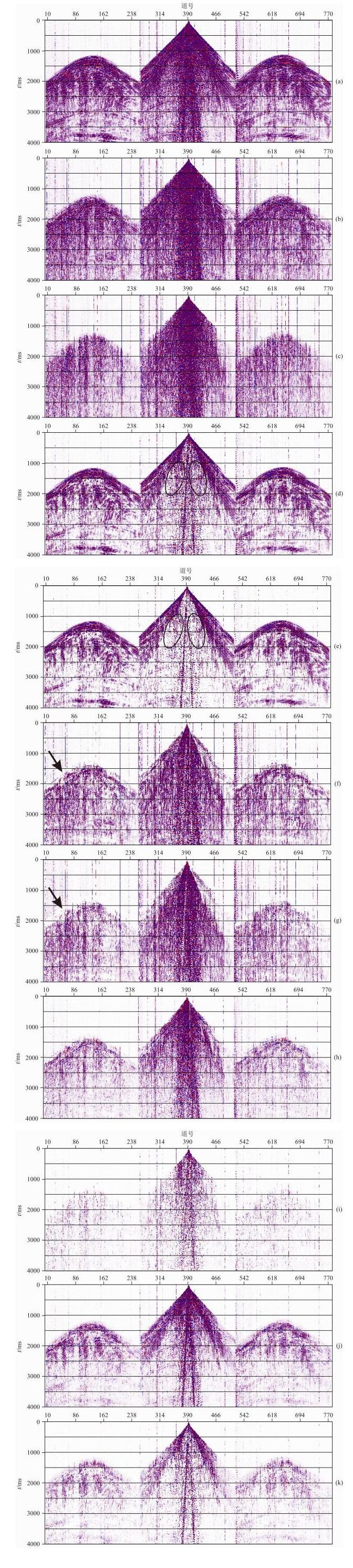
实际数据测试采用了四川西南新场靠近新851与新853井附近的3D3C地震数据，该工区的须二段为目标层段，裂缝广泛发育.须二段上覆地层发育多套不同方位的裂缝系统，所以我们采用了50 ms滑动时窗，对三分量单炮数据进行了矢量波场分离与偏移剖面上的快慢横波分离.单炮数据进行过程度较弱的随机噪声与面波压制以及三分量一体化振幅补偿.图 9所示为3D3C单炮数据的矢量波场分离结果，可以看出矢量波场分离后SV波与SH波泄露在分离后的P波记录上得到很好压制(如图 9d与9e的椭圆框处)；图 9f与9g的箭头指示处可以看出，在波场分离后的SV波与SH波记录上，P波泄露(主要为初至)得到衰减.图 9h与9i分别为Z分量上的SV波泄露与SH波泄露，这些横波泄露与波场分离后的SV波(图 9f)与SH波(图 9g)的时距曲线特性非常相似；同样，图 9j与9k显示的R分量与T分量上的P波泄露与波场分离后的P波(图 9e)时距曲线高度相似.所以，波型泄露虽然直接在三分量单炮记录(图 9a、9b和9c)难以用肉眼直接识别，实际上这些泄露的波场能量是很强的，如果不加以提取利用，后续的解释与反演结果都将不可靠.

图 9

Fig. 9

图 9 实际3D3C炮集数据矢量波场分离结果 (a) Z分量；(b) R分量；(c) T分量；(d) Z、R两分量波场分离后的PV波；(e) PV波与T分量波场分离后的P波；(f) Z、R两分量波场分离后的SV波；(g) PV波与T分量波场分离后的SH波；(h) Z分量上的SV波泄露；(i) Z分量上的SH波泄露；(j) R分量上的P波泄露；(k) T分量上的P波泄露. Fig. 9 Wave separation results of field 3D3C records (a) Z-component; (b) R-component; (c) T-component; (d) PV-wave after Z- and R-component wave separation; (e) P-wave after PV-wave and T-component wave separation; (f) SV-wave after Z- and R-component wave separation; (g) SH-wave after PV-wave and T-component wave separation; (h) SV mode leakage in Z-component; (i) SH mode leakage in Z-component; (j) P mode leakage in R-component; (k) P mode leakage in T-component.

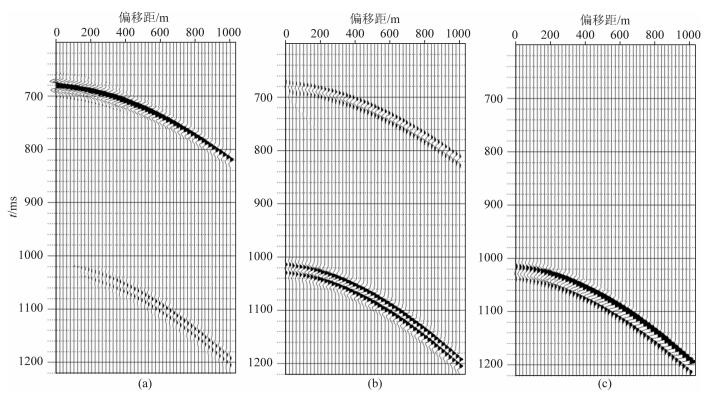
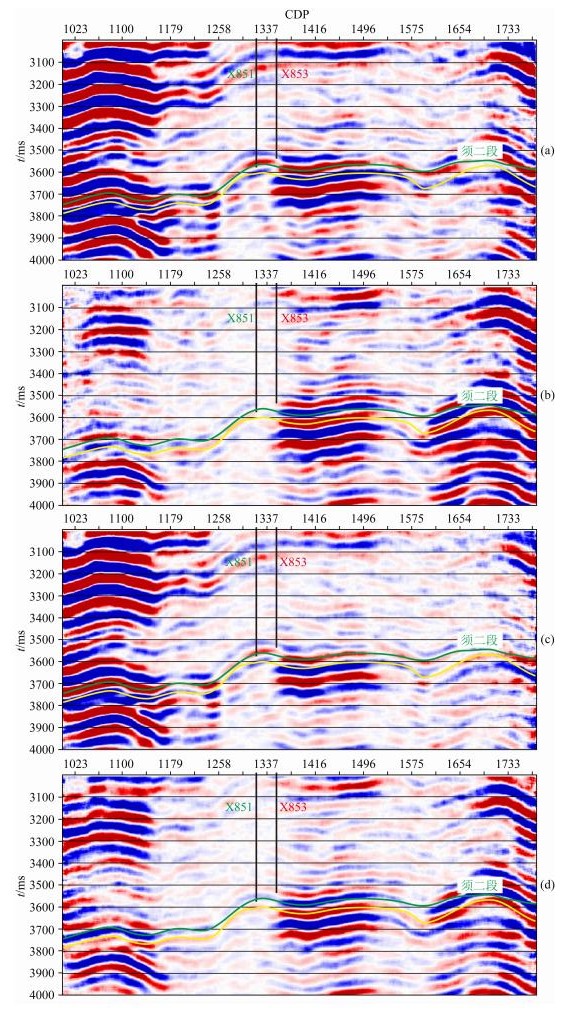
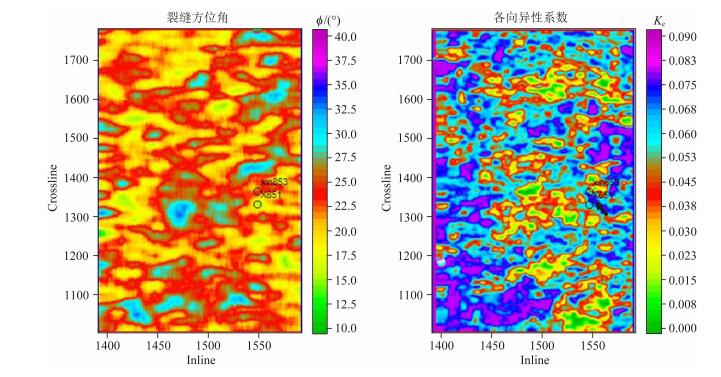
我们对波场分离后的三分量地震记录进行了三分量叠前时间偏移，得到转换横波PSV波剖面(图 10a)与PSH波剖面(图 10b)，再进一步进行剥层法快慢横波分离，得到PS1波剖面(图 10c)与PS2波剖面(图 10d).图 10中的绿色与黄色层位分别为须二段的PS1与PS2波反射层位，可见快、慢波分离前，PSV波与PSH波偏移剖面上都有PS1、PS2波的投影，PSV与PSH波场的能量视觉上很平均；快、慢波分离后，从浅至深的PS1、PS2波能量很好分离，并且S1波能量要明显强于S2波能量，时差也比较明显.图 11为提取的须二段沿层裂缝参数，可见该层段裂缝角度在正北偏西约18°~28°(图 11a).从各向异性系数图(图 11b)上可以看出，在箭头所指的新851与新853井之间以及蓝紫色区域的各向异性系数普遍在0.07以上，表明裂缝发育程度较高.该预测结果与该地区实际油气田开发动态资料相一致.

图 10

Fig. 10

图 10 剥层快、慢横波分离前后波场对比(滑动时窗为50 ms) 绿色与黄色层位分别在PS1与PS2剖面上拾取. (a) PSV波；(b) PSH波；(c) PS1波；(d) PS2波. Fig. 10 Comparison of layer-stripping fast and slow shear wave separation results The green and yellow horizons are picked on the PS1 and PS2 sections, respectively. (a) PSV-wave; (b) PSH-wave; (c) PS1-wave; (d) PS2-wave.

图 11

Fig. 11

图 11 须二段裂缝参数(正北方向为0°，逆时针方向为正) Fig. 11 Crack parameters of Xu Ⅱ member (the north azimuth is zero and the positive azimuth is anticlockwise)

本文提出一种适用于裂缝预测的方位各向异性介质的矢量波场分离方法，并对该方法进行了理论模型与实际数据的测试，得到的结论如下：

(1) 本文提出的方法不只是简单的对波型泄漏进行压制，而是在波场分离后通过矢量合成，恢复了纵、横波波场的矢量振幅；本文方法的核心是仿射坐标系的旋转变换，由于仿射坐标系不要求坐标轴正交，所以能够根据需要分离的波场，建立与之匹配的仿射变换矩阵.

(2) 当地层模型非水平时，纵波与分裂横波会投影到全部的三个分量上，所以单一的两分量变换，如Z、R分量变换，是无法将各向异性波场彻底分离的.本文提出的方法将多个两分量变换进行了组合，首先在叠前分离P、SV与SH波矢量振幅，再基于纯净SV与SH波剖面进行快慢横波的进一步分离，从而实现裂缝参数的精确预测.

(3) 模型实例与实际数据的应用表明该方法能够较好地实现纵、横波波场的分离，该方法有着良好的推广价值，为矢量地震数据的处理技术提供了一个新的思路.

谨此祝贺姚振兴先生从事地球物理教学科研工作60周年.