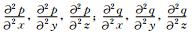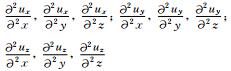2. 中国石油大学(北京) CNPC物探重点实验室, 北京 102249
2. CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum, Beijing 102249, China
有限差分方法由于其计算效率高、实现简单而被广泛应用于地震波动方程正演数值模拟中(Virieux,1984;王秀明等,2004;周竹生等,2007;Bansal and Sen, 2008;Di Bartolo et al., 2012).为了提高有限差分正演模拟的精度、效率以及稳定性,众多研究集中于有限差分模板的改进以及差分系数的求取(Moczo et al., 2000;Saenger et al., 2000;Finkelstein and Kastner, 2007;Song et al., 2013).高阶有限差分通常能够有效地压制数值频散,提高模拟精度(董良国等,2000;裴正林,2004;李振春等,2007;Du et al., 2009;Liu and Sen, 2009a,2009b).求取高阶差分系数的一种方法是泰勒级数展开(Dablain,1986;Liu and Sen, 2009a,2009b),该方法在波数较小的区域具有很高的精度,但是随着波数的增加频散误差逐渐增强.另一种求取差分系数的常用方法是利用数值优化算法,通过在有限波数或频率范围内极小化数值频散关系、相速度或群速度误差来获取最优化系数(Yang and Balanis, 2006;Zhou and Zhang, 2011;Chen,2012;Chu and Stoffa, 2012;梁文全等,2013;Wang et al., 2014).Liu(2013)利用最小二乘方法求取了空间域和时空域差分系数;此后,Liu(2014)将最小二乘方法应用到显式和隐式交错网格有限差分系数求取中.一般来说,最小二乘方法限制了优化目标函数的建立,而且使得其形式比较固定(Zhang and Yao, 2013).因此,Zhang和Yao(2013)利用最大范数法建立了优化目标函数,采用模拟退火算法对其进行求解.但是,全局优化算法需要多次迭代,计算过程比较耗时.Yang等(2016)利用采样近似方法求取了优化隐式差分系数;针对显式和隐式交错网格,Yan等(2016)将传统的泰勒级数展开与采样近似方法相结合求取了优化差分系数;Yang等(2017)利用Remez迭代算法求取了基于一范数所建立的优化目标函数.从本质上讲,Remez算法具有二次收敛性而且对初值不敏感,因此只需要三到四次的数值迭代就可以获得满意的计算结果(Remes, 1934a, 1934b, 1934c).针对二阶空间偏导数的显式有限差分离散,本文提出了一种新的优化差分系数方案.首先,结合泰勒级数展开与多点采样方法,利用最大范数建立优化目标函数,进而采用Remez算法对其进行求解,数值分析与模拟实验验证了本文方法的有效性.
在使用计算机进行正演模拟的过程中,由于计算区域的有限性,必然会导致人工截断边界的反射.吸收边界通常用于消除或减弱这种虚假边界的反射(Clayton and Engquist, 1977;Cerjan et al., 1985;Kosloff and Kosloff, 1986;Higdon,1991;Bérenger,1994;Zhou and McMechan, 2000;Heidari and Guddati, 2006).完全匹配层(PML)对不同角度的反射波都具有良好的吸收效果,在数值模拟中得到了广泛应用(Bérenger,1994;Zeng et al., 2001;Wang and Tang,2003;Komatitsch and Tromp, 2003;Hu et al., 2007;Gao and Zhang, 2008).但是,分裂式PML边界条件需要将原始波场分解成分量模式,在不同方向的匹配层中设置合适的阻尼衰减因子,整个实现过程比较复杂和耗时.非分裂PML边界条件通常需要更大的计算量和存储量(Komatitsch and Martin, 2007;Martin and Komatitsch, 2009;张鲁新等,2010;杜启振等,2011).为了有效解决这些问题,Liu和Sen(2010)提出了一种有效的混合吸收边界条件来处理人工边界反射的问题.在常规单程波边界条件的基础上,在波场的内部区域与边界之间增加过渡区域,通过线性加权内部的双程波波场与边界的单程波波场实现波场的平滑变化,从而减小人工虚假边界的反射.混合吸收边界在保证吸收效果的前提下极大地节省了计算量与存储量,到目前为止,已经在不同离散形式的波动方程中得到了成功应用(Liu and Sen, 2010,2011,2012).Ren和Liu(2013)将混合吸收边界条件推广到了频率域波动方程数值模拟中;任志明和刘洋(2014)提出了基于一阶Higdon单程波的弹性波混合吸收边界.本文将声波混合吸收边界条件(Liu and Sen, 2011)和弹性波混合吸收边界条件(Liu and Sen, 2012)推广到三维垂直对称轴横向各向同性(VTI)介质声波和弹性波数值模拟中.另外,根据各向异性特征,合理地调整了边界区域的波场速度值,有效地提高了吸收效果.针对三维计算量大的问题,本文将图形处理器(GPU)技术应用到数值模拟中.
本文的主要内容包括:介绍了三维VTI介质声波和弹性波波动方程;将泰勒级数展开和多点采样方法应用到显式空间频散关系中,利用最大范数建立优化目标函数并且采用Remez算法进行求解;将改进的混合吸收边界推广到三维VTI介质中;介绍了三维正演模拟的GPU实现流程;针对传统方法以及本文提出的方法,进行了数值精度分析以及在不同模型中的模拟实验;基于以上的对比分析,得出结论.
1 理论与方法 1.1 三维VTI介质声波和弹性波方程考虑到VTI介质波动方程在传播过程中的稳定性问题,本文选择含有限制性横波速度的三维声波方程,其形式如下(Fletcher et al., 2009):
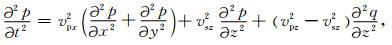
|
(1a) |
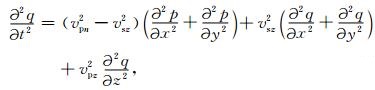
|
(1b) |
其中,t是时间项,x,y和z代表三个空间坐标轴,p(x, y, z, t)是标量压力场,q(x, y, z, t)是辅助波场.vpz是沿着对称轴方向的P波速度;vpx=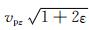
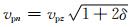
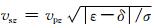
三维VTI介质中弹性波波动方程的形式如下(程玖兵等,2013):
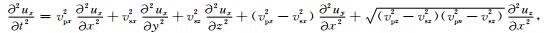
|
(2a) |
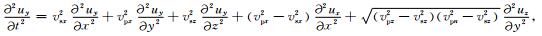
|
(2b) |

|
(2c) |
其中,ux(x, y, z, t)、uy(x, y, z, t)和uz(x, y, z, t)分别为沿着x、y和z三个方向的位移分量. vsx= 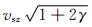
二阶空间偏导数的2M阶常规网格高阶有限差分的展开式为
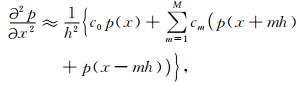
|
(3) |
其中,x是一个实变量,h是空间网格间距,cm是有限差分系数.
假设方程(3)具有如下形式的平面波解:
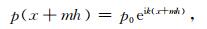
|
(4) |
其中,p0是一个常量,i是虚数单位,k代表空间波数.
将方程(4)代入方程(3)中,可以得到
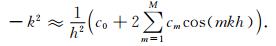
|
(5) |
当k=0时,方程(5)化简为
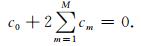
|
(6) |
将方程(6)代入方程(5)中可以得到
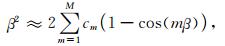
|
(7) |
其中,β=kh,并且β∈[0, π],β的实际变化范围为[0, b](0 < b < π).方程(7)代表显式有限差分的空间频散关系.
利用泰勒级数展开方程(7)右端的余弦函数,比较展开式中β的系数,可以得到(Liu and Sen, 2009a)
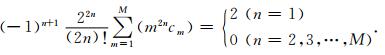
|
(8) |
方程(8)可以改写为如下的M阶线性方程组的形式(Liu and Sen, 2009a):
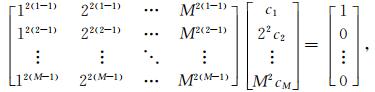
|
(9) |
通过求解方程(9),可以获得基于泰勒级数展开的有限差分系数.
对于频散关系式(7),在给定的波数区间内,利用左端项逼近右端的多项式可以获得优化的差分系数.Liu(2013)利用最小二乘方法极小化频散关系(7),从而获得最优化的差分系数.不同于前者的是,本文将采用最大范数法建立目标函数,用Remez算法求取目标函数获取最优化差分系数.
基于传统的泰勒级数展开方法,对于任意正整数L(L < M),均满足方程(8),因此可以构建如下的方程组:
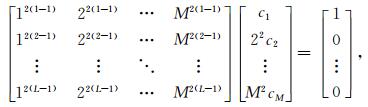
|
(10) |
方程(10)保证了差分系数的解具有M个自由度.
利用最大范数建立如下的目标函数:
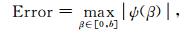
|
(11) |
其中,
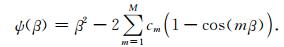
|
(12) |
方程(11)能够保证在给定的波数区间内,频散关系的计算结果不会超过给定的误差范围.通过采样近似方法求解方程(10)和(12)的结合体(Yan et al., 2016),可以获得优化的差分系数.然而,采样近似方法是在整个波数区间均匀选取样点,这样导致在一些非均匀节点所计算的误差会超出给定范围.鉴于此,利用Remez迭代算法获取的新的交换点能够在给定区间上完全满足精度要求.
基于Remez算法求取最优化差分系数的实现过程可以描述为:
(1) 引入一个新的常量A,在区间[0, b]上选择一系列均匀的参考点βi(i=1, 2, …, M),表示为
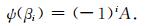
|
(13) |
令L=1,结合方程(10)和(13),构建如下的M阶线性方程组:
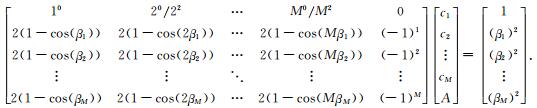
|
(14) |
求解方程(14)可以获得关于空间二阶显式有限差分系数cm和A.
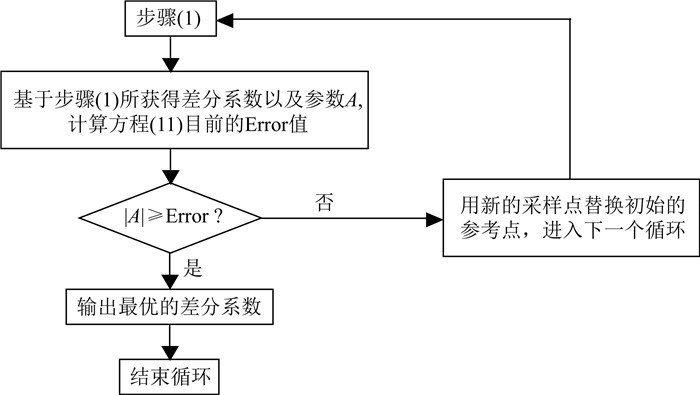
(2) 步骤(1)所选取的初始参考点是等间距的,这样就会导致目标函数的计算结果在一些非均匀点上超出给定的误差上限.为了克服这个问题,借助于Remez算法计算交换采样点的流程如图 1所示.
|
图 1 基于Remez迭代算法求取优化差分系数流程图 Fig. 1 Flowchart of computing optimal FD coefficients based on the Remez iteration algorithm |
(3) 需要注意的是在方程(13)的M个参考点上,ψ(βi)的计算结果是正负值交替出现的.因此,一定存在至少(M-1)个根使得ψ(β)=0,将区间[0, b]划分为M个间隔.通过计算每个给定间隔里极值点所对应的位置,可以获得新的交换参考点.
Remez迭代算法本质上具有二次收敛性以及对初值不敏感等性质,因此在整个计算过程中只需要三到四次迭代就可以获得满意的计算结果,在一定程度上有效控制了计算效率.
1.3 三维VTI介质混合吸收边界条件传统的PML吸收边界条件,由于其对于不同角度的反射波均具有良好的吸收效果,因此在声波和弹性波波动方程数值模拟中得到了广泛应用.但是,针对二阶波动方程,PML边界条件涉及求解时间三阶导数,增加了计算量和存储量(Komatitsch and Tromp, 2003).鉴于此,本文采用混合吸收边界条件对声波和弹性波数值模拟中的人工截断边界进行处理.
在这部分,本文首先将二维弹性波混合吸收边界条件(Liu and Sen, 2012)推广到三维VTI弹性介质中.基于各向异性特征,通过在边界区域合理调整节点速度来有效提高吸收效果.其次,将三维各向同性声学介质中的混合吸收边界条件(Liu and Sen, 2011)推广到三维VTI声学介质中.
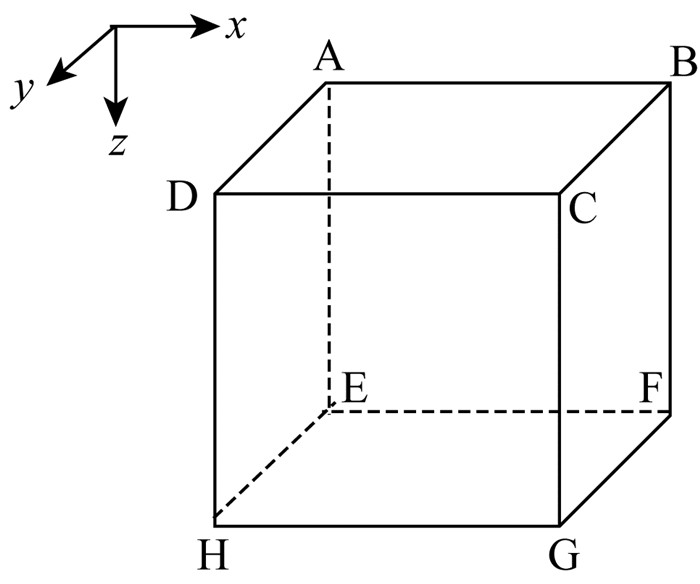
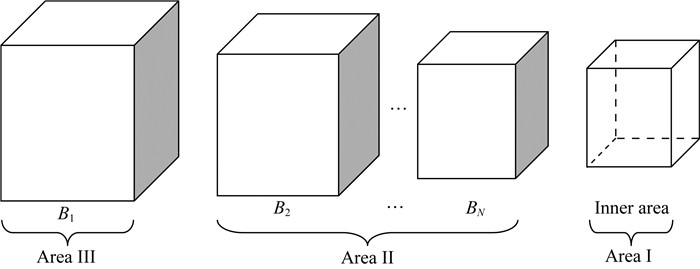
混合吸收边界通过在内部区域与边界区域之间增加一定厚度的过渡区域,通过加权平均外部的单程波波场与内部的双程波波场实现波场在过渡区域的平滑变化.首先需要将一个三维的计算区域(图 2)划分成三部分:内部(区域Ⅰ),过渡(区域Ⅱ:B2, B3, …, BN)和边界(区域Ⅲ:B1)(图 3).三维混合吸收边界条件的实现步骤如下(Liu and Sen, 2011):
|
图 2 三维计算区域示意图(Liu and Sen, 2011) Fig. 2 Schematic of 3D computational domain (Liu and Sen, 2011) |
|
图 3 三维数值模拟中混合吸收边界示意图(Liu and Sen, 2011) Fig. 3 Illustration of the HABCs for 3D numerical modeling (Liu and Sen, 2011) |
(1) 在区域Ⅰ,Ⅱ和Ⅲ内,求解双程波方程(1a)-(1b),(2a)-(2c),得到双程波波场:uitwo(i=1, 2, …, N);
(2) 在区域Ⅱ和Ⅲ内,求解单程波方程(详见下面内容),得到单程波波场:uione(i=1, 2, …, N);
(3) 在区域Ⅱ和Ⅲ内,加权平均双程波波场与单程波波场,得到:ui=wiuitwo+(1-wi)uione(i=1, 2, …, N).其中,ui是最终的波场,wi是加权系数,变化范围在0和1之间.简单的线性加权就可以达到良好的吸收效果,这里采用wi=(i-1)/N(i=1, 2, …, N).N代表的是吸收边界的层数.
混合吸收边界的关键是选择合适的单程波方程.根据之前的数值模拟实验(Liu and Sen, 2012),本文采用的是二阶Higdon单程波方程,三维情况下可以表示为
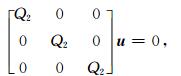
|
(15) |
其中,
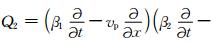

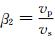
某一平面(ΩDCGH)(图 2)的波场值可以由下面的离散格式求解:
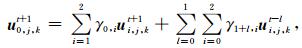
|
(16) |
其中,(i, j, k, t)代表的是(ih, jh, kh, tτ),γi, j可以由下面的方程计算得到(Higdon,1991):
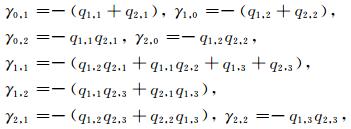
|
(17) |
以及
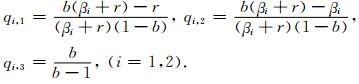
|
(18) |
r=vPτ/h,b是一个在0.3~0.5范围内的常数(Higdon,1991),本文b的取值为0.5.h为网格间距,τ为时间步长.
在两个平面(ΩDCGH和ΩDCBA)相交的棱上(LDC)(图 2),其波场值可以通过加权平均两个平面在相交区域的波场值获得
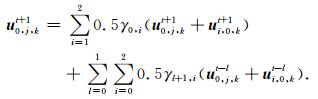
|
(19) |
在三个平面(ΩDCGH、ΩDCBA和ΩDAEH)相交的点上(PD)(图 2),其波场值可以通过加权平均三个平面在相交区域的波场值获得.因此,角点处波场的计算公式为
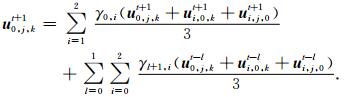
|
(20) |
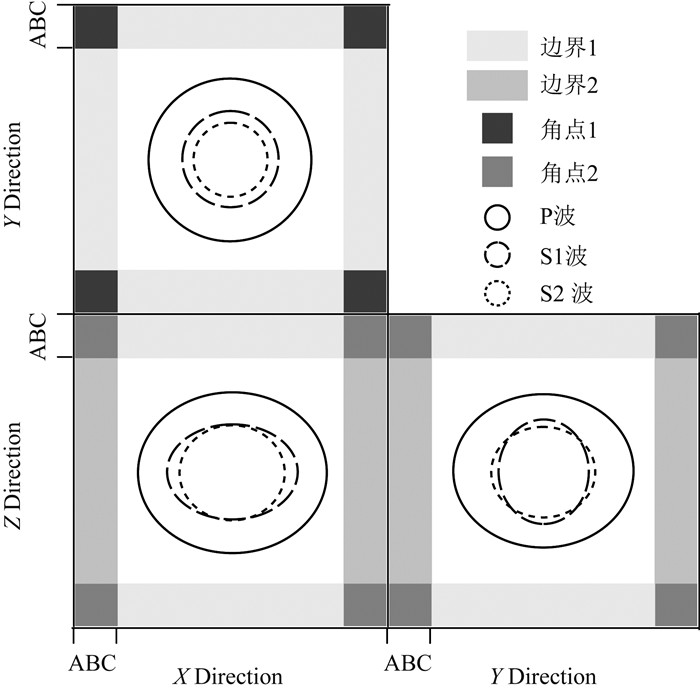
其他边界区域的波场值都可以通过与方程(16)、(19)和(20)相似的计算公式得到.另外,混合吸收边界的吸收效果依赖于边界区域速度值.不同于各向同性介质,地震波在各向异性介质中的传播速度与方向有关.对于三维VTI弹性介质混合吸收边界条件,本文提出一种有效的方法来估算边界区域的vp和vs,从而提高吸收效果.图 4为边界区域节点速度调整示意图,vp的计算公式为(Thomsen,1986)
|
图 4 三维混合吸收边界节点速度调整示意图 Fig. 4 Illustration of adjusting velocity in the absorption region for 3D HABCs |
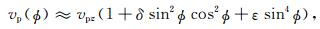
|
(21) |
如图 4所示,在边界1和角点1中ϕ=0,在边界2中ϕ=π/2,在角点2中ϕ=π/4.在VTI弹性介质中通常存在两种模式横波,本文在边界区域选择快横波速度.对于三维VTI介质声波方程数值模拟,选取Clayton单程波方程(Clayton and Engquist, 1977).声波混合吸收边界条件在三维VTI介质的实现过程与各向同性介质类似(Liu and Sen, 2011),节点速度的调整方案与弹性波吸收边界类似.
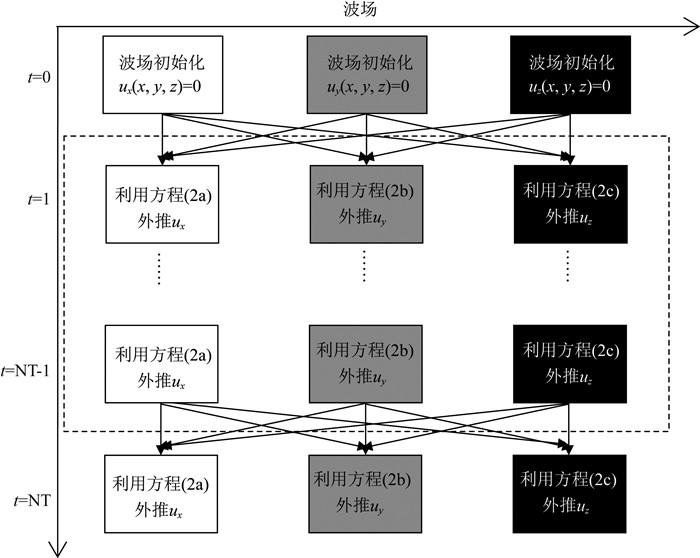
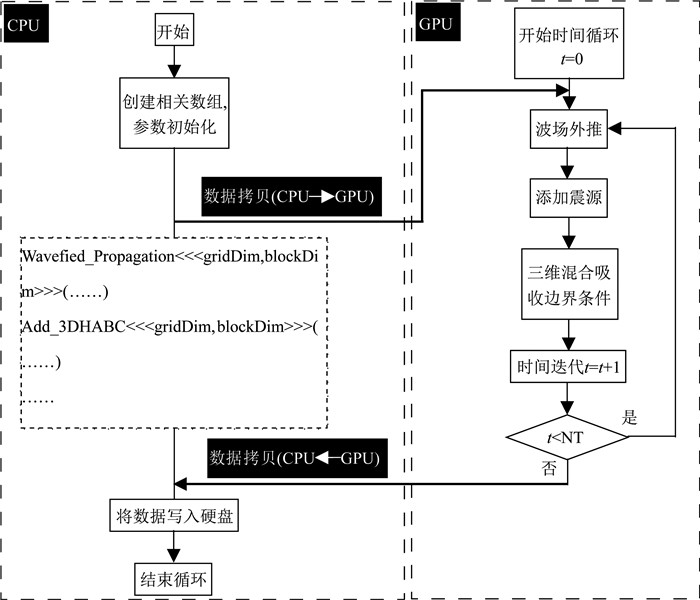
1.4 波动方程有限差分的GPU实现方程(1a)-(1b)和(2a)-(2c)可以通过时间二阶精度、空间高阶精度的方案进行离散求解.对于三维VTI介质中的地震波波动方程,表 1列出了在每个时间循环中需要求解的空间偏导数,主要涉及固定点三个轴向的导数.对于耦合的三维VTI弹性波方程(2a)-(2c),图 5展示了其具体的迭代求解流程,声波方程具有类似的实现流程.三维高阶有限差分通常需要很大的计算量,本文采用单个GPU卡加速运算,采用共享内存减小内存读取冗余度.基于GPU正演的流程大致可以分为:首先,将模型数据及各向异性参数从CPU复制到GPU中;其次,三维波场外推及混合吸收边界条件都在GPU上计算完成;最后,当波场递推到最大时刻时,结束整个循环,将结果输出.根据前面的描述,基于GPU三维波动方程有限差分正演模拟的流程如图 6所示.
|
|
表 1 三维VTI介质中需要求解的空间偏导数 Table 1 Spatial partial derivatives required to be calculated for 3D VTI medium |
|
图 5 利用有限差分迭代求解耦合三维VTI介质弹性波方程 Fig. 5 Iterative solution to 3D coupled elastic VTI wave equations with the FDM |
|
图 6 三维波动方程有限差分数值模拟GPU实现流程图 Fig. 6 Flowchart of GPU implementation for 3D wave equation modeling using the FDM |
根据方程(7),定义如下的ε(β)来衡量有限差分的空间数值频散:
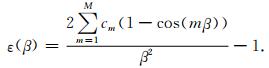
|
(22) |
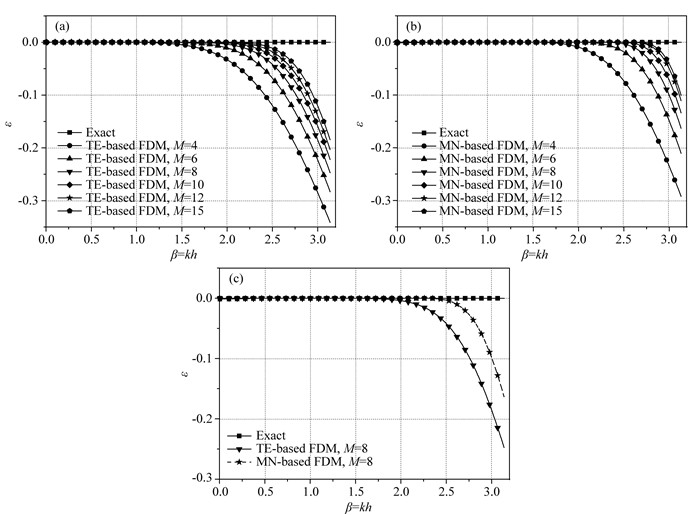
对于方程(22),若ε(β)为0时,不存在数值误差,若ε(β)远大于0时,数值误差就会越大.基于泰勒级数展开的差分系数可以从方程(6)获得,优化的差分系数可以利用方程(14)求取.为了比较传统方法与优化方法之间的数值误差,图 7给出了针对不同差分精度所计算的一些数值频散曲线.需要说明的是,在以下内容中,传统方法为泰勒级数展开有限差分方法,本文方法为基于最大范数优化有限差分方法.在这里,优化差分系数所选取的最大误差上限为η=10-4.由图 7可知:随着差分算子M的不断增加,频散误差总体呈下降趋势.此外,传统的泰勒级数展开方法在小波数区域具有很高的精度,但是在大波数区域误差较大;当给定相同的算子长度和误差上限时,与传统方法相比,优化方法不仅在小波数区域具有很高的精度,在大波数区域也能很好地压制数值频散.
|
图 7 不同差分算子长度所计算的频散误差 (a)传统方法;(b)本文方法;(c)不同方法之间的频散曲线对比. Fig. 7 Errors of numerical dispersions from different FD operator lengths (a) Conventional method; (b) Proposed method of this work; (c) Comparison of dispersion curves between different methods. |
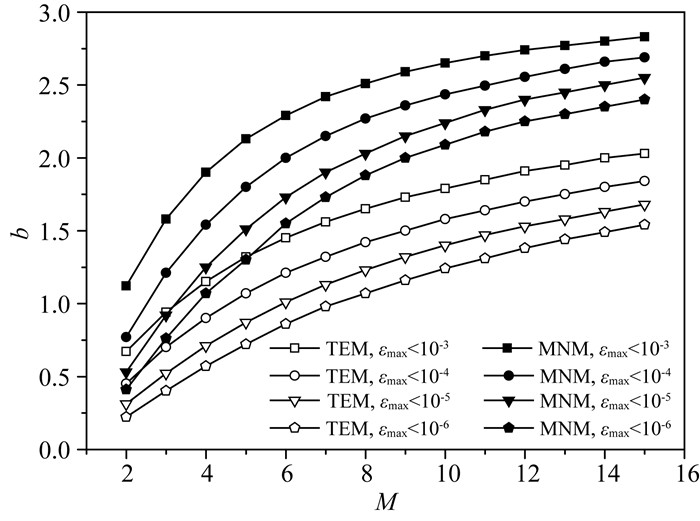
对于给定的误差上限η=10-3、η=10-4、η=10-5和η=10-6,图 8给出了针对传统方法和优化方法,计算的不同差分算子M所对应的b值,在相应区间内εmax < η.对于给定的η和M,相比于传统方法,优化方法能够在更大的波数区间压制数值频散.
|
图 8 针对不同最大误差,传统方法与本文方法所计算的随M变化的b值范围 Fig. 8 Variations of b with M for different maximum errors by the conventional method and proposed method |
与之前文献类似(Liu and Sen, 2009a),对于二阶空间偏导数显式有限差分方法,定义如下公式:
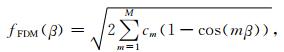
|
(23) |
因为β是fFDM(β)的精确值,针对不同的算子长度,对比了计算的fFDM(β)与β.另外,引入如下的误差函数来定量计算它们的精度(Liu and Sen, 2009a):
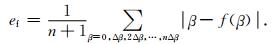
|
(24) |
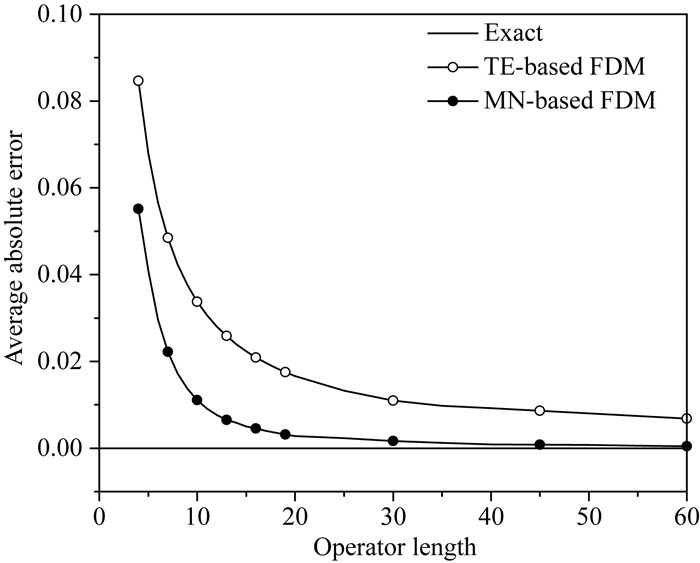
图 9给出了传统和优化差分系数所计算出的fFDM(β),其中,Δβ=0.001,n=3140.计算结果表明:随着有限差分算子长度的不断增加,误差逐渐减小;对于相同的算子长度,优化方法的误差小于传统方法.
|
图 9 针对不同算子长度,传统方法与本文方法所计算的平均绝对误差 Fig. 9 Average absolute errors of the conventional method and proposed method for different operator lengths |
在这部分,本文将采用多个数值算例来测试优化有限差分与混合吸收边界条件在三维VTI声波和弹性波方程数值模拟中的有效性和可靠性.
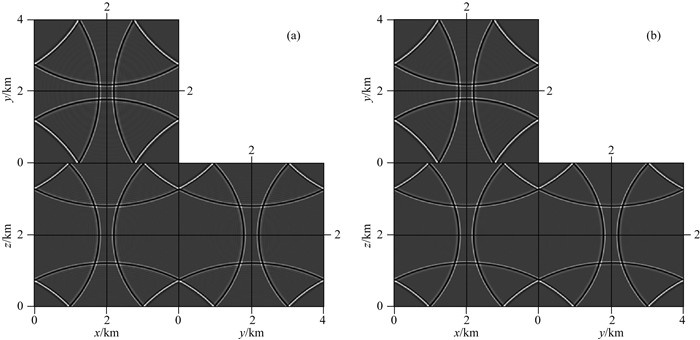
3.1 三维均匀模型正演模拟第一个例子针对均匀模型,用GPU实现三维声波VTI方程正演.图 10给出了基于传统和优化有限差分方法所计算的同一时刻的波场快照,图 11给出了基于优化有限差分和三维声波混合吸收边界条件所计算的不同时刻的波场快照,为简单起见,只展示了x分量.在这个例子中,模型尺寸为4000 m×4000 m×4000 m,网格间距为20 m×20 m×20 m,时间采样步长为0.001 s.P波速度和各向异性参数分别为vpz=2200 m·s-1,ε=0.20和δ=0.20.震源采用主频为25 Hz的雷克子波,置于模型中间产生振动.
|
图 10 三维均匀模型中声波VTI方程1500 ms时正演模拟波场快照,M=14 (a)传统方法;(b)本文方法. Fig. 10 Wavefield snapshots at 1500 ms computed by acoustic VTI wave equations for a 3D homogeneous model with M=14 (a) Conventional method; (b) Proposed method. |

|
图 11 三维均匀模型中利用本文方法所计算的声波VTI方程的正演模拟波场快照,M=14 (a)声波混合吸收边界条件,N=1(Clayton吸收边界条件);(b)声波混合吸收边界条件,N=5;(c)声波混合吸收边界条件,N=10.每一组图片包含两个时刻的波场快照切片,分别为1100 ms和2200 ms. Fig. 11 Wavefield snapshots computed by acoustic VTI wave equations using proposed method for a 3D homogeneous model with M=14 (a) Acoustic HABC (AHABC) with N=1 (Clayton ABC); (b) AHABC with N=5; (c) AHABC with N=10. Each figure includes three panels with two wavefield snapshots at 1100 ms and 2200 ms, respectively. |
第二个例子针对均匀模型,用GPU实现三维弹性波VTI方程正演.类似地,图 12和13给出了相应的波场快照.由于单层的三维弹性波混合吸收边界(Higdon吸收边界条件)随着传播时间的增大存在稳定性问题,在这里未做展示.在这个例子中,P波和S波的速度分别为vpz=3500 m·s-1和vsz=1900 m·s-1,各向异性参数分别为ε=0.20,δ=-0.10和γ=0.15.20 Hz的雷克子波置于模型中间产生振动,其他的模型参数与第一个例子相同.图 14和15分别给出了基于CPU和GPU的三维混合吸收边界条件接收到的记录差异,混合吸收边界的层数均为10.
|
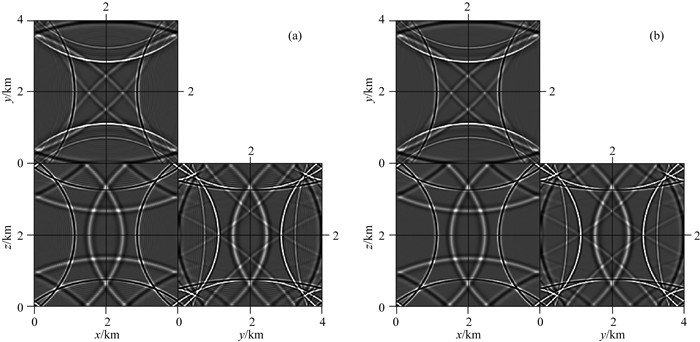
图 12 三维均匀模型中弹性波VTI方程1600 ms时正演模拟波场快照,M=8 (a)传统方法;(b)本文方法. Fig. 12 Wavefield snapshots at 1600 ms computed by elastic VTI wave equations for a 3D homogeneous model with M=8 (a) Conventional method; (b) Proposed method. |
|
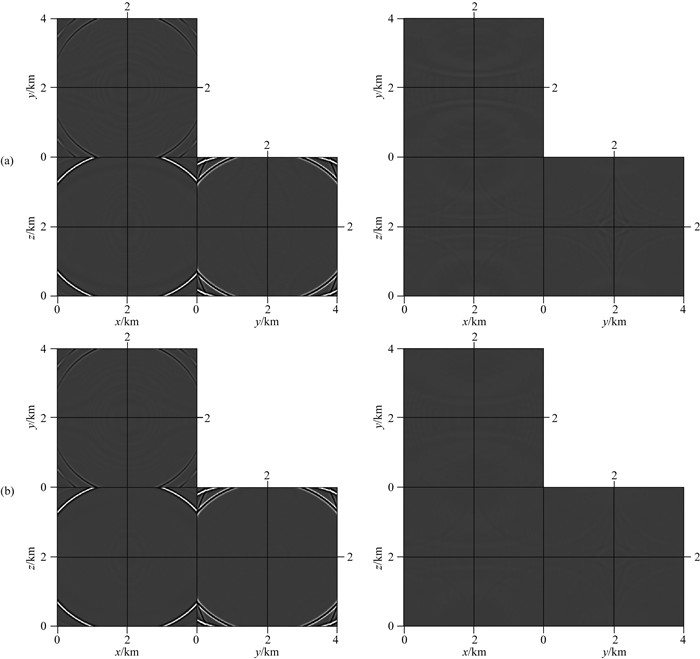
图 13 三维均匀模型中利用优化方法所计算的弹性波VTI方程的正演模拟波场快照,M=8 (a)弹性波混合吸收边界条件,N=5;(b)弹性波混合吸收边界条件,N=10.每一组图片包含两个时刻的波场快照切片,分别为1200 ms和2400 ms. Fig. 13 Wavefield snapshots computed by elastic VTI wave equations using proposed method for a 3D homogeneous model with M=8 (a) Elastic HABC (EHABC) with N=5; (b) EHABC with N=10. Each figure includes three panels with two wavefield snapshots at 1200 ms and 2400 ms, respectively. |
|
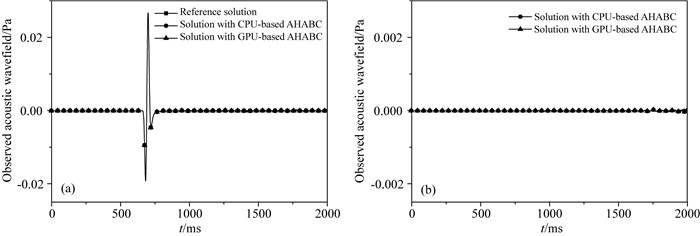
图 14 在(900 m, 900 m, 900 m)处接收到的声波波场,参考解是由扩大模型边界计算的 (a)参考解,基于CPU计算的声波混合吸收边界和基于GPU计算的声波混合吸收边界;(b)参考解与两种平台上的声波混合吸收边界的误差.需要说明的是在这例子中震源的主频变成20 Hz. Fig. 14 Received acoustic wavefield at (900 m, 900 m, 900 m) and reference solution computed by expanded model boundaries (a) Reference solution based on CPU- and GPU-based AHABCs; (b) Differences between the reference solution and the solutions from two AHABCs. Note that the main frequency of source in this example becomes 20 Hz. |
|
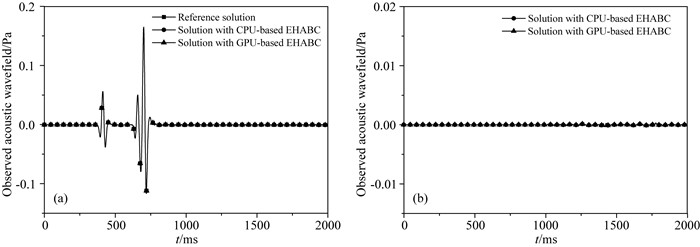
图 15 在(1200 m, 1200 m, 1200 m)处接收到的弹性波波场,参考解是由扩大模型边界计算的 (a)参考解,基于CPU计算的弹性波混合吸收边界和基于GPU计算的弹性波混合吸收边界;(b)参考解与两种平台上的弹性波混合吸收边界的误差.需要说明的是在这例子中震源的主频变成15 Hz. Fig. 15 Received elastic wavefield at (1200 m, 1200 m, 1200 m) and reference solution computed by expanded model boundaries (a) Reference solution based on CPU- and GPU-based EHABCs; (b) Differences between the reference solution and the solutions from two EHABCs. Note that the main frequency of source in this example becomes 15 Hz. |
(1) 基于传统泰勒级数展开有限差分的正演模拟结果在高波数区域会产生明显的空间数值频散,如图 10a和12a所示.当M=14和M=8,在高波数区域,基于优化有限差分的正演模拟精度(图 10b和12b)明显高于传统泰勒级数展开有限差分方法(图 10a和12a).
(2) 在三维VTI介质声波、弹性波正演模拟中,随着吸收层数的增加,混合吸收边界条件对人工边界反射的吸收效果逐渐提高.当N=10,可以获得满意的吸收效果,而且随着传播时间的增大,稳定性良好(图 11a-11c和13a-13b).
(3) 在三维均匀VTI介质中,当吸收层数为10时,基于CPU和GPU计算的声波和弹性波混合吸收边界都取得良好的吸收效果(图 14和15),两种计算平台之间的模拟误差可以忽略.因此验证了基于GPU正演模拟时混合吸收边界的可靠性与有效性.
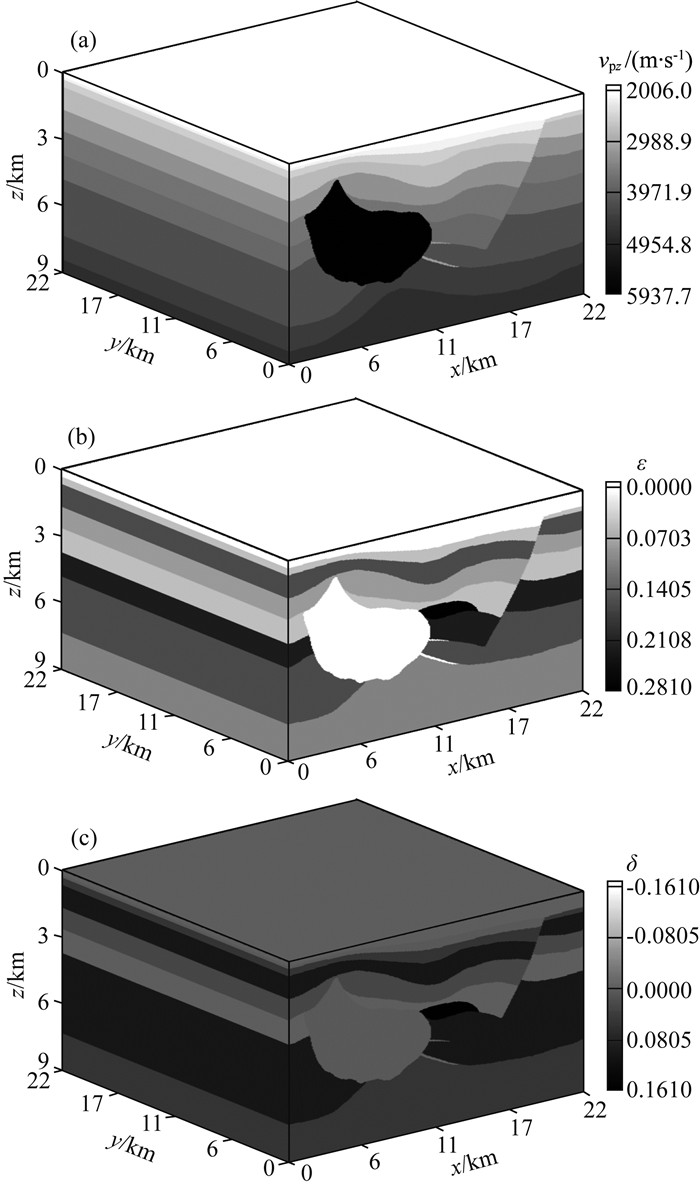
3.2 三维修改的Hess VTI模型正演模拟为了进一步验证本文所提出方法的优势,下面对三维修改的Hess VTI模型(图 16),用GPU实现声波和弹性波正演模拟.该非均质模型的大小为22000 m×22000 m×9000 m,重采样间隔为55 m×55 m×45 m,y方向的空间维度和间隔与x方向一致.模型参数主要包括:垂向P波速度(图 16a),Thomsen各向异性参数ε和δ(图 16b和16c).原始数据集中不包含S波速度vsz和S波各向异性参数γ,这里,在整个网格区域设置vsz/vpz=1/1.73和γ/ε=1/1.25.时间间隔是0.001 s,记录时长为4.0 s.对于VTI声波正演模拟,网格间距是20 m×20 m×20 m;对于VTI弹性波正演模拟,网格间距是15 m×15 m×15 m.震源均为20 Hz雷克子波,震源坐标为(x=11000 m,y=11000 m,z=300 m).接收点均匀分布在x方向上并且有(y=11000 m,z=300 m).利用三维VTI声波和弹性波方程在Hess VTI模型中进行正演模拟时,单层的声波混合吸收边界条件(Clayton吸收边界条件)和单层的弹性波混合吸收边界条件(Higdon吸收边界条件)均出现不稳定情况.因此综合考虑稳定性、吸收效果和计算效率,在这里采用10层的混合吸收边界条件对人工边界反射进行压制.为了简单起见,图 17和18仅给出了x方向的波场快照,图 19和20给出了相应的地震记录.表 2给出了在不同平台上的计算时间.
|
图 16 三维修改的Hess VTI模型 (a) vpz;(b) ε;(c) δ. Fig. 16 3D modified Hess VTI model |

|
图 17 三维修改的Hess VTI模型中声波波动方程所计算的1600 ms时刻的波场快照,M=12 (a)无吸收边界和传统方法;(b)声波混合吸收边界和传统方法;(c)无吸收边界和本文方法;(d)声波混合吸收边界和本文方法. Fig. 17 Wavefield snapshots at 1600 ms computed by acoustic wave equations for the 3D modified Hess VTI model with M=12 (a) Conventional method without AHABC; (b) Conventional method with AHABC; (c) Propsoed method without AHABC; (d) Proposed method with AHABC. |
|
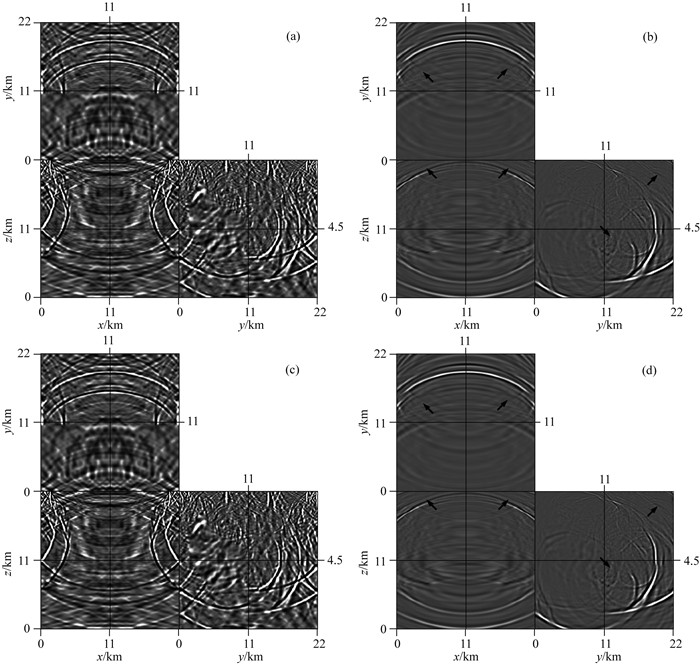
图 18 三维修改的Hess VTI模型中弹性波波动方程所计算的2000 ms时刻的波场快照,M=8 (a)无吸收边界和传统方法;(b)弹性波混合吸收边界和传统方法;(c)无吸收边界和本文方法;(d)弹性波混合吸收边界和本文方法. Fig. 18 Wavefield snapshots at 2000 ms computed by elastic wave equations for the 3D modified Hess VTI model with M=8 (a) Conventional method without EHABC; (b) Conventional method with EHABC; (c) Propsoed method without EHABC; (d) Proposed method with EHABC. |
|
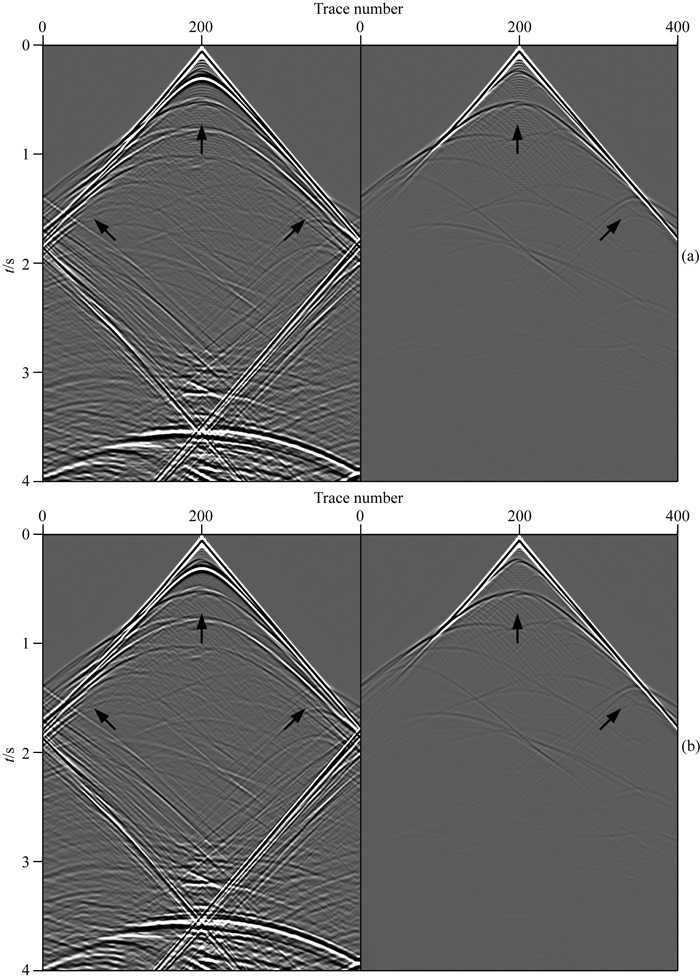
图 19 三维修改的Hess VTI模型中声波波动方程所计算的地震记录,M=12 (a)传统方法;(b)本文方法.每一张图左边无吸收边界,右边有吸收边界. Fig. 19 Seismograms computed by acoustic wave equations for the 3D modified Hess VTI model with M=12 (a) Conventional method; (b) Proposed method. Note that the left part of each figure has non-AHABC and the right part has AHABC. |
|
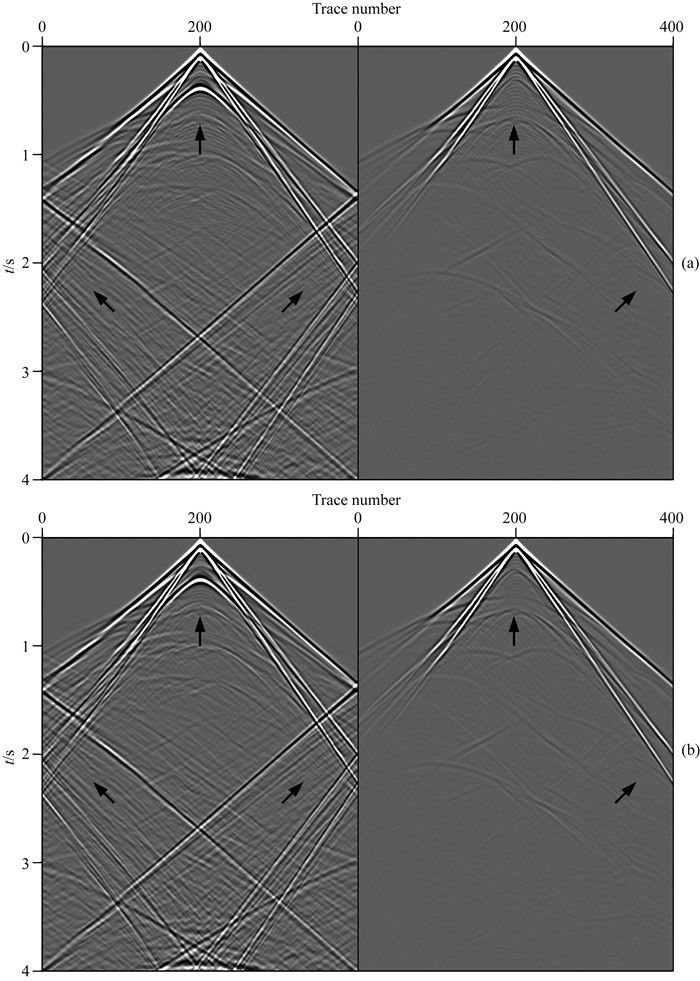
图 20 三维修改的Hess VTI模型中弹性波波动方程所计算的地震记录,M=8 (a)传统方法;(b)本文方法.每一张图左边无吸收边界,右边有吸收边界. Fig. 20 Seismograms computed by elastic wave equations for the 3D modified Hess VTI model with M=8 (a) Conventional method; (b) Proposed method. Note that the left part of each figure has non-EHABC and the right part has EHABC. |
|
|
表 2 三维修改的Hess VTI模型中地震波正演模拟计算时间 Table 2 Computational time for seismic wave modeling performed on the 3D modified Hess VTI model |
对比分析图 17a-17d,18a-18d,19a和19b以及20a和20b,可以观察到,对于相同长度的有限差分算子,在复杂构造及高波数区域(图中箭头所示区域),传统泰勒级数展开有限差分方法存在较强的数值频散(图 17a,17b,18a,18b,19a和20a).相比之下,基于最大范数优化有限差分能够在这些区域显著压制数值频散(图 17c,17d,18c,18d,19b和20b),有效提高模拟精度,而且优化方案不会耗费过多的计算资源(表 2).混合吸收边界条件在复杂的三维VTI声波和弹性波介质正演模拟中能够利用较少的吸收层数对边界处的人工反射产生良好的吸收效果(图 17b,17d,18b和18d),随着传播时间的增加,稳定性较高(图 19a,19b,20a和20b).此外,利用GPU进行三维有限差分正演数值模拟,能够显著地提高计算效率,最大程度地节省计算时间(表 2).
4 讨论当各向异性参数为零时,三维VTI声波方程可以退化到各向同性介质中,因此,本文采用各向同性介质中三维声波波动方程的稳定性条件来检验泰勒级数展开有限差分法和最大范数优化的有限差分法.稳定性函数由以下方程给出(Liu and Sen, 2009b):
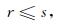
|
(25) |
其中,r代表Courant数,稳定性因子s具有如下的形式(Liu and Sen, 2009b):
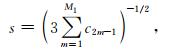
|
(26) |
M1=int((M+1)/2),int是取整函数.
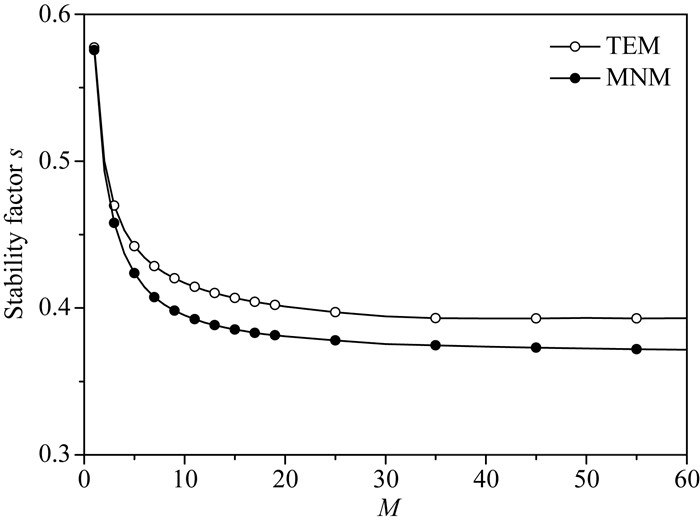
对于给定的误差上限η=10-4,图 21给出了传统方法以及本文优化方法计算出的稳定性因子s的变化规律.可以观察到,随着算子长度M的不断增加,稳定性逐渐变高,而且对于相同的算子长度,优化方法的稳定性略低于传统方法.
|
图 21 基于2M阶有限差分三维声波波动方程稳定性因子s的变化 Fig. 21 Variations of stability factor s with M for the 3D acoustic wave equation by the (2M)th-order FD schemes |
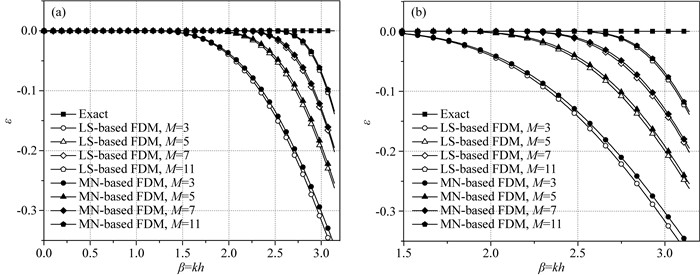
此外,本文比较了最小二乘优化(Liu,2013)和最大范数优化有限差分数值频散,图 22给出了不同算子长度下的频散曲线.最小二乘和最大范数优化差分系数的最大误差上限为η=10-4.由图可见,这两种优化方法在大波数区间均可以获得很高的精度,但是最大范数优化方法的效果略优于最小二乘优化方法.
|
图 22 针对不同差分算子,最小二乘和最大范数优化有限差分所计算的数值频散曲线 (a)最小二乘和最大范数优化有限差分计算的整个曲线图;(b) (a)的局部放大图. Fig. 22 Numerical dispersion curves for different FD operator lengths by the LS- and MN-based FDMs (a) Whole curves of LS- and MN-based FDMs; (b) Local magnification of (a). |
针对空间二阶偏导数的显式有限差分格式,本文给出了一种新的基于最大范数优化差分系数的方法.通过将传统的泰勒级数展开和多点采样方法应用于显式频散关系,然后利用最大范数建立直观有效的优化目标函数,利用Remez迭代算法求解该目标函数,从而获得最优化差分系数.将最大范数优化有限差分方法应用到三维VTI介质声波和弹性波方程数值求解中.相比较于传统的泰勒级数展开法,优化方法可以利用更小的算子长度获得同样的数值模拟精度,极大地减小了计算量.另外,本文将二维混合吸收边界成功推广到了三维VTI介质波动方程数值模拟中,根据各向异性特征,合理调整边界吸收区域的节点速度,从而有效地提高了吸收效果.同时,利用GPU提高了三维有限差分正演模拟的计算效率.数值精度分析以及多个模拟试验共同证明了本文方法的有效性.
致谢感谢审稿专家和编辑部的大力支持,感谢Hess公司提供的VTI模型数据,感谢开源软件平台Madagascar.
Bérenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
Bansal R, Sen M K. 2008. Finite-difference modelling of S-wave splitting in anisotropic media. Geophysical Prospecting, 56(3): 293-312. DOI:10.1111/j.1365-2478.2007.00693.x |
Cerjan C, Kosloff D, Kosloff R, et al. 1985. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 50(4): 705-708. DOI:10.1190/1.1441945 |
Chen J B. 2012. An average-derivative optimal scheme for frequency-domain scalar wave equation. Geophysics, 77(6): T201-T210. DOI:10.1190/geo2011-0389.1 |
Cheng J B, Kang W, Wang T F. 2013. Description of qP-wave propagation in anisotropic media Part Ⅰ:Pseudo-pure-mode wave equations. Chinese Journal of Geophysics (in Chinese), 56(10): 3474-3486. DOI:10.6038/cjg20131022 |
Chu C, Stoffa P L. 2012. Determination of finite-difference weights using scaled binomial windows. Geophysics, 77(3): W17-W26. DOI:10.1190/geo2011-0336.1 |
Clayton R W, Engquist B. 1977. Absorbing boundary conditions for acoustic and elastic wave equations. Bulletin of the Seismological Society of America, 67(6): 1529-1540. |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
Di Bartolo L, Dors C, Mansur W J. 2012. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation. Geophysics, 77(5): T187-T199. DOI:10.1190/geo2011-0345.1 |
Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese Journal of Geophysics (in Chinese), 43(3): 411-419. |
Du Q Z, Li B, Hou B. 2009. Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered-grid finite difference scheme. Applied Geophysics, 6(1): 42-49. DOI:10.1007/s11770-009-0008-z |
Du Q Z, Sun R Y, Zhang Q. 2011. Numerical simulation of three-component elastic wavefield in 2D TTI media in the condition of the combined boundary. Oil Geophysical Prospecting (in Chinese), 46(2): 187-195. |
Finkelstein B, Kastner R. 2007. Finite difference time domain dispersion reduction schemes. Journal of Computational Physics, 221(1): 422-438. DOI:10.1016/j.jcp.2006.06.016 |
Fletcher R P, Du X, Fowler P J. 2009. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
Gao H W, Zhang J F. 2008. Implementation of perfectly matched layers in an arbitrary geometrical boundary for elastic wave modelling. Geophysical Journal International, 174(3): 1029-1036. DOI:10.1111/gji.2008.174.issue-3 |
Heidari A H, Guddati M N. 2006. Highly accurate absorbing boundary conditions for wide-angle wave equations. Geophysics, 71(3): S85-S97. DOI:10.1190/1.2192914 |
Higdon R L. 1991. Absorbing boundary conditions for elastic waves. Geophysics, 56(2): 231-241. DOI:10.1190/1.1443035 |
Hu W, Abubakar A, Habashy T M. 2007. Application of the nearly perfectly matched layer in acoustic wave modeling. Geophysics, 72(5): SM169-SM175. DOI:10.1190/1.2738553 |
Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
Kosloff R, Kosloff D. 1986. Absorbing boundaries for wave propagation problems. Journal of Computational Physics, 63(2): 363-376. DOI:10.1016/0021-9991(86)90199-3 |
Li Z C, Zhang H, Liu Q M, et al. 2007. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm. Oil Geophysical Prospecting (in Chinese), 42(5): 510-515. |
Liang W Q, Yang C C, Wang Y F, et al. 2013. Acoustic wave equation modeling with new time-space domain finite difference operators. Chinese Journal of Geophysics (in Chinese), 56(10): 3497-3506. DOI:10.6038/cjg20131024 |
Liu Y, Sen M K. 2009a. A practical implicit finite-difference method:Examples from seismic modeling. Journal of Geophysics and Engineering, 6(3): 231-249. DOI:10.1088/1742-2132/6/3/003 |
Liu Y, Sen M K. 2009b. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
Liu Y, Sen M K. 2010. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation. Geophysics, 75(2): A1-A6. DOI:10.1190/1.3295447 |
Liu Y, Sen M K. 2011. 3D acoustic wave modelling with time-space domain dispersion-relation-based finite-difference schemes and hybrid absorbing boundary conditions. Exploration Geophysics, 42(3): 176-189. DOI:10.1071/EG11007 |
Liu Y, Sen M K. 2012. A hybrid absorbing boundary condition for elastic staggered-grid modeling. Geophysical Prospecting, 60(6): 1114-1132. DOI:10.1111/gpr.2012.60.issue-6 |
Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78(4): T113-T132. DOI:10.1190/geo2012-0480.1 |
Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
Martin R, Komatitsch D. 2009. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation. Geophysical Journal International, 179(1): 333-344. DOI:10.1111/gji.2009.179.issue-1 |
Moczo P, Kristek J, Halada L. 2000. 3D fourth-order staggered-grid finite-difference schemes:Stability and grid dispersion. Bulletin of the Seismological Society of America, 90(3): 587-603. DOI:10.1785/0119990119 |
Pei Z L. 2004. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface. Oil Geophysical Prospecting (in Chinese), 39(6): 629-634. |
Remes E Y. 1934a. Sur la détermination des polynômes d'approximation de degré donnée. Comm. Soc. Math. Kharkov, 10: 41-63. |
Remes E Y. 1934b. Sur le calcul effectiv des polynômes d'approximation des tschebycheff. Compt. Rend. Acade. Sc., 199: 337. |
Remes E Y. 1934c. Sur un procédé convergent d'approximations successives pour déterminer les polynômes d'approximation. Compt. Rend. Acade. Sc., 198: 2063-2065. |
Ren Z M, Liu Y. 2013. A hybrid absorbing boundary condition for frequency-domain finite-difference modeling. Journal of Geophysics and Engineering, 10(5): 054003. DOI:10.1088/1742-2132/10/5/054003 |
Ren Z M, Liu Y. 2014. Numerical modeling of the first-order elastic equations with the hybrid absorbing boundary condition. Chinese Journal of Geophysics (in Chinese), 57(2): 595-606. DOI:10.6038/cjg20140223 |
Saenger E H, Gold N, Shapiro S A. 2000. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion, 31(1): 77-92. DOI:10.1016/S0165-2125(99)00023-2 |
Song X L, Fomel S, Ying L X. 2013. Low rank finite-differences and low rank Fourier finite-differences for seismic wave extrapolation in the acoustic approximation. Geophysical Journal International, 193(2): 960-969. DOI:10.1093/gji/ggt017 |
Thomsen L. 1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
Virieux J. 1984. SH-wave propagation in heterogeneous media; Velocity-stress finite-difference method. Geophysics, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
Wang T, Tang X M. 2003. Finite-difference modeling of elastic wave propagation:A nonsplitting perfectly matched layer approach. Geophysics, 68(5): 1749-1755. DOI:10.1190/1.1620648 |
Wang X M, Zhang H L, Wang D. 2004. Modelling of seismic wave propagation in heterogeneous poroelastic media using a high-order staggered finite-difference method. Chinese Journal of Geophysics (in Chinese), 46(6): 842-849. |
Wang Y F, Liang W Q, Nashed Z, et al. 2014. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method. Geophysics, 79(5): T277-T285. DOI:10.1190/geo2014-0078.1 |
Yan H Y, Yang L, Li X Y. 2016. Optimal staggered-grid finite-difference schemes by combining Taylor-series expansion and sampling approximation for wave equation modeling. Journal of Computational Physics, 326: 913-930. DOI:10.1016/j.jcp.2016.09.019 |
Yang B, Balanis C A. 2006. Least square method to optimize the coefficients of complex finite-difference space stencils. IEEE Antennas and Wireless Propagation Letters, 5(1): 450-453. |
Yang L, Yan H Y, Liu H. 2016. Optimal implicit staggered-grid finite-difference schemes based on the sampling approximation method for seismic modelling. Geophysical Prospecting, 64(3): 595-610. DOI:10.1111/gpr.2016.64.issue-3 |
Yang L, Yan H Y, Liu H. 2017. Optimal staggered-grid finite-difference schemes based on the minimax approximation method with the Remez algorithm. Geophysics, 82(1): T27-T42. DOI:10.1190/geo2016-0171.1 |
Zeng Y Q, He J Q, Liu Q H. 2001. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Geophysics, 66(4): 1258-1266. DOI:10.1190/1.1487073 |
Zhang J H, Yao Z X. 2013. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. Journal of Computational Physics, 250: 511-526. DOI:10.1016/j.jcp.2013.04.029 |
Zhang L X, Fu L Y, Pei Z L. 2010. Finite difference modeling of Biot's poroelastic equations with unsplit convolutional PML and rotated staggered grid. Chinese Journal of Geophysics (in Chinese), 53(10): 2470-2483. DOI:10.3969/j.issn.0001-5733.2010.10.021 |
Zhou H B, McMechan G A. 2000. Rigorous absorbing boundary conditions for 3-D one-way wave extrapolation. Geophysics, 65(2): 638-645. DOI:10.1190/1.1444760 |
Zhou H B, Zhang G Q. 2011. Prefactored optimized compact finite-difference schemes for second spatial derivatives. Geophysics, 76(5): WB87-WB95. DOI:10.1190/geo2011-0048.1 |
Zhou Z S, Liu X L, Xiong X Y. 2007. Finite-difference modelling of Rayleigh surface wave in elastic media. Chinese Journal of Geophysics (in Chinese), 50(2): 567-573. |
程玖兵, 康玮, 王腾飞. 2013. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程. 地球物理学报, 56(10): 3474-2486. DOI:10.6038/cjg20131022 |
董良国, 马在田, 曹景忠, 等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411-419. |
杜启振, 孙瑞艳, 张强. 2011. 组合边界条件下二维三分量TTI介质波场数值模拟. 石油地球物理勘探, 46(2): 187-198. |
李振春, 张华, 刘庆敏, 等. 2007. 弹性波交错网格高阶有限差分法波场分离数值模拟. 石油地球物理勘探, 42(5): 510-515. |
梁文全, 杨长春, 王彦飞, 等. 2013. 用于声波方程数值模拟的时间-空间域有限差分系数确定新方法. 地球物理学报, 56(10): 3497-3506. DOI:10.6038/cjg20131024 |
裴正林. 2004. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟. 石油地球物理勘探, 39(6): 629-634. |
任志明, 刘洋. 2014. 一阶弹性波方程数值模拟中的混合吸收边界条件. 地球物理学报, 57(2): 595-606. DOI:10.6038/cjg20140223 |
王秀明, 张海澜, 王东. 2004. 利用高阶交错网格有限差分法模拟地震波在非均匀孔隙介质中的传播. 地球物理学报, 46(6): 842-849. |
张鲁新, 符力耘, 裴正林. 2010. 不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用. 地球物理学报, 53(10): 2470-2483. DOI:10.3969/j.issn.0001-5733.2010.10.021 |
周竹生, 刘喜亮, 熊孝雨. 2007. 弹性介质中瑞雷面波有限差分法正演模拟. 地球物理学报, 50(2): 567-573. |
 2018, Vol. 61
2018, Vol. 61