大地电磁测深法以天然交变电磁场为场源,通过在地表观测相互正交的电磁分量来获取地下构造的电性特征.近几十年来,大地电磁法被越来越多地用于深部构造研究以及油气和构造勘查中(Becken et al., 2011).常规的MT数据处理和解释往往忽略各向异性现象,其结果难以反映地下真实电性分布特征.由于地球构造应力场、地球介质形变、岩石裂隙、孔隙水及地质沉积等因素造成了地球介质的各向异性;大量实测MT数据也表明地球内部广泛存在电性各向异性(Rasmussen,1988;Mareschal et al., 1995;Bahr et al., 2000;Gatzemeier and Moorkamp, 2005).近年,大地电磁资料解释中呈现的深部各向异性构造特征,受到国内外学者越来越广泛的关注.Yin(2003, 2006)、Kirkby等(2015)进行了一维大地电磁各向异性正反演研究;同时学者们对二维大地电磁各向异性正演问题进行了研究(Reddy and Rankin, 1957;Pek and Verner, 1997;Li,2002).Heise等(2006)利用简单的一、二维各向异性模型分析了下地壳和上地幔大地电磁相位张量分离问题,指出根据相位分离不能直接判断地下介质存在各向异性.大地电磁二维各向异性反演也取得进展.Baba等(2006)考虑方位各向异性反演算法,Chen (2012)提出非线性共轭梯度反演算法, 黄一凡等(2016)采用二维对角各向异性反演算法.对于三维模型,Weidelt(1999)提出了基于交错网格的三维大地电磁各向异性有限差分算法,Gatzemeier和Moorkamp(2005)利用三维电导率模型研究下地壳和上地幔深部构造,Häuserer和Junge(2010)利用三维大地电磁正演方法构建三维各向异性模型解释乌干达西部大地电磁数据.
从模拟算法来说,三维MT正演主要包括:积分方程法(Farquharson et al., 2006),有限差分法(Liu and Becker, 1992;陈辉等,2011)和有限元法(Nam et al., 2007).有限差分法和积分方程法模拟起伏地表比较困难,积分方程法也难以对复杂多异常体进行模拟计算,而且它们的计算结果严重依赖网格剖分质量.基于非结构的有限元法可以利用合理的网格数量精确模拟复杂地电条件下的大地电磁响应(Usui,2015).
为提高复杂地电条件下(特别是各向异性)大地电磁的正演精度,本文利用面向目标自适应有限元法实现起伏地表和各向异性条件下三维大地电磁正演模拟.对于自适应策略,本文根据物性界面处垂向电流连续性估计后验误差(Ren et al., 2013),并用张量电导率与正演问题解的乘积作为改进的加权系数(殷长春等,2017),最后得到加权后验误差来驱动面向目标网格自适应.我们利用Yin(2003)的一维层状解析解验证本文算法的正确性;通过典型算例分析了各向异性对网格自适应的影响,证明了本文改进加权系数算法的优越性;最后分析了起伏地表条件大地电磁各向异性响应特征及其识别方法,证明本文算法的适用性.
1 正演算法 1.1 控制方程考虑到大地电磁(MT)测量频率范围内可以忽略位移电流,假设时谐因子为e-iωt,则电场满足的矢量亥姆霍兹方程为
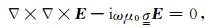
|
(1) |
式中μ0=4π×10-7H·m-1为真空磁导率,E为电场强度,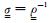
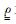
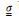
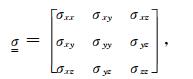
|
(2) |
其中x,y,z表示笛卡尔坐标系三个坐标方向. 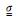
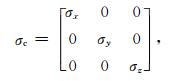
|
(3) |
则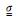
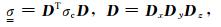
|
(4) |
其中D为总旋转矩阵,Dx,Dy,Dz分别为绕三个坐标轴的旋转矩阵(Yin, 2000)
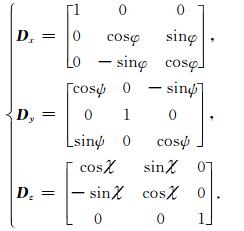
|
(5) |
为保证方程(1)中解的唯一性,我们在计算区域外边界设置狄利克雷边界条件.对于沿x方向极化的场源,对应上边界的边界条件为(殷长春等,2017)
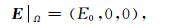
|
(6) |
式中Ω表示计算区域,E0表示上边界面的场值.对于其他边界,使用有限元法无需做任何处理(徐世浙,1994).
1.2 非结构矢量有限元法本文使用非结构矢量有限元法求解双旋度电场方程(1).矢量有限元法将自由度赋予棱边上,自动满足矢量场散度为零,消除了节点有限元的伪解效应(Jin,2002).此外,棱边与棱边的耦合弱于节点与节点的耦合,增加了总体矩阵的稀疏度.定义希尔伯特矢量空间H(curl, Ω)={Φ∈L2(Ω), ▽×Φ∈L2(Ω)}, 其中L2是希尔伯特空间中的平方可积函数,并在此空间下定义内积
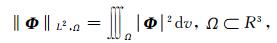
|
(7) |
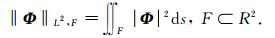
|
(8) |
利用伽辽金法离散控制方程(1),将其与四面体矢量基函数Φ做内积得到
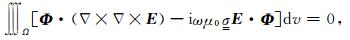
|
(9) |
(9) 式利用高斯分步积分可得
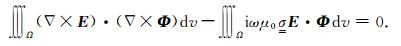
|
(10) |
将计算区域离散成小单元,并代入有限维函数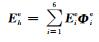
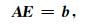
|
(11) |
其中,A为总体合成矩阵,b为与边界条件有关的右端项.求解方程组(11),可得任意区域内棱边电场值,则区域内任意位置电场可通过上述有限维函数插值得到,而磁场可通过Faraday定律得到,即
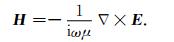
|
(12) |
在计算MT电磁响应后可通过定义阻抗张量计算视电阻率和相位,即
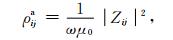
|
(13) |
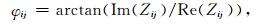
|
(14) |
其中i, j=x, y.(13)(14)式中的阻抗张量可通过求解两个极化方向的电磁场得到.
在各向异性介质中,阻抗张量依赖于各向异性主轴电阻率与场观测坐标系之间的夹角.借助于极坐标,可以进一步研究依赖于各向异性电阻率方向的阻抗张量.设极轴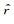
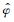
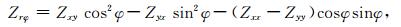
|
(15) |
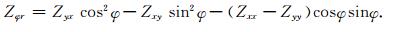
|
(16) |
在理论上,Zrφ等价于由极向电场和方位磁场计算的阻抗分量,而Zφr等价于由方位电场和极向磁场计算的阻抗分量.根据新的阻抗分量,按照公式(13)、(14)可以定义视电阻率ρrφa和ρφra及相位φrφ和φφr.
1.3 加权后验误差在自适应算法中直接使用后验误差指导网格剖分称为全局自适应算法.全局自适应算法所有单元的误差权重都相等.然而,我们只关心测量点的精度,这就需要增加测量区域的单元误差的权重,可以使用面向目标的自适应算法解决这一问题.在得到后验误差后,我们通过计算后验误差的权系数,得到加权后验误差,实现面向目标的自适应算法(Oden and Prudhomme, 2001).相比全局自适应算法,面向目标自适应算法可以重点加密计算点和异常体处的网格,在保证计算精度的情况下,使用更少的网格,进行快速三维正演.
1.3.1 后验误差估计在相邻单元i和j之间定义其公共面F,面两边电场的有限元解分别为E-和E+.假设面F从单元i指向单元j的单位法向量为nF.由电流密度法向连续性▽·j=0可得
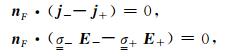
|
(17) |
j-和j+表示从两侧流过的面电流密度.在无限维希尔伯特空间,电流密度严格遵守公式(17).然而,利用有限元法求得的电流密度不满足该条件,本文利用有限维希尔伯特空间中电流密度在单元界面的不连续性估计后验误差(殷长春等,2017),其定义为
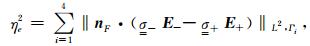
|
(18) |
其中Γi表示单元的第i个面.
1.3.2 后验误差权系数在地球物理电磁模拟问题中,主要关注的是测点附近场的计算精度.对于本文计算的电场方程,我们定义如下与局部电场相关的线性函数(Ren et al., 2013):
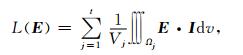
|
(19) |
其中,Vj表示第j个单元的体积,t表示需要加密测点的单元个数.
面向目标自适应算法的目的在于降低误差函数L(e),其中e=E-Eh表示正演解与精确解之间的差异.误差函数L(e)与加权系数w存在如下关系(Ren et al., 2013):
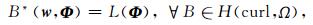
|
(20) |
其中,B*(w, Φ)表示B(w, Φ)的对偶形式,
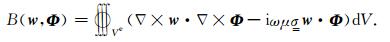
|
(21) |
求解(20)和(21)式可得加权系数.从公式(21)中可以看出,加权系数w实质上为电场的误差分布.设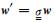
在得到电流密度后验误差及其权系数后,可以定义每个单元的电流密度加权后演误差为
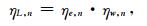
|
(22) |
其中,n表示第n个单元,ηw, n=‖w′‖L2, ηe, n由(18)式给出.
1.4 面向目标自适应策略本文面向目标自适应算法以殷长春等(2017)研发的针对各向同性目标体自适应策略为基础,在自适应过程中限制测点附近一定范围内单元的最大体积Vmax,以促进正演结果更快地收敛;为保证自适应算法的稳定性,对所有单元设置最小体积Vmin.
为了实现对特定单元加密,定义如下单元相对加权后验误差:
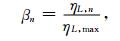
|
(23) |
其中ηL, max为所有单元中加权后验误差的最大值.
本文自适应策略算法过程主要为:
(1) 约束测点周边一定范围单元最大体积Vmax和所有单元的最小体积Vmin,设置自适应算法终止条件:最大迭代次数及最大棱边个数;
(2) 网格自适应迭代计算.不满足终止条件执行步骤(3),否则执行步骤(6);
(3) 若单元满足βn>βt和V>Vmin,则对该单元进行细化;
(4) 应用细化后的网格重新进行正演计算;
(5) 计算当前结果与前两次正演结果的相对误差,判断是否为非收敛点.若无非收敛点执行步骤(6),否则执行(2);
(6) 结束循环.
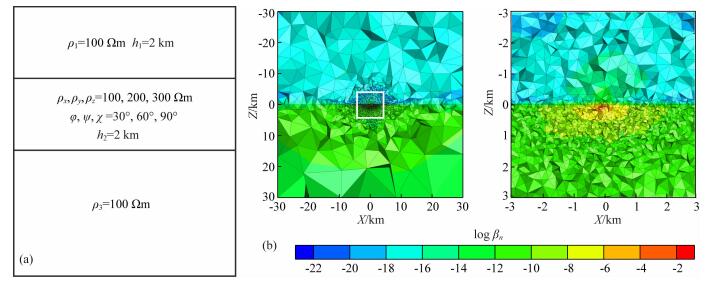
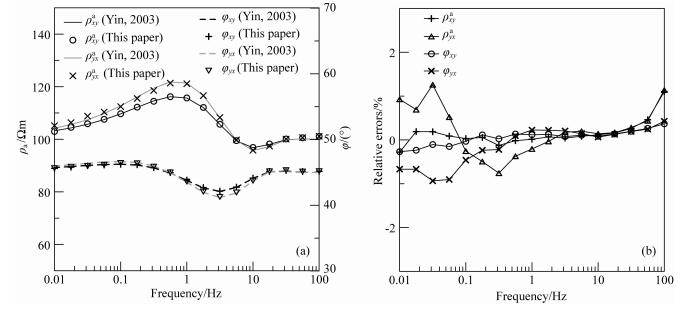
2 数值算例 2.1 精度验证首先假设一个简单的三层模型.如图 1a所示,第一层各向同性覆盖层电阻率为100 Ωm,厚度2 km.第二层为各向异性层,其中ρx、ρy和ρz分别为100、200和300 Ωm,各向异性电阻率三个旋转角φ、ψ和分别为30°、60°和90°,厚度为2 km.第三层为各向同性,电阻率为100 Ωm.从图 1可以看出观测点附近网格得到有效加密.我们利用Yin(2003)给出的任意各向异性解析解与本文三维大地电磁自适应结果进行对比.在频率0.01到100 Hz之间按对数等间隔取21个计算频点.图 2中的对比结果显示,本文程序与一维各向异性解析解最大相对误差小于2%,证明了本文程序的正确性.本文正演是在Intel(R) Xeon(R) CPU E5-2650 v2 @ 2.60 GHz,128 G内存工作站环境下进行的,表 1给出在频率为1 Hz时统计的网格自适应过程参数.结果表明,网格迭代三次达到收敛,正演计算累计耗时393 s.
|
图 1 (a) 三层各向异性介质模型;(b) 0.1 Hz自适应网格及局部放大效果 Fig. 1 (a) A 3-layer anisotropic model; (b) Mesh at x, z-plane for 0.1 Hz and a local view of the mesh in the white box |
|
图 2 (a) 本文算法结果与解析解对比;(b)相对误差 Fig. 2 (a) Comparison between our model results and analytical solutions; (b) Relative errors |
|
|
表 1 自适应迭代过程参数 Table 1 Parameters for iterative adaptive process |
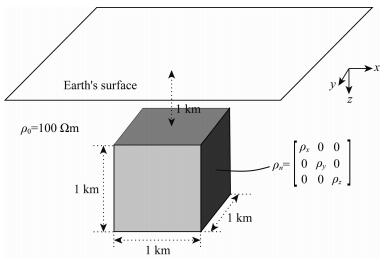
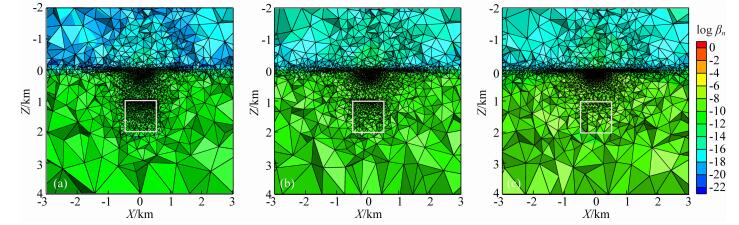
为分析各向异性对网格自适应的影响特征,假设半空间中存在一个三维各向异性体模型.如图 3所示,各向同性半空间电阻率为100 Ωm,三维异常体为三轴各向异性,其中,ρy=100 Ωm,ρz=1000 Ωm,ρx可变.异常体大小为1 km×1 km×1 km,顶面埋深1 km.我们计算模型在1 Hz时的大地电磁响应.从图 4中可以看出,当异常体ρy和ρz保持不变时,ρx为1 Ωm的时候异常体的网格最密,为10 Ωm时次之,而ρx为100 Ωm异常体处网格最稀疏,说明本文网格自适应算法由于引入电导率加权后验误差,有效地实现对测点和各向异性体加密,各向异性异常体最小主轴电阻率决定了异常体处网格加密程度.
|
图 3 各向同性半空间中存在一个三轴各向异性异常体 Fig. 3 A 3-axis anisotropic abnormal body embedded in an isotropic half-space |
|
图 4 各向同性半空间中存在各向异性三维异常体的自适应网格 (a) ρx/ρy/ρz=1/100/1000 Ωm;(b) ρx/ρy/ρz=10/100/1000 Ωm;(c) ρx/ρy/ρz=100/100/1000 Ωm. Fig. 4 Adaptive meshes for an anisotropic abnormal body embedded in an isotropic half-space |
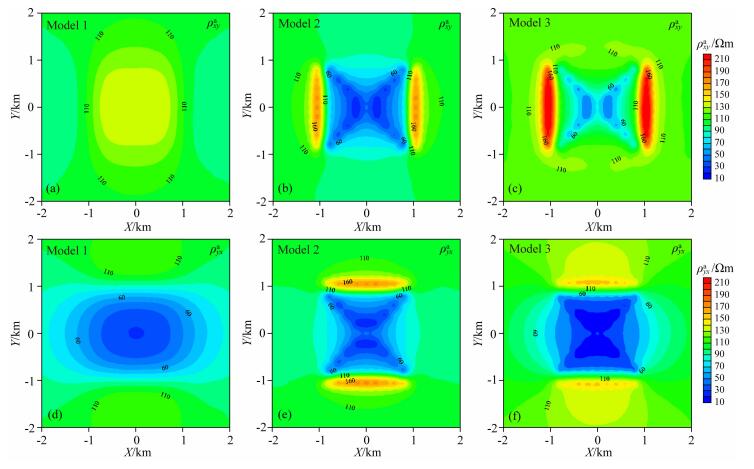
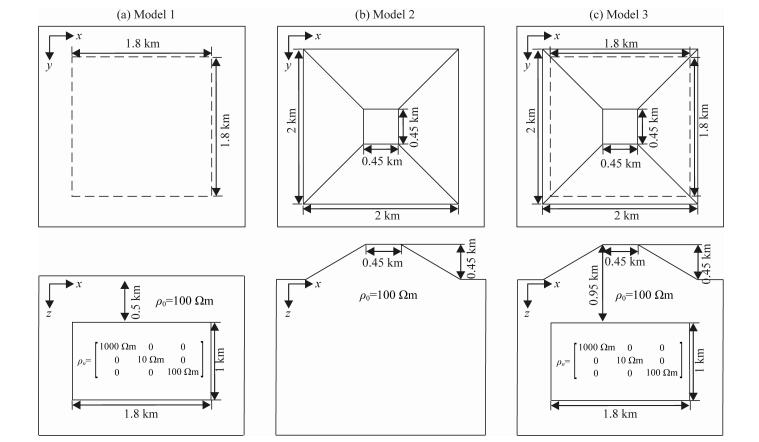
设置如图 5所示的三组模型:模型一为水平地表单个各向异性异常体模型,模型二为起伏地表半空间模型,模型三为含各向异性异常体的起伏地表模型,我们计算频率为2 Hz的MT响应,并分析地形和各向异性对MT响应的影响特征.图中假设均匀各向同性半空间电阻率100 Ωm,三维异常体的主轴电阻率ρx、ρy、ρz分别为1000 Ωm、10 Ωm和100 Ωm.
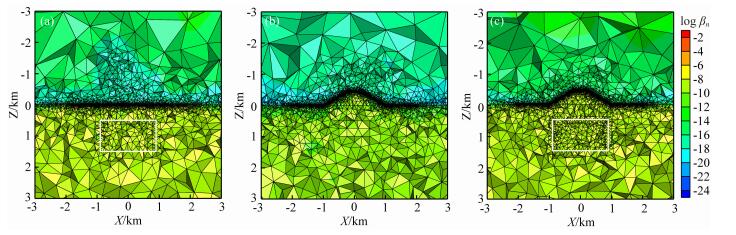
从图 6可以看出本文算法对图 5模型中的测点、异常体和地形都进行了有效地加密.
|
图 5 模型示意图 (a)模型一俯视图和切片图;(b)模型二俯视图和切片图;(c)模型三俯视图和切片图. Fig. 5 Schematic display of models (a) Plane view and section view of Model 1; (b) Plane view and section view of Model 2; (c) Plane view and section view of Model 3. |
|
图 6 图 5中模型自适应网格 (a)模型一;(b)模型二;(c)模型三. Fig. 6 Adaptive meshes for models in Fig. 5 (a) Model 1; (b) Model 2; (c) Model 3. |
图 7给出上述三个模型视电阻率ρxya和ρyxa响应.对于模型一,异常体主轴电阻率ρx为高阻,而主轴电阻率ρy为低阻.由图可见,ρxya在异常体上方表现为高阻,且高阻异常在y方向上有拉伸趋势;ρyxa在异常体上方表现为低阻,低阻异常在x方向有拉伸趋势.这种特征很容易解释.事实上,ρxya主要由x方向的极化电场决定,而ρyxa主要由y方向的极化电场决定.当电场沿高阻主轴x方向穿过异常体边界(ρx=1000 Ωm)时,由于电流密度在电性分界面的连续性,异常体内的电场大于围岩中的电场,所以异常体上方出现ρxya高阻异常;相反,当电场沿低阻主轴y方向穿过异常体边界(ρy=10 Ωm)时,电流密度的连续性导致异常体内的电场小于围岩中的电场,所以异常体上方出现ρyxa低阻异常.同样,由于在异常体附近电场沿极化方向变化梯度较大,导致分界面附近沿极化方向视电阻率梯度较大,而垂直极化方向视电阻率变化较缓慢.
对于模型二的纯地形模型,视电阻率在山峰的上方出现低阻异常.同时,视电阻率在电场极化方向两侧山脚处出现高阻畸变,这是由于电场在极化方向穿过绝缘空气介质和大地导电介质,介质之间巨大物性差异导致界面电场和视电阻率畸变.对于模型三,由于地形异常和地下异常体产生的异常叠加,导致山顶上ρxya值变高,而ρyxa值变得更低.
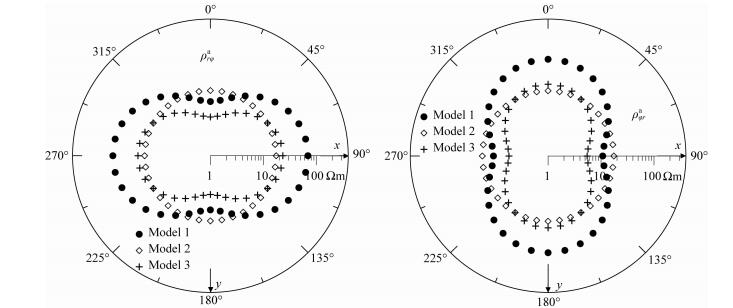
2.4 起伏地形条件下各向异性异常体识别本节将进一步研究地下介质各向异性识别问题.从2.3节模型讨论可知,虽然各向异性和地形模型的响应不同,但是起伏地形条件下各向异性效应和地形效应叠加在一起,难以直接从视电阻率响应中识别出地下介质的各向异性信息.为了识别起伏地形条件下异常体各向异性,我们针对2.3节给出的三种模型,研究极坐标系下地形中心点处视电阻率ρrφa和ρφra分布特征.图 8给出不同方位角下的ρrφa和ρφra分布.其中,从坐标原点到各点的矢量长度表示视电阻率大小,而方向表示极化电场测量方向.从图可以看出,对于模型二起伏地表各向同性模型,视电阻率ρrφa和ρφra为圆形分布;对于模型一无地形的各向异性模型和模型三起伏地表各向异性模型,ρrφa和ρφra的分布明显具有方向性.ρrφa在x轴方向最大,而在y方向最小.这是由于对于ρrφa,我们测量极向电场和方位磁场,在导电介质中电场受到介质电阻率影响大,而磁场在介质局部范围内变化很小,所以ρrφa在各向异性主轴方向会出现极大值,其长轴方向对应于各向异性主轴电阻率ρx,短轴方向对应ρy.对于ρφra,我们测量方位电场和极向磁场,导致ρφra分布与实际各向异性主轴正交,长轴对应各向异性主轴电阻率较小的方向,而短轴对应各向异性电阻率较大方向,这是典型的anisotropic paradox现象(Yin,2006).受地形屏蔽作用,起伏地表下各向异性异常体的异常受到压制,然而各向异性特征仍然可以从ρrφa和ρφra分布特征上识别出来.
|
图 8 图 5中三组模型在地形中心点处视电阻率ρrφa和ρφra分布图 Fig. 8 Polar plots of apparent resistivities ρrφa and ρφrafor 3 models in Fig. 5 |
为了进一步分析不同各向异性主轴方向MT响应特征及各向异性识别,我们对图 5中模型三的异常体各向异性电阻率张量绕x、y和z轴皆旋转0°,45°和90°.图 9展示了旋转后视电阻率ρrφa和ρφra的分布.从图 9a可以看出,由于在绕x轴旋转时x方向的电阻率不变ρx=1000 Ωm,y轴电阻率由10 Ωm变到100 Ωm,对应的ρrφa长轴位于x方向,在此方向上ρrφa值保持不变,而位于y轴方向的短轴视电阻率明显变大;由于anisotropic paradox, ρφra的分布与ρrφa正交.从图 9b可以看出,在绕y轴旋转时y方向的电阻率不变ρy=10 Ωm,而x方向的电阻率由1000 Ωm变为100 Ωm.由于x轴方向电阻率始终大于y方向,导致ρrφa长轴始终位于x方向,短轴位于y方向.长轴视电阻率变化明显,短轴保持不变,同理ρφra的分布与ρrφa正交.从图 9c可以看出,当异常体电阻率绕z轴转动时,随旋转角变大,异常体x轴电阻率由1000 Ωm变为10 Ωm,而y轴电阻率由10 Ωm变为1000 Ωm,ρrφa的分布与电阻率张量有良好的对应关系,而ρφra与实际电阻率分布呈现正交关系.ρrφa和ρφra这种分布特征有利于对地下异常体的各向异性特征进行识别.
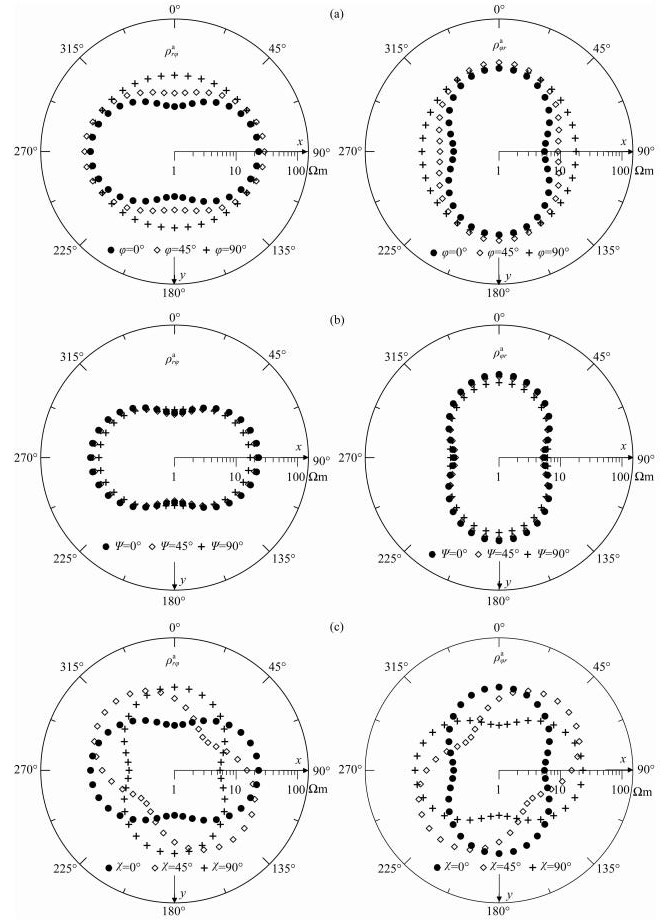
|
图 9 图 5模型三中异常体电阻率张量发生旋转时地形中心处ρrφa和ρφra极性图 (a)绕x轴旋转;(b)绕y轴旋转;(c)绕z轴旋转. Fig. 9 Polar plots of ρrφa and ρφra for Model 3 in Fig. 5 at the center of the topography (a) Rotation around x-axes; (b) Rotation around y-axes; (c) Rotation around z-axes. |
本文提出一种面向目标自适应有限元三维大地电磁各向异性正演模拟方法.通过与一维层状任意各向异性介质的解析解进行对比,验证了本文算法具有很高的精度.将所提出的自适应算法应用到大地电磁三维各向异性正演模拟中取得了很好的应用效果.通过大量模型试验,得出如下结论:
(1) 电阻率各向异性影响网格自适应结果,各向异性最小主轴电阻率决定自适应网格的疏密程度;
(2) 各向异性和起伏地形均对MT响应产生影响.山峰地形上方呈现低阻异常,在极化方向的山脚拐点处产生高阻异常,而各向异性依据极化方向和各向异性主轴之间的耦合关系,对MT响应产生不同影响;
(3) 根据极坐标下视电阻率ρrφa和ρφra分布,可以有效识别起伏地表情况下地下异常体各向异性主轴方向.
本文研究成果将为复杂地形条件下大地电磁各向异性数据三维反演提供理论基础.
致谢作者向吉林大学电磁“千人计划”研究团队成员在文章准备过程中提供的帮助表示感谢.特别对审稿人和编辑对本文提出的修改建议表示感谢.
Baba K, Chave A D, Evans R L, et al. 2006. Mantle dynamics beneath the East Pacific Rise at 17 S:Insights from the Mantle Electromagnetic and Tomography (MELT) experiment. Journal of Geophysical Research:Solid Earth, 111(B2): B02101. DOI:10.1029/2004JB003598 |
Bahr K, Bantin M, Jantos C, et al. 2000. Electrical anisotropy from electromagnetic array data:implications for the conduction mechanism and for distortion at long periods. Physics of the Earth and Planetary Interiors, 119(3-4): 237-257. DOI:10.1016/S0031-9201(00)00134-5 |
Becken M, Ritter O, Bedrosian P A, et al. 2011. Correlation between deep fluids, tremor and creep along the central San Andreas fault. Nature, 480(7375): 87-90. DOI:10.1038/nature10609 |
Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method. Chinese Journal of Geophysics, 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
Chen X. 2012. Two-dimensional constrained anisotropic inversion of magnetotelluric data. Postdam: Universität Potsdam.
|
Farquharson C G, Duckworth K, Oldenburg D W. 2006. Comparison of integral equation and physical scale modeling of the electromagnetic responses of models with large conductivity contrasts. Geophysics, 71(4): G169-G177. DOI:10.1190/1.2210847 |
Gatzemeier A, Moorkamp M. 2005. 3D modelling of electrical anisotropy from electromagnetic array data:hypothesis testing for different upper mantle conduction mechanisms. Physics of the Earth and Planetary Interiors, 149(3-4): 225-242. DOI:10.1016/j.pepi.2004.10.004 |
Häuserer M, Junge A. 2011. Electrical mantle anisotropy and crustal conductor:a 3-D conductivity model of the Rwenzori Region in western Uganda. Geophysical Journal International, 185(3): 1235-1242. DOI:10.1111/gji.2011.185.issue-3 |
Heise W, Caldwell T G, Bibby H M, et al. 2006. Anisotropy and phase splits in magnetotellurics. Physics of the Earth and Planetary Interiors, 158(2-4): 107-121. DOI:10.1016/j.pepi.2006.03.021 |
Huang Y F, Hu X Y, Han B. 2016. Forward and inverse modeling of the magnetotelluric field in 2D anisotropic media with an adaptive finite element method. Oil Geophysical Prospecting, 51(4): 809-820. |
Jin J M. 2002. The Finite Element Method in Electromagnetics. New York: Wiley-IEEE Press.
|
Kirkby A, Heinson G, Holford S, et al. 2015. Mapping fractures using 1D anisotropic modelling of magnetotelluric data:A case study from the Otway Basin, Victoria, Australia. Geophysical Journal International, 201(3): 1961-1976. DOI:10.1093/gji/ggv116 |
Li Y G. 2002. A finite-element algorithm for electromagnetic induction in two-dimensional anisotropic conductivity structures. Geophysical Journal International, 148(3): 389-401. DOI:10.1046/j.1365-246x.2002.01570.x |
Liu G M, Becker A. 1992. Evaluation of terrain effects in AEM surveys using the boundary element method. Geophysics, 57(2): 272-278. DOI:10.1190/1.1443240 |
Mareschal M, Kellett R L, Kurtz R D, et al. 1995. Archaean cratonic roots, mantle shear zones and deep electrical anisotropy. Nature, 375(6527): 134-137. DOI:10.1038/375134a0 |
Nam M J, Kim H J, Song Y, et al. 2007. 3D magnetotelluric modelling including surface topography. Geophysical Prospecting, 55(2): 277-287. DOI:10.1111/gpr.2007.55.issue-2 |
Oden J, Prudhomme S. 2001. Goal-oriented error estimation and adaptivity for the finite element method. Computers & Mathematics with Applications, 41(5-6): 735-756. |
Pek J, Verner T. 1997. Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophysical Journal International, 128(3): 505-521. DOI:10.1111/gji.1997.128.issue-3 |
Rasmussen T M. 1988. Magnetotellurics in southwestern Sweden:evidence for electrical anisotropy in the lower crust?, 93(B7):7897-7907. Journal of Geophysical Research:Solid Earth, 93(B7): 7897-7907. DOI:10.1029/JB093iB07p07897 |
Reddy I K, Rankin D. 1975. Magnetotelluric response of laterally inhomogeneous and anisotropic media. Geophysics, 40(6): 1035-1045. DOI:10.1190/1.1440579 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. Boundary element solutions for broad-band 3-D geo-electromagnetic problems accelerated by an adaptive multilevel fast multipole method. Geophysical Research Letters, 192(2): 473-499. |
Usui Y. 2015. 3-D inversion of magnetotelluric data using unstructured tetrahedral elements:applicability to data affected by topography. Geophysical Journal International, 202(2): 828-849. DOI:10.1093/gji/ggv186 |
Weidelt P. 1999. 3-D conductivity models:implications of electrical anisotropy. Three-Dimensional Electromagnetics, 7: 119-137. |
Xu S Z. 1994. The Finite-element Method in Geophysics. Beijing: Science Press.
|
Yin C C. 2000. Geoelectrical inversion for a one-dimensional anisotropic model and inherent non-uniqueness. Geophysical Journal International, 140(1): 11-23. DOI:10.1046/j.1365-246x.2000.00974.x |
Yin C C. 2003. Inherent nonuniqueness in magnetotelluric inversion for 1D anisotropic models. Geophysics, 68(1): 138-146. DOI:10.1190/1.1543201 |
Yin C C. 2006. MMT forward modeling for a layered earth with arbitrary anisotropy. Geophysics, 71(3): G115-G128. DOI:10.1190/1.2197492 |
Yin C C, Zhang B, Liu Y H, et al. 2017. A goal-oriented adaptive algorithm for 3D magnetotelluric forward modeling. Chinese Journal of Geophysics, 60(1): 327-336. DOI:10.6038/cjg20170127 |
陈辉, 邓居智, 谭捍东, 等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究. 地球物理学报, 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
黄一凡, 胡祥云, 韩波. 2016. 自适应有限元法的大地电磁二维各向异性正反演. 石油地球物理勘探, 51(4): 809-820. |
徐世浙. 1994. 地球物理中的有限单元法. 北京: 科学出版社.
|
殷长春, 张博, 刘云鹤, 等. 2017. 面向目标自适应三维大地电磁正演模拟. 地球物理学报, 60(1): 327-336. DOI:10.6038/cjg20170127 |
 2018, Vol. 61
2018, Vol. 61