2. 页岩油气富集机理与有效开发国家重点实验室, 北京 100083;
3. 中国石化页岩油气勘探开发重点实验室, 北京 100083;
4. 中国石化石油勘探开发研究院, 北京 100083
2. National Key Laboratory of Corporation of Shale Oil/Gas Enrichment Mechanism and Effective Development, SinoPEC, Beijing 100083, China;
3. SinoPEC Key Laboratory of Shale Oil/Gas Exploration and Production Technology, Beijing 100083, China;
4. SinoPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
页岩油气作为一种非常规能源,近些年来在国内外受到越来越多的关注.岩石物理方法已经成为寻找页岩油气富集地段的重要方法之一,利用岩石物理建模方法可以建立岩石组分、孔隙度、孔隙形态以及流体性质与岩石整体弹性参数之间的联系.
对页岩岩石物理模型的研究在早期可以追溯到Vernik和Nur(1992)基于各向异性Backus平均理论,针对属于富有机质黑色页岩的北美Bakken页岩,进行了岩石物理建模研究.另外,Hornby等(1994)利用各向异性自相容近似(SCA)和差分等效介质(DEM)理论进行页岩岩石物理建模,考虑黏土矿物和微裂缝等复杂物性特征的几何分布.Carcione(2000)针对富含有机质成分的页岩利用黏弹各向异性理论讨论了其各向异性衰减特征.Sayers(2005, 2013)也对富有机质页岩中干酪根对页岩弹性参数的影响进行了研究.近年来,许多学者利用岩石物理建模方法,讨论了页岩的组成和其精细结构:Mba和Prasad(2010)分析了页岩中矿物组分与弹性各向异性的关系;Spikes(2011)基于统计学方法研究了裂缝密度参数的不确定性以及孔隙形态对页岩弹性参数影响;Jiang和Spikes(2013)利用自相容模型和Chapman理论建立岩石物理模型对海恩斯维尔页岩进行了参数估计;Guo等(2014)开发了页岩各向异性参数井中反演方法;邓继新等(2015)利用实验室观察和岩石物理建模手段讨论了龙马溪组页岩的微观结构和地震岩石物理特征.
黏土作为页岩岩石的重要组分之一,其弹性参数的选取决定着岩石物理建模的准确性.针对页岩中的黏土矿物,Han等(1986)利用统计学分析讨论了墨西哥湾黏土的弹性参数.除实验统计方法外,还可以利用岩石物理模型研究黏土矿物的弹性参数:Sayers(2005)通过岩石物理模型研究了黏土矿物的分布与页岩各向异性参数之间的关系;Bayuk等(2007)通过微观尺度的岩石物理模型,计算了黏土矿物的各向异性参数;Ortega等(2009)进一步研究了纳米尺度上黏土颗粒的微观结构,以及对应的岩石物理分析方法.Caicione等(2011)利用Backus平均计算页岩中黏土颗粒定向对其地震弹性性质及各向异性的影响;Guo等(2014)在研究Barnett页岩各向异性岩石物理建模过程中,提出黏土压实指数参数CL,用于描述黏土定向排列引起的速度变化.
相比于碳酸盐岩等其他地层,页岩地层其组分更为复杂,且具有不同微观物性特征,使得页岩地层呈现各向异性.研究区为四川龙马溪组页岩地层,其黏土组分含量较高,并且黏土成分复杂,存在定向排列的特征,本文着重考虑黏土矿物的弹性参数对岩石物理建模的影响,同时考虑页岩中定向排列的裂缝以及地层倾角的影响,建立TTI(Tilted Transversely Isotropic)介质模型,并基于岩石物理模型进行各向异性参数反演.
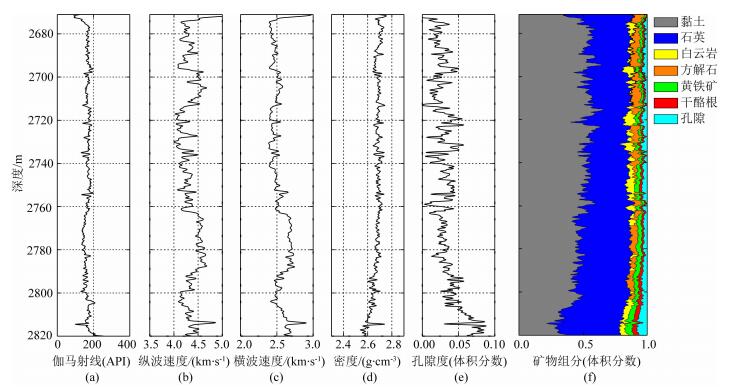
1 研究区岩石物理模型特征分析图 1所示为四川盆地下志留统龙马溪组页岩气储层测井数据.研究层段岩性主要为页岩、含粉砂质页岩和碳质页岩.
|
图 1 页岩测井曲线图 (a)伽马射线; (b)纵波速度; (c)横波速度; (d)密度; (e)孔隙度; (f)组分体积比. Fig. 1 Well-log curves of shale formation (a) Gamma ray; (b) P-wave velocity; (c) S-wave velocity; (d) Density; (e) Porosity; (f) Volume ratio of composition. |
图 1e为孔隙度曲线,显示页岩地层总体孔隙度较低,介于2%~3%之间.图 1f给出该层段组成页岩的各个组分的体积分数,可以看出龙马溪组页岩的主要矿物组分为黏土和石英,约占总体积的80%,其他矿物包括白云岩、方解石、黄铁矿.地层TOC(Total Organic Carbon,总有机碳)含量稳定,约为1.5%.各个组分的弹性参数如表 1所示.
|
|
表 1 龙马溪组页岩各个矿物组分的弹性参数 Table 1 Elastic properties of components in shale of Longmaxi Formation |
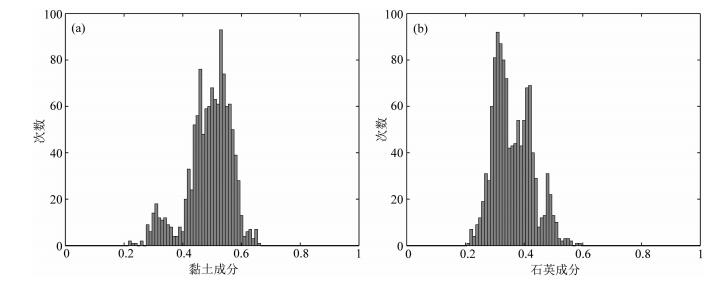
图 2a和图 2b分别为页岩储层黏土矿物和石英矿物的统计直方图,可以看出该层段总体上黏土含量大于石英含量,并且黏土含量介于40%~60%,石英含量介于25%~45%,因此在岩石物理建模过程中需要重点考虑黏土的影响.
|
图 2 部分组分含量统计直方图 (a)黏土矿物; (b)石英矿物. Fig. 2 Statistical histogram of partial components of clay (a) and quartz (b) |
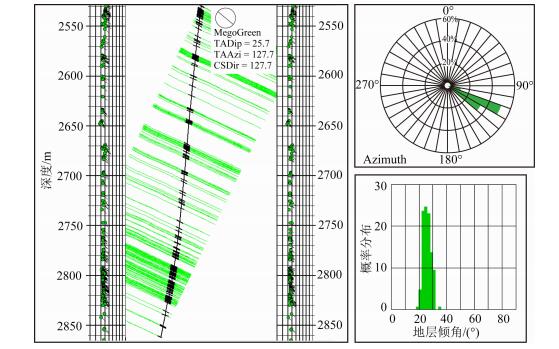
图 3为目的层位的井旁构造图,可以看出该层位倾向比较稳定倾向南东,地层倾角较高,为18°~32°.
|
图 3 井旁构造图 Fig. 3 Side-borehole structure of the target formation |
图 4为部分典型层段FMI (Formation MicroScanner Image,地层微电阻率扫描成像)成像图,表明岩性主要为黑色泥质页岩,成层性明显,并且层间微裂缝发育.页岩岩层发育微裂缝的主要原因是黏土矿物的应力释放和黏土矿物的脱水作用,定向排列的微裂缝使得页岩的各向异性特征明显.

|
图 4 FMI成像测井图 Fig. 4 FMI image well-log |
泥页岩的裂缝系统是油气的主要储集空间和运移通道,但是由于受限于测井仪器纵向分辨率,岩石的微观结构无法直接测量,更重要的是,在井中直接测量横向各向同性介质的各向异性参数存在困难.
因此,有必要建立岩石物理模型,计算泥页岩的复杂矿物组分、有机质、孔隙-裂缝系统等微观结构如何影响岩石的弹性各向异性,并进一步开发裂缝和各向异性参数的反演方法.
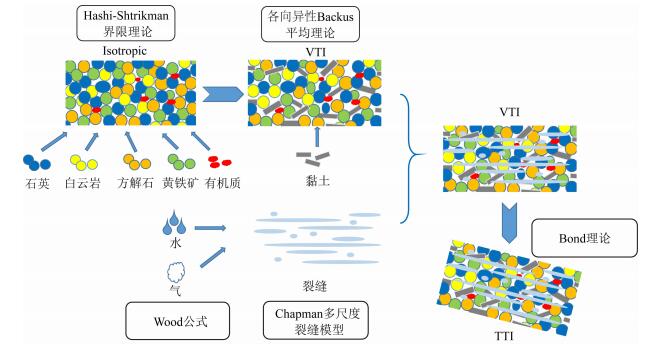
2 页岩各向异性岩石物理建模流程 2.1 岩石物理建模流程如图 5所示为具有横向各向同性弹性特征的页岩储层的岩石物理建模流程图,包括:(1)利用Hashi-Shtrikman界限理论(附录Ⅰ),计算非黏土类矿物(石英、白云岩、石灰岩、黄铁矿)及有机质干酪根的各向同性弹性参数.基于前人的研究,假设干酪根在空间上呈随机的团块状分布;(2)利用各向异性Backus平均理论(附录Ⅱ)将黏土矿物与上述非黏土类矿物、干酪根混合,计算具有VTI(Transversely isotropy with a vertical axis)各向异性的固体基质的弹性模量,并且考虑黏土矿物弹性参数的非均质性;(3)利用Wood公式求取孔隙-裂缝空间中混合流体(气和水)的弹性参数;(4)利用Chapman理论(附录Ⅲ)将多尺度孔隙-裂缝系统引入固体基质,得到具有VTI各向异性的页岩储层弹性参数;(5)利用Bond变换(附录Ⅳ),计算地层倾斜情况下页岩储层的TTI弹性各向异性参数.
|
图 5 岩石物理建模流程图 Fig. 5 Flow chart of rock physics modeling |
上述岩石物理模型中,步骤(2)中黏土矿物纵横波速度和步骤(3)中裂缝密度为待定参数,其他参数可由测井数据确定或估计,因此为设计岩石物理反演算法方便,模型输出的弹性系数矩阵可以写为
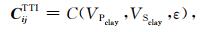
|
(1) |
其中CijTTI为TTI模型的弹性系数矩阵,VPclay和VSclay分别为黏土矿物的纵横波速度,ε为平行层理的孔隙或微裂缝的密度.根据岩石物理定义,在测井孔隙度已知的情况下,裂缝密度ε与孔隙纵横比α之间的关系为
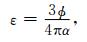
|
(2) |
因此(1)式可以改写为
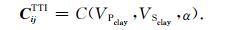
|
(3) |
下面设计岩石物理反演算法,由测井数据计算这三个参数.
2.2 对黏土矿物的分析如图 2所示,页岩储层中黏土矿物比例较高,因此在岩石物理模型中,黏土矿物的速度大小对建模结果影响显著.表 2给出前人对不同地区的黏土矿物测量得到的结果,不同地区的黏土矿物速度相差明显.黏土速度差异的重要影响因素,在于黏土矿物的成分复杂,并且呈现各向异性定向排列特征(Guo et al., 2014).一方面,黏土中具有不同弹性模量的矿物组分的变化,会导致黏土混合物速度的变化;另一方面,黏土矿物的定向排列特征又使得页岩在垂直方向的速度发生变化.针对上述分析,本文提出将黏土矿物的垂向纵、横波速度作为待定的拟合参数,而非直接利用其他地区已有的黏土矿物参数,通过岩石物理建模设计反演流程,预测黏土矿物的弹性参数.
|
|
表 2 前人对于不同地区黏土矿物纵横波速度的测量结果 Table 2 Elastic properties of clay in different areas from previous work |
研究区页岩储层主要为水和气填充,本文假设其主要充填于微观孔隙和定向排列的裂缝中,利用Chapman多尺度裂缝岩石物理模型,考虑流体充填的孔隙-裂缝系统的影响,计算水平缝密度ε变化引起的扰动ΔCchapman(ε),得到岩石整体的弹性系数矩阵为
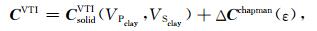
|
(4) |
其中,CsolidVTI(VPclay, VSclay)为固体骨架的弹性系数矩阵.
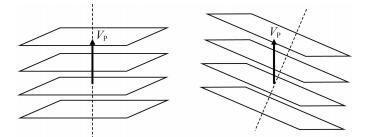
2.4 TTI介质模型如图 3所示,龙马溪组页岩地层倾角较大,测井测得的速度方向将不再沿着地层对称轴方向(如图 6所示),此时VTI介质模型并不能完全描述倾斜页岩层,需要用Bond变换建立TTI介质模型进行地层倾角校正.
|
图 6 水平地层与倾斜地层示意图 Fig. 6 Schematic of horizontal and tilt strata |
以建模过程中的黏土纵波速度、黏土横波速度以及孔隙纵横比作为拟合参数,以测井得到的纵波速度和横波速度作为约束来进行岩石物理反演.因此,反演过程中对于每一个测井点有三个拟合参数,但只有两个确定的约束条件(测井纵波速度和横波速度),属于欠定问题.因此,为了得到符合真实条件的解,需要对待定参数进行约束.本文基于贝叶斯理论框架利用测井测得的纵波数据和横波数据进行约束以及待反演参数的先验信息进行反演.根据贝叶斯理论,后验概率分布为
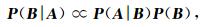
|
(5) |
其中事件A代表测井测得的纵横波速度,事件B代表待反演的参数,P(B)为事件B发生的先验概率,P(A|B)为似然函数,P(B|A)为后验概率.
本文假设黏土矿物的纵、横波速度满足高斯分布,其均值取Han等人的测量结果(表 2).同时,假设孔隙纵横比参数α以10为底的对数也满足高斯分布,考虑到孔隙纵横比在不同地区随岩性的变化较大,因此选取较大的方差.邓继新等(2015)针对研究区页岩样本进行的分析统计表明,大部分孔隙的纵横比介于0.1~0.2之间,因此本文选取lg(α)=-1作为均值.由此,待反演的三个参数符合三元高斯分布
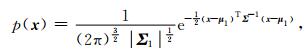
|
(6) |
其中,x为黏土矿物纵、横波速度和孔隙纵横比以10为底的对数所组成的参数向量,μ1为参数的均值所组成的向量,Σ1为参数向量的协方差矩阵.协方差矩阵反映各个变量偏离均值的程度以及不同变量之间的相关性.本文假设黏土矿物纵、横波速度为正相关关系,即纵波速度变大横波速度也变大,其协方差可通过前人研究的黏土纵、横波速度统计得到,同时假设孔隙纵横比与黏土的纵、横波速度没有相关性,即协方差为0,因此给出这三个参数的协方差矩阵为
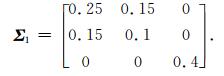
|
(7) |
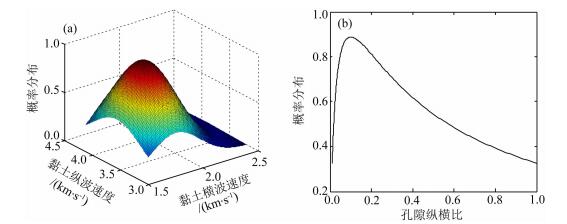
分别画出黏土纵、横波速度和孔隙纵横比的先验概率分布函数如图 7a和图 7b所示.同时,认为黏土速度不会超过伊利石(纵波速度为4.32 km·s-1,横波速度为2.52 km·s-1)的速度,将伊利石的速度作为黏土矿物纵、横波速度的上限.孔隙纵横比的概率密度曲线如图 7b所示,为了避免反演结果过度依赖初始值的选取,选取较大的方差.
|
图 7 模型参数的先验概率分布图 Fig. 7 Distribution of prior probability |
为建立反演的目标函数,假设模型的正演结果与测井约束参数之间的残差,即似然函数,也满足二元高斯分布
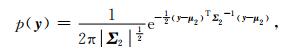
|
(8) |
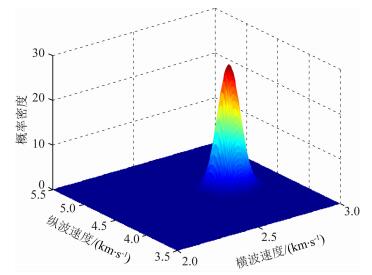
式中,y为TTI模型的垂向纵、横波速度所组成的向量,μ2为测井纵、横波速度组成的向量,Σ2为协方差矩阵,决定着对模型解偏离实际测井速度的容忍程度,概率分布函数如图 8所示.结合拟合参数的先验概率分布,可以得到后验概率分布
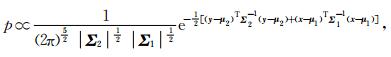
|
(9) |
|
图 8 似然函数概率分布图 Fig. 8 Distribution of likelihood function |
后验概率密度最大的点即对应着最优解.因此,可以得到目标函数为
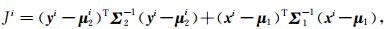
|
(10) |
其中,Ji为第i个测井点的目标函数,yi为第i个测井点的岩石物理建模得到的纵、横波速度组成的向量,μ2i为第i个测井点的实测纵、横波速度组成的向量,xi为第i个测井点黏土纵、横波速度和孔隙纵横比所组成的向量,μ1i为第i个测井点黏土纵、横波速度和孔隙纵横比的先验均值所组成的向量,并且yi为xi的函数.当目标函数最小时取得最优解.
本文利用粒子群(Particle Swarm Optimization, PSO)算法进行最优化搜索.粒子群算法最早由Eberhart和Kennedy(1995)提出.该方法的基本概念源于对鸟群觅食行为的研究,即假设一群鸟在随机搜寻食物,在这个区域里只有一块食物,而所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远.那么找到食物的最优策略是搜寻目前离食物最近的鸟的周围区域.PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题.在PSO中,每个优化问题的潜在解都可以想象成d维搜索空间上的一个点,称之为“粒子”(Particle),所有的粒子都有一个被目标函数决定的适应值(Fitness Value),每个粒子还有一个速度决定它们飞翔的速度和距离,然后粒子们就追随当前的最优粒子在解空间中进行迭代搜索.在每一代中,粒子通过跟踪两个“极值”来更新自己,一个为粒子本身目前找到的最优解Pbest,另一个为所有粒子目前找到的最优解Gbest.
标准粒子群算法速度和位置进化方程为:
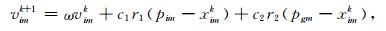
|
(11) |
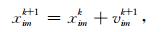
|
(12) |
其中,下标i表示第i个粒子;下标m表示粒子的第m维;ω为惯性权值;常数c1和c2为学习因子;r1和r2是取值范围[0, 1]之间的随机数;vimk和vimk+1分别表示第k和第k+1次迭代时第i个粒子的速度矢量的第m维分量;ximk和ximk+1分别表示第k和第k+1次迭代时第i个粒子的位置矢量的第m维分量;pim是第i个粒子的个体最佳位置Pbest的第m维分量;pgm是种群最好位置Gbest的第m维分量.搜索时,粒子的位置可以被限定在一个范围内,粒子只能在设定的搜索范围内进行迭代更新.
本文利用粒子群算法进行最优化搜索的参数如表 3所示.
|
|
表 3 粒子群算法的参数表 Table 3 Parameters of particle swarm optimization algorithm |
为了讨论反演算法的准确性,本文设计了一个理论模型,其固体矿物的体积分数、孔隙度以及流体饱和度参数如表 4所示,各个矿物的弹性参数如表 1所示,并且取孔隙纵横比为0.1.
|
|
表 4 理论模型组分参数 Table 4 Parameters of theoretical model |
通过如图 5所示的岩石物理建模流程正演得到TTI模型在垂直方向的纵波速度VP=3.9167 km·s-1,横波速度VS=2.3881 km·s-1.将黏土矿物的纵、横波速度和孔隙纵横比参数作为待反演的参数,输入几组不同先验均值信息来验证反演算法的准确性,其参数和反演结果如表 5所示.
|
|
表 5 四组不同的输入以及反演结果 Table 5 Four different inputs and results of inversion |
输入1为模型的真实解,可以看出当先验信息十分准确时,可以反演得到几乎准确的结果;输入2中黏土矿物的纵横波速度准确,而孔隙纵横比输入不准确,其反演结果有一定误差,但仍然接近模型的真实解;输入3中孔隙纵横比输入准确,而黏土矿物的纵横波速度输入不准确,其反演结果有较小误差;输入4中孔隙纵横比输入和黏土矿物的纵横波速度均不准确,其反演结果存在一定误差,但仍可以接受.
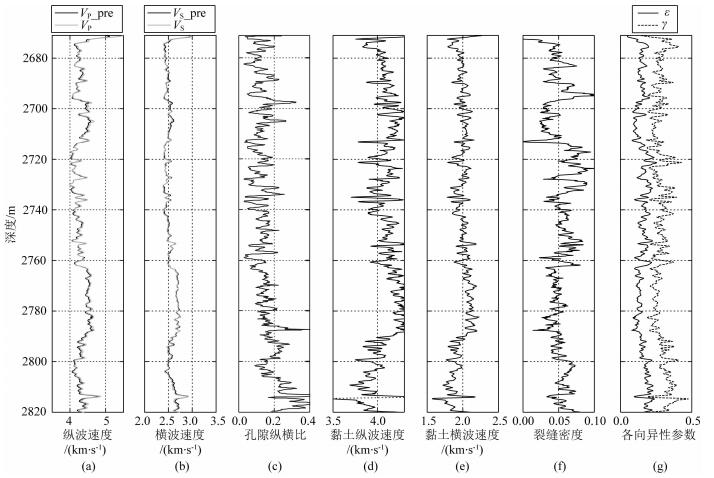
3.3 实际应用及分析图 9为对龙马溪组页岩层逐个测井点进行岩石物理反演的结果,图 9a和图 9b分别为TTI介质模型垂向纵、横波速度和实际速度测井曲线的对比图,黑色线段所表示的是TTI介质模型垂向纵、横波速度,灰色线段所表示的是测井实测的纵横波速度.可以看出,利用公式(10)所示的目标函数进行约束,并利用粒子群智能算法搜索最优解进行反演,计算得到的纵、横波速度与测井曲线吻合度高,拟合残差小, 说明反演目标函数有较强的约束力,反演算法具有可行性.
|
图 9 反演结果图 (a)模型纵波速度与测井纵波速度; (b)模型横波速度与测井横波速度; (c)孔隙纵横比; (d)黏土矿物纵波速度; (e)黏土矿物横波速度; (f)裂缝密度; (g)各向异性参数. Fig. 9 Results of rock physics inversion (a) P-wave velocity of well-log and model; (b) S-wave velocity of well-log and model; (c) Pore aspect ratio; (d) P-wave velocity of clay; (e) S-wave velocity of clay; (f) Microcrack density; (g) Anisotropy parameters. |
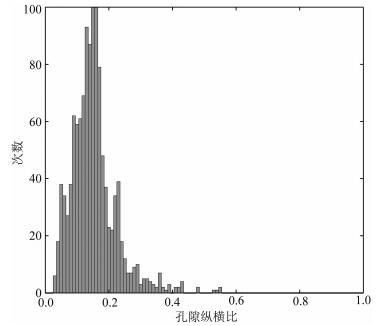
图 9c为岩石物理反演得到的孔隙纵横比曲线,结合图 10所示的孔隙纵横比统计直方图,可以看到,龙马溪组页岩层段的孔隙纵横比集中在0.1~0.3之间,总体孔隙纵横比与邓继新等(2015)对邻区龙马溪组页岩孔隙纵横比的统计结果相符合.
|
图 10 孔隙纵横比统计直方图 Fig. 10 Statistical histogram of aspect ratio of pores |
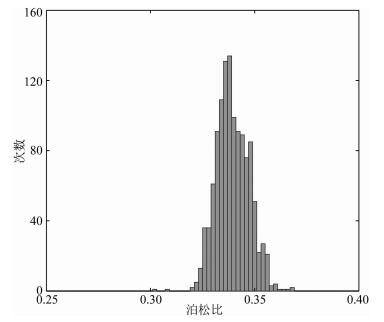
图 9d和图 9e分别给出反演得到的黏土矿物的纵横波速度,反演得到的黏土纵、横波速度整体大于先验速度均值(Han等人测得的黏土纵、横波速度),可能原因是龙马溪组页岩中的黏土成分相比于墨西哥湾黏土其中的伊利石含量更高,而伊利石具有较高的纵、横波速度.反演结果说明本文提出的反演策略能够反映黏土矿物组分变化对速度的影响.并且,反演得到的黏土矿物的泊松比稳定,介于0.34~0.35之间(图 11).同时,反演得到的黏土矿物纵、横波速度在一定范围内变化,这可能与黏土矿物沿平行层理方向定向排列有关.
|
图 11 泊松比统计直方图 Fig. 11 Statistical histogram of Poisson ratio |
图 9f给出计算得到的裂缝密度曲线,与图 9g计算的各向异性参数具有一定的相关性(图 12).因此,反映出水平裂缝能够增强地层的VTI各向异性.并且反演得到的横波各向异性参数γ大于纵波各向异性参数ε.页岩储层整体横波各向异性参数大于纵波各向异性参数的原因仍不很明确,需结合地质理论、岩心测量结果和测井数据做进一步分析.
|
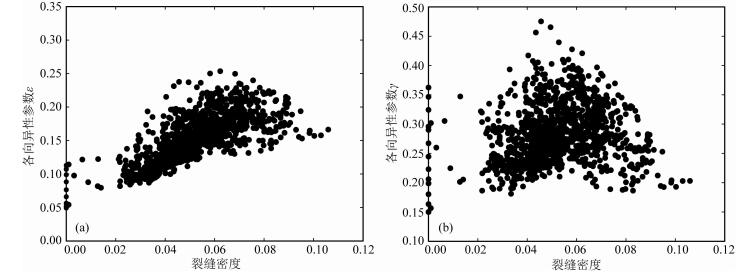
图 12 各向异性参数与裂缝密度的交汇图 (a)纵波各向异性参数ε与裂缝密度; (b)横波各向异性参数γ与裂缝密度. Fig. 12 Crossplots of anisotropy parameters versus crack density (a) ε versus crack density; (b) γ versus crack density. |
图 12a所示为裂缝密度与纵波各向异性参数ε的交汇图,可以看出这两个参数之间具有明显的正相关性;而图 12b所示的裂缝密度与横波各向异性参数γ的交汇图,其相关性不明显.这说明页岩层间微裂缝主要引起纵波各向异性,而横波的传播受流体填充的裂缝的影响较小.
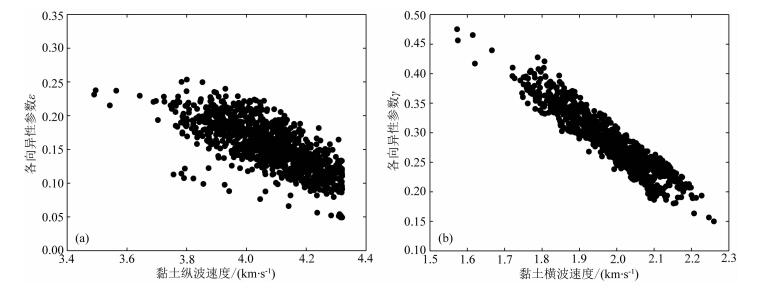
图 13a和图 13b分别为纵波各向异性参数ε与黏土纵波速度的交汇图和横波各向异性参数γ与黏土横波速度的交汇图,两者都存在明显的负相关关系,且横波各向异性参数与黏土横波速度之间的相关性更强.黏土的速度变化反映了其定向排列特征,速度越小其定向排列特征越明显,各向异性参数越大.因此,黏土的定向排列特征是造成页岩各向异性的重要因素,且是造成页岩横波各向异性的主要因素.
|
图 13 各向异性参数与黏土速度的交汇图 (a)纵波各向异性参数ε与黏土纵波速度; (b)横波各向异性参数γ与黏土横波速度. Fig. 13 Crossplots of anisotropy parameters versus clay velocity (a) ε versus P-wave velocity of clay; (b) γ versus S-wave velocity of clay. |
(1) 根据研究区页岩特征提出岩石物理建模方法,通过各向异性Backus平均理论考虑黏土矿物成分和定向排列规律的影响,利用Chapman理论考虑定向排列的多尺度裂缝系统造成的页岩各向异性,同时还考虑地层倾角对岩石物理建模的影响.基于模型的反演结果,验证了建模方法对研究区裂缝型泥页岩储层的有效性.
(2) 基于先验约束和粒子群算法搜索的反演方法能够比较准确地反演得到黏土矿物的弹性参数、孔隙形态参数以及裂缝密度参数,同时先验信息越准确,反演结果越接近真实情况,在先验信息存在误差的情况下,也能得到较合理的结果.
(3) 利用本文岩石物理反演方法对龙马溪组页岩层的反演结果表明:孔隙纵横比总体符合前人的统计结果,黏土矿物的纵、横波速度总体大于Han等人的统计结果并且在一定范围内变化明显,这可能与其较高的伊利石含量和黏土矿物存在定向排列特征有关.
(4) 研究区页岩储层各向异性特征受层间微裂缝和各向异性黏土矿物的综合影响,纵波各向异性参数受层间微裂缝和各向异性黏土的综合影响,而横波各向异性参数则主要受各向异性黏土的影响.对这一规律的深入理解,还需要在岩石学、岩石物理学和地震波动力学的基础上做更深入研究.
附录Ⅰ Hashi-Shtrikman界限理论
在Hashi-Shtrikman界限(Hashin and Shtikman, 1963)基础上,Berryman(1995)给出多种矿物的界限理论公式为:
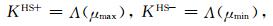
|
(A1) |
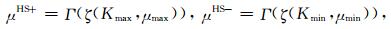
|
(A2) |
其中:
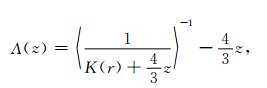
|
(A3) |
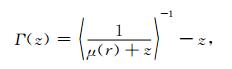
|
(A4) |
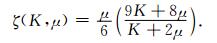
|
(A5) |
通过该理论,计算非黏土矿物及干酪根组成的混合物的弹性模量.
Ⅱ 各向异性Backus平均理论
Backus(1962)在长波极限下,提出由多层横向各向同性材料组成的层状介质对应的等效各向异性的弹性模量为:
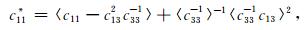
|
(A6) |
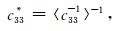
|
(A7) |
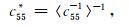
|
(A8) |
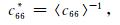
|
(A9) |
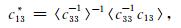
|
(A10) |
其中,符号〈a〉表示对a取加权平均.
Ⅲ Chapman多尺度裂缝系统理论
Chapman(2003)和Chapman等(2003)提出多尺度裂缝岩石物理模型,描述岩石的复杂孔缝系统,以及地震波动引起的流体喷射流动等现象.岩石弹性张量为复数并且与频率有关:
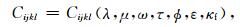
|
(A11) |
其中,λ和μ为无裂缝岩石的拉梅系数,ω为频率,τ为时间尺度参数,ϕ为孔隙度,ε为裂缝密度,κf为流体的体积模量.
对于具有多尺度孔隙和裂缝系统的岩石,各向异性弹性张量Cijkl为在各向同性背景Cijkliso上加入孔隙和裂缝引起的扰动:
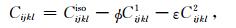
|
(A12) |
其中,Cijkl1和Cijkl2分别为孔隙和裂缝的贡献.
Ⅳ Bond变换
设在坐标系ox1x2x3中,弹性系数矩阵Cij经过坐标变换后的矩阵用C′ij表示,坐标变换矩阵用M表示,即有
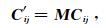
|
(A13) |
其中,M定义为一个6×6的变换矩阵,
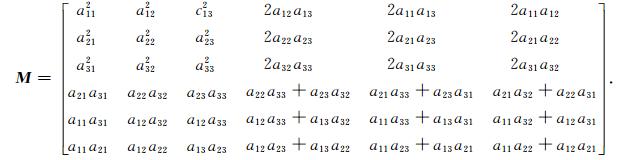
|
(A14) |
定义绕x3轴逆时针转的角度为方位角φ,绕x2轴逆时针转的角度为极化角θ,方位角与极化角跟矩阵M的对应关系为
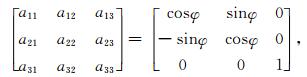
|
(A15) |
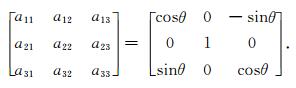
|
(A16) |
Backus G E. 1962. Long-wave elastic anisotropy produced by horizontal layering. Journal of Geophysical Research, 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427 |
Bayuk I O, Ammerman M, Chesnokov E M. 2007. Elastic moduli of anisotropic clay. Geophysics, 72(5): D107-D117. DOI:10.1190/1.2757624 |
Berryman J G. 1995. Mixture theories for rock properties. //Rock Physics & Phase Relations: A Handbook of Physical Constants. Washington, D C: American Geophysical Union, 205-228.
|
Carcione J M. 2000. A model for seismic velocity and attenuation in petroleum source rocks. Geophysics, 65(4): 1080-1092. DOI:10.1190/1.1444801 |
Carcione J M, Helle H B, Avseth P. 2011. Source-rock seismic-velocity models:Gassmann versus Backus. Geophysics, 76(5): N37-N45. DOI:10.1190/geo2010-0258.1 |
Castagna J P, Batzle M L, Eastwood R L. 1985. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics, 50(4): 571-581. DOI:10.1190/1.1441933 |
Chapman M. 2003. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity. Geophysical Prospecting, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
Chapman M, Maultzsch S, Liu E R, et al. 2003. The effect of fluid saturation in an anisotropic multi-scale equant porosity model. Journal of Applied Geophysics, 54(3-4): 191-202. DOI:10.1016/j.jappgeo.2003.01.003 |
Deng J X, Wang H, Zhou H, et al. 2015. Microtexture, seismic rock physical properties and modeling of Longmaxi Formation shale. Chinese Journal of Geophysics, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
Eastwood R L, Castagna J P. 1986. Interpretation of Vp/Vs ratios from sonic logs. //Danbom S H, Domenico S N. Shear Wave Exploration. Geophysical Developments No. I, Society of Exploration Geophysicists. Tulsa, Oklahoma.
|
Guo Z Q, Li X Y, Liu C. 2014. Anisotropy parameters estimate and rock physics analysis for the Barnett Shale. Journal of Geophysics and Engineering, 11(6): 065006. DOI:10.1088/1742-2132/11/6/065006 |
Han D H, Nur A, Morgan D. 1986. Effects of porosity and clay content on wave velocities in sandstones. Geophysics, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
Hashin Z, Shtrikman S. 1963. A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics & Physics of Solids, 11(2): 127-140. |
Hornby B E, Schwartz L M, Hudson J A. 1994. Anisotropic effective-medium modeling of the elastic properties of shales. Geophysics, 59(10): 1570-1583. DOI:10.1190/1.1443546 |
Jiang M J, Spikes K T. 2013. Estimation of reservoir properties of the haynesville shale by using rock-physics modelling and grid searching. Geophysical Journal International, 195(1): 315-329. DOI:10.1093/gji/ggt250 |
Kennedy J, Eberhart R. 1995. Particle swarm optimization. //Proceedings of the IEEE International Conference on Neural Networks. Perth, WA: IEEE, 1942-1948.
|
Mba K, Prasad M. 2010. Mineralogy and its contribution to anisotropy and kerogen stiffness variations with maturity in the Bakken Shales. //2010 SEG Annual Meeting. Denver, Colorado: SEG, 2612-2616.
|
Ortega J A, Ulm F J, Abousleiman Y. 2009. The nanogranular acoustic signature of shale. Geophysics, 74(3): D65-D84. DOI:10.1190/1.3097887 |
Sayers C M. 2005. Seismic anisotropy of shales. Geophysical Prospecting, 53(5): 667-676. DOI:10.1111/gpr.2005.53.issue-5 |
Sayers C M. 2013. The effect of kerogen on the elastic anisotropy of organic-rich shales. Geophysics, 78(2): D65-D74. DOI:10.1190/geo2012-0309.1 |
Spikes K T. 2011. Modeling elastic properties and assessing uncertainty of fracture parameters in the Middle Bakken Siltstone. Geophysics, 76(4): E117-E126. DOI:10.1190/1.3581129 |
Tosaya C A. 1982. Acoustic properties of clay-bearing rocks. Stanford, CA: Stanford University.
|
Vernik L, Nur A. 1992. Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics, 57(5): 727-735. DOI:10.1190/1.1443286 |
邓继新, 王欢, 周浩, 等. 2015. 龙马溪组页岩微观结构、地震岩石物理特征与建模. 地球物理学报, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
 2018, Vol. 61
2018, Vol. 61


