速度模型描述了地震波在地下介质中传播时速度的变化情况,是地震数据处理和解释中最基础、最重要的参数之一,因而速度建模是地震资料处理解释中的关键步骤.速度模型的质量影响偏移成像的效果,也影响着地震和地质解释结果的准确性.随着勘探的需要,对速度模型质量的要求原来越高,传统的速度建模方法,例如叠加速度分析、射线层析成像和偏移速度分析等,在精度和分辨率上并不能提供高质量的模型,尤其是在一些地质条件比较复杂的地区,往往不能达到地震处理和解释的要求.
全波形反演(Full Waveform Inversion, FWI)是一种高精度、高分辨率的地下速度反演方法,能得到地下介质中更多细节的速度变化特征.它利用地震资料中的振幅和相位信息通过最小化模拟数据与实际观测数据之间的误差来重构地下介质的速度模型,可以为叠前深度偏移成像提供高精度高分辨率的速度模型.但由于实际观测到的数据一般都是有缺陷的,存在严重的噪声干扰,且受初始速度模型不精确、子波未知、波动方程等多方面因素的影响,导致波场与要反演的速度之间关系更弱,非线性更强,使全波形反演达不到预期的效果.
全波形反演技术的研究始于20世纪80年代,Lailly(1983)和Tarantola(1984)首先提出了全波形反演方法,并在时间域得到实现.而后Pratt(1999)、Pratt和Shipp(1999)提出频率域的全波形反演,用较少离散频率的数据就能获得较好的反演结果,在保证反演精度的前提下大大提高了计算效率.近些年来,随着计算机硬件的高速发展,研究者们在传统全波形反演理论基础上,更多考虑的是反演精度和计算效率的提高.Krebs等(2009)将震源编码技术引入全波形反演算法中,将多个炮编码成超级炮从而节约了正演时间,提高计算效率.Shin和Cha(2008, 2009)提出拉普拉斯域的全波形反演方法,可以得到一个更为准确的初始速度模型,然后再进行常规的全波形反演建模,并在合成数据中验证了方法的有效性.Wang和Rao(2009)提出了基于剥层法和深度权重法的全波形反演,大大提高了模型深部的反演效果,同时也增强了反演的稳定性.Fei等(2012)提出一种低频补偿技术,降低了反演对低频数据的依赖性.Li等(2012)提出基于压缩感知技术的全波形反演算法,根据数据的稀疏性来减少计算量,提高效率.van Leeuwen等(van Leeuwen and Herrmann, 2013;Herrmann and van Leeuwen, 2014)使用罚函数来构造目标函数,降低了反演的非线性和对初始模型的依赖性,减少了存储量和计算量,提高了效率,同时扩大了目标函数搜索空间.Han等(2013)、韩淼(2014)结合震源编码、主成分分析和变网格等技术提出一种高效联合的全波形反演方法,在不损失反演精度的前提下大幅度提高了计算效率.Esser等(2015)将基于罚函数的目标函数与凸约束结合应用,在反演不连续点或突变点时效果明显.胡勇等(2017)提出解调包络方法重构数据中的低频信息,并与低通滤波技术结合,有效降低了全波形反演的非线性性.
全变差(Total Variation,TV)约束方法是一种非光滑约束,在求解不连续解的问题中得到广泛应用.它由Rudin等(1992)提出,主要是用于图像的去噪处理,能有效的处理解的不连续性,重构图像中的一些间断点,保留边缘信息.近几年来,全变差约束已经应用在电法成像(Chung et al., 2005)、图像去噪(屈勇等,2011)、偏移速度分析(Anagaw,2009;Anagaw and Sacchi, 2012)、混合数据偏移(卢昕婷等,2015)等领域.由于地下介质通常是不规则的,存在许多不连续的构造,速度变化不连续,全变差约束的应用可以有效保留这些不连续的特征.Hinge损失函数是支持向量机成功的关键,而且属于一种非光滑约束,可以用来估量模型的预测值与真实值的不一致程度,本文将其作为约束项应用于全变差约束的全波形反演方法中.
本文提出一种基于Hinge损失函数的垂向全变差约束全波形反演算法,采用原-对偶混合梯度法(Zhu and Chan, 2008;Esser et al., 2010;Zhang et al., 2011)求解目标函数的最优化问题,通过数值实验测试表明:全变差约束的全波形反演方法能更好地反演地下高速体,有效的重构速度不连续界面,提高反演效果,而基于Hinge损失函数的垂向全变差约束全波形反演方法在保证反演精度的前提下,大大降低了反演对初始速度模型的依赖程度,在含噪声数据的应用中也可以看出该方法有良好的抗噪性.
1 方法原理 1.1 常规频率域全波形反演全波形反演是一个最优化的问题,它通过对观测波场与理论波场的残差求取极小值来构造目标函数进行迭代更新,最终重构地下介质的参数模型.当前常用的目标函数主要是通过数据残差的L2范数来构建,即:
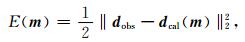
|
(1) |
E(m)表示目标函数,dobs表示实际观测数据,dcal表示模拟地震数据,m为地下介质模型,声波全波形反演中即为地下介质中的声波速度.在(1)式中的dcal=Pu,P为模拟数据与波场之间的转换因子,u是通过正演模拟得到的波场.
本文是基于常密度声波方程进行的数值模拟,目标函数对m求一阶导数可以得到梯度矩阵,公式为
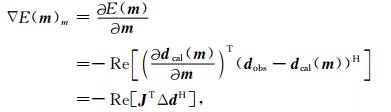
|
(2) |
对目标函数求二阶导数可以得到近似Hessian矩阵,公式为
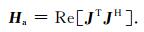
|
(3) |
根据高斯牛顿法可以得到模型的更新量为
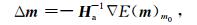
|
(4) |
根据梯度投影法(Bertsekas,1999;Bonettini et al., 2009),模型更新量可以表示为
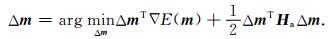
|
(5) |
假设m是一个n×n的速度模型,网格间距为h,用(i, j)代表各个网格点坐标,其中i=1, 2, …, n,j=1, 2, …, n,则在纵向和横向两个方向的梯度分别为

|
(6) |
全变差被定义为
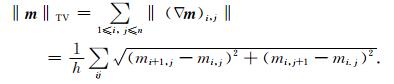
|
(7) |
为方便起见,定义矩阵Al∈RN×2,对m重排序,l=1, …, N,N=n×n,可以得到(8)式的离散表示为
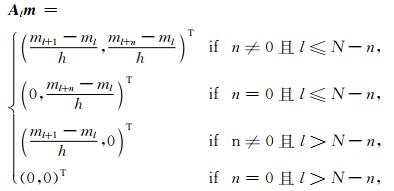
|
(8) |
其中ml=m(j-1)n+i,Alm表示m在第l个点的离散梯度,因此可以得到:
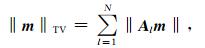
|
(9) |
可以看出全变差相当于模型每个点离散梯度二范数的和.
1.3 垂向全变差约束的全波形反演将全变差约束项应用于常规全波形反演算法中,可以得到基于全变差约束的目标函数,公式为
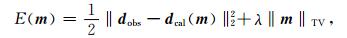
|
(10) |
式中λ是正则化参数,用来调节全变差约束项在目标函数中的权重作用.
通常情况下,地下介质速度随着深度的增加而呈现增大趋势,为了减少全波形反演中由于速度错误的更新使反演陷入局部极小值,使用垂直方向的全变差分量的Hinge损失函数的一范数来约束模型深度方向的更新,此时目标函数可以表示为
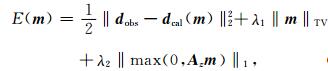
|
(11) |
其中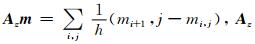
注意到,(11)式具有等价的优化形式为

|
(12) |
τ是与λ1有关的一个正常数,ξ是与λ2有关的一个正常数,τ值和ξ值越小,全变差约束项以及垂向全变差约束项在目标函数中的权重作用越大,本文中先求取真实模型的τtrue和ξtrue,然后根据τtrue和ξtrue选取反演中的τ值和ξ值.此时的反演问题可以表示为

|
(13a) |

|
(13b) |
对于全变差约束的问题,近些年来研究者们提出了许多高效的解法,本文采取一种改正的原-对偶混合梯度法(PDHGMp)来求解上述问题,首先定义‖Am‖ TV的对偶范数为

|
(14) |
‖·‖ 1的对偶范数相当于求最大值.
根据PDHGMp,解式(13)的全变差约束问题相当于求解(15)式问题的鞍点(Δm, p1, p2),p1、p2是拉格朗日乘子,公式为

|
(15) |
式(15)可以转化为三个求解最小值的子问题:
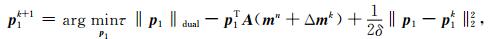
|
(16a) |
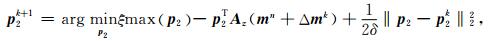
|
(16b) |

|
(16c) |
其中,δ和α为迭代步长,满足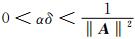
解(16)式中三个子问题可以得到对应的迭代公式为
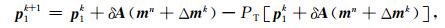
|
(17a) |
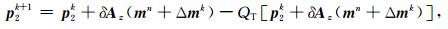
|
(17b) |
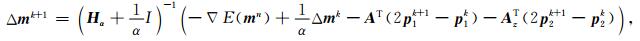
|
(17c) |
PT、QT为投影算子,公式为
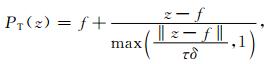
|
(18a) |
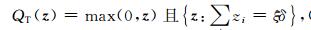
|
(18b) |
其中f为T={z:‖z-f‖2≤τδ}的中心点.迭代的停止条件为:

|
(19a) |
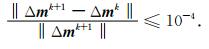
|
(19b) |
为了验证本文方法的有效性,截取BP模型的右半部分进行测试,如图 1a所示,截取的模型网格大小为111×373,网格间距为20 m,横向长约7.5 km,纵向深2.2 km,速度变化范围在1500~4800 m·s-1,模型中存在一个典型的高速体,在深度约500 m处有明显的速度突变界面.观测系统如图 1b所示,共187个检波点94炮,检波点间距为40 m,炮间距为80 m.震源为15 Hz雷克子波,起始反演频率为2 Hz,频率范围为2~30 Hz,频率间隔为1 Hz.

|
图 1 部分BP真实模型(a)及观测系统(b) Fig. 1 Part of the real BP model (a) and recording geometry (b) |
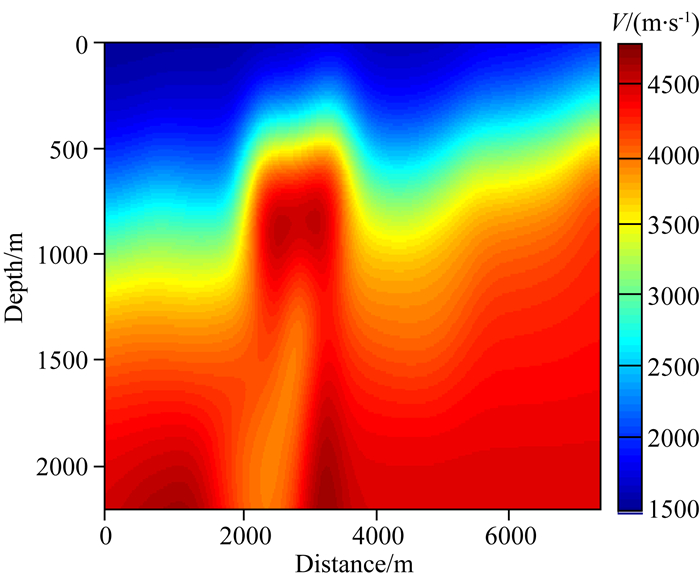
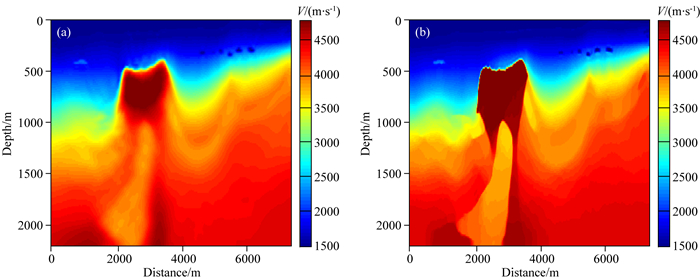
首先测试常规全变差约束的全波形反演方法,即不含垂向全变差约束项.图 2是通过对真实速度模型做平滑后得到的初始速度模型,图 3a是常规全波形反演的结果,图 3b是τ=0.8τtrue时全变差约束的全波形反演结果.从图 3a中可以看到盐丘顶部的轮廓基本已经重构出来,顶部界面已经很清晰,但是深部反演效果不佳,尤其是1000 m以下盐丘的边缘很模糊.与常规波形反演结果相比,全变差约束后的反演结果整个盐丘的轮廓已经重构出来,顶部界面和底部界面都很清晰,1000 m以下深部的速度界面也能清晰的重构出来.
|
图 2 初始模型 Fig. 2 Initial model |
|
图 3 反演结果 (a)常规全波形反演;(b)全变差约束的全波形反演. Fig. 3 Inversion results (a) Conventional full waveform inversion; (b) TV constraint full waveform inversion. |
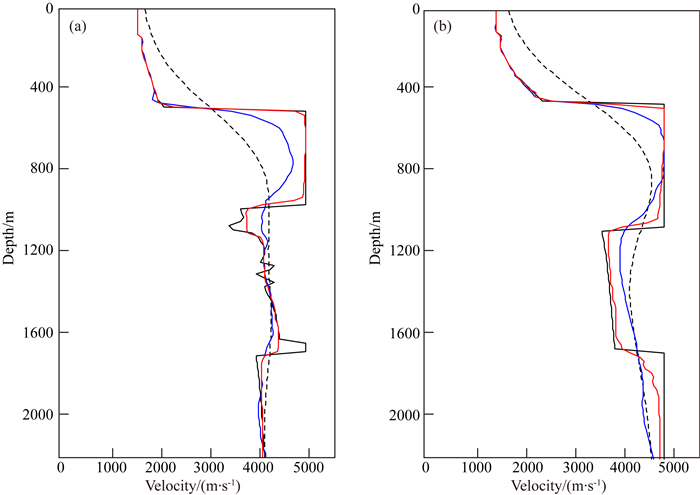
从真实模型、初始模型、常规全波形反演结果和全变差约束的全波形反演结果中提取模型水平距离为2260 m和3100 m处的纵向速度曲线进行对比,如图 4所示,相比于常规波形反演结果,全变差约束的反演结果与真实速度拟合更好,尤其是在速度突变点,效果更加明显.由此可见全变差约束的全波形反演方法对于存在高速体这种不连续速度界面的重构更加有效,可以获得更加精确的反演结果.
|
图 4 x=2260 m(a)和x=3100 m(b)处纵向速度曲线对比,分别为真实模型(黑色实线)、初始模型(黑色虚线)、常规全波形反演结果(蓝色)和全变差约束的全波形反演结果(红色) Fig. 4 Vertical velocity comparison at x=2260 m(a) and x=3100 m(b) including true models (black solid lines), initial models (black dashed lines), conventional full waveform inversion results (blue line) and TV constraint full waveform inversion results (red line), respectively |
用反演结果与真实模型的相似程度Eres来评价反演的精度,公式为

|
(20) |
minv表示反演得到的速度模型,mtrue表示真实模型.BP模型试验两种方法反演结果的精度对比如表 1所示,表中模型迭代次数为每个频率模型更新的最大迭代次数,经过相同的迭代次数,全变差约束的全波形反演方法反演精度要明显高于常规全波形反演.
|
|
表 1 BP模型反演精度分析 Table 1 Accuracy analysis of BP model inversion |
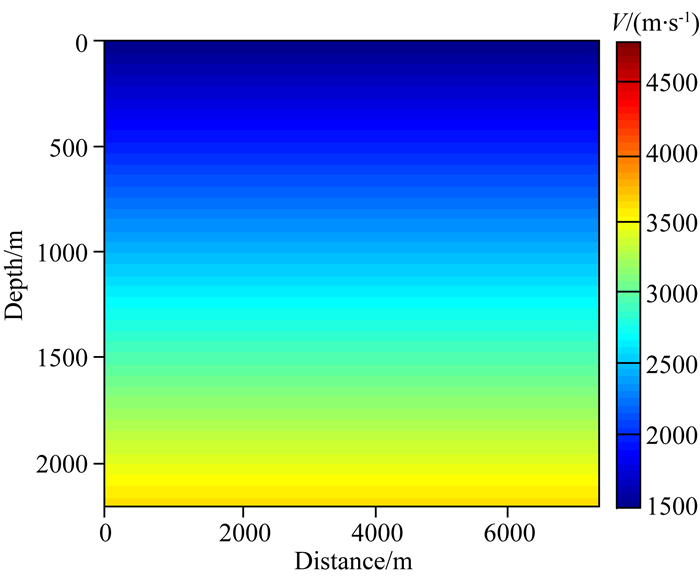
全波形反演算法中,初始模型的质量决定了正演模拟的地震记录与实际数据匹配时的误差,如果误差较大就会出现“周波跳跃”现象,使反演陷入局部极小值,影响反演结果的准确性.如图 5是一个线性的初始速度模型,与真实模型相比,没有明显的构造.图 6a是τ=0.75τtrue时对应的全变差约束全波形反演算法的反演结果,可以看出重构范围仅局限在高速体顶部界面处,深部没有明显变化.
|
图 5 线性初始模型 Fig. 5 Linear initial model |
|
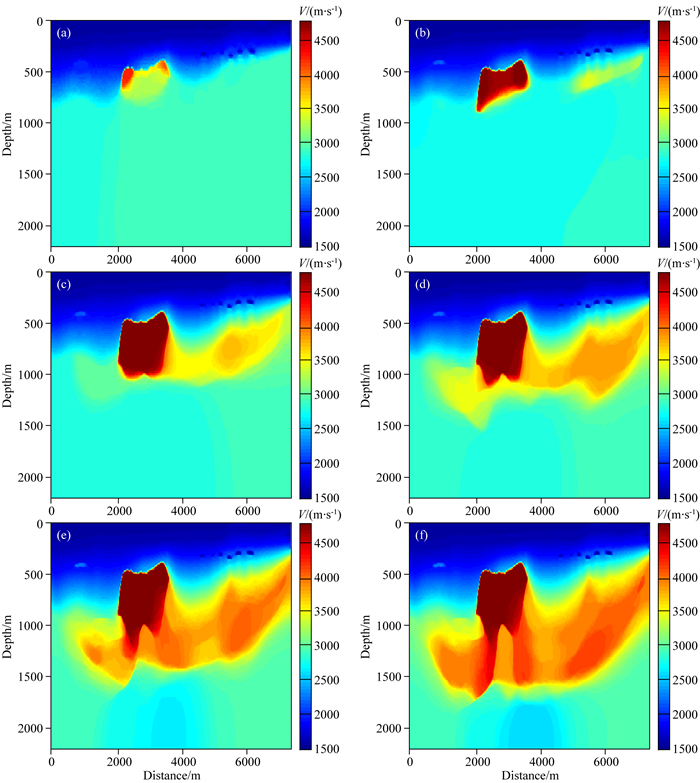
图 6 τ取不同值时全变差约束的全波形反演循环迭代的反演结果 (a) τ=0.75τtrue; (b) τ=0.8τtrue; (c) τ=0.85τtrue; (d) τ=0.9τtrue; (e) τ=0.95τtrue; (f) τ=0.98 τtrue. Fig. 6 Inversion results of TV constraint full waveform inversion in cyclic iteration for different values of τ (a) τ=0.75 τtrue; (b) τ=0.8τtrue; (c) τ=0.85τtrue; (d) τ=0.9τtrue; (e) τ=0.95τtrue; (f) τ=0.98τtrue. |
以图 6a为初始模型,将τ值增大,以减小全变差约束在反演中的约束作用,其他参数不变,再进行全变差约束的全波形反演速度建模,图 6b是τ=0.8τtrue时的反演结果,图 6c是以图 6b为初始模型τ=0.85τtrue时的反演结果,图 6d是以图 6c为初始模型τ=0.9τtrue时的反演结果,图 6e是以图 6d为初始模型τ=0.95τtrue时的反演结果,图 6f是以图 6e为初始模型τ=0.98τtrue时的反演结果.对比之后可以看出,通过逐渐增大τ值而进行的循环迭代反演,在每次反演结果中模型的重构深度都有明显的增大,高速体顶部已经重构出来,但是模型深部仍然没有得到重构,当τ值足够大时,深部重构效果没有明显改善,且高速体中深部界面的反演结果与真实模型相比误差较大,可见在全变差约束的全波形反演方法中,初始模型的精度对反演结果的影响仍然较大.
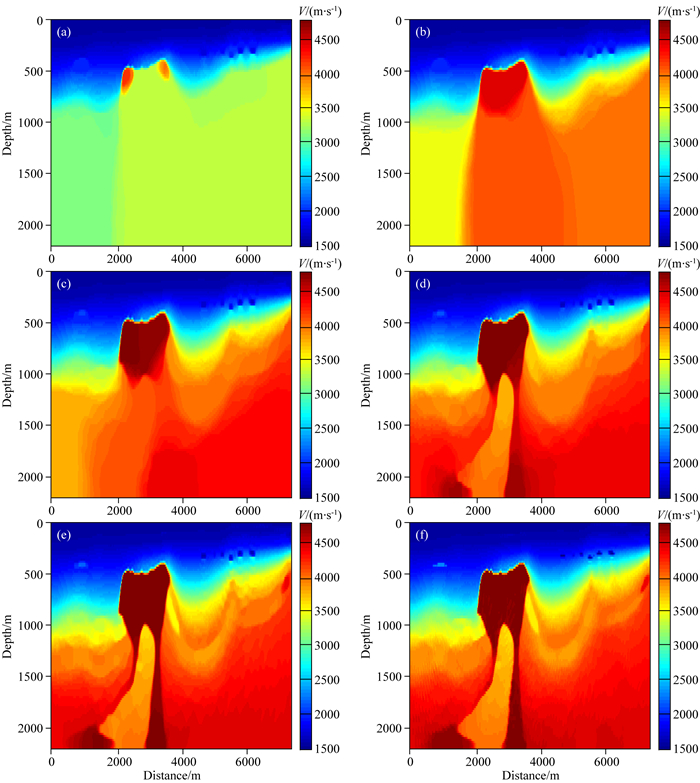
2.3 垂向全变差约束全波形反演方法测试在基于Hinge损失函数的垂向全变差约束全波形反演算法测试中,同样以图 5中的线性模型为初始模型,采用逐渐增大阈值循环迭代的策略.在整个反演中取τ=0.8τtrue不变,图 7a是ξ=0.04ξtrue时垂向全变差约束全波形反演的结果,可以看出只有模型浅部的速度变化趋势得到了重构,逐渐增大ξ值,图 7b是以图 7a为初始模型ξ=0.1ξtrue时的反演结果,图 7c是以图 7b为初始模型ξ=0.2ξtrue时的反演结果,图 7d是以图 7c为初始模型ξ=0.3ξtrue时的反演结果,图 7e是以图 7d为初始模型ξ=0.6ξtrue时的反演结果,图 7f是以图 7e为初始模型ξ=0.9ξtrue时的反演结果,也就是最终反演结果,可见模型中的高速体已经得到很好的重构,界面清晰,在高速体两侧的速度变化趋势也与真实模型相符.基于Hinge损失函数的垂向全变差约束全波形反演方法可以从一个较低精度的初始模型,甚至仅是一个线性的初始模型,通过逐渐增大阈值循环迭代的反演策略得到同样高精度的反演结果.
|
图 7 ξ取不同值时垂向全变差约束的全波形反演循环迭代的反演结果 (a) ξ=0.04ξtrue; (b) ξ=0.1ξtrue; (c) ξ=0.2ξtrue; (d) ξ=0.3ξtrue; (e) ξ=0.6ξtrue; (f) ξ=0.9ξtrue. Fig. 7 Inversion results of vertical TV constraint full waveform inversion in cyclic iteration for different values of ξ (a) ξ=0.04ξtrue; (b) ξ=0.1ξtrue; (c) ξ=0.2ξtrue; (d) ξ=0.3ξtrue; (e) ξ=0.6ξtrue; (f)ξ=0.9ξtrue. |
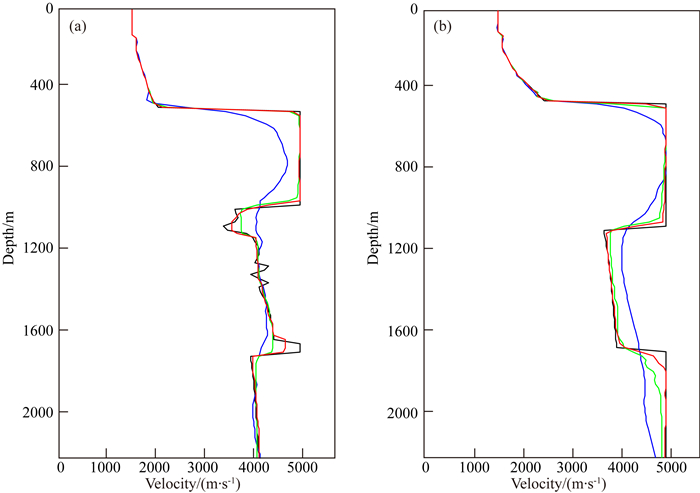
从真实模型、无约束的常规全波形反演结果、全变差约束的全波形反演结果和垂向全变差约束的全波形反演结果中提取模型水平距离为2260 m和3100 m处的纵向速度曲线进行对比,如图 8所示,相比于常规波形反演结果,全变差约束和垂向全变差约束的反演结果与真实速度都能很好拟合,尤其是在速度突变点,两种约束后的方法的反演精度更高,而以线性模型为初始模型的垂向全变差约束的反演结果精度甚至更高,这也说明了这种基于Hinge损失函数的垂向全变差约束全波形反演方法在保证反演精度的同时,大大降低了对初始速度模型的依赖程度.
|
图 8 x=2260 m(a)和x=3100 m(b)处纵向速度曲线对比,分别为真实模型(黑色实线)、常规全波形反演结果(蓝色)、全变差约束的全波形反演结果(绿色)和垂向全变差约束全波形反演结果(红色) Fig. 8 Vertical velocity comparison at x=2260 m(a) and x=3100 m(b) including true models (black solid lines), conventional full waveform inversion results (blue lines), TV constraint full waveform inversion results (green lines and vertical TV constraint full waveform inversion results (red lines), respectively |
实际野外采集的数据存在严重的噪声干扰,全波形反演技术对噪声较为敏感,只有数据信噪比较高的情况下才能获得理想的结果.本文通过在数据中加入高斯噪声来测试全变差约束的全波形反演技术的抗噪能力,信噪比为SNR=-5.
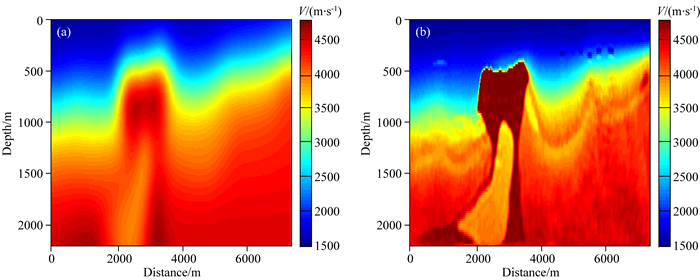
取τ=0.9τtrue,如图 9b是以图 9a为初始模型的全变差约束的全波形反演结果,尽管噪声对反演结果有一定影响,但仍然能将高速体重构出来,浅部界面比较清晰,深部反演效果不理想.
|
图 9 含噪数据测试 (a)初始模型; (b)全变差约束全波形反演结果. Fig. 9 Tests on noisy data (a) Initial model; (b) TV constraint full waveform inversion. |
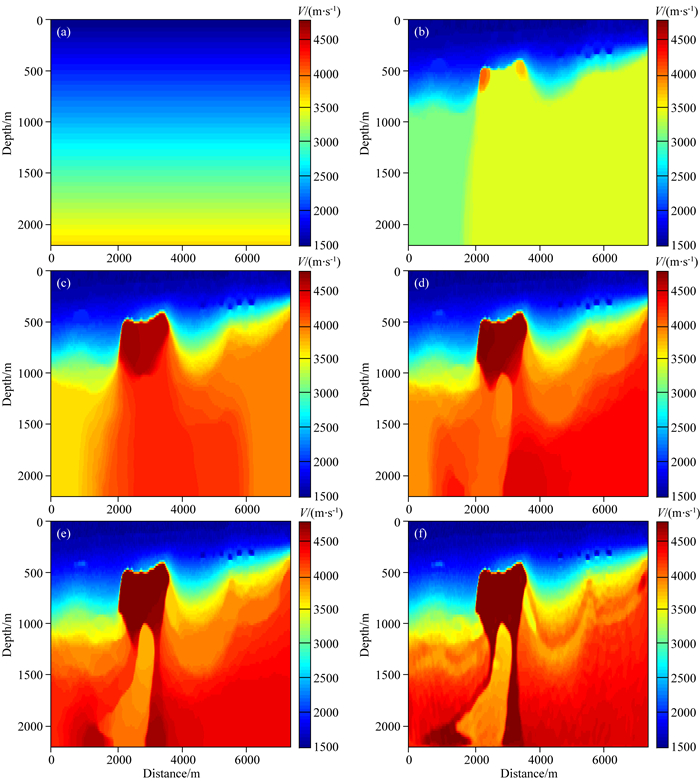
在垂向全变差约束的全波形反演方法中,仍然采用线性的初始速度模型,如图 10a,在整个反演中取τ=0.9τtrue不变.图 10b是ξ=0.1ξtrue时垂向全变差约束全波形反演的结果,图 10c是以图 10b为初始模型ξ=0.15ξtrue时的反演结果,图 10d是以图 10c为初始模型ξ=0.3ξtrue时的反演结果,图 10e是以图 10d为初始模型ξ=0.6ξtrue时的反演结果,图 10f是以图 10e为初始模型ξ=0.9ξtrue时的反演结果.可见在噪声影响下,反演结果存在一定扰动,但垂向全变差约束的全波形反演算法仍然可以将高速体重构出来,而且反演结果要优于常规全变差约束的反演结果.可见垂向全变差约束的全波形反演方法具有较好的抗噪性.
|
图 10 ξ取不同值时含噪数据垂向全变差约束的全波形反演结果 (a)线性初始模型; (b) ξ=0.1ξtrue; (c) ξ=0.15ξtrue; (d) ξ=0.3ξtrue; (e) ξ=0.6ξtrue; (f) ξ=0.9ξtrue. Fig. 10 Inversion results of vertical TV constraint full waveform inversion with a noisy data for different values of ξ (a) Initial linear model; (b) ξ=0.1ξtrue; (c) ξ=0.15ξtrue; (d) ξ=0.3ξtrue; (e) ξ=0.6ξtrue; (f) ξ=0.9ξtrue. |
基于全变差约束的全波形反演算法能有效重构介质中的速度不连续界面.全变差约束属于非光滑约束,将TV范数作为正则化约束项,在有高速体存在、速度变化剧烈的区域,能有效处理不平滑点,提高反演精度,但该方法对初始速度模型的精度仍然有一定要求.
基于Hinge损失函数的垂向全变差约束全波形反演方法在保证反演精度的同时,大大降低了对初始速度模型的依赖程度.将Hinge损失函数和TV范数同时作为目标函数的正则化约束项不仅可以精确重构速度不连续界面,而且能够约束模型深度方向的速度更新,避免产生错误的迭代而使反演陷入局部极小值,反演结果表明它能从一个质量很差的初始模型同样得到高精度的反演结果,速度变化趋势与真实模型相符,含噪数据的测试也证明了垂向全变差约束的全波形反演算法具有较好的抗噪性.
本文采用逐渐增大阈值的循环迭代反演策略.反演最初由于初始模型精度较低,因此使用较小的阈值来增大垂向全变差约束项在反演中的权重,最大程度的约束反演,避免陷入局部极小值,然后逐渐增大阈值,减小全变差约束项的权重,并将每一个较小阈值的反演结果作为较大阈值反演的初始模型,使模型中深部以及更多细节变化逐渐得到精确的重构,反演结果验证了这种反演策略的有效性.尽管多次反演增加了时间成本,但在初始模型精度较低的情况下能获得高精度的反演结果也是值得的.
Anagaw A Y. 2009. Total variation and adjoint state methods for seismic wavefield imaging. Edmonton, Alberta: University of Alberta.
|
|
Anagaw A Y, Sacchi M D.
2012. Edge-preserving seismic imaging using the total variation method. Journal of Geophysics and Engineering, 9(2): 138-146.
DOI:10.1088/1742-2132/9/2/138 |
|
Bertsekas D P. 1999. Nonlinear Programming. 2nd ed. Belmont: Athena Scientific.
|
|
Bonettini S, Zanella R, Zanni L.
2009. A scaled gradient projection method for constrained image deblurring. Inverse Problems, 25(1): 015002.
DOI:10.1088/0266-5611/25/1/015002 |
|
Chung E T, Chan T F, Tai X C.
2005. Electrical impedance tomography using level set representation and total variational regularization. Journal of Computational Physics, 205(1): 357-372.
DOI:10.1016/j.jcp.2004.11.022 |
|
Esser E, Guasch L, van Leeuwen T, et al. 2015. Automatic salt delineation-Wavefield Reconstruction Inversion with convex constraints. //SEG Technical Program Expanded Abstracts. New Orleans, Louisiana: SEG, 1337-1343.
http://www.researchgate.net/publication/299907682_Automatic_salt_delineation_-_Wavefield_Reconstruction_Inversion_with_convex_constraints |
|
Esser E, Zhang X Q, Chan T F.
2010. A general framework for a class of first order primal-dual algorithms for convex optimization in imaging science. SIAM Journal on Imaging Sciences, 3(4): 1015-1046.
DOI:10.1137/09076934X |
|
Fei T W, Luo Y, Qin F H, et al. 2012. Full waveform inversion without low frequencies: A synthetic study. //2012 SEG Annual Meeting. Las Vegas, Nevada: SEG, 4609-4613.
https://www.researchgate.net/publication/268454503_Full_waveform_inversion_without_low_frequencies_A_synthetic_study |
|
Han M. 2014. Methods and application of full waveform inversion for abyssal seismic data (in Chinese). Changchun: Jilin University.
|
|
Han M, Han L G, Liu C C, et al.
2013. Frequency-domain auto-adapting full waveform inversion with blended source and frequency-group encoding. Applied Geophysics, 10(1): 41-52.
DOI:10.1007/s11770-013-0367-3 |
|
Herrmann F J, van Leeuwen T. 2014. A penalty method for PDE-constrained optimization: WIPO, WO/2014/172787. 2014-10-30.
|
|
Hu Y, Han L G, Xu Z, et al.
2017. Demodulation envelope multi-scale full waveform inversion based on precise seismic source function. Chinese J. Geophys. (in Chinese), 60(3): 1088-1105.
DOI:10.6038/cjg20170321 |
|
Krebs J R, Anderson J E, Hinkley D, et al.
2009. Fast full-wavefield seismic inversion using encoded sources. Geophysics, 74(6): WCC105.
DOI:10.1190/1.3215771 |
|
Lailly P. 1983. The seismic inverse problem as a sequence of before stack migrations. //Proceedings of the Conference on Inverse Scattering, Theory and Application. Philadelphia: Society for Industrial and Applied Mathematics, 206-220.
|
|
Li X, Aravkin A Y, van Leeuwen T, et al.
2012. Fast randomized full-waveform inversion with compressive sensing. Geophysics, 77(3): A13-A17.
DOI:10.1190/geo2011-0410.1 |
|
Lu X T, Han L G, Zhang P, et al.
2015. Direct migration method of multi-source blended data based on total variation. Chinese J. Geophys. (in Chinese), 58(9): 3335-3345.
DOI:10.6038/cjg20150926 |
|
Pratt R G.
1999. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in a physical scale model. Geophysics, 64(3): 888-901.
DOI:10.1190/1.1444597 |
|
Pratt R G, Shipp R M.
1999. Seismic waveform inversion in the frequency domain, Part 2:Fault delineation in sediments using crosshole data. Geophysics, 64(3): 902-914.
DOI:10.1190/1.1444598 |
|
Qu Y, Cao J X, Zhu H D, et al.
2011. An improved total variation technique for seismic image denoising. Acta Petrolei Sinica (in Chinese), 32(5): 815-819.
|
|
Rudin L I, Osher S, Fatemi E.
1992. Nonlinear total variation based noise removal algorithms. Physica D, 60(1-4): 259-268.
DOI:10.1016/0167-2789(92)90242-F |
|
Shin C, Cha Y H.
2008. Waveform inversion in the Laplace domain. Geophysical Journal International, 173(3): 922-931.
DOI:10.1111/gji.2008.173.issue-3 |
|
Shin C, Cha Y H.
2009. Waveform inversion in the Laplace-Fourier domain. Geophysical Journal International, 177(3): 1067-1079.
DOI:10.1111/gji.2009.177.issue-3 |
|
Tarantola A.
1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266.
DOI:10.1190/1.1441754 |
|
van Leeuwen T, Herrmann F J.
2013. Mitigating local minima in full-waveform inversion by expanding the search space. Geophysical Journal International, 195(1): 661-667.
DOI:10.1093/gji/ggt258 |
|
Wang Y H, Rao Y.
2009. Reflection seismic waveform tomography. Journal of Geophysical Research:Solid Earth, 114(B3): B03304.
|
|
Zhang X Y, Burger M, Osher S.
2011. A unified primal-dual algorithm framework based on bregman iteration. Journal of Scientific Computing, 46(1): 20-46.
DOI:10.1007/s10915-010-9408-8 |
|
Zhu M Q, Chan T. 2008. An efficient primal-dual hybrid gradient algorithm for total variation image restoration. CAM Report 08-34. 1-29.
|
|
韩淼. 2014. 深水区地震全波形反演策略与应用. 长春: 吉林大学.
http://cdmd.cnki.com.cn/Article/CDMD-10183-1014268080.htm |
|
胡勇, 韩立国, 许卓, 等.
2017. 基于精确震源函数的解调包络多尺度全波形反演. 地球物理学报, 60(3): 1088–1105.
DOI:10.6038/cjg20170321 |
|
卢昕婷, 韩立国, 张盼, 等.
2015. 基于全变分原理的多震源混合数据直接偏移方法. 地球物理学报, 58(9): 3335–3345.
DOI:10.6038/cjg20150926 |
|
屈勇, 曹俊兴, 朱海东, 等.
2011. 一种改进的全变分地震图像去噪技术. 石油学报, 32(5): 815–819.
DOI:10.7623/syxb201105011 |
|
 2018, Vol. 61
2018, Vol. 61


