2. 中国科学院地质与地球物理研究所, 岩石圈演化国家重点实验室, 北京 100029;
3. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101
2. State Key Laboratory of Lithospheric Evolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. CAS Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China
地震波逆时偏移是现行偏移方法中精确的成像方法之一,它包含了全波场的信息,具有不受横向变速和高陡倾角的影响、成像清晰、相位准确等特点(Baysal et al., 1983; McMechan and Fuis, 1987; Chang and McMechan, 1986, 1989, 1990; 张智等, 2013; Lan et al., 2014a).叠前逆时偏移主要分为三个部分: (1)由震源激发的源波场沿着时间方向正向延拓,(2)由地震记录作为边值问题的接收波场沿着时间方向逆向延拓,(3)应用成像条件得到叠前逆时偏移成像结果.近二三十年,自逆时偏移提出以来,人们一直从以上三个方面对逆时偏移进行完善和改进.
地震波场延拓作为逆时偏移的核心环节,为了提高地震波场延拓的精度和效率,学者们进行着各种努力.Dablain(1986)采用高阶有限差分算子求解双程波动方程,不仅提高了计算精度,而且减少了计算量和存储量;同年,Virieux(1986)在地震波场数值模拟中引入交错网格有限差分方法,进一步提高了数值模拟的精度和效率;Wang(2000)提出一种双变网格(变网格和变时间步长)的波场延拓方法,Soubaras和Zhang(2008)提出了求解双程波动方程的两步显式更新方法,这两种方法极大地提高了有限差分波场延拓的计算效率;Zhang Y和Zhang G Q(2009)采用单步延拓法实现逆时深度偏移,即利用平方根算子将双程波动方程转化成类似单程波动方程的一阶偏微分方程形式,提出了真振幅的逆时偏移方法.随着计算机技术的迅速发展,GPU/CPU协同计算和集群计算机系统取得了飞速的发展,计算能力也得以大幅度提高(刘红伟等, 2010a).刘红伟等(2011)基于传统的阶梯状近似实现了GPU上的声波叠前逆时偏移高阶有限差分算法.
成像条件是逆时偏移中另一项重要内容,它直接关系到成像的质量和计算效率.常用的成像条件包括零延迟互相关(Yoon et al., 2004)、激发时间(Chang and McMechan, 1986)、振幅比(Claerbout, 1971)、倾斜校正(Costa, 2009)和坡印廷(Yoon et al., 2004)成像条件,以及针对成像假象提出基于单程波(Liu et al., 2007)、无反射双程地震波(Baysal et al., 1984)等成像条件.已有许多学者对这些成像条件在保幅、分辨率、计算效率,以及成像剖面中由直达波和回折波等产生的噪声做了比较深入的讨论(Hanitzsch, 1997; Schleicher et al., 2007; Chattopadhyay and McMechan, 2008; Robert, 2009).其中,激发时间成像条件,无需存储震源波场,但仅仅利用了初至或者最大振幅波场,且成像剖面在量纲上不是反射系数,图像不够清晰.互相关成像条件,采用波场传播的最大相干性成像原理, 即地震波到达地下某一反射界面的波场与地表接收到的波场逆时延拓至该反射界面的波场具有最大相干性.由于互相关成像条件沿着波路径成像,导致地震波在与界面无关的传播路径上产生高振幅、低频的假象,这些假象会掩盖来自界面的有效信号,因此需要采用一定的手段对逆时偏移波路径中的假象进行压制或去除(Kaelin and Guitton, 2006; Karazincir and Gerrard, 2006; 刘红伟等, 2010b; 杜启振等, 2013).
除了逆时偏移算法本身的难点问题,随着地震勘探的深入,地震波成像技术也逐渐朝着能够适应地表起伏、复杂构造和横向变速的方向发展.剧烈的地形起伏给地震勘探工作提出了严峻的挑战,如数据采集困难、数据质量差、散射干扰严重、静校正不准确、成像效果不佳等问题(阎世信等, 2000; 夏竹等, 2004; Deng, 2006; 杨旭明和裴正林, 2008).对于采集自起伏地表的数据,传统基于平缓构造的探测方法在处理复杂地表地区采集的地震数据时受到限制,许多传统处理技术已经不再适用(Rajasekaran and McMechan, 1995).因此,起伏地形在一定程度上制约了地震探测的发展,成为地球内部精细结构探测的瓶颈之一.自20世纪80年代以来,专门处理起伏地表及界面的针对性处理方法受到了重视并得到了广泛的研究(Ilan et al., 1975; Jih et al., 1988; Tessmer et al., 1992, Tessmer and Kosloff, 1994; Nielsen et al., 1994; Rial et al., 1992; Toshinawa and Ohmachi, 1992; Wang and Takenaka, 2001; Rawlinson and Sambridge, 2004a, 2004b, 2005; 孙建国, 2007; 徐义, 2008; 刘红伟等, 2011; Lan et al., 2014a, 2014b, 2016; 孙章庆等, 2012a, 2012b; 侯爵等, 2014; 曲英铭等, 2015; Wang et al., 2015; Liu et al., 2017; Wang et al., 2017).目前,起伏地表的相关研究工作已经成为国际研究的热点问题之一.由于我国西部多为山地地区,广泛分布着剧烈的起伏地表,因此发展起伏地表下的地震偏移成像方法具有广阔的应用前景和实用价值.
传统的逆时偏移方法采用有限差分法进行波场延拓,基于此的逆时偏移通常仅适用于水平地表,因此传统基于有限差分法的逆时偏移方法对起伏地表地震资料处理存在一定的困难(Robertsson and Holliger, 1997; Zhang and Klemperer, 2005).近几年,发展的贴体网格地形“平化”策略被广泛应用于处理起伏地表的走时场、地震波场正演模拟与偏移成像问题(Lan and Zhang, 2012, 2014b, 2016; 兰海强等, 2011;刘志强等, 2016, 2017).最近,不少学者(Huang et al., 2015; Wang et al., 2015, 2017; Liu et al., 2017)开展了声波方程的起伏地表逆时偏移和最小二乘逆时偏移的工作.借助贴体网格和坐标变换,本文将笛卡儿坐标系物理空间的不规则模型转化为曲线坐标系计算空间的规则模型,理论上实现了对起伏地表模型的精确处理.在贴体网格模型参数化基础上,将笛卡儿坐标系的波动方程变换到曲线坐标系,发展了起伏地形地震数据的弹性波逆时偏移方法,并对工业界的标准Marmousi模型及盐丘模型等进行修正并开展了逆时偏移数值试验研究,验证地形平化策略逆时偏移成像方法的有效性,并展示其在起伏地表复杂地质问题中的巨大应用潜力.
1 基于贴体网格模型参数化的地形“平化”策略起伏地表条件下的地震波波场正演模拟是逆时偏移成像的核心,如何灵活、准确地对复杂起伏地表模型进行准确的地质描述至关重要.按照介质的空间分布特征可以将地球介质分为连续介质和离散介质两种类型(李飞等, 2013).连续介质主要应用于基于射线理论的几何地震学,在地震波波场数值模拟中使用较少;离散介质主要用于地震波场正演模拟、程函方程走时场计算等.本文重点研究基于离散介质描述并考虑地形起伏的地震波正演模拟和偏移成像.离散介质一般对地球介质空间按照一定的网格单元进行划分,可以看作是对连续介质的抽样.网格化方法的实质是解决如何将求解区域精确离散化表示的问题,亦即将空间上连续的计算区域剖分为若干个子区域,并确定各个区域中每个空间节点的物理参数值(Thompson et al., 1985; Hvid, 1995).
起伏地表模型网格化方法的基本思想是将模型进行网格剖分,利用网格的变化来适应地表的起伏性和不规则性.现如今,起伏地形下的模型网格化常用方法主要有阶梯网格近似法(Sun et al., 2011; 孙章庆, 2011)、规则矩形网格扩展法(Hole, 1992; Zelt and Smith, 1992)、不等距网格剖分法(孙章庆等, 2012a, 2012b)、三角形网格剖分法(Kimmel and Sethian, 1998; Sethian and Vladimirsky, 2000; Yu et al., 2010; Lelièvre et al., 2011; Bai et al., 2012)、混合网格剖分法(Rawlinson and Sambridge, 2004a, 2004b, 2005; 孙章庆, 2011, 孙章庆等, 2012a)以及曲线网格剖分法(Hestholm and Ruud, 1994, 1998; Dong, 2005; 王祥春和刘学伟, 2005; Hestholm et al., 2006; 蒋丽丽和孙建国, 2008; 孙建国和蒋丽丽, 2009; 刘一峰和兰海强, 2012; Lan and Zhang, 2011a, 2013; Lan et al., 2014a, 2014b, 2016; Lan and Chen, 2018)等.与笛卡儿坐标系下的网格化方法相比,曲线坐标系下的网格化(曲线网格)法在地表模型的建立时没有对地表位置做任何近似处理,也未对地表起伏形态作折线连接的假设.因此,笛卡儿坐标系下的起伏地表问题在被转化为曲线坐标系下的水平地表问题后,波动方程求解算法的整体实现与常规水平地表条件下的算法相同并且无精度损失,这种基于坐标变换的方法被认为是起伏地表模型的理想处理手段之一.
对于曲线网格,其网格生成主要有两种方法,即坐标变换法(Hestholm and Ruud, 1994, 1998; Dong, 2005; Hestholm et al., 2006; 王祥春和刘学伟,2005)和贴体网格法(蒋丽丽和孙建国, 2008; 孙建国和蒋丽丽, 2009; 刘一峰等, 2012; 兰海强等, 2012; Lan and Zhang, 2011a, 2013, Lan et al., 2014a, 2014b, 2016).为了获得优良的模拟效果,尤其是对近地表附近的地震波传播进行精确模拟,最理想的做法是采用一种求解区域边界与坐标系的坐标轴一一平行的坐标系,使其各坐标轴恰与计算区域的边界相适应,这种坐标系称为贴体坐标系(Body fitted coordinates),生成的网格被相应地称为贴体网格(Body fitted grid)(Thompson et al., 1985).使用贴体坐标系生成贴体网格的方法原则上是把物理空间(笛卡儿坐标系)上的一些不规则区域变换成为计算空间(曲线坐标系)上的规则区域(图 1).在进行贴体网格剖分时,地表处的网格与地表地形相吻合.随着远离地表,网格逐渐接近于矩形(兰海强等, 2012),这种方法在数值计算上是对起伏地表的精确无损描述.
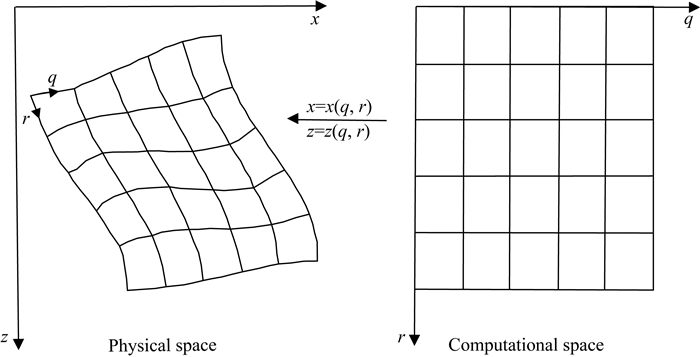
|
图 1 计算空间和物理空间映射示意图(Lan and Zhang, 2011a) Fig. 1 Mapping between computational space and physical space in two dimensions (Lan and Zhang, 2011a) |
在不考虑外力的情况下,笛卡儿坐标系(物理空间)下各向同性介质中的二维弹性波波动方程(Kelly et al., 1976)为:
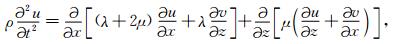
|
(1) |
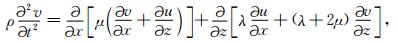
|
(2) |
其中,u, v分别是沿x, z轴方向的位移分量;ρ为介质密度;λ, μ是Lame常数,为空间位置坐标的实函数.为了实现起伏地表下的弹性波波场数值模拟,我们采用贴体网格模型参数化将笛卡儿坐标系下的非规则物理区域映射为曲线坐标系的规则计算区域(见附录).
两个坐标系下的空间偏导数可以利用如下的链式求导规则建立联系:
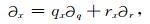
|
(3) |
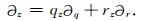
|
(4) |
基于上述链式规则对方程(1)和(2)进行坐标变换(即所谓的“平化”),可得到曲线坐标系(计算空间)中的波动方程:
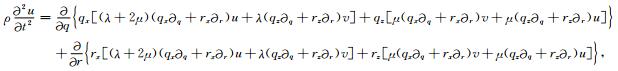
|
(5) |
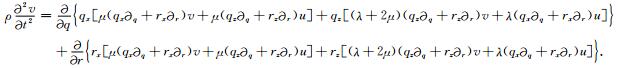
|
(6) |
我们称方程(5)和(6)为地形“平化”策略下各向同性介质中与地形有关的弹性波波动方程.
为了对方程(5)和(6)进行离散得到其差分格式,我们对曲线坐标系下的规则求解区域用如下网格点进行离散:
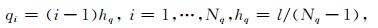
|
(7) |
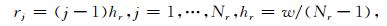
|
(8) |
式中,l, w分别为矩形区域的长度与宽度,hq, hr>0且分别表示沿q, r方向的网格间距.
笛卡儿坐标系与曲线坐标系下的地震波场同样也可以建立如下的对应关系:
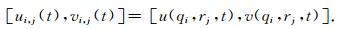
|
(9) |
引入下列差分算子表示符(Appelö and Petersson, 2009):
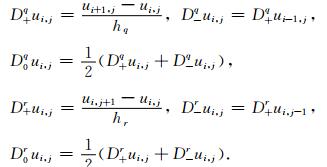
|
(10) |
方程(5)和(6)右边部分的空间导数包含了四种基本类型,可以分别按照以下方式来离散:
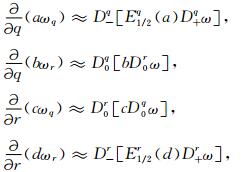
|
(11) |
式中,ω表示u或v,a, b, c, d为度量导数和弹性参数的组合.E为求平均算子:
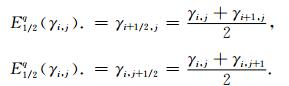
|
(12) |
利用(11)式,对方程(5)和(6)的空间导数项进行近似计算,忽略角标(i, j)可得:
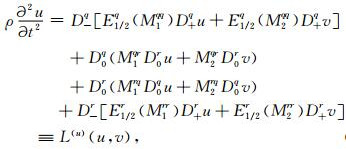
|
(13) |
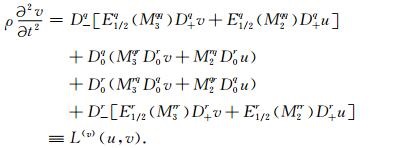
|
(14) |
在网格点中,(qi, rj), (i, j)∈[1, Nq]×[1, Nr)],其中索引M为:
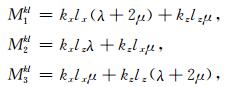
|
(15) |
式中,k, l表示q或r;kx, kz, lx, lz由公式(16)来计算:
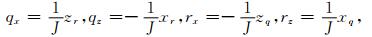
|
(16) |
其中,J=xqzr-xrzq(兰海强等, 2011, 2012; 刘一峰和兰海强, 2012; Lan et al., 2014a, 2014b).
在时间离散上,我们采用二阶精度的中心差分进行离散,波动方程(5)和(6)的全离散方程形式如下:
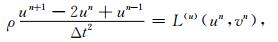
|
(17) |
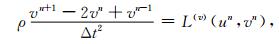
|
(18) |
其中,L(u)和L(v)分别为水平分量和垂直分量的空间离散算子(详见(13)和(14)式).
2.2 震源加载及边界条件处理在地震波场数值模拟过程中,我们用雷克子波作为震源时间函数,空间上以指数衰减形式描述震源能量随距离的振幅衰减.震源项S的表达式可以简写为:
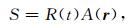
|
(19) |
其中,R(t)表示雷克子波,A(r)表示振幅衰减.
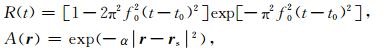
|
(20) |
其中,f0为雷克子波的频率;t0为震源子波的延迟时间,一般取为子波的主周期t0=1/f0;rs为震源的空间坐标;α为空间衰减系数.
由于爆炸力源为无旋场,可以表示为一个标量场的散度场.因此,爆炸源的等效体力f可以表示为:
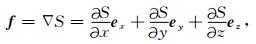
|
(21) |
通过坐标变换,我们获得了爆炸源在二维曲线坐标系下的分量形式:
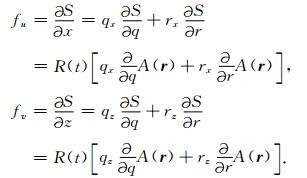
|
(22) |
在笛卡儿坐标系下,振幅衰减项A(r)作为空间坐标(x, y)的函数,即A(x, y);在曲线坐标系下,A(r)是变量(q, r)的函数,即A(q, r).A(q, r)对空间求导的离散表达式为:
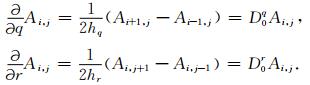
|
(23) |
将上述离散形式代入到式(22)中,可以得到爆炸源的离散表达式:
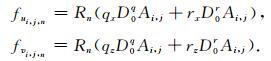
|
(24) |
在地震波场数值模拟中,由于受到计算资源的限制,通常选取有限的区域进行地震波传播模拟,而在区域边界会产生虚假反射.为了消除来自模型边界的虚假反射,人们提出了多种吸收边界条件.完全匹配层吸收边界(Perfectly Matched Layers,PML)被证实为最有效的边界条件之一,本文采用PML吸收边界条件用于起伏地表地震波场数值模拟中的人工截断边界条件处理(Berenger, 1994; Collino and Tsogka, 2001).有关起伏地表下自由边界和PML边界条件的细节问题,请详见参考文献(Lan and Zhang, 2011b, 2012; Lan et al., 2016; 刘志强等, 2016, 2017).
3 基于贴体网格“平化”策略的逆时偏移成像在贴体网格模型参数化的基础上,我们开展了贴体网格中的弹性波逆时偏移成像方法研究.逆时偏移是一种以矢量波动理论为基础的深度域偏移方法,它基于波动方程在震源处激发正向传播的震源波场,并对地表记录到的地震波场进行逆时波场延拓,然后利用成像条件对地下各成像点进行成像.总体上,叠前逆时偏移分为三个部分:一是作为初值问题的震源波场正向延拓,即求解起伏地表下各向同性介质弹性波方程(5)和(6)来实现震源波场的正向外推;二是作为边值问题的检波器波场的逆时外推,即求解震源项为零并将检波点处的地震记录作为边值约束从接收的最大时间开始沿着时间方向逆向延拓直至零时刻;三是成像条件的应用,即对震源波场和检波器波场应用互相关成像条件,叠加所有时刻和炮点的成像值获得最终的逆时偏移成像结果.
在偏移成像过程中,我们采用震源照明度归一化互相关成像条件,即将互相关成像条件的偏移图像除以震源照明强度,这样不仅可以部分消除震源附近的假象同时从成像值中消除了震源强度的影响,并且成像结果接近于反射系数,其数学表达式为:
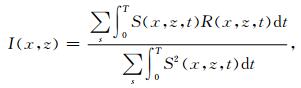
|
(25) |
其中,S(x, z, t), R(x, z, t)分别表示震源与检波器波场;
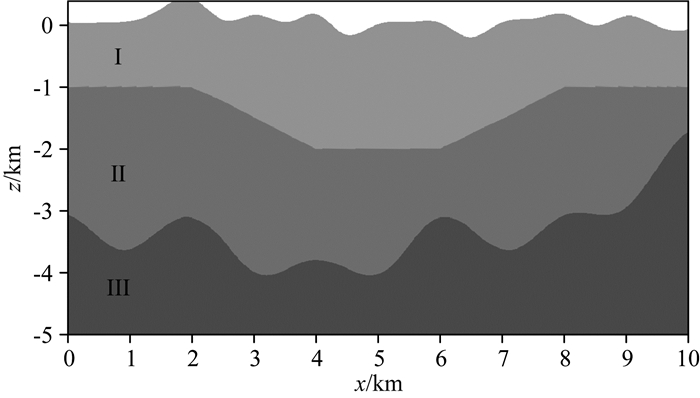
通过三个数值试验来验证本文起伏地表下逆时偏移成像方法的有效性和准确性.模型1为一个构造相对简单的三层起伏地表模型,地表和地下界面均剧烈起伏(图 2);模型2选取地震勘探中标准的强非均匀介质Marmousi模型,并将其改造,生成地表起伏的Marmousi模型(图 5);模型3构建了地表起伏的盐丘模型(图 7).
|
图 2 模型1的P波速度模型 Fig. 2 P-wave velocity of Model 1 |
|
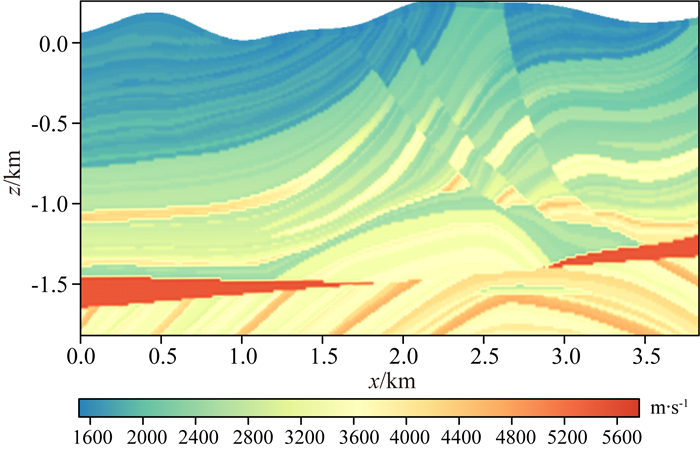
图 5 Marmousi P波速度模型 Fig. 5 P-wave velocity of Marmousi model |
|
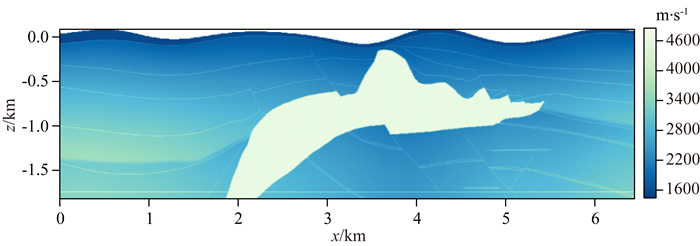
图 7 盐丘P波速度模型 Fig. 7 P-wave velocity of Salt model |
首先,为了验证本文方法对起伏地表的成像能力,我们设计了一个地表起伏的三层模型,如图 2所示.模型尺寸为10 km×5 km,地表起伏达0.4 km,表 1给出了地下各层的介质参数.用该模型来检测本文逆时偏移成像方法的灵活性和准确性.
|
|
表 1 模型1的介质参数 Table 1 Parameters of Model 1 |
我们采用1001×501的贴体网格对模型进行离散,计算时间步长取τ=1 ms,最大接收时间为T=5.5 s.图 3为模型的贴体网格剖分示意图.震源位于地表,主频为10 Hz的爆炸源,以等炮间距(10个网格点一炮)布置,共计101炮.

|
图 3 模型1的贴体网格化示意图 Fig. 3 Sketch for body fitted gridding of Model 1 |
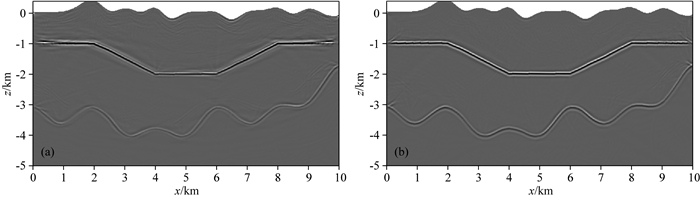
对每炮的偏移成像结果进行拉普拉斯滤波处理,并将101炮的成像结果叠加,得到最终的成像结果(图 4),可见贴体网格“平化”策略下的逆时偏移方法可灵活地处理地表和地下界面起伏的情况,且地下界面成像清晰连续.
|
图 4 拉普拉斯滤波后的101炮叠加的模型1逆时偏移成像结果 (a)水平分量的成像结果; (b)垂直分量的成像结果. Fig. 4 Reverse time migration results of Model 1 (a) Horizontal component image; (b) Vertical component image. |
我们对工业界的标准Marmousi模型进行改造,设计了图 5所示的具有地表起伏的Marmousi模型.
对于该复杂模型,我们采用767×364的贴体网格进行离散,网格间距5 m.计算时间步长同样取τ=0.5 ms,最大接收时间取T=6.0 s.震源布置在地表,为15 Hz主频的爆炸源,总共77炮,炮间距50 m.
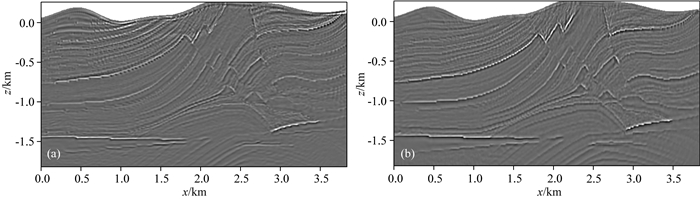
采用基于震源边照明度的归一化互相关成像条件进行偏移成像,在成像后进行逐炮拉普拉斯滤波以压制高振幅、低频假象,叠加的成像结果如图 6所示.由图可见,Marmousi模型的精细结构得到了良好的恢复,Marmousi模型右下部的气/油帽的空间形态与位置均得到了准确成像.
|
图 6 Marmousi模型偏移成像结果 (a)水平分量的成像结果; (b)垂直分量的成像结果. Fig. 6 Reverse time migration results of Marmousi model (a) Horizontal component image; (b) Vertical component image. |
基于工业界的标准盐丘模型,我们设计了具有起伏地表的盐丘模型,如图 7所示.发布的模型仅有P波速度模型,介质的相应S波速度及密度模型由经验关系式给出.
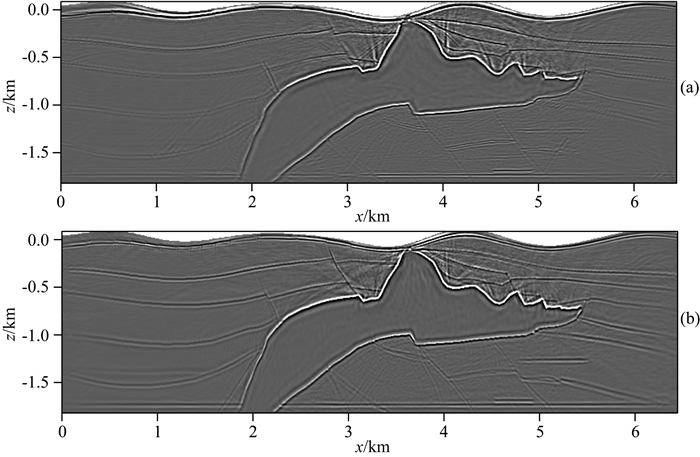
采用网格密度为1290×300的贴体网格对该盐丘模型进行网格剖分,网格间距5 m.计算时间步长为τ=0.5 ms,最大接收时间为T=5.0 s.震源布置于地表,为15 Hz主频的爆炸源,炮间距为75 m,共计86炮.采用归一化互相关成像条件并对每炮成像结果进行拉普拉斯滤波处理,多炮叠加后得到最终的成像结果如图 8所示.
|
图 8 盐丘模型逆时偏移成像结果 (a)水平分量的成像结果; (b)垂直分量的成像结果. Fig. 8 Reverse time migration results of Salt model (a) Horizontal component image; (b) Vertical component image. |
由图 8可见,成像结果(尤其是垂直分量的成像结果)与偏移速度模型(图 7)的构造界面信息吻合较好,地下界面得以清晰正确地归位,表明该方法对起伏地表下的复杂几何模型、甚至是强非均匀介质盐丘模型依然展现出良好的适用性.
5 讨论在起伏地表模型的地震波场正演模拟计算过程中,采用贴体网格技术进行模型剖分.受到地表起伏的影响,为了适应地表的起伏形态,贴体网格在空间展布上往往呈不同程度的扭曲,即贴体网格的各向异性.兰海强等(2012)对不同的网格密度、震源深度及地形起伏程度引起的各向异性强弱对坐标变换法地震波数值模拟的影响进行了深入研究.随着贴体网格的各向异性增强,用坐标变换法模拟地表起伏区域的地震波场误差增大,且计算效率和稳定性降低.因此,贴体网格的质量对地震波场正演模拟的稳定性和计算精度具有重要影响,高质量的贴体网格(边界正交且贴体网格的疏密与地形起伏程度具有较好的一致性)能够保证该方法具有更好的稳定性,反之则可导致稳定性降低甚至无法计算,这些结论对于本文方法的实际应用具有重要指导意义.
在实际应用中,当复杂几何模型涉及到较大的曲率变化而致使贴体网格呈现较强的各向异性时,应该对贴体网格的生成进行质量控制,以保证生成的贴体网格能够满足后期波场正演模拟和偏移成像的精度要求.基于贴体网格的地形“平化”策略强烈依赖于贴体网格的质量,当速度模型涉及较陡的地形时,常规方法生成的贴体网格精度较低.鉴于此,未来将重点开展有效的高质量贴体网格生成方法,推进该方法的适用范围.
6 结论针对山地地震勘探资料处理的难点问题,即起伏地表问题,我们在贴体网格模型参数化的基础上,采用各向同性介质中与地形有关的波动方程进行波场延拓,发展了与地形有关的弹性波逆时偏移成像方法.在地震逆时偏移成像中,采用稳定的归一化零延迟互相关成像条件获取地下介质的高分辨率构造界面图像.三层模型的逆时偏移成像结果验证了基于地形“平化”策略叠前逆时偏移成像方法的成像能力.选取工业界的标准强非均匀介质Marmousi和盐丘模型并对其改造生成具有地形起伏的Marmousi及盐丘模型,开展了起伏地表下复杂地质模型逆时偏移成像试验,结果清晰准确地再现了原有模型,表明该方法对起伏地表地震资料有良好的适应性和有效性,可望在山地、盆山边界等复杂地表地区地震勘探中发挥重要作用.
附录 笛卡儿坐标和曲线坐标的转换(1) 笛卡儿坐标和曲线坐标的变换
贴体网格法采用一种曲线网格来剖分起伏地表模型,其网格形态需要保证网格线的正交性,因此贴体网格需要专门的网格生成技术,而不是通过一个简单的映射函数来建立(蒋丽丽和孙建国, 2008; 孙建国等, 2009; 刘一峰等, 2012).生成贴体网格的方法主要有保角变换法、代数法及偏微分方程法等(Thompson et al., 1985; Hvid, 1995; 蒋丽丽和孙建国, 2008; 孙建国和蒋丽丽, 2009).微分方程法是目前广泛应用的贴体网格生成方法,它通过求解一个偏微分方程来确定与计算平面上规则区域中各节点相应的物理平面上节点位置的方法.该方法生成的网格光滑、均匀,同簇网格线之间不会相交,且方便调整网格疏密.鉴于微分方程法生成贴体坐标的优越性及广泛性,本文在数值模拟中采用求解泊松椭圆型偏微分方程来构造贴体网格坐标系,生成贴体网格.
对于二维问题,常用椭圆型偏微分方程作为转换方程,其形式为:
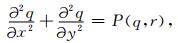
|
(A1) |
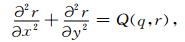
|
(A2) |
其中,(x, y)是物理域的坐标值;(q, r)是计算域的坐标值;P, Q为调节因子.当P=0, Q=0时,该方程是拉普拉斯方程;否则,该方程是泊松方程.在复杂边界条件下,直接求解上述方程有一定困难,但可通过坐标逆变换,即由矩阵计算域中的网格节点坐标(q, r),反求物理域的坐标点(x, y),即:
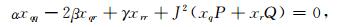
|
(A3) |
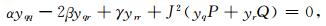
|
(A4) |
其中,α=xr2+yr2;γ=xq2+yq2;β=xqxr+yqyr;J=xqyr-xryq. P, Q的形式(Thomas and Middlecoff, 1980)为:
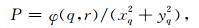
|
(A5) |
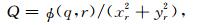
|
(A6) |
其中,边界上的φ、ϕ值有:
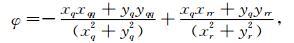
|
(A7) |
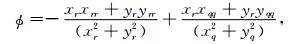
|
(A8) |
内部节点的φ、ϕ值由边界值通过线性插值得到,从而进一步得到各节点的P, Q值.xq2+yq2与xr2+yr2起到了可以把边界上设定的网格线分布密度向区域内部传递的作用.方程(A3)和(A4)即为曲线坐标变换的控制方程,若解出该方程,即得出x=x(q, r),z=z(q, r),那么就可以确定出物理平面和计算平面之间对应点的关系.
(2) 坐标变换的度量导数
贴体网格生成之后,物理空间中的不规则模拟区域与计算空间的规则区域中的网格点就一一对应起来,即:
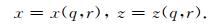
|
(A9) |
由链锁规则,有:
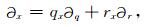
|
(A10) |
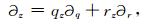
|
(A11) |
这里qx表示∂q(x, z)/∂x,qz,rx,rz的意义也类似,这些导数叫做度量导数(Appelö and Petersson, 2009; Lan and Zhang, 2011a).最终我们会得到度量导数之间的关系:
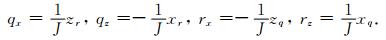
|
(A12) |
其中,J=xqzr-xrzq.值得注意的是,即使映射关系式(A9)有解析的形式,度量导数依然通过数值的方式来计算,以避免使用守恒形式的运动方程时系数偏导数引起的假源项(Thompson et al., 1985).
Appelö D, Petersson N A.
2009. A stable finite difference method for the elastic wave equation on complex geometries with free surfaces. Communications in Computational Physics, 5(1): 84-107.
|
|
Bai C Y, Li X L, Wang Q L, et al.
2012. Multiple arrival tracking within irregular triangular or tetrahedral cell model. Journal of Geophysics and Engineering, 9(1): 29-38.
DOI:10.1088/1742-2132/9/1/004 |
|
Baysal E, Kosloff D D, Sherwood J W C.
1983. Reverse time migration. Geophysics, 48(11): 1514-1524.
DOI:10.1190/1.1441434 |
|
Baysal E, Kosloff D D, Sherwood J W C.
1984. A two-way nonreflecting wave equation. Geophysics, 49(2): 132-141.
DOI:10.1190/1.1441644 |
|
Berenger J P.
1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200.
DOI:10.1006/jcph.1994.1159 |
|
Chang W F, McMechan G A.
1986. Reverse-time migration of offset vertical seismic profiling data using the excitation-time imaging condition. Geophysics, 51(1): 67-84.
DOI:10.1190/1.1442041 |
|
Chang W F, McMechan G A.
1989. Wave field processing of data from the 1986 program for array seismic studies of the continental lithosphere Ouachita experiment. Journal of Geophysical Research:Solid Earth, 94(B12): 17781-17792.
DOI:10.1029/JB094iB12p17781 |
|
Chang W F, McMechan G A.
1990. 3D acoustic prestack reverse-time migration. Geophysical Prospecting, 38(7): 737-755.
DOI:10.1111/gpr.1990.38.issue-7 |
|
Chattopadhyay S, McMechan G A.
2008. Imaging conditions for prestack reverse-time migration. Geophysics, 73(3): S81-S89.
DOI:10.1190/1.2903822 |
|
Claerbout J F.
1971. Toward a unified theory of reflector mapping. Geophysics, 36(3): 467-481.
DOI:10.1190/1.1440185 |
|
Collino F, Tsogka C.
2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics, 66(1): 294-307.
DOI:10.1190/1.1444908 |
|
Costa J C, Silva Neto F A, Alcantara R M, et al.
2009. Obliquity-correction imaging condition for reverse time migration. Geophysics, 74(3): S57-S66.
DOI:10.1190/1.3110589 |
|
Dablain M A.
1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66.
DOI:10.1190/1.1442040 |
|
Deng Z W. 2006.
Seismic Prospecting in Complex Mountains (in Chinese). Beijing: Petroleum Industry Press.
|
|
Dong L G.
2005. Numerical simulation of seismic wave propagation under complex near surface conditions. Progress in Exploration Geophysics (in Chinese), 28(3): 187-194.
|
|
Douma H, Yingst D, Vasconcelos I, et al.
2010. On the connection between artifact filtering in reverse-time migration and adjoint tomography. Geophysics, 75(6): S219-S223.
DOI:10.1190/1.3505124 |
|
Du Q Z, Zhu Y T, Zhang M Q, et al.
2013. A study on the strategy of low wavenumber noise suppression for prestack reverse-time depth migration. Chinese Journal of Geophysics (in Chinese), 56(7): 2391-2401.
DOI:10.6038/cjg20130725 |
|
Fletcher R P, Fowler P J, Kitchenside P, et al.
2006. Suppressing unwanted internal reflections in prestack reverse-time migration. Geophysics, 71(6): E79-E82.
DOI:10.1190/1.2356319 |
|
Guitton A, Kaelin B, Biondi B.
2007. Least-squares attenuation of reverse-time-migration artifacts. Geophysics, 72(1): S19-S23.
DOI:10.1190/1.2399367 |
|
Hanitzsch C.
1997. Comparison of weights in prestack amplitude-preserving Kirchhoff depth migration. Geophysics, 62: 1812-1816.
DOI:10.1190/1.1444282 |
|
Hestholm S, Ruud B.
1994. 2D finite-difference elastic wave modelling including surface topography. Geophysical Prospecting, 42(5): 371-390.
DOI:10.1111/gpr.1994.42.issue-5 |
|
Hestholm S, Ruud B.
1998. 3-D finite-difference elastic wave modeling including surface topography. Geophysics, 63(2): 613-622.
DOI:10.1190/1.1444360 |
|
Hestholm S, Moran M, Ketcham S, et al.
2006. Effects of free-surface topography on moving-seismic-source modeling. Geophysics, 71(6): T159-T166.
DOI:10.1190/1.2356258 |
|
Hole J A.
1992. Nonlinear high-resolution three-dimensional seismic travel time tomography. Journal of Geophysical Research:Solid Earth, 97(B5): 6553-6562.
DOI:10.1029/92JB00235 |
|
Hou J, Zhang Z J, Lan H Q, et al.
2014. Progress in numerical simulation of seismic wave propagation under an undulating surface. Progress in Geophysics (in Chinese), 29(2): 488-497.
DOI:10.6038/pg20140203 |
|
Huang J P, Li C, Wang R R, et al.
2015. Plane-wave least-squares reverse time migration for rugged topography. Journal of Earth Science, 26(4): 471-480.
DOI:10.1007/s12583-015-0556-5 |
|
Hvid S L. 1995. Three dimensional algebraic grid generation. Department of Fluid Mechanics, Technical University of Denmark.
|
|
Ilan A, Ungar A, Alterman Z.
1975. An improved representation of boundary conditions in finite difference schemes for seismological problems. Geophysical Journal International, 43(3): 727-745.
DOI:10.1111/gji.1975.43.issue-3 |
|
Jiang L L, Sun J G.
2008. Source terms of elliptic system in grid generation. Global Geology (in Chinese), 27(3): 298-305.
|
|
Jih R S, McLaughlin K L, Der Z A.
1988. Free-boundary conditions of arbitrary polygonal topography in a two-dimensional explicit elastic finite-difference scheme. Geophysics, 53(8): 1045-1055.
DOI:10.1190/1.1442541 |
|
Kaelin B, Guitton A. 2006. Imaging condition for reverse time migration. //76th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts. .
http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=SEGEAB000025000001002594000001&idtype=cvips&prog=normal |
|
Karazincir M H, Gerrard C M. 2006. Explicit high-order reverse time pre-stack depth migration. //76th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=SEGEAB000025000001002353000001&idtype=cvips&prog=normal |
|
Kelly K R, Ward R W, Treitel S, et al.
1976. Synthetic seismograms:a finite-difference approach. Geophysics, 41(1): 2-27.
DOI:10.1190/1.1440605 |
|
Kimmel R, Sethian J.
1998. Fast marching methods on triangulated domains. Proceedings of the National Academy of Science, 95: 8341-8435.
|
|
Lan H Q, Liu J, Bai Z M.
2011. Wave-field simulation in VTI media with irregular free surface. Chinese Journal of Geophysics (in Chinese), 54(8): 2072-2084.
DOI:10.3969/j.issn.0001-5733.2011.08.014 |
|
Lan H Q, Zhang Z J.
2011a. Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface. Bulletin of the Seismological Society of America, 101(3): 1354-1370.
DOI:10.1785/0120100194 |
|
Lan H Q, Zhang Z J.
2011b. Comparative study of free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation. Journal of Geophysics and Engineering, 8(2): 275-286.
DOI:10.1088/1742-2132/8/2/012 |
|
Lan H Q, Zhang Z, Xu T, et al.
2012. Effects due to the anisotropic stretching of the surface-fitting grid on the traveltime computation for irregular surface by the coordinate transforming method. Chinese Journal of Geophysics (in Chinese), 55(10): 3355-3369.
DOI:10.6038/j.issn.0001-5733.2012.10.018 |
|
Lan H Q, Zhang Z J.
2013. Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface. Geophysical Journal International, 193(2): 1010-1026.
DOI:10.1093/gji/ggt036 |
|
Lan H Q, Zhang Z J, Chen J Y, et al.
2014a. Reverse time migration from irregular surface by flattening surface topography. Tectonophysics, 627: 26-37.
DOI:10.1016/j.tecto.2014.04.015 |
|
Lan H Q, Chen J Y, Zhang Z J.
2014b. A fast sweeping scheme for calculating p wave first-arrival travel times in transversely isotropic media with an irregular surface. Pure and Applied Geophysics, 171(9): 2199-2208.
DOI:10.1007/s00024-014-0836-5 |
|
Lan H Q, Chen J Y, Zhang Z J, et al.
2016. Application of a perfectly matched layer in seismic wavefield simulation with an irregular free surface. Geophysical Prospecting, 64(1): 112-128.
DOI:10.1111/1365-2478.12260 |
|
Lan H Q, Chen L.
2018. An upwind fast sweeping scheme for calculating seismic wave first-arrival travel times for models with an irregular free surface. Geophysical Prospecting, 66(2): 327-341.
DOI:10.1111/gpr.2018.66.issue-2 |
|
Lelièvre P G, Farquharson C G, Hurich C A.
2011. Inversion of first-arrival seismic traveltimes without rays, implemented on unstructured grids. Geophysical Journal International, 185(2): 749-763.
DOI:10.1111/gji.2011.185.issue-2 |
|
Li F, Xu T, Wu Z B, et al.
2013. Segmentally iterative ray tracing in 3-D heterogeneous geological models. Chinese Journal of Geophysics (in Chinese), 56(10): 3514-3522.
DOI:10.6038/cjg20131026 |
|
Liu F Q, Morton S A, Leveille J P, et al. 2007. Reverse-time migration using one-way wavefield imaging condition. //77th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
http://www.researchgate.net/publication/249861878_Reverse-time_migration_using_one-way_wavefield_imaging_condition |
|
Liu H W, Li B, Liu H, et al.
2010a. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese Journal of Geophysics (in Chinese), 53(7): 1725-1733.
DOI:10.3969/j.issn.0001-5733.2010.07.024 |
|
Liu H W, Liu H, Zou Z, et al.
2010b. The problems of denoise and storage in seismic reverse time migration. Chinese Journal of Geophysics (in Chinese), 53(9): 2171-2180.
DOI:10.3969/j.issn.0001-5733.2010.09.017 |
|
Liu H W, Liu H, Li B, et al.
2011. Pre-stack reverse time migration for rugged topography and GPU acceleration technology. Chinese Journal of Geophysics (in Chinese), 54(7): 1883-1892.
DOI:10.3969/j.issn.0001-5733.2011.07.022 |
|
Liu Q C, Zhang J F, Gao H W.
2017. Reverse-time migration from rugged topography using irregular, unstructured mesh. Geophysical Prospecting, 65(2): 453-466.
DOI:10.1111/gpr.2017.65.issue-2 |
|
Liu Y F, Lan H Q.
2012. Study on the numerical solutions of the eikonal equation in curvilinear coordinate system. Chinese Journal of Geophysics (in Chinese), 55(6): 2014-2026.
DOI:10.6038/j.issn.0001-5733.2012.06.023 |
|
Liu Z Q, Sun J G, Sun H, et al.
2016. Mimetic finite-difference numerical simulation of seismic wave based on the adaptive grid. Chinese Journal of Geophysics (in Chinese), 59(12): 4654-4665.
DOI:10.6038/cjg20161225 |
|
Liu Z Q, Sun J G, Sun H, et al.
2017. A perfectly matched layer absorbing boundary condition under the curvilinear coordinate system. Journal of Jilin University (Earth Science Edition), 47(6): 1875-1884.
|
|
McMechan G A, Fuis G S.
1987. Ray equation migration of wide-angle reflections from southern Alaska. Journal of Geophysical Research:Solid Earth, 92(B1): 407-420.
DOI:10.1029/JB092iB01p00407 |
|
Nielsen P, If F, Berg P, et al.
1994. Using the pseudospectral technique on curved grids for 2D acoustic forward modelling. Geophysical Prospecting, 42(4): 321-341.
DOI:10.1111/gpr.1994.42.issue-4 |
|
Qu Y M, Huang J P, Li Z C, et al.
2015. Elastic wave modeling and pre-stack reverse time migration of irregular free-surface based on layered mapping method. Chinese Journal of Geophysics (in Chinese), 58(8): 2896-2911.
DOI:10.6038/cjg20150823 |
|
Qu Y M, Huang J P, Li Z C, et al.
2015. Elastic wave modeling and pre-stack reverse time migration of irregular free-surface based on layered mapping method. Chinese Journal of Geophysics (in Chinese), 58(5): 544-560.
DOI:10.6038/cjg20150823 |
|
Rajasekaran S, McMechan G A.
1995. Prestack processing of land data with complex topography. Geophysics, 60(6): 1875-1886.
DOI:10.1190/1.1443919 |
|
Rawlinson N, Sambridge M.
2004a. Wave front evolution in strongly heterogeneous layered media using the fast marching method. Geophysical Journal International, 156(3): 631-647.
DOI:10.1111/gji.2004.156.issue-3 |
|
Rawlinson N, Sambridge M.
2004b. Multiple reflection and transmission phases in complex layered media using a multistage fast marching method. Geophysics, 69(5): 1338-1350.
DOI:10.1190/1.1801950 |
|
Rawlinson N, Sambridge M.
2005. The fast marching method:an effective tool for tomographic imaging and tracking multiple phases in complex layered media. Exploration Geophysics, 36(4): 341-350.
DOI:10.1071/EG05341 |
|
Rial J A, Saltzman N G, Ling H.
1992. Earthquake-induced resonance in sedimentary basins. American Scientist, 80(6): 566-578.
|
|
Robert G C. 2009. Reverse time migration with random boundaries. 79th Annual International Meeting, SEG Expanded Abstracts, 28: 2809-2813.
http://www.researchgate.net/publication/242554950_Reverse_time_migration_with_random_boundaries |
|
Robertsson J O A, Holliger K.
1997. Modeling of seismic wave propagation near the earth's surface. Physics of the Earth and Planetary Interiors, 104(1-3): 193-211.
DOI:10.1016/S0031-9201(97)00045-9 |
|
Schleicher J, Costa J C, Novais A.
2008. A comparison of imaging conditions for wave-equation shot-profile migration. Geophysics, 73(6): S219-S227.
DOI:10.1190/1.2976776 |
|
Sethian J A, Vladimirsky A.
2000. Fast methods for the eikonal and related Hamilton-Jacobi equations on unstructured meshes. Proceedings of the National Academy of Sciences of the United States of America, 97(11): 5699-5703.
DOI:10.1073/pnas.090060097 |
|
Soubaras R, Zhang Y. 2008. Two-step explicit marching method for reverse time migration. //78th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
http://www.researchgate.net/publication/269065330_Twostep_explicit_marching_method_for_reverse_time_migration |
|
Sun J G.
2007. Methods for numerical modeling of geophysical fields under complex topographical conditions:a critical review. Global Geology (in Chinese), 26(3): 345-362.
|
|
Sun J G, Jiang L L.
2009. Orthogonal curvilinear grid generation technique used for numeric simulation of geophysical fields in undulating surface condition. Oil Geophysical Prospecting (in Chinese), 44(4): 494-500.
|
|
Sun J G, Sun Z Q, Han F X.
2011. A finite difference scheme for solving the eikonal equation including surface topography. Geophysics, 76(4): T53-T63.
DOI:10.1190/1.3580634 |
|
Sun Z Q. 2011. The seismic traveltimes and raypath computation under undulating Earth's surface condition (in Chinese). Changchun: Jilin University.
|
|
Sun Z Q, Sun J G, Han F X.
2012a. The comparison of three schemes for computing seismic wave traveltimes in complex topographical conditions. Chinese Journal of Geophysics (in Chinese), 55(2): 560-568.
DOI:10.6038/j.issn.0001-5733.2012.02.018 |
|
Sun Z Q, Sun J G, Han F X.
2012b. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3D undulating surface condition. Chinese Journal of Geophysics (in Chinese), 55(7): 2441-2449.
DOI:10.6038/j.issn.0001-5733.2012.07.028 |
|
Tessmer E, Kosloff D, Behle A.
1992. Elastic wave propagation simulation in the presence of surface topography. Geophysical Journal International, 108(2): 621-632.
DOI:10.1111/gji.1992.108.issue-2 |
|
Tessmer E, Kosloff D.
1994. 3-D elastic modeling with surface topography by a Chebychev spectral method. Geophysics, 59(3): 464-473.
DOI:10.1190/1.1443608 |
|
Thompson J E, Warsi Z U A, Mastin C W. 1985. Numerical Grid Generation, Foundations and Applications. Amsterdam: North-Holland.
|
|
Toshinawa T, Ohmachi T.
1992. Love-wave propagation in a three-dimensional sedimentary basin. Bulletin of the Seismological Society of America, 82(4): 1661-1677.
|
|
Virieux J.
1986. P-SV wave propagation in heterogeneous media:velocity-stress finite-difference method. Geophysics, 51(4): 889-901.
DOI:10.1190/1.1442147 |
|
Wang X C, Liu X W.
2005. Downward continuing the seismic record of topography using coordination transformated method. Progress in Geophysics (in Chinese), 20(3): 677-680.
|
|
Wang Y. 2000. Reverse-time migration by a variable time-step and space-grid method. //70th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
http://www.researchgate.net/publication/240735805_Reverse-time_migration_by_a_variable_time-step_and_space-grid_method |
|
Wang Y, Zhou H, Chen H M, et al.
2015. Acoustic reverse time migration and perfectly matched layer in boundary-conforming grids by elliptic method. Journal of Applied Geophysics, 122: 53-61.
DOI:10.1016/j.jappgeo.2015.08.013 |
|
Wang Y, Zhou H, Yuan S Y, et al.
2017. A fourth order accuracy summation-by-parts finite difference scheme for acoustic reverse time migration in boundary-conforming grids. Journal of Applied Geophysics, 136: 498-512.
DOI:10.1016/j.jappgeo.2016.12.002 |
|
Wang Y B, Takenaka H.
2001. A multidomain approach of the Fourier pseudospectral method using discontinuous grid for elastic wave modeling. Earth, Planets and Space, 53(3): 149-158.
DOI:10.1186/BF03352372 |
|
Xia Z, Zhang S H, Wang X J.
2004. Discussion on near-surface characters and structures in complex area of western China. Oil Geophysical Prospecting (in Chinese), 38(4): 414-424.
|
|
Xu Y.
2008. Prestack reverse-time migration by the grid method. Progress in Geophysics (in Chinese), 23(3): 839-845.
|
|
Yan S X, Liu H S, Yao X G. 2000.
Mountain Geophysical Exploration Technology (in Chinese). Beijing: Petroleum Industry Press.
|
|
Yang X M, Pei Z L.
2008. Study on feature of elastic wavefield in complex near surface. Oil Geophysical Prospecting (in Chinese), 42(6): 658-664.
|
|
Yoon K, Marfurt K J, Starr W. 2004. Challenges in reverse-time migration. //74th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
http://www.researchgate.net/publication/249858659_Challenges_in_reverse-time_migration |
|
Yu S J, Liu R Z, Cheng J L.
2010. A minimum traveltime ray tracing global algorithm on a triangular net for propagating plane waves. Applied Geophysics, 7(4): 348-356.
DOI:10.1007/s11770-010-0263-z |
|
Zelt C A, Smith R B.
1992. Seismic traveltime inversion for 2-D crustal velocity structure. Geophysical Journal International, 108(1): 16-34.
DOI:10.1111/gji.1992.108.issue-1 |
|
Zhang Y, Zhang G Q.
2009. One-step extrapolation method for reverse time migration. Geophysics, 74(4): A29-A33.
DOI:10.1190/1.3123476 |
|
Zhang Y, Sun J. 2009. Practical issues of reverse time migration: true amplitude gathers, noise removal and harmonic-source encoding. //Beijing 2009 International Geophysical Conference and Exposition. Beijing, China: SEG.
http://www.publish.csiro.au/ex/ASEG2009ab033 |
|
Zhang Z, Liu Y S, Xu T, et al.
2013. A stable excitation amplitude imaging condition for reverse time migration in elastic wave equation. Chinese Journal of Geophysics (in Chinese), 56(10): 3523-3533.
DOI:10.6038/cjg20131027 |
|
Zhang Z J, Klemperer S L.
2005. West-east variation in crustal thickness in northern Lhasa block, central Tibet, from deep seismic sounding data. Journal of Geophysical Research:Solid Earth, 110(B9): B09403.
DOI:10.1029/2004JB003139 |
|
邓志文. 2006.
复杂山地地震勘探. 北京: 石油工业出版社.
|
|
董良国.
2005. 复杂地表条件下地震波传播数值模拟. 勘探地球物理进展, 28(3): 187–194.
|
|
杜启振, 朱钇同, 张明强, 等.
2013. 叠前逆时深度偏移低频噪声压制策略研究. 地球物理学报, 56(7): 2391–2401.
DOI:10.6038/cjg20130725 |
|
侯爵, 张忠杰, 兰海强, 等.
2014. 起伏地表下地震波传播数值模拟方法研究进展. 地球物理学进展, 29(2): 488–497.
DOI:10.6038/pg20140203 |
|
蒋丽丽, 孙建国.
2008. 基于Poisson方程的曲网格生成技术. 世界地质, 27(3): 298–305.
|
|
兰海强, 刘佳, 白志明.
2011. VTI介质起伏地表地震波场模拟. 地球物理学报, 54(8): 2072–2084.
DOI:10.3969/j.issn.0001-5733.2011.08.014 |
|
兰海强, 张智, 徐涛, 等.
2012. 贴体网格各向异性对坐标变换法求解起伏地表下地震初至波走时的影响. 地球物理学报, 55(10): 3355–3369.
DOI:10.6038/j.issn.0001-5733.2012.10.018 |
|
李飞, 徐涛, 武振波, 等.
2013. 三维非均匀地质模型中的逐段迭代射线追踪. 地球物理学报, 56(10): 3514–3522.
DOI:10.6038/cjg20131026 |
|
刘红伟, 李博, 刘洪, 等.
2010a. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725–1733.
DOI:10.3969/j.issn.0001-5733.2010.07.024 |
|
刘红伟, 刘洪, 邹振, 等.
2010b. 地震叠前逆时偏移中的去噪与存储. 地球物理学报, 53(9): 2171–2180.
DOI:10.3969/j.issn.0001-5733.2010.09.017 |
|
刘红伟, 刘洪, 李博, 等.
2011. 起伏地表叠前逆时偏移理论及GPU加速技术. 地球物理学报, 54(7): 1883–1892.
DOI:10.3969/j.issn.0001-5733.2011.07.022 |
|
刘一峰, 兰海强.
2012. 曲线坐标系程函方程的求解方法研究. 地球物理学报, 55(6): 2014–2026.
DOI:10.6038/j.issn.0001-5733.2012.06.023 |
|
刘志强, 孙建国, 孙辉, 等.
2016. 基于自适应网格的仿真型有限差分地震波数值模拟. 地球物理学报, 59(12): 4654–4665.
DOI:10.6038/cjg20161225 |
|
刘志强, 孙建国, 孙辉, 等.
2017. 曲线坐标系下的完全匹配层吸收边界条件. 吉林大学学报(地球科学版), 47(6): 1875–1884.
|
|
曲英铭, 黄建平, 李振春, 等.
2015. 分层坐标变换法起伏自由地表弹性波叠前逆时偏移. 地球物理学报, 58(8): 2896–2911.
DOI:10.6038/cjg20150823 |
|
孙建国.
2007. 复杂地表条件下地球物理场数值模拟方法评述. 世界地质, 26(3): 345–362.
|
|
孙建国, 蒋丽丽.
2009. 用于起伏地表条件下地球物理场数值模拟的正交曲网格生成技术. 石油地球物理勘探, 44(4): 494–500.
|
|
孙章庆. 2011. 起伏地表条件下的地震波走时与射线路径计算. 长春: 吉林大学.
http://cdmd.cnki.com.cn/Article/CDMD-10183-1011105855.htm |
|
孙章庆, 孙建国, 韩复兴.
2012a. 针对复杂地形的三种地震波走时算法及对比. 地球物理学报, 55(2): 560–568.
DOI:10.6038/j.issn.0001-5733.2012.02.018 |
|
孙章庆, 孙建国, 韩复兴.
2012b. 三维起伏地表条件下地震波走时计算的不等距迎风差分法. 地球物理学报, 55(7): 2441–2449.
DOI:10.6038/j.issn.0001-5733.2012.07.028 |
|
王祥春, 刘学伟.
2005. 变换坐标系下相移法起伏地表地震波场延拓. 地球物理学进展, 20(3): 677–680.
|
|
夏竹, 张少华, 王学军.
2004. 中国西部复杂地区近地表特征与表层结构探讨. 石油地球物理勘探, 38(4): 414–424.
|
|
徐义.
2008. 格子法在起伏地表叠前逆时深度偏移中的应用. 地球物理学进展, 23(3): 839–845.
|
|
阎世信, 刘怀山, 姚雪根. 2000.
山地地球物理勘探技术. 北京: 石油工业出版社.
|
|
杨旭明, 裴正林.
2008. 复杂近地表弹性波波场特征研究. 石油地球物理勘探, 42(6): 658–664.
|
|
张智, 刘有山, 徐涛, 等.
2013. 弹性波逆时偏移中的稳定激发振幅成像条件. 地球物理学报, 56(10): 3523–3533.
DOI:10.6038/cjg20131027 |
|
 2018, Vol. 61
2018, Vol. 61

