地球物理学报  2018, Vol. 61 Issue (3): 1118-1135   PDF    
引用本文
王赟, 杨春, 芦俊. 2018. 薄互层弹性波反演面临的困境. 地球物理学报, 61(3): 1118-1135, doi: 10.6038/cjg2018L0404.  
Wang Y, Yang C, Lu J. 2018. Dilemma faced by elastic wave inversion in thinly layered media. Chinese J. Geophys. (in Chinese), 61(3): 1118-1135, doi: 10.6038/cjg2018L0404.  
薄互层弹性波反演面临的困境
王赟, 杨春, 芦俊     
中国地质大学(北京)地球物理与信息技术学院, 地质过程与矿产资源国家重点实验室, 北京 100083
收稿日期 2017-07-03, 2018-01-25 收修定稿
基金项目: 国家自然科学基金项目（41425017，41604119，41574126）和国家十三五重大专项"薄层地震波场特征与反演研究"专题（2016ZX05002-005-008）联合资助
第一作者简介: 王赟, 男, 1969年生, 博士, 教授、博士生导师, 1998年毕业于中国科学院地球物理研究所, 现从事地震各向异性理论与多分量地震技术的研究. E-mail: yunwang@mail.iggcas.ac.cn
通讯作者: 芦俊, E-mail: lujun615@163.com
摘要：对于薄互层地震传播特征的研究我们已有了充分的认识，这是一种完全不同于现有的基于厚层单阻抗差界面地震反射理论的、具有频率依赖性的调谐反射.因而也使得对具有N层结构的弹性介质薄互层反演时，现有有限带宽的基于空间-频率域采样的地震观测难以规避多解性问题.长波长假设下的薄互层VTI近似似乎可以为我们提供一种待反演弹性参数只有5个的可行性方案，使得我们可以将薄互层背景下任一目标薄层的反演看作VTI厚层介质背景下单薄层的反演.但是，我们首先面临薄互层VTI近似的误差和适用性条件等问题；其次，既使对于单薄层厚度的反演，目前地震领域也未能提供一种通用有效的解决方案，实际地震勘探中薄层厚度的预测依然是一个悬而未决的难题.因此在此基础上再进行单薄层的物性参数、裂缝隙和流体的预测则更叠加了难以预知的多解性.显然单纯P波已难以应对，弹性波的介入成为必然；而且单薄层含裂缝与流体的预测更需要横波分裂和双相介质理论的支撑.可以预见的是，除了纵、横波速度，薄互层反射系数的频率依赖性是我们试图给出相对可靠的、单薄层物性精细刻画必须使用的一种重要地震属性.
关键词: 薄互层      VTI      单薄层      弹性波      反演     
Dilemma faced by elastic wave inversion in thinly layered media
WANG Yun, YANG Chun, LU Jun     
School of Geophysics and Information Technology, China University of Geosciences, State Key Laboratory of Geological Processes and Mineral Resources(GPMR), Beijing 100083, China
Abstract: It's well known that there is a great difference of reflecting characteristics between an interface and a thin-bed, mainly because of frequency interference. Though lots of researches have been contributed to this field, under the condition that the seismic data is only recorded as limited frequency band and sparse space sampling, the elastic inversion in thinly layered media was faced with 3N parameters unknown and seriously ambiguity. Maybe a feasible policy is that only 5 elastic parameters (including 3 Thomsen parameters) need to be predicted based on the approximation of vertically transverse isotropy, so that we can simplify the inversion of thinly layered media as a thin-bed inversion in the VTI background. However, first we need to re-consider the accuracy of quasi-VTI theory and its applicable conditions; secondly, we have to solve the problems encountered by thin-bed inversion. Unfortunately, the thin-bed thickness is still difficult to be predicted precisely, though many studies had been given to this topic since the last century. And more than that, if the elastic attributes, especially fractures and fluids need to be detected in a thin-bed, the inversion of thin-bed will become a more complex mathematical problem. Obviously, only P-wave can't afford to face this challenge, and PS-wave information should be used jointly. Especially, frequency-dependent reflectance of the thin-bed is another important seismic attribute needed to be utilized sufficiently, so that the thin-bed can be delineated precisely and finely.
Key words: Thinly layered media    Vertically transverse isotropy    Thin-bed    Elastic wave    Inversion    
0 引言

对于深部地球动力学研究，上地壳稳定沉积的盆地或克拉通是典型的低频地震探测下的薄互层模型；化石能源探测针对的广泛分布的陆相或海陆交互相沉积地层也是典型的薄互层.随着我国油气、煤炭等资源开发的不断深入，薄(互)层储层、岩性储层、碳酸盐岩缝洞型储层、非常规油气等复杂储层及煤层成为勘探的重点.在我国东部以及一些西部盆地，绝大多数的中、新生代陆相含油气、含煤盆地大都以薄层砂、泥岩沉积为主，并夹有少量的碳酸盐岩、页岩及膏盐层，这些地层岩性和厚度横向变化较大，而且单层厚度远远低于目前地震勘探的垂向分辨率，以薄层或其互层的形式存在(王濮等，2007；陈继松和常旭，1987).

地震技术从国外引进中国石油工业之初，由于国外的油气勘探主要针对的是海相厚层储层，因此，当时的地震技术是建立在层状介质厚层反射理论基础上的，即单阻抗差界面的反射(许云，1981；沃特斯，1983).而我国初期阶段主要是以勘探开发构造油气藏为主，套用的也是厚层的地震反射理论.几十年来，随着构造油气藏的开发殆尽，岩性油气藏等更复杂的油气藏的勘探开发日益紧迫，建立在单阻抗差界面、厚层反射理论基础之上的地震技术受到越来越多的挑战，存在不可接受的误差(Gochioco, 1991, 1992；张川等，2015).因此，开展针对薄互层地震传播的专项研究，建立适用于薄互层的地震波理论，以期获得对薄层、薄互层的定性或定量预测分析，提高储层的预测精度，对油气以及煤炭等化石能源的地震勘探开发来说具有重要的理论及现实意义.

早在20世纪，薄层反射的特殊性就引起了国内外众多学者的关注(Postma，1955；Krey and Helbig, 1956；Widess, 1973；唐文榜，1987；Gochioco, 1991, 1992；袁子龙等，1996).纵观薄层正演研究，主要分为以下三个思路进行.

一是将问题简化，只考虑平面纵波垂直入射情况下PP波的地震响应(Treitel and Robinson, 1966；Widess，1973；Chung and Lawton, 1995a，1995b).但这些研究忽略了转换波和层间多次波的影响.Koefoed和de Voogd (1980)曾指出，上述研究只有在薄层与围岩的声阻抗比值位于0.5和2之间时，转换波及层间多次波对薄层反/透射的影响很小时才成立.

二是任意入射角情况下利用时间延迟建立的薄层反/透射关系式(Meissner and Meixner, 1969；Liu and Schmitt, 2003).Pan和Innanen(2013)在Liu的基础上，进行了单一薄层在弹性介质下的AVO(Amplitude versus Offset, 振幅随偏移距变化)/AVF(Amplitude versus Frequency, 振幅随频率变化)特征研究，表明声学介质不适合单一薄层AVO研究.

三是利用层状介质传播矩阵理论研究薄层问题(布列霍夫斯基赫，1960；Kennett，1974；Kennett and Kerry, 1979；Carcione et al., 1991; Carcione，2001；Sayers，1998；Chen and Liu, 2006；Sidler and Holliger, 2010).此时的研究给出了任意入射角条件下的多层介质纵、横波反射系数谱理论，进一步简化给出了单个薄层的纵波反射系数谱计算公式，从而获得了在薄层条件下不同频率成分的纵波反射系数谱数学关系式；且在薄层的反射中考虑了所有可能的波型转换和所有类型的多次波.

由于薄互层在我国煤田与油气勘探中的主要目的层中具有代表性，我们国家对于薄互层地震反射的研究给予了较多的关注.国家自然科学基金委员会曾在九五油储重大专项中给予了充分的讨论，所获得的关于薄层反射与单阻抗差界面反射的差异认知也被大量的研究证实(孙树海和牛彦良，1991；郭智奇等，2016).一个明显的标志是2010年前的研究主要局限于均匀各向同性纵波反射的情况，此后关于薄层弹性波和各向异性的研究明显增多(杨春颖等，2017).

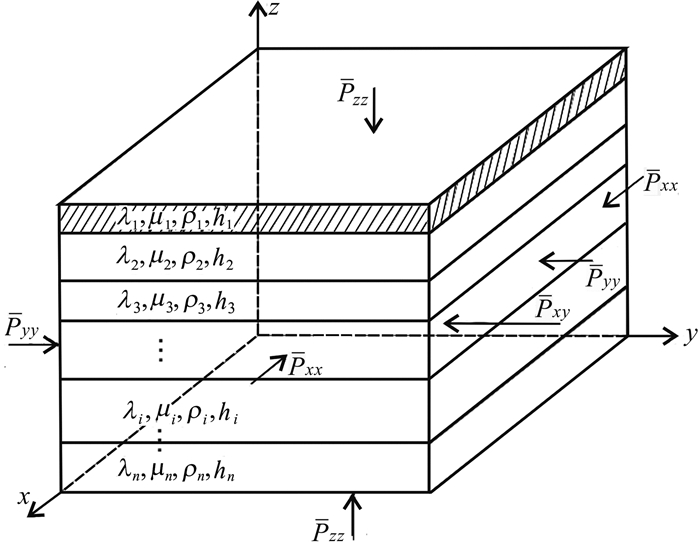
1 薄互层反演的难点 1.1 薄互层反演问题的提出

由于薄层的调谐效应和地震信号的有限频带宽度，以及相对层厚的长波长特征使得薄互层反演成为超越地震分辨率极限的反演.例如，对于图 1所示的一个典型的水平层状薄互层模型，在薄互层的顶界面，不论我们获得是透射波或者反射波，对于具有N层结构的薄互层，在已知有限的接收信息基础上欲获得每层介质的速度、密度和厚度参数是一个严重欠定的地球物理反问题.虽然地震技术可以通过加密采样点的方式使用尽可能多的物理点上反射或透射信号来降低这种反问题的多解性，但对于这种水平层状、可近似为横向各向同性的介质层，在已满足空间和时间采样率的条件下，加密并不会增加额外的、可有效提高反演矩阵秩的非相关信息(张永刚等，2010).也就是说，这种典型的薄互层模型不具有可实现唯一解反演的数学完备性.

图 1 具有N层结构的薄互层模型(张中杰和何樵登，1990) Fig. 1 Sketch map of N thin layers model (Zhang and He, 1990)

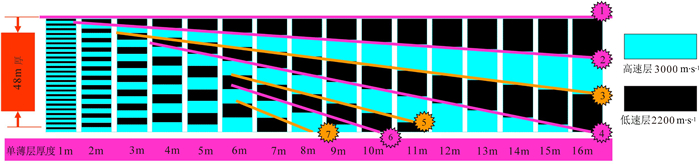
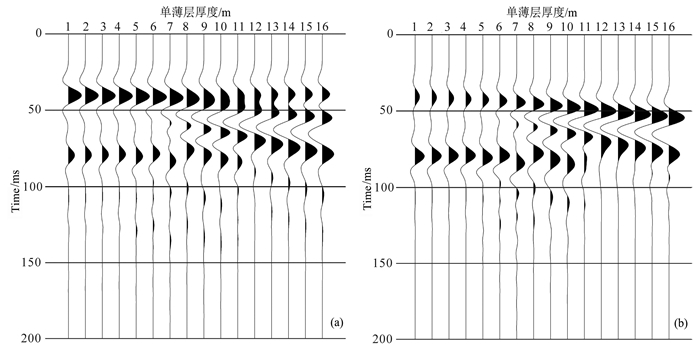
既使对于一种最简单的、理想的韵律型薄互层，如图 2所示，设薄互层只由两种岩性(或具有阻抗差异的)介质互层组成，分别为高速层及低速层，且假设不同深度的相同岩性介质具有相同的速度和密度，而唯一不同的是单薄层厚度.即针对图 2模型，固定薄互层的总厚度为48 m；但两种互层的岩性层厚度分别从1 m逐渐增厚到16 m.如图 3模拟的地震反射波场显示(子波设置为主频50 Hz的Ricker子波)，这种韵律型的薄互层随着单层厚度的变化，反射特征发生了巨大的变化；对于薄层厚度很小的情况，如图中左半部分反射波形所示，薄互层除了顶和底还具有相对稳定的反射标志，互层中间的反射不具有与地质结构的一一对应性(Ellison et al., 2004；李国发等，2011)，呈现"白"反射现象，因此针对这种薄互层的反演已缺失了可利用的、可唯一对应的地震反射异常.

图 2 不同厚度薄层叠置形成的韵律型薄互层模型 Fig. 2 The rhythm thin inter-bed models constituted by the overlapped thin layers with variable thicknesses
图 3 图 2模型在不同上覆介质情况下的反射特征(自激自收记录，从左至右互层厚度为1~16 m) (a)上覆水层的薄互层反射波场；(b)上覆松散沉积的薄互层反射波场. Fig. 3 Reflection characteristics of the model illustrated in Fig. 2 with different overburden media (from left to right the thickness of single bed varies from 1 meter to 16 meters) (a) Reflections of thin inter-bed models with overlying water in zero offset; (b) Reflections of thin inter-bed models with overlying loose sediment in zero offset.
1.2 薄互层反演研究现状

目前，有以下两种方法实现这种薄互层的地震反演.一种方法是将高频先验信息加入到地震反演中，如宽带约束反演(Mansfield，1989；杨谦和李正文，1996)、随机反演(Sams et al., 1999；Francis，2005；Srivastava and Sen, 2010；王保丽等，2015)等.宽带约束反演综合利用地质及测井资料，建立高分辨率阻抗初始模型，将地震资料作为约束条件，利用随机迭代算法对初始模型进行修正，从而得到高分辨率反演结果.该方法对初始模型的依赖性强，容易陷入局部极小值；在井少的地区，反演结果不可靠.随机反演也称为地质统计学反演，其实质是基于地震资料约束测井信息的内插和外推，并利用随机模拟技术将不同尺度和方向上的数据相融合，反演结果分辨率较高，但多解性强、运算效率低，制约着该技术的应用.

另一种方法是拓宽地震频带降低薄层调谐作用，从而提高反演结果的分辨率.这种方法对初始模型依赖较小，在井少的地区也可以得到较为合理的高分辨率反演结果，一直是地震反演的重点研究领域.其中的谱反演技术(Puryear and Castagna, 2008；Chopra et al., 2009；刘万金等，2013)在频率域建立目标函数，充分利用地震资料中被压制的相对高频和低频信息，反演结果具有较高的分辨率，但也存在抗噪性差、可信度低、运算速度慢等问题.较为成熟的方法是分频反演，该技术把地震资料分成多个频段，使用回归法分别进行反演并将不同频段的反演结果累加，提高了反演分辨率(宿淑春和王晓华，2000).在分频反演的基础上，还有研究者将振幅与频率的关系作为独立信息引入叠后反演，获得了分辨率较高的反演结果(于建国等，2006)；有的研究了多井约束分频非线性地震波阻抗反演算法，获得了低、中、高全频段波阻抗剖面(崔炯成等，2007).有研究则进一步将AVA (amplitude versus angle)分析技术与分频段信息结合，将分频反演方法推广到叠前(张繁昌等，2008).分频反演虽然可以提高分辨率，但带通滤波产生的多频带数据体地质意义不明确，且存在高频假象，降低了反演的可信度.

谱分解技术在薄层地震反演中已得到广泛的应用，但受限于地震反射频带宽度的有限性，常用的谱分解方法还是难以实现对薄层的高精度反演.韩利等(2016)在此基础上借助稀疏反演复谱分解技术提高了谱分解刻画薄储层的时间分辨率.杜伟维等(2017)则通过井约束下的波形指示反演尝试对薄砂体进行刻画，但依然受限于砂体厚度要足够大且砂体的反射与波形一一对应的假设.近十几年，随着数学变换技术的发展，相继出现利用小波等不同尺度的数学变换力图实现不同尺度层序识别和反演的研究(Chakraborty and Okaya, 1995；高静怀等, 1997, 2006)，其实质也是将薄层反射按不同的频率分解以实现不同尺度薄层的识别(杜世通，2004；夏竹等，2005；赵军龙和李娜，2008；任金峰等，2013).也有研究曾对小波多尺度分频技术与贝叶斯反演算法联合做出了有意义的尝试(杨千里和吴国忱，2016；Li et al., 1996；黄捍东等，2011)，使得薄储层的识别能力有所提升.另有波形反演和地震瞬时属性等技术也曾在薄层问题上做过有益的探索(Sirgue and Pratt, 2004；高静怀等，2005).由于薄互层对于我国煤炭和油气资源勘探的意义和典型性，对于薄层的研究还是以国内的最为关注(赵继龙等，2014；韩利等，2016)，且尤以我国东部地区的油田应用与尝试为主(李占东等，2011；李雪英等，2012).但大量的实验证明薄互层的反演多解性极强，是目前勘探地震面临的主要问题(黄捍东等，2009；凌云等，2010).

1.3 基于Zoeppritz方程的反演

对于薄层或薄互层的反演出现上述问题的主要原因在于目前的地震反演技术仍是建立在单阻抗差界面反射的Zoeppritz方程及其各种近似公式基础上.Lu等(2015)和石瑛等(2015)虽然基于入射角道集和精确Zoeppritz方程进行了薄层反演的探索，反演精度比近似公式有所提高，但仍然未能解决薄层的反演问题.

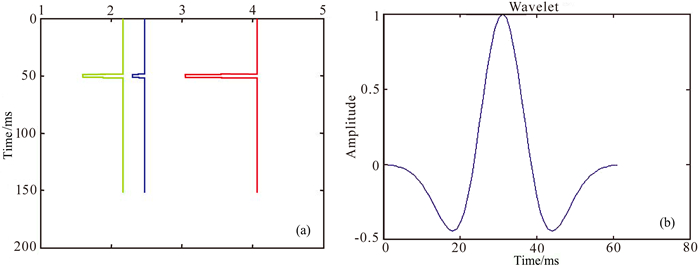
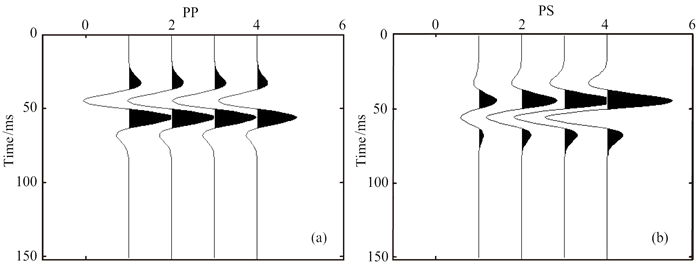
1.3.1 单薄层模型的Zoeppritz方程模拟与反演

即使对于如表 1和图 4a所示的简单的、水平层状煤层单薄层模型，其中绿色为横波速度，红色为纵波速度，单位km·s-1；蓝色为密度，单位g·cm-3；设子波为Ricker子波，如图 4b所示，采用Zoeppritz方程进行阻抗差界面反射的模拟可得如图 5所示的PP与PS波AVA道集.其中PS波道集进行了DIW(Dynamic Image Wrapping, 动态图像匹配)层位匹配压缩(蒋雪珍等，2017)使之压缩到PP波的走时时间轴上；即合成记录为入射角道集，纵坐标为纵波走时，横坐标为道编号，对应入射角为道号乘以10°，例如：道号4对应入射角40°.

表 1 单薄层模型参数 Table 1 The parameters of single thin layer model
图 4 (a) 薄煤层模型; (b) Ricker子波，主频30 Hz Fig. 4 (a) Thin coal seam model; (b) Ricker wave with 30 Hz dominant frequency
图 5 合成地震记录的AVA道集: (a) PP波的入射角道集；(b) PS波的入射角道集 Fig. 5 Synthetic seismogram, AVA gathers, of which the figure (a) and (b) represent PP-and PS-wave respectively

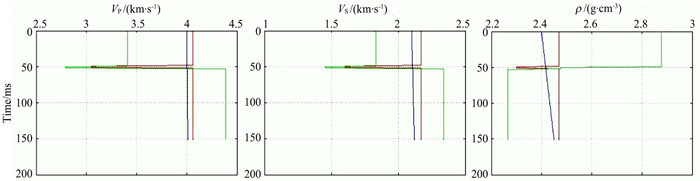
反演采用四种方法：PP波单独Aki方程反演、PS波单独周竹生方程反演(周竹生，1993)、PP波Zoeppritz方程反演、PP波+PS波Zoeppritz方程联合反演(Lu et al., 2015)，如图 6—图 9所示，其中初始模型为均匀线性模型.

图 6 PP波单独Aki方程反演结果 红色：真实模型，蓝色：初始模型，绿色：反演结果；以下各图颜色标示相同. Fig. 6 Inversion results of PP wave by Aki equation Red: real model, blue: initial model, green: inversion results; the colors of following figures is same.
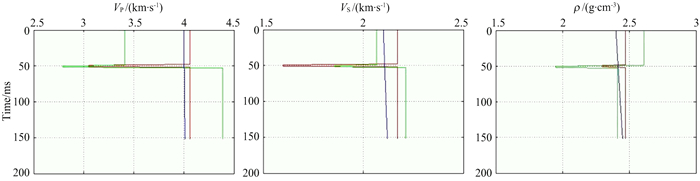
图 7 PS波单独周竹生方程反演结果 Fig. 7 Inversion results of PS wave by Zhou′s equation
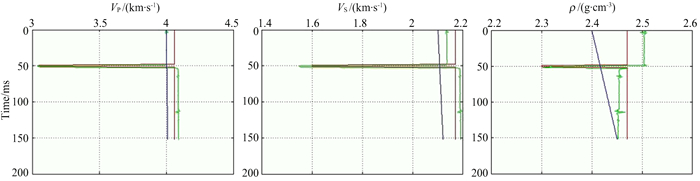
图 8 PP波单独Zoeppritz方程反演结果 Fig. 8 Inversion results of PP wave by accurate Zoeppritz equation
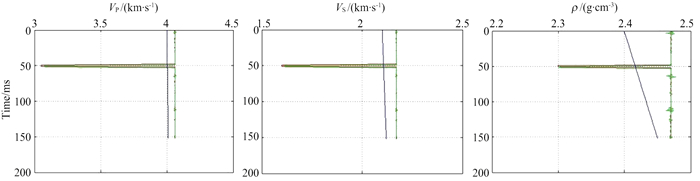
图 9 PP波+PS波Zoeppritz方程联合反演结果(红线与绿线几乎重合) Fig. 9 Joint inversion results of PP and PS waves by accurate Zoeppritz equation in which the red and green lines coincided

从上述反演结果对比可知，虽然四种方法对于煤层位置的反演都较为准确，但明显地，基于Zoeppritz方程的物性参数反演精度较高，且联合反演效果优于单纯波的反演.在三个物性反演图中，尽管初始模型用的是线性模型，Zoeppritz方程反演结果(图中以绿线显示)基本与真实模型重合；虽然存在局部的微弱扰动，但也可以证明当被反演的地震反射波场是用Zoeppritz方程模拟生成时，利用Zoeppritz方程反演可以获得较好的反演结果.

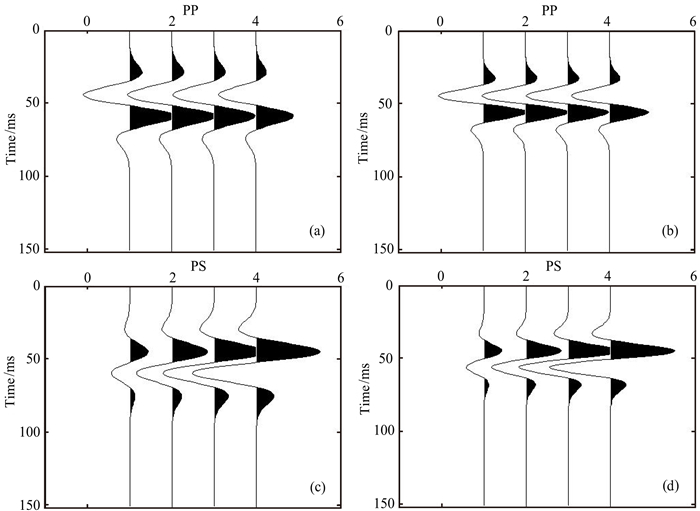
1.3.2 单薄层模型的薄层模拟与Zoeppritz反演

前面模型的模拟还是采用了单阻抗差界面反射系数公式进行的薄层模拟，反演也是基于Zoeppritz方程，非近似公式的使用明显取得了较高的反演精度.但实际地震记录是薄层反射，大量的正演模拟研究已经证明薄层与单阻抗差界面反射的差异.为此，对中间薄层采用反射率法模拟，可获得如图 10所示的PP波与PS波的薄层反射，显然，此模拟结果由于考虑了层间转换波、多次波和薄层反射的调谐效应，与单阻抗差界面反射模拟所显示的顶、底反射叠加存在明显的差异(张川等，2015).

图 10 薄层反射与阻抗差界面反射的模拟对比 (a) PP波薄层反射率模拟; (b) PP波薄层Zoeppritz一次反射模拟; (c) PS波薄层反射率模拟; (d) PS波薄层Zoeppritz一次反射模拟. Fig. 10 Simulation comparison of interfacial reflection between thin layer and impedance difference interface (a) PP wave simulated by thin layer reflectivity; (b) PP-wave simulated by Zoeppritz primary reflection; (c) PS wave simulated by thin layer reflectivity; (d) PS wave simulated by Zoeppritz primary reflection.

依然采用上述的反演方法和初始模型，只是待反演的数据发生了变化，反演结果如图 11—图 13所示.此例中不再进行单纯PP波的Zoeppritz方程反演试验.

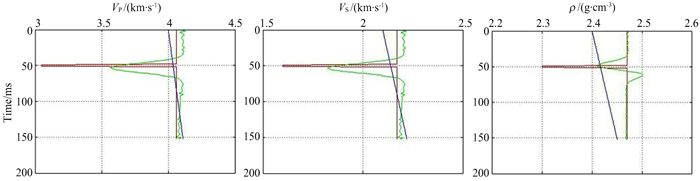
图 11 薄层反射率模拟的PP波单独Aki方程反演结果 Fig. 11 Inversion results of PP wave by Aki equation
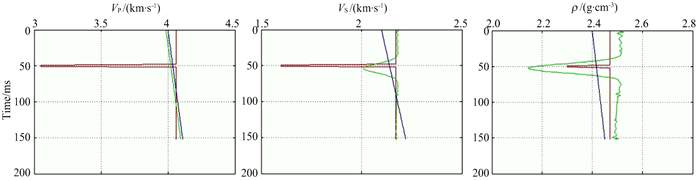
图 12 薄层反射率模拟的PS波单独周竹生方程反演结果 Fig. 12 Inversion results of PS wave by Zhou′s equation
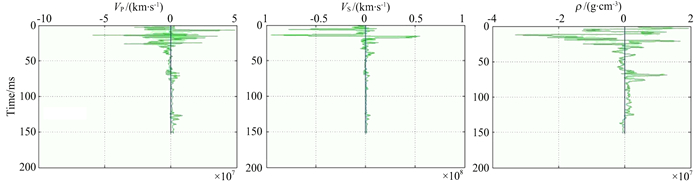
图 13 薄层反射率模拟的PP波+PS波联合Zoeppritz方程精确反演结果 Fig. 13 Joint inversion results of PP and PS waves by accurate Zoeppritz equation

显然对于薄层反演，简单的、近似线性的方法还可以得到一个具有很大误差的结果，而基于精确Zoeppritz方程的反演，涉及大型反演矩阵计算和迭代(Lu et al., 2015)，由于奇异值的存在，反演无法收敛，呈震荡状态.由此可以证明：对于薄层反射，现有的基于Zoeppritz方程及其各种近似的反演要么存在较大误差，要么反演结果不可信.

2 长波长假设下的薄互层VTI近似

长波长条件下薄互层可以近似为VTI介质，这一结论已被物理实验及数值模拟等大量的研究所证实.在薄互层的各向异性等效研究方面，Postma(1955)针对层状各向同性介质，利用界面上的应力、位移连续性，结合运动方程首先提出薄互层在满足一定波长与厚度比条件下可以近似为拟各向异性介质，即横向各向同性介质.Backus(1962)首次给出了薄互层长波长假设下各向异性近似的弹性参数计算方法.Melia和Carlson(1984)通过玻璃与树脂的叠层物理模型实验讨论了薄互层的拟各向异性效应与波长、层厚的关系.Helbig(1984a, 1984b)同时针对各向异性和波场传播，讨论薄互层等效各向异性公式的推导，在此基础上对P波和SH波进行了模拟分析；并从勘探地震面对的复杂薄互层目标论证了研究TI介质的意义.Zykov等(1984)通过针对冰与黏土制作的韵律型薄互层模型进行的超声物理实验，对比了拟各向异性近似理论值与实验观测值，并讨论了温度和含水饱和度对各向异性系数的影响.Lyakhovitskiy(1984)从大尺度地球动力学的角度讨论了薄互层所引起的拟各向异性存在的三个问题：1)薄互层各向异性假设成立依赖于薄层纵、横波速度比，2)SV型面波相速度交叉点与弹性参数的关系，3)与薄互层相比，讨论了不同类型TI介质弹性参数的计算方法差别.Levshin和Ratnikova(1984)则通过横向非均匀介质、薄互层与厚层模型超第一临界角的数值模拟对比说明了薄互层拟各向异性近似可能存在误导，大角度与横向非均匀性也会引起体波与面波的横波分离现象.Carcione等(1991)通过一维和二维数值模拟证明了薄互层的长波长假设不仅与波长与薄层厚度比有关，还与入射角和单薄层的物性差异有关.Kerner(1992)通过数值模拟分析讨论了随机分布薄互层的弹性波场各向异性特征，并指出存在波长与薄层厚度比值的中间过渡带，此时波场特征同时受各向异性和散射的影响.Foldstad和Schoenberg(1992)对于薄互层引起的TI各向异性效应进行了讨论，从数值上证明了当薄层厚度满足各向异性近似的条件时，再进一步降低层厚对薄互层的透射波场已经没有影响.Imhof(2003)通过声波测井曲线制作的薄互层模型与数值模拟讨论了薄互层非均匀性，包括薄互层的结构尺度对地震波反射、透射的影响，以及与频率的关系.而国内早期只有李跃等(1995)，徐果明等(1996)通过物理实验及数值模拟证明了薄互层拟各向异性的近似及传播矩阵法模拟的可行性.

2.1 拟各向异性近似存在的问题

针对图 3所示的N层薄层所形成的薄互层模型，Postma(1955)在薄层的厚度极薄假设条件下给出了各向异性介质的刚度系数计算公式.从上述理论近似可以看出，对于薄互层VTI近似，薄互层的反射已与频率无关，可以用6个物性参数有效地刻画具有N层结构的综合效应.毋庸置疑，这给薄互层的反演提供了一种可能的捷径.但这种近似是存在假设条件的.在该近似公式的推导过程中存在薄层厚度较小的假设，这一假设也是消除了薄层的频率依赖性的基本条件之一.

为了简化问题，我们只讨论由两层介质形成的韵律型薄互层，如图 2所示.为使得讨论问题具有广泛的代表性，设定两种互层结构，一种互层结构由阻抗差异很小的砂岩和泥岩组成，用以表征弱阻抗差的韵律型薄互层；另一种为煤层与泥岩互层的结构，用以表征具有强阻抗差的韵律型薄互层.通过改变薄互层中两种介质层厚度的比值以及互层的个数，在第一临界角之内，利用薄互层反射率法精确公式计算了不同频率情况下薄互层顶界面的反射系数和薄互层近似成VTI介质时的顶界面反射系数，并将两种方法计算的反射系数进行对比以分析VTI近似的误差.

2.2 厚度比值k对韵律型薄互层的VTI近似及其误差的影响

当薄互层为韵律层，并且两种岩性层厚度比值为1/k时，横向各向同性介质的5个弹性参数和密度可简化为：

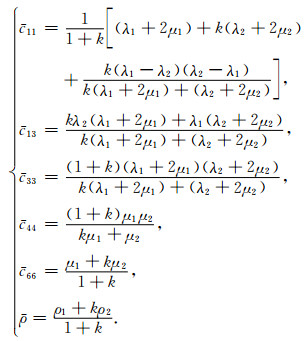
(1)

式中λ1, μ1, ρ1, λ2, μ2, ρ2分别为韵律型薄互层中两种介质的拉梅常数及密度；c11、c13、c33、c44、c66为等效VTI介质的5个刚性系数；符号"-"表示等效或近似.

对于一般的韵律型薄互层，根据VTI介质的Thomsen参数和刚性系数的关系(王赟等，2017)，并将vP2=(λ+2μ)/ρ和vS2=μ/ρ代入Thomsen参数中，可得到韵律型薄互层等效为VTI层时的速度和Thomsen参数的表达式：

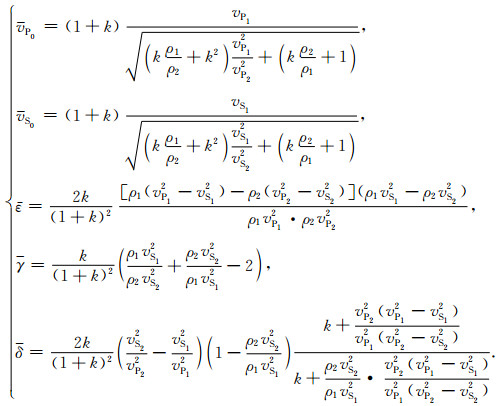
(2)

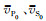
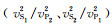
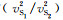
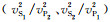
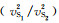
式中，分别表示等效介质在垂直方向的纵波和横波速度.由(2)式可以看出，ε与介质横纵波速度比的平方有关；γ与两种介质横波速度比值的平方有关；δ与介质横纵波速度比值的平方以及两种介质横波速度比值的平方都有关；且三参数ε、γ、δ与两种介质的密度比ρ1/ρ2有关，也与互层的厚度比k有关.进一步分析不难发现，当组成互层单元的两种岩性层厚度相同时，即k=1时，ε与γ取得最大值，各向异性增强；而当1/k趋近于0，即其中一层厚度远大于另一层厚度时，各向异性减弱.

2.3 阻抗差强弱对韵律层VTI近似各向异性强度的影响

对于两种典型的韵律型薄互层，设用砂岩和泥岩组成的韵律型薄互层的速度、密度参数如表 2所示；用煤和泥岩组成韵律型薄互层的速度、密度参数如表 3所示，显然煤与泥岩的组合形成了强阻抗差界面.通过改变砂岩与泥岩的厚度比值、煤与泥岩的厚度比值，计算相对应的Thomsen参数如表 4所示.对于这两种不同强、弱阻抗差韵律层等效的VTI介质参数，显然强阻抗差韵律层呈现明显的速度各向异性.

表 2 砂岩、泥岩物性参数 Table 2 Physical parameters of sandstone and mudstone
表 3 煤、泥岩物性参数 Table 3 Physical parameters of coal and mudstone
表 4 韵律型薄互层的等效Thomsen参数 Table 4 The equivalent Thomsen parameters of rhythmic thin inter-beds

由于Thomsen各向异性理论存在弱各向异性假设，因此有必要讨论不同各向异性发育程度时Thomsen理论计算所得相速度的精度.针对上述两种模型分析可知(李磊，2008)：当ε和δ都小于0.1时，Thomsen的速度比较精确；当ε－δ=0时，即使ε和δ都比较大，Thomsen的速度精确解和近似解也是相近的；当ε和δ增大(大于0.1)，尤其两者符号相反时，Thomsen速度的误差增大，误差与入射角有关.经(2)式简化后的韵律型薄互层的Thomsen参数中ε和δ的符号总是相反，因此Thomsen速度在ε或δ大于0.1且符号相反时是不精确的.

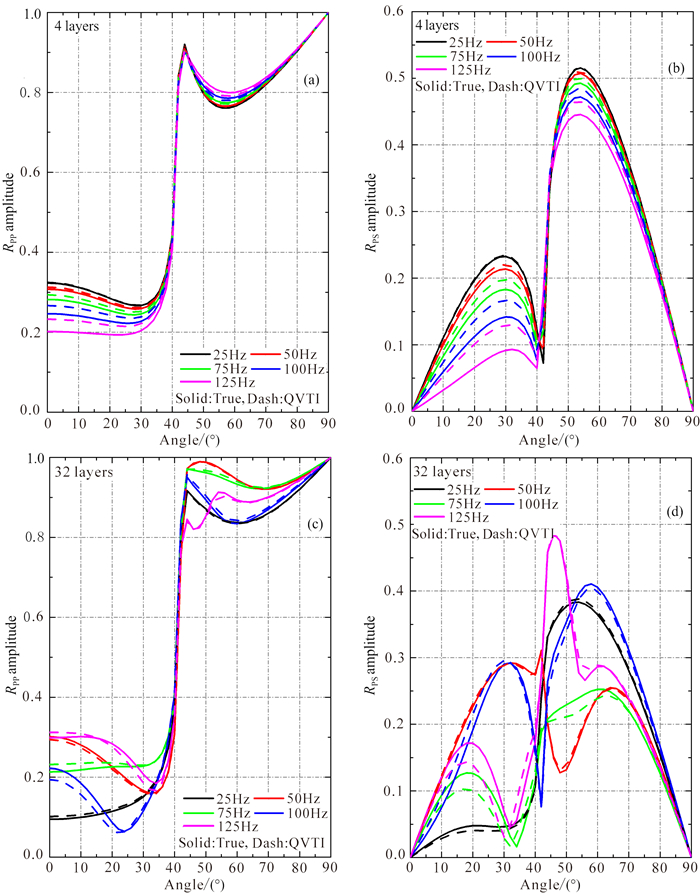
2.4 互层单元数量对薄互层反射系数的影响

以典型砂泥岩韵律型薄互层模型为例，设模型参数如表 5所示，两种岩性单薄层(例如，均为1 m)组合为一个互层单元，模拟并分析不同入射波频率(25、50、75、100、125 Hz)下1~25个互层单元情况下韵律层的精确及VTI近似反射PP、PS波系数.以2个和16个互层单元(分别对应4 m和32 m厚度韵律互层)为例对比不同入射波频率下薄互层反射系数精准解及VTI近似解，如图 14所示，图中不同颜色曲线表示入射P波频率的变化，实线为精确解，虚线为VTI(QVTI)近似解.总结发现：(1)当互层单元数量较少的情况下，不同频率薄互层反射系数随着入射角变化的趋势一致；互层单元增大到一定程度时，薄互层反射系数随着入射角变化的趋势将随频率的变化而变化，PS波反射曲线变化尤为明显；(2)互层单元数量较小的情况下，随着入射波频率的增加，VTI近似误差增大，该现象在PS波AVA曲线的极大值位置处表现尤为明显；相同入射频率下，PS波反射系数的近似精度高于PP波反射系数；(3)互层单元数量较大的情况下，对于PP波反射系数振幅而言，除125 Hz情况以外，VTI近似误差随着入射波频率的增加而增大；而PS波由于在不同频率下具有不同的变化趋势，VTI近似误差随着入射波频率变化较为复杂；总的近似精度特征表现为小角度范围内(入射角＜30°)，低频情况下的近似精度优于高频情况.即这种对比模拟可以证实，由于VTI近似不再依赖于频率，而实际薄互层的精确反射是频率依赖的，因此，薄互层的VTI近似存在近似条件，不能简单地搬用.

表 5 砂泥岩韵律型薄互层模型的弹性参数 Table 5 Elastic parameters of sandstone and mudstone rhythmic thin inter-beds
图 14 砂泥岩薄互层精准反射系数与VTI近似反射系数的对比 (a) 2个互层单元情况下反射PP波AVA曲线；(b) 2个互层单元情况下反射PS波AVA曲线；(c) 16个互层单元情况下反射PP波AVA曲线；(d) 16个互层单元情况下反射PS波AVA曲线. Fig. 14 Comparison of accurate reflection coefficient and quasi anisotropic approximate reflection coefficient of sandstone and mudstone thin inter-beds (a) The AVA curve of reflected PP wave of two inter layer units; (b) The AVA curve of reflected PS wave of two inter layer units; (c) The AVA curve of reflected PP wave of sixteen inter layer units; (d) The AVA curve of reflected PS wave of sixteen inter layer units.
3 薄互层拟各向异性反演的可能性

针对砂泥岩形成的薄互层，国际上常用N/G(net-to-gross，净砂厚度比)来描述地层的互层结构(Stovas et al., 2006；Vernik et al., 2002)，其中N表示砂岩累计厚度，G表示互层的总厚度；这主要是基于油气勘探目的层是寻找砂体的这个初衷展开的研究.对于煤系地层，由于我国的陆相沉积主要是煤与泥岩的交叠，也可以定义煤与煤系地层的厚度比来简化薄互层的反演.但若只是反演煤的总厚度离解决煤田地质中的诸多问题还有很大的距离(杨春等，2014).

3.1 P波各向异性分析

过去20多年，人们对HTI介质P波AVO属性进行了大量的研究并取得一定的进步.首先Rüger和Tsvankin(1995, 1997)提出用P波方位AVO分析方法来检测裂缝；进一步推广在弱各向异性介质中利用线性简化的PP波反射系数来表述各向异性AVO特征(Rüger，1998).Ramos和Davis(1997)也曾尝试在美国Cedar Hill煤层气田应用AVO方法检测煤层裂隙，但该方法并未考虑煤层作为薄层时反射调谐效应的存在.Pérez等(1999)成功地将P波方位AVO分析用于检测裂缝之中.后来Rüger(2002)则进一步给出了HTI介质PP波反射系数近似方程；Hall和Kendall(2003)在此基础上用海底三分量地震的P波AVO分析预测了天然裂缝的特征；国内杨勤勇等(2006)通过物理实验证实了裂缝导致纵波方位各向异性的存在，并将其应用在检测裂缝的工作中.尽管业界已认识到Rüger的这个公式只适用于描述厚层介质的界面反射系数，对于薄层不一定适用，但人们现在还没有意识到这个问题的严重性.

而对于煤系地层，煤层含裂隙后将进一步复杂化薄互层结构的介质模型，虽可能假设为VTI背景下的垂直裂缝的存在，但此时需要用OA(Orthorhombic Anisotropy，正交各向异性)介质进行近似，单纯的TI介质反演是无法逼近真实解的.由于早期研究(Postma，1955；Backus，1962)发现横向各向同性的单薄层叠置组成的薄互层可以近似为厚层的VTI介质，从而使得OA介质的研究可以放到厚层的VTI介质背景下去讨论，并把含裂缝的VTI单薄层的反问题作为一个特殊目的层进行讨论.

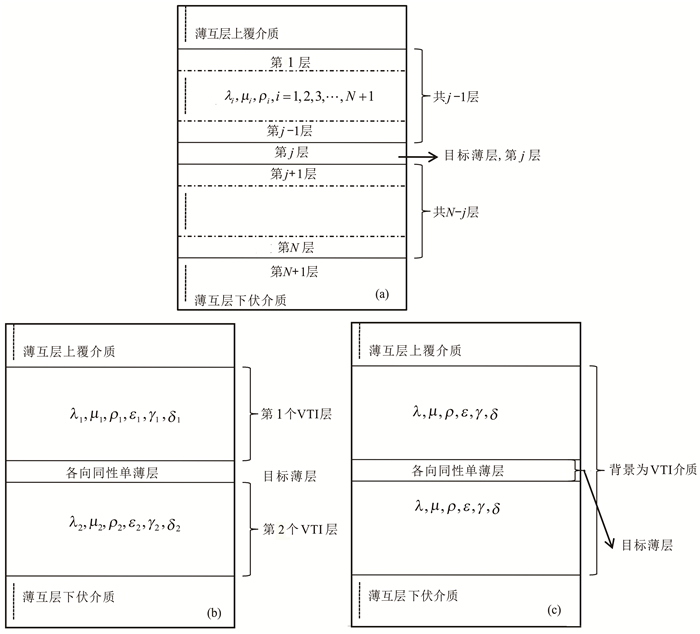
3.2 VTI近似下的单薄层反演策略

对于图 15a所示的具有N层结构的薄互层，无论是深部地球物理研究还是油气勘探，我们并不是对所有的地层均感兴趣；因此可假设第i层是我们待反演的目标单薄层.则可以将薄互层的反演问题简化为如图 15b所示的近似过程，即实际的薄互层反演转化为两层厚层VTI介质夹持的单一各向同性(或各向异性，当考虑每一个单薄层同时又是VTI介质情况)薄层的反演问题，或更进一步简化为图 15c所示的厚层、VTI背景下的单一薄层反演.这一反演当然不仅限于薄层厚度的反演，更多的是薄层的物性和含裂缝隙、流体等更精细的特征.即中间的目标薄层可能是各向同性的，也可能是各向异性的，甚至是双相介质的.但总之，薄互层的反演有可能通过VTI近似简化为VTI厚层和单薄层的反演，因此，单薄层的反演是基础.

图 15 薄互层反演的简化与转化策略 Fig. 15 Simplification and transformation of inversion of thin layered media
3.3 单薄层厚度的反演

单薄层的反演首先涉及到厚度的反演，薄层厚度的预测对于勘探地震也是首要的目标.领域早就关注了薄层厚度的预测问题，且早期的研究主要利用叠后地震信息，讨论垂直入射下薄层的振幅响应.Widess(1973)认为在薄层厚度等于λd/8(λd为薄层反射P波对应的主频)的情况下，反射波形显示为入射子波的一阶导数形态；且反射子波振幅是薄层厚度的函数的线性极限.在假设薄层顶、底介质具有相同的声速与密度、震源子波可近似为正弦子波的条件下，反射子波的波峰值是薄层厚度和反射系数的函数.Koefoed和de Voogd(1980)认为在不考虑透射损失和多次波的条件下，层厚度的振幅响应若偏离线性函数小于10%时，可以将该层定义为薄层.Kallweit和Wood(1982)进一步指出，Ricker提出的零曲率标准(Ricker, 1953)不仅能够用来定义振幅相同、极性相反情况下的薄层，还能够定义振幅相同、极性相同的薄层；在弱反射和薄层厚度小于八分之一波长λ的条件下振幅响应是薄层厚度的函数；de Voogd和den Rooijen(1983)也获得了类似的结论.

尽管Chung和Lawton(1995a)给出基于正弦近似的Widess方法的扩展公式：

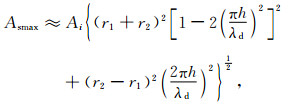
(3)

式中Asmax表示正弦近似下的地震反射波振幅，Ai表示地震子波的振幅，h表示薄层厚度，λd表示主频对应的纵波主波长，r1和r2分别表示顶、底界面的反射系数振幅.此公式适用于任意薄层模型.和基于Ricker零相位子波的表达式(Chung and Lawton, 1995b)相比，

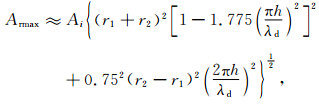
(4)

公式中Armax表示Ricker子波近似下的地震反射波振幅，其他参数与正弦近似中参数定义相同.对于任意薄层反射，在难以保证薄层反射为正弦或零相位子波的情况下，薄层厚度的反演依然是个难题.尽管基于分频扫描的谱分解方法一直在尝试解决这一问题(孙鲁平等，2009；苑春方等，2014)，但有限的地震反射频率带宽是难以获得薄层厚度准确结果的根本制约因素，这也是至今薄层厚度的预测仍不能满足油气和煤田勘探开发需要的主要原因之一(Yang et al., 2016).

3.4 单薄层的AVO属性分析

由于Aki给出了单阻抗差界面反射的简化AVO公式，从而使得AVO分析成为叠前地震反演的主要工具.按照这一思路，我们也可以把薄层的PP波反射近似简化为

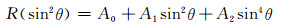
(5)

的形式(Yang et al., 2017)，其中A0为截距，表示垂直入射情况下PP波反射，A1项为AVO曲线线性变化段的斜率，表示薄层反射随入射角近似线性变化的快慢，而A2则表示非线性变化段的加速度.因为此时Ai(i=0，1，2)参数是关于频率的复函数，显然，对于薄层反射，常规AVO分析技术不能搬用；而且，我们首先还是必须解决垂直入射情况下的单薄层反演问题.

在Yang等(2017)给出的单薄层PP波反射解析表达近似式的基础上，对于垂直入射情况下的单薄层的反射，可以获得如下所示的反射系数能谱公式：

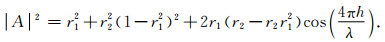
(6)

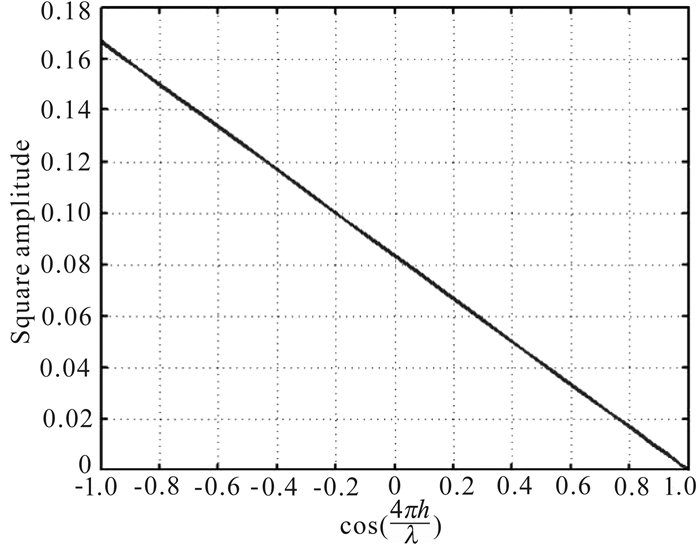
根据单薄层的反射能谱的变化规律(如图 16)，总能找到两个特征点，例如两轴的截距或斜率，解析获得单薄层顶、底界面的反射系数.此时获得的四个解分别对应顶、底界面反射系数极性相同或相反四个模型的情况，即阻抗递增或递减，高阻抗或低阻抗薄层四种情况.

图 16 振幅平方谱随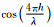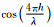的变化 Fig. 16 Amplitude squared spectrum versus

在Gardner公式的约束下，根据求得的薄层顶、底界面的反射系数，进一步可以获得单薄层相对于围岩的阻抗或速度差异，且可以证明这一计算方法的误差在10%以内.但显然这两个特征点的获得需要宽频带的地震数据.地震频带的有限性，使得分频讨论获得图 16所示的特征曲线成为难点，因此最基本的问题又回到了薄层厚度与波长关系的讨论上.可见，对于单薄层反演，薄层厚度的确定是基础；也是进行更进一步的薄层频变AVO分析和反演的基础.

4 结论与讨论

在薄层反演不同于厚层反演讨论的基础上，本文围绕着薄互层的反演首先从数值实例的角度论证了现行反演理论、方法技术面对薄层问题时的不适应性，重点讨论了薄互层复杂的反射特征及其反演所面临的诸多问题.通过国内外对于薄互层问题研究现状的分析，以及本文所依次展开论述的内容，不难获得以下认识：

(1) 在有限频带的地震反射信息基础上，即使PP波和PS波联合，力图反演薄互层的完整结构和物性显然也是严重病态的反问题.薄互层在长波长假设下的VTI近似是薄互层实现粗线条反演的可能途径之一.

(2) 长波长假设下薄互层的VTI近似是有条件的，不仅在于公式推导过程中所明确的简单的单层极薄的假设，从而消除了薄层反射的频率依赖性；大量的研究表明，薄互层的结构、互层单元的物性差异、互层单元的厚度比都影响着各向异性参数的大小，也影响着VTI近似的精度；VTI近似精度具有频率依赖性，表征为频率越低、互层单元越薄，VTI近似精度越高.

(3) 在VTI近似的理论框架下，薄互层的反演问题可以化简为厚层介质背景下单薄层的反演，从而使得3N个弹性参数的反演问题化简为5个弹性参数反演，及其在此背景下的单薄层3个参数的反演，使得薄互层的反演成为可能.

回顾单薄层的反演发展历程我们不难发现，即使对于薄层厚度的反演，现有的理论和方法尚不完备，非正弦和非零相位Ricker子波情况下薄层反射波振幅与厚度的关系尚需进一步的拓展；针对叠后地震特征点法所展示的可能实现薄层物性差异反演也需要宽频带的地震数据支撑.因此，薄互层的反演问题回归到VTI介质反演和单薄层厚度、物性反演这一通常认为很简单的起点上，其中薄层反演的频率依赖性是需要重点开发的方向之一.

当然，若考虑薄互层或单薄层中还发育垂直裂缝，或考虑裂缝和孔隙的双相或多相介质情况时，反演将变得更加复杂.但显然，VTI假设下的厚层与单薄层的反演是基础，是实现更复杂薄互层结构反演的出发点；且弹性波联合反演应该是可行的、降低多解性、提高反演精度的有力工具.

致谢

谨此祝贺姚振兴先生从事地球物理教学科研工作60周年.感谢与大庆油田物探院王建民总工关于薄互层反演问题的探讨给了我们很大的启发.

参考文献
Backus G E. 1962. Long-wave elastic anisotropy produced by horizontal layering. Journal of Geophysical Research, 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427
Brekhovskikh L M. 1960. Waves in Layered Media. Beijing: Academic Press.
Carcione J M, Kosloff D, Behle A. 1991. Long-wave anisotropy in stratified media:a numerical test. Geophysics, 56(2): 245-254. DOI:10.1190/1.1443037
Carcione J M. 2001. Wave Fields in Real Media:Wave Propagation in Anisotropic, Anelastic and Porous Media. Amsterdam: Pergamon.
Chakraborty A, Okaya D. 1995. Frequency-time decomposition of seismic data using wavelet-based methods. Geophysics, 60(6): 1906-1916. DOI:10.1190/1.1443922
Chen J S, Chang X. 1987. The seismic response of thin reservoir and its quantitative interpretation. Oil Geophysical Prospecting, 22(4): 386-399.
Chen T S, Liu Y. 2006. Multi-component AVO response of thin beds based on reflectance spectrum theory. Applied Geophysics, 3(1): 27-36. DOI:10.1007/s11770-006-0004-5
Cheng L Z, Yang C, Ye S G, et al. 2014. Analysis of two typical thin bed elastic parameter prediction using multi-wave joint inversion. Coal & Geology Exploration, 42(1): 68-71.
Chopra S, Castagna J, Xu Y. 2009. Thin-bed reflectivity inversion and some applications. First Break, 27: 17-24.
Chung H M, Lawton D C. 1995a. Frequency characteristics of seismic reflections from thin beds. Canadian Journal of Exploration Geophysics, 31(1-2): 32-37.
Chung H M, Lawton D C. 1995b. Amplitude responses of thin beds:Sinusoidal approximation versus Ricker approximation. Geophysics, 60(1): 223-230. DOI:10.1190/1.1443750
Cui J C, Wu M, Li W X, et al. 2007. Nonlinear high-resolution impedance inversion method and its application. Geophysical Prospecting for Petroleum, 46(1): 1-12.
de Voogd N, den Rooijen H. 1983. Thin-layer response and spectral bandwidth. Geophysics, 48(1): 12-18. DOI:10.1190/1.1441400
Du S T. 2004. Seismic data interpretation of high resolution under sequence frame. Petroleum Geophysics, 2(4): 66-77.
Du W W, Jin Z J, Di Y X. 2017. The application of seismic waveform indicator inversion and characteristic parameter simulation to thin reservoir prediction. Chinese Journal of Engineering Geophysics, 14(1): 56-61.
Ellison S J, Imhof M G, Çoruh C, et al. 2004. Modeling offset-dependent reflectivity for time-lapse monitoring of water-flood production in thin-layered reservoirs. Geophysics, 69(1): 25-36. DOI:10.1190/1.1649372
Foldstad P G, Schoenberg M. 1992. Low-frequency propagation through fine layering. //62nd Annual International Meeting, SEG Expanded Abstracts. Houston: SEG, 1279-1281.
Francis A. 2005. Limitations of deterministic and advantages of stochastic seismic inversion. CSEG Recorder, 30(2): 5-11.
Gao J H, Wang W B, Zhu G M. 1997. Wavelet transform and instantaneous attributes analysis. Chinese J. Geophys. (Acta Geophysica Sinica), 40(6): 821-832.
Gao J H, Chen F, Chen S M. 2005. Using seismic instantaneous attributes to analyze thin interbeds. Coal Geology & Exploration, 33(3): 67-71.
Gao J H, Wan T, Chen W C, et al. 2006. Three parameter wavelet and its applications to seismic data processing. Chinese J. Geophys., 49(6): 1802-1812.
Gochioco L M. 1991. Tuning effect and interference reflections from thin beds and coal seams. Geophysics, 56(8): 1288-1295. DOI:10.1190/1.1443151
Gochioco L M. 1992. Modeling studies of interference reflections in thin-layered media bounded by coal seams. Geophysics, 57(9): 1209-1216. DOI:10.1190/1.1443336
Guo Z Q, Liu C, Li X Y, et al. 2016. Modeling and analysis of frequency-dependent AVO responses in inelastic stratified media. Chinese J. Geophys., 59(2): 664-672. DOI:10.6038/cjg20160223
Hall S A, Kendall J. 2003. Fracture characterization at Valhall:application of P-wave amplitude variation with offset and azimuth (AVOA) analysis to a 3D ocean-bottom data set. Geophysics, 68(4): 1150-1160. DOI:10.1190/1.1598107
Han L, Liu C C, Zhang Y M, et al. 2016. Seismic complex spectral decomposition and its application on hydrocarbon detection. Chinese J. Geophys., 59(3): 1095-1101. DOI:10.6038/cjg20160329
Helbig K. 1984a. Anisotropy and dispersion in periodically layered media. Geophysics, 49(4): 364-373. DOI:10.1190/1.1441672
Helbig K. 1984b. Transverse isotropy in exploration seismics. Geophys. J. R. astr. Soc., 76(1): 79-88. DOI:10.1111/j.1365-246X.1984.tb05024.x
Huang H D, Zhang R W, Zhao D, et al. 2009. Seismic inversion and detection of thin-layer gas-bearing sandstone by attributes coupling. Oil Geophysical Prospecting, 44(2): 185-189.
Huang H D, Zhao D, Ren D Z, et al. 2011. A thin bed inversion method based on Bayes theory. Oil Geophysical Prospecting, 46(6): 919-924.
Imhof M G. 2003. Scale dependence of reflection and transmission coefficients. Geophysics, 68(1): 322-336. DOI:10.1190/1.1543218
Jiang X Z, Lu J, Wang Y. 2017. PP-and PS-waves matching directly based on dynamic image warping. Chinese J. Geophys., 60(3): 1106-1117. DOI:10.6038/cjg20170322
Kallweit R S, Wood L C. 1982. The limits of resolution of zero-phase wavelets. Geophysics, 47(7): 1035-1046. DOI:10.1190/1.1441367
Kennett B L N. 1974. Reflections, rays, and reverberations. Bulletin of the Seismological Society of America, 64(6): 1685-1696.
Kennett B L N, Kerry N J. 1979. Seismic waves in a stratified half space. Geophys. J. R. astr. Soc., 57(3): 557-583. DOI:10.1111/gji.1979.57.issue-3
Kerner C. 1992. Anisotropy in sedimentary rocks modeled as random media. Geophysics, 57(4): 564-576. DOI:10.1190/1.1443270
Koefoed O, de Voogd N. 1980. The linear properties of thin layers, with an application to synthetic seismograms over coal seams. Geophysics, 45(8): 1254-1268. DOI:10.1190/1.1441122
Krey T, Helbig K. 1956. A theorem concerning anisotropy of stratified media and its significance for reflection seismics. Geophysical Prospecting, 4(3): 294-302. DOI:10.1111/gpr.1956.4.issue-3
Levshin A, Ratnikova L. 1984. Apparent anisotropy in inhomogeneous media. Geophys. J. R. astr. Soc., 76(1): 65-69. DOI:10.1111/j.1365-246X.1984.tb05022.x
Li G F, Yue Y, Xiong J L, et al. 2011. Experimental study on seismic amplitude attribute of thin interbed based on 3D model. Oil Geophysical Prospecting, 46(1): 115-120.
Li L. 2008. Applicability of Thomsen approximate formula in transversely isotropic media. Geophysical Prospecting for Petroleum, 47(2): 116-122.
Li X G, Sacchi M D, Ulrych T J. 1996. Wavelet transform inversion with prior scale information. Geophysics, 61(5): 1379-1385. DOI:10.1190/1.1444061
Li X Y, Chen S M, Wang J M, et al. 2012. Forward modeling studies on the time-frequency characteristics of thin layers. Chinese J. Geophys., 55(10): 3410-3419. DOI:10.6038/j.issn.0001-5733.2012.10.024
Li Y, Xu G M, Shi J X, et al. 1995. Experiment in equivalent anisotropy of thin interbedded medium. Oil Geophysical Prospecting, 30(4): 513-517.
Li Z D, Zhao W, Li Y, et al. 2011. Feasibility study and application of development seismic inversion. Oil & Gas Geology, 32(54): 797-806.
Ling Y, Guo X Y, Gao J, et al. 2010. The technical challenges on the development trend of reservoir geophysics. Geophysical Prospecting for Petroleum, 49(4): 319-335.
Liu W J, Zhou H, Yuan S Y, et al. 2013. Applications of spectral inversion in seismic attribute interpretation. Oil Geophysical Prospecting, 48(3): 423-428.
Liu Y B, Schmitt D R. 2003. Amplitude and AVO responses of a single thin bed. Geophysics, 68(4): 1161-1168. DOI:10.1190/1.1598108
Lu J, Yang Z, Wang Y, et al. 2015. Joint PP and PS AVA seismic inversion using exact Zoeppritz equations. Geophysics, 80(5): R239-R250. DOI:10.1190/geo2014-0490.1
Lyakhovitskiy F M. 1984. Transverse isotropy of thinly layered media. Geophys. J. R. astr. Soc.,, 76(1): 71-77. DOI:10.1111/j.1365-246X.1984.tb05023.x
Mansfield G. 1989. Interactive broadband constrained inversion. Exploration Geophysics, 20(2): 253-255. DOI:10.1071/EG989253
Meissner R, Meixner E. 1969. Deformation of seismic wavelets by thin layers and layered boundaries. Geophysical Prospecting, 17(1): 1-27. DOI:10.1111/gpr.1969.17.issue-1
Melia P J, Carlson R L. 1984. An experimental test of P-wave anisotropy in stratified media. Geophysics, 49(4): 374-378. DOI:10.1190/1.1441673
Pan W Y, Innanen K A. 2013. AVO/AVF analysis of thin beds in elastic media. //SEG Technical Program Expanded Abstracts 2013. SEG, 373-377.
Pérez M A, Gibson R L, Toksöz M N. 1999. Detection of fracture orientation using azimuthal variation of P-wave AVO responses. Geophysics, 64(4): 1253-1265. DOI:10.1190/1.1444632
Postma G W. 1955. Wave propagation in a stratified medium. Geophysics, 20(4): 780-806. DOI:10.1190/1.1438187
Puryear C I, Castagna J P. 2008. Layer-thickness determination and stratigraphic interpretation using spectral inversion:theory and application. Geophysics, 73(2): R37-R48. DOI:10.1190/1.2838274
Ramos A C B, Davis T L. 1997. 3-D AVO analysis and modeling applied to fracture detection in coalbed methane reservoirs. Geophysics, 62(6): 1683-1695. DOI:10.1190/1.1444268
Ren J F, Liao Y T, Sun M, et al. 2013. A method for quantitative division of sequence stratigraphy with high-resolution based on wavelet transform and its application. Progress in Geophysics, 28(5): 2651-2658. DOI:10.6038/pg20130546
Ricker N. 1953. Wavelet contraction, wavelet expansion, and the control of seismic resolution. Geophysics, 18(4): 769-792. DOI:10.1190/1.1437927
Rüger A, Tsvankin I. 1995. Azimuthal variation of AVO response for fractured reservoirs. //65th Annual International Meeting, SEG, Expanded Abstracts. SEG, 1103-1106.
Rüger A, Tsvankin I. 1997. Using AVO for fracture detection:analytic basis and practical solutions. The Leading Edge, 16(10): 1429-1434. DOI:10.1190/1.1437466
Rüger A. 1998. Variation of P-wave reflectivity with offset and azimuth in anisotropic media. Geophysics, 63(3): 935-947. DOI:10.1190/1.1444405
Rüger A. 2002. Reflection coefficients and azimuthal AVO analysis in anisotropic media. Society of Exploration Geophysicists, No.10.
Sams M S, Atkins D, Said N, et al. 1999. Stochastic inversion for high resolution reservoir characterisation in the Central Sumatra Basin. //SPE Asia Pacific Improved Oil Recovery Conference. Kuala Lumpur, Malaysia: Society of Petroleum Engineers, 257-260.
Sayers C. 1998. Long-wave seismic anisotropy of heterogeneous reservoirs. Geophys. J. Int., 132(3): 667-673. DOI:10.1046/j.1365-246X.1998.00456.x
Sidler R, Holliger K. 2010. Seismic reflectivity of the sediment-covered seafloor:effects of velocity gradients and fine-scale layering. Geophys. J. Int., 181(1): 521-531. DOI:10.1111/gji.2010.181.issue-1
Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies. Geophysics, 69(1): 231-248. DOI:10.1190/1.1649391
Shi Y, Lu J, Yang Z, et al. 2015. Joint PP-and PS-wave inversion of gathers with average incident angles. Chinese J. Geophys., 58(12): 4617-4627.
Srivastava R P, Sen M K. 2010. Stochastic inversion of prestack seismic data using fractal-based initial models. Geophysics, 75(3): R47-R59. DOI:10.1190/1.3379322
Stovas A, Landro M, Avseth P. 2006. AVO attribute inversion for finely layered reservoirs. Geophysics, 71(3): C25-C36. DOI:10.1190/1.2197487
Su S C, Wang X H. 2000. Development of dividing frequency impedance inversion and its application. Journal of the University of Petroleum, China (Edition of Natural Science), 24(1): 85-87.
Sun L P, Zheng X D, Li J S, et al. 2009. Thin-bed thickness calculation formula and its approximation using peak frequency. Applied Geophysics, 6(3): 234-240. DOI:10.1007/s11770-009-0033-y
Sun S H, Niu Y L. 1991. The application of AVO technique under the condition of thin interbed series. Chinese J. Geophys. (Acta Geophysica Sinica), 34(1): 99-106.
Treitel S, Robinson E A. 1966. Seismic wave propagation in layered media in terms of communication theory. Geophysics, 31(1): 17-32. DOI:10.1190/1.1439729
Tang W B. 1987. On resolution of a thin seam in reflection seismic exploration. Chinese J. Geophys. (Acta Geophysica Sinica), 30(6): 641-652.
Vernik L, Fisher D, Bahret S. 2002. Estimation of net-to-gross from P and S impedance in deep water turbidite. The Leading Edge, 21(4): 380-387. DOI:10.1190/1.1471602
Wang B L, Yin X Y, Ding L X, et al. 2015. Study of fast stochastic inversion based on FFT-MA spectrum simulation. Chinese J. Geophys., 58(2): 664-673. DOI:10.6038/cjg20150227
Wang P, Jin Z K, Li G F, et al. 2007. Detection of thin-layer biodastic limestone based on seismic attributes. Geophysical Prospecting for Petroleum, 46(4): 390-393.
Wang Y, Liu Y Y, Zhang M G. 2017. Seismic Equivalent Medium Theory for Fractured Anisotropy. Beijing: Science Press: 49-52.
Waters K H. 1983. Reflection Seismology (in Chinese). Xu Y, Wu C X Trans. Beijing: Petroleum Industry Press.
Widess M B. 1973. How thin is a thin bed?. Geophysics, 38(6): 1176-1180. DOI:10.1190/1.1440403
Xia Z, Liu C Y, Wei W B, et al. 2005. Frequency attributes characters of seismic traces in time domain and division of stratigraphic sequence. Oil Geophysical Prospecting, 40(5): 550-560.
Xu G M, Li Y, Ni S D, et al. 1996. Research on equivalent azimuthal isotropy of thin interbed medium. Oil Geophysical Prospecting, 31(6): 792-805.
Xu Y. 1981. Seismic model of layer structure and its theory. Geophysical Prospecting for Petroleum, 20(1): 1-16.
Yang C, Wang Y, Yang D Y. 2014. Discussion on seismic recognition of deformed coal. Journal of China Coal Society, 39(S2): 465-470.
Yang C, Wang Y, Wang Y H. 2016. Reflection and transmission coefficients of a thin bed. Geophysics, 81(5): N31-N39. DOI:10.1190/geo2015-0360.1
Yang C, Wang Y, Lu J. 2017. Weak impedance difference approximations of thin-bed PP-wave reflection responses. J. Geophys. Eng., 14(4): 1010-1019. DOI:10.1088/1742-2140/aa6dd8
Yang C Y, Yang C, Chen S Q, et al. 2017. An analysis of seismic responses in thin anisotropic-viscoelastic reservoirs. Chinese J. Geophys., 60(1): 316-326. DOI:10.6038/cjg20170126
Yang Q, Li Z W. 1996. Broadband constrained inversion of data and its application. Geophysical Prospecting for Petroleum, 35(4): 37-42.
Yang Q L, Wu G C. 2016. Multi-scale seismic inversion method based on Bayesian theory. Chinese J. Geophys., 31(3): 1246-1256. DOI:10.6038/pg20160343
Yang Q Y, Zhao Q, Wang S X, et al. 2006. P-wave azimuthal anisotropy and its application in detection of fractures. Geophysical Prospecting for Petroleum, 45(2): 177-181.
Yu J G, Han W G, Liu L H. 2006. Frequency-divided inversion and application. Oil Geophysical Prospecting, 41(2): 193-197.
Yuan C F, Peng S P, Tang S Q, et al. 2014. Improvement of function between thin-bed composite amplitude and its thickness. Journal of China Coal Society, 39(10): 2083-2086.
Yuan Z L, Yang B, Wang J G. 1996. Study and application of the forward modeling of thin-layer and thin-interlay in the domains of time and frequency. Geophysical Prospecting for Petroleum, 35(3): 14-20.
Zhang C, Yang C, Wang Y. 2015. Discussion on elastic reflection and transmission coefficients of thin-bed and single interface models. Coal Geology & Exploration, 43(2): 86-90.
Zhang F C, Liu J, Yin X Y, et al. 2008. Modified Cauchy-constrained seismic blind deconvolution. Oil Geophysical Prospecting, 43(4): 391-396.
Zhang Y G, Wang Y, Yin J J. 2010. Single point high density seismic data processing analysis and initial evaluation. OGP, 45(2): 201-207.
Zhang Z J, He J D. 1990. Apparent anisotropy produced by the coupling of N thin-layered media. Journal of Changchun University of Earth Science, 20(2): 223-231.
Zhao J L, Li N. 2008. Application of wavelet transform to high resolution sequence analysis. Progress in Geophysics, 23(4): 1230-1235.
Zhao J L, Xiong R, Chen G, et al. 2014. Seismic inversion of frequency divisions reconstruction and its application thin interbedded sand reservoir prediction. Journal of Southwest Petroleum University (Science & Technology Edition)(in Chinese), 36(4): 47-54.
Zhou Z S. 1993. AVO analysis of P-SV and SH waves. OGP, 28(4): 430-438.
Zykov Y D, Lyakhovitskiy F M, Chervinskaya O P. 1984. Experimental investigation of transverse isotropy in ice/clay thin-layered periodic models. Geophys. J. R. astr. Soc., 76(1): 269-272. DOI:10.1111/j.1365-246X.1984.tb05044.x
布列霍夫斯基赫. 1960. 分层介质中的波. 杨训仁译. 北京: 科学出版社.
陈继松, 常旭. 1987. 储油薄层的地震响应及定量解释. 石油地球物理勘探, 22(4): 386–399.
崔炯成, 吴眉, 李维新, 等. 2007. 高分辨率非线性地震波阻抗反演方法和应用. 石油物探, 46(1): 1–12.
杜世通. 2004. 层序框架下的地震高分辨率资料解释. 油气地球物理, 2(4): 66–77.
杜伟维, 金兆军, 邸永香. 2017. 地震波形指示反演及特征参数模拟在薄储层预测中的应用. 工程地球物理学报, 14(1): 56–61.
高静怀, 王文秉, 朱光明. 1997. 小波变换与信号瞬时特征分析. 地球物理学报, 40(6): 821–832.
高静怀, 陈凤, 陈树民. 2005. 利用地震瞬时谱属性进行薄互层分析. 煤田地质与勘探, 33(3): 67–71.
高静怀, 万涛, 陈文超, 等. 2006. 三参数小波及其在地震资料分析中的应用. 地球物理学报, 49(6): 1802–1812.
郭智奇, 刘财, 李向阳, 等. 2016. 非弹性层状介质地震波频变AVO响应模拟及分析. 地球物理学报, 59(2): 664–672.
韩利, 刘春成, 张益明, 等. 2016. 地震复谱分解技术及其在烃类检测中的应用. 地球物理学报, 59(3): 1095–1101.
黄捍东, 张如伟, 赵迪, 等. 2009. 地震反演与属性耦合检测薄层含气砂岩. 石油地球物理勘探, 44(2): 185–189.
黄捍东, 赵迪, 任敦占, 等. 2011. 基于贝叶斯理论的薄层反演方法. 石油地球物理勘探, 46(6): 919–924.
蒋雪珍, 芦俊, 王赟. 2017. 基于动态图像变形的PP与PS波层位直接匹配. 地球物理学报, 60(3): 1106–1117.
李国发, 岳英, 熊金良, 等. 2011. 基于三维模型的薄互层振幅属性实验研究. 石油地球物理勘探, 46(1): 115–120.
李磊. 2008. 横向各向同性介质Thomsen近似公式的适用范围. 石油物探, 47(2): 116–122.
李雪英, 陈树民, 王建民, 等. 2012. 薄层时频特征的正演模拟. 地球物理学, 55(10): 3410–3419. DOI:10.6038/j.issn.0001-5733.2012.10.024
李跃, 徐果明, 施行觉, 等. 1995. 薄互层等效各向异性的实验研究. 石油地球物理勘探, 30(4): 513–517.
李占东, 赵伟, 李阳, 等. 2011. 开发地震反演可行性研究及应用——以大庆长垣北部油田为例. 石油与天然气地质, 32(5): 797–806. DOI:10.11743/ogg20110520
凌云, 郭向宇, 高军, 等. 2010. 油藏地球物理面临的技术挑战与发展方向. 石油物探, 49(4): 319–335.
刘万金, 周辉, 袁三一, 等. 2013. 谱反演在地震属性解释中的应用. 石油地球物理勘探, 48(3): 423–428.
任金峰, 廖远涛, 孙鸣, 等. 2013. 基于小波变换的高精度层序地层定量划分研究及其应用. 地球物理学进展, 28(5): 2651–2658. DOI:10.6038/pg20130546
石瑛, 芦俊, 杨震, 等. 2015. 平均入射角道集PP波与PS波联合反演. 地球物理学报, 58(12): 4617–4627.
宿淑春, 王晓华. 2000. 分频波阻抗反演方法及其应用. 石油大学学报(自然科学版), 24(1): 85–87.
孙鲁平, 郑晓东, 李劲松, 等. 2009. 基于峰值频率的薄层厚度计算公式及其近似. 应用地球物理, 6(3): 234–240.
孙树海, 牛彦良. 1991. 薄互层条件下AVO技术的应用. 地球物理学报, 34(1): 99–106.
唐文榜. 1987. 地震反射法中薄煤层分辨能力的研究. 地球物理学报, 30(6): 641–652.
王保丽, 印兴耀, 丁龙翔, 等. 2015. 基于FFT-MA谱模拟的快速随机反演方法研究. 地球物理学报, 58(2): 664–673.
王濮, 金振奎, 李国发, 等. 2007. 薄层生物碎屑灰岩的地震属性检测. 石油物探, 46(4): 390–393.
王赟, 刘媛媛, 张美根. 2017. 裂缝各向异性地震等效介质理论. 北京: 科学出版社: 49-52.
沃特斯K H. 1983. 反射地震学——能源勘探的工具. 许云, 吴荣祥译. 北京: 石油工业出版社.
夏竹, 刘超颖, 魏文博, 等. 2005. 地震道时间域频率属性特征和地层层序划分. 石油地球物理勘探, 40(5): 550–560.
徐果明, 李跃, 倪四道, 等. 1996. 薄互层等效横向各向同性的研究. 石油地球物理勘探, 31(6): 792–805.
许云. 1981. 地震层状构造理论与地震模型——Ⅰ.理论评述. 石油物探, 20(1): 1–16.
杨春, 王赟, 杨德义. 2014. 构造煤的地震可识别性特征. 煤炭学报, 39(S2): 465–470.
杨春颖, 杨春, 陈双全, 等. 2017. 各向异性衰减薄层地震响应特征研究. 地球物理学报, 60(1): 316–326.
杨谦, 李正文. 1996. 地震资料宽带约束反演方法及应用. 石油物探, 35(4): 37–42.
杨千里, 吴国忱. 2016. 基于贝叶斯理论的多尺度地震反演方法. 地球物理学进展, 31(3): 1246–1256. DOI:10.6038/pg20160343
杨勤勇, 赵群, 王世星, 等. 2006. 纵波方位各向异性及其在裂缝检测中的应用. 石油物探, 45(2): 177–181.
于建国, 韩文功, 刘力辉. 2006. 分频反演方法及应用. 石油地球物理勘探, 41(2): 193–197.
苑春方, 彭苏萍, 唐申强, 等. 2014. 薄层复合波振幅与厚度函数关系的改进. 煤炭学报, 39(10): 2083–2086.
袁子龙, 杨冰, 王建国. 1996. 薄层、薄互层地震反射时间域与频率域正演模拟研究及应用. 石油物探, 35(3): 14–20.
张川, 杨春, 王赟. 2015. 关于薄层与单界面模型弹性反射透射系数的讨论. 煤田地质与勘探, 43(2): 86–90.
张繁昌, 刘杰, 印兴耀, 等. 2008. 修正柯西约束地震盲反褶积方法. 石油地球物理勘探, 43(4): 391–396.
张永刚, 王赟, 尹军杰. 2010. 单点高密度地震数据处理分析与初步评价. 石油地球物理勘探, 45(2): 201–207.
张中杰, 何樵登. 1990. N个薄层介质组合引起的视各向异性. 长春地质学院学报, 20(2): 223–231.
赵军龙, 李娜. 2008. 小波变换在高分辨率层序地层分析中的应用. 地球物理学进展, 23(4): 1230–1235.
赵继龙, 熊冉, 陈戈, 等. 2014. 分频重构反演及在薄互层储层预测中的应用. 西南石油大学学报(自然科学版), 36(4): 47–54. DOI:10.11885/j.issn.1674-5086.2012.11.19.06
周竹生. 1993. P-SV波和SH波的AVO分析. 石油地球物理勘探, 28(4): 430–438.