2. 中国科学院大学, 北京 100049;
3. 中国石油大学(华东)地球科学与技术学院, 青岛 266580
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Geosciences, China University of Petroleum(East China), Qingdao 266580, China
地震波衰减作为地震波在地球介质中传播的一个重要基本特征, 无论是对于地震学研究还是对于含油气储层描述等都至关重要.一般而言, 引起地震波衰减的主要原因包括几何扩散、界面反射与透射、多次反射、非均质散射、以及岩石的本征衰减作用.在这些作用中, 岩石的本征衰减作用将地震波的机械能转化为内能.其余作用均为弹性过程, 即将地震波能量在空间上进行重分配.对平面波而言, 如果只考虑地震波在宏观均匀的岩石中传播, 地震波的振幅衰减则主要由岩石的微观或介观非均质体散射以及岩石的本征衰减特性决定.区分和确定不同物理机制的衰减作用对于准确认识岩石物理性质和岩石内部结构特征意义重大.虽然有关岩石的本征衰减与非均质散射衰减的区分在地震学中得到了广泛而深入的研究, 但是相关研究在勘探地震学中并不多见.特别地, 对于岩石物理实验测量的衰减而言, 区分散射和本征衰减的研究尤为缺乏.
在地震学中, 散射被认为是岩石非均质性的体现, 其在地震图上表现为明显且持续存在的尾波(Aki, 1969; Aki and Chouet, 1975).Wu(1985)通过在频率域求解辐射传输方程(radiative transfer equation)发现具有不同地震散射率(seismic albedo)的介质, 其对应的能量密度-距离曲线的形状不同.Frankel和Wennerberg(1987)则通过数值模拟和能流理论发现尾波的整体衰减与岩石的本征衰减特性有关, 而尾波振幅与直达波能量之比可以作为计算散射衰减的一种方法.基于这些相关的理论研究, 地震学中利用地震图的S波数据开展了大量区分散射和本征衰减的研究工作(比如, Fehler et al., 1992; Hoshiba, 1993; Jemberie and Langston, 2005).另一方面, 由于散射作用的强弱由非均质体尺度与地震波长的相对大小决定(吴如山和谢小碧, 2014), 而沉积地层内的非均质体尺寸相对于勘探地震波长而言一般较小, 非均质散射作用在勘探地震中常被忽略.然而, 沉积地层的层状非均质性却被认为可能引起较强散射作用(Hackert and Parra, 2000).这种散射作用最初是由O′Doherty和Anstey(1971)设想提出, 并在其后得到完善的数学描述(Shapiro and Zien, 1993).为了区分这种散射作用与沉积地层的本征衰减作用, Hackert和Parra(2000)基于Dvorkin等(1994)提出的Biot/Squirt(BISQ)本征衰减机制, 对一套薄互层沉积序列的本征衰减与散射衰减作用进行了对比分析.
对于岩石物理实验而言, 有关散射衰减和本征衰减的讨论并不多见, 两种衰减机制的相对重要性也不确定.比如, Sams等(1997)就认为其实验室测量的衰减是岩石的本征衰减, 散射作用不明显.其原因归结于岩石无明显的层理.相反, Guo和Fu(2007)则通过对尾波Q的计算发现非均质散射作用很强, 其采用的岩石也是一块无明显层理的常规储层砂岩.即使是这样, Guo和Fu(2007)仍视谱比法衰减为岩石的本征衰减.严格说来, 谱比法衰减是一种直达波衰减, 表征的是直达波振幅的整体衰减, 而其中必然包括了非均质体散射的影响.并且, 岩石的非均质体类型不仅包含岩性分层, 也包括岩石本身具备的孔隙性、含流体性等.为了同时考虑岩石的非均质散射特性和本征吸收特性对实验室衰减测量结果的影响, 本文应用Frankel和Wennerberg(1987)提出的能流理论来描述超声脉冲传输实验中弹性波的能量损失过程与尾波生成机制.通过引入能流理论, 得到一种测量直达波衰减的方法, 即能流法.文章通过理论推导和实验对比展示了谱比法与能流法测量衰减结果的一致性.这两种直达波衰减的一致性暗示了谱比法衰减中存在着散射的作用, 而这一结论仅仅透过谱比法的理论是无从得知的.换而言之, 本文通过引入能流理论, 给出了在使用谱比法时, 判断其衰减结果中是否存在非均质散射的一种方法.确定实验室测量的谱比法衰减中是否存在着散射的作用, 对于地震岩石本身的基础研究具有十分重要的意义.在地震岩石物理的相关研究中, 有大量的本征衰减物理模型(比如, Johnston et al., 1979)需要准确的实验数据用于模型验证.如果用于验证本征衰减物理模型的实验数据中包含了散射作用的干扰, 这将会对验证过程本身的可信度产生巨大的影响.当然, 基于未被准确验证的理论模型开展相关应用, 其可信度可能也会大打折扣.
本文的行文安排如下.第一部分首先介绍了本研究所采用的高温高压超声脉冲传输实验的基本情况.还分析了一块无衰减铝样和一块饱油砂岩样品的基本波形特征.基于实验波形特征, 第二部分通过引入能流理论来描述实验条件下的弹性波衰减过程, 并利用能流理论测量直达波衰减.同时, 通过理论推导展示了能流法衰减同谱比法衰减的一致性.第三部分, 依据实验波形数据, 介绍了谱比法和能流法的衰减测量过程, 对比分析了谱比法和能流法的直达波衰减测量结果, 并结合一个现有的喷射流模型(Gurevich et al., 2010)展示了由其计算的本征衰减同谱比法衰减的差异.
1 超声脉冲传输实验 1.1 实验装置与实验步骤本研究采用的高温高压超声脉冲传输实验装置的核心部分结构如图 1所示.在该实验装置中, 样品的围限压力(confining pressure, Pc)由一个普通三轴加压装置实现, 孔隙压力(pore pressure, Pp)通过注入压力釜内均衡的孔隙流体压力实现.温度是通过加热包裹样品的橡胶套(rubber jecket)来实现.样品两端的高温高压超声探头将纵、横波换能器集成于其中.激发换能器(transducer)中的纵、横波压电陶瓷芯片(P/S piezoelectric ceramic)受两侧电极(electrodes)的控制而振动, 将电信号转化为机械振动信号; 接收换能器则将接收到的机械振动信号通过电极转化为电信号, 并由计算机系统记录下来.以激发换能器(图 1底部换能器)为例, 该换能器主要由三大组件构成, 即压电组件(电极与压电陶瓷芯片)、前端声学组件(front acoustic port, 也就是所谓的matching layer)和后端声学组件(back acoustic port, 也就是所谓的backing material).换能器的压电组件实现机械能与电能的转换, 适当厚度的前端声学组件可以提升换能器的性能, 适当材质的后端声学组件则可以吸收换能器内向后传播的弹性波以削弱换能器的激振噪声(ringing effect)(Zhou et al., 2014).高温高压探头的最外层是金属材质的保护层(metal outer casing), 保证换能器在高温高压条件下能正常运行.另外, 此实验设备中纵、横波换能器主频均为1 MHz.需要注意, 高温高压超声脉冲传输法实验装置是一个极为复杂的声学测量系统, 我们在此对其基本结构特征予以描述, 是为了便于理解由其获得实验波形的基本过程, 以及其中可能存在的对于实验波形的影响因素.

|
图 1 高温高压超声脉冲传输实验装置结构示意图 Fig. 1 Physical setup for the high pressure-temperature ultrasonic pulse transmission method |
利用上述实验设备, 我们针对一块直径为3.8 cm长度为7.6 cm的柱体常规储层砂岩岩心以及一块与岩心同等尺寸的铝样, 在稳定的温度条件(20 ℃室温, 不加热)和不同的压力条件下, 进行了超声脉冲传输实验.在针对岩心的实验测量过程中, 岩石的围限压力(Pc)设置为65 MPa不变, 孔隙压力(Pp)由5 MPa开始, 以5 MPa为压力间隔逐步增大到60 MPa.特别地, 当孔隙压力大于20 MPa后, 孔隙压力间隔调整为10 MPa.孔隙流体为轻质油, 孔隙压力平衡后记录对应的实验波形数据.铝样的波形来自于围限压力为65 MPa下的实验测量结果.铝样和岩样的尺寸形状、耦合条件、以及测量参数设置等均完全相同.由上述实验步骤, 得到不同压力条件下的岩样和铝样的波形数据如图 2所示.

|
图 2 岩样和铝样的纵波(a)、横波(b)波形 Fig. 2 P-wave (a) and S-wave (b) waveform recordings of the rock and the aluminum |
对于实验室衰减测量而言, 波形记录是基础实验数据, 深入理解波形数据中蕴含的信息以及其影响因素是利用实验数据开展相关研究的基础.首先, 我们将超声脉冲传输实验的完整波形记录从时间上分为两部分:一部分是首先到达接收点的波组, 称为直达波(direct wave); 其余部分, 即直达波之后的所有波组, 统称为尾波(coda), 如图 2中所示.需要注意, 之所以这样规定, 是因为通常所说的“尾波”是指由介质非均质散射引起的滞后于直达波的波形记录(Aki, 1969).在理想条件下, 尾波与非均质散射可以认为是相互对应的.但是, 在超声脉冲传输实验中却并不一定如此.如图 2所示, 由于换能器性能问题、实验耦合条件、以及可能存在的边界反射(付博烨等, 2016)等因素的影响, 即使是均匀的铝样, 其直达波波组之后仍然存在着明显的波形记录.特别地, 本研究中的实验设备和实验条件仍无法消除铝样直达波后的波形记录.也就是说, 在本研究中, 与铝样对应的岩石的尾波, 可能并非完全来自于岩石的非均质散射.尤其当岩石异常均匀时, 岩石的尾波可能完全与岩石的非均质散射无关.为了便于讨论, 本研究中所说尾波不严格指代非均质散射作用.
为了便于理解岩样的波形特征, 理解与岩样尺寸、形状和测试条件相当的铝样的波形特征尤为重要.如图 2中所示, 不论是纵波还是横波, 铝样波形的最大振幅位于直达波波组中, 尾波振幅相对直达波的振幅普遍较弱.即换能器激发的绝大部分振动能量向前经过样品传播至接收端, 只有少量振动能量向后传播经过反射和后端声学组件的吸收作用后再向前传播至接收端.当然, 不排除耦合条件的影响, 波在铝样中传播时出现边界反射等情况也可能对铝样尾波造成影响.可见, 即使是均匀无衰减的铝样, 其波形特征也是十分复杂的.然而, 铝样波形的一些特定特征却是可以确定的.首先, 对于1 MHz左右的弹性波而言, 由于铝样为均匀介质, 其不存在非均质散射作用; 并且, 铝的品质因子Q ≈ 150000, 其本征衰减也约为零.换而言之, 铝样波形中的尾波必来自于实验设备和实验条件的影响, 而这些影响可以认为近似等同地影响着岩样的波形.其次, 由于铝样可以近似视为无衰减介质, 如果已知铝样中波阵面的尺寸和形状, 那么由波阵面上的弹性波能量积分可以确定换能器激发的弹性波总能量.
对岩样而言, 其波形特征相对于铝样的更为复杂.直观而言, 图 2中无论是纵波还是横波, 岩样的波形中都存在着明显的尾波.而且随着孔隙压力的增大, 尾波振幅逐渐增大, 直达波振幅逐渐减小.岩石波形的这种压力变化特征暗示了岩石中可能存在的非均质散射作用.即随着孔隙压力的增大, 岩石的非均质散射作用增强, 更多的波能量滞后到达接收点, 表现为尾波振幅的相对增大.另外, 由于岩石的非弹性性质, 比如流体黏滞性和弹性波导致的流体流动现象(Biot, 1956a, 1956b, 1962; Mavko and Nur, 1975, 1979)等, 会导致直达波和尾波振幅均随时间衰减, 即所谓的本征衰减作用或本征吸收作用.因此, 很难确定岩石的直达波振幅相对于铝样直达波振幅的衰减, 有多少来自于岩石的非均质散射作用, 有多少来自于本征衰减作用.
2 谱比法衰减的散射与本征吸收特性就实验衰减测量而言, 谱比法(Toksöz et al., 1979)是一种最常用的实验测量方法.虽然谱比法测量的衰减在实际中应用广泛, 但是其测量结果中来自非均质散射作用的影响是否存在, 是否可以忽略, 仍不甚明确.虽然可以借助岩石非均质体尺寸与弹性波波长的相对大小大致确定岩石中非均质散射作用的大小, 但是确定岩石的非均质体尺寸本身就比较困难, 况且岩石的非均质性在不同尺度上都存在.因此, 利用岩石的波形特征辨别其非均质散射特征是一种可行而简便的方法.下面, 我们将地震学中的一个能流理论引入到岩石的超声脉冲传输实验中, 借以理解本征衰减作用和非均质散射作用对岩石波形的影响.除此之外, 我们将利用该理论推导出一种计算直达波衰减的实验方法, 并进一步讨论通过该方法测量的衰减与谱比法衰减的内在关联.
2.1 能流理论Frankel和Wennerberg(1987)通过数值模拟和能流理论研究了实际地球介质中传播的弹性波的本征衰减和非均质散射作用.在其描述的能流理论中, 地震波在由震源向外球面扩散过程中, 波阵面(直达波)遇非均质体后, 向波阵面包裹的球内散射部分波能量, 造成了波阵面上总能量的非均质散射衰减; 而散射到波阵面以内的波能量, 在球内由于非均质散射而均匀分布于其中, 并最终体现为波形记录中的尾波.在直达波向外传播以及尾波在球内随机散射的过程中, 直达波和尾波都持续受到岩石的本征衰减作用.在这个理论中, 忽略了波型转换和波的相位信息, 完全以弹性波能量的形式处理相应的能量衰减过程.同时, 该理论还认为, 能流模型不论是对于单次散射还是多次散射等情形均适用.需要注意, 能流理论中的“散射衰减”(1/Qs)是指波阵面上总能量向后散射造成的非均质散射衰减.而在一般的非均匀介质多次散射理论中, “散射衰减”是指弹性波在非均质体处发生散射而引发的在入射方向上的功率损失, 其不限制散射方向.并且, 在一般的非均匀介质多次散射理论中, 一般通过构建考虑散射作用的波动方程, 或者与之相应的能量传输方程, 来描述介质的多次散射作用(Wu, 1985).可见, 能流理论中“散射衰减”的定义与一般的非均匀介质散射理论中“散射衰减”的定义是不同的, 它们通过不同的方式描述了弹性波传播的散射衰减作用.探讨能流理论与一般散射理论的区别和联系超出了本文的研究范畴, 本文中将采用能流理论中的相关概念及结论来表征岩石的非均质散射和本征衰减过程.
依据能流理论的基本假设及适用条件, 对于本研究中使用的储层砂岩而言, 利用能流理论描述其弹性波的传播过程是可行的.首先, 该储层砂岩为一块分选性较好的纯石英砂岩, 泥质含量很低, 孔隙度为20%, 渗透率为40.3 mD(1 mD≈10-15m2), 石英颗粒粒径为0.1~0.3 mm(如图 3所示).其次, 弹性波主频为1 MHz, 岩石的纵波速度约为3500 m·s-1, 横波速度约为2000 m·s-1.如果将饱和流体的孔隙视为岩石的非均质体, 将石英视为岩石的稳定背景基质, 那么其非均质体的尺寸可以由石英的粒径来近似表征.由于孔隙具备一定的连通性, 实际的非均质体尺寸将略高.因此, 此非均匀介质的相关长度a在0.1~1 mm之间.利用地震波在非均匀介质中传播的尺度法则可知, 该砂岩位于大角度散射(Mie散射)的区域(0.1 < ka < 10,k为波数)(吴如山和谢小碧, 2014).这就意味着, 向波阵面之后的大角度散射的情况是可能存在的.另外, 岩样长度L为7.6 cm, 岩石的L/a~102, 在直达波到达接收端时, 其后的散射波也有足够时间以均匀分布于岩石中.这一现象在Zhang等(2014)针对柱体岩心的非均质散射波场模拟中也得到了验证.

|
图 3 实验砂岩样品的铸体薄片 Fig. 3 Thin sections of the sandstone sample tested |
假设换能器激发的弹性波总能量为W, 并且假设通过岩石的弹性波只存在本征衰减作用, 忽略实验设备对弹性波能量的吸收作用.根据能流理论, 岩石中弹性波的本征衰减作用可表示为

|
(1) |
WT表示排除本征衰减后的弹性波总能量, ω为圆频率, Qi为岩石的本征衰减品质因子.在换能器激发弹性波的那一瞬间, 即t = 0时, 所有波能量都集中于直达波中.随着直达波向接收端传播, 即t>0时, 当直达波波阵面遇到非均质体, 一部分直达波能量被散射到波阵面之后, 造成了直达波的散射衰减, 从而形成了尾波.直达波的散射衰减作用表示为(Frankel and Wennerberg, 1987)

|
(2) |
其中WD表示直达波的总能量, Qs为直达波的散射衰减品质因子.联立公式(1)和(2)可知,

|
(3) |
其中,

|
(4) |
QD为直达波衰减对应的品质因子.如公式(4)所示, 直达波波阵面上的总能量损失等于直达波波阵面上的本征衰减与非均质散射衰减之和.
反过来, 如果要测量直达波的总衰减, 可直接对公式(3)两边取对数, 即得

|
(5) |
根据公式(5)可知, 只要能获知换能器激发的总能量W, 接收端直达波波阵面上的总能量WD, 以及该弹性波的圆频率ω, 则可以计算出弹性波的直达波衰减.结合本研究所采用的实验设备情况(图 1), 参照铝样的波形特征(即铝样不存在明显的边界反射作用), 将激发换能器激发的波阵面近似视为平面.通过对铝样波形对应的波能量在接收端处整个波阵面上积分, 计算出换能器激发的总机械能W.类似地, 将岩石直达波波形对应的波能量在接收端处整个波阵面上积分, 即可得到直达波波阵面上的总能量WD.Frankel和Wennerberg(1987)指出, 波阵面上的弹性波总能量与地震波振幅的关系可表示为

|
(6) |
其中,

|
(7) |
I为波形的振动能量积分, A(t)为t时刻的波形振幅, t1和t2为波形积分的时窗, S为波阵面的面积, v为介质的速度, d是一个比例常数.由此, 柱体岩心中传播的弹性波的总能流W为

|
(8) |
其中,

|
(9) |
tend为铝样波形的截止记录时间, 下标1代指铝样.假设岩石的直达波初至时间为td, 直达波完全到达接收换能器的时间为t′d, 那么岩石直达波波阵面上的总能量WD为

|
(10) |
其中,

|
(11) |
下标2代指岩石.由于实验波形均来自于同一接收换能器, 铝样和岩样仅仅相当于充当一个滤波器的作用, 所以公式(8)与公式(10)中的d相同.由此, 公式(5)可转化为

|
(12) |
公式(12)是基于能流理论, 结合超声脉冲传输实验的波形特征, 推导得到的直达波衰减测量公式.也就是说, 只要对几何形状完全一致的铝样和岩样, 按照相同的实验条件和实验步骤进行实验, 那么就可以在已知波阵面几何特征的前提下, 利用两个样品的完整波形数据, 计算出岩石的直达波衰减值.
2.2 能流法衰减与谱比法衰减能流法与谱比法均是描述介质中弹性波衰减的方法, 但是它们的理论方法过程是完全不同的.谱比法的理论体系中没有对介质的非均质散射作用和本征衰减作用详做区分, 而以一个统一的衰减系数来表征弹性波在介质中的振幅衰减; 相反, 能流理论则针对岩石的非均质散射和本征衰减作用进行了分别考虑.但是, 这两种方法也存在着一定的相似性.比如, 将公式(12)改写为

|
(13) |
对比于Toksöz等(1979)中的公式(5)可知, 两个公式在形式上具有相似性.并且, 两者测量的衰减在物理意义上是一致的, 都是直达波衰减.下面, 我们将以理论推导的方式展示两者在测得的直达波衰减上的一致性.
在谱比法中, Toksöz等假设超声脉冲传输实验中的铝样和岩样的振幅分别可表示为

|
(14) |

|
(15) |
其中, x表示弹性波传播的距离, G(x)为与样品形状等相关的几何因子, k为波数, α(f)为频率相关的衰减系数, 其频率相关性表示为

|
(16) |
γ与岩石的品质因子Q的关系为

|
(17) |
v为速度.与能流法中一样, 下标1和2分别代指铝样和岩样.将公式(14)和(15)分别代入公式(9)和(11)中, 并将公式(13)的左侧改写为

|
(18) |
由于我们假设柱体岩心中的波阵面为平面, 即可以忽略几何扩散对直达波能量的影响.并且, 考虑到实验设备等引发的铝样尾波能量总体较弱, 可以假设铝样的所有机械能在平面波假设下集中于铝样的直达波中.即铝样的振幅集中于初至td1和直达波截止时间td1′之间.令T=t′d-td为岩石直达波的视周期, T′=td1′-td1为铝样的直达波视周期, 那么, 公式(18)可化解为

|
(19) |
将公式(19)右侧的积分化解得

|
(20) |
一般而言, 由于岩石的高频衰减比铝样的强, 岩石的主频会向低频方向移动(Quan and Harris, 1997).所以, 一般地, T′ < T, 但是两者的差异不会很大.因此,

|
(21) |
又由于铝样的衰减几乎为零, 即α1(f)≈0.对于长度为x=L的岩心而言, td=L/v, 取公式(20)的实部得

|
(22) |
至此, 我们应用谱比法的基本假设代入公式(13)左侧对ln(I1/I2)进行了化解, 并得到了公式(22).公式(22)中的品质因子Q2是谱比法理论中定义的岩石的品质因子.对比公式(13)与公式(22)可知, 谱比法衰减1/Q2与能流法衰减1/QD均可由ln(I1/I2)的频率项求得, 即两种方法求解的岩石衰减是一致的.
谱比法衰减与能流法衰减的一致性有助于理解谱比法衰减中包含的非均质散射作用, 同时也使得利用能流理论解释直达波衰减的构成成为可能.虽然本文中并没有像Frankel和Wennerberg(1987)就散射Qs及尾波的相关内容做更深入讨论, 但是其基本结论在此依然适用.即直达波的非均质散射衰减越强, 被散射到直达波波阵面之后的尾波能量将相对越强.对于满足能流理论的孔隙岩石而言, 如果岩石的非均质散射越强, 那么其超声脉冲传输实验波形的直达波振幅将越弱, 尾波振幅将越强.相反, 相对较弱的尾波振幅可能意味着直达波衰减更多地反映岩石的本征衰减特性.
需要注意, 如前所述, 实际的实验过程受到诸多因素的影响, 导致超声脉冲传输实验波形的尾波可能不完全来自于岩石的非均质散射作用.一个简单可行的方法是, 通过对比铝样和岩样的尾波波形特征, 来确定实验条件及仪器设备的影响.如果两者的尾波波形特征极其相似, 那么岩石的非均质散射可能是较弱的, 直达波衰减中的非均质散射作用因而可以忽略.相反, 如果岩石的尾波振幅较铝样的异常明显, 那么这可能意味着岩石具有较强的非均质散射作用.更具体地说, 岩石可能具备较好的孔渗条件, 或者较强的岩性不均匀性等.当然, 对于这种情况下的直达波衰减, 不论其来自于谱比法还是能流法, 其中的非均质散射作用可能都是不能忽略的.
3 实验衰减测量基于实验波形测量岩石的弹性波衰减, 对研究岩石本身结构特征、含油气储层描述、以及研究地球深部构造都具有实际意义.谱比法和本文导出的能流法都是利用岩石的直达波波形数据, 结合一块参考铝样的波形数据, 用于估算岩石的直达波衰减.两种方法在理论构建上差异较大, 在实际实施过程中也差异明显.下面, 我们将分别就两种方法的具体实施过程予以描述, 并对比两种方法的测量结果.为了直观展示谱比法衰减中可能存在的散射作用, 文中还利用Gurevich等的喷射流模型计算了岩石的本征衰减, 并与谱比法衰减进行对比.
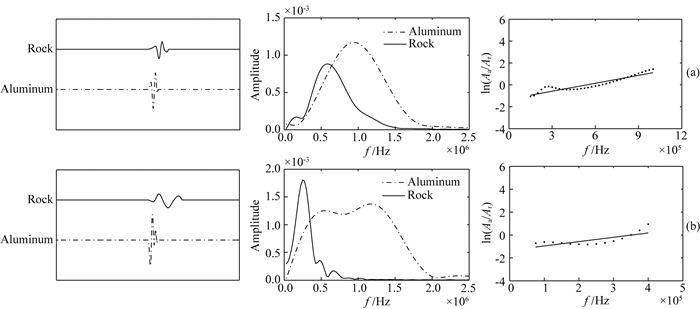
3.1 谱比法衰减测量谱比法衰减的测量主要依靠岩样与参考铝样的直达波波形数据.其具体实施步骤包括:(1)从完整的波形数据中截取岩样和铝样的直达波波形数据, (2)对岩样和参考铝样的直达波波形进行频谱分析并得到两者的谱比, (3)依据岩样与铝样的谱比数据拟合岩石的品质因子Q.以本研究中孔隙压力为10 MPa的岩石波形数据和铝样波形数据为例.首先, 将铝样和岩样的直达波波形数据从完整的波形数据中提取出来, 这里我们选取直达波初至后两个周期的波形作为直达波波形数据, 如图 4中左侧波形所示.接下来, 对铝样和岩样的直达波波形进行频谱分析, 得到两者的振幅谱(图 4中部), 以及两者的谱比(如图 4右侧散点).最后, 依据Toksöz等(1979)的做法, 在岩石纵、横波直达波的主频范围内对谱比进行拟合, 将本研究中岩石的纵波谱比频段选取在0.1 MHz到1 MHz之间, 横波谱比频段选取在0.05 MHz到0.5 MHz之间, 拟合曲线如图 4右侧所示.谱比衰减拟合公式为:
|
图 4 10 MPa孔隙压力下样品的纵波(a)、横波(b)波形, 频谱和谱比 Fig. 4 P-wave (a) and S-wave (b) direct waveform recordings, amplitude spectrum, and spectral ratios of samples when pore pressure is under 10 MPa |

|
(23) |
γ2与岩石的品质因子Q的关系由公式(17)给出, x为样品长度, f为频率, 下标1, 2分别指铝样和岩样.由谱比ln(A1/A2)关于频率f的斜率即可求得岩石的品质因子Q.
3.2 能流法衰减测量与谱比法不同, 能流法需要铝样的完整波形数据, 以计算总能量W.能流法的具体实施步骤包括:(1)截取岩石的直达波波形数据并获取铝样的完整波形数据(波形记录时间足够长, 截止时间在波形稳定且振幅微弱处), (2)对岩石直达波进行频谱分析, 确定其主频, (3)根据公式(9), (11)和(12)计算直达波衰减1/QD.以本研究中不同孔隙压力条件下岩石的波形数据以及对应的铝样波形数据为基础(图 2), 截取岩石直达波波形(截取方法与谱比法的一致), 如图 5所示.不同压力条件下的岩石直达波主频标注于图 5中.与之对应, 不同有效压力(Peff=Pc-Pp)条件下岩石的速度如图 6中所示(方形散点为饱和轻质油岩石的速度, 圆形散点为干燥岩石的速度).铝样的纵波速度为6500 m·s-1, 横波速度为3200 m·s-1.由于本实验中波形的采样频率为10 MHz, 利用常规的梯形数值积分方法就可以计算得到较高精度的岩石直达波波形振动积分I2和铝样波形振动积分I1.

|
图 5 岩石的纵波(a)、横波(b)直达波波形及铝样的完整波形 Fig. 5 P-wave (a) and S-wave (b) direct waves of the rock and the full waveform recording of the aluminum |

|
图 6 不同压力条件下干燥和饱油岩石的纵波(a)、横波(b)速度 Fig. 6 P-wave (a) and S-wave (b) velocities of the dry and oil-saturated rock under different stress conditions |
谱比法与能流法在不同压力条件下的直达波衰减对比, 如图 7所示.由图可知, 两种实验方法测量的直达波衰减呈现出良好的一致性, 与2.2节中的理论推导相呼应.图 7中, 纵、横波直达波衰减的增大与孔隙压力的增大是相匹配的.虽然纵、横波的直达波衰减特征相似, 衰减数值相近, 但两者却有着很大的不同.正如图 5中所示, 纵波衰减和横波衰减在每一个压力点上的直达波主频不同.也就是说, 纵波和横波衰减不在同一频率下, 对比讨论两者的数值差异缺乏合理性.然而, 纵波和横波衰减共同体现出的压力相关性却值得分析.

|
图 7 岩石的纵波(a)、横波(b)谱比法衰减与能流法衰减 Fig. 7 Energy flux attenuation and spectral ratio attenuation of the rock for P-wave (a) and S-wave (b) |
就本研究中的储层砂岩而言, 岩石的速度、直达波波形、以及直达波衰减都呈现出良好的压力相关性.首先, 不论是干燥还是饱油的岩石, 其速度均随着有效压力(Peff=Pc-Pp)的增大(即围压不变, 孔隙压力的减小)而增大(图 6).并且, 当有效压力较低(Peff < 40 MPa)时, 速度与有效压力呈非线性相关; 当有效压力较高(Peff>40 MPa)时, 速度与有效压力呈线性相关.岩石的这种压力-速度关系有可能与不同压力条件下岩石的孔隙结构特征有关.即速度与压力非线性相关性可能是由于岩石中存在着不同纵横比的软空隙(微裂缝、孔隙吼道等), 而速度与压力的线性相关性则来自于岩石中硬孔隙(粒间孔、溶蚀孔等)的孔隙变形(邓继新等, 2015).其次, 岩石的衰减也体现出类似的压力相关性(图 7).当孔隙压力大于20 MPa以后, 直达波衰减随着压力明显增大.孔隙压力为60 MPa时的直达波衰减约为20 MPa下的2.5倍.可见, 相对于速度, 衰减对于孔隙压力的变化更为敏感.衰减与孔隙压力的相关性也可能与岩石中软孔隙的开闭有关.一方面, 孔隙流体的注入导致软孔隙的张开与扩张, 可能导致岩石的喷射流作用(Mavko and Nur, 1975, 1979)加强, 即岩石的本征衰减增强.另一方面, 裂缝的张开与扩展可能会增大非均质体的尺寸, 尺寸与波长相当的非均质体(含流体孔隙)数量也可能上升, 非均质散射作用因而得以加强.
有关压力通过本征衰减作用对岩石在不同频率范围内的弹性波速度和衰减的影响, 可以应用Gurevich等(2010)提出的喷射流(squirt flow)模型予以描述.在Gurevich等提出的这个喷射流模型中, 通过一个具有二元孔隙结构的岩石物理模型, 表征喷射流作用对饱和流体岩石动态弹性性质的影响.特别地, 该模型考虑了频率和压力对岩石弹性模量的影响.表 1给出了本研究中所采用的砂岩及其饱和的轻质油的基本物理性质参数.岩石的二元孔隙结构可以通过最优化拟合(本文使用最小二乘拟合)岩石的干燥和饱和速度来确定, 如图 6所示.一旦确定了岩石的二元孔隙结构, 那么就可以确定任意压力和频率条件下, 岩石的弹性波速度和衰减(详见Gurevich et al., 2010).对应于不同压力条件下的纵、横波直达波主频, 我们利用Gurevich等的喷射流模型计算得到了本研究中砂岩的喷射流本征衰减(1/Q), 如图 8所示.对比于相同压力条件下的谱比法衰减, 由图 8可知, 在本实验中, 喷射流衰减作用明显低于直达波整体的衰减作用.也就是说, 在本实验中, 谱比法衰减中很可能是包含了散射的作用, 而且散射的作用相对于本征衰减作用并不弱.值得一提的是, Gurevich等提出的喷射流模型是众多本征衰减物理模型中的一种, 其可能不能绝对准确地反映岩石的整体本征衰减作用.但是, 就岩石物理学近几十年有关本征衰减物理机制的研究看来, 弹性波导致流体流动所描述的本征衰减机制, 可能是最重要的本征衰减物理机制(Winkler and Nur, 1982; Müller et al., 2010).总而言之, 在本实验中, 非均质散射作用对谱比法衰减的影响很可能是不可忽略的.

|
图 8 岩石的纵波(a)、横波(b)谱比法衰减与喷射流衰减 Fig. 8 Spectral ratio attenuation and squirt flow attenuation of the rock for P-wave (a) and S-wave (b) |
|
|
表 1 饱油砂岩的基本物理性质 Table 1 Physical properties of the oil-saturated sandstone |
就本实验中弹性波衰减的频率相关性而言, 其物理实质仍相当复杂.首先, 无论是谱比法还是能流法, 为了简化研究, 实际上都隐含地采用了一个常Q假设(衰减系数与频率线性相关).大量的实验研究表明, 在超声实验频段内采用常Q模型是可行的(可参看Jackson and Anderson(1970)给出的综述).当然, 也有大量物理模型用以表征岩石Q值的频率相关性(可参考Sato et al.(2012)中给出的综述).但是, Q与频率相关的衰减物理模型现阶段仍不完善.虽然一些物理模型对于衰减测量结果的物理解释是有意义的, 但应用其进行可行的衰减测量仍较为困难.从本研究的实验结果看来, 此砂岩的直达波波形的视周期随着孔隙压力的增大而增大, 主频向低频方向移动.这可能是因为, 孔隙流体的注入导致了岩石的微观结构的改变(Dvorkin et al., 1991), 弹性波中高频信号的损失增强, 进而导致岩石呈现出相应的频率特征(Quan and Harris, 1997).除此之外, 孔隙流体在不同孔压条件下的黏性的变化(Batzle and Wang, 1992), 孔隙结构变化导致的喷射流特征频率的变化(Gurevich et al., 2010)也可能是导致这种频率相关性的原因.特别地, 横波的主频漂移较纵波的更为明显.这有可能是由于岩石的横波衰减与纵波衰减存在着特定的内在联系(Gurevich et al., 2010).
最后, 需要注意, 能流理论本身是以一种唯象的方式来描述直达波的非均质散射与本征衰减过程, 其并未涉及导致岩石本征衰减和非均质散射的具体物理机制.将能流理论引入到超声脉冲传输实验中用于直达波衰减的测量, 是一种分析不同物理机制对衰减测量结果影响的尝试.能流法在计算直达波衰减方面当然也存在一定的不足, 比如, 铝样波形就可能受到各种实验条件的影响, 进而导致计算的总能量W出现误差.但是, 在比较理想的实验条件下, 通过能流法测量的直达波衰减依然是可信的.
4 结论本文通过能流理论描述了超声脉冲传输实验中柱体岩心内弹性波的非均质散射与本征衰减过程, 并以此导出一种测量直达波衰减的方法.结合谱比法的理论假设, 文章进一步从理论的角度展示了能流法与谱比法一致性.文中还针对一块储层砂岩进行了不同压力条件下的超声脉冲传输实验.岩石的速度和衰减都呈现出明显的压力和频率相关性.在实验中, 应用能流法和谱比法测量的直达波衰减也呈现出较好的一致性.能流理论的引入可以从理论上有区分地描述直达波中的非均质散射作用和本征衰减作用, 这是谱比法所不具备的.通过本文的相关理论和实验分析发现, 在超声脉冲传输实验中利用谱比法测量衰减, 其很可能会受到非均质散射的影响.如果要利用谱比法衰减数据进行相关理论模型验证和实际应用, 非均质散射的影响应当受到重视.最后, 将能流理论引入到实验中, 可以帮助理解尾波与直达波非均质散射的潜在关系, 为定性地评估直达波衰减中的非均质散射作用提供了一种简单可行的方法.
致谢谨此祝贺姚振兴先生从事地球物理教学科研工作60周年.
Aki K.
1969. Analysis of the seismic coda of local earthquakes as scattered waves. Journal of Geophysical Research, 74(2): 615-631.
DOI:10.1029/JB074i002p00615 |
|
Aki K, Chouet B.
1975. Origin of coda waves:Source, attenuation, and scattering effects. Journal of Geophysical Research, 80(23): 3322-3342.
DOI:10.1029/JB080i023p03322 |
|
Batzle M, Wang Z J.
1992. Seismic properties of pore fluids. Geophysics, 57(11): 1396-1408.
DOI:10.1190/1.1443207 |
|
Biot M A.
1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. 1. Low-frequency range. J. Acoust. Soc. Am., 28(2): 168-178.
|
|
Biot M A.
1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid. 11. Higher frequency range. J. Acoust. Soc. Am., 28(2): 179-191.
|
|
Biot M A.
1962. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 33(4): 1482-1498.
DOI:10.1063/1.1728759 |
|
Deng J X, Zhou H, Wang H, et al.
2015. The influence of pore structure in reservoir sandstone on dispersion properties of elastic waves. Chinese Journal of Geophysics (in Chinese), 58(9): 3389-3400.
DOI:10.6038/cjg20150931 |
|
Dvorkin J, Mavko G, Nur A.
1991. The effect of cementation on the elastic properties of granular material. Mech. Mater., 12(3-4): 207-217.
DOI:10.1016/0167-6636(91)90018-U |
|
Dvorkin J, Nolen-Hoeksema R, Nur A.
1994. The squirt-flow mechanism:macroscopic description. Geophysics, 59(3): 428-438.
DOI:10.1190/1.1443605 |
|
Fehler M, Hoshiba M, Sato H, et al.
1992. Separation of scattering and intrinsic attenuation for the Kanto-Tokai region, Japan, using measurements of S-wave energy versus hypocentral distance. Geophysical Journal International, 108(3): 787-800.
|
|
Fu B Y, Fu L Y, Wei W, et al.
2016. Boundary-reflected waves and ultrasonic coda waves in rock physics experiments. Applied Geophysics (in Chinese), 13(4): 667-682.
DOI:10.1007/s11770-016-0583-8 |
|
Frankel A, Wennerberg L.
1987. Energy-flux model of seismic coda:Separation of scattering and intrinsic attenuation. Bulletin of the Seismological Society of America, 77(4): 1223-1251.
|
|
Guo M Q, Fu L Y.
2007. Stress associated coda attenuation from ultrasonic waveform measurements. Geophys. Res. Lett., 34: L09307.
DOI:10.1029/2007GL029582 |
|
Gurevich B, Makarynska D, de Paula O B, et al.
2010. A simple model for squirt-flow dispersion and attenuation in fluid-saturated granular rocks. Geophysics, 75(6): N109-N120.
DOI:10.1190/1.3509782 |
|
Hackert C L, Parra J O.
2000. Analysis of multiscale scattering and poroelastic attenuation in a real sedimentary rock sequence. J. Acoust. Soc. Am., 107(6): 3028-3034.
DOI:10.1121/1.429433 |
|
Hoshiba M.
1993. Separation of scattering attenuation and intrinsic absorption in Japan using the multiple lapse time window analysis of full seismogram envelope. Journal of Geophysical Research, 98(B9): 15809-15824.
DOI:10.1029/93JB00347 |
|
Jackson D D, Anderson D L.
1970. Physical mechanisms of seismic-wave attenuation. Review of Geophysics and Space Physics, 8(1): 1-63.
DOI:10.1029/RG008i001p00001 |
|
Jemberie A L, Langston C A.
2005. Site amplification, scattering, and intrinsic attenuation in the Mississippi Embayment from coda waves. Bulletin of the Seismological Society of America, 95(5): 1716-1730.
DOI:10.1785/0120040203 |
|
Johnston D H, Toksoz M N, Timur A.
1979. Attenuation of seismic waves in dry and saturated rocks:Ⅱ. Mechanisms. Geophysics, 44(4): 691-711.
|
|
Mavko G, Nur A.
1975. Melt squirt in the asthenosphere. Journal of Geophysical Research, 80(11): 1444-1448.
DOI:10.1029/JB080i011p01444 |
|
Mavko G, Nur A.
1979. Wave attenuation in partially saturated rocks. Geophysics, 44(2): 161-178.
DOI:10.1190/1.1440958 |
|
Müller T M, Gurevich B, Lebedev M.
2010. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review. Geophysics, 75(5): 75A147-75A164.
DOI:10.1190/1.3463417 |
|
O'Doherty R F, Anstey N A.
1971. Reflections on amplitudes. Geophysical Prospecting, 19(3): 430-458.
DOI:10.1111/j.1365-2478.1971.tb00610.x |
|
Quan Y, Harris J M.
1997. Seismic attenuation tomography using the frequency shift method. Geophysics, 62(3): 895-905.
DOI:10.1190/1.1444197 |
|
Sams M S, Neept J P, Worthington M H, et al.
1997. The measurement of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 62(5): 1456-1464.
DOI:10.1190/1.1444249 |
|
Sato H, Fehler M C, Maeda T. 2012. Seismic Wave Propagation and Scattering in the Heterogeneous Earth. 2nd ed. New York, USA:Springer.
|
|
Shapiro S A, Zien H.
1993. The O'Doherty-Anstey formula and localization of seismic waves. Geophysics, 58(5): 736-740.
DOI:10.1190/1.1443458 |
|
Toksöz M N, Johnston D H, Timur A.
1979. Attenuation of seismic waves in dry and saturated rocks:1. Laboratory measurements. Geophysics, 44(4): 681-690.
DOI:10.1190/1.1440969 |
|
Winkler K W, Nur A.
1982. Seismic attenuation:Effects of pore fluids and frictional-sliding. Geophysics, 47(1): 1-15.
DOI:10.1190/1.1441276 |
|
Wu R S.
1985. Multiple scattering and energy transfer of seismic waves-Separation of scattering effect from intrinsic attenuation -Ⅰ. Theoretical modelling. Geophysical Journal of the Royal Astronomic Society, 82(1): 57-80.
DOI:10.1111/j.1365-246X.1985.tb05128.x |
|
Zhang Y, Fu L Y, Zhang L X, et al.
2014. Finite difference modeling of ultrasonic propagation (coda waves) in digital porous cores with un-split convolutional PML and rotated staggered grid. Journal of Applied Geophysics, 104: 75-89.
DOI:10.1016/j.jappgeo.2014.02.012 |
|
Zhou Q F, Lam K H, Zheng H R, et al.
2014. Piezoelectric single crystal ultrasonic transducers for biomedical applications. Prog. Mater. Sci., 66: 87-111.
|
|
邓继新, 周浩, 王欢, 等.
2015. 基于储层砂岩微观孔隙结构特征的弹性波频散响应分析. 地球物理学报, 58(9): 3389–3400.
DOI:10.6038/cjg20150931 |
|
付博烨, 符力耘, 魏伟, 等.
2016. 超声岩石物理实验尾波观测中边界反射的影响分析. 应用地球物理, 13(4): 667–682.
|
|
吴如山, 谢小碧.
2014. 地震学百科知识(十二)——地震波散射. 国际地震动态(6): 31–36.
DOI:10.3969/j.issn.0235-4975.2014.06.007 |
|
 2018, Vol. 61
2018, Vol. 61

