地震波正演模拟是模拟地震波在介质中的传播过程,研究其传播特性与地球介质参数的关系.通过正演模拟以达到对实际观测地震记录的最优逼近.有限差分方法能够准确描述地下介质分布状况及波在各种介质中的传播规律.但是这种方法存在一个无法回避的缺点——数值频散的问题.在弹性波正演模拟的过程当中,为了提高差分精度,减小数值频散,许多学者做了大量的研究工作.
地球物理学家最早提出有限差分解决波的传播问题要追溯到40多年前.那时大部分的研究都是基于二阶位移量的有限差分正演模拟.Alterman和Karal(1968)将有限差分方法应用于均匀介质的地震波数值模拟当中.Boore(1972)将其应用于非均匀介质的地震波传播当中.Kelly等(1974)真正实现了有限差分制作合成地震记录的方法.在此之后针对有限差分不同网格分析的文章大量的涌现,如何提高计算的精度及效率是学者们关注的重点.Madariage(1976)提出了一种较为先进的交错网格有限差分方法,并首先将其应用于模拟弹性介质内圆形扩展破裂产生的波动.Crase(1990)将高阶差分方法运用到求解二阶弹性波方.Graves(1996)给出了三维速度应力方程交错网格有限差分弹性波传播的模拟方法.Saenger等(2000)用交错网格有限差分模拟了二维和三维黏弹性介质中波的传播.董良国等(2008)对一维弹性波高阶交错网格有限差分方法进行了进一步实现.Higdon等(2008)对交错网格有限差分方法的边界问题强反射问题进行了有效解决.近年来数值模拟正演的研究工作仍然在高速发展.
断层是油气藏中非常重要的地质特征之一.现在随着地震勘探程度的逐渐提高,储量较小,低幅度构造的勘探逐渐受到重视.复杂断块油藏是受众多断层切割,且复杂化的断块圈闭所形成的一类比较特殊的油藏.在这类油藏中断层是其中至关重要的组成部分,怎样进行精细的构造解释将成为断块油田制定勘探及开发措施的关键.因此,如何做好断层断面波的成像及分析工作也就变得尤为关键.
断层相对于平层的成像照明度较低,断面波同相轴不容易识别,断层波形容易发生畸变.这些问题导致利用常规有限差分正演模拟进行断面波正演工作会产生强烈的数值频散,给断面波的正演分析带来更大的阻碍.这就不得不使我们采用更高精度的高阶交错网格有限差分方法进行数值模拟,从而减小数值频散的干扰,提高正演模拟的精度.
本文利用高阶交错网格有限差分方法从采集因素的采集方向和电缆长度,地质因素的地层倾角,断距,反射系数以及处理因素的偏移成像三个方面对断面波成像的影响因素进行分析.通过正演论证,得出只有采用合理的采集参数才能提高断面波的照明度;只有在断层解释时有效结合地质因素才能提高断层解释的精度;只有利用合理的偏移方法才能使断层正确归位,偏移成像更加准确.
1 高阶交错网格有限差分算法交错网格差分的主要思想是将空间的导数值在两个空间网格的中间进行计算,这样做的好处是在不增加计算量的情况下提高差分方程的精度.主体网格与交错网格两者相差半个网格间距.为了满足差分格式的需要,需要对差分方程的参数定义在主体网格和交错网格上(李国平等,2011).
对于空间高阶差分格式,在交错网格技术中,变量的导数是在相应网格点之间的半程上计算的.为此,采用下式计算一阶空间导数:
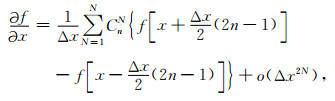
|
(1) |
其中CnN是待定系数,它是确定一阶空间导数的2N阶差分精度的关键.将(1)式在x处用Taylor公式展开整理,并通过解矩阵方程从而可以确定CnN.
对各向同性介质速度应力弹性波方程给出10阶空间差分精度的差分格式,相应的差分网格如图 1所示,参数定义如表 1所示.最终交错网格有限差分格式为
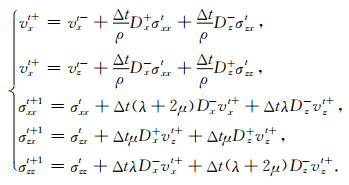
|
(2) |
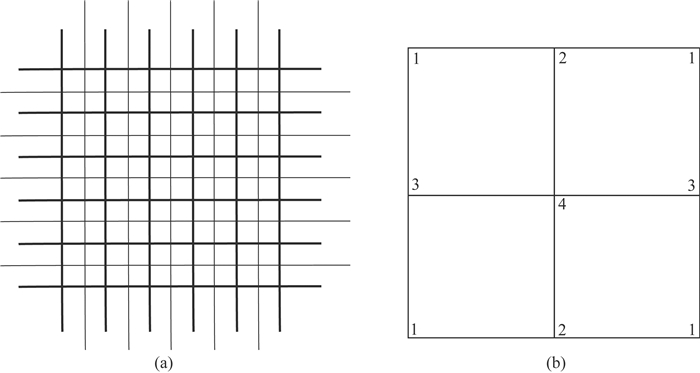
|
图 1 (a) 交错网格及(b)单元网格参数定义 Fig. 1 (a) Staggered grid difference format and (b)Unit grid parameter definition |
|
|
表 1 弹性波场分量和弹性参数的空间位置 Table 1 The spatial position of elastic wave field and elastic parameters |
式中,t±表示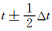
有限差分法是用有限的离散值来代替连续的介质,这样必然会产生数值频散问题.减小这种误差最有效的方法就是减小空间网格,从而增加空间采样率.但是这样做的弊端是成倍增加了计算时间.利用以上提出的高阶交错网格有限差分方法既可以在空间上减小计算网格,从而增加了采样率,而且还有效缩短了计算时间,提高了计算效率.所以利用高阶交错网格有限差分方法进行断层断面波正演分析工作是十分必要且有效的.
2 断面波成像影响因素正演分析由于断面两侧具有不同岩性,或者不同地质年代的地层直接接触,断层面本身就是一个良好的波阻抗界面.这种阻抗界面可以使地震波传播轨迹发生变化,产生的反射波即为断面波.由于断面波是一种界面反射波,所以它具有一般界面反射波的特点.但是由于它是断层面产生的反射波,所以断面波又有它不同与平界面反射波的特点.由于断面倾角一般都大于地层倾角,所以断面波是大倾角反射波.在水平叠加剖面上,同向轴比较陡直,和一般反射波同向轴产状不协调,常和它们交叉,产生干涉.由于断面波是断层面上的反射波,所以在断面波附近,经常伴随有绕射波和回转波等干扰(吕公河等,2006).
在地震资料采集及处理过程中,采集因素,地质因素,及处理因素对地震资料偏移成像的品质均有影响.本文主要从采集因素中的采集方向和电缆长度,地质因素当中的断层倾角,断距和反射系数及处理因素中的偏移成像方法等因素一一展开进行断面波成像正演研究.
2.1 采集因素对断面波成像的影响在地震采集过程中,采集参数对地震资料品质有较大影响.合理的采集参数可以提高地震资料的信噪比和分辨率(蒋先艺等,2003).对于断层断面波成像的研究,主要的影响因素是采集方向和电缆长度,其他参数相对于以上两个参数影响较小.所以本文主要针对采集方向和电缆长度进行正演模拟研究.
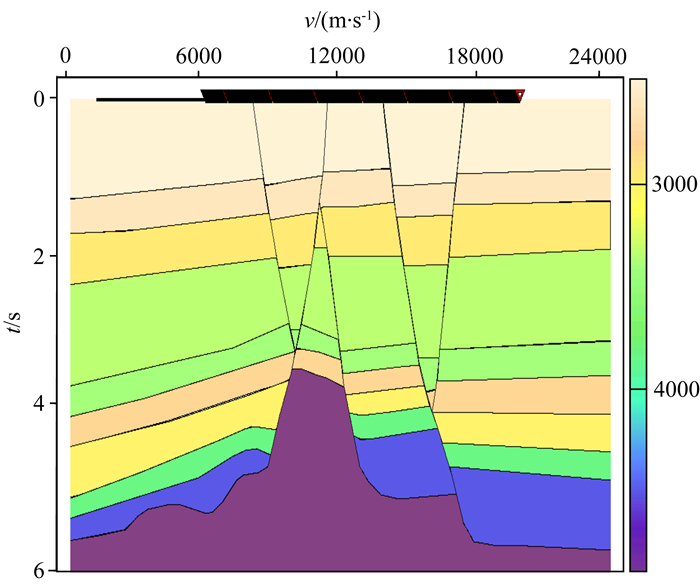
2.1.1 采集方向对断面波成像的影响对于采集方向,沿着断层的倾向,可分为上倾放炮下倾接收和下倾放炮上倾接收两种情况.本文针对渤海海域具有代表性的秦皇岛某区块X型断层进行模型正演.实际地震剖面与速度模型如图 2和图 3所示.

|
图 2 秦皇岛30区块X型断层 Fig. 2 X type fault in Block 30 of Qinhuangdao |
|
图 3 速度模型 Fig. 3 Velocity model |
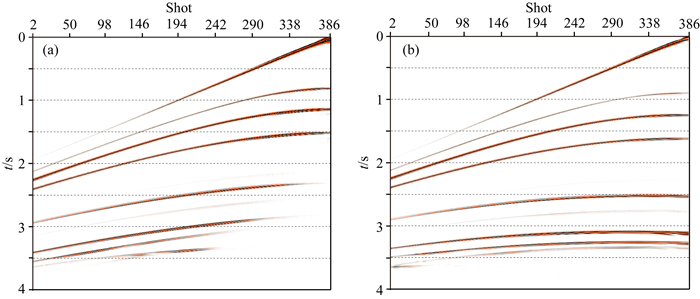
图 4为采集方向相反,其他采集参数相同的正演单炮记录.图 4a中近偏移距信息有很多缺失.相反,图 4b中近偏移距信息没有缺失.从而说明采集方向不同,采集到的反射信息量有较大差别.本文统一规定正演模拟海上的观测系统,右侧放炮左侧接收为正方向,同理,左侧放炮右侧接收为负方向.
|
图 4 正演单炮记录 (a)正方向;(b)反方向. Fig. 4 Forward single shot (a) In positive direction; (b) In negative direction. |
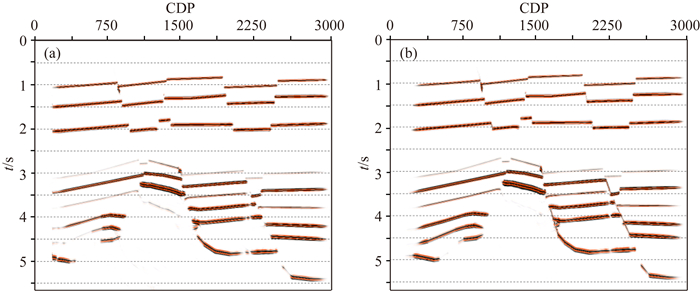
图 5(a,b)分别为两种采集方向数据得到的偏移结果.从结果中可看出,断面波有效成像的断层,其采集方向均为上倾接收下倾放炮.从而得到论断:沿着断层的倾向,上倾接收下倾放炮更有利于断面波成像;反之上倾放炮下倾接收不利于断面波成像.所以在设计采集方向时,无论拖缆采集或海底电缆采集,采集方向应尽量沿着断层的倾向进行采集设计,这样可以有效提高断面波成像的质量.

|
图 5 时间偏移剖面 (a)正向采集; (b)反向采集. Fig. 5 Migration profile in time domain (a) In positive direction; (b) In negative direction. |
目前海上地震资料采集主要分为拖缆采集和海底电缆采集,虽然海底电缆采集可以提供更宽的方位角和覆盖次数,但是由于采集成本较高,因此拖缆采集仍然占有重要地位.在众多的采集参数中,电缆长度对地震资料品质的影响很大.增加电缆长度可以增加覆盖次数,进而提高信噪比.但是增加电缆长度会增加采集成本,致使收益下降.过长电缆长度的中远偏移距信息还会降低资料的分辨率,所以在设计电缆长度时,应根据具体地质目标采用恰当的缆长(Vermeer,2009).
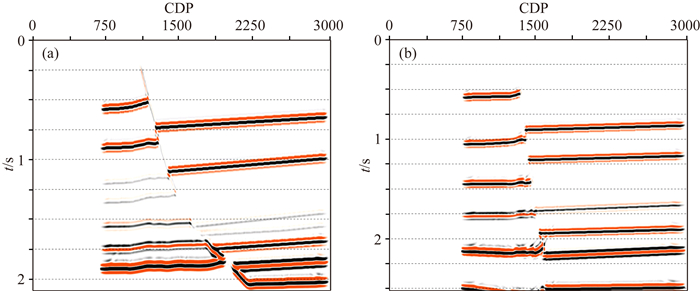
本文利用1800 m和4800 m的电缆长度进行数据正演.当缆长为1800 m时,由于断层倾角较陡,近偏移距接收不到断层反射信息.但是当缆长为4800 m时,即使近偏移距接收断层反射信息较少,但是偏移距足够大,远偏移距可以接收大量的有效信号,弥补了近偏移距接收不到反射信号的缺陷.图 6a和6b分别为电缆长度为1800 m和4800 m正演数据的叠前时间偏移剖面.由结果中可知,当电缆长度为1800 m时,断层断面波不能成像;当电缆长度为4800 m时,断层倾向与采集方向一致的断层断面波有效成像.从而得出结论:增加电缆长度可以有效增加中远偏移距的采集信息,增加了照明范围,利于断层断面波成像;反之,减小电缆长度会降低照明范围,不易于断面波成像.
|
图 6 时间偏移剖面 (a)缆长1800 m; (b)缆长4800 m. Fig. 6 Migration profile in time domain (a) The cable length is 1800 m; (b) The cable length is 4800 m. |
除采集因素外,断层本身的性质对断面波成像影响也很大.例如断层倾角、断距、阻抗差等.本文分别对断面波成像影响较大的断层倾角及对断面波波形影响较大的阻抗差异进行了正演分析.
2.2.1 断层倾角对断面波成像的影响断层相对于正常地层具有倾角陡,界面两层速度差异大等特点.如果方位角、采集密度、电缆长度、偏移孔径等参数没有达到断层成像需求时,这些特点就会导致断层照明度变低,断面波成像模糊或不能成像.
本文首先在断层其他参数不变的前提下,对断层倾角进行了正演模拟,建立正演模型参考的断层是渤海垦利某油田的边界断层.该断层从水面一直断至基底,倾角由浅至深逐渐变陡,断面两侧速度横向变化不大,利于研究断层倾角对断面波成像的影响.
本文模拟的断层倾角由浅至深逐渐变大,模拟的断层角度由浅至深为35°~45°,45°~60°,60°~70°,70°~75°,采集方向为沿断层倾向上倾接收下倾放炮.叠前时间偏移结果如图 7所示.

|
图 7 时间偏移剖面 (a)倾角为35°~45°; (b)倾角为45°~55°; (c)倾角为60°~70°; (d)倾角为70°~75° Fig. 7 Migration profile in time domain (a) The dip angle is 35°~45°; (b) The dip angle is 45°~55°; (c) The dip angle is 60°~70°; (d) The dip angle is 70°~75°. |
由以上偏移结果可知,对于生产中广泛应用的射线域Kirchhoff叠前时间偏移,当断层倾角小于60°时,断面波成像清晰;当断层倾角大于60°时,断面波成像不清或不能成像.
2.2.2 断层断距对断面波成像的影响本文针对断层断距对断面波成像的影响进行了正演分析,图 8a和8b分别为倾角为45°时减小断层断距的成像剖面和倾角为60°时增大断层断距的成像剖面.
|
图 8 时间偏移剖面 (a)倾角45°; (b)倾角60°. Fig. 8 Migration profile in time domain (a) The dip angel is 45°; (b) The dip angel is 60°. |
由以上两图的比较中可知,当断层倾角为45°时,减小断层断距,断面波成像效果依然很好;当断层倾角增大到60°时,增加断层断距,断面波依然不能有效成像.由以上现象可得出,影响断面波成像的主要因素是断层倾角,断层断距对断面波成像的影响较小.
2.2.3 阻抗差异对断面波成像的影响本文对图 9中各段断层的反射系数与振幅值进行了相关统计,统计的结果表明反射系数与振幅值成正比关系,如图 9所示.

|
图 9 反射系数与振幅成正比关系 Fig. 9 The reflection coefficient is proportional to the amplitude |
阻抗差异对断面波成像的影响很大.当阻抗差异较大时,断面波振幅值相应增大,断面波容易成像并识别.当阻抗差异较小时,断面波振幅值相应减小,偏移剖面上断面波模糊导致无法识别.
反射系数的极性变化导致断面波波形极性产生变化,反射系数的极性可分为正反射系数和负反射系数.波形的极性反转与断层两盘速度值差异量没有关系,而由断层两盘速度差是否有反转所决定,如图 10所示.
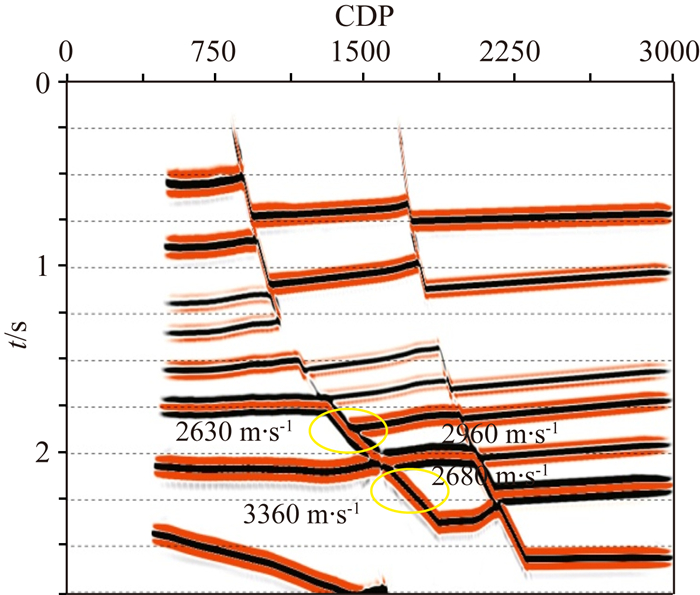
|
图 10 速度反转决定断面波波形极性反转 Fig. 10 Fault surface wave polarity inversion is decided by velocity inversion |
对于同一套断层,解释人员往往习惯于把断层位置解释在同一种波形极性位置,很少考虑波形极性反转的情况.如果遇到这种波形极性反转的情况,就会给解释断层带来很大的误差.所以对于断面波的解释工作,应当考虑速度参数,判断是否有波形极性反转,若有极性反转,应及时调整解释思路,避免解释误差的产生.
图 11为垦利某区块断层的解释方案,在没有考虑波形极性反转之前,断层位置统一解释在波峰位置,但是由于速度原因导致断面波波形极性发生反转,上述解释方案造成解释断层位置严重偏差.通过参考速度参数,分析出断层真实位置为峰和谷中间位置,从而调整了解释方案.调整解释方案后的断层位置北移约80 m,如图 12所示.通过上述实际数据的论证得出:对于断面波的解释工作,参考速度参数非常必要,若断面波波形极性出现反转,应及时调整解释思路,避免解释误差的产生.
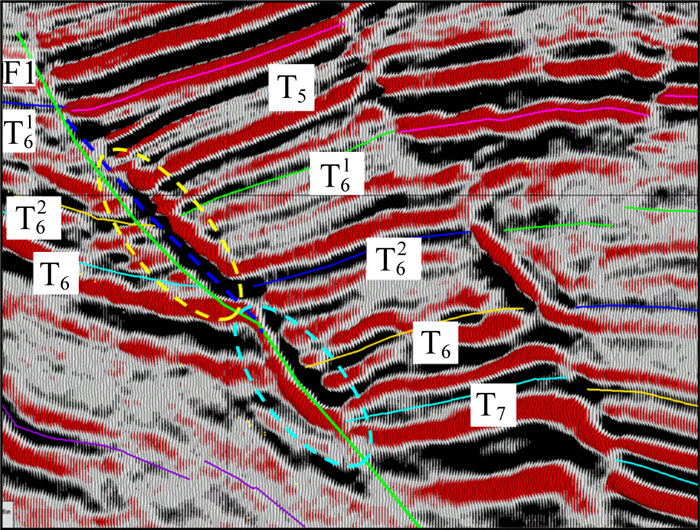
|
图 11 极性反转断面波解释方案 Fig. 11 Interpretive version of the fault surface wave polarity inversion |
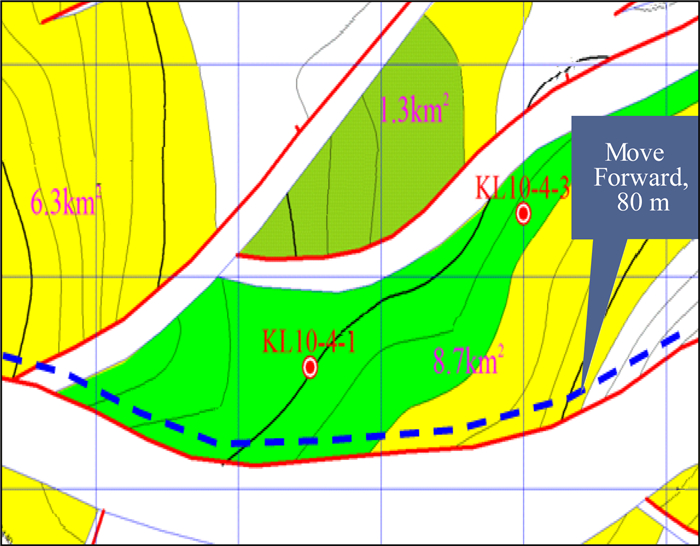
|
图 12 调整解释方案后断层位置 Fig. 12 Fault positions after adjusting the interpretive version |
地震资料处理的各个环节对断面波成像的影响很大.去噪环节影响断面波的信噪比,反褶积的环节影响断面波的分辨率,速度建模及偏移成像的环节影响断面波能否正确成像与归位.这些环节当中偏移成像对断面波的影响最为敏感,所以本文主要对偏移成像的影响进行正演分析(张慧和李振春,2011).
实际生产中,虽然叠前深度偏移发展迅速,但是叠前时间偏移仍然占据主导地位(张秀红等2003).叠前时间偏移速度容易获取,计算成本低,计算效率高,在地质条件不是特别复杂的地区成像精度较高,所以这种偏移方法往往受到地震资料处理者的喜爱.但是这种偏移方法的前提条件是横向速度变化小,如果遇到横向速度变化大的地层或断层,偏移质量会明显下降.遇到这种情况,往往考虑叠前深度偏移,这种偏移方法是解决复杂地质体非常有效的手段.本文分别利用Kirchhoff叠前时间偏移和Kirchhoff叠前深度偏移对断面波成像的影响进行了正演分析,正演速度模型及两种偏移方法结果如图 13,14(a, b)所示.
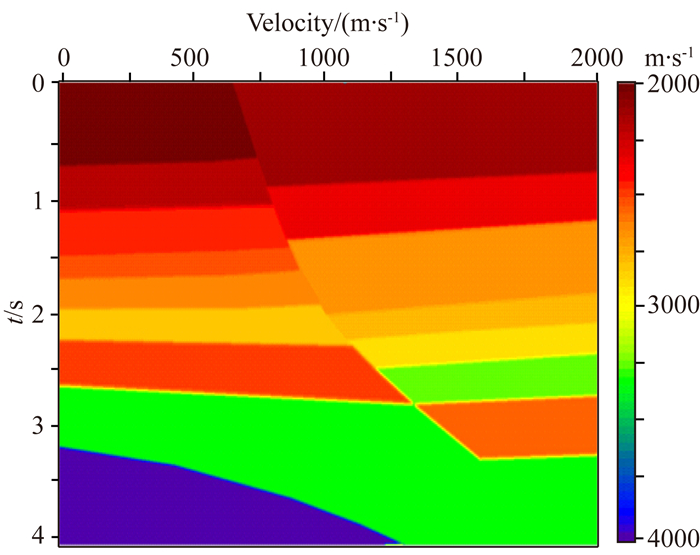
|
图 13 正演速度模型 Fig. 13 Forward velocity model |
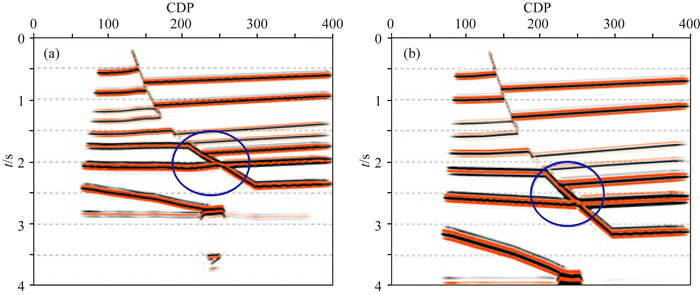
|
图 14 (a) 叠前时间偏移剖面; (b)叠前深度偏移剖面 Fig. 14 (a) Prestack time migration profile; (b) Prestack depth migration profile |
由图 14a和14b的比较中可看出,断层附近同相轴出现明显的上翘或下拉假象,出现这种情况的原因是由于叠前时间偏移应用的是均方根速度,没有考虑速度横向变化给偏移成像带来的影响,从而造成假象的产生.叠前深度偏移不会出现这种假象,这种偏移方法应用的速度是深度域层速度,充分考虑了速度横向的变化,所以不会出现同相轴的上翘或者下拉.由以上的分析中可知,对于断层两盘速度差异量不大的断层,叠前时间偏移可以得到很好的效果,误差不大;但是如果断层两侧速度横向变化非常大,叠前时间偏移就会产生很大的误差,这时候应当考虑采用叠前深度偏移来解决偏移带来的误差.
3 结论本文正演采用高阶交错网格有限差分方法,这种数值模拟方法可以在保证计算效率的同时有效压制数值频散,给断面波成像的分析带来可靠的保障.本文主要从采集因素、地质因素及处理因素出发对断面波成像的影响进行了正演分析,通过正演分析得出以下结论:
(1) 采集因素:沿着断层的倾向,上倾接收下倾放炮这种采集方式更有利于断面波成像;考虑电缆长度对断面波成像影响,应与多项处理步骤综合在一起定量计算,并与正演论证有效结合,最终计算出最佳的成像电缆长度.
(2) 地质因素:影响断面波成像的主要因素是断层倾角大小,断层的断距对断面波成像的影响较小;断层反射系数与断面波振幅值成正比关系,阻抗差异的大小直接影响断面波成像的照明度;断层上下两盘速度变化是引起断面波波形极性反转的主要原因,对于断层解释,应当结合速度参数,防止解释误差.
(3) 处理因素:偏移方法对断面波成像的影响非常大,当断层两侧速度差别不大时,利用叠前时间偏移可以满足成像精度;当横向速度变化较大时,利用叠前时间偏移误差增大,这时应当采用叠前深度偏移方法,确保断层正确归位与成像.
Alterman Z, Karal E C Jr.
1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of the Seismological Society of America, 58(1): 367-398.
|
|
Boore D M.
1972. Finite difference methods for seismic wave propagation in heterogeneous materials. Methods in Computational Physics:Advances in Research and Applications, 11: 1-37.
DOI:10.1016/B978-0-12-460811-5.50006-4 |
|
Crase E. 1990. High-order (space And Time) finite-difference modeling of the elastic wave equation.//60th Annual International Meeting, SEG. Expanded Abstracts, 987-991.
|
|
Dong L G, Ma Z T, Cao J Z, et al.
2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese Journal of Geophysics, 43(3): 37-41.
|
|
Graves R.
1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bulletin of the Seismological Society of America, 86(4): 1091-1106.
|
|
Higdon R L.
2008. Absorbing boundary conditions for elastic waves. Geophysics, 1991, 56(2): 231-241.
|
|
Jiang X Y, He Z H, Huang D J.
2003. New concept for seismic data acquisition. Computing Techniques for Geophysical and Geochemical Exploration, 25(2): 130-134.
|
|
Kelly K R, Ward R W, Treitel S, et al.
1974. Synthetic seismograms:a finite-difference approach. Geophysics, 41(1): 2-27.
|
|
Li G P, Yao F C, Shi Y M, et al.
2011. Several key issues of finite-difference seismic wave numerical simulation. Progress in Geophysics, 26(2): 469-476.
|
|
Lü G H, Yin C, Zhou X H, et al.
2006. Precious simulation of seismic illumination based on acquired targets. Oil Geophysical Prospecting, 41(3): 258-261.
|
|
Madariage R.
1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666.
|
|
Saenger E H, Gold N, Shapiro S A.
2000. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion, 31(1): 77-92.
DOI:10.1016/S0165-2125(99)00023-2 |
|
Vermeer G J O.
2009. Wide-azimuth towed-streamer data acquisition and simultaneous sources. The Leading Edge, 28(8): 950-958.
DOI:10.1190/1.3192843 |
|
Zhang H, Li Z C.
2011. Seismic wave simulation method based on dual-variable grid. Chinese Journal of Geophysics, 54(1): 77-86.
DOI:10.3969/j.issn.0001-5733.2011.01.009 |
|
Zhang X H, Qiao D J, Tian X Q.
2003. Deep 3-D seismic data acquisition techniques. Oil Geophysical Prospecting, 38(4): 358-362.
|
|
董良国, 马在田, 曹景忠, 等.
2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 37–41.
|
|
蒋先艺, 贺振华, 黄德济.
2003. 地震数据采集新概念. 物探化探计算技术, 25(2): 130–134.
|
|
李国平, 姚逢昌, 石玉梅, 等.
2011. 有限差分法地震波数值模拟的几个关键问题. 地球物理学进展, 26(2): 469–476.
|
|
吕公河, 尹成, 周星合, 等.
2006. 基于采集目标的地震照明度的精确模拟. 石油地球物理勘探, 41(3): 258–261.
|
|
张慧, 李振春.
2011. 基于双变网格算法的地震波正演模拟. 地球物理学报, 54(1): 77–86.
DOI:10.3969/j.issn.0001-5733.2011.01.009 |
|
张秀红, 乔大军, 田新琦.
2003. 深层三维地震勘探数据采集技术. 石油地球物理勘探, 38(4): 358–362.
|
|
 2018, Vol. 61
2018, Vol. 61

