2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266071
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
在油气勘探开发方面,地应力不仅与地层的变形破裂、油气的运移聚集以及储层的压裂施工改造等众多问题有关,还对具有低孔低渗特点的页岩储层的开采与开发有着不可替代的作用.因此,研究地应力不仅有助于了解地质构造的形成、演化以及断层的形态和分布而且还能够指导井网的布置、设计以及水力压裂等,在油气勘探、开发和生产方面都具有重要的意义(李志明和张金珠,1997).
Heim(1905—1912)首先提出了地应力的概念,它是指存在于地层中未受工程扰动的天然应力,并假设原岩应力在各个方向上均相等,即静水应力状态.1926年,金尼克修正了Heim的静水压力假说,并给出了针对均匀各向同性介质的地应力公式,称为金尼克模型.但该模型计算的应力不够准确,需要根据实际工区添加校正项(如孔隙度和构造应力等附加项)以提高应力预测的精度(Biot and Willis, 1957;Bourgoyne et al., 1986).1932年,Liearace首次对某工区地应力进行了测量,随后发展了孔壁岩石破坏法(Leeman,1964;Haimson,1968;Cornet and Valette, 1984, Cornet, 1986;Stephasson, 1983a, 1983b;Zoback,2007)、弹性应变恢复法(Mathar,1934;Hast,1969;Amadei and Stephasson, 1997;Zang and Stephanson, 2010)、岩芯法(Voight,1968;Simmons, et al., 1974;Sugawara, et al., 1978;Logan and Teufel,1978;Teufel,1983;Gies,1987;Warpinski and Teufel, 1989;Matsuki and Takeuchi, 1993)等地应力测量方法,但是地应力测量只能得到岩体某点的应力大小和方向,所测得数据有限;为了得到沿井深连续分布的分层地应力剖面,开展了利用测井资料计算地应力的方法,国内外许多专家学者对此做了相关研究,但是该方法不能得到连续的地应力剖面.Cleary(1993)提出了一个不含泊松比的应力计算模型,通过不断调整应力曲线,使其与应力测量数据点达到最佳吻合的方法得到模型中的系数.以上地应力计算模型都是基于各向同性介质的基本假设下,而实际地层是各向异性介质,因此基于各向同性介质假设下的公式所计算的应力与实际应力不匹配.Iverson(1995)利用各向异性泊松比替换了金尼克模型中的各向同性泊松比,一定程度上解决了计算的应力与实际应力不匹配的问题,但是难以直接获得其公式中的相关参数.Gray等(Gray et al, 2010a, 2010b, 2010c, 2012; Gray, 2011)提出了基于地震数据估算地应力的方法,利用该方法估算了水平应力差异比,即最大和最小水平应力差与最大水平应力的比值(Differential Horizontal Stress Ratio),它是指示储层中水平两个方向应力差异大小的指示因子.水平应力差异比较小的区域表明该区域适用于压裂开发,且易于形成复杂的裂缝网,有助于页岩气藏的勘探开发,但是该方法只是基于HTI(Horizontal Transverse Isotropy)介质,而实际页岩通常等效为正交各向异性介质,既含有大量的高角度裂缝又具有很强的水平层理特征.马妮等(2017)推导了正交各向异性介质的地应力计算公式,并对该公式进行了验证,同时提出了正交各向异性水平应力差异比(即ODHSR,Orthorhombic Differential Horizontal Stress Ratio)的概念.
本文依据正交各向异性介质理论的地应力计算公式(马妮等,2017),利用叠前方位地震数据估算了正交各向异性水平应力差异比(ODHSR).首先,根据方位弹性阻抗方程,利用6个不同方位、不同入射角的叠前方位地震数据反演方位弹性阻抗数据体,通过反演得到的方位弹性阻抗数据体提取储层的弹性参数和各向异性参数;其次,根据正交各向异性介质理论的地应力计算公式,利用得到的弹性参数和各向异性参数估算地层的ODHSR;最后选取某工区的叠前方位地震数据对该方法进行了实际应用.实际应用结果表明,根据正交各向异性介质理论的地应力计算公式,通过叠前方位地震数据反演得到的ODHSR能够指导水力压裂改造,提高储层的渗透率和采收率,在油气勘探和开发方面有着十分重要的作用.
1 方法原理 1.1 基于方位各向异性的弹性阻抗方程叠前地震反演方法由于其能够较为准确的提取丰富的储层信息,且反演方法稳定可靠,因此,被广泛的应用于储层预测和流体识别等方面(印兴耀等, 2014, 2015, 印兴耀和刘欣欣,2016;宗兆云等, 2012a, 2012b;Zong et al., 2012, 2013).随着人类社会发展对油气需求的日益增长,泥页岩及裂缝型储层等非常规储层逐渐成为油气勘探的研究重点.裂缝型储层是指包含近垂直裂缝的储层,包括具有各向同性背景的HTI储层和水平层理背景的OA储层,其是实际地层中较为常见的形式,具有较大的勘探潜力和开发前景.而常规的叠前地震反演方法很难满足泥页岩、裂缝型储层等复杂非常规储层的勘探要求,特别是存在较强各向异性特征的非常规储层,因此发展针对裂缝型储层等非常规储层的叠前方位地震反演方法显得尤为重要.Ruger(1996)推导了HTI介质的方位反射系数近似方程,使针对裂缝型储层的叠前方位地震反演成为可能,该反射系数近似公式另一种以纵横波速度、密度以及各向异性参数表征的形式为
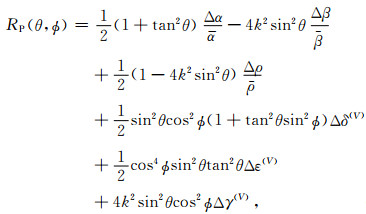
|
(1) |
其中,α、β和ρ分别为纵波速度、横波速度和密度,θ为入射角,ϕ为方位角,Δα/α、Δβ/β和Δρ/ρ分别为纵波速度反射系数、横波速度反射系数和密度反射系数,Δδ(V)、Δε(V)和Δγ(V)为上下介质各向异性参数的差值.
叠前方位地震反演方法中的方位各向异性弹性阻抗方法具有较好的抗噪性和稳定性,且能够充分利用方位地震数据的方位各向异性信息,因而在裂缝型储层预测方面具有广泛的应用.陈天胜等(2006)以HTI介质的方位反射系数近似方程为基础,根据Connolly(1999)推导弹性阻抗方程的思想,将方位反射系数等价为
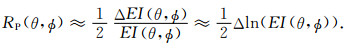
|
(2) |
利用微分转换关系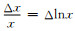
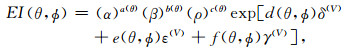
|
(3) |
其中,a=(1+tan2θ),b=-8k2sin2θ,c=(1-4k2sin2θ),d=sin2θcos2ϕ(1+tan2θsin2ϕ),e=cos4ϕsin2θtan2θ,f=8k2sin2θcos2ϕ.
由于方位各向异性弹性阻抗方程的量纲会随着入射角和方位角的变化出现剧烈变化的不稳定现象,因此为了得到可靠预测地应力的弹性参数和各向异性参数,需要对方位各向异性弹性阻抗做标准化处理(Whitcombe,2002),得到标准化的方位弹性阻抗方程为
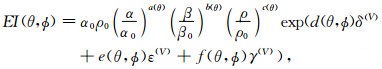
|
(4) |
其中,α0、β0和ρ0分别为纵波速度、横波速度和密度的均值.利用经过标准化的方位弹性阻抗方程进行叠前方位地震反演能够得到稳定且可靠的反演结果.
1.2 基于方位弹性阻抗的各向异性参数反演方法为了能够从弹性阻抗数据体中反演出稳定的弹性参数和各向异性参数数据体,需要对方程(4)进行线性化处理,即

|
(5) |
其中,EI0=α0ρ0.从方程(5)可以看出利用线性化后的方位弹性阻抗方程提取弹性参数和各向异性参数至少需要6个不同方位角、不同入射角的弹性阻抗数据体.将6个不同方位、不同入射角的弹性阻抗方程写成矩阵形式为

|
(6) |
利用已知的α、β、ρ、δ(V)、ε(V)和γ(V)测井数据以及井旁道方位弹性阻抗值计算公式(6)中各参数对应的常系数.将叠前方位弹性阻抗反演得到的6个不同方位、不同入射角的弹性阻抗代入公式(6)中,结合各参数对应的常系数,通过求解可得到各采样点处的纵波速度α、横波速度β、密度ρ和各向异性参数ε(V)、δ(V)、γ(V).利用HTI介质与VTI介质各向异性参数的关系(Thomsen,1986),即
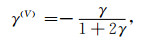
|
(7) |
可以得到VTI介质的各向异性参数γ,用于计算正交各向异性介质的地应力.
1.3 基于正交各向异性介质的地应力反演方法正交各向异性介质是由周期性的水平薄互层和垂直的定向裂缝构成的各向异性介质,又叫做OA介质,它具有三个相互正交的对称面,是与实际页岩储层最相符的各向异性介质模型.根据线性滑动理论(Schoenberg and Sayers, 1995),OA介质的柔度矩阵可以近似等价为具有垂直对称轴的横向各向同性(VTI)背景介质柔度矩阵与扰动裂缝柔度矩阵的和.VTI背景介质的刚度矩阵表示为
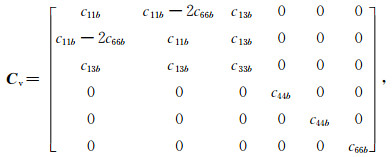
|
(8) |
其中,cijb为VTI介质的弹性常数.根据Schoenberg和Sayers(1995),扰动裂缝柔度矩阵Sf简化为
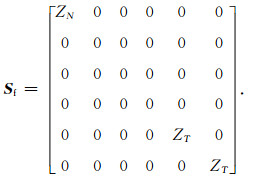
|
(9) |
根据Schoenberg和Sayers提出的线性滑动理论,将OA介质的柔度矩阵近似表示为
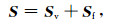
|
(10) |
其中,Sv为柔度矩阵,其是刚度矩阵Cv的逆矩阵.在弹性形变范围内,根据广义胡克定律,弹性介质的应力和应变关系表示为
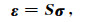
|
(11) |
其中,ε是应变张量,σ是应力张量,S是柔度张量(柔度矩阵).将公式(11)表示为矩阵形式,假设存在垂直方向的主应力和两个水平方向的主应力,且假设地下岩石是有界的,不能移动,则水平方向的应变为零(Iverson,1995),可得水平方向上应变与应力的关系表达式.
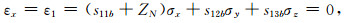
|
(12) |
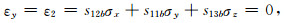
|
(13) |
其中,sijb为VTI介质的柔度系数.根据Thomsen各向异性参数表达式,利用公式(12)和(13),可以得到正交各向异性介质的地应力近似公式(马妮等,2017):
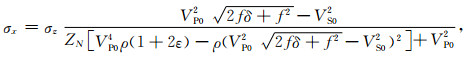
|
(14) |
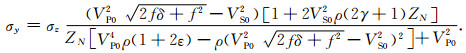
|
(15) |
利用最大水平地应力σy和最小水平地应力σx推导了正交各向异性水平应力差异比(ODHSR)近似公式,将其命名为正交各向异性水平应力差异比(ODHSR),它是最大水平地应力σy和最小水平地应力σx的差除以最大水平地应力σy所得的比值,是表示水平应力相对变化的储层参数,能够评价地层是否易于压裂成网.在进行水力压裂时,ODHSR低值表明该区域地层容易压裂成裂缝的网状结构,高值则表明该区域地层容易形成定向排列的裂缝,不利于有效的提高储层的渗透率,达到预期的增产效果.由于ODHSR低值区域为进行水力压裂最佳区域,因此ODHSR较为理想的取值范围为0~0.2,但根据实际工区的情况其范围可能会更为广泛.ODHSR近似公式为
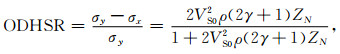
|
(16) |
其中,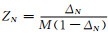
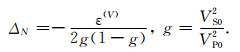
|
λ和μ为各向同性介质的拉梅参数,ΔN为裂缝的法向弱度,其数值变化范围为0~1.ODHSR综合考虑了HTI介质的裂缝扰动性质和VTI介质的水平层理特征,更符合实际的页岩储层,它的值越低,表明最大水平地应力与最小水平地应力的值越接近,地层的延展性越差,越容易压裂成网,因此可以将其作为评价页岩油气储层是否易于压裂成网的重要因子.根据ODHSR近似公式,利用基于方位弹性阻抗的各向异性参数反演方法提取的弹性参数和各向异性参数可以估算的地层的ODHSR,得到某个区域连续的ODHSR剖面,有助于寻找最佳进行水力压裂的区域.
2 数值模拟分析 2.1 弹性参数对ODHSR的影响利用ODHSR近似公式研究单一弹性参数数值变化对ODHSR的影响.模型参数设为:当地层的横波速度从1500 m·s-1变为3000 m·s-1,变化间隔为30 m·s-1时,纵波速度为4300 m·s-1,密度为2400 kg·m-3,γ为0.025,ZN单独与ΔN相关,ΔN从0.01变为0.8,变化间隔约为0.2;当地层的密度从1800 kg·m-3变为3000 kg·m-3,变化间隔为50 kg·m-3时,纵波速度为4300 m·s-1,横波速度为2300 m·s-1,γ为0.025,ZN单独与ΔN相关,ΔN从0.01变为0.8,变化间隔约为0.2.单一弹性参数变化对ODHSR的影响如图 1所示.
|
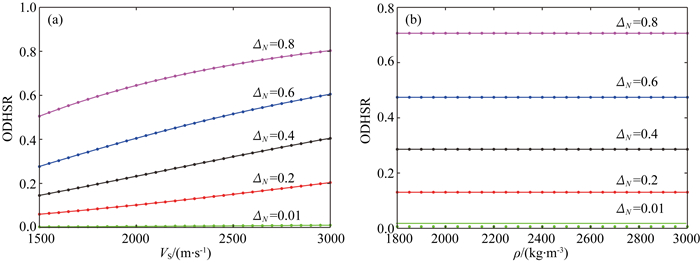
图 1 弹性参数对ODHSR的影响 Fig. 1 Effect of elastic parameters on ODHSR |
图 1a为横波速度对ODHSR的影响,图 1b为密度对ODHSR影响.从图 1a中可以看出,ODHSR随横波速度的增加都呈上升趋势,且ODHSR数值变化幅度随裂缝法向弱度的增加呈先增大后减小的趋势.当横波速度不变时,裂缝的法向弱度越大,ODHSR值越大.因此,横波速度与法向弱度对ODHSR较为敏感,当横波速度和法向弱度的估算值存在误差时,ODHSR估算值会存在一定误差.从图 1b中可以看出,随着密度的增加,ODHSR值保持不变,这表明ODHSR值不受密度的影响,这是因为法向柔度公式中隐含的密度项消除了ODHSR近似公式中密度的影响.因此,利用ODHSR近似公式估算ODHSR时,不会出现因密度反演不稳定而造成ODHSR估算值不稳定的问题.
2.2 各向异性参数对ODHSR的影响利用ODHSR近似公式研究单一各向异性参数数值变化对ODHSR的影响.模型参数设为:当VTI介质各向异性参数γ从0变为0.5,变化间隔为0.01时,纵波速度为4300 m·s-1,横波速度为2300 m·s-1,密度为2400 kg·m-3,ZN单独与ΔN相关,ΔN从0.01变为0.8,变化间隔约为0.2.VTI介质各向异性参数γ对ODHSR的影响如图 2所示.
|
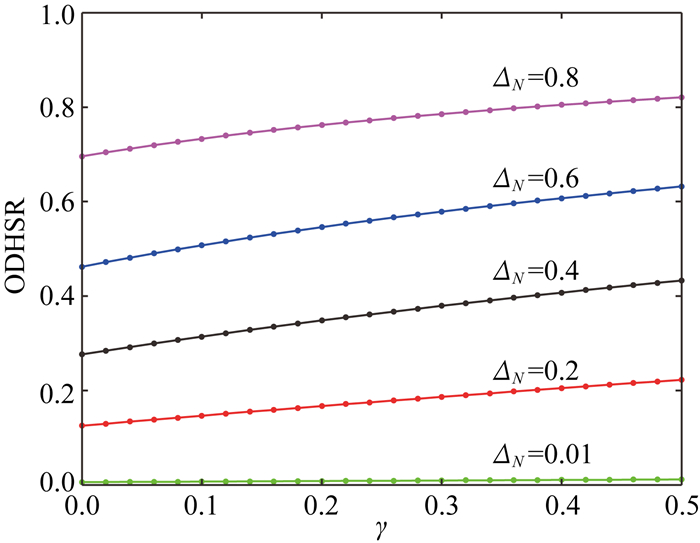
图 2 VTI介质各向异性参数γ对ODHSR的影响 Fig. 2 Effect of anisotropy parameter γ of VTI media on ODHSR |
由图 2可以看出,ODHSR数值随VTI介质各向异性参数γ的增大而增大.当VTI介质各向异性参数γ不变时,裂缝的法向弱度越大,ODHSR值越大.为了研究同一条件下不同参数变化对ODHSR估算值的影响程度,分别假设某单一参数存在10%误差(即增加或减少10%的误差),其他参数数值不变时引起的ODHSR变化量(某单一参数变化后估算的ODHSR与原始参数估算的ODHSR之间的差值).模型参数设为:纵波速度为4300 m·s-1,横波速度为2300 m·s-1,密度为2400 kg·m-3,ZN单独与ΔN相关,ΔN从0变为1,变化间隔约为0.01.结果如图 3所示.
|
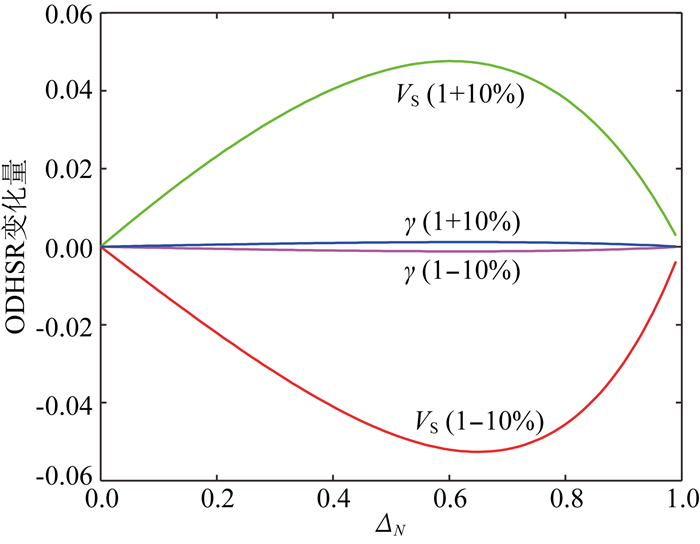
图 3 不同参数存在10%误差时对ODHSR估算值的影响 Fig. 3 Effect of different parameter which has 10% error on ODHSR |
图 3中绿色曲线和红色曲线分别为横波速度增加10%和减小10%误差时引起的ODHSR变化量,蓝色曲线和品红色曲线分别为VTI介质各向异性参数γ增加10%和减小10%误差时引起的ODHSR变化量.从图中可以看出,横波速度变化对ODHSR估算值的影响远远大于VTI介质各向异性参数γ产生的影响,当VTI介质各向异性参数γ存在误差时,对ODHSR估算值的影响较小,但通过数值分析发现,VTI介质各向异性参数γ数值越大(即VTI介质水平层理特征越明显),其数值发生变化时对ODHSR估算值产生的影响越大.
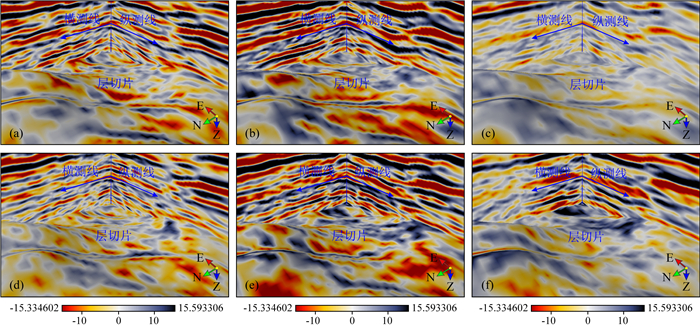
3 实际应用分析实际资料来自中国东部某全方位地震勘探工区,该工区具有较为复杂的断裂构造,裂缝系统较为发育,本文利用基于正交各向异性介质的地应力反演方法估算该工区的ODHSR,寻找易于压裂成网的区域,指导水力压裂的实施.首先对全方位地震数据进行一系列处理得到6个方位且每个方位包含3个入射角的共18个分方位部分角度叠加道集,然后选取其中6个叠前方位地震数据进行叠前方位弹性阻抗反演,方位地震数据如图 4所示,反演得到的6个不同方位、不同入射角的弹性阻抗数据体如图 5所示,最后通过基于方位弹性阻抗的各向异性参数反演方法从弹性阻抗数据体中提取地层的纵波速度、横波速度、密度和HTI介质的各向异性参数,结果如图 6所示.
|
图 4 实际工区不同方位部分角度叠加道集 (a)方位角ϕ=15°,入射角θ=8°;(b)方位角ϕ=15°,入射角θ=16°;(c)方位角ϕ=15°,入射角θ=24°;(d)方位角ϕ=105°,入射角θ=8°;(e)方位角ϕ=105°,入射角θ=16°;(f)方位角ϕ=105°,入射角θ=24°. Fig. 4 Stack data of different azimuths for fractured reservoir (a) Azimuth angle ϕ=15°, incident angle θ=8°; (b) Azimuth angle ϕ=15°, incident angle θ=16°; (c) Azimuth angle ϕ=15°, incident angle θ=24°; (d) Azimuth angle ϕ=105°, incident angle θ=8°; (e) Azimuth angle ϕ=105°, incident angle θ=16°; (f) Azimuth angle ϕ=105°, incident angle θ=24°. |
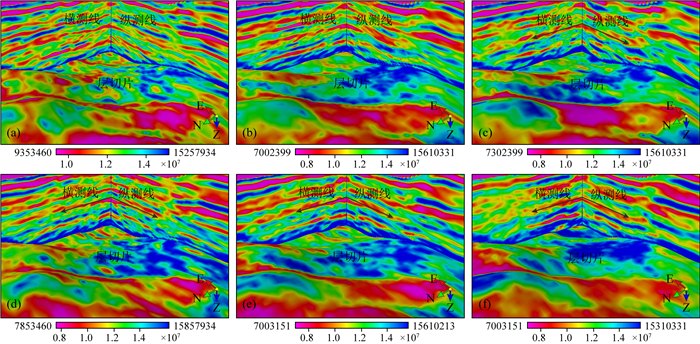
|
图 5 实际工区方位各向异性弹性阻抗反演结果 (a)方位角ϕ=15°,入射角θ=8°;(b)方位角ϕ=15°,入射角θ=16°;(c)方位角ϕ=15°,入射角θ=24°;(d)方位角ϕ=105°,入射角θ=8°;(e)方位角ϕ=105°,入射角θ=16°;(f)方位角ϕ=105°,入射角θ=24°. Fig. 5 Azimuthal anisotropic EI inverted results for fractured reservoir (a) Azimuth angle ϕ=15°, incident angle θ=8°; (b) Azimuth angle ϕ=15°, incident angle θ=16°; (c) Azimuth angle ϕ=15°, incident angle θ=24°; (d) Azimuth angle ϕ=105°, incident angle θ=8°; (e) Azimuth angle ϕ=105°, incident angle θ=16°; (f) Azimuth angleϕ=105°, incident angle θ=24°. |

|
图 6 弹性参数和各向异性参数反演结果(纵横测线剖面和层切片) (a)纵波速度;(b)横波速度;(c)密度;(d) ε(V);(e) δ(V);(f) γ(V). Fig. 6 Inversion result of elastic parameters and anisotropy parameters including inline, crossline and horizontal slicer. (a) P-wave velocity; (b) S-wave velocity; (c) Density; (d) ε(V); (e) δ(V); (f) γ(V). |
根据HTI介质与VTI介质各向异性参数的关系,利用HTI介质的各向异性参数γ(V)计算VTI介质的各向异性参数γ,VTI介质各向异性参数γ的纵横测线剖面和层切片如图 7所示.

|
图 7 VTI介质的各向异性参数γ (纵横测线剖面和层切片) Fig. 7 Anisotropy parameter γ of VTI media (inline, crossline and horizontal slicer) |
利用地层的弹性参数和各向异性参数计算地层的ODHSR,ODHSR层切片如图 8所示.

|
图 8 ODHSR的层切片 Fig. 8 Horizontal slicer of ODHSR |
从图 8可以看出,井A所在区域为ODHSR低值区域,在该处进行水力压裂能够形成复杂的裂缝网状结构,有利于页岩气储层的水力压裂改造,提高储层的渗透率和采收率,因此利用ODHSR计算公式得到的ODHSR层切片能够找到储层中ODHSR低值区域,可以有效的指导页岩的水力压裂施工,影响着压裂的增产效果.综上所述,ODHSR参数在页岩油气开采和勘探方面有着极其重要的作用.
4 结论本文探讨了基于正交各向异性介质的地应力反演方法,利用叠前方位地震数据估算了地层的正交各向异性水平应力差异比,它是评价地层是否适用于压裂成网的主要参数.首先,基于方位弹性阻抗方程,将6个不同方位、入射角的叠前方位地震数据反演得到6个方位弹性阻抗数据体;其次利用得到的方位弹性阻抗数据体提取地层的弹性参数和各向异性参数;然后,根据HTI介质与VTI介质各向异性参数的关系,通过HTI介质的各向异性参数γ(V)得到VTI介质的各向异性参数γ;最后根据ODHSR近似公式,利用地层的弹性参数和各向异性参数估算地层的正交各向异性水平应力差异比(ODHSR).实际资料反演结果表明:根据ODHSR近似公式,利用叠前方位地震数据估算地层的正交各向异性水平应力差异比(ODHSR)既考虑了水平层理特征的作用又考虑了垂直裂缝的影响,更符合实际的页岩储层,能够较为有效的预测储层中容易压裂成网的区域,指导水力压裂的开发.
Amadei B, Stephansson O. 1997. Rock Stress and Its Measurement. London: Chapman & Hall.
|
|
Biot M A, Willis D G.
1957. The elastic coefficients of the theory of consolidation. Journal Applied Mechanics, 24: 594-601.
|
|
Bourgoyne A T, Millheim K K, Chenevert M E, et al. 1986. Applied Drilling Engineering. Richardson, Texas: Society of Petroleum Engineers.
|
|
Chen T S, Wei X C, Liu Y.
2006. New approximation formula for calculation of elastic Impedance in anisotropic media. Geophysical Prospecting for Petroleum, 45(6): 563-569.
|
|
Cleary M P. 1993. Mechanics, Modeling, and Implementation of Hydraulic Fracturing Using the GRI FRACPRO System. Short Course Notes. Houston, Texas.
|
|
Connolly P.
1999. Elastic impedance. The Leading Edge, 18(4): 438-452.
DOI:10.1190/1.1438307 |
|
Cornet F H, Valette B.
1984. In situ stress determination from hydraulic injection test data. Journal of Geophysical Research:Solid Earth, 89(B13): 11527-11537.
DOI:10.1029/JB089iB13p11527 |
|
Cornet F H. 1986. Stress determination from hydraulic tests on preexisting fractures-the H. T. P. F. method. //ISRM International Symposium. Stockholm, Sweden: International Society for Rock Mechanics and Rock Engineering, 301-312.
|
|
Gies R M.
1987. An improved method for viewing micro pore systems in rocks with the polarizing microscope. SPE Formation Evaluation, 2(2): 209-214.
DOI:10.2118/13136-PA |
|
Gray F D, Schmidt D P, Delbecq F. 2010a. Optimize shale gas field development using stresses and rock strength derived from 3D seismic data. //80th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts.
|
|
Gray F D, Anderson P F, Logel J, et al. 2010b. Estimating in-situ, anisotropic, principal stresses from 3D seismic. //72nd EAGE Conference and Exhibition Incorporating. SPZ, EAGE.
|
|
Gray F D, Anderson P F, Logel J, et al. 2010c. Principle stress estimation in shale plays using 3D seismic. GeoCanada2010.
|
|
Gray F D. 2011. Methods and systems for estimating stress using seismic data. United States Patent Application 20110182144. 2011-07-28.
|
|
Gray F D, Anderson P F, Logel J, et al.
2012. Estimation of stress and geomechanical properties using 3D seismic data. First Break, 30(3): 59-68.
|
|
Haimson B C. 1968. Hydraulic fracturing in porous and nonporous rock and its potential for determining in situ stresses at great depth[Ph. D. thesis]. Minneapolis: University of Minnesota.
|
|
Hast N.
1969. The state of stress in the upper part of the earth's crust. Tectonophysics, 8(3): 169-211.
DOI:10.1016/0040-1951(69)90097-3 |
|
Iverson W P. 1995. Closure Stress Calculations in Anisotropic Formations. //65th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts.
|
|
Leeman E R.
1964. The measurement of stress in rocks. Journal of the South African Institute of Mining and Metallurgy, 65(2): 45-114.
|
|
Li Z M, Zhang J Z. 1997.
In-Situ Stress and Petroleum Exploration & Development. Beijing: Petroleum Industry Press.
|
|
Logan J M, Teufel L M. 1978. The prediction of massive hydraulic fracturing from analyses of oriented cores. //19th U. S. Symposium on Rock Mechanics. Reno, Nevada: American Rock Mechanics Association, 340-347.
|
|
Ma N, Yin X Y, Sun X Y, et al.
2017. The in-situ stress seismic prediction method based on the theory of orthorhombic anisotropic media. Chinese Journal of Geophysics, 60(12): 4766-4775.
DOI:10.6038/cjg20171218 |
|
Mathar J.
1934. Determination of initial stresses by measuring the deformation around drilled holes. Trans. ASME, 56: 249-254.
|
|
Matsuki K, Takeuchi K.
1993. Three-dimensional in situ stress determination by anelastic strain recovery of a rock core. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 30(7): 1019-1022.
|
|
Ruger A. 1996. Reflection coefficients and azimuthal AVO analysis in anisotropic media[Ph. D. thesis]. Colorado: Colorado School of Mines.
|
|
Schoenberg M, Sayers C M.
1995. Seismic anisotropy of fractured rock. Geophysics, 60(1): 204-211.
DOI:10.1190/1.1443748 |
|
Simmons G, Siegfried R W, Feves M L.
1974. Differential strain analysis:a new method for examining cracks in rocks. Journal of Geophysical Research, 79(29): 4383-4385.
DOI:10.1029/JB079i029p04383 |
|
Stephansson O. 1983a. Rock stress measurement by sleeve fracturing. //5th ISRM Congress. Melbourne, Australia: International Society for Rock Mechanics and Rock Engineering, F129-F137.
|
|
Stephansson O.
1983b. Sleeve fracturing for rock stress measurements in boreholes. Proc. Int. Symp. Essais en Place, In Situ Testing, 2: 571-578.
|
|
Sugawara K, Kameoka Y, Saito T, et al.
1978. A study on core discing of rock. Journal of the Mining Institute of Japan, 94(1089): 797-803.
|
|
Teufel L W. 1983. Determination of in-situ stress from anelastic strain recovery measurements of oriented core. //53th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 421-430.
|
|
Thomsen L.
1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966.
DOI:10.1190/1.1442051 |
|
Voight B.
1968. Determination of the virgin state of stress in the vicinity of a borehole from measurements of a partial anelastic strain tensor in drill cores. Felsmechanik und Ingenieurgeologi, 6(4): 201-215.
|
|
Warpinski N R, Teufel L W.
1989. In-situ stresses in low-permeability, nonmarine rocks. Journal of Petroleum Technology, 41(4): 405-414.
DOI:10.2118/16402-PA |
|
Whitcombe D N.
2002. Elastic impedance normalization. Geophysics, 67(1): 60-62.
DOI:10.1190/1.1451331 |
|
Yin X Y, Cao D P, Wang B L, et al.
2014. Research progress of fluid discrimination with pre-stack seismic inversion. Oil Geophysical Prospecting, 49(1): 22-34, 46.
|
|
Yin X Y, Zong Z Y, Wu G C.
2015. Research on seismic fluid identification driven by rock physics. Science China Earth Sciences, 58(2): 159-171.
DOI:10.1007/s11430-014-4992-3 |
|
Yin X Y, Liu X X.
2016. Research status and progress of the seismic rock-physics modeling methods. Geophysical Prospecting for Petroleum, 55(3): 309-325.
|
|
Zang A, Stephansson O. 2010. Stress field of the earth's crust. Netherlands: Springer.
|
|
Zoback M D. 2007.
Reservoir geomechanics. New York: Cambridge University Press.
|
|
Zong Z Y, Yin X Y, Wu G C.
2012. AVO inversion and poroelasticity with P-and S-wave moduli. Geophysics, 77(6): N17-N24.
DOI:10.1190/geo2011-0214.1 |
|
Zong Z Y, Yin X Y, Wu G C.
2012a. Fluid identification method based on compressional and shear modulus direct inversion. Chinese Journal of Geophysics, 55(1): 284-292.
DOI:10.6038/j.issn.0001-5733.2012.01.028 |
|
Zong Z Y, Yin X Y, Zhang F, et al.
2012b. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio. Chinese Journal of Geophysics, 55(11): 3786-3794.
DOI:10.6038/j.issn.0001-5733.2012.11.025 |
|
Zong Z Y, Yin X Y, Wu G C. 2013. AVAZ inversion and stress evaluation in heterogeneous medium. //83th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 428-432.
|
|
陈胜天, 魏修成, 刘洋.
2006. 一种新的各向异性弹性阻抗近似公式. 石油物探, 45(6): 563–569.
|
|
李志明, 张金珠. 1997.
地应力与油气勘探开发. 北京: 石油工业出版社.
|
|
马妮, 印兴耀, 孙成禹, 等.
2017. 基于正交各向异性介质理论的地应力地震预测方法. 地球物理学报, 60(12): 4766–4775.
|
|
印兴耀, 曹丹平, 王保丽, 等.
2014. 基于叠前地震反演的流体识别方法研究进展. 石油地球物理勘探, 49(1): 22–34, 46.
|
|
印兴耀, 宗兆云, 吴国忱.
2015. 岩石物理驱动下地震流体识别研究. 中国科学:地球科学, 45(1): 8–21.
|
|
印兴耀, 刘欣欣.
2016. 储层地震岩石物理建模研究现状与进展. 石油物探, 55(3): 309–325.
|
|
宗兆云, 印兴耀, 吴国忱.
2012a. 基于叠前地震纵横波模量直接反演的流体检测方法. 地球物理学报, 55(1): 284–292.
|
|
宗兆云, 印兴耀, 张峰, 等.
2012b. 杨氏模量和泊松比反射系数近似方程及叠前地震反演. 地球物理学报, 55(11): 3786–3794.
|
|
 2018, Vol. 61
2018, Vol. 61


