类似于日、月引潮力，地球自转变化导致的离心力变化也会引起地球变形、重力变化以及海洋极潮(Wahr，1985).地球自转变化包括自转轴地心位置的变化(即极移，polar motion)和自转速率的变化.极移引起的重力变化被称为重力极潮，主要由周期为12个月的周年项(Annual wobble，简称AW)和周期约为14个月的Chandler项(Chandler wobble，简称CW)组成.相比于重力极潮，自转速率变化引起的重力变化很小(比重力极潮约小两个数量级)，在研究中常可以忽略(Wahr，1985；Xu et al., 2004).海洋极潮，即海平面高度的变化，是海洋对地球自转变化导致的离心力变化的响应，也会引起地球的负荷形变和重力变化，但影响非常小，在研究中也常可以忽略(Wahr，1985).重力极潮的检测和研究一直以来是高精度重力场研究中的基本问题之一(陈晓东，2010).由于重力极潮振幅较小(在中纬地区，重力极潮的峰-峰振幅仅为10~13 μGal，1 μGal=10^-8 m·s^-2)且周期较长，而传统的弹簧重力仪仪器漂移很大、灵敏度较低、线性量程较窄，因此直到有着低仪器漂移、高灵敏度、极宽动态线性测量范围特性的超导重力仪(Goodkind，1991；Sun et al., 1999)被广泛应用于高精度重力场观测，重力极潮的检测和研究才成为可能.近年来，利用超导重力仪研究重力极潮，主要是通过对比观测重力极潮和理论重力极潮估算极潮的潮汐因子(包括振幅因子δ和相位滞后κ).极潮潮汐因子与勒夫数相关，确定极潮潮汐因子可以为了解地球形变、地球内部构造和物理参数提供约束，也可以为台站进行重力极潮改正提供参考.

在估算长周期极潮的潮汐因子之前，需要消除仪器漂移.以往的研究(例如Harnisch and Harnisch, 2001，2006；Xu et al., 2004；Ducarme et al., 2006；Chen et al., 2009)通常使用数学模型(多项式或指数)来拟合仪器漂移.Hu等(2007)和徐华君等(2008)则利用小波方法将超导重力仪重力残差滤波到极潮所在的频段范围(256~512天)，有效地消除了仪器漂移，避免了简单数学模型拟合长期仪器漂移(尤其是当漂移出现突变)的不准确性及常规带通滤波后得到的较宽频带上大的局部信号的干扰，从而获得了高精度的极潮潮汐因子.类似于小波分析，集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法本质上也相当于一个二进(dyadic)滤波器组(Wu and Huang, 2009，2010)，但区别于小波分析需要选择基小波函数，EEMD所用的基是基于自身信号获得的(即自适应性)，尤其适用于包含非线性、非平稳过程的现象研究.鉴于EEMD的这些特性，近两年来该方法已经被用来进行极移方面的研究，例如Ding和Shen(2015)利用EEMD在1962—2013年的极移时间序列中观测到了周期约为531天的信号，Wang等(2015)利用EEMD从长达7年的超导重力仪观测数据中提取了长周期信号(包含重力极潮).

受上述研究启发，本研究采用EEMD方法从超导重力仪观测数据中提取重力极潮信号(包括周年项和Chandler项)，消除仪器漂移，并结合最小二乘匹配法来估算Chandler周期的极潮潮汐因子.由于重力极潮的周年项受到环境效应(如全球海平面、大气和水文循环的周年变化)的严重影响，而这些影响还难以精确地模型化，因此本文我们不考虑周年项的极潮潮汐因子.

本文利用我国武汉(C032)、奥地利Vienna(C025)、德国Potsdam(T018)、比利时Membach(C021)、比利时Brussels(T003)5个超导重力仪台站的观测资料来进行重力极潮的研究，这些观测资料均是从全球地球动力学计划(Global Geodynamics Project，GGP)数据库网站(http://isdc.gfz-potsdam.de/igets-data-base/)下载的已修正干扰(尖峰、阶跃、间断、地震)的1 h采样观测记录.表 1给出了所使用的超导重力仪台站位置信息及观测数据时间范围和长度.在进行EEMD分解之前，需要扣除台站局部重力合成潮，并将重力残差按相应时间间隔重采样成1天的数据序列.这里台站局部重力合成潮是根据Eterna软件(Wenzel，1996)调和分析得到的潮汐参数和Tamura(1987)引潮位展开表、并按下式计算得到：

表 1 Table 1

表 1 超导重力仪观测资料 Table 1 Superconducting gravimeter observations considered in this study 台站名 台站坐标 观测时间 观测天数 武汉/中国 30.5159°N， 114.4898°E 1997-12-21至 2012-04-30 5245 Vienna/奥地利 48.2489°N， 16.3565°E 1997-07-02至 2006-12-30 3469 Potsdam/德国 52.3806°N， 13.0682°E 1992-06-30至 1998-10-06 2290 Membach/比利时 50.6093°N， 6.0066°E 1997-03-31至 2011-12-30 5388 Brussels/比利时 50.7986°N， 4.3581°E 1987-08-01至 2000-09-21 4801

表 1 超导重力仪观测资料 Table 1 Superconducting gravimeter observations considered in this study

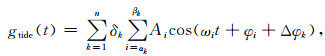
(1)

式中n为波群数，α_k和β_k分别为第k个波群在引潮位展开表中的始、末位置，A_i、ω_i、φ_i分别为第k个波群中第i个潮波的理论振幅、角频率和初始相位，δ_k和Δφ_k分别为第k个波群的振幅因子和相位滞后(许厚泽，2010).

为了估算极潮潮汐因子，除了超导重力仪观测资料外，还需要计算台站的理论重力极潮.对于刚体地球，理论重力极潮的计算公式(详见Wahr，1985)为

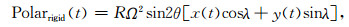
(2)

式中R(6.371×10⁶ m)为平均地心半径，Ω(7.292115×10^-5 rad·s^-1)为平均地球自转角速度，θ、λ分别为观测点的余纬(co-latitude)和西经(western longitude)，x(t)、y(t)为天球历书极(Celestial Ephemeris Pole)相对于国际参考极(International Reference Pole)的瞬时极坐标，这里我们使用国际地球自转服务中心(International Earth Rotation Service，IERS)提供的EOPC04极坐标资料.

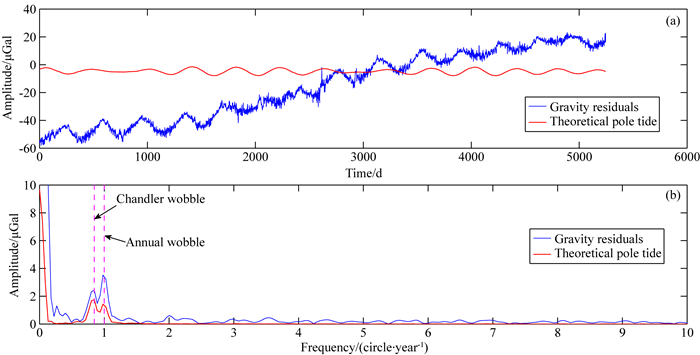
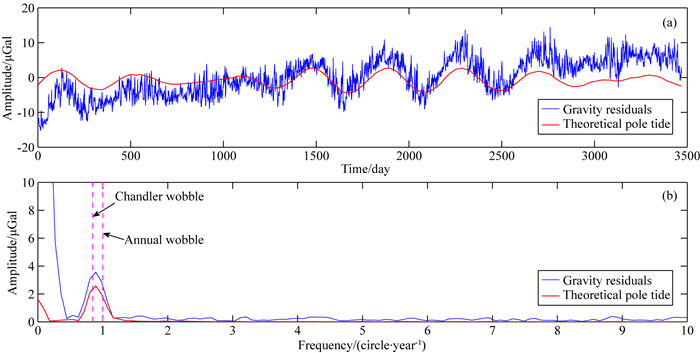
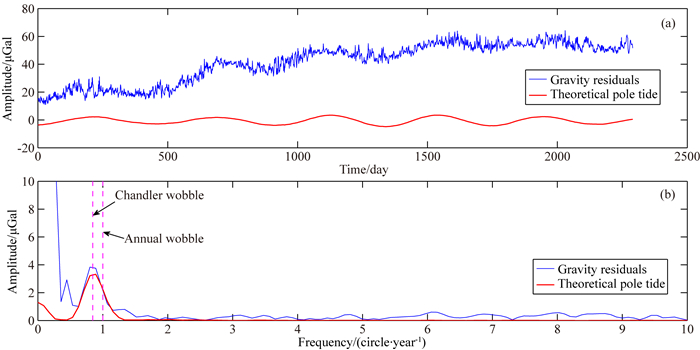
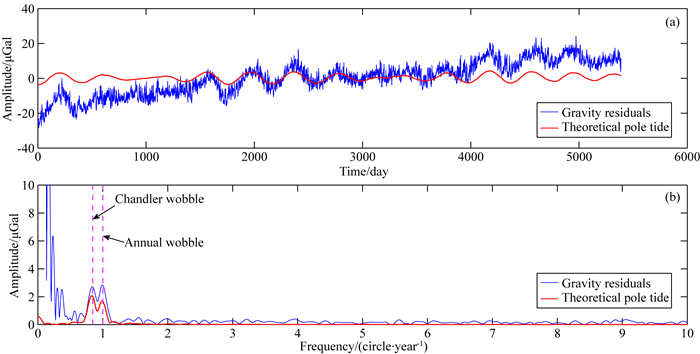
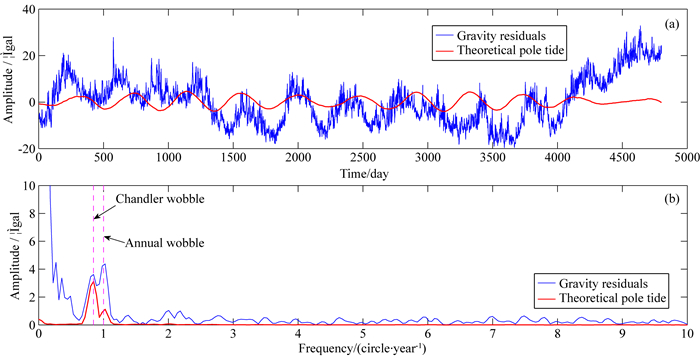
图 1—5给出了我国武汉(C032)、奥地利Vienna (C025)、德国Potsdam(T018)、比利时Membach(C021)、比利时Brussels(T003)5个超导重力仪台站的观测重力残差、理论重力极潮及它们对应的傅里叶振幅谱，其中蓝线对应观测重力残差，红线对应理论重力极潮，箭头分别标注了重力极潮Chandler项(432天)和周年项(365.25天)的理论频率(周期).从图中可以看出，这些观测重力残差存在明显的仪器漂移，使得其振幅谱的低频段具有较高的能量.另外，从这些台站的振幅谱中还可以明显看到对应于重力极潮Chandler项和周年项的谱峰，不过在Vienna台和Potsdam台，重力极潮的Chandler项和周年项并没有区分开来，这是由于观测时间不够长，理论上至少需2364天((1/365.25-1/432)^-1=2364)才能将两者分开.

图 1

Fig. 1

图 1 武汉台观测重力残差、理论重力极潮(a)及其振幅谱(b) Fig. 1 Time fluctuations of the gravity residuals (blue) and the theoretical pole tide (red) (a) and their corresponding amplitude spectra (b) at Wuhan

图 2

Fig. 2

图 2 Vienna台观测重力残差、理论重力极潮(a)及其振幅谱(b) Fig. 2 Time fluctuations of the gravity residuals (blue) and the theoretical pole tide (red) (a) and their corresponding amplitude spectra (b) at Vienna

图 3

Fig. 3

图 3 Potsdam台观测重力残差、理论重力极潮(a)及其振幅谱(b) Fig. 3 Time fluctuations of the gravity residuals (blue) and the theoretical pole tide (red) (a) and their corresponding amplitude spectra (b) at Potsdam

图 4

Fig. 4

图 4 Membach台观测重力残差、理论重力极潮(a)及其振幅谱(b) Fig. 4 Time fluctuations of the gravity residuals (blue) and the theoretical pole tide (red) (a) and their corresponding amplitude spectra (b) at Membach

图 5

Fig. 5

图 5 Brussels台观测重力残差、理论重力极潮(a)及其振幅谱(b) Fig. 5 Time fluctuations of the gravity residuals (blue) and the theoretical pole tide (red) (a) and their corresponding amplitude spectra (b) at Brussels

根据系统是否线性，信号有线性与非线性之分；根据各阶统计量(如：自相关函数、功率谱密度)是否都与时间无关，信号又有平稳与非平稳之分(张贤达，2002).在实际中，系统通常不是线性的，信号也很难满足平稳性的定义.由于受到大气、地下水、地震、地壳运动、仪器噪声、极移等非线性、非平稳过程的影响，超导重力仪重力观测记录实际上也属于非线性、非平稳信号(Vaníček，1971；Smylie et al., 1993；尹晖和Pagiatakis，2005；Crossley and Hinderer, 2009；Wang et al., 2015).对于非线性、非平稳现象，不能期望用一个预先决定的基去拟合所有的物理现象，而应该从自身信号中获得一个自适应基.经验模态分解法(Empirical Mode Decomposition, EMD)是一种分析非线性、非平稳信号的局部自适应方法，能将任意复杂信号分解为有限个分量，同时相比于傅里叶分析以正弦函数为基、小波分析以基小波函数为基，所用的基是基于自身信号获得的，这里每一个分量称为一个固有模态函数(Intrinsic Mode Function，IMF)，对应一个特征时间尺度(或频率)，只涉及一种振荡模式，且极值点个数与零点个数最多相差一个、局部极大值点和局部极小值点构成的两条包络线平均值为零(Huang et al., 1998；Flandrin et al., 2004；Huang and Wu, 2008；Wu and Huang, 2010；Tary et al., 2014).具体过程如下：

① 利用三次样条曲线插值拟合获得信号的局部极大值、局部极小值包络线.

② 在任意时刻，求出局部极大值和局部极小值的平均值m₁(t)，再与原信号x(t)作差，得到h₁(t)=x(t)-m₁(t).若h₁(t)满足固有模态函数的条件，则得到第一个固有模态函数分量c₁(t)=h₁(t)；否则，将h₁(t)作为新信号重复①、②两个步骤，如此下去，直到求得c₁(t).

③ 将c₁(t)从原信号分离得到残余项r₁(t)：r₁(t)=x(t)-c₁(t).

④ 将r₁(t)作为新信号重复上述筛选过程，如此下去，得到：

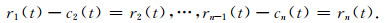
筛选过程直到残余项r_n(t)是一个单调函数或仅包含一个极值以致于不能再分解出固有模态函数为止.最终得到：

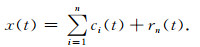
(3)

尽管EMD方法自适应而高效，然而仍存在一些不足，尤其是模态混叠问题，即一个IMF包含了不同时间尺度(或频率)的多个信号，或者相同时间尺度(或频率)的信号分布在多个IMF中.为了缓解模态混叠问题，Wu和Huang(2009)提出了EEMD方法，该方法是通过在原信号x(t)中添加白噪声序列，再利用EMD方法将添加了白噪声序列的信号分解成若干个IMF，重复多次且每次添加不同的白噪声序列，最后取多次分解得到的相应IMF的算术平均值作为最终结果，同时这些白噪声序列会互相抵消而不影响最终结果.下面给出应用EEMD方法的一个数值例子，设合成非平稳信号s(t)是两个线性调频信号之和：

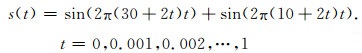
(4)

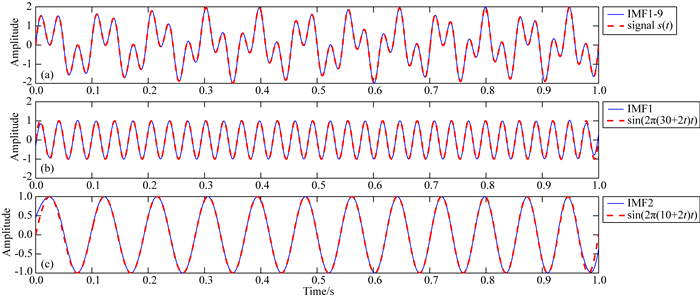
利用EEMD方法，s(t)分解为9个IMF(为了方便，从这以后EEMD分解得到的残余项r_n(t)也叫做IMF)，这些IMF之和与s(t)基本吻合(如图 6a中蓝线和红线)，而IMF1(第一个IMF写作IMF1，第二个IMF写作IMF2，依次类推)与线性调频信号sin(2π(30+2t)t)几乎一致(如图 6b中蓝线和红线)，IMF2与线性调频信号sin(2π(10+2t)t)几乎一致(如图 6c中蓝线和红线)，其余IMF之和的能量可忽略，从而证明了EEMD分离、提取信号的能力.

图 6

Fig. 6

图 6 合成信号s(t)的EEMD分解 (a)红线为s(t)，蓝线为所有IMF之和；(b)红线为sin(2π(30+2t)t)，蓝线为IMF1；(c)红线为sin(2π(10+2t)t)，蓝线为IMF2. Fig. 6 The decomposition of the synthetic signal s(t) using EEMD (a) The synthetic signal s(t) (red) and the sum of all the IMFs (IMF1-9, blue); (b) sin(2π(30+2t)t) (red) and the first IMF (IMF1, blue); (c) sin(2π(10+2t)t) (red) and the second IMF (IMF2, blue).

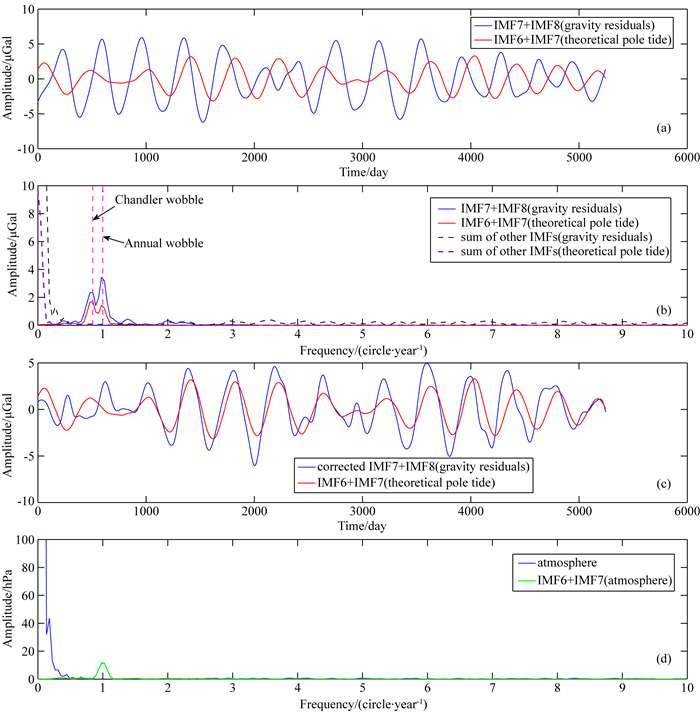
下面以武汉台为例，利用EEMD方法提取重力极潮信号.武汉台重力残差和理论重力极潮均可分解成12个IMF.图 7a给出了重力残差的第7、8个IMF之和(蓝线)及理论重力极潮的第6、7个IMF之和(红线)，图 7b给出了重力残差的第7、8个IMF之和的振幅谱(蓝线)及剩余IMF之和的振幅谱(黑色虚线)、理论重力极潮的第6、7个IMF之和的振幅谱(红线)及剩余IMF之和的振幅谱(紫色虚线).从图中可以看出，对于重力残差，第7、8个IMF之和包含了重力极潮信号，而剩余IMF之和包含了与其他频段(尤其是低频)信号有关的全部信息；对于理论重力极潮，第6、7个IMF之和包含了重力极潮信号，剩余IMF之和包含了更低频信号.这样，利用某些IMF的组合，EEMD方法自适应地提取出重力极潮信号(在0上下波动)，消除了仪器漂移并过滤掉极潮频段以外的大部分噪声信号.另外，为了更好地改正局部大气效应，我们也对气压数据进行了EEMD分解.图 7d给出了气压的振幅谱(蓝线)，以及气压经EEMD分解后得到的对应于极潮频段的第6、7个IMF之和的振幅谱(绿线).类似于图 7b，图 7d中也存在对应于频率为1 circle/year (即周期为1年)的谱峰，由此推测重力的周年变化与大气的周年变化有关.

图 7

Fig. 7

图 7 武汉台EEMD分解结果 (a)蓝线是重力残差的第7、8个IMF之和(IMF7+IMF8)，红线是理论重力极潮的第6、7个IMF之和(IMF6+IMF7)；(b)蓝线是重力残差的第7、8个IMF之和(IMF7+IMF8)的振幅谱，黑色虚线是重力残差剩余IMF之和的振幅谱，红线是理论重力极潮的第6、7个IMF之和(IMF6+IMF7)的振幅谱，紫色虚线是理论重力极潮剩余IMF之和的振幅谱，箭头分别标注了重力极潮Chandler项(432天)和周年项(365.25天)的理论频率；(c)蓝线是重力残差的第7、8个IMF之和(IMF7+IMF8)改正大气效应后的结果，红线仍是理论重力极潮的第6、7个IMF之和(IMF6+IMF7)；(d)蓝线是气压的振幅谱，绿线是气压数据经EEMD分解后得到的对应于极潮频段的第6、7个IMF之和(IMF6+IMF7)，这里气压的第6、7个IMF之和(IMF6+IMF7)用来进行(c)中提到的大气效应改正. Fig. 7 EEMD for Wuhan (a) Time fluctuations of the sum of IMF7 and IMF8 (IMF7+IMF8, blue) for the gravity residuals and the sum of IMF6 and IMF7 (IMF6+IMF7, red) for the theoretical pole tide; (b) Amplitude spectra of the sum of IMF7 and IMF8 (IMF7+IMF8, blue) for the gravity residuals, the sum of the other IMFs (IMFs except for IMF7 and IMF8, black) for the gravity residuals, the sum of IMF6 and IMF7 (IMF6+IMF7, red) for the theoretical pole tide and the sum of the other IMFs (IMFs except for IMF6 and IMF7, purple) for the theoretical pole tide. Arrows indicate the frequencies of Chandler wobble (period of about 432 days) and Annual wobble (period of about 365.25 days), respectively; (c) Time fluctuations of the sum of IMF7 and IMF8 (IMF7+IMF8, blue) for the gravity residuals after correcting for local atmospheric pressure effects on gravity variations in the pole tidal band, and the sum of IMF6 and IMF7 (IMF6+IMF7, red) for the theoretical pole tide; (d) Amplitude spectra of the local atmospheric pressure (blue) and the sum of IMF6 and IMF7 (IMF6+IMF7, green) derived from the local atmospheric pressure based on EEMD. The sum of IMF6 and IMF7 (IMF6+IMF7, green) are used to estimate local atmospheric pressure effects on gravity variations in the pole tidal band as mentioned in (c).

事实上，EEMD提取重力极潮(或者重力极潮频段的气压信号)相当于滤波，但区别于傅里叶分析需要选择截止频率、小波分析需要选择基小波函数，这种滤波是基于自身信号的自适应的、后验的过程.利用气压的EEMD滤波结果(即第6、7个IMF之和)对重力残差的EEMD滤波结果(即第7、8个IMF之和)进行大气重力效应改正(导纳值法)后，重力残差的EEMD滤波结果与理论重力极潮的EEMD滤波结果更加符合(如图 7c).

下面仍以武汉台为例，利用最小二乘匹配法估算Chandler周期的极潮潮汐因子(包括振幅因子δ和相位滞后κ).类似于前人的研究(例如Harnisch and Harnisch, 2001，2006；Xu et al., 2004；Hu et al., 2007；徐华君等，2008)，这里利用两个周期分别为365.25天和432天的正弦函数相加来最小二乘拟合上述3.2节中提取到的重力极潮信号，从而将极潮中的周年项和Chandler项分离.对于重力残差的滤波结果(即图 7c中蓝线)、理论重力极潮的滤波结果(即图 7b、7c中红线)，分别有

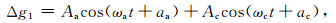
(5)

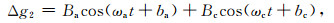
(6)

式中Δg₁、Δg₂分别用来拟合重力残差和理论重力极潮的滤波结果，下角标a、c分别代表重力极潮的周年项和Chandler项，ω_a、ω_c分别为2π/365.25、2π/432 rad/天.利用最小二乘方法，可以估算出参数A_a、A_c、B_a、B_c、a_a、a_c、b_a、b_c，进而估算出Chandler周期的极潮潮汐因子：

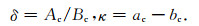
(7)

武汉台Chandler周期的极潮潮汐因子为：δ=1.2116±0.0141，κ=13.4757°±0.6664°.该极潮潮汐因子具有较高的精度.我们又利用Hu等(2007)和徐华君等(2008)提出的小波方法提取重力极潮、并利用最小二乘匹配法估算了武汉台Chandler周期的极潮潮汐因子：δ=1.2244±0.0128，κ=11.5856°±0.5985°.对比EEMD和小波方法的结果，发现二者在同一数量级，仅存在较小差异，这进一步证明了EEMD结果的正确性和可靠性.

表 2给出了基于EEMD方法得到的其他4个台站Chandler周期的极潮潮汐因子，同时给出了前人基于其他消除仪器漂移方法得到的结果.从表中可以看出，本文基于EEMD得到的Chandler周期的极潮振幅因子δ大体上与前人结果相符合(除Brussels台结果偏小一些外)，精度(即均方根误差)相当.对于Brussels台，我们又利用小波方法估算了极潮振幅因子δ，发现与EEMD方法得到的结果相同，因此推断本文结果较前人结果偏小的原因可能是数据预处理的不同，考虑到Brussels台观测数据质量较差，数据预处理的不同很容易影响最终估算结果.另外，由于海洋极潮、局部效应(如地下水)的影响(Boy et al., 2000；Ducarme et al., 2006)，本文基于EEMD得到的各台站Chandler周期的极潮振幅因子δ与理论潮汐模型DDW99(Dehant et al., 1999)给出的理论值1.16有一定的差距.对于相位滞后κ，Hu等(2007)已经指出由于方法本身原因，不同方法得到的结果差异可能很大，不过本文基于EEMD得到的精度更高一些.同时，进一步考虑到超导重力观测记录的非线性、非平稳性以及EEMD方法的自适应性，本文结果更客观地反映了实际物理过程.

表 2 Table 2

表 2 基于不同消除仪器漂移方法得到的各台站Chandler周期的极潮潮汐因子 Table 2 Pole tide gravimetric factors at the Chandler period at each station derived from different methods for eliminating the instrumental drift 台站 消除仪器漂移方法 观测时间 Chandler wobble δ κ(°) Vienna EEMD(本研究) 1.2189±0.0137 4.8908±0.6476 小波滤波(Hu et al., 2007) 1997—2004 1.2092±0.0127 -5.7917±1.3345 漂移模型(Harnisch and Harnisch, 2006) 1995—2003 1.20±0.13 5.0 Potsdam EEMD(本研究) 1.0733±0.0213 0.9122±1.1481 漂移模型(Harnisch and Harnisch, 2006) 1992—1998 1.11±0.08 0.9 漂移模型(Xu et al., 2004) 1992—1998 1.2350±0.0205 5.28±0.95 Membach EEMD(本研究) 1.2863±0.0132 3.0747±0.5868 小波滤波(Hu et al., 2007) 1995—2005 1.1960±0.0119 0.6487±0.9126 漂移模型(Harnisch and Harnisch, 2006) 1996—2003 1.18±0.13 2.4 漂移模型(Xu et al., 2004) 1995—2000 1.2613±0.0187 -4.97±0.85 Brussels EEMD(本研究) 1.1074±0.0149 5.9989±0.7747 小波滤波(Hu et al., 2007) 1987—2000 1.1820±0.0338 -0.5967±2.0926 漂移模型(Harnisch and Harnisch, 2006) 1982—2000 1.15±0.14 0.7 漂移模型(Xu et al., 2004) 1987—2000 1.1848±0.0504 -6.36±2.43

表 2 基于不同消除仪器漂移方法得到的各台站Chandler周期的极潮潮汐因子 Table 2 Pole tide gravimetric factors at the Chandler period at each station derived from different methods for eliminating the instrumental drift

利用GGP项目的5个超导重力仪台站观测资料，结合调和分析得到的观测重力潮汐参数及最新引潮位展开表、极移资料分别分离台站重力固体潮、计算理论重力极潮，在此基础上，采用局部自适应的EEMD方法分别从观测重力残差、理论重力极潮中提取Chandler项和周年项，从而消除仪器漂移及极潮频段以外的大部分噪声信号.同时，利用EEMD方法从台站同址观测的气压数据中提取重力极潮频段的信号，用于更好地改正局部大气效应、估算极潮潮汐因子.

基于两个周期分别为365.25天和432天的正弦函数相加来最小二乘拟合提取到的重力极潮信号，将周年项和Chandler项分离，进而估算出Chandler周期的极潮潮汐因子，这些极潮潮汐因子与前人基于其他消除仪器漂移方法得到的结果相符合，精度相当.尽管利用EEMD提取重力极潮(或极潮频段信号)相当于滤波，但不同于傅里叶分析和小波分析以特定数学函数为基，EEMD所用的基是基于自身信号获得的，因此本文结果更客观地反映实际非线性、非平稳的物理过程.另外，采用不同于最小二乘分离法的时间域或频率域拟合回归分析方法(Hu et al., 2007)，并进一步扣除海洋极潮、局部水文效应等的影响，有望进一步提高Chandler周期的极潮潮汐因子的精度.

感谢全球地球动力学计划(GGP)数据中心提供超导重力数据，感谢N. E. Huang研究小组提供EEMD程序.