地球物理学报  2018, Vol. 61 Issue (12): 4954-4964   PDF    
引用本文
王潇, 杨锴. 2018. 基于二维VTI拟声波程函方程的椭圆各向异性立体层析反演. 地球物理学报, 61(12): 4954-4964, doi: 10.6038/cjg2018M0212.  
Wang X, Yang K. 2018. Anisotropic elliptical stereotomography based on the 2D quasi-acoustic eikonal equation for VTI media. Chinese J. Geophys. (in Chinese), 61(12): 4954-4964, doi: 10.6038/cjg2018M0212.  
基于二维VTI拟声波程函方程的椭圆各向异性立体层析反演
王潇, 杨锴     
同济大学海洋地质国家重点实验室, 上海 200092
收稿日期 2018-04-06, 2018-07-19 收修定稿
基金项目: 国家自然科学基金面上项目（41574098，41630964）资助
第一作者简介: 王潇, 男, 1995年生, 硕士研究生, 研究方向为地震波的传播、成像与反演.E-mail:15316808190@qq.com
通讯作者: 杨锴, 男, 1972年生, 理学博士, 教授, 博士生导师, 研究方向为地震波的传播、成像与反演.E-mail:yang_kai@tongji.edu.cn
摘要：基于二维VTI介质拟声波程函方程，应用射线扰动理论建立了该方程控制下的数据空间各参数对于模型空间各个参数之间的线性关系，从而获得二维VTI介质拟声波程函方程的各向异性立体层析核函数.考虑到拟声波近似程函方程中η参数与ε和δ存在强烈耦合，本文首先探讨椭圆各向异性情形，为二维拟声波程函方程椭圆各向异性立体层析算法奠定了理论基础.同时也为日后推广到非椭圆各向异性情况提供了一种获得高质量初始模型的可靠途径.理论数据算例证实了Fréchet核函数求取的正确性以及在此基础上设计的工作流程实现两参数反演的可行性.
关键词: 二维VTI介质拟声波程函方程      椭圆各向异性立体层析      Fréchet核函数     
Anisotropic elliptical stereotomography based on the 2D quasi-acoustic eikonal equation for VTI media
WANG Xiao, YANG Kai     
State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China
Abstract: Stereo-tomography is a distinctive tomography method. The theory and application of isotropic stereo-tomography have been fully developed in the past two decades. In this paper, we apply the ray perturbation theory to the 2D elliptical quasi-acoustic eikonal equation for VTI media from which the linear relation between the stereo-tomographic data components and the model components for qP-wave is derived. Thus the theoretical foundation of 2D VTI stereo-tomography based on the 2D quasi-acoustic eikonal equation is established. Different from the previous anisotropic stereo-tomography which is derived in general anisotropic media, the kinematic information of converted wave mode and the polarization vectors are not necessarily taken into account as a data component in this approach, thus its applicability is more promising. The sensitivity analysis and two synthetic data examples demonstrate the correctness of the derived Fréchet derivatives and the applicability of the presented work-flow of this method.
Keywords: 2D quasi-acoustic eikonal equation for VTI media    Anisotropic elliptical stereotomography    Fréchet kernal    
0 引言

各向异性在地下介质中广泛存在，实践中早已经发现，对于大偏移距地震数据而言，若不考虑各向异性会导致成像与速度估计发生很大误差.这促使近年来学术界和工业界在研究基于地震波的反演、成像及储层建模技术时，必须将算法从各向同性拓展到各向异性.基于走时的各向异性层析成像已经有大量工作(Chapman and Pratt, 1992；卢明辉等，2005；Zhou et al., 2008; Wang and Tsvankin, 2013；刘玉柱等，2014；黄光南等，2015).不同于走时层析，立体层析是一种极具特色的运动学层析反演方法.从数据空间的利用方面来说，立体层析堪称利用了最为丰富的数据空间信息.该方法将射线出射到地表的慢度水平分量(即地表地震记录中同相轴的斜率)以及射线出射到地表的坐标也纳入到数据空间，是对传统走时的层析成像的丰富和扩展.各向同性介质下立体层析的理论与实践已经有大量工作(Billette and Lambare, 1998；Billette et al, 2003; 倪瑶等，2013；Prieux et al., 2013；李振伟等，2014；任丽娟等，2014；Chauris et al., 2015; Li et al., 2015；王宇翔等，2016；杨锴等，2016；邵炜栋等，2017；Xing et al., 2017).

各向异性立体层析方法研究则相对较少.Barbosa等(2008)讨论了椭圆与非椭圆各向异性介质中立体层析Fréchet导数的求取以及分辨率矩阵问题.不过该文仅基于分辨率矩阵探讨了实施各向异性立体层析联合反演的可能性，没有对其偏导数敏感度与多参数联合反演做任何测试.Nag等(2010)以PP/PS波数据空间为例推导了适用于一般各向异性的立体层析Fréchet导数公式.周嘉欣等(2018)在邵炜栋等(2017)的基础上提出了适应于三角网格剖分模型的VTI介质立体层析算法.其中Nag等(2010)的工作从理论上而言适用于最一般的各向异性介质，但是在实际应用方面它要求提取转换波信息以及极化矢量方向，同时其模型空间的介质参数部分直接面对的是弹性系数，其实用性相对有限.

Alkhalifah(2000)提出的拟声波方程程函方程为简化各向异性立体层析提供了一种可能.在这个方程中，横波信息被完全忽略.基于该方程实施射线扰动理论分析可以构建适用于TI介质中拟声波(qP波)的立体层析核函数，从而建立起TI介质中qP波的运动学信息与速度、各向异性参数以及射线初始相空间之间的线性关系.注意上述线性关系中涉及的数据空间分量和模型空间分量相比Nag等(2010)提出的大为减少，同时其模型空间的各向异性参数直接用Thomsen参数表达，不需在反演中直接处理弹性系数.因此利用拟声波程函方程计算立体层析核函数不但降低了各向异性立体层析反演对数据空间的要求，同时也完全适应工业界多年来采集到的大量纵波勘探数据，具有不错的应用潜力.

本文基于射线扰动理论(Farra and Madariaga, 1987)对二维VTI介质拟声波程函方程进行了扰动分析.考虑到拟声波程函方程中的η参数同时依赖于ε和δ，本文着重探讨椭圆各向异性介质下ε=δ即η=0时立体层析核函数的求取以及相应的敏感度分析，为实现基于二维VTI介质拟声波程函方程的椭圆立体层析反演奠定了理论基础，同时也为日后推广到非椭圆各向异性情况提供了一种获得可靠的初始模型的途径.理论数据算例证实了核函数求取的正确性以及在此基础上实施多参数联合反演的可行性.

1 立体层析简介

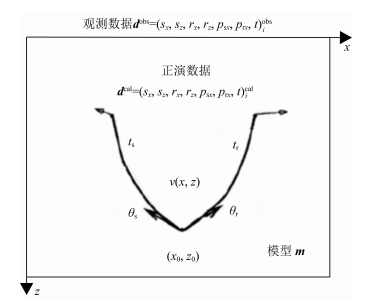
考虑到论文的自洽性，在推导各向异性立体层析线性关系之前，有必要对二维各向同性立体层析的模型空间、数据空间及Fréchet导数矩阵建立过程做一简要回顾.图 1a显示了一根从炮点S出发、到地下反射点X反射、回到地表R的射线.从透射的角度，不妨将其理解为从X出发、分别以入射角θs与反射角θr发射至炮点和检波点的两根透射射线.当速度正确时，两根透射射线分别以正确的出射方向、正确的走时达到正确的炮点和检波点位置.这样构成的立体层析数据空间各分量为：d=[Sx, Rx, T, Psx, Prx].其中Sx、Rx为炮检点坐标；T为走时；Psx、Prx为炮检点处的射线参数水平分量.地下的模型空间m=(X0, Z0, θs, θr, V)，其中X0、Z0为地下反射点X的坐标；θs、θr分别代表从炮点一侧与检波点一侧出射的地下张角, V代表地下介质速度信息.假设Pslope为局部相干同相轴的斜率，根据几何关系以及射线理论中慢度矢量的定义得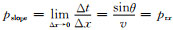：.该式表明共炮数据上同相轴的斜率对应于检波点处慢度矢量的水平分量Psx，由炮检互易原理可知，共检波点数据上同相轴的斜率必对应于炮点处慢度矢量的水平分量Prx.Billette和Lambare(1998)指出，由于Prx、Psx(共炮道集和共检波点道集数据内同相轴的斜率)被引入层析数据空间，使得反演中地震波在炮检点处的局部传播方向得到强有力的约束.具体的优势体现在：(1)在实际应用中无需拾取连续的反射同相轴，只要选择连续性好、信噪比高的局部波包即可；(2)将反射问题化为透射问题，回避了传统反射层析中速度与反射层深度耦合的问题.由于在数据空间中引入了Prx、Psx，模型空间也随之扩大，在反演速度的同时还可以同时反演出反射点的位置以及反射层的倾角.这使得立体层析反演成为射线类层析反演方法中唯一一种可以同时反演速度、反射点位置以及局部倾角的层析反演方法.

图 1 二维立体层析数据空间各分量与模型空间各分量 Fig. 1 Model and data components in 2D stereotomography data space

众所周知，任何一种层析反演方法都必须建立数据空间扰动与模型空间扰动的线性关系，即：

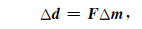
(1)

这样利用观测到的数据残差就可以计算出模型空间的扰动量，达到更新初始模型的目的.其中关键是建立方程(1)所示的F矩阵：即Fréchet偏导数矩阵公式.Fréchet偏导数矩阵的物理意义是数据空间任一分量关于模型空间任一分量的敏感度.(2)式展示了二维各向同性立体层析Fréchet偏导数矩阵，除了第一行走时关于模型空间各分量的偏导数根据走时积分方程即可得到外.其余元素需通过二维各向同性程函方程实施射线扰动分析(Farra and Madariaga, 1987)得到，其中σ为针对矩阵中每一行的数量级不同设置的均衡系数.其推导细节请查阅(Billette and Lambare, 1998)或杨锴等(2016)，这里不再赘述.公式(2)为

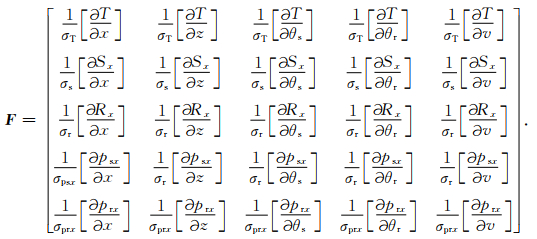
(2)

2 基于VTI介质拟声波程函方程建立立体层析所需线性关系

与(2)式所示的各向同性立体层析Fréchet导数矩阵推导过程不同，本文的二维qP波立体层析Fréchet导数矩阵将基于二维VTI介质拟声波程函方程导出.二维VTI介质拟声波程函方程的汉密尔顿形式为(Alkhalifah，2000)：

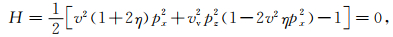
(3)

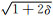
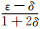
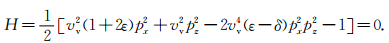
其中, 垂直速度vv(x, y)=vp0(x, y); v(x, y)=vnmo(0)(x, y)=vp0(x, y) ; η(x, y)=.将η与v的关系式带入(3)式中，得到只含有垂向速度vv和Thomsen表征的各向异性参数ε、δ的汉密尔顿算子，公式为

(4)

本文仅仅讨论椭圆各向异性即ε=δ的情形，因此(4)式简化为

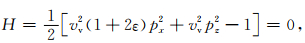
(5)

由Hamiltonian方法可得相应的射线追踪一阶微分方程组为

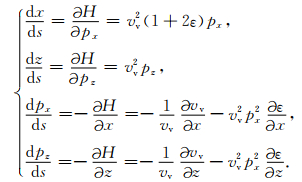
(6)

对(5)式求取关于初始相空间参数对射线场的一阶影响，有：

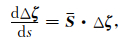
(7)

其中初始相空间的扰动信息为Δζ=(δX0，δP0)=(Δx0, Δz0, Δpx0, Δpz0)T.

除了考虑初始相空间扰动外, 还要考虑各向异性参数扰动(δε)和垂直速度参数扰动(δvv)对射线场的一阶效应.根据Farra和Madariaga(1987)，汉密尔顿算子H可以近似写为背景汉密尔顿算子H0与扰动汉密尔顿算子ΔH之和，公式为

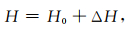
(8)

考虑到椭圆各向异性假设，有：

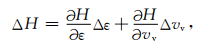
(9)

对(8)、(9)带入(7)式，有：

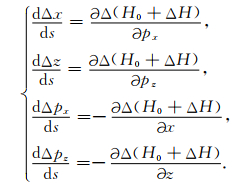
(10)

将(9)展开并忽略高阶小量做线性近似并以矩阵形式表达，即：

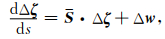
(11)

其中Δζ的含义同上，而.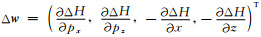

(11) 式表达了模型空间中的初始射线场扰动(δx0, δP0)T(或曰初始相空间扰动)与垂直速度和各向异性参数扰动(δvv, δε)对射线轨迹上任意一点的射线场扰动(δx, δP)T之间的线性关系.利用传播矩阵理论容易求得：

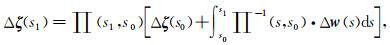
(12)

其中s0代表射线出射时刻，s1代表射线传播的最终时刻.∏(s1, s0)表示从射线出射起到最终到达时的传播矩阵.利用(12)式即可建立二维VTI椭圆各向异性介质下拟声波立体层析所需的，除了走时t之外其他数据分量对模型空间各分量之间的一阶扰动关系，其中各项的详细形式请参见附录A.

走时t关于对模型空间各分量之间的一阶扰动关系推导思路如下：在傍轴射线追踪中, 是以ds(微小的走时量)为射线积分变量，当中心射线到达地表或者指定界面的时候，傍轴射线用掉同样的走时t.但是傍轴射线的终点可能不在地表或者界面上.这时候傍轴射线需要补加一段.这一段就是走时差产生的地方.所以得到走时t与模型空间分量之间的一阶扰动关系就是建立走时差与模型空间扰动的线性关系.

根据周嘉欣等(2017)，这一段补加的走时dtu计算公式为

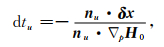
(13)

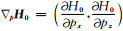
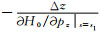
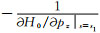
在二维问题中，当射线射到地表时且认为地表水平时，nu=(0, 1).且δx=(Δx, Δz)，(射线追到地表时的数值)，带入到上公式得：dtu=，所以求走时扰动关系即是求空间扰动量z关于模型空间的一阶线性关系与的乘积，具体形式请参见附录B.

3 二维VTI介质下拟声波各向异性立体层析线性关系敏感度测试以及反演策略

如前所述，求取Fréchet导数的目的就是为了获得数据空间各分量和模型空间各分量之间的线性关系.原则上说，在获得了二维VTI椭圆各向异性介质下拟声波立体层析所需的所有Fréchet偏导数的求取公式后，就可以建立形如(1)式的线性方程组实施二维VTI椭圆各向异性介质下拟声波立体层析反演.因此在反演实施之前考察这些Fréchet导数所代表的敏感性的正确性是非常必要的.

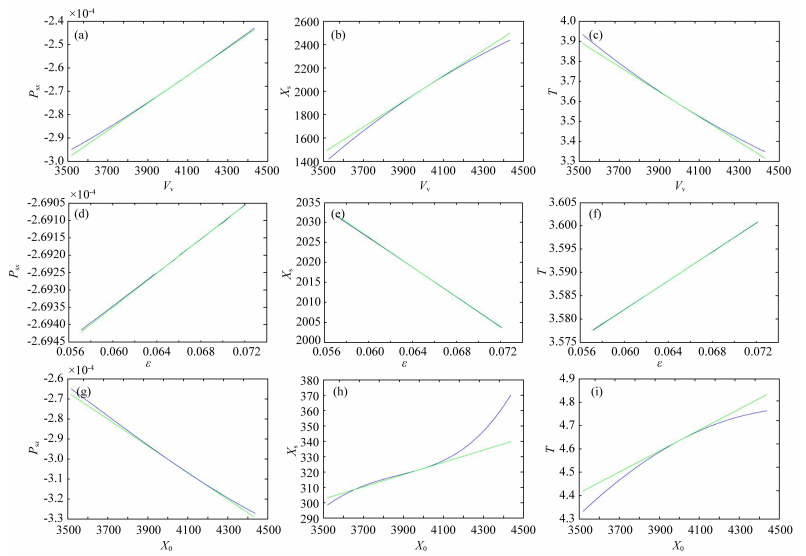
首先我们在某光滑速度模型下由地下向地表出射一对射线.具体的参数为射线出射点坐标为x0=4000 m, z0=3500 m处，出射到Z=0 m观测面时的信息为Sx=2502 m，Rx=6498 m，Psx=-0.000269，Prx=0.000367.本次敏感度测试是在初始模型参数的基础上，对射线出射点信息以及介质参数进行±10%的扰动后，分别统计数据空间各个分量相应变化得到的.考虑到炮点和检波点存在的互易性，因此测试仅限于炮点一侧的数据空间分量关于某些模型空间参数的敏感度.图 2a-i显示了炮点坐标Sx、炮点一侧射线参数水平分量Psx及走时t关于Vv、ε、出射点横坐标x0的敏感度分析.

图 2 数据空间炮点一侧分量对部分模型空间分量δ(Ts，Sx，Psx)/δ(Vv，ε，x0)的敏感度分析 (a) Psx/Vv；(b) Sx/Vv；(c) t/Vv；(d) Psx/ε；(e) Sx/ε；(f) t/ε；(g) Psx/x0；(h) Sx/x0；(i) t/x0. Fig. 2 Sensitivity analysis of the Fréchet derivatives for some selected data components (Ts, Sx, Psx) with respect to some selected model components (Vv, ε, x0) of the 2D qP-wave anisotropic stereotomography

图 2中蓝色曲线代表数据空间某分量与模型空间某分量的变化关系，可以看到二者之间存在着良好的联动关系.注意数据空间某分量对模型空间某分量的敏感值，即Fréchet导数所代表的绿色直线与蓝色曲线在考察点处相切，证明之前数据空间各分量和模型空间各分量之间的线性关系的推导是正确的.基于这些线性关系建立的线性方程组是可以用于反演的.

在敏感度测试通过之后即可制定相应的反演策略.考虑到各向异性参数ε对地震波运动学信息的影响明显弱于垂直速度Vv.本文VTI介质下拟声波二维各向异性立体层析的反演策略如下：(1)首先基于观测到的数据空间进行常规的各向同性二维立体层析，其反演结果可以视为是初始Vv速度模型；(2)固定P波速度，单独反演各向异性参数ε；(3)将第一轮获得Vv与第二轮获得的各向异性参数ε作为初始参数输入，实施两参数联合反演得到更为可靠的Vv与ε反演结果.

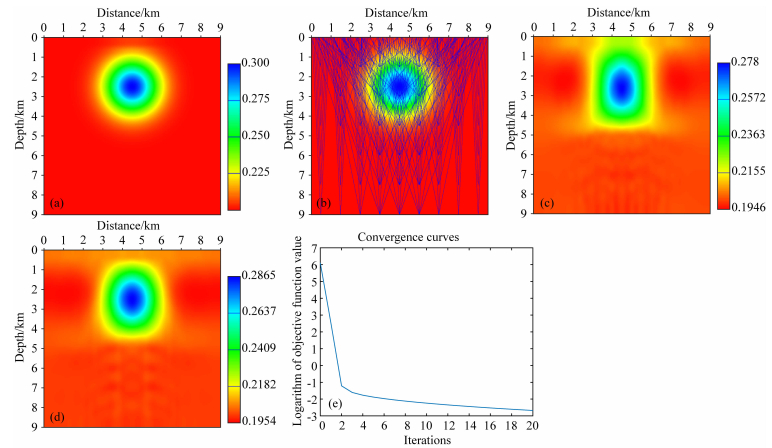
4 理论数据测试 4.1 理论数据反演实验1(给定反射点位置以及Vv为正确，单独反演各向异性参数ε)

首先实施一个最为简单的实验：在图 3a所示的光滑速度模型中进行二维VTI介质拟声波程函方程正演模拟得到立体层析数据空间.于地下布设6行9列共46个散射点，每一列散射点的横坐标从0.5 km开始，每隔1 km放置一个；每一行散射点的纵坐标从1.5 km开始，每隔1.5 km放置一个，每一个散射点出射若干对射线到地表，地表接收到的完整射线共计340对.基于正演得到的数据空间(走时、P参数水平分量以及射线地表出射点横坐标)，固定Vv及散射点坐标为正确，进行各向异性参数ε的单参数反演，各向异性参数初始为一个常背景.图 3a显示了ε的真实模型；图 3b显示了地下射线对信息；图 3c显示了第二轮的ε的反演结果；图 3d显示了最终的ε反演结果；图 3e显示了目标泛函的下降曲线.从反演结果和泛函下降曲线都可以看出由于散射点坐标和Vv为设置为正确，使得线性方程组的可逆性得到了充分保证，反演结果非常令人满意，同时也进一步证实了关于ε的偏导数推导是正确无误的.

图 3 固定Vv与散射点坐标单独反演ε (a) ε真实模型；(b)射线对信息；(c)第二轮ε反演结果；(d)最终ε反演结果；(e)目标泛函下降曲线. Fig. 3 2D anisotropic triangulated stereo-tomography inversion of ε only (a) True ε model; (b) Ray-pairs simulated; (c) Inverted ε after 2nd iterations; (d) Final inverted ε; (e) Decline of the cost function during iterations.s
4.2 理论数据反演实验2(分步骤反演ε和Vv)

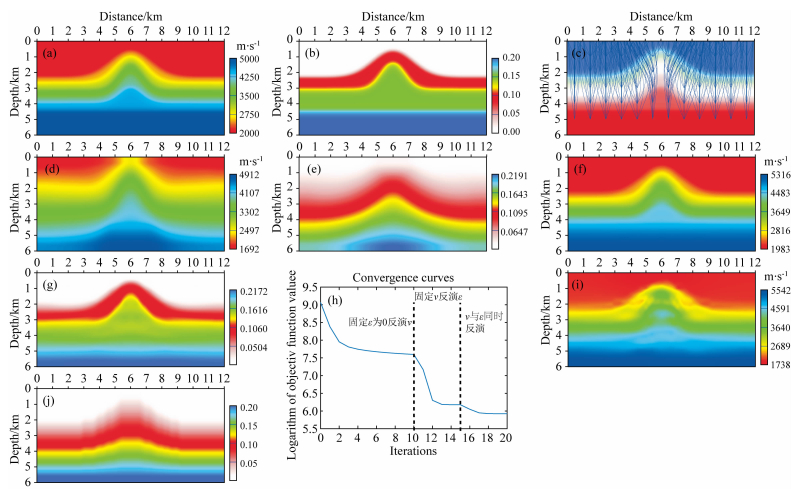
第二个实验用于验证上一节提出的反演策略是否有效.首先在图 4a所示的光滑穹隆状速度模型中进行二维VTI介质拟声波射线正演得到立体层析数据空间.于地下布设5行12列共60个散射点，每一列散射点的横坐标从1 km开始到5 km，每隔1 km放置一列；每一行散射点的纵坐标从0.9 km开始，每隔1 km放置一个，每一个散射点出射若干对射线到地表，地表接收到的完整射线共计560对.基于正演得到的数据空间(走时、P参数水平分量以及射线地表出射点横坐标)，首先实施一个常规的各向同性立体层析反演.各向同性立体层析反演的初始模型为一个垂直梯度模型，这里不再展示.图 4d、4e显示了各向同性立体层析反演之后获得的Vv剖面和ε剖面.图 4f、4g显示了将图 4d、4e作为初始模型输入，实施各向异性立体层析反演之后获得的最终Vv剖面和ε剖面.图 4h显示了目标泛函的下降曲线.从反演结果和泛函下降曲线可以看出上述策略能够保证椭圆各向异性介质中的立体层析反演获得不错的结果.同时也要注意到由于立体层析模型空间变大，需要同时联合反演很多模型分量，因此在实施真正的联合反演之前，通过循序渐进的策略和步骤获得好的初始模型信息是非常重要的.图 4i、4j显示了基于梯度初始模型的直接联合立体层析反演结果，两个参数的初始模型均为梯度模型.可以看到直接反演效果不佳，无论Vv剖面还是ε剖面都失真严重.

图 4 固定散射点坐标联合反演 (a) Vv真实模型；(b) ε的真实模型；(c)正演射线对信息；(d)各向同性立体层析反演Vv；(e)固定Vv反演ε；(f)基于图(d)、图(e)所示模型联合反演Vv的结果；(g)基于图(d)、图(e)所示模型联合反演ε的结果；(h)泛函收敛曲线；(i)直接基于梯度初始模型联合反演Vv的结果；(j)直接基于梯度初始模型联合反演ε的结果. Fig. 4 Final inverted anisotropic parameters with a final joint inversion (a) True Vv model; (b) True ε model; (c) Ray-pairs simulated; (d) Vv inverted by isotropic stereotomography; (e) Inverted ε with fixed Vv; (f) Final Vv by joint inversion; (g) Final ε by joint inversion; (h) Convergence curves; (i) Vv by joint inversion based on an initial gradient model; (j) ε by joint inversion based on an initial gradient model.
5 结论

不同于前人直接将扰动理论用于一般各向异性弹性介质的程函方程，本文将射线扰动理论应用于二维VTI介质拟声波程函方程，建立了该方程控制下的数据空间各参数对于模型空间各个参数之间的线性关系从而得到了二维VTI椭圆各向异性立体层析所需的核函数.相比前人需要将多分量数据和极化矢量作为数据空间输入，本文算法是一种更为实用的、适用于qP波的二维各向异性立体层析算法.该算法非常适合于工业界常规采集得到的大量单分量地震数据据.理论数据算例证实了Fréchet导数的正确性以及分步骤反演的可行性，为日后推广到非椭圆各向异性情况提供了一种获得高质量初始模型的可靠途径.

附录A 二维VTI椭圆各向异性介质中P参数与X坐标关于模型空间参数的一阶扰动关系推导

将正文中初始相空间与介质参数对数据空间的一阶扰动公式(11)重写为式(A1)，即：

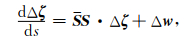
(A1)

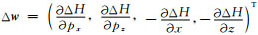
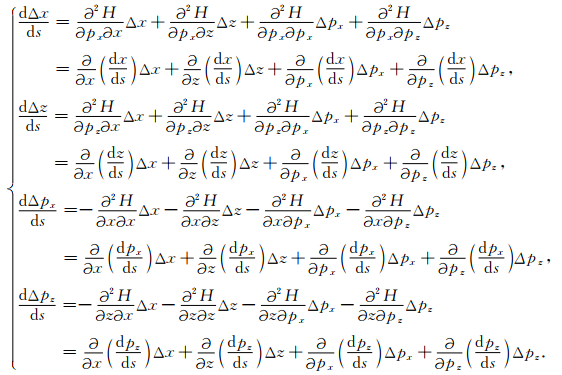
其中Δζ的含义同上，而.(A1)中等式右边第一项的显示表达为

(A2)

将H算子的形式带入即可将(A2)进一步展开为

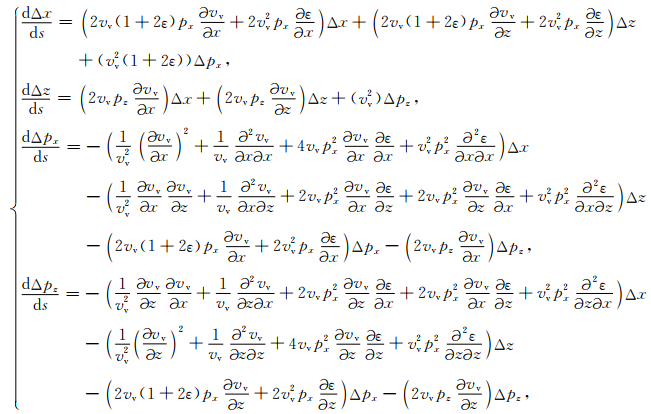
(A3)

对(A1)中等式右边第二项的显示表达推导，首先将正文中公式(12)重写为

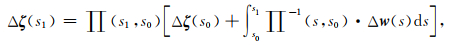
(A4)

其显示表达为

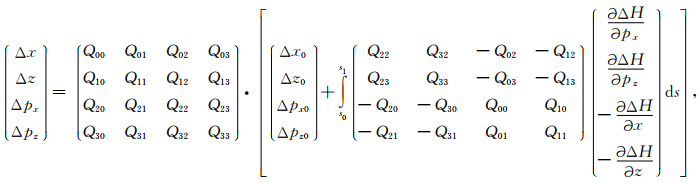
(A5)

其中右端第一项的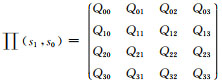.该矩阵是以一个4×4的单位矩阵作为初始条件，实施龙格库塔求解傍轴射线追踪方程组得到的.

式(A4)中的Δw(s)项的显示表达为

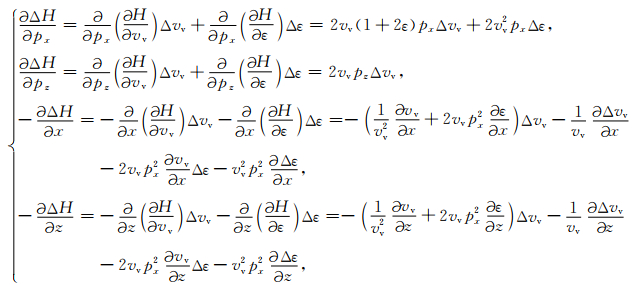
(A6)

地表出射点处横坐标x对模型空间各个参数的导数表达为

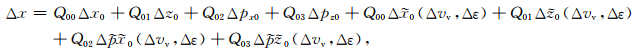
(A7)

其中：

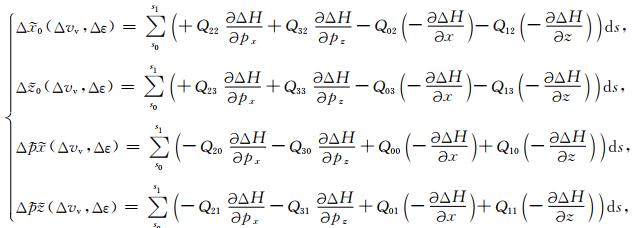
(A8)

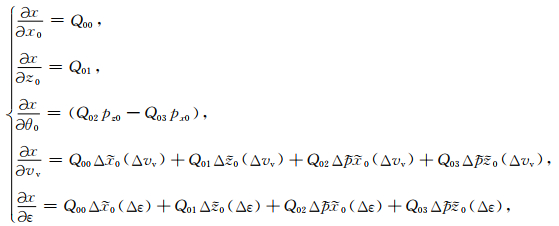
(A9)

地表出射炮点处慢度水平分量px对模型空间各个参数的导数表达为

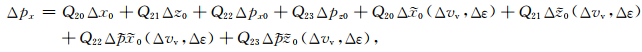
(A10)

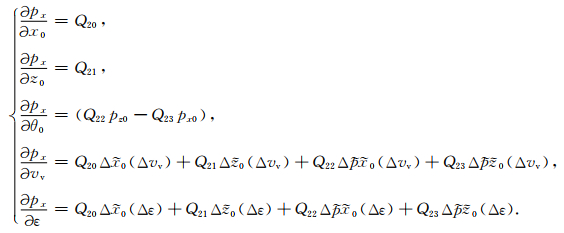
(A11)

附录B 二维VTI椭圆各向异性介质中走时t关于模型空间参数的一阶扰动关系推导

已知公式有：

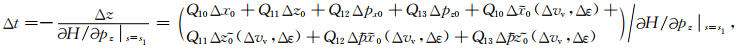
(B1)

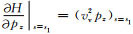
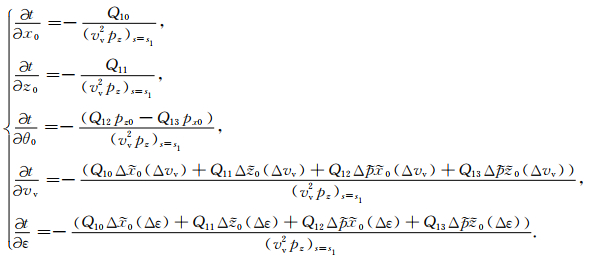
其中，s1表示中心射线到达地表的时刻，可得:

(B2)

References
Alkhalifah T. 2000. An acoustic wave equation for anisotropic media. Geophysics, 65(4): 1239-1250. DOI:10.1190/1.1444815
Barbosa B, Costa J, Gomes E, et al. 2008. Resolution analysis for stereotomography in media with elliptic and anelliptic anisotropy. Geophysics, 73(4): R49-R58. DOI:10.1190/1.2917853
Billette F, Lambare G. 1998. Velocity macro-model estimation from seismic reflection data by stereotomography. Geophysical Journal International, 135(2): 671-690. DOI:10.1046/j.1365-246X.1998.00632.x
Billette F, Le Bégat S, Podvin P, et al. 2003. Practical aspects and applications of 2D stereotomography. Geophysics, 68(3): 1008-1021. DOI:10.1190/1.1581072
Chapman C H, Pratt R G. 1992. Traveltime tomography in anisotropic media-Ⅰ. Theory. Geophysical Journal International, 109(1): 1-19. DOI:10.1111/gji.1992.109.issue-1
Chauris H, Noble M S, Lambaré G, et al. 2015. Migration velocity analysis from locally coherent events in 2-D laterally heterogeneous media, Part Ⅰ:Theoretical aspects. Geophysics, 67(67): 1202-1212.
Farra V, Madariaga R. 1987. Seismic waveform modeling in heterogeneous media by ray perturbation theory. Journal of Geophysical Research:Solid Earth, 92(B3): 2697-2712. DOI:10.1029/JB092iB03p02697
HUANG Guang-Nan, ZHOU Bing, DENG Ju-Zhi, et al. 2015. Traveltime tomography of qP reflection waves in anisotropic TI media. Chinese Journal of Geophysics, 58(6): 2035-2045. DOI:10.6038/cjg20150618
Li Z W, Yang K, Xiong K. 2015. Towards an Edge-preserving Stereotomography with a Practical Model Regularization Technique.//Proceedings of the 77th EAGE Conference & Exhibition. Madrid, Spain: EAGE.
Liu Y Z, Wang G Y, Dong L G, et al. 2014. Joint inversion of VTI parameters using nonlinear traveltime tomography. Chinese Journal of Geophysics (in Chinese), 57(1): 99-115. DOI:10.6038/cjg20141026
Lu M H, Tang J H, Yang H Z, et al. 2005. P-wave traveltime analysis and Thomsen parameters inversion in orthorhombic media. Chinese Journal of Geophysics (in Chinese), 48(5): 1167-1171.
Nag S, Alerini M, Ursin B. 2010. PP/PS anisotropic stereotomography. Geophysical Journal International, 181(1): 427-452. DOI:10.1111/gji.2010.181.issue-1
Ni Yao, Yang Kai, Chen Baoshu. 2013. Stereotomography inversion method:theory and application testing. Geophysical Prospecting for Petroleum, 52(2): 121-130.
Prieux P, Lambaré G, Operto S, et al. 2013. Building starting models for full waveform inversion from wide-aperture data by stereotomography. Geophysical Prospecting, 61(S1): 109-137.
Shao W D, Yang K, Xing F Y, et al. 2017. Stereo-tomography in squared-slowness triangulated model. Chinese Journal of Geophysics (in Chinese), 60(9): 3574-3586. DOI:10.6038/cjg20170923
Wang X X, Tsvankin I. 2013. Ray-based gridded tomography for tilted transversely isotropic media. Geophysics, 78(1): C11-C23. DOI:10.1190/geo2012-0066.1
Wang Y X, Yang K, Yang X C, et al. 2016. A high-density stereo-tomography method based on the gradient square structure tensors algorithm. Chinese Journal of Geophysics (in Chinese), 59(1): 218-276. DOI:10.6038/cjg20160122
Xing F Y, Yang K, Xue D, et al. 2017. 3D stereo-tomography applied to the deep-sea data acquired in the South China Sea. Applied Geophysics, 14(3): 142-153.
Yang K, Xing F Y, Li Z W, et al. 2016. 3D stereo-tomography based on the non-reduced Hamiltonian. Chinese Journal of Geophysics (in Chinese), 59(9): 3366-3378. DOI:10.6038/cjg20160920
Zhou B, Greenhalgh S, Green A. 2008. Nonlinear traveltime inversion scheme for crosshole seismic tomography in tilted transversely isotropic media. Geophysics, 73(4): D17-D33. DOI:10.1190/1.2910827
Zhou J X, Xiong K, Yang K. 2017. On the correction of the Frechet derivatives of stereotomography in Cartesian coordinate. Geophysical Prospecting for Petroleum, 56(4): 491-499.
Zhou J X, Yang K, Shao W D. 2019. 2D QP anisotropic stereo-tomography for VTI media in triangulated model. Chinese Journal of Geophysics (in Chinese). DOI:10.6038/cjg2019L0473.inPress
黄光南, ZHOU Bing, 邓居智, 等. 2015. 各向异性TI介质qP反射波走时层析成像. 地球物理学报, 58(6): 2035-2045. DOI:10.6038/cjg20150618
李振伟, 杨锴, 倪瑶, 等. 2014. 基于立体层析反演的偏移速度建模应用研究. 石油物探, 53(4): 444-452. DOI:10.3969/j.issn.1000-1441.2014.04.010
刘玉柱, 王光银, 董良国, 等. 2014. VTI介质多参数联合走时层析成像方法. 地球物理学报, 57(1): 99-115. DOI:10.6038/cjg20141026
卢明辉, 唐建侯, 杨慧珠, 等. 2005. 正交各向异性介质P波走时分析及Thomsen参数反演. 地球物理学报, 48(5): 1167-1171. DOI:10.3321/j.issn:0001-5733.2005.05.026
倪瑶, 杨锴, 陈宝书. 2013. 立体层析反演方法理论分析与应用测试. 石油物探, 52(2): 121-130.
任丽娟, 孙小东, 李振春. 2014.基于特征波属性参数的立体层析速度反演方法研究.//CPS/SEG北京2014国际地球物理会议摘要. http://www.cqvip.com/QK/92065X/201703/672487134.html
邵炜栋, 杨锴, 邢逢源, 等. 2017. 慢度平方三角网格立体层析反演方法. 地球物理学报, 60(9): 3574-3586. DOI:10.6038/cjg20170923
王宇翔, 杨锴, 杨小椿, 等. 2016. 基于梯度平方结构张量算法的高密度二维立体层析反演. 地球物理学报, 59(1): 218-276. DOI:10.6038/cjg20160122
杨锴, 邢逢源, 李振伟, 等. 2016. 基于非降阶汉密尔顿算子的三维立体层析反演. 地球物理学报, 59(9): 3366-3378. DOI:10.6038/cjg20160920
周嘉欣, 熊凯, 杨锴. 2017. 直角坐标系下立体层析FRECHET导数求取修正问题探讨. 石油物探, 56(4): 491-499. DOI:10.3969/j.issn.1000-1441.2017.04.004
周嘉欣, 杨锴, 邵炜栋. 2019. 慢度平方三角网格模型VTI介质二维QP波各向异性立体层析反演. 地球物理学报. DOI:10.6038/cjg2019L0473