2. 山东科技大学测绘科学与工程学院, 青岛 266590
2. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
在过去的20年间,欧美先后实施了CHAMP、GRACE、GOCE、Swarm等一系列具有重力场测量功能的卫星观测任务,获取了全球高精度高分辨率的重力场观测数据,全球重力场模型精度、时间分辨率和空间分辨率不断改善,在全球范围内获得了巨大的科学成功并实现广泛的社会应用.与卫星跟踪卫星技术相比,以GOCE卫星为代表的卫星重力梯度测量技术以其对重力场信号的高敏感性得到了广泛关注,利用其可以获取高精度的地球重力场中短波信息,这对于大地测量的发展具有跨时代的意义.利用卫星重力梯度数据确定重力场,在理论上归结为求解卫星重力梯度测量边值问题,在数据处理的角度上则是在建立观测数据与地球重力位模型球谐系数函数模型和统计模型的基础上,结合一定的参数估计方法进行求解.在利用卫星重力梯度数据确定地球重力场的经典理论方法中,有直接法、空域法和时域法等(Bruinsma et al., 2014; Pail et al., 2011; Sneeuw, 2003).
在利用卫星重力梯度数据确定地球重力场的过程中,由于重力梯度仪的测量带宽限制,在测量带宽(5~100 mHz)以下的重力梯度观测误差呈现1/f的频谱分布(ESA, 1999, 2006),这使得重力梯度观测值中含有强相关的有色噪声,相应观测值的协方差阵为满阵.在海量的观测数据前提下,难以直接对该矩阵进行最小二乘处理.在空域或者时域中,数据间的相关性可以利用自协方差函数进行模型化,这适用于小数据量的情况.此时,不同观测类型、不规则分布的数据均可以得到有效处理,并获得统一的数学模型.对于海量观测值,协方差阵会随着数据量的增大而快速增大,此时协方差阵的求逆、乘积等直接处理过程会变得非常困难.在此情况下,一般的处理方式是引入额外的限制条件,例如等间距数据,无数据空白等,使得协方差阵具有特殊结构(Schuh, 1996, 2003),例如Toeplitz矩阵、循环矩阵,从而可以快速处理.
在利用卫星重力梯度数据反演地球重力场的过程中,国内外学者针对有色噪声的处理多有研究.Schuh(1996, 2003)和Brockmann等(2015)利用ARMA模型滤波器提出了一种函数模型的去相关滤波方法,并将该思想应用到求解大型线性方程系统中. Klees和Broersen(2002),Klees等(2003)基于噪声功率谱密度或噪声时间序列,提出了一种求解ARMA滤波器系数的统计方法,获得了不错的效果.Migliaccio等(2004)基于空域方法提出了地球重力场求解中的有色噪声的维纳滤波方法,该方法可通过迭代处理得到较好的解算结果.Ditmar等(2007)提出了一种卫星数据中的不稳定噪声的数据加权策略,该方法通过共轭梯度方法实现重力场的求解,并已应用到CHAMP数据求解地球重力场中.Piretzidis和Sideris(2017)将自适应滤波应用于卫星重力梯度数据处理中,实测结果表明,与EGM2008模型相比,重力梯度观测值的均方根误差达到了63~84 mE.国内,钟波等(2012)通过仿真数据研究了卫星重力梯度数据的AR去相关滤波方法,刘晓刚等(2012)根据卫星重力梯度测量的有色噪声特性,对Wiener、AR和FIR滤波器进行了系统设计和测试,结果表明AR滤波效果要优于其他两种滤波方法.高秀鹤等(2015)联合重力梯度数据垂直分量和重力数据,有效实现了全张量重力梯度数据的噪声滤除.从相关研究来看,目前针对卫星重力梯度观测数据的有色噪声处理方法中,AR滤波模型的处理精度要优于维纳滤波模型,且多以Schuh(1996, 2003)提出的理论方法为基础,以AR、MA和ARMA等有理分式模型为主要滤波模型.相较而言,ARMA滤波模型具有设计简单,阶数不高,计算负担小等优点.但如何根据观测数据的先验信息,确定最优的ARMA滤波模型仍是需要重点研究的课题.本文在前人的研究基础上,提出了一种最优ARMA模型的构建方法,应用于卫星重力梯度有色噪声滤波处理中,最后通过卫星重力梯度数据确定地球重力场的直接法进行了数值仿真分析,验证了该滤波模型的有效性.
1 ARMA最优滤波模型的构建方法一个线性移不变离散时间系统可以表示为以下差分方程的形式(Schuh, 1996, 2003):
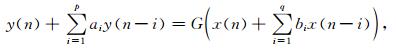
|
(1) |
其中,p, q分别为常系数ai, bi的个数,x(n)为输入过程,y(n)为输出过程,G为系统增益.相应的系统函数为:
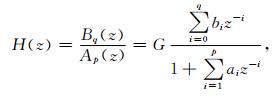
|
(2) |
系统函数式(2)中的p和q值决定了系统的类型:当p=0, q>0时,为卷积滤波器,亦称为滑动平均滤波器,表示为MA(q).当p>0, q=0时,为递归滤波器,表示为AR(p);当p>0, q>0时,为自回归滑动平均滤波器,表示为ARMA(p,q).AR、MA和ARMA滤波器均为有理分式模型,是平稳随机信号处理中最常用的线性模型(张玲华和郑宝玉, 2003).
在信号处理中(张玲华和郑宝玉, 2003),当滤波器的单位脉冲响应为一个有限长序列,称为有限长单位脉冲响应滤波器,简称FIR(finite impulse response)滤波器,此时滤波器的输出信号仅仅与有限长度的系统输入有关,例如MA滤波器.当滤波器的单位脉冲响应为无限长序列,称为无线长单位脉冲响应滤波器,简称IIR(infinite impulse response)滤波器,此时滤波器中存在反馈回路,输出信号与系统输入信号和系统已输出信号均有关,例如AR和ARMA滤波器.MA滤波模型为线性相位,稳定性好,其输出仅仅与有限长度的系统输入有关,但系统输入长度的确定给滤波器的设计带来了一定困难.AR模型和ARMA模型多为非线性相位,存在反馈回路,其输出信号与系统输入信号和系统已输出信号均有关.在卫星重力梯度数据处理中,由于重力梯度仪测量特性的限制,梯度观测值间存在一定的相关性,这种相关性的度量标准无法获取,即梯度值序列间的相关性会随着时间间隔的增加逐渐减弱,但却不一定完全消失.加之从设计方式、求解难易程度和计算效率上考虑,本文选择了ARMA滤波器开展梯度观测值有色噪声的滤波方法研究.
1.1 ARMA模型阶数的选取准则在数字信号处理理论中,ARMA阶数的选取准则一般可表示为(Jones, 1974; Tong, 1975; Broersen, 2000; de Waele and Broersen, 2003):
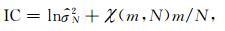
|
(3) |
其中,χ(m, N)为罚系数,对应于具体的选取准则;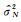
当χ(m, N)=2时,称为AIC准则(Akaike Information Criterion Rule);当χ(m, N)=2N/(N-m-1)时,称为改进的AIC准则(Corrected AIC Rule);当χ(m, N)=ν时,一般取ν∈[2, 6],称为GIC准则(Generalized Information Criterion Rule);当χ(m, N)=lnN时,称为BIC准则(Bayesian Information Criterion Rule).在确定模型的阶数时,本文选择了应用较为广泛、性能较佳的GIC准则.
1.2 ARMA最优模型的构建
当进行ARMA模型参数估计时,首先需要估计AR参数作为ARMA模型的初始输入,然后进行迭代求解.AR初始参数估计有高阶AR方法、高阶MA方法、高阶COV方法以及高阶RINV方法等(Klees et al., 2003; Broersen and de Waele, 2005; Kizilkaya and Kayran, 2006).四种方法均采用一高阶AR模型
一般情况下,四种方法总会有一种方法能够得到最优的ARMA模型参数.但是,在一些情况下,求解可能会存有一定的数值问题,尤其是高阶AR方法和高阶COV方法,此时无法得到适当的AR初始参数.本文采用了高阶MA方法进行AR初始参数的估计.该方法利用一源于高阶AR模型CM(z)的脉冲响应进行初始AR参数的估计.AR模型CM(z)依据Levinson-Durbin迭代方法求解Yule-Walker方程获得(Kaderli and Kayhan, 2000; Kay and Marple, 1981; Sandgren and Stoica, 2005).
1) 高阶AR模型CM(z)的估计AR模型的正则方程可表示为:

|
(4) |
式中,ci为待求的高阶AR模型系数,Rx(m)为时差为m的有色噪声自相关函数,可通过对噪声先验功率谱密度函数进行离散傅里叶逆变换求得(Klees et al., 2003):
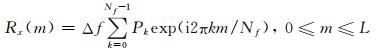
|
(5) |
式中,Pk对应于频率fk=kΔf的噪声功率谱密度(Power Spectrum Density,PSD)函数,Nf为频域采样数,Δf=1/(NfΔt)为频率分辨率,Δt为时域采样间隔,L为最大的计算时差,一般不大于Nf/2.卫星重力梯度观测值的误差PSD模型在卫星发射前一般由地面实验室标定给出,卫星发射后,可利用先验重力场模型对该误差PSD模型进行修正.
方程式(4)亦称作尤勒-沃克(Yule-Walker)方程,可用如下的Levinson-Durbin递推算法进行求解:
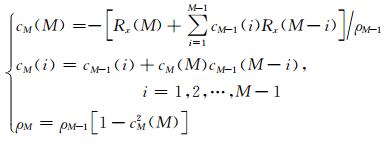
|
(6) |
在式(4)中令M=1,得到一阶AR模型对应的尤勒-沃克方程,求解得到模型系数c1(1)和最小预测误差功率ρ1(此处将预测误差功率G2用ρ表示)为:
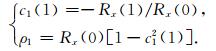
|
(7) |
此即递推的初始条件,利用式(6)即可得到M阶AR模型的M个系数cM(i)(i=1, 2, …, M)和G.
2) ARMA模型AR初始参数的估计
首先,利用高阶AR模型CM(z)估计脉冲响应G(z),即:
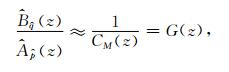
|
(8) |
其中,
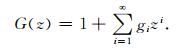
|
(9) |
该过程可直接利用简单的多项式除法求解,或者将该估计过程视作以单位脉冲序列作为输入信号的滤波过程来求解.脉冲响应的长度M0满足远大于M即可.
然后,利用最小二乘方法求解如下的超定系统:
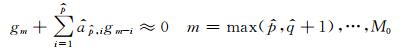
|
(10) |
式中,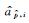
3) ARMA最优模型参数的确定
在利用上述方法求取ARMA模型的初始AR参数后,利用(11)式计算相应的MA参数:
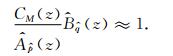
|
(11) |
最后利用
为了减少计算量,ARMA模型的类型仅限于
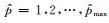

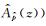

在卫星重力梯度数据确定地球重力场时,可基于引力梯度观测值的球函数表达式直接在卫星位置处建立观测方程,从而实现卫星重力场模型的高精度恢复,该直接解算方法没有任何近似和假设,所以精度较高.截至目前,欧空局(European Space Agency,ESA)发布的GOCE卫星重力场模型中,利用直接法解算的DIR模型已发布了5代.但是,当重力场模型的恢复阶数达到200阶时,所要求解的球谐系数未知数达到了4万余个,设计矩阵和协方差阵更是与观测值个数相关,这时的求解属于大型最小二乘问题.在利用海量重力梯度观测值的求解过程中,梯度观测值误差呈现有色噪声特性,方差协方差阵为非对角阵,因此除了提高计算机的性能外,需要利用重力梯度观测值的误差特性进行有色噪声滤波处理,实现重力梯度观测值的“白化”处理.
利用最小二乘平差准则,直接法的观测方程可以表示为:
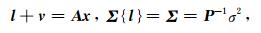
|
(12) |
其中,l为观测向量,A为设计矩阵,x为未知参数向量,P为权阵,σ2为单位权方差.正定对称阵Σ为观测值的方差协方差阵,代表了观测值的精度及观测值间的相关程度.
假定观测值满足等间隔周期采样,那么协方差阵将具有循环Toeplitz结构(Schuh, 1996, 2003),令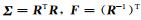
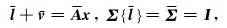
|
(13) |
其中,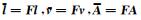
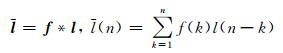
|
(14) |
或者
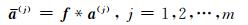
|
(15) |
其中,f为F的第一列,a(j)为设计矩阵A的第j列.该卷积过程可看作一离散线性移不变滤波过程,向量f代表了滤波器的脉冲响应.
根据重力梯度观测值PSD模型,采用ARMA滤波方法构建白化滤波器,在假定观测值满足等间隔采样条件下,可以利用协方差阵的特殊结构实现白化滤波处理.在实现卫星重力梯度数据有色噪声滤波,提高法方程态性的同时,解决了大型最小二乘问题的求解难题.需要指出的是,ARMA滤波方法可以在时域内或者频域内进行.时域方法的优点是在获得观测数据的同时,可以进行滤波处理,避免了超大型矩阵的存储.频域方法的优点则是,在计算条件允许的情况下,可以利用FFT算法实现滤波过程的快速处理,提高计算效率.本文在对梯度数据进行ARMA滤波处理时采用了时域滤波方法.
考虑到重力梯度观测值的海量特征,在利用直接法进行重力场模型的求解过程中,对设计矩阵进行了分块处理,基于并行算法采用了多个线程同时计算,设计矩阵和法方程的分块表达式如下:
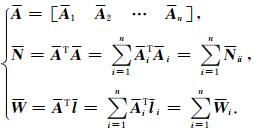
|
(16) |
由此通过ARMA最优滤波算法和分块求解策略可实现卫星重力梯度数据确定地球重力场模型的高精度快速计算.需要说明的是,相关研究表明(Schuh, 2003),ARMA滤波器的暖机时间为90个采样左右,即经过90个采样后,滤波器的频谱特性能够与重力梯度观测值的频谱特性倒数保持一致性.因此,在进行重力场计算时,需要对各数据分块的起始采样数据进行剔除处理.
2.2 仿真分析采用EGM2008模型的前300阶,给定初始轨道根数:轨道长半径6628.000 km,偏心率0.001,轨道倾角96.7°,升交点赤经0.0°,近地点角距0.0°,平近点角0.0°,模拟了30天的卫星轨道数据.依据模拟的卫星轨道信息,基于EIGEN-GL04C模型,利用球谐综合方法仿真了30天、5 s采样的引力梯度数据.在有色噪声的模拟过程中,由于GOCE卫星重力梯度仪的设计指标为3.2 mE,其校准后的实际在轨性能仅能达到10 mE左右(Rummel et al., 2011).考虑到未来我国重力梯度卫星的精度指标要优于GOCE卫星,本文仍然采用ESA给出的GOCE重力梯度仪先验误差功率谱密度(ESA, 1999, 2006)近似解析表达式(17),基于高阶AR模型(10000阶),仿真得到了30天、5 s采样的GOCE重力梯度测量分量Vzz有色噪声序列:
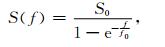
|
(17) |
其中,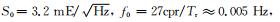
图 1给出了基于AR模型和先验误差功率谱密度模拟的有色噪声时间序列.

|
图 1 模拟的有色噪声时间序列 Fig. 1 Simulated color noise time series |
在ARMA滤波器阶数的选择时,依据前文所述方法和GIC准则,获得了最优ARMA滤波模型.如图 2所示.从图中可以看出,ARMA模型具有局部极小值ARMA(8, 7)和ARMA(34, 33),当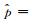

|
图 2 ARMA最优滤波模型阶数的确定 Fig. 2 Determination of the optimal ARMA filter degree |
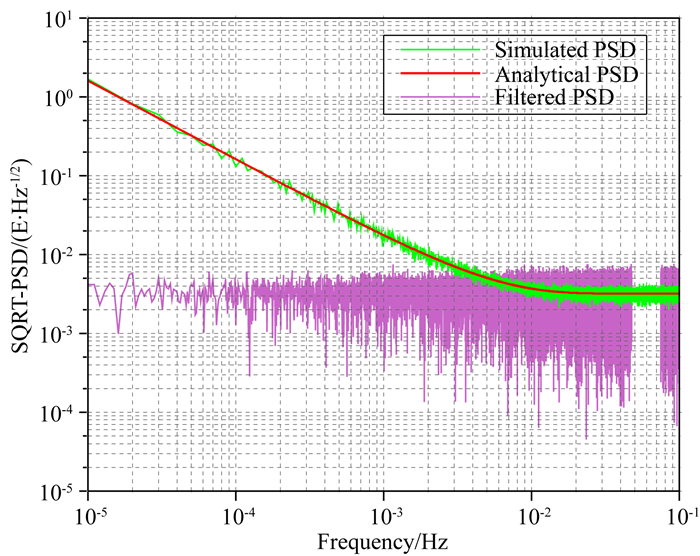
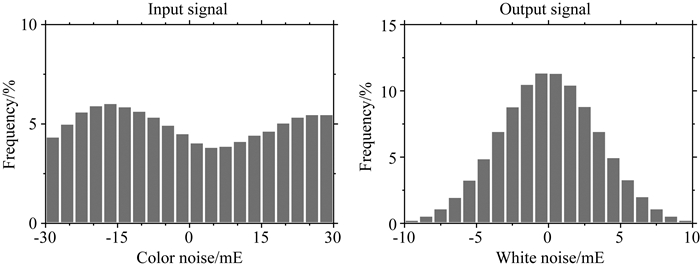
利用获得的最优ARMA时域滤波器,对模拟的有色噪声时间序列进行了ARMA时域滤波处理.图 3给出了ARMA滤波前后的噪声时间序列PSD,图 4给出了滤波前后的噪声时间序列统计直方图.从图中可以看出,滤波前噪声呈现有色噪声特性,呈非正态分布,且与先验的误差PSD模型保持了很好的一致性;滤波后噪声PSD呈现白噪声特性和明显的正态分布,相关性得到了极大地消弱,ARMA时域滤波获得了很好的滤波效果.
|
图 3 ARMA滤波前后的噪声时间序列PSD Fig. 3 PSD of the noise time series before and after ARMA filtering |
|
图 4 ARMA滤波前后的噪声时间序列统计直方图 Fig. 4 Statistical histogram of the noise time series before and after ARMA filtering |
利用球谐综合方法,基于EIGEN-GL04C重力场模型模拟了30天,5 s采样的重力梯度观测值.对其加入了模拟的有色噪声,在未进行滤波处理和进行ARMA滤波处理的情况下分别利用直接法求解重力场模型,求解过程中未采用任何的正则化方法.
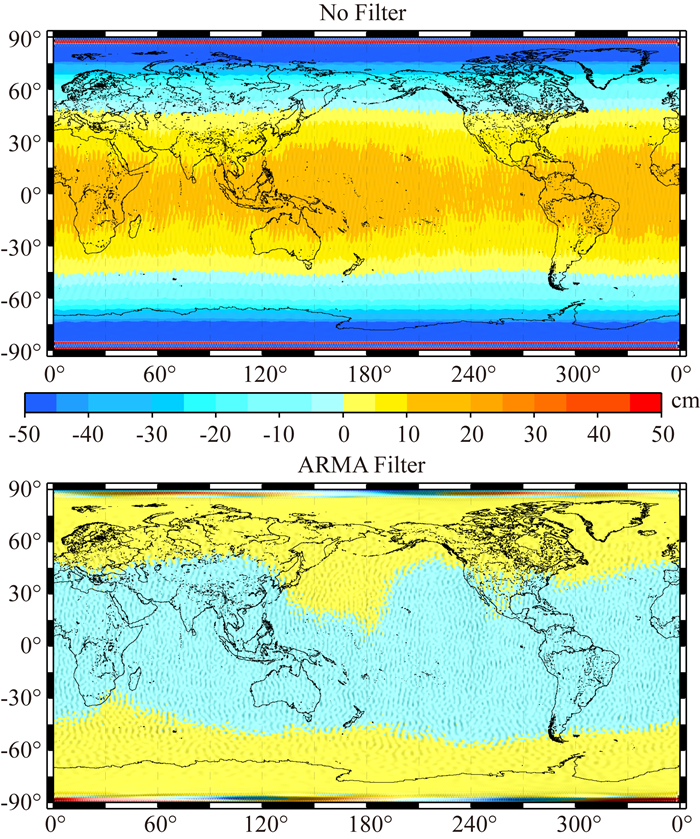
图 5-图 7分别给出了滤波前后的模型阶误差、球谐系数误差谱、全球大地水准面误差分布,表 1给出了ARMA滤波前后纬度±83°间的大地水准面误差统计.从图 5中可以看出,ARMA滤波前后的模型阶误差存在明显差异,滤波前的阶误差在高阶项较之原始信号的均方差(黑色实线)要大,即噪声占优,而滤波后的噪声水平得到了明显抑制,信噪比明显改善,模型阶误差的精度通过滤波处理提高了约两个数量级.滤波前后的球谐系数误差谱(如图 6所示)显示,球谐系数的求解精度提高了1~2个数量级.对比滤波前后的大地水准面误差(如图 7所示),可以看出无论对于低纬度地区还是两极区域,大地水准面均得到了明显改善.非极空白区域的大地水准面精度从米级提高到了分米级水平.表 1的统计量化分析则表明,未进行滤波的大地水准面误差均方差在26.999 m,ARMA滤波有效改善了法方程的态性,大地水准面的误差均方差也提高至0.603 m.由此可见,ARMA滤波方法对于实现卫星重力梯度数据中有色噪声的“白化”处理是有效的,可显著提升重力场模型的求解精度.

|
图 5 ARMA滤波前后的模型阶误差 Fig. 5 Gravity field model degree errors before and after ARMA filtering |

|
图 6 ARMA滤波前后的球谐系数误差谱 Fig. 6 Error spectrum of spherical harmonic coefficients before and after ARMA filtering |
|
图 7 ARMA滤波前后大地水准面误差 Fig. 7 Geoid errors before and after ARMA filtering |
|
|
表 1 ARMA滤波前后大地水准面误差统计 Table 1 Statistics of geoid errors before and after ARMA filtering |
受到重力梯度仪的测量特性限制和观测值采样率影响,利用卫星重力梯度数据直接求解地球重力场模型属于超大型最小二乘问题.本文在前人的研究基础上,对该最小二乘问题存在的有色噪声滤波模型构建和处理问题进行了系统研究:
大型最小二乘问题中数据的去相关处理问题一般多利用有理分式AR、MA和ARMA模型进行.本文基于AR初始参数的高阶MA估计方法和GIC准则,提出了一种最优ARMA滤波模型的构建方法,并成功应用于直接法确定卫星重力梯度重力场模型解算中.结合法方程的分块求解策略,基于欧空局提供的重力梯度对角线分量功率谱密度模型,确定的最优ARMA滤波器为ARMA(76, 75).数值仿真结果表明,滤波后噪声PSD呈现白噪声特性和明显的正态分布,相关性得到了极大地消弱,观测值噪声水平和法方程的态性得到了明显改善,模型阶误差、球谐系数和大地水准面精度均得到了显著提升,有效实现了卫星重力梯度观测值的“白化”滤波处理.
需要指出的是,本文研究仅采用了重力梯度对角线Vzz分量开展相关数值分析验证工作,后续工作中将对全张量观测值的联合滤波处理问题进行进一步研究.
Brockmann J M, Schuh W D, Kargoll B. 2015. A case study on the potential of robust decorrelation filter design for a reprocessing of a gravity field model from GOCE data. EGU General Assembly Conference.//EGU General Assembly Conference Abstracts. Vienna, Austria.
|
Broersen P M T. 2000. Finite sample criteria for autoregressive order selection. IEEE Transactions on Signal Processing, 48(12): 3550-3558. DOI:10.1109/78.887047 |
Broersen P M T, de Waele S. 2005. Automatic identification of time-series models from long autoregressive models. IEEE Transactions on Instrumentation and Measurement, 54(5): 1862-1868. DOI:10.1109/TIM.2005.853232 |
Bruinsma S L, Förste C, Abrikosov O, et al. 2014. ESA's satellite-only gravity field model via the direct approach based on all GOCE data. Geophysical Research Letters, 41(21): 7508-7514. DOI:10.1002/2014GL062045 |
deWaele S, Broersen P M T. 2003. Order selection for vector autoregressive models. IEEE Transactions on Signal Processing, 51(2): 427-433. DOI:10.1109/TSP.2002.806905 |
Ditmar P, Klees R, Liu X. 2007. Frequency-dependent data weighting in global gravity field modeling from satellite data contaminated by non-stationary noise. Journal of Geodesy, 81(1): 81-96. |
ESA. 1999. Gravity field and steady-state ocean circulation mission. Report for mission selection of the four candidate earth explorer missions, ESA Publications Division. ESA SP-1233 (1).
|
ESA. 2006.GOCE L1b products user handbook. Technical Note, OCE-GSEG-EOPGTN-06-0137.
|
Gao X H, Yu P, Zhao Y. 2015. Noise attenuation of vertical components of full tensor gravity gradient data. Global Geology (in Chinese), 34(1): 203-209. |
Jones R. 1974. Identification and autoregressive spectrum estimation. IEEE Transactions on Automatic Control, 19(6): 894-898. DOI:10.1109/TAC.1974.1100730 |
Kaderli A, Kayhan A S. 2000. Spectral estimation of ARMA processes using ARMA-Cepstrum recursion. IEEE Signal Processing Letters, 7(9): 259-261. DOI:10.1109/97.863151 |
Kay S M, Marple S L. 1981. Spectrum analysis-a modern perspective. Proceedings of the IEEE, 69(11): 1380-1419. DOI:10.1109/PROC.1981.12184 |
Kizilkaya A, Kayran A H. 2006. ARMA model parameter estimation based on the equivalent MA approach. Digital Signal Processing, 16(6): 670-681. DOI:10.1016/j.dsp.2006.08.010 |
Klees R, Broersen P. 2002. How to Handle Colored Noise in Large Least-Squares Problems. Building the Optimal Filter. Delft: Delft University Press.
|
Klees R, Ditmar P, Broersen P. 2003. How to handle colored observation noise in large least-squares problems. Journal of Geodesy, 76(11-12): 629-640. DOI:10.1007/s00190-002-0291-4 |
Liu X G, Wu B, Wang X M, et al. 2012. Design of color noise filter in GOCE satellite gravimetry mission. Progress in Geophysics (in Chinese), 27(3): 856-860. DOI:10.6038/j.issn.1004-2903.2012.03.004 |
Migliaccio F, Reguzzoni M, Sansò F. 2004. Space-wise approach to satellite gravity field determination in the presence of coloured noise. Journal of Geodesy, 78(4-5): 304-313. DOI:10.1007/s00190-004-0396-z |
Pail R, Bruinsma S, Migliaccio F, et al. 2011. First GOCE gravity field models derived by three different approaches. Journal of Geodesy, 85(11): 819-843. DOI:10.1007/s00190-011-0467-x |
Piretzidis D, Sideris M G. 2017. Adaptive filtering of GOCE-derived gravity gradients of the disturbing potential in the context of the space-wise approach. Journal of Geodesy, 91(9): 1069-1086. DOI:10.1007/s00190-017-1010-5 |
Rummel R, Yi W Y, Stummer C. 2011. GOCE gravitational gradiometry. Journal of Geodesy, 85(11): 777-790. DOI:10.1007/s00190-011-0500-0 |
Sandgren N, Stoica P. 2005. On moving average parameter estimation. Systems and Control Division, Uppsala University, Sweden.
|
Schuh W D. 1996. Tailored numerical solution strategies for the global determination of the Earth's gravity field. Mitteilungen der geodätischen Institute der TU Graz, Folge 81.
|
Schuh W D. 2003. The processing of band-limited measurements:filtering techniques in the least squares context and in the presence of data gaps. Space Science Reviews, 108(1-2): 67-78. |
Sneeuw N. 2003. Space-wise, time-wise, torus and rosborough representations in gravity field modelling. Space Science Reviews, 108(1-2): 37-46. |
Tong H. 1975. Autoregressive model fitting with noisy data by Akaike's information criterion (Corresp.). IEEE Transactions on Information Theory, 21(4): 476-480. DOI:10.1109/TIT.1975.1055402 |
Zhang L H, Zheng B Y. 2003. Stochastic Signal Processing (in Chinese). Beijing: Tsinghua University Press.
|
Zhong B, Ning J S, Luo Z C, et al. 2012. Simulation study of rigorous gravity field recovery by combining GOCE satellite orbit and gravity gradient data. Geomatics & Information Science of Wuhan University (in Chinese), 37(10): 1215-1220. |
高秀鹤, 于平, 赵玥. 2015. 全张量重力梯度数据垂直分量噪声滤除方法研究. 世界地质, 34(1): 203-209. DOI:10.3969/j.issn.1004-5589.2015.01.26 |
刘晓刚, 吴杉, 王献民, 等. 2012. GOCE卫星重力测量中有色噪声滤波器设计. 地球物理学进展, 27(3): 856-860. DOI:10.6038/j.issn.1004-2903.2012.03.004 |
张玲华, 郑宝玉. 2003. 随机信号处理. 北京: 清华大学出版社.
|
钟波, 宁津生, 罗志才, 等. 2012. 联合GOCE卫星轨道和重力梯度数据严密求解重力场的模拟研究. 武汉大学学报(信息科学版), 37(10): 1215-1220. |
 2018, Vol. 61
2018, Vol. 61


