2. 国土资源部地球物理电磁法探测技术重点实验室, 廊坊 065000;
3. 青海省第三地质矿产勘查院, 西宁 810000
2. Laboratory of Geophysical EM Probing Technologies, Ministry of Land and Resources, Hebei Langfang 065000, China;
3. The Third Institution of Qinghai Geological Mineral Prospecting, Xining 810000, China
经典的磁异常解释方法通常假设不存在剩磁,并认为退磁的作用可以忽略不计(Li and Oldengurg, 1996;Pilkington, 1997),大量的实例应用说明这样近似在多数情况下是合理的,然而当剩磁强、磁化率高时,这样处理出现的误差会明显增大(Guo et al., 2001;Shearer, 2005;刘双等, 2012).刘双等(2012)通过分析指出当磁化率κ≥1.0 SI时,考虑退磁与不考虑退磁的相对偏差高达30%;在剩磁的影响下,经典反演方法得到的磁化强度方向与实际的偏差可能超过15°(Shearer, 2005).强磁性体的磁测资料解释是很常见的问题,块状粗粒的钛磁铁矿和磁赤铁矿的磁化率在1.0~6.0 SI之间(Clark and Emerson, 1991),具有强剩磁的火山岩与磁铁矿磁性相当,剩余磁化强度可达到200 A·m-1(张昌达和董浩斌, 2011),玄武岩磁铁矿不仅有很高的磁化率,还有很强的剩余磁化强度.对于强磁性体,忽略退磁和剩磁中的任意一项都会引起很大的误差,更复杂的是同时存在强剩磁和高磁化率的情况,因此有必要分析忽略退磁或剩磁对磁测数据解释的影响.
经典的重磁位泊松公式假设磁化率和感应磁化强度为线性关系,不能考虑退磁作用,虽可以引入退磁系数来计算退磁场,但非二次曲面形体的退磁系数不为常数,因此退磁改正的计算方法适用范围非常有限,只能计算部分简单规则形体的磁异常.对于复杂形体考虑退磁的正演,研究者们采用了数值积分的方法.早在1963年Vogel提出了一种逐次逼近的迭代算法,通过反复计算单元体内部的磁场实现磁异常的计算;Sharma(1966, 1968)将磁性体划分为一系列磁性均匀的小矩形棱柱单元,由每个单元积分方程的解计算任意形态非均匀磁化地质体的磁场;方华竹(1978)用加约束的赛德尔迭代法求解关于有效磁荷面密度的积分方程,然后计算得到稳定磁场中多个任意形状强磁性均质三度体的磁异常;Eskola和Tervo(1980)将磁性空间划分为线性均匀的磁导率和剩磁组成的子区间,利用面积分的方法来求解高磁化率下的静磁学问题;王书惠(1980, 1981)利用有限元计算强磁性复杂形体的磁异常,并指出不需要引入均匀磁化假定,还能同时考虑磁各向异性、退磁效应、剩磁三种因素的影响(王书惠,1985);Furness(1999)提出了一种在磁性体表面放置偶层计算磁场的面积分算法,能够同时考虑剩磁和感磁;Purss(2005)在高磁化率复杂形体磁场的迭代计算方法中,将非椭球形状地质体用一组不同半径和磁矩的球体表示,通过多次迭代计算球体间的相互作用,能够较精确得到复杂形体近似的退磁系数;Lelievre(2003, 2006)实现了基于有限体积法的高磁化率形体正反演计算;Kostrov(2007)在体积分法的基础上提出利用三角单元的体积分求解二维问题,很大程度上克服了体积分法的缺陷,能够精确地计算相对磁导率大和离磁性体距离小的磁场.
相对考虑退磁和剩磁的正演,近年来研究者们对复杂磁化条件下的反演解释更加关注.李媛媛等(2010)系统总结了考虑退磁影响的磁场正反演研究的发展方向.由于退磁和剩磁都会导致磁化方向发生改变,研究者们提出先估计异常体的磁化方向(Dannemiller and Li, 2006; Gerovska, 2009; Chen et al., 2017;Li et al., 2017),然后利用得到的磁化方向计算磁性的三维分布,或者利用弱受磁化方向影响的模量数据反演(Shearer, 2004, 2005; Li et al., 2010, 2012; Pilkington and Beiki, 2013; Guo et al., 2014; Li and Li, 2014; Liu et al., 2015; 李泽林等, 2015; Zhou et al., 2015; Krahenbuhl and Li, 2007, 2017),也有不少学者提出一些磁化强度矢量反演方法,避开了磁化方向的影响(王妙月等, 2004;Lelièvre et al., 2009;;Ellis et al., 2012; 刘双等,2013;Ou and Feng, 2015; Li and Sun, 2015, 2016; Liu et al., 2013, 2017).尽管在各种复杂磁化条件下的磁场正反演计算方面已经取得了不少成果,然而对于同时考虑退磁和剩磁的正演模拟分析还不够,对剩磁的退磁改正认识模糊,为此本文详细分析了退磁作用对剩磁的影响,这对深入开展考虑退磁和剩磁的磁异常反演研究,提高磁法勘探效果和应用水平具有指导意义.
1 有限体积法正演 1.1 控制方程根据静磁学理论,若设B为磁感应强度,μ0为真空中的磁导率,μ为介质磁导率,Mr为剩余磁化强度,H为磁场强度,对于线性各向同性的磁介质满足控制方程:
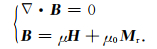
|
(1) |
引入标量磁位U,那么磁场强度H=-∇U,将其代入方程得到关于U的方程:
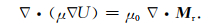
|
(2) |
求解方程(2)得到U,并根据Mi=κH和B=μH+μ0Mr分别计算得到感应磁化强度Mi和磁感应强度B.
1.2 控制方程离散化和求解控制方程在整个介质空间内都成立,对(1)式中方程在体积为V的单元体内积分,并运用高斯定理,可将方程写成:
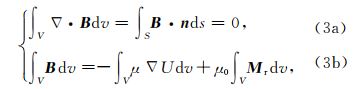
|
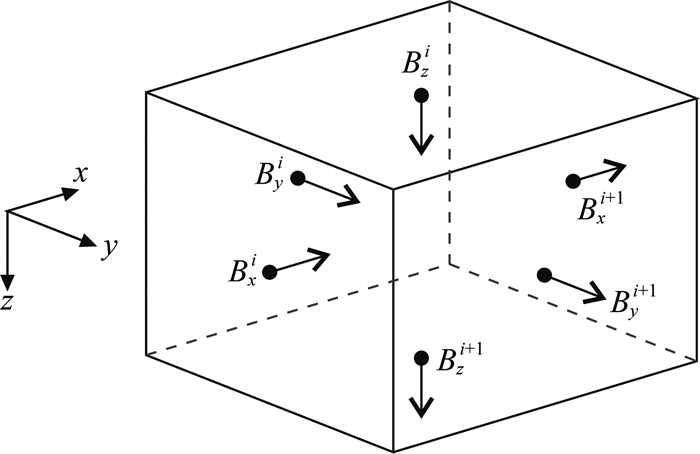
将地下空间剖分为规则的网格单元,设每个网格单元的磁化率和剩余磁化强度为常数,并采用图 1所示的方式采样磁场分量.其中n为单元体表面的外法向单位矢量,并假设每个表面的磁通量为其磁场分量平均值与面积的乘积,磁场分量的采样位置位于每个表面的中心点上,并且每个面上磁场分量的平均值等于中心点上的分量值(图 1).那么可以将公式(3a)中积分方程离散化为如下形式:
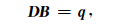
|
(4) |
|
图 1 磁场分量位置示意图 Fig. 1 Location of magnetic field components |
其中D是与单元大小有关的梯度矩阵,B向量是单元表面上待求的磁感应强度分量,q是边界条件系数组成的向量.
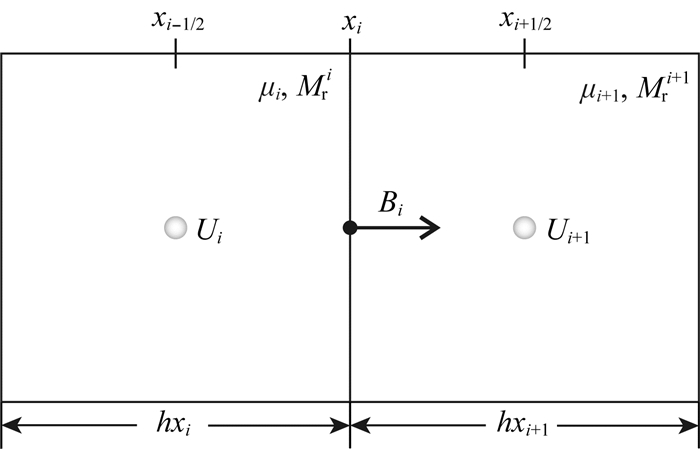
对于(3b)式,仅考虑对Bx分量的积分,如图 2所示,设相邻网格单元磁导率分别为μi、μi+1,x方向的剩余磁化强度分别为Mri、Mri+1,网格单元中心磁位为Ui、Ui+1,网格单元边长为hxi、hxi+1,可以得到:

|
(5) |
|
图 2 Bx分量积分示意图 Fig. 2 Diagram of the integral of the Bx component |
假设Bix在整个积分段不变,并作
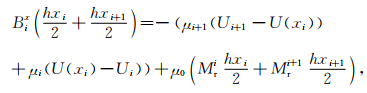
|
(6) |
在(6)式中假设在xi处的磁位由线性插值得到:
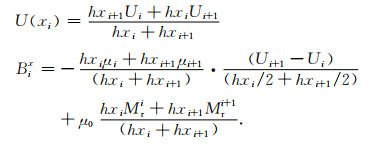
|
(7) |
设Yx是由hxi/(hxi+hxi+1)和hxi+1/(hxi+hxi+1)组成的稀疏矩阵,m和U向量分别是单元网格的磁导率和磁位,Gx是由±1/(hxi/2+hxi+1/2)组成的稀疏矩阵,Mrx向量是剩余磁化强度的x分量,可以将(7)式写成Bx=-XxGxU+μ0YxMrx,其中Xx=diag(Yxm)是由向量Yxm组成的对角矩阵,扩展到三维可以写成如下形式:
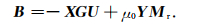
|
(8) |
代入到(4)式中将B消去后得到了关于磁位U的方程:
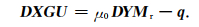
|
(9) |
设磁异常为Bs,正常地磁场为B0,可以得到磁异常Bs的表达式:
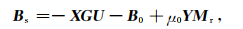
|
(10) |
方程(9)为Ax=b形式的大型稀疏线性方程组,利用拟最小残差法,预条件共轭梯度法等求解就可以得到磁位,代入(10)式计算得到规则网格上的磁异常Bs,然后根据观测点和网格的相对位置关系得到观测点上的磁异常.
1.3 边界条件处理在求解方程时需要建立相应的边界条件.如果选取的计算区域足够大,磁性体对外边界的贡献几乎为零,可认为外边界处的磁场近似为地磁场.这样的做法虽比较精确,但在足够大的区域必然会降低计算的效率.如果计算区域太小,磁性体对边界的影响是不可忽略的,此时仅将地磁场作为边界条件,会降低计算的精度.为了兼顾计算效率和计算精度,首先设计了有限的计算空间,然后用一些规则模型在边界处的磁场近似代替磁性体对边界的影响.
任何复杂的形体在离观测点有一定距离之后,可以近似当作点源来处理,因此将研究区内磁性体在边界处的磁场可以近似等效为单个球体的磁场.磁化率为κ,剩余磁化强度为Mr,体积为V的球体受地磁场B0磁化后在P点产生的磁感应强度可以表示为(Blakely, 1996):
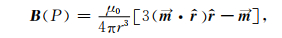
|
(11) |
其中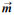


其中等效球体的体积和磁性体的相等,等效球体的磁化率是磁性体的加权平均值,而等效球体的中心坐标(xc,yc,zc)按磁性体磁化率的大小加权得到.按照上述方法处理后,得到磁性体近似在边界处的磁场,加上地磁场便可以计算得到方程(4)中q的值.
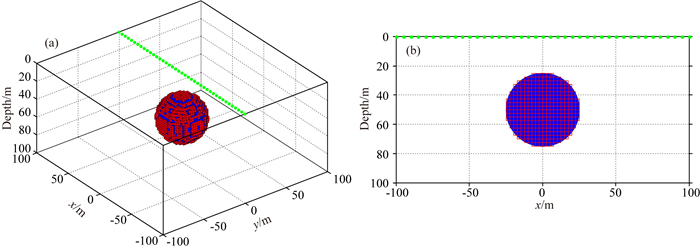
2 模型正演分析 2.1 球体模型为验证三维有限体积法计算的正确性,并分析忽略剩磁或剩磁改正项导致的计算误差,设计了图 3所示的球体模型.球体的退磁系数为常数,因此可以利用退磁改正公式计算磁异常.采用规则网格剖分,设计的规则网格单元体(图 3中红色网格模型)与球体模型(图 3中蓝色模型)的体积相同.球体模型中心埋深50 m,半径为25.07 m,网格的大小为2.5 m×2.5 m×2.5 m,四组实验中模型磁化率分别为0.01 SI,0.1 SI,1.0 SI和6.0 SI;地磁场大小T0=50000 nT,地磁倾角I0=60°,偏角D0=0°.假设球体剩余磁化强度为常量,磁化强度大小Mr=19.89 A·m-1,剩余磁化倾角Ir=50°,偏角Dr=60°;观测点分布在x=-100~100 m,y=0 m,高程为0 m的直线上,点距为5 m.
|
图 3 模拟球体模型示意图 红色为网格模型,蓝色为球体模型,绿色点为观测点位置. Fig. 3 Diagram of the simulation sphere model The red lines are grid models, the blue region is the sphere, and the green points are the observation points. |
在磁化场H0作用下,退磁系数为N的磁性体受磁化后,按退磁改正公式计算,其磁化强度M=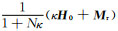
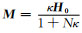

|
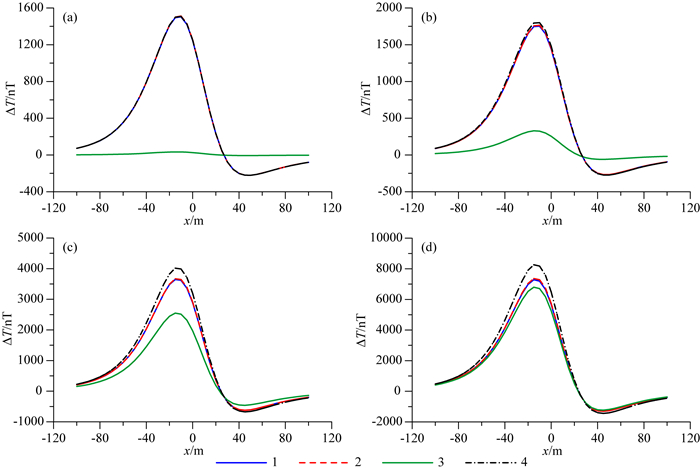
图 4
不同方法正演的球体ΔT异常
(a)模型磁化率κ=0.01 SI,Q=50; (b)模型磁化率κ=0.1SI,Q=5;
(c)模型磁化率κ=1.0 SI,Q=0.5; (d)模型磁化率κ=6.0 SI,Q=0.083 1-退磁改正计算结果;2-有限体积法计算结果; 3-忽略剩磁计算结果;4-忽略剩磁改正项计算结果. Fig. 4 The total-field anomaly of the sphere using different methods (a) κ=0.01 SI, Q=50; (b) κ=0.1 SI, Q=5; (c) κ=1 SI, Q=0.5; (d) κ=6 SI, Q=0.083. Curve 1-the result of demagnetization correction, Curve 2-the result of finite volume method, Curve 3-the result of ignoring remanence, Curve 4-the result of ignoring remanence correction. |
从图 4中可以看出,对于不同磁化率大小的模型,曲线1和曲线2几乎完全重合.表 1中比较了有限体积法与退磁改正计算结果的偏差,由于利用网格模型模拟球体和局部截断的误差,导致随着模型磁化率的增加,最大偏差和平均偏差逐渐增大,但是相对偏差均保持在4%以下,说明了利用有限体积法计算磁异常的正确性.对于忽略剩磁的正演曲线3,与退磁改正的偏差随着Q的增加而增加,说明存在强剩磁时,忽略剩磁产生误差较大.曲线4与曲线3相比更加接近曲线2,可见忽略剩磁改正项的偏差相对忽略剩磁小,并且会随着模型磁化率的增大而增加.
|
|
表 1 有限体积法计算结果偏差表 Table 1 Deviation analysis of the finite volume method |
如果以退磁改正结果为标准,那么忽略剩磁的结果与退磁改正的异常幅值相对偏差为
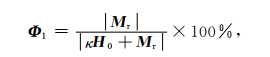
|
(12) |
忽略剩磁改正项的结果与退磁改正的异常幅值相对偏差为
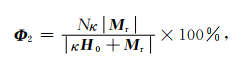
|
(13) |
其中|κH0+Mr|≤|κH0|+|Mr|,那么Φ1≥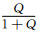
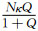
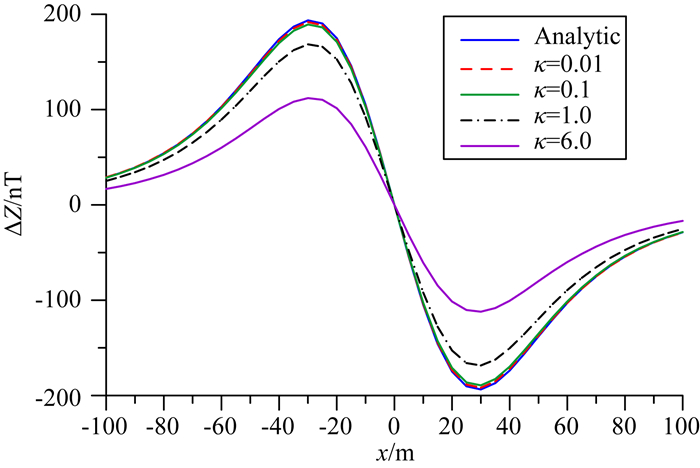
通常认为感应磁化强度和剩余磁化强度矢量相加即得到了总的磁化强度,并没有注意到退磁作用也会导致剩磁发生变化.从球体的正演模拟中可以看到,同时考虑退磁和剩磁的正演结果与忽略剩磁改正项的磁异常存在偏差,而且这种偏差随着模型磁化率的增加而变大,为了进一步分析退磁作用对剩磁的影响,在图 3的观测条件下设计了如图 5所示的长方体模型,大小为40 m×20 m×20 m长方体上顶面埋深40 m,模型剩余磁化强度大小Mr=19.89 A·m-1,剩余磁化倾角Ir=0°,磁化偏角Dr=0°,模型的磁化率大小设为0.01 SI、0.1 SI、1.0 SI和6.0 SI四种情况.为了单独分析退磁作用对剩磁的影响,设地磁场大小T0=0,那么感应磁化强度为零,异常都是由剩磁引起的.图 6是用有限体积法计算得到的垂直分量ΔZ异常曲线,其中analytic曲线是假设剩余磁化强度为常量按照解析公式计算得到,其他曲线由有限体积法计算的得到.从正演结果中发现模型磁化率为0.01 SI和0.1 SI时,analytic曲线和这两种情况的结果非常接近,而磁化率增大到1.0 SI和6.0 SI之后,有限体积法正演结果变小,与解析计算的结果存在了较大偏差.从以上的模拟结果可以看出,退磁作用影响了剩磁,使得剩磁引起的磁异常幅值变小,而且磁化率越大这种影响越明显.

|
图 5 长方体模型示意图 红色为长方体模型,绿色点为观测点位置,蓝色平面为切片图位置. Fig. 5 Diagram of the cuboid model The red region is the cuboid, the green points are the observation points, and the blue plane is a vertical slice. |
|
图 6 不同磁化率长方体模型的垂直分量ΔZ异常 Fig. 6 The vertical-component anomaly of the cuboid model with different susceptibilities |
为说明剩磁的退磁改正问题,前人提出真剩余磁化强度Mr和有效剩余磁化强度M′r的概念,并用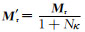

|
图 7 长方体内部磁化强度分布图 (a)模型磁化率κ=0.01 SI;(b)模型磁化率κ=6.0 SI. Fig. 7 Internal magnetization distributions of the cuboid (a) κ=0.01 SI; (b) κ=6.0 SI. |
为分析影响有效剩余磁化强度的因素,将图 5中磁化率为6.0 SI长方体模型的剩余磁化方向Ir设为90°,计算得到的长方体内部磁化强度分布如图 8a所示;将图 5中磁化率为6.0 SI长方体模型长宽高比设置为1:1:1,剩余磁化方向Ir=0°,计算得到的长方体内部磁化强度分布如图 8b所示.将这两组结果和图 7b中的磁化强度相比,对于不同剩磁方向和不同比例的模型,不仅磁化强度形态表现的不同,磁化强度的大小也各不相同,由此看见,退磁作用对剩磁的影响不仅与磁化率相关,而且与剩磁的方向和磁性体的形态相关.
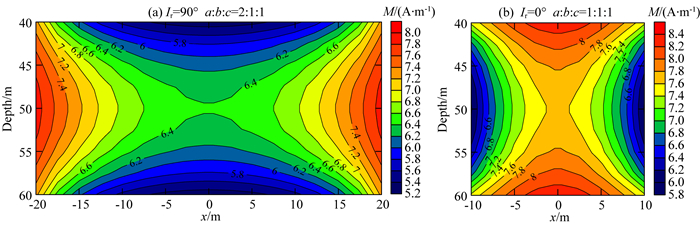
|
图 8 模型内部磁化强度分布图 (a)垂直磁化长方体; (b)水平磁化立方体. Fig. 8 Internal magnetization distributions of the model (a) Vertically magnetized cuboid; (b) Horizontally magnetized cube. |
为了分析复杂情况下同时考虑退磁和剩磁的磁异常特征,设计了由两个走向相同、倾向相反的板状体构成的组合模型.地磁场大小T0=50000 nT,地磁倾角I0=60°,偏角D0=5°.设置板状体A的剩余磁化强度Mr=39.79 A·m-1,剩余磁化倾角Ir=85°,磁偏角Dr=-25°,板状体B剩余磁化强度为0,板状体的磁化率图 9中所示.
|
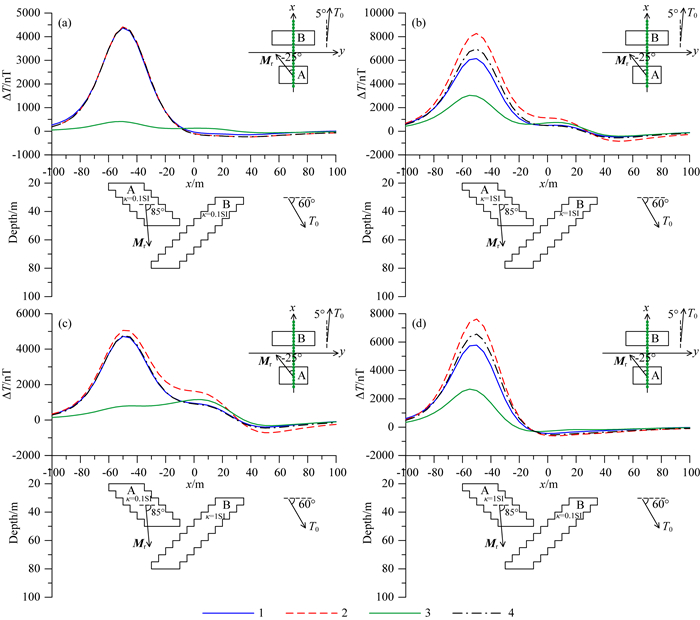
图 9 不同方法正演的组合模型ΔT异常 1-同时考虑退磁和剩磁计算结果;2-忽略退磁计算结果; 3-忽略剩磁计算结果;4-忽略剩磁改正项计算结果. Fig. 9 The total-field anomaly of the combination model using different methods Curve 1: the result of simultaneous consideration for demagnetization and remanence, Curve 2: the result of ignoring demagnetization, Curve 3: the result of ignoring remanence, Curve 4: the result of ignoring remanence correction. |
利用四种方法计算得到组合模型的磁异常.图 9a中的曲线1、曲线2、曲线4几乎完全重合,可见板状体磁化率均为0.1 SI时,忽略退磁或忽略剩磁改正项产生的误差均非常小.而此时Q=10,曲线3与曲线1差异非常明显,忽略剩磁产生了很大的误差.图 9b中板状体磁化率均为1 SI,不论忽略剩磁还是剩磁,均与同时考虑退磁和剩磁的结果存在较大差异,且忽略退磁时,异常幅值偏大,忽略剩磁时,异常幅值偏小.图 9a中曲线4和曲线1几乎完全重合,图 9b中两者差异变大,可见板状体A的磁化率增大后,忽略剩磁改正项的误差也会增大.
将图 9a中板状体B的磁化率从0.1 SI增大到1 SI得到图 9c的结果,与图 9a相比,图 9c中的曲线2与曲线1偏差变大,曲线4依然同曲线1基本重合;将图 9b中板状体B的磁化率从1 SI减小为0.1 SI得到图 9d的结果,对比发现板状体B的磁化率减小后,忽略退磁的误差也随之减小,而忽略剩磁改正项的误差基本没有变化.这两组对比中板状体B的磁化率变化后,忽略剩磁改正项的误差变化不明显.
为进一步对比忽略剩磁改正项的误差,将图 9中忽略剩磁改正项的结果与同时考虑退磁和剩磁的结果相减得到误差对比图(图 10中曲线a,b,c,d对应于图 9a,图 9b,图 9c,图 9d的误差值).图 10中曲线a与曲线c相似,曲线b与曲线d相似,曲线a和c的值小于曲线b和d的值,并且它们不是两两相等的.板状体A具有剩磁,当板状体A与B磁化率单独变化时,忽略剩磁改正项的误差主要与板状体A的磁化率相关;虽然板状体B不存在剩磁,当其磁化率变化时,忽略剩磁改正项的误差也会发生改变.由此可见退磁作用对剩磁的影响不仅主要与磁性体自身磁性参数相关,还会因为临近强磁性体的作用发生改变.

|
图 10 忽略剩磁改正项的误差对比 Fig. 10 Error comparisons of ignoring remanence correction |
青海灶火河西预查区位于北昆仑岩浆弧带与祁漫塔格缝合带的交接部位,工区大面积被第四系风积物所覆盖,平均厚度在60 m以上,工区内矿产以接触矽卡岩型的铁多金属矿(化)为主,其次为气液充填型细脉状黄铜矿化.2012—2013年青海省第三地质矿产勘查院在预查区圈定了6条铁多金属矿体,1条铜铅锌矿化体,发现的矿体基本呈似层状、透镜状不规则状,赋存于大理岩和花岗闪长岩外接触带的矽卡岩中.根据工区岩矿石磁性统计结果(表 2),该区磁性最强的是磁铁矿矿石,不仅有较高的磁化率还有很强的剩磁,按磁化率和剩磁平均值计算科尼斯布格比Q=2.1,黄铜矿化磁铁矿矿石、磁铁矿化矽卡岩等呈中强磁性,磁性变化范围大,是主要的干扰异常,中等磁性和弱磁性的岩石则构成了背景场.
|
|
表 2 灶火河西地区主要岩矿石磁性参数统计表 Table 2 Magnetic parameters statistics of main ores in the Zaohuohexi area |
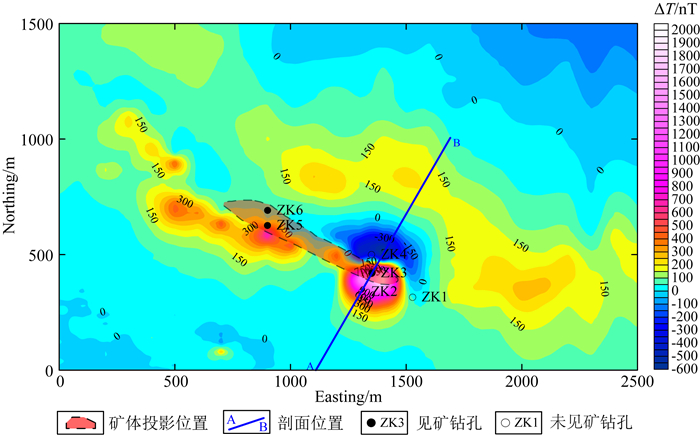
预查区中南部C5磁异常形态规则、呈带状北西西向展布,异常长1.6 km、宽约400 m,异常南正北负,曲线尖锐,强度高(峰值达1980 nT)、梯度陡,是区内最强的磁异常带.通过施工钻孔,圈定出的磁铁矿体埋深由东向西逐渐增加,且厚度逐渐变薄.AB线在矿体东段,经过异常幅值位置,根据钻孔控制的矿体位置和形态正演了AB线的磁异常.由物性统计表,模型的磁化率和剩磁均按平均值计算,磁铁矿矿石的剩磁倾角取35°(图 11).
|
图 11 灶火河西工区C5磁异常等值线平面图 Fig. 11 The magnetic anomaly map of C5 in the Zaohuohexi area |
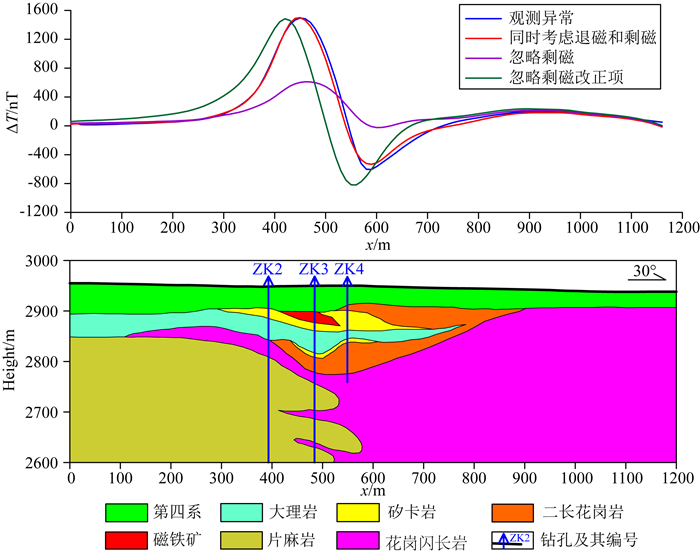
AB剖面的磁异常正演计算结果如图 12所示.由于该区磁铁矿的剩磁较强,忽略剩磁计算结果的幅值明显比观测值小,极大值偏差达到900 nT,忽略剩磁改正项的幅值与观测值接近,但是异常的位置向210°方位偏移了30 m,与观测值之间的均方差到达370 nT,而同时考虑退磁和剩磁的计算结果和观测异常一致,与观测值间的均方差小于40 nT.磁铁矿的磁化率计算值只有0.37 SI,但由于剩磁较强,导致忽略剩磁或剩磁改正项时产生了较大的误差.这里只是由地质模型正演了磁异常,若按忽略剩磁或剩磁改正项的方法进行解释,必然会导致解释出现偏差,由此可见强磁性岩体的资料处理解释中有必要同时考虑退磁和剩磁.
|
图 12 灶火河西工区AB剖面磁异常正演图 Fig. 12 Forward modeling of the magnetic anomaly of profile AB in the Zaohuohexi area |
本文探讨了基于有限体积法同时考虑退磁和剩磁的磁异常正演方法,推导了采用有限体积法计算的离散表达式,由球体模型的磁异常计算验证了有限体积法的正确性,通过对理论模型和实测数据进行正演计算得到以下认识:
(1) 由退磁改正作为对比标准分析了几种近似计算的误差,忽略剩磁的相对误差与科尼斯布格比Q相关;忽略剩磁改正项的误差相对较小,并且与磁化率相关;而对于Q值较大岩体,忽略剩磁相比忽略退磁作用将产生更大的误差.
(2) 在无地磁场的情况下对模型进行正演计算,单独分析了退磁作用对剩磁的影响,结果表明退磁作用使得剩磁引起的磁异常幅值变小,而且导致模型内部磁化强度分布不均匀,这种影响随着磁化率增大而更加明显,由此说明了对剩磁进行退磁改正的合理性.
(3) 通过分析不同条件下模型内部磁化强度的特征,说明退磁作用对剩磁的影响不仅随着磁化率增加而增大,而且会因为剩磁的方向和磁性体的形态发生变化.组合模型的计算对比表明,退磁作用对剩磁的影响还会因为临近强磁性体的作用发生改变.退磁作用对剩磁的影响使得对剩磁的处理解释更加复杂.
综上所述,由于退磁作用的影响导致剩磁也需要进行改正,这样增加了强磁性体异常解释的难度.本文虽然只是从正演上进行了分析,但要提高强磁性体解释的准确性有必要开展同时考虑退磁和剩磁的反演方法研究.
Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press..
|
Chen C, Yu P, Rao C. 2017.Estimating the magnetization direction based on the 3D susceptibility inversion of the total magnitude anomaly. SEG Technical Program Expanded Abstracts. 1834-1838. http://www.onepetro.org:443/conference-paper/SEG-2017-17781520
|
Clark D A, Emerson D W. 1991. Notes on rock magnetization characteristics in applied geophysical studies. Exploration Geophysics, 22(3): 547-555. DOI:10.1071/EG991547 |
Dannemiller N, Li Y G. 2006. A new method for determination of magnetization direction. Geophysics, 71(6): L69-L73. DOI:10.1190/1.2356116 |
Ellis R G, Wet B D, Macleod I N. 2012. Inversion of magnetic data for remanent and induced sources. Aseg Extended Abstracts, 2012(1): 1-4. |
Emerson D W, Clark D A, Saul S J, et al. 1985. Magnetic exploration models incorporating remanence, demagnetization and anisotropy:HP 41C handheld computer algorithms. Exploration Geophysics, 16(1): 1-122. DOI:10.1071/EG985001 |
Eskola L, Tervo T. 1980. Solving the magnetostatic field problem (a case of high susceptibility) by means of the method of subsections. Geoexploration, 18(2): 79-95. DOI:10.1016/0016-7142(80)90022-8 |
Fang H Z. 1978. Calculation of magnetic anomaly of three-degree magnetic body with arbitrary shape. Acta Geologica Sinica (in Chinese), 52(01): 63-78. |
Furness P. 1999. A versatile integral equation technique for magnetic modelling. Journal of Applied Geophysics, 41(4): 345-357. DOI:10.1016/S0926-9851(99)00005-1 |
Gerovska D, Araúzo-Bravo M J, Stavrev P. 2009. Estimating the magnetization direction of sources from southeast Bulgaria through correlation between reduced-to-the-pole and total magnitude anomalies. Geophysical Prospecting, 57(4): 491-505. DOI:10.1111/gpr.2009.57.issue-4 |
Guo L H, Meng X H, Zhang G L. 2014. Three-dimensional correlation imaging for total amplitude magneticanomaly and normalized source strength in the presence of strong remanent magnetization. Journal of Applied Geophysics, 111: 121-128. DOI:10.1016/j.jappgeo.2014.10.007 |
Guo W W, Dentith M C, Bird R T, et al. 2001. Systematic error analysis of demagnetization and implications for magnetic interpretation. Geophysics, 66(2): 562-570. DOI:10.1190/1.1444947 |
Kostrov N P. 2007. Calculation of magnetic anomalies caused by 2D bodies of arbitrary shape with consideration of demagnetization. Geophysical Prospecting, 55(1): 91-115. DOI:10.1111/gpr.2007.55.issue-1 |
Krahenbuhl R A, Li Y G. 2007. Influence of self-demagnetization effect on data interpretation in strongly magnetic environments. ASEG Extended Abstracts, 2007(1): 1-4. |
Krahenbuhl R A, Li Y G. 2017. Investigation of magnetic inversion methods in highly magnetic environments under strong self-demagnetization effect. Geophysics, 82(6): J83-J97. DOI:10.1190/geo2016-0676.1 |
Lelievre P G. 2003. Forward modelling and inversion of geophysical magnetic data[M.S. thesis]. Vancouver: University of British Columbia.
|
Lelievre P G, Oldenburg D W. 2006. Magnetic forward modelling and inversion for high susceptibility. Geophysical Journal International, 166(1): 76-90. DOI:10.1111/gji.2006.166.issue-1 |
Lelievre P G, Oldenburg D W. 2009. A 3D total magnetization inversion applicable when significant, complicated remanence is present. Geophysics, 74(3): L21-L30. DOI:10.1190/1.3103249 |
Li J P, Zhang Y T, Yin G, et al. 2017. An approach for estimating the magnetization direction of magnetic anomalies. Journal of Applied Geophysics, 137: 1-7. DOI:10.1016/j.jappgeo.2016.12.009 |
Li S L, Li Y G. 2014. Inversion of magnetic anomaly on rugged observation surface in the presence of strong remanent magnetization. Geophysics, 79(2): J11-J19. DOI:10.1190/geo2013-0126.1 |
Li Y G, He Z X, Liu Y X. 2012. Application of magnetic amplitude inversion in exploration for volcanic units in a basin environment. Geophysics, 77(5): B219-B225. DOI:10.1190/geo2012-0008.1 |
Li Y G, Oldenburg D W. 1996. 3-D inversion of magnetic data. Geophysics, 61(2): 394-408. DOI:10.1190/1.1443968 |
Li Y G, Shearer S E, Haney M M, et al. 2010. Comprehensive approaches to 3D inversion of magnetic data affected by remanent magnetization. Geophysics, 75(1): L1-L11. DOI:10.1190/1.3294766 |
Li Y G, Sun J J. 2015.Towards geology differentiation using magnetization inversions.International Workshop and Gravity, Electrical & Magnetic Methods and their Applications, 350-353.
|
Li Y G, Sun J J. 2016. 3D magnetization inversion using fuzzy c-means clustering with application to geology differentiation. Geophysics, 81(5): J61-J78. DOI:10.1190/geo2015-0636.1 |
Li Y Y, Yang Y S, Liu T Y. 2010. Magnetic forward and reverse modelling of 3D bodies of arbitrary shape withconsideration of demagnetization:progress and prospect. Progress in Geophysics (in Chinese), 25(02): 627-634. |
Liu S, Liu T Y, Gao W L, et al. 2012. The Influence of demagnetization on magnetic data Interpretation. Geophysical and Geochemical Exploration (in Chinese), 36(04): 602-606. |
Liu S, Feng J, Gao W L, et al. 2013. 2D inversion for borehole magnetic data in the presence of significant remanence and demagnetization. Chinese Journal of Geophysics (in Chinese), 56(12): 4297-4309. |
Liu S, Hu X, Liu T, et al. 2013. Magnetization vector imaging for borehole magnetic data based on magnitude magnetic anomaly. Geophysics, 78(6): D429-D444. DOI:10.1190/geo2012-0454.1 |
Liu S, Hu X, Xi Y, et al. 2015. 2D sequential inversion of total magnitude and total magnetic anomaly data affected by remanent magnetization. Geophysics, 80(3): K1-K12. DOI:10.1190/geo2014-0019.1 |
Liu S, Hu X, Zhang H, et al. 2017. 3D Magnetization Vector Inversion of Magnetic Data:Improving and Comparing Methods. Pure & Applied Geophysics, 174(12): 4421-4444. |
Li Z L, Yao C L, Zheng Y M, et al. 2015. 3D data-space inversion of magnetic amplitude data. Chinese Journal of Geophysics (in Chinese), 58(10): 3804-3814. |
Ou Y, Feng J. 2015. Joint magnetization vector inversion of surface and borehole magnetic data. International Workshop and Gravity, Electrical & Magnetic Methods and their Applications, 73-76. https://www.sciencedirect.com/science/article/pii/S0926985117300794
|
Pilkington M. 1997. 3-D magnetic imaging using conjugate gradients. Geophysics, 62(4): 1132-1142. DOI:10.1190/1.1444214 |
Pilkington M, Beiki M. 2013. Mitigating remanent magnetization effects in magnetic data using the normalized source strength. Geophysics, 78(3): J25-J32. DOI:10.1190/geo2012-0225.1 |
Sharma P V. 1968. Demagnetization effect of a rectangular prism. Geophysics, 33(1): 132-134. DOI:10.1190/1.1439915 |
Sharma P V. 1966. Rapid computation of magnetic anomalies and demagnetization effects caused by bodies of arbitrary shape. Pure and Applied Geophysics, 64(1): 89-109. DOI:10.1007/BF00875535 |
Shearer S, Li Y G. 2004. 3D Inversion of magnetic total gradient data in the presence of remanent magnetization. 74th SEG Annual Meeting Expanded Abstracts, 774-777. http://adsabs.harvard.edu/abs/2004AGUFMNG31B0871S
|
Shearer S E. 2005. Three-dimensional inversion of magnetic data in the presence of remanent magnetization[Master's thesis].Colorado: Colorado School of Mines.
|
Vogel A. 1963. The application of electronic computers to the calculation of effective magnetisation. Geophysical Prospecting, 11(1): 51-58. DOI:10.1111/gpr.1963.11.issue-1 |
Wang M Y, Di Q Y, Xu K, et al. 2004. Magnetization vector inversion equations and 2D forward and inversed model study. Chinese Journal of Geophysics (in Chinese), 47(03): 528-534. |
Wang S H. 1980. Calculating the effective magnetization and magnetic anomaly of inhomogeneous magnetized magnetic bodies (two-dimensional) using Finite element method. Geology and Exploration (in Chinese), 09: 49-57. |
Wang S H. 1981. On the theory using the finite element method to solve direct problem of magnetic exploration. Chinese Journal of Geophysics (in Chinese), 24(02): 207-217. |
Wang S H. 1985. Finite element-boundary element method used to solve the direct problem of magnetic prospecting under complicated conditions. Chinese Journal of Geophysics (in Chinese), 28(06): 618-630. |
Wu X Z. 1979. Remanence should be corrected for demagnetization?. Geophysical and Geochemical Exploration (in Chinese), 3(03): 70-72. |
Zhou J J, Meng X H, Guo L H, et al. 2015. Three-dimensional cross-gradient joint inversion of gravity andnormalized magnetic source strength data in the presence of remanent magnetization. Journal of Applied Geophysics, 119: 51-60. DOI:10.1016/j.jappgeo.2015.05.001 |
Zhang C D, Dong H B. 2011. Remanent magnetizationin the interpretation of magnetic anomaly. Geophysical and Geochemical Exploration (in Chinese), 35(01): 1-6. |
方华竹. 1978. 任意形状强磁性三度体磁异常的计算. 地质学报, 52(01): 63-78. |
李媛媛, 杨宇山, 刘天佑. 2010. 考虑自退磁影响的三维复杂形体磁场正反演研究进展与展望. 地球物理学进展, 25(02): 627-634. DOI:10.3969/j.issn.1004-2903.2010.02.036 |
刘双, 刘天佑, 高文利, 等. 2012. 退磁作用对磁测资料解释的影响. 物探与化探, 36(04): 602-606. |
刘双, 刘天佑, 冯杰, 等. 2013. 强剩磁强退磁条件下的二维井中磁测反演. 地球物理学报, 56(12): 4297-4309. DOI:10.6038/cjg20131232 |
李泽林, 姚长利, 郑元满, 等. 2015. 数据空间磁异常模量三维反演. 地球物理学报, 58(10): 3804-3814. DOI:10.6038/cjg20151030 |
王妙月, 底青云, 许琨, 等. 2004. 磁化强度矢量反演方程及二维模型正反演研究. 地球物理学报, 47(03): 528-534. DOI:10.3321/j.issn:0001-5733.2004.03.025 |
王书惠. 1980. 用有限元法计算非均匀磁化磁性体(二度)的有效磁化强度和磁异常. 地质与勘探, 09: 49-57. |
王书惠. 1981. 关于用有限元法作磁法勘探正演计算的理论问题. 地球物理学报, 24(02): 207-217. DOI:10.3321/j.issn:0001-5733.1981.02.009 |
王书惠. 1985. 解复杂条件下磁法正问题的有限元-边界元法. 地球物理学报, 28(06): 618-630. DOI:10.3321/j.issn:0001-5733.1985.06.008 |
吴宣志. 1979. 剩磁要不要作退磁改正. 物探与化探, 3(03): 70-72. |
张昌达, 董浩斌. 2011. 磁异常解释中的剩余磁化问题. 物探与化探, 35(01): 1-6. |
 2018, Vol. 61
2018, Vol. 61

