2. 徐州医科大学公共教育学院, 江苏徐州 221004
2. School of Basic Education, Xuzhou Medical University, Jiangsu Xuzhou 221004, China
在煤炭开采时经常会遇到煤矿水害问题,如何查明或定位含水地质异常体是水害防治中的重要环节.目前常用的探测方法之一是矿井瞬变电磁法.20世纪90年代,地面瞬变电磁法被移植到矿井巷道中并开展了一系列的方法技术试验研究(于景邨,2001),因该方法具有对低阻体敏感、横向分辨率较高、体积效应较小等优点(于景邨,2007;牛之琏,2007),引起了国内外学者的重视,随后开展了大量的研究工作,主要包括:Krivochieva和Chouteau(2002)计算了全空间1D层状介质模型的瞬变电磁响应,陈丁等(2015)采用核函数法计算均匀全空间中矩形回线源瞬变电磁响应,Yu等(2008)研究了矿井瞬变电磁法的时深转换,杨海燕等(2010)研究了矿井瞬变电磁法全空间视电阻率解释方法,刘志新(2008)采用有限元法数值模拟矿井瞬变电磁场,杨海燕(2009)采用时域有限差分法数值模拟了矿用多匝小回线源瞬变电磁场,胡博(2010)采用边界元法数值模拟了矿井瞬变电磁场,程久龙等(2014a)采用粒子群优化算法研究了矿井瞬变电磁法的反演,Cheng等(2015)研究了矿井瞬变电磁和矿井直流电法间的联合反演,程久龙等(2016)研究了利用矿井瞬变电磁超前探测数据进行合成孔径成像,范涛等(2016)利用瞬变电磁虚拟波场成像研究检测井下煤层气水力压裂效果.
近20年的大量实际探测实践工作表明这种方法能取得较好的效果,但由于常规的矿井瞬变电磁法是将发射线圈和接收线圈均布设在矿井巷道中,接收线圈距离异常体相对较远,因而其纵向分辨率相对较低(程久龙等,2014b).
联想到地面瞬变电磁法的一个分支——地面-钻孔瞬变电磁(或地井电磁法),该方法将源布设于地表,而将接收线圈做成细长型的圆柱体并放入钻孔中从上至下或从下至上依次观测.Dyck(1981)利用本征电流环系统地研究了板状体和球体的地井电磁法响应.Dyck和West(1984)使用本征电流法正演模拟了自由空间中导电板和球的电磁响应,并借助这两种模型分析实测孔中电磁数据而获得目标体参数.Eaton和Hohman(1984)使用直接显式有限差分法计算2D导电异常体的钻孔瞬变电磁响应.West和Ward(1988)利用积分方程法研究了导电半空间中3D破裂带和水平导电板的钻孔瞬变电磁响应.Newman等(1989)利用积分方程法分别研究了导电、半导电和高阻围岩时的钻孔瞬变响应.在实际应用方面,国外进行了大量的硫化金属矿的探测实验(Thomas,1987;Bishop et al., 1987).
国内对钻孔中瞬变电磁法的研究起步较晚,宋汐瑾等(2011)采用G-S逆拉氏变换正演计算了包含井眼泥浆、套管、水泥环和轴对称多层介质模型的电磁场响应.孟庆鑫和潘和平(2012, 2013)利用时域有限差分法数值模拟了包含低阻体的均质半空间中的磁偶源和线源激励的瞬态场.
大量的实际探测结果表明地面-钻孔瞬变电磁法在垂向分辨率、探测深度方面相对优于传统的地面瞬变电磁法.结合煤矿水害精细探测的迫切需求及地面-钻孔瞬变电磁法的优势,本文将地面钻孔中瞬变电磁法移植到矿井巷道中,将源布设于巷道内,而将接收线圈置于钻孔中,形成矿井巷道-钻孔瞬变电磁法.选取煤层底板受水害威胁的代表性地层为研究对象,建立底板含低阻地质异常体的三维地电模型,表征底板砂岩层构造发育所形成的含水体.采用积分方程法,进行全空间条件下巷道-钻孔瞬变电磁场响应数值模拟.
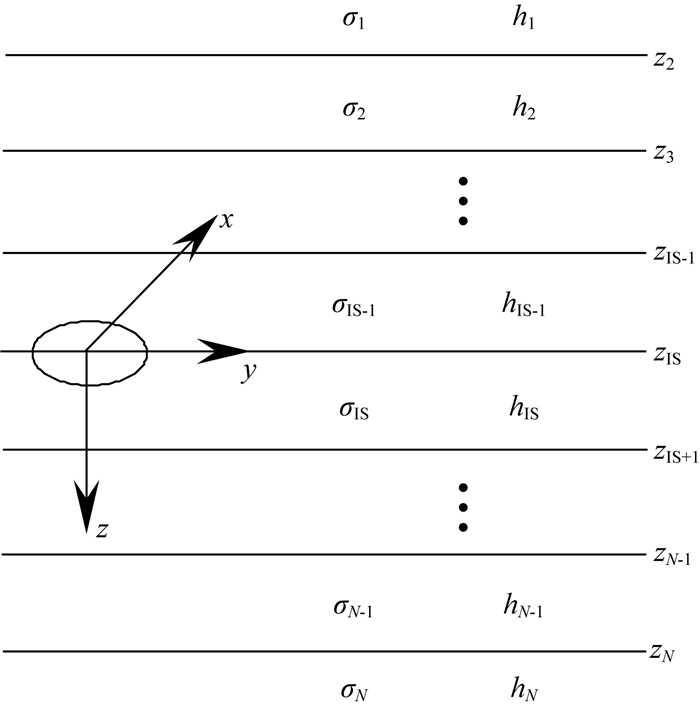
1 理论基础 1.1 全空间水平层状介质瞬变电磁响应图 1所示的是全空间1D水平层状介质模型,共N层,每层介质是均匀、各向同性的,第i层的顶界面深度为Zi,厚度为hi,电导率为σi,并假设每层介质的磁导率均为μ0.源为水平圆回线源或垂直磁偶源,并位于第IS-1层的底界面处.若源不在实际的层界面处,可以引入一个虚拟的层界面z=zIS.选用柱坐标系,z轴向下.水平圆回线源在第i层深度z处产生的电磁场(Das,1995)为
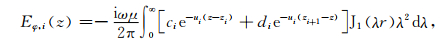
|
(1) |
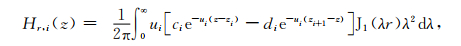
|
(2) |
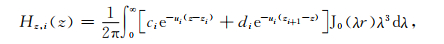
|
(3) |
|
图 1 全空间一维模型示意图 Fig. 1 Sketch map of whole space 1D model |
其中z表示深度,ui2=λ2-ki2,ki表示第i层的波数,ci和di表示第i层的系数,并且c1=0, dN=0.
电磁场所满足的边界条件(Das,1995)为
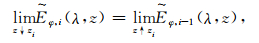
|
(4) |
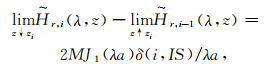
|
(5) |
其中a为回线半径,M为磁矩,δ为克罗尼克函数.
设源上方各层的系数比为Ri-=ci/di,源下方各层的系数比为Ri+=di/ci.
由边界条件(4)和(5)可得
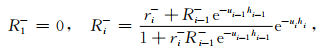
|
(6) |
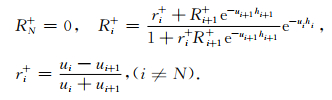
|
(7) |
对于ZIS界面,由公式(4)和公式(5)得
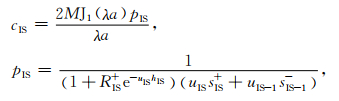
|
(8) |
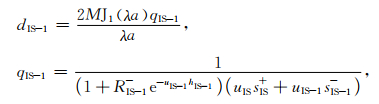
|
(9) |
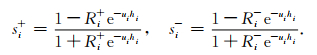
|
(10) |
进而源上方各层的系数为
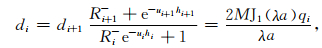
|
(11) |
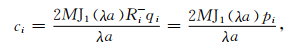
|
(12) |
源下方各层的系数为
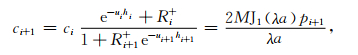
|
(13) |
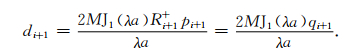
|
(14) |
全空间水平层状介质中水平圆回线源的电磁场公式为
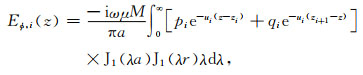
|
(15) |
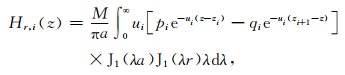
|
(16) |
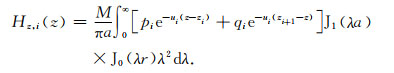
|
(17) |
公式(15)—(17)的计算采用数字滤波法(Anderson,1979;Guptasarma and Singh, 1997),一般地,当a>r时,选择J1(λa)为滤波器;当a<r时,选择J1(λr)或J0(λr)为滤波器.
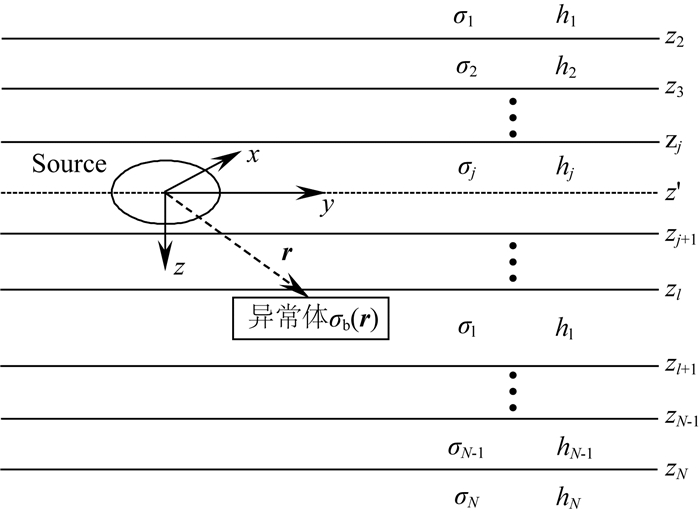
1.2 全空间积分方程基本原理图 2所示的是含异常体的全空间层状介质模型纵剖面示意图,共N层,源位于第j层,异常体位于第l层,第m层的电导率为σm,厚度为hm,异常体电导率为σb,场源是磁源(不接地回线).
|
图 2 含异常体全空间层状介质模型示意图 Fig. 2 Sketch map of whole space layered medium containing body |
可用等效的散射电流代替异常体对电磁场的贡献(Harrington,2001),那么总电磁场(E, H)可分解为激励场(Ei, Hi)和散射场(Es, Hs),即
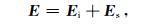
|
(18) |
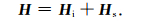
|
(19) |
激励场是由所施加的场源引起,而散射场是由异常体所引起.激励场的求解采用公式(15)—(17).散射场所满足的赫姆霍兹方程(Wannamaker et al., 1984)为
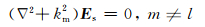
|
(20) |
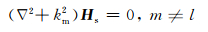
|
(21) |
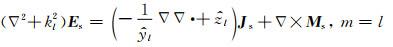
|
(22) |
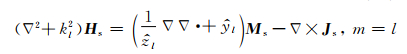
|
(23) |
其中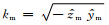
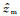
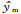
在方程(22)和方程(23)中,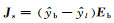
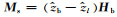
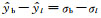
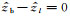
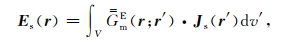
|
(24) |
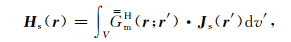
|
(25) |
其中,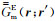
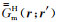
将激励场加到方程(24)和(25)上得总场(Hohmann, 1983):
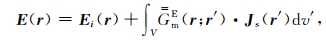
|
(26) |
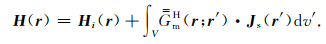
|
(27) |
将异常体剖分成N个小单元,假定每个小单元内的电导率和总电场为常数,则每个小单元内散射电流为常数,则方程(26)和(27)可近似为
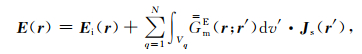
|
(28) |
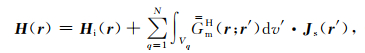
|
(29) |
对于异常体内部的场点,方程(28)可变为
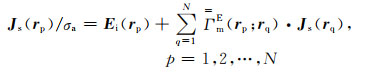
|
(30) |
其中σa=σb-σl, 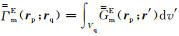
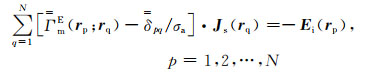
|
(31) |
写成矩阵形式为
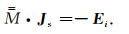
|
(32) |
如果p = q,则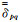
通过张量格林函数的互易性和张量格林函数元素的物理意义验证散射场的正确性.电性源张量格林函数的元素分别表示x、y和z三个方向上的单位电偶源分别在x、y和z三个方向上所产生的电磁场,而Key(2009)发表的文章中提供了电偶源1D正演程序Diplo1D.通过对比所编程序和Diplo1D的结果一致,从而验证了所编程序的正确性.具体的对比过程和对比结果参见文献(胡俊华,2014).
Newman等(1989)使用积分方程法数值模拟了含有低阻板状目标体的地面-钻孔瞬变电磁响应并将该方法应用到实测钻孔数据,取得了成功,从而验证了积分方程法模拟地面钻孔瞬变电磁响应的有效性.与地面-钻孔瞬变电磁法相比,矿井全空间巷道-钻孔瞬变电磁只是将源布设在巷道中,源距离低阻地质异常体更近,通过类比的方法,使用积分方程法模拟全空间巷道-钻孔瞬变电磁法也是有效的.
2 数值模拟与计算结果分析 2.1 地质模型的建立宏观上典型的煤田地层主要包括:第四系盖层、煤系砂岩层、煤层和灰岩层,巷道在煤层中开拓,低阻地质异常体主要是含水异常体.电性参数:空气层电阻率为105 Ωm、第四系覆盖层电阻率为50 Ωm,砂岩电阻率为100 Ωm,煤层电阻率为1000 Ωm,灰岩电阻率为2000 Ωm,含水低阻地质异常体电阻率为1 Ωm,矿井巷道中湿度一般较大,故将巷道空间电阻率设为5000 Ωm.
建立如图 3所示背景模型,从上至下依次为空气层、第四系覆盖层、砂岩层、煤层、砂岩层和灰岩层.其厚度第四系覆盖层100 m,顶板砂岩层200 m,煤层10 m,底板砂岩层250 m,而空气层和基底灰岩层厚度无限大.这种模型的地质意义是盖层表示浅部的第四系地层,含煤砂岩层可表示二叠纪和石炭纪的石盒子组、山西组和太原组等,灰岩层可表示为煤系基底.
|
图 3 宏观上典型煤田地层模型示意图 Fig. 3 Sketch map of typical coal field strata |
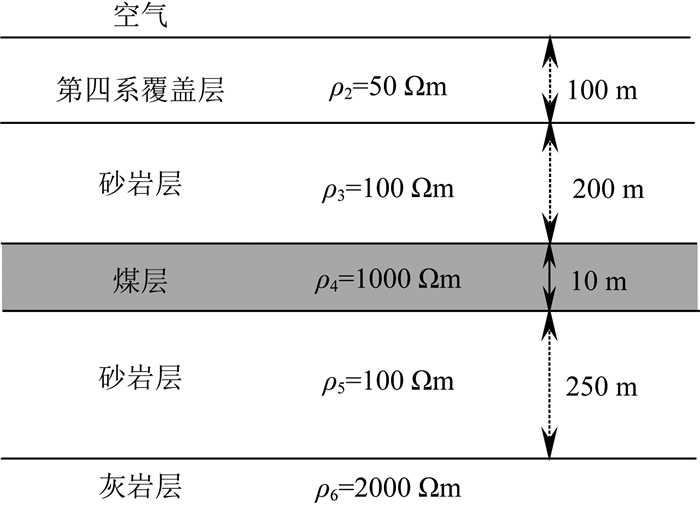
为了后文理解钻孔瞬变电磁响应,此处有必要介绍水平板状体中的涡流和伽伐尼电流(Newman et al., 1986).
图 4a是自由空间中水平导电板状体受到磁源激发而在其中形成的感应涡流(实线)和由该涡流感应的磁场(虚线)示意图.在激励源关断的瞬间感应出涡流,该涡流以及由其激发的磁场随时间的增加逐渐衰减.对于图示位置及流向的激发源,水平导电板状体中的感应涡流的方向为逆时针方向,由该涡流所感应出的左侧磁场方向为逆时针方向,而右侧磁场方向为顺时针方向.
|
图 4 水平板中涡电流和伽伐尼电流示意图 (a)涡电流;(b)伽伐尼电流. Fig. 4 Sketch of vortex currents and Galvanic currents in a horizontal thin plate (a) Vortex currents; (b) Galvanic currents. |
图 4b是导电围岩中水平导电板状体的伽伐尼电流示意图.由于围岩导电,激励源关断后的随时间衰减的磁场将在导电围岩中感应出电流,如果水平板状体比围岩更加导电,则该电流会向水平板状体汇集.对比图 4a和图 4b可以发现涡流和伽伐尼电流所感应出的磁场是不同的.一般地,导电围岩中异常体的瞬变电磁响应是涡电流和伽伐尼电流的复杂的综合作用.
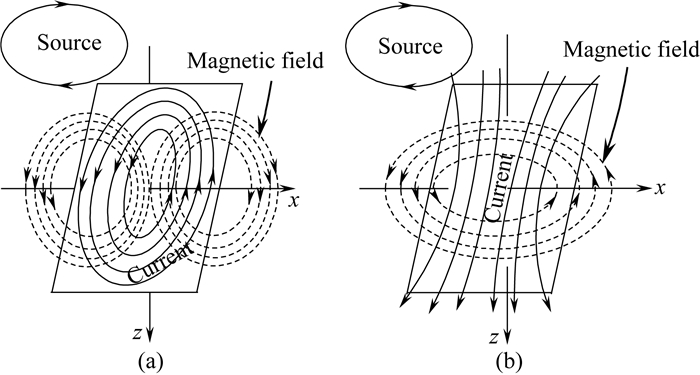
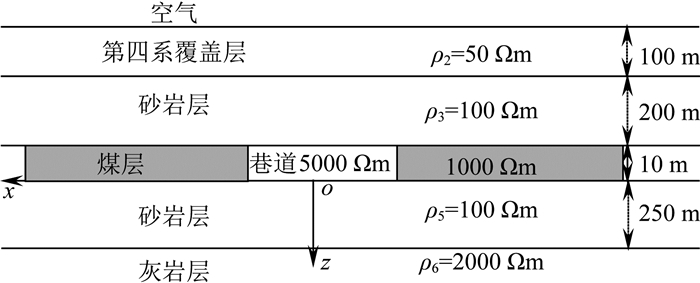
2.3 全空间3D地电模型正演模拟 2.3.1 巷道对钻孔瞬变电磁响应的影响由于是研究矿井全空间中巷道对瞬变电磁响应的影响,回线半径不可能很大,故可将回线半径设为5 m,供电电流1A,中心坐标(0, 0, 0),回线源位于巷道层底板;接收线圈:起点(0, 10, 0),终点(0, 10, 200),钻孔中测点间距10 m,其他深度处的瞬变电磁响应通过样条插值求出(下同).
建立如图 5所示的地电模型,它是将图 3所示背景层模型的第四层改为巷道层并插入两块煤层.煤层的大小为x向延伸范围为-155~155 m,中间空出10 m,用于模拟巷道,y向延伸范围为-150~150 m,煤层块体的剖分尺寸为10 m.根据积分方程理论,总场分为激励场和散射场,此时,激励场来自于水平层状介质(从上至下依次为空气层、第四系盖层、砂岩层、巷道层、砂岩层和灰岩层),而散射场来自于巷道侧帮的煤层块体,也即将煤层块体作异常体处理.
|
图 5 巷道两侧帮做异常体处理模型示意图 Fig. 5 Sketch map of roadway sides being regarded as body |
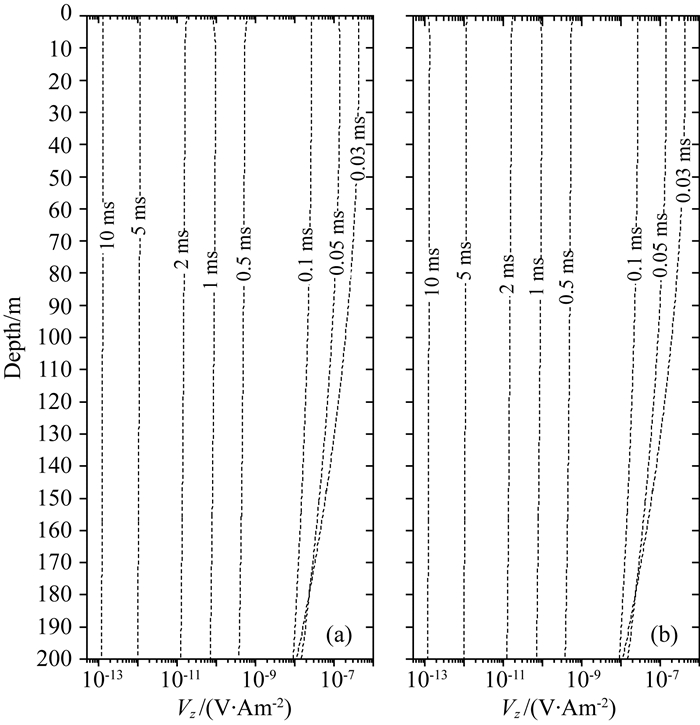
图 6是将巷道两个侧帮做异常体处理后的钻孔瞬变电磁Vz响应的激励场和总场随孔深变化曲线(以下称为Vz钻孔剖面)对比图,虚线表示响应的极性为负.从图中可以看出,Vz响应的激励场和总场除幅值有微小的变化外,两者的形态基本一致,即均表现为0.03 ms和0.05 ms时刻,深度约0~100 m内,响应曲线为近直线,在100~200 m内,随着深度的增加,Vz响应的幅值迅速减小,而在图示其他时刻,Vz曲线为近直线,表明相对高阻的巷道侧帮对钻孔中Vz响应的影响较小.
|
图 6 侧帮做异常体处理后钻孔瞬变电磁Vz响应 (a)激励场;(b)总场. Fig. 6 Comparison of TEM Vz profiles between primary fields and total fields when roadway sides are regarded as body (a) Primary fields; (b) Total fields. |
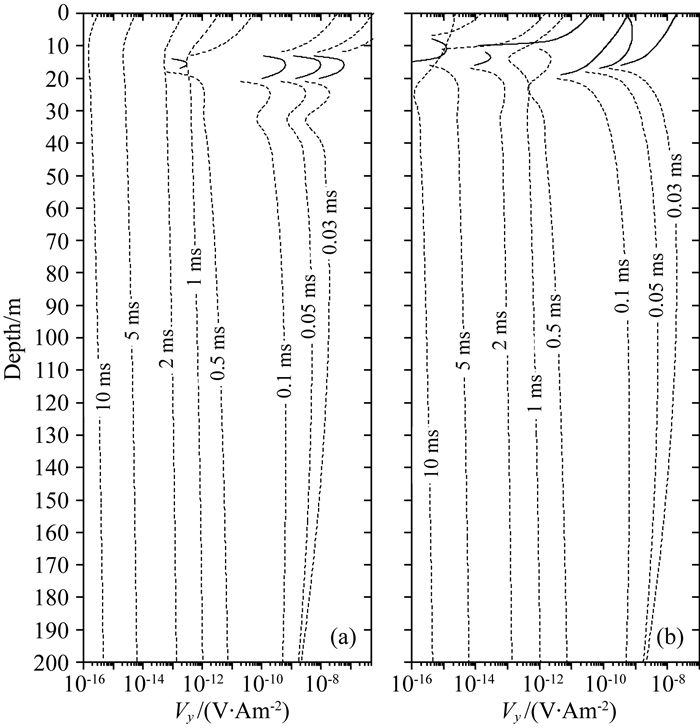
图 7是将巷道两个侧帮做异常体处理后的钻孔瞬变电磁Vy响应的激励场和总场随孔深变化曲线(以下称为Vy钻孔剖面)对比图,虚线表示响应的极性为负,实线表示响应的极性为正(下同).从图中可以看出,在浅部约30 m以内,Vy响应的激励场和总场的差异相对较大;而在30 m以下二者除幅值有微小的变化外,其曲线形态基本一致,即在图示时刻均表现为近直线.表明相对高阻的巷道侧帮对钻孔中Vy响应除浅部(约30 m内)影响相对较大外,对深部影响较小.
|
图 7 侧帮做异常体处理后钻孔瞬变电磁Vy响应 (a)激励场;(b)总场. Fig. 7 Comparison of TEM Vy profiles between primary fields and total fields when roadway sides are regarded as body (a) Primary fields; (b) Total fields. |
需要说明的是,由于对称性,此时Vx响应为0,Vy响应表示的是感应电动势的水平分量,而Vz响应表示的是感应电动势的垂向分量(下同).
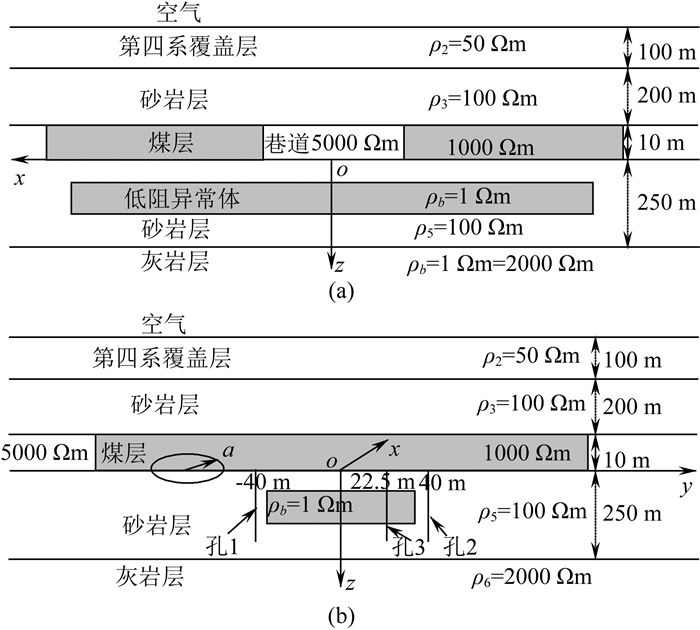
2.3.2 底板含异常体时的钻孔瞬变电磁响应 2.3.2.1 存在巷道时的钻孔瞬变电磁响应建立如图 8所示的地电模型,它是在图 5所示模型的第五层,即底板砂岩层内插入一个低阻异常体,其尺寸:-150 m≤x≤150 m,-30 m≤y≤30 m,75 m≤z≤85 m,剖分网格为10 m,异常体的中心埋深为80 m,其中心在底板的投影点为原点.回线源位于巷道层底板,半径a为5 m,回线中心为(0, -50, 0),电流1 A;钻孔孔位为孔1(0, -40, 0)、孔2(0, 40, 0)和孔3(0, 22.5, 0),分别表示钻孔位于源和异常体之间、钻孔和源分立异常体两侧及钻孔穿过异常体,钻孔竖直向下,深度200 m,测点间距10 m.使用积分方程法数值模拟如图 8所示的地电模型时,将巷道侧帮和底板低阻异常体均作异常体进行处理.
|
图 8 含侧帮和底板低阻异常体模型示意图 (a)横截面示意图;(b)纵剖面示意图. Fig. 8 Sketch map of typical coal field strata containing roadway sides and body located in coal seam floor (a) Cross section; (b) Longitudinal section. |
为了减少计算时间,此处没有考虑巷道侧帮和底板低阻异常体之间的耦合,也即分别计算出巷道侧帮和底板低阻异常体的散射场,然后两者相加,再加上激励场,最后进行频时转换到时间域.
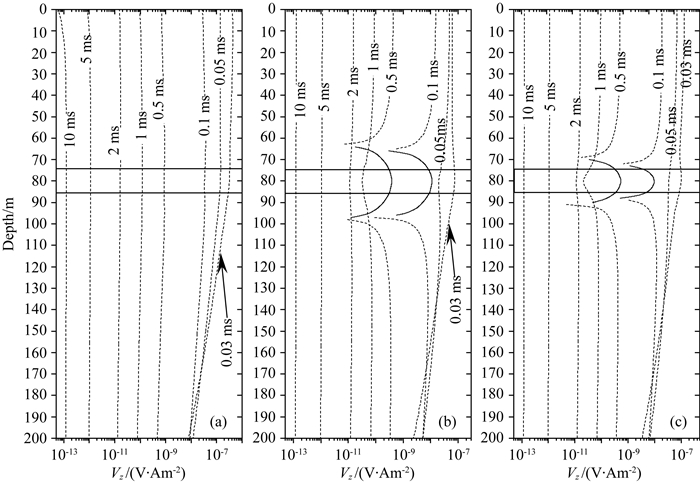
图 9是巷道侧帮存在时底板含低阻异常体地电模型三个孔的Vz剖面.图中的矩形框表示的是异常体的横截面(下同).图 9a是图 8b所示模型中孔1的Vz剖面,从图中可以看出,仅在0.03 ms和0.05 ms时刻约80 m深度处(异常体中心埋深)形成拐点,其他时刻曲线形态为近直线.
|
图 9 巷道侧帮和底板低阻异常体存在时的孔1、孔2和孔3中Vz曲线对比图 (a)孔1 Vz曲线;(b)孔2 Vz曲线;(c)孔3 Vz曲线. Fig. 9 Comparison of TEM Vz profiles of drillhole 1 and drillhole 2 and drillhole 3 when coal seam floor body and roadway sides exist (a) Vz profile of drillhole 1; (b) Vz profile of drillhole 2; (c) Vz profile of drillhole 3. |
图 9b是图 8b所示模型中孔2的Vz剖面,从图中可以看出,在0.03 ms时刻,约80 m深度处,Vz曲线出现峰值.而在0.05 ms、0.1 ms、0.5 ms、1 ms和2 ms时刻,Vz曲线表现为约80 m深度处形成了极性相反的异常响应.而在5 ms之后Vz曲线形态表现为近直线.
图 9c是图 8b所示模型中孔3的Vz剖面,从图中可以看出,其Vz曲线和图 9b相比除了异常响应的幅值减弱之外,基本一致.从图 9中还可以看出钻孔2中异常响应的幅值最大,钻孔3中异常响应幅值次之,钻孔1中异常响应最弱,所以孔2中Vz剖面对异常体的纵向分量率最高,孔3中Vz剖面的纵向分辨率次之,孔1中Vz剖面的纵向分辨率最低.
将图 8中底板低阻异常体看做水平导电板状体,则可借助3.2节中涡电流和伽伐尼电流解释三个孔中的Vz响应曲线.孔1、孔2和孔3中由源感应出的一次磁场的垂直分量方向向上.孔1中由涡电流感应的磁场的垂直分量方向向下;由伽伐尼电流感应的磁场的垂直分量方向也向下;孔2中由涡电流感应的磁场的垂直分量方向向下;由伽伐尼电流感应的磁场的垂直分量方向向上.
对于孔1,因为一次磁场的垂直分量向上,而涡流磁场的垂直分量和伽伐尼电流磁场的垂直分量均向下,但前者大于后者,所以Vz钻孔剖面上表现为负极性响应.
对于孔2,一次磁场的垂直分量向上,伽伐尼电流磁场垂直分量向上,而涡流磁场的垂直分量向下.在0.03 ms时刻伽伐尼电流磁场起主导作用,所以此时间道在异常体中心埋深处形成峰值;在0.05 ms、0.1 ms、0.5 ms、1 ms和2 ms时刻,涡流磁场起主导作用,所以这些时间道上出现极性为正的异常响应;在5 ms之后则是全空间层状介质响应起主导作用.故5 ms和10 ms两个时刻的Vz响应曲线为负极性的近直线.钻孔3中Vz响应的解释类似于钻孔2.
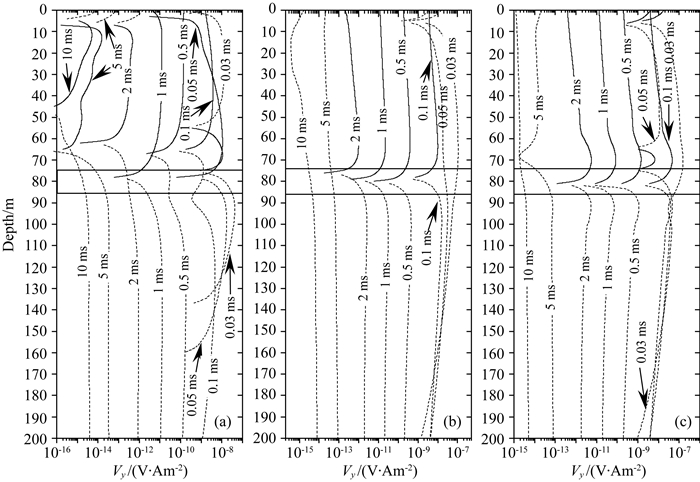
图 10是巷道侧帮存在时底板含低阻异常体地电模型三个孔的Vy剖面.图 10a是图 8b所示模型中孔1的Vy剖面,从图中可以看出,在0.03 ms时刻,在异常体上方形成了极性为正的异常响应.在0.05 ms、0.1 ms、0.5 ms和1 ms时刻,异常响应逐渐增强,表现为在经过异常体中心时响应的极性从上到下由正转为负,零点对应异常体中心.而在后续时刻,异常响应逐渐减弱.
|
图 10 巷道侧帮和底板低阻异常体存在时的孔1、孔2和孔3中Vy曲线对比图 (a)孔1 Vy曲线;(b)孔2 Vy曲线;(c)孔3 Vy曲线. Fig. 10 Comparison of TEM Vy profiles of drillhole 1 and drillhole 2 and drillhole 3 when coal seam floor body and roadway sides exist (a) Vy profile of drillhole 1; (b) Vy profile of drillhole 2; (c) Vy profile of drillhole 3. |
图 10b是图 8b所示模型中孔2的Vy剖面,从图中可以看出,在0.03 ms和0.05 ms时刻,曲线整体上表现为负极性的近直立曲线.在0.1 ms、0.5 ms、1 ms和2 ms时刻,约在异常体中心处发生极性反转,从上至下由正转为负.在5 ms之后,Vy响应表现为负极性的近直线.
图 10c是图 8b所示模型中孔3的Vy剖面.对比图 10b和图 10c可以发现,图 10c中Vy响应曲线上除异常响应的延续时间有所增加外,其曲线响应特征和图 10b类似.
纵向对比图 10a和图 7可以发现,底板低阻异常体的存在使得Vy钻孔剖面上低阻异常体上方的极性反转,引起显著变化.横向对比图 10a、图 10b和图 10c可以发现,在异常体的纵向分辨率方面,图 10b和图 10c较高,而图 10a较低.
仍采用涡电流和伽伐尼电流来解释三个孔中的Vy响应.孔1、孔2和孔3中由源感应出的一次磁场的水平分量方向向右.而孔1中由涡电流感应的磁场的水平分量的方向在异常体上方向左,在异常体下方向右;由伽伐尼电流感应的磁场的水平分量的方向在异常体上方向左,在异常体下方向右;孔2中由涡电流感应的磁场的水平分量的方向在异常体上方向右,在异常体下方向左;由伽伐尼电流感应的磁场的水平分量的方向在异常体上方向左,在异常体下方向右.
对于Vy钻孔剖面,由于围岩导电,涡流磁场不起主导作用,起主导作用的是伽伐尼电流磁场响应.对于孔1,异常体上方一次磁场水平方向向右,而伽伐尼电流磁场水平方向向左,二者方向相反;在异常体下方一次磁场水平方向向右,伽伐尼电流磁场水平方向也向右,二者方向相同,故而图 10a的Vy钻孔剖面上,异常体上方的极性为正,异常体下方的极性为负.对于孔2,一次磁场水平分量方向和伽伐尼电流磁场水平分量方向与孔1中的类似,只是孔2中0.03 ms、0.05 ms、5 ms和10 ms时刻,全空间地层的Vy响应起主导作用,而中间四个时刻起主导作用的是伽伐尼电流磁场响应.孔3中Vy响应的解释类似于孔2.
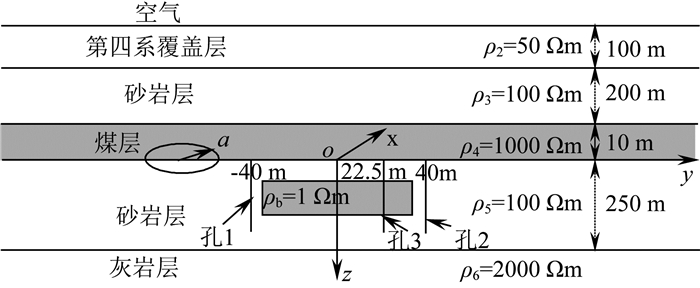
2.3.2.2 不存在巷道时的钻孔瞬变电磁响应为了进一步研究巷道对钻孔瞬变电磁响应的影响,下面对比分析如图 11所示地电模型的钻孔瞬变电磁响应.图 11所示模型是将图 8所示模型的第4层完全变为煤层,也即不考虑巷道,其他模型参数不变.
|
图 11 底板含异常体全空间层状模型示意图 Fig. 11 Sketch map of typical coal field strata with coal seam floor containing body |
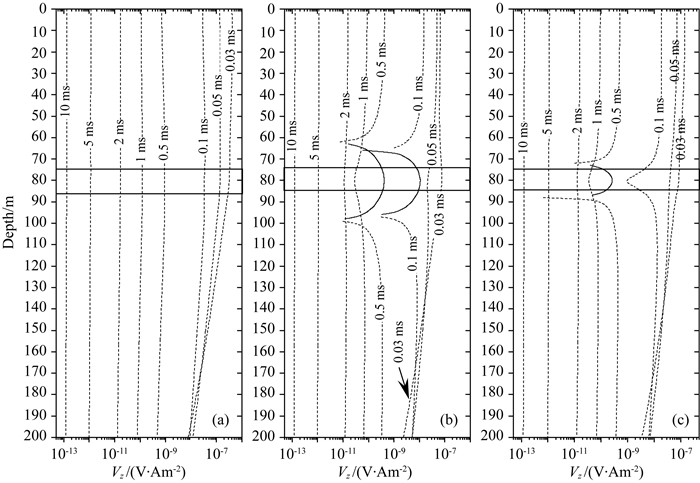
图 12是图 11所示模型中三个孔的Vz钻孔剖面.通过对比图 12a和图 9a、图 12b和图 9b,图 12c和图 9c可以发现三类孔中的Vz响应除了幅值有微小的变化外,其曲线形态基本一致,也即相对高阻的巷道侧帮和相对高阻的巷道层对三类孔中的Vz钻孔剖面影响较小.
|
图 12 仅底板含低阻异常体时的孔1、孔2和孔3中Vz曲线对比图 (a)孔1 Vz曲线;(b)孔2 Vz曲线;(c)孔3 Vz曲线. Fig. 12 Comparison of TEM Vz profiles of drillhole 1 and drillhole 2 and drillhole 3 when coal seam floor body exists (a) Vz profile of drillhole 1; (b) Vz profile of drillhole 2; (c) Vz profile of drillhole 3. |
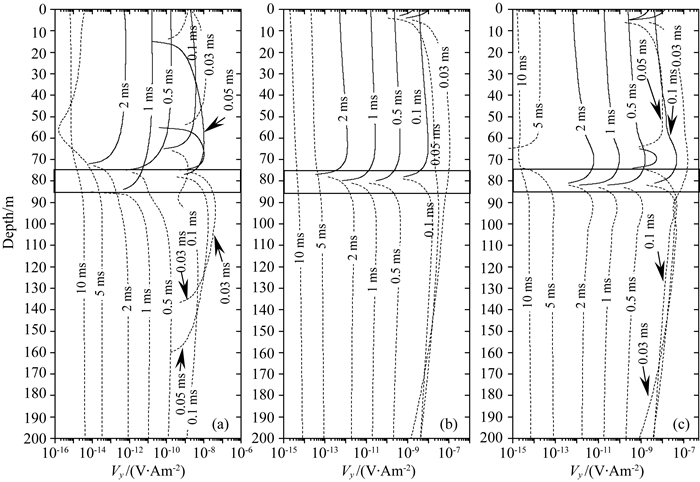
图 13是图 11所示模型中三个孔的Vy钻孔剖面.对比图 13a和图 10a可以发现,除了异常响应影响时间减小之外基本类似;对比图 13b和图 10b、图 13c和图 10c可以发现,两种模型下这两类钻孔中的Vy响应基本类似.
|
图 13 仅底板含低阻异常体时的孔1、孔2和孔3中Vy曲线对比图 (a)孔1 Vy曲线;(b)孔2 Vy曲线;(c)孔3 Vy曲线. Fig. 13 Comparison of TEM Vy profiles of drillhole 1 and drillhole 2 and drillhole 3 when coal seam floor body exists (a) Vy profile of drillhole 1; (b) Vy profile of drillhole 2; (c) Vy profile of drillhole 3. |
由以上分析可知,相对高阻的巷道层对底板低阻异常体的异常响应影响较小,因而在下文中不考虑巷道的影响.
在底板低阻异常体的纵向分辨率方面,三类孔中的Vy剖面和孔2中的Vz剖面的分辨能力较强,孔3中的Vz剖面对异常体的纵向分辨率次之,孔1中的Vz剖面对异常体的纵向分辨率最低.三类孔的Vy剖面的分辨能力相对强于Vz剖面.
在异常响应的延续时间方面,三类孔中Vy剖面上异常响应延续时间相对较长,孔2和孔3中的Vz剖面上异常响应延续时间次之,孔1中Vz剖面基本无法反映异常体.在响应幅值方面,三类孔的Vz剖面强于Vy剖面
在实际观测时,不仅要观测瞬变电磁响应的垂向分量,也要观测水平分量,因为垂向分量的幅值较强,而水平分量上异常响应的延续时间较长,纵向分辨率较高.
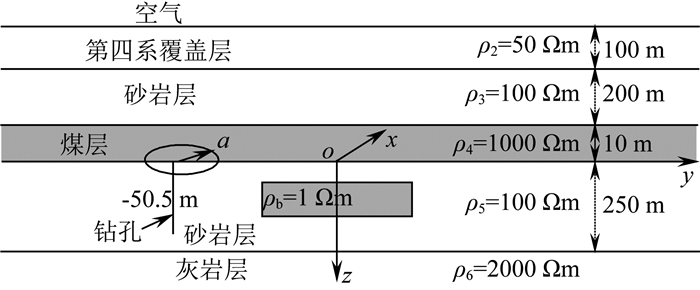
2.3.3 回线内部时钻孔瞬变电磁响应建立如图 14所示的地电模型,它与图 11所示模型类似,其他参数不变,只是孔位变为(0, -50.5, 0).
|
图 14 钻孔位于回线内部时地电模型示意图 Fig. 14 Sketch map of typical coal field strata with coal seam floor containing body and drillhole in loop |
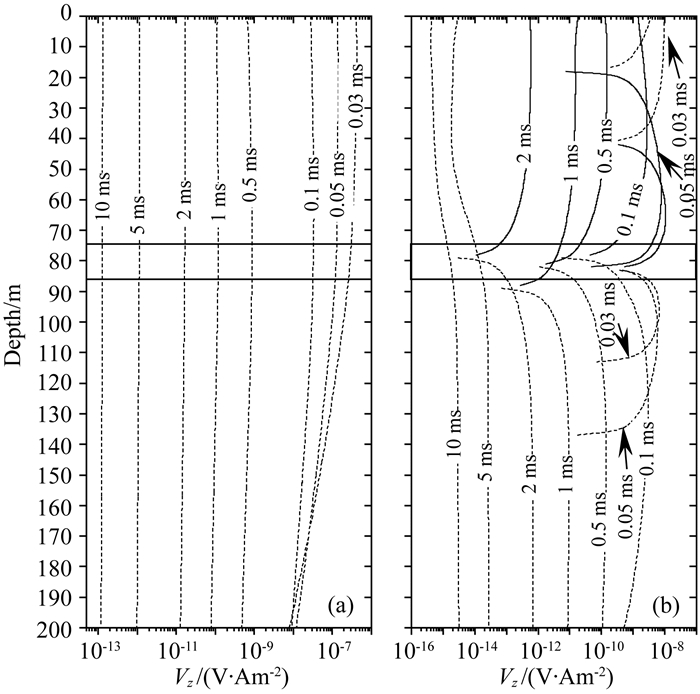
图 15是图 14所示地电模型的钻孔Vz和Vy剖面.从图 15a中可以看出,在钻孔Vz剖面上,Vz响应曲线与图 9a基本类似,即仅在早期0.03 ms和0.05 ms时刻有相对较为明显的拐点,图示其他时刻Vz曲线表现为近直线.
|
图 15 图 14所示模型的钻孔Vz剖面和Vy剖面 (a) Vz钻孔剖面;(b) Vy钻孔剖面. Fig. 15 TEM Vz and Vy profiles of geoelectric model of Fig. 14 (a) Vz profile; (b) Vy profile. |
从图 15b可以看出,在钻孔Vy响应曲线上,Vy响应曲线和图 13a的Vy响应曲线基本类似,即在0.03 ms、0.05 ms、0.1 ms、0.5 ms、1 ms和2 ms时刻,异常响应较为明显,表现为在异常体上方Vy响应为正极性(0.03 ms和0.05 ms时刻,异常体上方仅部分Vy曲线的极性为正),而在异常体下方,Vy响应为负极性.
3 结论本文将回线源布设在巷道底板,而将接收线圈机放置在钻孔内,从上至下依次进行观测.选取煤层底板受水害威胁的代表性地层为研究对象,建立表征煤层底板砂岩层构造发育形成含水体的三维数学模型,利用积分方程法进行数值模拟.计算结果表明:
(1) 使用两个煤层块体模拟巷道侧帮时,相对高阻的侧帮对孔内感应电动势的垂向分量影响较小,而对孔内感应电动势的水平分量除浅部约30 m内影响较大外,对深部影响较小.
(2) 当煤层底板含水平低阻板状异常体时,①在三类孔的水平感应电动势剖面上,中期,由浅至深,响应的极性从正转为负,零点对应异常体中心;②在孔2和孔3的垂向感应电动势剖面上,中期约在异常体中心出现极性相反的异常响应.
在对异常体的纵向分辨率方面,三类孔中的水平感应电动势剖面和孔2的垂向感应电动势剖面上较高,而孔1和孔3的垂向感应电动势剖面上较低.在异常响应的延续时间方面,孔内感应电动势的水平分量相对优于垂向分量.但响应的幅值方面,孔内感应电动势的垂向分量强于水平分量.因此,实际观测时不仅要观测瞬变电磁的竖直分量,也需要观测水平分量.
Anderson W L. 1979. Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering. Geophysics, 44(7): 1287-1305. DOI:10.1190/1.1441007 |
Bishop J R, Lewis R J G, Macnae J C. 1987. Down-hole electromagnetic surveys at Renison Bell, Tasmania. Exploration Geophysics, 18(3): 265-277. DOI:10.1071/EG987265 |
Chen D, Cheng J L, Huang Q S, et al. 2015. Time domain transient electromagnetic responses from a rectangular loop in homogeneous whole-space. Journal of China Coal Society (in Chinese), 40(12): 2865-2873. |
Cheng J L, Li M X, Xiao Y L, et al. 2014a. Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space. Chinese J. Geophys. (in Chinese), 57(10): 3478-3484. DOI:10.6038/cjg20141033 |
Cheng J L, Li F, Peng S P, et al. 2014b. Research progress and development direction on advanced detection in mine roadway working face using geophysical methods. Journal of China Coal Society (in Chinese), 39(8): 1742-1750. |
Cheng J L, Li F, Peng S P, et al. 2015. Joint inversion of TEM and DC in roadway advanced detection based on particle swarm optimization. Journal of Applied Geophysics, 123: 30-35. DOI:10.1016/j.jappgeo.2015.09.008 |
Cheng J L, Chen D, Xue G Q, et al. 2016. Synthetic aperture imaging in advanced detection of roadway using the mine transient electromagnetic method. Chinese J. Geophys. (in Chinese), 59(2): 731-738. DOI:10.6038/cjg20160230 |
Das U C. 1995. A reformalism for computing frequency-and time-domain EM responses of a buried, finite-loop source in a layered earth.//SEG Technical Program Expanded Abstracts. Houston, TX: SEG, 811-814.
|
Dyck A V. 1981. A method for quantitative interpretation of wideband, drill-hole EM surveys in mineral exploration[Ph. D. thesis]. Toronto: University of Toronto. https://tspace.library.utoronto.ca/handle/1807/69194
|
Dyck A V, West G F. 1984. The role of simple computer models in interpretations of wide-band, drill-hole electromagnetic surveys in mineral exploration. Geophysics, 49(7): 957-980. DOI:10.1190/1.1441741 |
Eaton P A, Hohmann G W. 1984. The influence of a conductive host on two -dimensional borehole transient electromagnetic responses. Geophysics, 49(7): 861-869. DOI:10.1190/1.1441732 |
Fan T, Cheng J Y, Wang B L, et al. 2016. Experimental study on imaging method of TEM pseudo wave-field to detect the effect of underground coal-bed gas hydraulic fracturing. Journal of China Coal Society (in Chinese), 41(7): 1762-1768. |
Guptasarma D, Singh B. 1997. New digital linear filters for Hankel J0 and J1 transforms. Geophysical Prospecting, 45(5): 745-762. DOI:10.1046/j.1365-2478.1997.500292.x |
Harrington R F. 2001. Time-Harmonic Electromagnetic Fields. New York: IEEE Press.
|
Hohmann G H. 1983. Three-dimensional EM modeling. Geophysical Surveys, 6(1-2): 27-53. DOI:10.1007/BF01453994 |
Hu B. 2010. Numerical simulation of mine transient electromagnetic field by boundary element method[Ph. D. thesis] (in Chinese). Xuzhou: China University of Mining and Technology.
|
Hu J H. 2014. Study of the transient electromagnetic response using integral equation method[Master's thesis] (in Chinese). Wuhan: China University of Geosciences.
|
Jiang S F, Xiang S H. 2007. An efficient method to calculate the Sine and Cosine transform. Chinese Journal of Engineering Geophysics (in Chinese), 4(5): 512-515. |
Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. DOI:10.1190/1.3058434 |
Krivochieva S, Chouteau M. 2002. Whole-space modeling of a layered earth in time-domain electromagnetic measurements. Journal of Applied Geophysics, 50(4): 375-391. DOI:10.1016/S0926-9851(02)00164-7 |
Liu Z X. 2008. Study on the distribution and application of mine transient electromagnetic field[Ph. D. thesis] (in Chinese). Xuzhou: China University of Mining and Technology.
|
Meng Q X, Pan H P. 2012. Numerical simulation analysis of surface-hole TEM responses. Chinese J. Geophys. (in Chinese), 55(3): 1046-1053. DOI:10.6038/j.issn.0001-5733.2012.03.035 |
Meng Q X, Pan H P. 2013. 3D FDTD numerical simulation for transient electromagnetic of magnetic source in borehole. Journal of Central South University (Science and Technology) (in Chinese), 44(2): 649-655. |
Newman G A, Hohmann G W, Anderson W L. 1986. Transient electromagnetic response of a three-dimensional body in a layered earth. Geophysics, 51(8): 1608-1626. DOI:10.1190/1.1442212 |
Newman G A, Anderson W L, Hohmann G W. 1989. Effect of conductive host rock on borehole transient electromagnetic responses. Geophysics, 54(5): 598-608. DOI:10.1190/1.1442687 |
Niu Z L. 2007. Principle of Time Domain Electromagnetic Method (in Chinese). Changsha: Central South University Press.
|
Song X J, Dang R R, Guo B L, et al. 2011. Research on transient electromagnetic response of magnetic source in borehole. Chinese J. Geophys. (in Chinese), 54(4): 1122-1129. DOI:10.3969/j.issn.0001-5733.2011.04.028 |
Thomas L. 1987. Short note:A simple interpretation aid for downhole time-domain electromagnetic anomalies. Exploration Geophysics, 18(3): 349-351. DOI:10.1071/EG987349 |
Wannamaker P E, Hohmann G W, SanFilipo W A. 1984. Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations. Geophysics, 49(1): 60-74. DOI:10.1190/1.1441562 |
West R C, Ward S H. 1988. The borehole transient electromagnetic response of a three-dimensional fracture zone in a conductive half-space. Geophysics, 53(11): 1469-1478. DOI:10.1190/1.1442427 |
Yang H Y. 2009. Study on numerical simulation and distribution regularity of transient electromagnetic field with mine-used multi small loop[Ph. D. thesis] (in Chinese). Xuzhou: China University of Mining and Technology.
|
Yang H Y, Deng J Z, Zhang H, et al. 2010. Research on full-space apparent resistivity interpretation technique in mine transient electromagnetic method. Chinese J. Geophys. (in Chinese), 53(3): 651-656. DOI:10.3969/j.issn.0001-5733.2010.03.020 |
Yu J C. 2001. Study on theory and application technology of mine transient electromagnetic method[Ph. D. thesis] (in Chinese). Xuzhou: China University of Mining and Technology.
|
Yu J C. 2007. Mine Transient Electromagnetic Prospecting (in Chinese). Xuzhou: China University of Mining and Technology Press.
|
Yu J C, Wang Y Z, Liu J, et al. 2008. Time-depth conversion of transient electromagnetic method used in coal mines. J. China Univ. Mining Technol., 18(4): 546-550. |
陈丁, 程久龙, 黄琪嵩, 等. 2015. 矿井瞬变电磁矩形回线源瞬变电磁响应. 煤炭学报, 40(12): 2865-2873. |
程久龙, 李明星, 肖艳丽, 等. 2014a. 全空间条件下矿井瞬变电磁法粒子群优化反演研究. 地球物理学报, 57(10): 3478-3484. DOI:10.6083/cjg20141033 |
程久龙, 李飞, 彭苏萍, 等. 2014b. 矿井巷道地球物理方法超前探测研究进展与展望. 煤炭学报, 39(8): 1742-1750. |
程久龙, 陈丁, 薛国强, 等. 2016. 矿井瞬变电磁法超前探测合成孔径成像研究. 地球物理学报, 59(2): 731-738. DOI:10.6038/cjg20160230 |
范涛, 程建远, 王保利, 等. 2016. 应用瞬变电磁虚拟波场成像方法检测井下煤层气水力压裂效果的实验研究. 煤炭学报, 41(7): 1762-1768. |
胡博. 2010.矿井瞬变电磁场数值模拟的边界元法[博士论文].徐州: 中国矿业大学. http://cdmd.cnki.com.cn/article/cdmd-10290-2010280166.htm
|
胡俊华. 2014.瞬变电磁积分方程法正演模拟研究[硕士论文].武汉: 中国地质大学. http://cdmd.cnki.com.cn/Article/CDMD-10491-1014340971.htm
|
蒋淑芬, 向淑晃. 2007. 一种正余弦变换的高效算法. 工程地球物理学报, 4(5): 512-515. DOI:10.3969/j.issn.1672-7940.2007.05.022 |
刘志新. 2008.矿井瞬变电磁场分布规律与应用研究[博士论文].徐州: 中国矿业大学. http://cdmd.cnki.com.cn/Article/CDMD-10290-2008196425.htm
|
孟庆鑫, 潘和平. 2012. 地-井瞬变电磁响应特征数值模拟分析. 地球物理学报, 55(3): 1046-1053. DOI:10.6038/j.issn.0001-5733.2012.03.035 |
孟庆鑫, 潘和平. 2013. 井中磁源瞬变电磁三维时域有限差分数值模拟. 中南大学学报, 44(2): 649-655. |
牛之琏. 2007. 时间域电磁法原理. 长沙: 中南大学出版社.
|
宋汐瑾, 党瑞荣, 郭宝龙, 等. 2011. 井中磁源瞬变电磁响应特征研究. 地球物理学报, 54(4): 1122-1129. DOI:10.3969/j.issn.0001-5733.2011.04.028 |
杨海燕. 2009.矿用多匝小回线源瞬变电磁场数值模拟与分布规律研究[博士论文].徐州: 中国矿业大学. http://cdmd.cnki.com.cn/article/cdmd-10290-2009222851.htm
|
杨海燕, 邓居智, 张华, 等. 2010. 矿井瞬变电磁法全空间视电阻率解释方法研究. 地球物理学报, 53(3): 651-656. DOI:10.3969/j.issn.0001-5733.2010.03.020 |
于景邨. 2001.矿井瞬变电磁法理论与应用技术研究[博士论文].徐州: 中国矿业大学. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y392169
|
于景邨. 2007. 矿井瞬变电磁法勘探. 徐州: 中国矿业大学出版社.
|
 2018, Vol. 61
2018, Vol. 61


