2. 中国国土资源航空物探遥感中心, 北京 100083;
3. 中国地质科学院地质研究所, 北京 100037
2. China Aero Geophysical Survey & Remote Sensing Center for Land and Resources, Beijing 100083, China;
3. Institute of Geology, Chinese Academy of Geological Sciences, Beijing 100037, China
20世纪的科技革命产生了计算机辅助制图技术,使地质构造图的制作实现了数字化.但是计算机辅助制图并没有实现地质构造图的制作自动化,其中的地质构造要素仍然是人工选取和定位的,而不是通过计算机计算出来的.在21世纪,地质学和大地构造学应该走向定量,通过地质构造要素的数学物理分析达到用计算机自动制作区域构造图的目的,使大地构造图件的绘制具有客观标准.另一方面,地球物理探测取得的关于地壳构造的数据是定量的,地壳探测取得的各种地球物理场中包含有大量地壳构造信息,如果提取出这些信息,可以在数学物理普适规律指导下计算出关于地壳构造的有关图件.基于这个目的,本文探讨了区域重力场的高阶谱矩理论,并将它应用于地质构造要素分析,创建了输入区域重力场并用计算机制作地壳变形带分布图的方法技术.本文讨论区域重力场的高阶谱矩理论和应用,在塔里木等地的资料进行了方法试验,取得了预期的效果.
2 表面和位场的高阶谱矩在x, y, z组成的笛卡尔直角坐标系中,任意地形表面和二维位场表面都可以用二维函数z(x, y)来表征(Ardalan, 2005; Riley, 1974).其中(x, y)为平面直角坐标;z表示高程和位场函数.根据傅里叶变换理论(Longust-Higgins,1962;Yanagi et al., 2001), 二维函数z(x, y)的二维傅里叶变换为
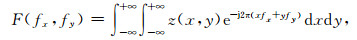
|
(1) |
式中,fx和fy别代表x和y两个相互垂直方向上的波数.表面函数的二维功率谱密度可以用傅里叶变换的形式表示为
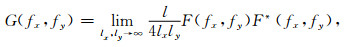
|
(2) |
式中,F*(fx, fy)表示共轭的傅里叶变换.对离散数据进行计算时,假定区域含有M×N个采样点.在x方向以间隔Δx等间距采样,在y方向上以间隔Δy等间距采样,且采样点数分别为M和N,则表面函数的二维离散傅里叶变换式为
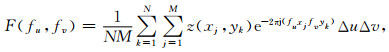
|
(3) |
式中fu,fv是离散空间频率(即波数),
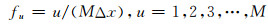
|
(4) |
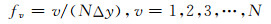
|
(5) |
对于连续的表面函数,相应的p+q阶功率谱密度表为
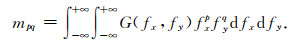
|
(6) |
不同于二维傅里叶变换的全部分析方式,工程界把谱矩用作局部分析.例如, 对表面提取二阶谱矩时, 采用滑动窗口提取每个网格点处附近面元的高程或位场幅值,计算每个窗口面元的二阶谱矩及统计不变量.将计算结果定位于面元中心点,并逐点移动滑动窗口,完成计算表面的二阶谱矩.把高程函数z(x, y)视为随机函数,由随机过程理论可知,随机变量的p+q阶谱矩mpq为(Longust-Higgins,1962)
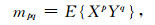
|
(7) |
式中X,Y分别为变量x,y的随机函数.对应z(x, y)的离散p+q阶谱矩波数域表达式为
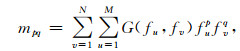
|
(8) |
由(8) 式可见, 谱矩的积分核是频谱和波数幂的乘积,谱矩分析揭示随机过程的复合结构及其和各周期成分的响应模式.区域位场分布取决于地下场源的分布,而地下场源的分布是随机的,因此区域位场分布可当作随机过程对待.区域位场函数f=f(x, y)是一个单值的二维连续可微函数,它也代表区域位场幅值面的轮廓.谱矩的元可由以下公式计算, 当r=0时, 就是场强度的方差,即
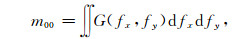
|
(9) |
当r=2时,场的二阶谱矩等于f(x, y)偏导数的自协方差与互协方差函数.二阶谱矩的元为
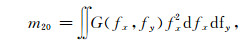
|
(10) |
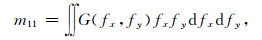
|
(11) |
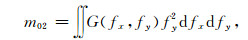
|
(12) |
令偏导数向量
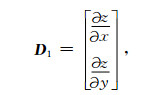
|
(13) |
则场的偏导数的协方差矩阵可写为
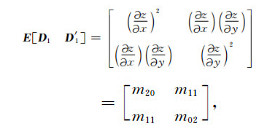
|
(14) |
即, m20为x方向上的斜率əz/əx的方差;m02是y方向上的斜率əz/əy的方差;m11是əz/əx与əz/əy的协方差.
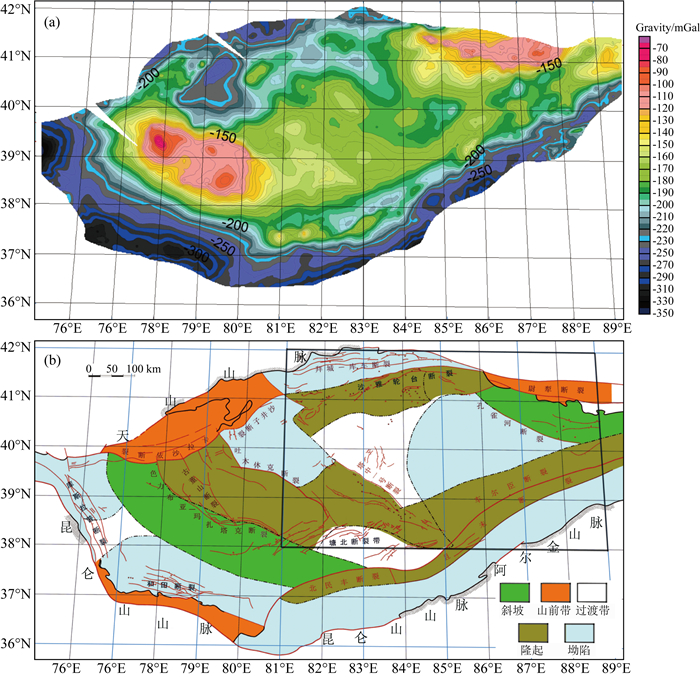
以中国西北的塔里木盆地为例,图 1a为区域布格重力异常图,图 1b为区域大地构造图(杨文采,2010;Hou et al., 2011).由图可见,区域布格重力异常和大地构造趋势基本一致;重力异常南北向斜率大,东西向斜率变化小.计算的塔里木盆地布格重力场的二阶谱矩的三个元见图 2.由图可见,x方向上斜率的方差m20数值小,反映重力场东西向斜率变化小.y方向上的斜率的方差m02数值大,反映重力场南北向斜率变化大.二阶谱矩的这两个元高值分布在盆地四周的造山带;造山带地壳变形剧烈,重力异常斜率变大,斜率的方差也加大.m11是一个新参数,将在下面讨论.
|
图 1 (a)塔里木盆地区域布格重力异常图,(b)为区域大地构造图 Fig. 1 (a) Regional gravity field f(x, y) and (b) tectonic map in Tarim Basin |

|
图 2 计算的塔里木盆地区域布格重力场的二阶谱矩: (a) m20; (b) m02; (c) m11 Fig. 2 Order-2 spectral moments (SM) estimation, corresponding to (a) m20, (b) m02, (c) m11 |
根据(6—8) 式,区域位场的四阶谱矩的元定义为
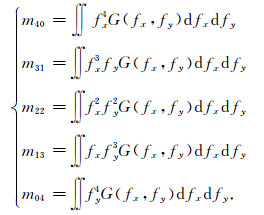
|
(15) |
m40, m31, m22, m13和m04分别等于区域布格重力场二阶导数的自协方差或互协方差,令场的二阶导数向量为
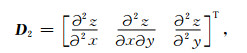
|
则二阶导数的协方差矩阵可写为
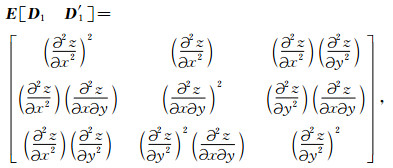
|
(16) |
或
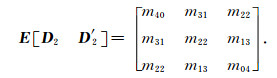
|
(17) |
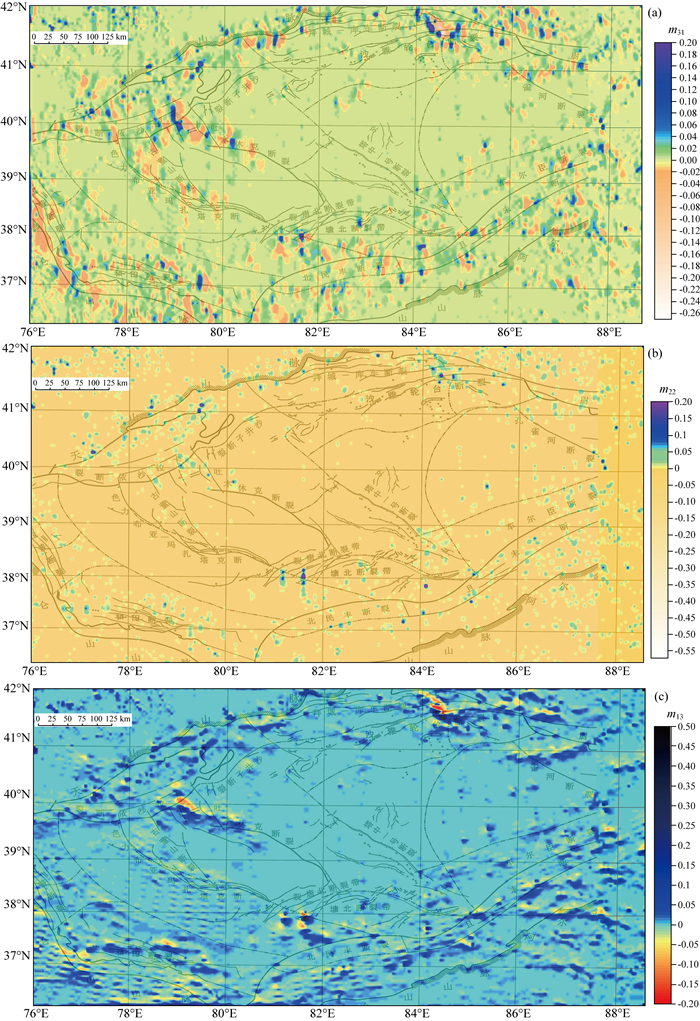
二阶导数的协方差矩阵分别表示表面曲率的变化情况.如四阶谱矩m40和m04反映场x与y方向上的二阶水平导数协方差.四阶谱矩三个元m22,m31和m13是三个新参数,代表x与y方向上二阶水平导数的互协方差.如此计算的塔里木盆地四阶谱矩的三个互协方差元m22,m31和m13示如图 3.由图可见,m31为x方向上的曲率主导的方差,数值小,反映重力场东西向曲率变化小.m13是y方向上的曲率主导的方差;数值大,反映重力场南北向曲率变化大.四阶谱矩的这两个元高值主要分布在盆地四周的造山带;造山带地壳变形剧烈,重力异常曲率变化大,曲率的方差也加大.m22是x与y方向上的曲率的协方差,强异常只出现在构造结点上,值得进一步研究讨论.
|
图 3 计算的塔里木盆地区域布格重力场的四阶谱矩三个元: (a) m31,(b) m22, (c) m13 Fig. 3 Three order-4 spectral moments, corresponding to (a) m31, (b) m22, (c) m13 |
不难看出频谱分析和谱矩分析有相关之处.例如,频率域场一阶偏导数协方差与二阶谱矩m20和m02对应,频率域场二阶偏导数协方差与四阶谱矩m40和m04对应.早在1970年代,位场数据处理中一阶二阶导数等线性滤波就已经有应用(Sybery, 1972; Cianciara and Marcar, 1975; 杨文采等, 1978).但是,谱矩分析的互协方差元给出了新参数,如二阶谱矩元m11和四阶谱矩三个元m22,m31和m13,它们只与场幅值面的轮廓有关.因此,谱矩分析能比频谱分析提供更多的与幅值面轮廓有关的几何信息.
在空间域进行计算时,位场表面对应的离散二阶谱矩表达式为
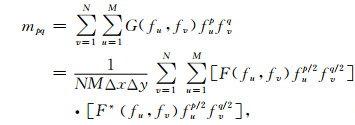
|
(18) |
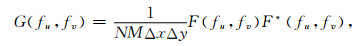
|
(19) |
其中函数F(fu,fv)为位场的离散傅里叶变换.令p=2, q=0,则表面二阶谱矩的三个元可表示为
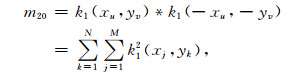
|
(20) |
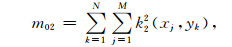
|
(21) |

|
(22) |
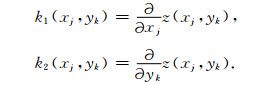
|
(23) |
不过,上述谱矩的元一般不能直接应用于幅值面轮廓有关的信息提取,这是因为它们与坐标系方向的选取有关.因此,首先要计算与坐标选取无关的统计不变量.任何表面的二阶谱矩可以用统计不变量M2和Δ2来表示为(黄逸云,1984;1985;Yanagik, 2001)
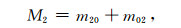
|
(24) |
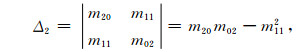
|
(25) |
M2是表面斜率的方差,场的方向导数模越大,M2越大.Δ2是表面梯度方向性效应的一种度量.场的方向导数互协方差m11减小,梯度各向异性增强,Δ2增大.
类似地,四阶谱矩统计不变量M4和Δ4分别为
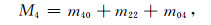
|
(26) |

|
(27) |
式(26—27) 中M4反映表面曲率的方差.Δ4是表面曲率方向性效应的一种度量.四阶谱矩的元m04的含义为x方向二阶功率谱矩自协方差;m40的含义为y方向二阶功率谱矩自协方差.m22的含义为正交方向二阶导数互协方差,m31的含义为x方向加权二阶导数互协方差,m13的含义为y方向加权二阶导数互协方差.由于本文篇幅有限,不能进一步讨论四阶谱矩的应用问题;但是可以估计,它们对浅层变形带定位和场源弯曲点定位可能有用.
3 位场二阶谱矩在地壳构造分析上的应用由于大地构造图件目前还是大地构造学家根据地表地质和地球物理资料的综合分析勾画出来的,因此,大地构造学家在制图时的主观推测便不可避免,使不同的大地构造学家勾画出不同的大地构造图件,缺乏客观的评价标准.另一方面,地球物理探测取得的关于地壳构造的图件是定量的,取得的各种地球物理场数据中包含有大量地壳构造信息.如果把这些信息提取出来,可以在数学物理普适规律指导下计算出有关地壳构造的大地构造图件.
圈定地壳变形带是地质构造学的基础研究内容之一,目前主要通过地表观测取得资料.由于露头和视角的限制,有不少隐伏的地壳变形带容易被忽略,而且地表观测的许多断裂延深并不大,没有深入地壳内部,使地壳变形带的制图产生错觉.地壳变形带在地壳中呈现为特殊岩石矿物组成的脊椎形条带,在物理性质上体现为脊椎形的密度急变带.根据重力学可知,这种脊椎形的物质密度急变带将产生脊椎形的布格重力异常带.因此,区域布格重力异常中包含有地壳变形带的信息.把这些信息提取出来,有可能计算出区域地壳变形带图件,为地质构造分析提供客观的证据.
在应用地球物理中,曾制作出区域重力梯度图,用于大地构造学研究,但是效果欠佳.究其原因可知,区域布格重力梯度异常只能反映少数最强烈的地壳变形,而许多地壳变形带,尤其是比较古老的地壳变形带在重力梯度图上常常没有反映.地壳变形带是历次地质作用在地壳中留下的刻痕,前期地质作用留下的刻痕不断为后期地质作用留下的刻痕改造和冲淡,因此前期变形带在布格重力梯度图中反映微弱,只利用梯度的幅度信息不能全面圈定地壳变形带.
那么,还有什么信息可用于圈定地壳变形带呢?答案为几何信息,即区域重力异常的各向异性度.变形带脊椎形的物质密度急变带产生脊椎形的布格重力异常,重力异常脊椎形的量化参数就是表面轮廓各向异性度高.不管是老的还是新的变形带,都产生地表面轮廓各向异性度高的重力异常.因此,如果要增强弱变形带的显示,应提取与表面轮廓各向异性度成正相关的参数,它称为脊形化系数.
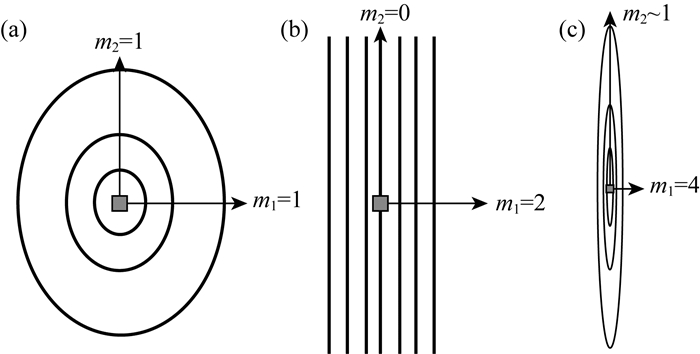
场表面轮廓的各向异性信息至今还没有在区域重力图解析上应用过.由于二阶谱矩的互协方差元m11给出了与场的几何信息有关的新参数,可预期二阶谱矩分析可成为提取地壳变形特征有用的数学工具.图 4上有3种不同的表面轮廓,图 4a是球缺形的表面轮廓,表示穹窿构造的重力场;其x方向的坡度设为单位,即m1=1, 其y方向的坡度也为单位,即m2=1;m1和m2的乘积也为1.图 4b是阶梯形的表面轮廓,表示正断层或逆断层的重力场;其x方向的坡度m1=2,其y方向的坡度m2=0;m1和m2的乘积为0.图 4c是脊椎形体的表面轮廓,表示地壳变形带一段的重力场;其x方向的坡度m1=4, 其y方向的坡度m2在1和0之间;m1和m2的乘积为不为0.由此可知,3种不同的表面轮廓对应3种不同的表面轮廓参数.由于二阶谱矩的三个元表征了重力场幅度表面轮廓,可知地壳变形带的脊形化系数与二阶谱矩有关.
|
图 4 提取3种不同的表面轮廓特征的图解 (a)球缺形; (b)阶梯形; (c)对应地壳变形带的脊形. Fig. 4 Illustration of characteristic parameters of three different surfaces (a) Part of a ball; (b) A step; (c) Ridge. |
地壳变形带的定位计算要用去除了地形影响之后的布格重力异常,例如图 1a所示的塔里木盆地布格重力异常.为了计算位场的脊形化系数,对地壳变形带准确定位,我们参照自动控制论中的刻痕分析方法(Huang,1984;1985;杨叔子等,2007;Sun and Yang, 2014;Sun et al., 2015, 2016; 杨文采等,2015a),同时使用两个二阶谱矩的统计不变量M2和Δ2来描述脊形化系数,将这种综合参数定义为

|
(28) |
脊形化系数Λ值变化区间为[0, 1],与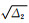
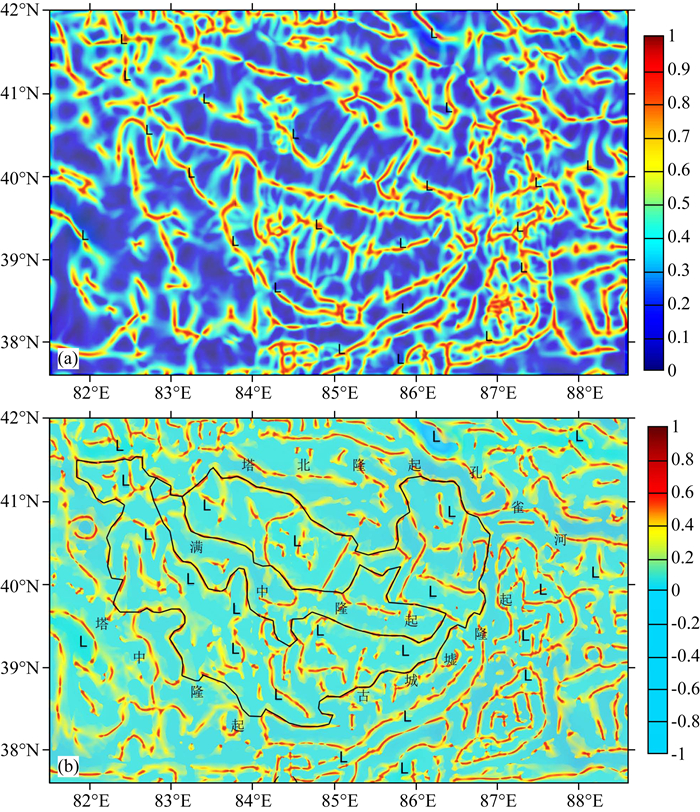
大别山地区基岩出露,我们曾选取大别山地区来验证脊形化系数对地壳变形带定位的效果(Yang and Sun, 2016).试验表明脊形化系数大于0.5的刻痕与地表地质测定的地壳变形构造带吻合.我们还选取塔里木盆地核心地区的满加尔坳陷,来验证未有基岩出露的覆盖区谱矩分析的效果.满加尔坳陷位于塔里木盆地东北部,布格重力异常计算的面积示如图 1b的方框内,图 1a对应区显示有其布格重力异常,作为计算的原始数据.为了油气勘探的需要,我们把原始数据分解为沉积盆地浅层、深层和结晶基底的重力异常三部分,分别作为计算脊形化系数的输入(侯遵泽和杨文采,2011;杨文采等, 2001, 2015a).计算输出的浅层(0~5 km)和深层(5~11 km)脊形化系数示如图 5a和图 6a.图中的脊形化系数大于0.5的刻痕揭示了地表看不见的地壳变形构造带.比较图 5a和图 6a可见,浅层和深层的地壳变形构造带有明显不同,表明塔里木浅部中新代的构造演化和深层中新代的构造演化有明显区别.在作者的前文中对有关图像进行了初步的解释(杨文采等,2015b),因篇幅限制,本文不再重复.
|
图 5 谱矩分析计算的滿加尔坳陷浅层脊形化系数图(a)和对应边界系数图(b);字母“H”表示高密度,字母“L”表示低密度 Fig. 5 The ridge coefficient map of the shallow layer (a) and the boundary ridge coefficient map (b), Notations are Chinese structure names, and letter "H" denotes high density disturbance, "L" denotes low density disturbance |
|
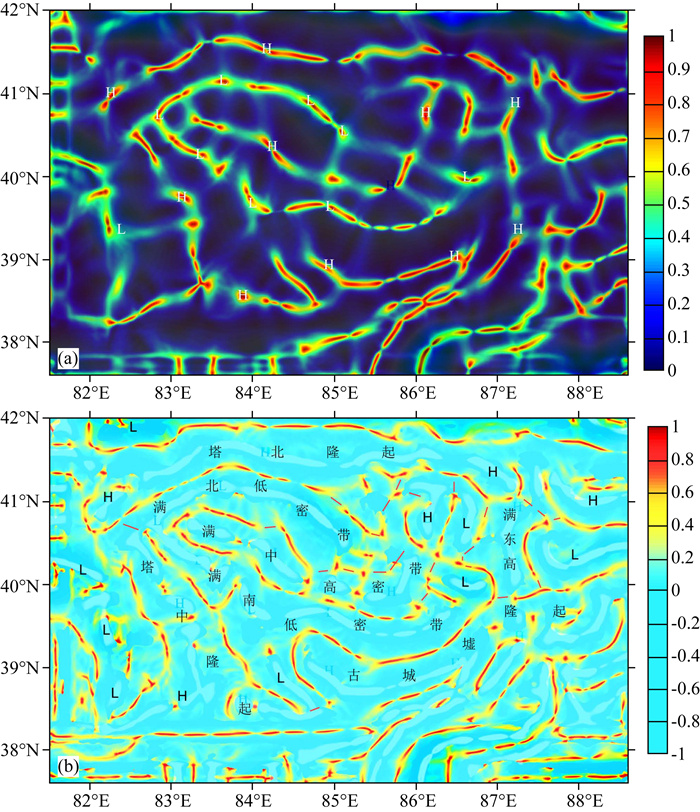
图 6 谱矩分析计算的滿加尔坳陷深层脊形化系数图(a)和对应边界系数图(b); 字母“H”表示高密度,字母“L”表示低密度. Fig. 6 The ridge coefficient map of the deep layer showed (a) and the boundary ridge coefficient map (b) Notations are Chinese structure names, and letter "H" denotes high density disturbance, "L" denotes low density disturbance |
重力场谱矩方法中的刻痕分析揭示了地表看不见的地壳变形构造带.计算脊形化系数还为用计算机自动制作区域地质构造图跨出了关键的一步.但是,这一步还未实现地壳构造图的制作.制作大地构造图首先要划分活动的和稳定的构造单元,造山带属于活动的构造单元,地壳变形作用强烈;克拉通属于稳定的构造单元,地壳变形作用不强烈.因此,强与弱的脊形化系数区的边界代表了活动的和稳定的构造单元的边界.二阶谱矩的统计不变量M2是表面斜率的方差,见(25) 式,M2越大场的方向导数模越大,它反映脊形化系数梯度较大区的边界.为了准确地对脊形化系数梯度值较小区的边界追踪定位,还要对与相关的脊形化系数作进一步增强处理,使追踪的构造单元边界更加连续和精细(孙艳云和杨文采,2014;Sun et al., 2015, 2016).因此,要提取的构造边界系数MΛ包含两项:
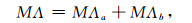
|
(29) |
其中第一项与脊形化系数的方向导数模M2有关,第二项与脊形化系数进一步作增强有关.在提取构造单元边界信息时单元划分越窄边界的定位越准确,因此计算时对这两项采用的窗口要求是不一样的.
在(29) 式中MΛa和MΛb为构造边界系数的分量,由下式计算
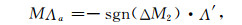
|
(30) |
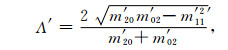
|
(31) |
其中m′ 20、m′ 02及m′ 11为以M2为输入数据,在每一个面元内提取的M2表面二阶谱矩的三个元,Δ为拉普拉斯算子,ΔM2的符号用来区分是“谷”还是“峰”的边界系数.同样,M2作为初始数据,采用滑动窗口w2对M2表面进行刻痕边界增强处理求MΛb;采用含有Mβ×Nβ个采样点的窗口计算.假定在x方向以间隔Δx等间距采样,在y方向上以间隔Δy等间距采样,且采样点数分别为Mβ和Nβ,
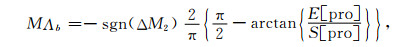
|
(32) |
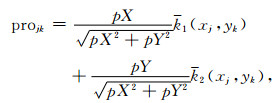
|
(33) |
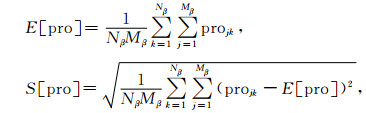
|
(34) |
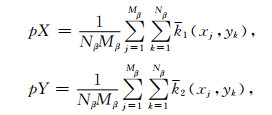
|
(35) |

|
(36) |
满加尔坳陷浅层和深层脊形化系数已经示如图 5a和图 6a,揭示了地表看不见的地壳变形构造带.按公式(29—36) 计算刻痕的满加尔坳陷构造边界系数示如图 5b和图 6b,揭示了地表看不见的构造单元及其边界.比较两图的(a)和(b)可见,所有地壳变形构造带和构造单元的走向变化一致,构造单元边界围绕变形构造带分布,其图像可为大地构造分区提供客观的依据.比较图 5b和和图 6b可见,塔里木盆地浅部中新代的构造和深层古新代的构造有分区明显区别.关于这些新制作图像的地质含义,笔者已发文作了初步分析(杨文采等,2015b;孙艳云等,2015).
把塔里木盆地作为一级构造,满加尔坳陷就是其中具有低密度扰动的二级构造.用区域重力场小波多尺度分析及刻痕分析等新方法的结合,可以确定满加尔坳陷内部深层三级构造密度扰动带的分布及其边界.图 6b中用字母“L”标明等效层低密度扰动中心位置;用“H”标明等效层高密度扰动中心位置.脊形化系数Λ>0.5的线条都与标明“L”成“H”的等效层密度扰动中心对应,Λ大的线条多数反映断裂裂隙带的轴线.扰动边界刻痕系数MΛ线条反映等效层中高密度扰动带中“脊”与“谷”的边界.沉积盆地内的沉积岩密度较结晶岩低,所以盆地或坳陷边缘会有密度急变的“边界刻痕”,不同深度上的盆地边缘也可以为多尺度刻痕分析方法识别并检测.综合脊形化系数图和边界刻痕系数图,可以准确确定盆地深和浅等效层中高和低密度扰动带的分布及其边界.盆地浅层大范围局部高电阻率分布区与高大地热流分布区和高密度分布区大致吻合,主要反映构造活动与构造上隆.综合脊形化系数图和边界刻痕脊形化系数图(图 5和图 6),圈定了深层满中高密度扰动带和满南、满北低密度扰动带,为深层油气勘探提供重要基础资料.
5 结论(1) 由于区域重力场的高阶谱矩包含了场轮廓面的几何信息,可用于地质构造要素的分析计算,为地质构造要素选取和定位的计算机自动制图提供了理论依据.
(2) 由地面布格重力场的二阶谱矩的统计不变量的计算,可导出表征地壳变形带的脊形化系数,用于计算机自动制作区域地壳变形带分布图.
(3) 脊形化系数强弱区的边界代表了活动的和稳定的构造单元之间的边界.在计算脊形化系数的基础上,还可进一步计算其二阶谱矩的统计不变量并作进一步增强处理,计算构造单元的边界系数,对地壳构造单元边界作连续和精细的追踪.
(4) 文中介绍了脊形化系数和边界系数的计算方法,以及用在塔里木盆地进行地壳构造分析的结果.圈定了塔里木深层满中高密度扰动带和满南和满北低密度扰动带,为深层油气勘探提供重要基础资料.
(5) 文中还介绍了塔里木盆地四阶谱矩的计算结果(图 3),但尚未对四阶谱矩的地学应用进行讨论,有待将来深入研究.
| Ardalan A A, Safari A. 2005. Global height datum unification: a new approach in gravity potential space. Journal of Geodesy, 79(9): 512-523. DOI:10.1007/s00190-005-0001-0 | |
| Cianciara B, Marcak H. 1975. Interpretation of graviti anomalies by means of local power spectra. Geophysical Prospecting, 24(2): 273-286. | |
| Hou Z Z, Yang W C. 2011. Multi-scale inversion of density structure from gravity anomalies in Tarim Basin. Science China Earth Sciences, 54(3): 399-409. DOI:10.1007/s11430-011-4169-2 | |
| Huang Y Y. 1984. The characterization of three-dimensional radom surface topography. Journal of Zhejiang University, 18(2): 138-148. | |
| Huang Y Y. 1985. Geometrical interpretation and graphical solution of second order spectrum moments and statistical invariants for random surface characterization. Journal of Zhejiang University, 19(6): 143-153. | |
| Longust-Higgins M S. 1962. The statistical geometry of random surfaces in hydrodynamic instabity.//13th Symp. Applied Math. Amer. Math. Soc., 105-143. | |
| Riley K F. 1974. Mathematical Methods for the Physical Sciences. New York: Cambridge University Press. | |
| Sun Y Y, Yang W C. 2014. Recognizing and extracting the information of crustal deformation belts from the gravity field. Chinese J. Geophys., 57(5): 1578-1587. DOI:10.6038/cjg20140521 | |
| Sun Y Y, Yang W C, Yu C Q. 2015. Multi-scale scratch analysis in Qinghai-Tibet Plateau and its geological implications. Pure and Applied Geophysics, 173(4): 1197-1210. | |
| Sun Y Y, Yang W C, Yu C Q. 2015a. Crustal density deformation zones of Qinghai-Tibet Plateau and their geological implications. Chinese J. Geophys., 58(11): 4115-4128. DOI:10.6038/cjg20151119 | |
| Sun Y Y, Yang W C, Zeng X Z, et al. 2016. Edge enhancement of potential field data using spectral moments. Geophysics, 81(1): G1-G11. DOI:10.1190/GEO2014-0430.1 | |
| Sybery F J R. 1972. A Fourier method for the regional-residual problem of potential fields. Geophysical Prospecting, 20(1): 47-75. DOI:10.1111/gpr.1972.20.issue-1 | |
| Yanagi K, Hara S, Endoh T. 2001. Summit identification of anisotropic surface texture and directionality assessment based on asperity tip geometry. International Journal of Machine Tools and Manufacture, 41(13-14): 1863-1871. DOI:10.1016/S0890-6955(01)00050-5 | |
| Yang S Z, Wu Y, Xuan J P, et al. 2007. Time Series Analysis in Engineering Application. (2nd ed). Wuhan: Huazhog University of Science and Technology Press: 158-206. | |
| Yang W C, Guo A Y, Zhao J X, et al. 1978. Theory and methods for interpretation of gravity and magnetic anomalies in the frequency domain. Bulletin of Institute of Geophysical and Geochemical Prospecting, 78(2): 134-178. | |
| Yang W C, Shi Z Q, Hou Z Z, et al. 2001. Discrete wavelet transform for multiple decomposition of gravity anomalies. Chinese J. Geophys., 44(4): 534-541. DOI:10.3321/j.issn:0001-5733.2001.04.012 | |
| Yang W C. 2010. Tectonophysics of Paleo-Tethyan. Beijing: Beijing Petroleum Pub: 1-443. | |
| Yang W C, Sun Y Y, Hou Z Z. 2015a. The multi-scale scratch analysis method for quantitative interpretation of regional gravity field. Chinese J. Geophys., 58(2): 520-531. DOI:10.6038/cjg20150215 | |
| Yang W C, Sun Y Y, Yu C Q, et al. 2015b. Multi-scale scratch analysis of gravity field and deep structures in Manjar depression. Acta Geologica Sinica, 89(2): 211-221. | |
| Yang W C, Sun Y Y. 2016. Discovering crustal deformation bands by processing regional gravity field. Acta Geologica Sinica (English Edition), 90(1): 66-74. DOI:10.1111/1755-6724.12642 | |
| 侯遵泽, 杨文采. 2011. 塔里木盆地多尺度重力场反演与密度结构. 中国科学:地球科学, 41(1): 29–39. | |
| 黄逸云. 1984. 三维随机表面形貌的识别. 浙江大学学报, 18(2): 138–148. | |
| 黄逸云. 1985. 随机表面二阶谱矩和统计不变量的几何解释及其图解法. 浙江大学学报, 19(6): 143–153. | |
| 孙艳云, 杨文采. 2014. 从重力场识别与提取地壳变形带信息的方法研究. 地球物理学报, 57(5): 1578–1587. DOI:10.6038/cjg20140521 | |
| 孙艳云, 杨文采, 于常青. 2015a. 青藏高原地壳密度变形带及构造分区. 地球物理学报, 58(11): 4115–4128. DOI:10.6038/cjg20151119 | |
| 杨叔子, 吴雅, 轩建平, 等. 2007. 时间序列分析的工程应用(下). (2版). 武汉: 华中科技大学出版社: 158-206. | |
| 杨文采, 郭爱缨, 谢玉清, 等. 1978. 重磁异常频率域解释的理论与方法. 物化探研究报导, 78(2): 134–178. | |
| 杨文采, 施志群, 侯遵泽, 等. 2001. 离散小波变换与重力异常多重分解. 地球物理学报, 44(4): 534–541. DOI:10.3321/j.issn:0001-5733.2001.04.012 | |
| 杨文采. 2010. 东亚古特提斯域大地构造物理学. 北京: 石油工业出版社: 1-443. | |
| 杨文采, 孙艳云, 侯遵泽, 等. 2015a. 用于区域重力场定量解释的多尺度刻痕分析方法. 地球物理学报, 58(2): 520–531. DOI:10.6038/cjg20150215 | |
| 杨文采, 孙艳云, 于常青, 等. 2015b. 重力场多尺度刻痕分析与满加尔坳陷深层构造. 地质学报, 89(2): 211–221. | |
 2017, Vol. 60
2017, Vol. 60


