2. 中国地震局黄土地震工程重点实验室, 兰州 730000
2. Key Laboratory of Loess Earthquake Engineering, Lanzhou Institute of Seismology, China Earthquake Administration, Lanzhou 730000, China
远震P波接收函数是研究台站下方地壳和上地幔结构的一种经典方法, 它将三分量波形记录的两个水平分量旋转为径向和切向分量, 用垂直分量分别对径向和切向分量作反褶积得到时间序列(Langston,1979;Yuan et al., 1997;Shen et al., 2015;Shen et al., 2017).接收函数计算过程中消除了震源和传播路径对波形的影响, 结果仅与接收台站下方地球介质的结构特征有关.接收函数波形上的每个波峰(波谷)都对应着某个间断面的一次转换波或多次波.因此接收函数方法是研究台站下方间断面的一种有效地震学工具.由于接收函数中震相到时较易测量且较为稳定, 因此利用到时信息确定界面深度是接收函数最为广泛的一种应用.较经典方法为Zhu和Kanamori(2000)提出的利用接收函数确定Moho面深度和波速比的H-k搜索叠加方法.该方法通过叠加不同震中距和方位角的接收函数, 有效抑制了横向结构的变化, 从而获得平均地壳模型.该方法实现过程简单、稳定性好, 被广泛应用于不同地区地壳结构的研究(如, Ramesh et al., 2002; Pan and Niu, 2011).近年来, 陆续有研究者对该方法进行了研究和发展.李翠芹等(2014)讨论了P波速度(α)变化对H-k方法结果的影响;Ma和Zhou(2007)结合接收函数与面波频散曲线, 用合理的P波速度作为H-k搜索叠加方法的初始值, 使其对H-k方法结果的影响减小, 从而得到更加精确的地壳厚度和波速比;Shen等(2011)利用该方法确定了青藏高原东北缘地区地壳厚度和波速比;司少坤等(2014)讨论了界面倾斜和各向异性对接收函数H-k搜索叠加方法的影响, 并对这种影响进行了校正.
接收函数中不仅包含震相的到时信息, 还包含幅度信息, 且幅度和界面的速度跃变、密度跃变及各向异性等性质密切相关.因此利用接收函数幅度可对界面不同参数的跃变进行研究.国外已有学者尝试利用接收函数方法研究速度和密度跃变(Owens et al., 1984;Ammon et al., 1990;Julià et al., 2000).Niu和James(2002)使用单台宽频带记录的接收函数幅度估计出Kaapvaal地区下方Moho面的速度和密度跃变;Julià(2007) 提取了西班牙中部和印度地盾地区两个固定台站长期观测记录的接收函数幅度, 研究了台站下方Moho面的结构特性.但在实际资料的处理中, 影响接收函数幅度的因素较多, 如Moho面多次波和深层界面一次波的相互干扰、衰减、滤波因子和浅层结构等.这些因素导致提取接收函数幅度信息面临较大困难, 所以该方法一直没有得到广泛应用, 在国内相关方面的研究报道较少.
近年来, 随着观测仪器越来越精密, 研究者得到了大量高质量的数据, 有可能捕捉到来自地球内部精细结构的信息, 使得接收函数中一些弱震相(多次波)的稳定性和分辨能力都有较大提高.因而有可能在接收函数上量取到一次波和多次波准确稳定的幅度信息, 进行台站下方界面速度和密度跃变的研究.
本文主要目的为探索利用接收函数一次波和多次波幅度确定Moho面速度和密度跃变的方法.为此, 通过单层模型的理论计算和理论地震图的数值试验, 我们提出了确定速度和密度跃变的δβ-δρ扫描叠加方法;并以青藏高原东北缘地区两个台站为例, 利用该方法确定了台站下方Moho面的速度和密度跃变.
2 影响接收函数幅度因素分析接收函数包括所有震相的到时和幅度信息, 影响震相幅度的最主要因素是界面的反射和透射系数(Aki and Richards, 2002).图 1为单层模型中P波入射界面的射线路径及对应的接收函数, 其中Ps为一次透射转换震相, PpPs、PpSs和PsPs为多次反射震相.从图中看出, PpSs和PsPs震相射线路径虽稍有不同, 但走时相同, 所以PpSs和PsPs的幅度叠加可用PpSs+PsPs整体处理.由于直达P波与界面的S波速度和密度跃变基本无关, 只与浅部的S波速度有关(Aki and Richards, 2002;Ammon,1991;Julià, 2007),所以不考虑其对界面的影响; 幅度较小的震相, 对研究界面的速度跃变和密度跃变影响较小, 且淹没在噪声之中无法分辨, 因此可忽略.综上所述, 本文主要考虑一次转换波和多次波反射、透射系数对震相幅度的影响.
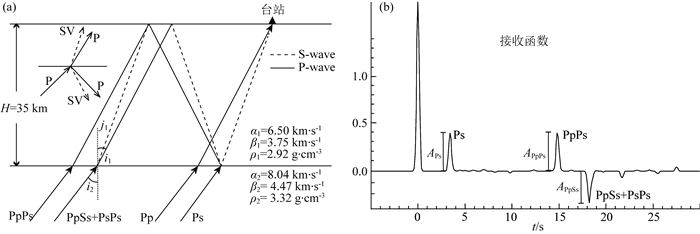
|
图 1 震相射线路径和接收函数示意图(单层模型) Fig. 1 Schematic diagram showing ray paths of main phases and synthetic receiver functions for one-layer model |
为了定量分析反射和透射系数对震相幅度的影响, 在此引入Aki和Richards(2002)的反射透射理论:
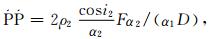
|
(1) |
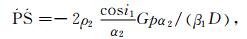
|
(2) |
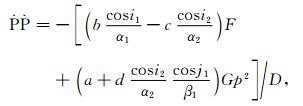
|
(3) |
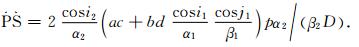
|
(4) |
式中, 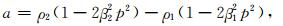
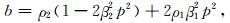
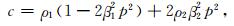
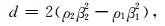
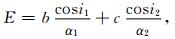
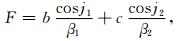
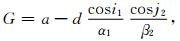
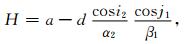
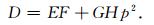
其中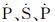
考虑震源为单一脉冲信号.当入射波为远震波时, 穿过界面的P波可近似是平行的.在不考虑衰减的情况下(φ≈1), 根据公式(1)-(4) 近似得到
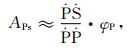
|
(5) |
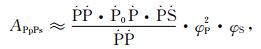
|
(6) |
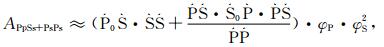
|
(7) |
其中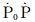
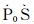
从上述公式看出, 接收函数幅度主要与入射角i、上下界面速度和介质的密度有关.其中i和射线参数(p=(sini)/V;V=α, β)有关.p可由震中距和震源深度计算得到(Crotwell et al., 1999).当给定震中距时, 震相幅度主要受到界面速度和密度的影响.
假设震中距为70°, 对应p为0.05506 s·km-1, 界面上下层的P(S)波速度跃变δv和密度跃变δρ分别取0~30%的变化范围, 由(5)-(7) 式计算得到震相幅度, 绘制α、β和ρ存在如下跃变的三种组合方式对应的震相幅度等值线图(见图 2).根据该图可作如下分析:
|
图 2 P(S)波速度和密度跃变对一次波和多次波反射透射系数的影响 (a-c) Ps和PpPs幅度随速度和密度变化的等值线;(d-f) Ps和(PpSs+PsPs)幅度随速度和密度变化的等值线.δα代表界面上下层P波速度跃变量, δβ为S波速度跃变量, δρ为密度跃变量(δv=(v2-v1)/v1, v=α, β, ρ). (c)和(f)中Ps幅度为0. Fig. 2 Influence of P(S) wave velocity and density contrasts on the reflection and transmission coefficients (a-c) Contours of Ps and PpPs amplitudes changing with velocity and density. (d-f) Contours of Ps and PpSs+PsPs amplitudes changing with velocity and density. δα is P wave velocity contrast across the interface, δβ is S wave velocity contrast, δρ is density contrast (δv=(v2-v1)/v1, v=α, β, ρ). The amplitude of Ps is zero in (c) and (f). |
(1) δβ-δρ约束震相幅度, δα=0.可看出, Ps幅度值与纵轴(δρ)夹角较小, 近似平行;Ps幅度与横轴(δβ)夹角较大, 近似垂直.当δρ很大时, Ps幅度几乎不发生变化;当δβ很小时, Ps幅度有明显的变化.这说明Ps幅度对δρ不敏感, 而对δβ非常敏感;同理, PpPs和PpSs幅度对δβ和δρ都比较敏感(图 2a和2d).
(2) δα-δβ约束震相幅度, δρ=0.Ps、PpPs和PpSs+PsPs都不随横轴(δα)变化, 说明P波速度对震相幅度影响甚小(图 2b和2e).
(3) δα-δρ约束震相幅度, δβ=0.PpPs和PpSs+PsPs幅度不随δα变化, 没有Ps震相(图 2c和2f).
以上分析表明, 一次波和多次波幅度对S波速度都敏感, 对P波速度都不敏感, 多次波对密度较为敏感.这进一步验证了前人的结果(Owens et al., 1984;Ammon et al., 1990;Julià et al., 2000;Julià,2007).
虽然接收函数的幅度主要受透射系数和反射系数的影响, 但严格意义上讲, 实际接收函数是由地动位移作反褶积得到的.因一次透射波和多次波引起的地动位移都包含入射和地表反射的影响, 地表的地动位移受入射波和地表反射共同作用, 所以反射透射系数的计算值(公式(5)-(7))并不能完全代表接收函数最真实的幅度.对此, 我们通过反射透射矩阵法(Ma et al., 2012)计算理论接收函数, 考查地表反射对接收函数造成的影响.
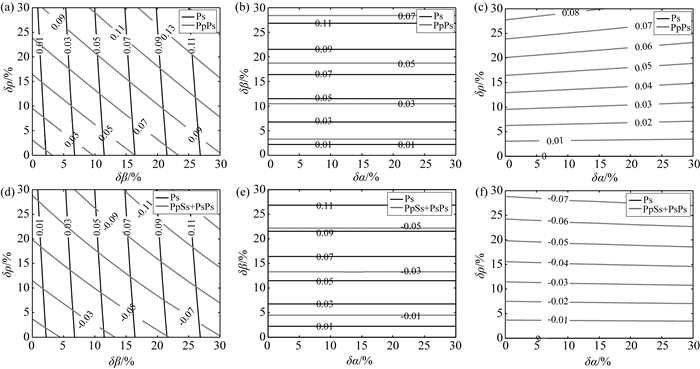
利用反射透射矩阵法, 构建δα、δβ和δρ从0~30%、步长为0.1%的不同组合模型, 选取震中距为70°, 计算不同模型对应的理论接收函数.接收函数中包括所有震相信息, 通过一次波和多次波的走时信息来提取其幅度值, 绘制δα、δβ和δρ不同组合模型对应的接收函数幅度等值线(图 3).比较图 2a和图 3a可看出, 反射透射矩阵法中考虑地表反射和其他波形影响时得到的震相幅度与通过反射、透射系数比值法得到结果基本一致.因此, 在一定的误差范围内, 界面的速度和密度跃变可近似用反射、透射系数比值来约束.
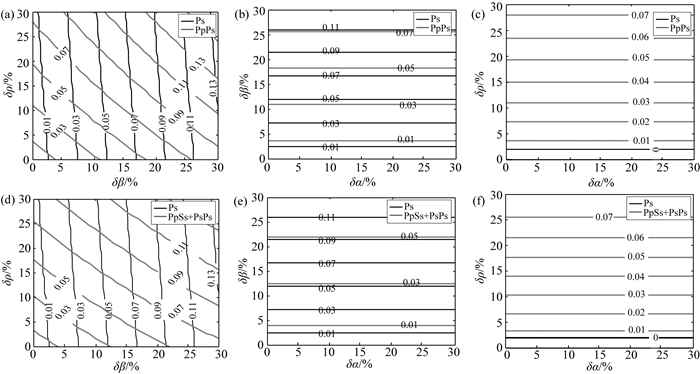
|
图 3 P(S)波速度和密度跃变对接收函数幅度的影响 (a-c) Ps和PpPs幅度随速度和密度变化的等值线;(d-f) Ps和(PpSs+PsPs)幅度随速度和密度变化的等值线.δα代表界面上下层P波速度跃变量, δβ为S波速度跃变量, δρ为密度跃变量(δv=(v2-v1)/v1, v=α, β, ρ). (c)和(f)中Ps幅度为0. Fig. 3 Influence of P(S) wave velocity and density contrasts on amplitudes of receiver functions (a-c) Contours Ps and PpPs amplitudes changing with velocity and density. (d-f) Contours of Ps and PpSs+PsPs amplitudes changing with velocity and density. δα is P wave velocity contrast across the interface, δβ is S wave velocity contrast, δρ is density contrast (δv=(v2-v1)/v1, v=α, β, ρ). The amplitude of Ps is zero in (c) and (f). |
以上从简单模型出发, 推导了影响接收函数幅度的主要因素, 即界面上下层的密度和速度跃变.对于三分量观测波形(垂向Z、径向R和切向T), 在数据处理过程中需对数据进行不同滤波的反褶积, 会对接收函数幅度产生较大影响.下面通过计算理论地震图对此作进一步分析.
3 理论接收函数数值试验地球具有吸收和衰减的性质, 它并不是完全弹性的, 且衰减因子和幅度之间并不是简单的线性关系.为了和观测地震数据处理过程进行对比, 利用反射率法(Ma et al., 2013)先计算理论地震图, 再采取与处理观测资料相同的方法, 通过反褶积计算接收函数.考虑不同速度和密度组合模型的接收函数幅度的变化, 采用不同滤波因子计算接收函数, 进而分析其对接收函数幅度的影响, 最终确定界面的速度和密度跃变.
3.1 界面速度、密度跃变对接收函数幅度敏感性数值试验下面通过计算理论地震图反褶积得到接收函数, 对前述结果进行进一步检验.以图 1所示速度密度模型为例, 首先选取震源为爆炸源, 利用反射率法(Ma et al., 2013)来计算震中距为70°的理论地震图, 并利用时间域迭代反褶积方法, 计算理论接收函数(Ligorría and Ammon, 1999).
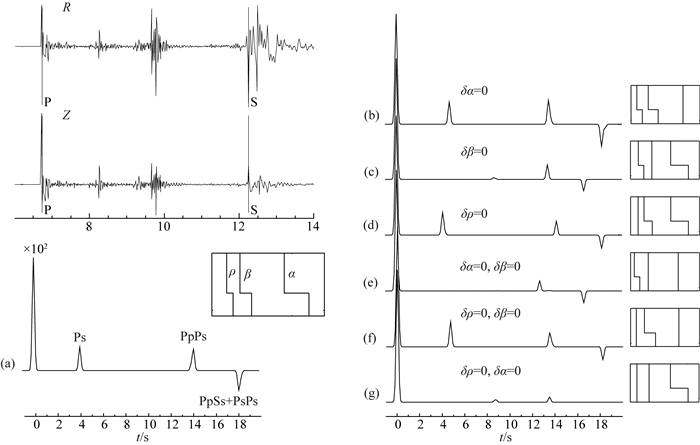
我们选取速度和密度跃变的不同组合来测试接收函数对α、β和ρ的敏感性.图 4给出了速度和密度跃变的不同组合方式对应的理论接收函数的计算结果.图 4a为IASP91模型径向和切向的理论地震图及对应接收函数;图 4b为当P波速度不发生跃变(δα=0) 时的接收函数, 各震相幅度与图 4a对比无明显变化;当δβ=0时图 4c所得结果与图 4a比较, Ps幅度减小到0, PpPs和PpSs幅度相对减小;当δρ=0时Ps幅度无明显变化(图 4d), PpPs和PpSs幅度减小;图 4e-4g为只有一个参数发生跃变得到的接收函数.结果表明:P(S)波速度和密度跃变对接收函数幅度的敏感性不同, 一次波仅对β变化敏感, 多次波对β和ρ变化都敏感, 接收函数震相幅度对α都不敏感(Owens et al., 1984;Ammon et al., 1990;Julià et al., 2000).这与理论计算得到的结果(图 2)一致.
|
图 4 速度和密度跃变的不同组合方式对应的接收函数理论计算值(单层模型) (a) IASP91模型径向和切向的理论地震图及对应接收函数;(b—g) α、β、ρ三个参数的6种组合情况下震相Ps、PpPs和PsPs+PpSs幅度的变化. Fig. 4 Synthetic receiver functions of models with different velocity and density jumps (one-layer model) (a) Synthetic seismograms (left-hand panel) of IASP91 model with constant P-and S-velocity and density; (b—g) Synthetic receiver functions for one-layer model shown in the insets panel, corresponding to a zero P-velocity contrast (δα=0), a zero S-velocity contrast (δβ=0), and a zero density contrast (δρ=0). |
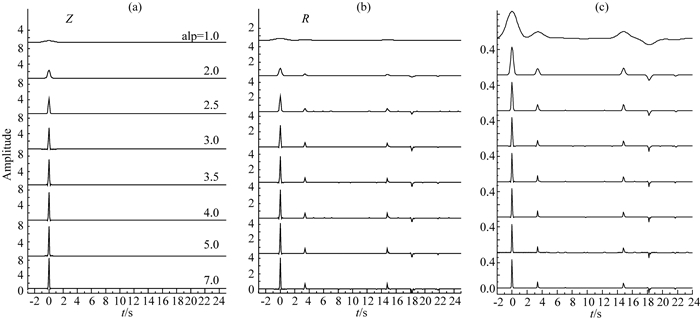
由于不同滤波器对接收函数幅度的影响不同, 本文尝试了用不同高斯滤波因子(alp)计算理论接收函数, 以考察alp不同时接收函数幅度的变化.选取IASP91模型用反射率法计算震中距为70°的理论地震图(Ma et al., 2013), 采用不同alp值, 在时间域计算接收函数(Ligorría and Ammon, 1999).由于不同alp对应的接收函数幅度相差很大, Ammon(1990)提出了利用垂向Z接收函数最大峰值幅度对径向R接收函数作归一化处理来提取幅度的方法.利用该方法对不同alp的接收函数幅度进行了对比(图 5).当alp逐渐增大时, R(Z)向接收函数震相的到时不变, 但是波形变得尖锐, 其幅度逐渐增大(图 5a,5b);图 5c为Z向接收函数对R向接收函数作归一后得到的结果, 从中可看出随alp值的增大, 其接收函数震相变窄, 幅度不随alp发生较大变化, 近似相等.提取其最大峰值发现, 虽然Ammon(1990)提出了利用垂向接收函数幅度对径向接收函数归一化, 但是消除alp的影响后得到的幅度还是存在微小差异.这种差别可能来自滤波过程中的非线性影响, 在后面的观测资料中将再作具体讨论.
|
图 5 垂向和径向接收函数 (a—b)震中距为70°时不同alp对应的垂向(Z)和径向(R)接收函数;(c)用Z接收函数对R接收函数作归一化后的结果. Fig. 5 Vertical and radial synthetic receiver functions with different Gaussian filter factors (a—b) Vertical and radial receiver function with different alp in 70° epicenter distance; (c) Normalization results of R function using Z receiver function. |
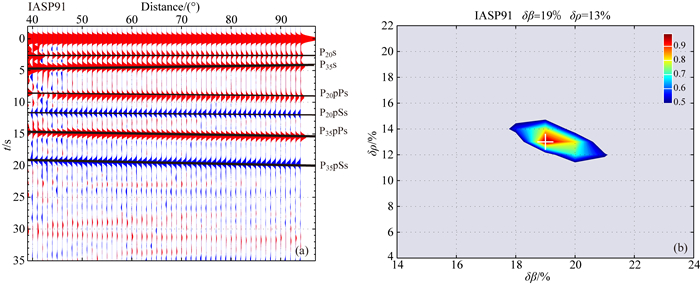
为了和观测资料相对应, 采取和处理实际资料相同的方式.选取IASP91模型, 震中距范围为40°~95°, 步长为1°, 利用反射率法(Ma et al., 2013)计算理论地震图.以该理论地震图作为观测资料, 选滤波窗(alp=1), 在时间域作反褶积计算接收函数(图 6a).图中显示走时在5 s、15 s和20 s附近存在清晰的一次波(P35s)、多次波(P35pPs和P35pSs+P35sPs).
|
图 6 IASP91模型接收函数以及接收函数幅度约束速度跃变、密度跃变 Fig. 6 Receiver functions of the IASP91 model and the results from δβ-δρ scan stacking method |
利用接收函数约束Moho面速度和密度跃变的方法与H-k搜索叠加方法(Zhu and Kanamori, 2000)类似, 是在δβ(上下层S波速度跃变量)和δρ(上下层介质的密度跃变量)组成的空间进行搜索, 选取δβ和δρ的变化范围为0~30%, 搜索步长为0.01%.在搜索过程中, 每搜索一次, 可根据公式(5)-(7) 计算震相幅度的理论值.在一次波和多次波的到时(tP35s, tP35pPs和tP35pSs)附近t±2 s提取其幅度的最大值, 即为接收函数幅度的观测值, 从而得到不同震中距的一次波和多次波幅度的理论值和观测值.对于每一个δβ和δρ都可算出不同震中距震相的理论值;不同震中距的观测值和理论值之间的差别, 用misfit(δβ, δρ)表示, 可作为衡量速度、密度跃变是否接近实际值的标准.misfit(δβ, δρ)定义为
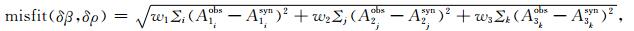
|
(8) |
其中A1、A2和A3分别为震相P35s、P35pPs和P35pSs+P35sPs的幅度, Aobs为观测值, Asyn为理论计算值, ∑表示对不同射线参数的网格扫描叠加, wi为一次波(Ps)和多次波(PpPs和PpSs+PsPs)的权重因子.对于权重因子的选取, 可由震相幅度的清晰度和受干扰程度来确定, 一般而言一次波Ps震相幅度较为清晰且波形简单, 干扰少, 权重相对稍高一些, 具体需经多次选取、实验得到最佳权重关系.
根据公式(8) 计算misfit(δβ, δρ).其值最小时所对应的δβ和δρ为间断面的速度跃变和密度跃变的最优值.在整个δβ和δρ的空间扫描寻找最优值, 最终得到较精确的速度跃变和密度跃变(图 6b).图中横坐标是上下界面速度跃变δβ%, 纵坐标为密度跃变δρ%, “+”符号为界面速度跃变和密度跃变的最优值.在绘制图形时取misfit(δβ, δρ)倒数后归一, 使最优值接近1, 定义误差范围≥0.95.
对于IASP91模型, 35 km深度间断面的速度跃变为(19±0.5)%, 密度跃变为(13±0.5)%.初始模型中δβ=19.2%, δρ=13.69%, 这与初始速度和密度模型相一致, 说明该方法对于研究间断面的速度、密度跃变是有效的.
4 观测资料处理为进一步检验该方法在观测资料处理中的有效性, 我们将该方法应用到了位于青藏高原东北缘地区甘肃地震台网的高台(GTA)台和兰州(LZH)台, 研究各台站下方Moho面速度和密度跃变.
选取GTA台2009-2015年震中距为40°~95°、震级MS大于5.5且Z分量上P波初动清晰、信噪比较好的546条地震记录, 并截取P波初动前20 s和后150 s的地震记录.将Z-N-E三分量观测波形的两个水平分量(N-E)旋转到径向(R)和切向(T), 旋转后Z向记录和R向记录在时间域作迭代反褶积获得R向观测接收函数(Ligorría and Ammon, 1999).且分别计算了高斯滤波因子alp为1、2和5的不同频率接收函数.图 7a-7c为根据上述方法计算的GTA台接收函数.图中Moho面Pms、PmpPs和PmsPs+PmpSs的震相清晰, 这保证了提取接收函数幅度是可行的.分别利用Z向接收函数对R向接收函数作归一(Ammon,1990), 消除滤波器带来的影响.根据H-k搜索叠加得到的厚度和波速比分别为51 km和1.7(Ma and Zhou, 2007), 可计算出Moho面一次转换波和多次反射波的到时(tPms, tPmpPs和tPmpSs), 在t±2 s范围查找幅度最大值, 即为观测幅度值.
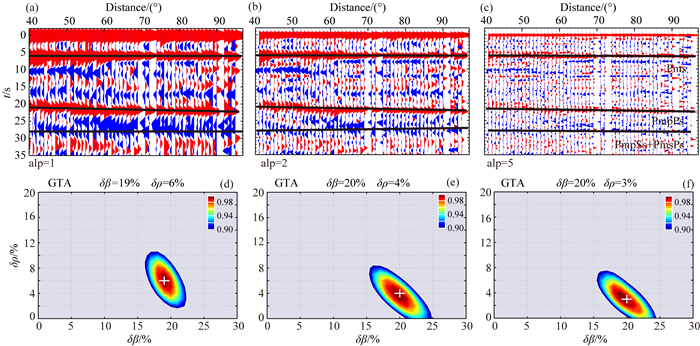
|
图 7 GTA台观测数据的接收函数及下方Moho面速度和密度跃变 (a—c) alp=1、2、5对应的径向接收函数; (d—f)分别为不同alp对应GTA台下方Moho面速度和密度跃变. Fig. 7 Receiver functions of GTA station and the results from δβ-δρ scan stacking method (a—c) Radial receiver functions with alp= 1, 2 and 5; (d—f) S-wave velocity and density contrasts across the Moho corresponding to different alps. |
分别选取δβ和δρ从0~30%, 步长为0.01%, 代入公式(5)-(7) 计算不同震中距的理论幅度值.将量取的GTA台观测接收函数震相幅度和理论幅度代入misfit(δβ, δρ);选定权重(w1:w2:w3=0.4:0.3:0.3), 在δβ和δρ变化范围内扫描搜索misfit(δβ, δρ)的最小值, 对应变量δβ和δρ数值则为GTA台下方Moho面速度和密度跃变(图 7d-7f).图 7d中给出了alp=1时, GTA台下方Moho面速度跃变为(19±1)%, 密度跃变为(6±2)%;图 7e给出了alp=2时, δβ≈(20±1)%, δρ≈(4±2)%;图 7f为alp=5时, δβ≈(20±1)%, δρ≈(3±1)%.比较图 7d-7f结果可看出, 滤波因子不同时速度跃变比较稳定, 都集中在(19~20)%, 而密度跃变稳定性略有不足, 其误差范围为(3~6)%, 存在一定的差异.
对于LZH台观测资料, 选择震中距为40°~95°、震级MS为5.5级以上、初至P波清晰的606条地震记录.采用和计算GTA台相似的步骤, 得到LZH台下方Moho面速度和密度跃变(图 8).图 8a-8c分别为alp=1、2、5时对应的LZH台观测资料的径向接收函数, 黑线位置为Moho面Pms、PmpPs和PmsPs+PmpSs的震相.LZH台速度跃变和密度跃变结果如图 8d-8f:当alp=1时, Moho面速度跃变为(21±2)%, 密度跃变为(6±3)%;当alp=2时δβ≈(20±2)%, δρ≈(8±3)%;当alp=5时, δβ≈(19±2)%, δρ≈(10±3)%.比较图 8d-8f看出, 滤波因子变化时速度跃变比较稳定, 处于(19~21)%之间;而密度跃变范围为(6~10)%, 误差较大.
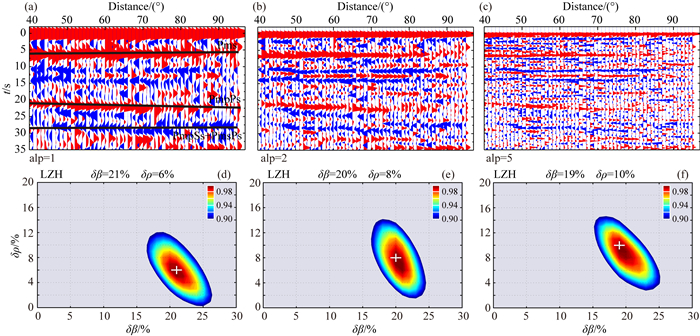
|
图 8 LZH台观测数据的接收函数及下方Moho面速度和密度跃变 (a—c)分别为alp=1、2、5对应的径向接收函数; (d—f)分别为不同alp对应LZH台下方Moho面速度和密度跃变. Fig. 8 Receiver functions of LZH station and the results from δβ-δρ scan stacking method (a—c) Radial receiver functions with alp= 1, 2 and 5; (d—f) S-wave velocity and density contrasts across the Moho corresponding to different alps. |
GTA和LZH台下方Moho面的速度跃变分别约为(19±2)%和(20±2)%, 密度跃变最小值分别为(3±2)%和(8±3)%.比较图 7和图 8, GTA台接收函数Moho面震相比LZH台清晰, 震相附近干扰或其他震相叠加较少;两台站下方Moho面的速度跃变在对应不同滤波因子时都比较稳定, 在20%附近;GTA台下方Moho面密度跃变相对LZH台小, 但两个台站得到结果中Moho面密度跃变存在的不确定性相对较大.
5 讨论在第2节中我们根据理论计算对比了地表反射对接收函数幅度的影响.下面是考虑地表反射情况下实际资料的处理结果.选取震中距为70°, 对反射透射矩阵法和反射透射系数比值法得到的震相幅度进行比较(图 9a).两种计算方法得到的Ps(黑线)幅度完全重合, 吻合得较好;PpPs的幅度稍有差异(红线和蓝线), 当δρ变化小时幅度差异较小, 当δρ变化大时(超过20%)幅度差异较大.在本文处理结果中密度跃变总体较小, 可近似用反射透射系数比值法分析速度和密度跃变.
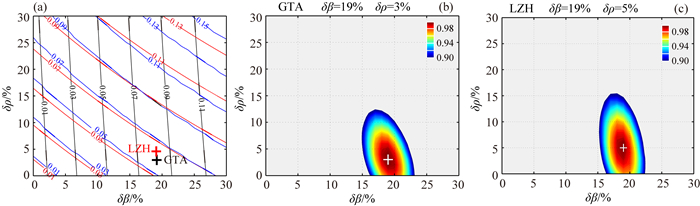
|
图 9 反射透射矩阵法和反射透射系数比值法对应的震相幅度及GTA台和LZH台Moho面速度和密度跃变 (a) Ps和PpPs幅度随速度和密度变化的数值, “+”为GTA台和LZH台下方Moho面速度和密度跃变最优值;(b—c)考虑地表反射等因素得到的GTA台和LZH台下方Moho面速度和密度跃变. Fig. 9 Constraining receiver function amplitudes with different methods and the results from δβ-δρ scan stacking for GTA and LZH stations (a) Contours of Ps and PpPs amplitudes changing with velocity and density; (b—c) Constraining S-wave velocity and density contrasts across the Moho below GTA and LZH stations considering surface reflection. |
为进一步考察地表反射影响, 我们利用反射透射矩阵法约束GTA台和LZH台下方Moho面的速度跃变和密度跃变.选取滤波窗(alp=1), 用相同的(δβ-δρ)扫描叠加方法对幅度的理论值(理论接收函数幅度由反射透射矩阵法计算)(Ma et al., 2012)和观测值作misfit(δβ, δρ), 得到各台站下方Moho面δβ和δρ(图 9b和9c).其结果与反射透射系数比值法得到的S波速度跃变和密度跃变比较, 两种方法GTA台和LZH台获得的S波速度跃变值(19±2)%和(20±2)%较接近, 密度跃变值(3±3)%和(5±3)%, 误差范围较大.
在处理观测资料时, 由于各种干扰或地下介质的物质属性不同, 接收函数幅度的观测值和理论值之间会存在差异.震相Pms的观测值和理论值基本吻合, 而多次波的幅度存在较多的不确定信息.由于一次波比多次波简单, 影响因素也较少, 所以提取的精度较高.多次波携带的信息复杂, 它与速度、密度跃变都有关.另外, P波和S波的衰减对多次波影响较大, 台站下方深部结构对多次波的干扰或叠加的可能性较大.界面的S波速度跃变只和一次转换波有关, 所以稳定性较好.
为了进一步分析结果的合理性, 以及震相(Pms、PmpPs和PmpSs+PmsPs)对界面速度和密度跃变的影响, 对misfit(δβ, δρ)中权重w进行了调整.针对GTA台和LZH台观测资料, 给定Pms和PmpPs震相(w1:w2:w3=0.6:0.4:0.0), 及给定Pms和PmpSs+PmsPs震相(w1:w2:w3=0.6:0.0:0.4), 所得结果如图 10(GTA)、图 11(LZH).比较两种震相组合所得到结果发现, 速度跃变基本不发生变化, 而密度跃变却发生较大的变化, 分析原因可能是密度跃变受多次波的影响, 而两个多次波对结果的影响差距较大.因此, 相比两个波形幅度约束速度和密度跃变模型, 由三个震相Pms、PmpPs和PmpSs+PmsPs幅度同时约束界面速度和密度跃变的精度较高.各个台站权重的选取应以前人的研究作为先验信息, 以提高结果的可靠性.但不同alp得出的速度和密度跃变还是存在微小的差别, 可能还受其他因素的影响.该方法所得密度跃变值的不确定性虽然相对较大, 但是至少提供了密度跃变值的重要信息, 是前人工作的进一步发展.
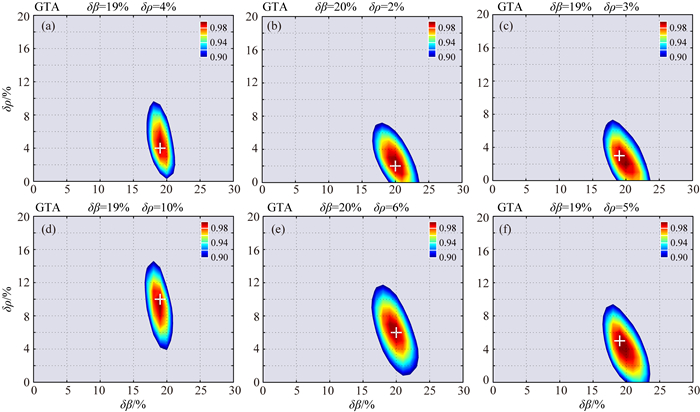
|
图 10 GTA台下方Moho面的速度和密度跃变 (a—c) Pms和PmpPs幅度确定的速度和密度跃变;(d—f) Pms和PmpSs+PmsPs幅度确定的速度和密度跃变. Fig. 10 Velocity and density contrasts across the Moho below GTA station (a—c) Velocity and density contrasts determined by Pms and PmpPs amplitudes; (d—f) Velocity and density contrasts determined by Pms and PmpSs+PmsPs amplitudes. |
|
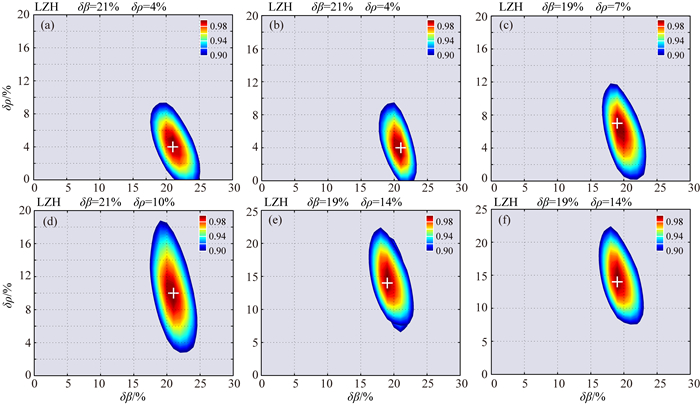
图 11 LZH台下方Moho面的速度和密度跃变 (a—c) Pms和PmpPs幅度确定的速度和密度跃变;(d—f) Pms和PmpSs+PmsPs幅度确定的速度和密度跃变. Fig. 11 Velocity and density contrasts across the Moho below LZH station (a—c) Velocity and density contrasts determined by Pms and PmpPs amplitudes; (d—f) Velocity and density contrasts determined by Pms and PmpSs+PmsPs amplitudes. |
从图 11a-11c中可以看出, 由震相Pms和PmpPs幅度确定出的密度跃变与图 11e-11f (Pms和PmpSs+PmsPs)得出的值存在较大差异, 这可能是由于PmpSs+PmsPs幅度观测值偏大造成的.产生这种现象的原因可能是在LZH台下方200 km左右存在一个低速层, 其一次波和Moho面PmpSs+PmsPs震相发生了叠加, 使其幅度观测值偏大.
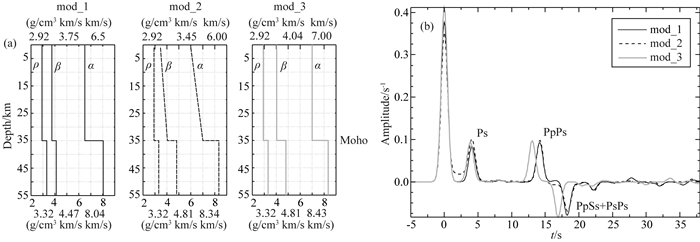
在本文以上的数值试验中, 都使用了速度相同的单层地壳模型考察速度、密度跃变对接收函数幅度的影响, 在处理实际资料中也是参考前人结果取地壳平均速度作为Moho面以上的速度.但是实际情况比单层模型要复杂许多, 如速度随着深度会逐渐增加.为了考察不同地壳速度结构对接收函数幅度的影响, 我们构建了如图 12a所示的三个不同地壳模型.模型1和模型3为速度不同的单层地壳模型, 模型2地壳速度随深度线性增加, 但其平均速度和模型1相同, 三个模型速度和密度跃变都相同.图 12b为三个模型所对应的理论接收函数.可看出模型1(黑实线)和模型2(黑虚线)的接收函数到时和幅度都吻合较好, 这说明接收函数幅度对于随深度线性变化的速度结构不敏感, 主要受速度和密度跃变的影响.另外, 模型1和模型3(灰实线)相比较, 在地壳平均速度差异较大的情况下, 接收函数震相到时差别较大, 而幅度变化较小, 这也表明接收函数幅度对界面上速度大小不是很敏感, 而对上下界面的速度和密度变化量敏感.这个数值试验也表明, 虽然实际地壳结构比简单一维模型复杂很多, 但是这种复杂速度结构对接收函数幅度影响较小, 主要影响接收函数幅度的因素还是速度和密度跃变.因此本文利用接收函数幅度约束速度和密度跃变的方法是可行的.
|
图 12 不同模型的接收函数 (a)速度模型, 三个模型在界面的速度跃变都取δα=23%;δβ=19%(其中δα和δβ分别为速度、密度跃变百分比, 和图 2对应), 模型一Moho上界面参数为:α=6.5 km·s-1, β=3.75 km·s-1, ρ=2.92 g·cm-3, 下界面的参数为:α=8.04 km·s-1, β=4.47 km·s-1, ρ=3.32 g·cm-3;模型二和模型三的界面参数详见图; (b)三个模型计算得到的接收函数结果, 其中Ps为一次波, PpPs和PpSs+PsPs为多次波. Fig. 12 Synthetic receiver functions for different models (a) Velocity model, the S wave velocity leap on Moho's upper interface is all the same, δα=23%, δβ=19%. The parameters of the upper interface in the first model are: α=6.5 km·s-1, β=3.75 km·s-1, ρ=2.92 g·cm-3, the parameters of the lower interface in the first model are: α=8.04 km·s-1, β=4.47 km·s-1, ρ=3.32 g·cm-3. The interface parameters of model two and model three are in this figure; (b) The results of receiver functions calculated by three models. PpPs and PpSs+PsPs are multiple waves. |
本文细致分析了界面速度跃变和密度跃变对接收函数幅度的影响;提出了用Pms、PmpPs和PmpSs+PmsPs三个震相来确定Moho面速度和密度跃变的δβ-δρ扫描叠加方法.由于一次波提取精度高, 计算得到的速度跃变较稳定可靠, GTA台和LZH台下方Moho面的速度跃变都在(19~20)%;由于多次波可能受到的干扰较多, 提取精度较低, 获得的密度跃变较复杂, 但可以据此估计密度跃变的参考值.GTA台观测资料与LZH台相比较精度较高, 可能是因台站周围环境较好、噪声少使得观测资料质量较高, 且多次波相对更为清晰、干扰较少, 所以速度、密度跃变比较稳定.
目前, 利用地震学信息确定Moho面速度和密度跃变的工作较少.本文的创新在于尝试用接收函数幅度确定Moho面速度和密度的跃变范围.该方法适用于波形清楚、干扰较少、接收函数一次波和多次波受其他震相干扰少的情形.在某些区域, 实际的地下结构可能非常复杂, 特别是当岩石圈中存在复杂结构时, 会对接收函数中Moho的多次波产生 较强干扰, 不能可靠稳定地提取到Moho对应震相的幅度信息, 此时无法利用本文的方法对Moho面速度和密度跃变进行约束, 这也是目前该方法存在的局限性.在未来的工作中将通过复杂模型的理论地震图数值试验对方法进行进一步的改进.
致谢地震波形观测资料由甘肃省地震台网中心提供, 中国地震台网中心的马延路博士提供了计算理论地震图和理论接收函数的程序, 资料分析中用了Lawrence Livermore实验室的SAC软件.两位审稿人对该稿件提出了建设性意见.在此一并表示感谢.
| Aki K, Richards P G. 2002. Quantitative Seismology. Sausalito: University Science Books: 146-202. | |
| Ammon C J. 1991. The isolation of receiver effects from teleseismic P waveforms. Bulletin of the Seismological Society of America, 81(6): 2504-2510. | |
| Ammon C J, Randall G E, Zandt G. 1990. On the nonuniqueness of receiver function inversions. Journal of Geophysical Research: Solid Earth, 95(B10): 15303-15318. DOI:10.1029/JB095iB10p15303 | |
| Crotwell H P, Owens T J, Ritsema J. 1999. The TauP toolkit: flexible seismic travel-time and ray-path utilities. Seismological Research Letters, 70(2): 154-160. DOI:10.1785/gssrl.70.2.154 | |
| Julià J. 2007. Constraining velocity and density contrasts across the crust-mantle boundary with receiver function amplitudes. Geophysical Journal International, 171(1): 286-301. DOI:10.1111/gji.2007.171.issue-1 | |
| Julià J, Ammon C J, Herrmann R B, et al. 2000. Joint inversion of receiver function and surface wave dispersion observations. Geophysical Journal International, 143(1): 99-112. DOI:10.1046/j.1365-246x.2000.00217.x | |
| Langston C A. 1979. Structure under Mount Rainier, Washington, inferred from teleseismic body waves. Journal of Geophysical Research-Atmospheres, 84(B9): 4749-4762. DOI:10.1029/JB084iB09p04749 | |
| Li C Q, Shen X Z, Qin M Z. 2014. The effect of P wave velocity on the H-k stacking results of receiver function. Acta Seismologica Sinica, 36(3): 480-490. DOI:10.3969/j.issn.0253-3782.2014.03.013 | |
| Ligorría J P, Ammon C J. 1999. Iterative deconvolution and receiver-function estimation. Bulletin of the Seismological Society of America, 89(5): 1395-1400. | |
| Ma Y L. 2013. YASEIS: Yet Another computer program to calculate synthetic SEIS mograms for a spherically multi-layered Earth model.//EGU General Assembly. Vienna, 15: 5596. | |
| Ma Y L, Wang R J, Zhou H L. 2012. A note on the equivalence of three major propagator algorithms for computational stability and efficiency. Earthquake Science, 25(1): 55-64. DOI:10.1007/s11589-012-0831-9 | |
| Ma Y L, Zhou H L. 2007. Crustal thicknesses and Poisson's ratios in China by joint analysis of teleseismic receiver functions and Rayleigh wave dispersion. Geophysical Research Letters, 34(12): L12304. DOI:10.1029/2007GL029848 | |
| Niu F L, James D E. 2002. Fine structure of the lowermost crust beneath the Kaapvaal craton and its implications for crustal formation and evolution. Earth and Planetary Science Letters, 200(1-2): 121-130. DOI:10.1016/S0012-821X(02)00584-8 | |
| Owens T J, Zandt G, Taylor S R. 1984. Seismic evidence for an ancient rift beneath the Cumberland Plateau, Tennessee: A detailed analysis of broadband teleseismic P waveforms. Journal of Geophysical Research: Solid Earth, 89(B9): 7783-7795. DOI:10.1029/JB089iB09p07783 | |
| Pan S Z, Niu F L. 2011. Large contrasts in crustal structure and composition between the Ordos Plateau and the NE Tibetan Plateau from receiver function analysis. Earth and Planetary Science Letters, 303(3-4): 291-298. DOI:10.1016/j.epsl.2011.01.007 | |
| Ramesh D S, King R, Yuan X. 2002. Receiver function analysis of the North American crust and upper mantle. Geophysical Journal International, 150(1): 91-108. DOI:10.1046/j.1365-246X.2002.01697.x | |
| Shen X Z, Liu M, Gao Y, et al. 2017. Lithospheric structure across the northeastern margin of the Tibetan Plateau: Implications for the plateau's lateral growth. Earth and Planetary Science Letters, 459: 80-92. DOI:10.1016/j.epsl.2017.11.027 | |
| Shen X Z, Mei X P, Zhang Y S. 2011. The crustal and upper-mantle structures beneath the northeastern margin of Tibet. Bulletin of the Seismological Society of America, 101(6): 2782-2795. DOI:10.1785/0120100112 | |
| Shen X Z, Yuan X H, Ren J S. 2015. Anisotropic low-velocity lower crust beneath the northeastern margin of Tibetan Plateau: Evidence for crustal channel flow. Geochemistry, Geophysics, Geosystems, 16(12): 4223-4236. DOI:10.1002/2015GC005952 | |
| Si S K, Tian X B, Zhang H S, et al. 2014. Multiple sinusoidal tapers method to estimate receiver function. Chinese Journal of Geophysics, 57(3): 789-799. DOI:10.6038/cjg20140309 | |
| Yuan X H, Ni J, Kind R, et al. 1997. Lithospheric and upper mantle structure of southern Tibet from a seismological passive source experiment. Journal of Geophysical Research: Solid Earth, 102(B12): 27491-27500. DOI:10.1029/97JB02379 | |
| Zhu L P, Kanamori H. 2000. Moho depth variation in southern in southern California from teleseismic receiver functions. Journal of Geophysical Research: Solid Earth, 105(B2): 2969-2980. DOI:10.1029/1999JB900322 | |
| 李翠芹, 沈旭章, 秦满忠. 2014. P波速度对接收函数H-k搜索叠加结果的影响分析. 地震学报, 36(3): 480–490. DOI:10.3969/j.issn.0253-3782.2014.03.013 | |
| 司少坤, 田小波, 张洪双, 等. 2014. 接收函数提取的多正弦窗方法. 地球物理学报, 57(3): 789–799. DOI:10.6038/cjg20140309 | |
 2017, Vol. 60
2017, Vol. 60


