2. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2. Function Laboratory of Marine Geo-Resource Evaluation and Exploration Technology, Qingdao National Laboratory for Marine Science and Technology, Shandong Qingdao 266071, China;
3. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
高信噪比的地震资料是地震高分辨率处理、解释、岩性参数反演及属性分析等诸项研究的前提和基础.因此如何提高地震数据的信噪比是地震数据处理中的一个重要环节.目前在实际地震资料处理中压制随机噪声的技术主要有f-k方法(Liu et al., 2012)、小波变换方法(刘洋等,2009;张一和成礼智, 2011)、离散余弦变换方法(陆文凯,2011)、基于结构中值滤波噪声衰减(王伟等,2012;Liu et al., 2006)和多项式拟合方法等(Lu et al., 2009;林红波等,2011).但随机噪声具有不确定性,仅存在统计特性(Liu et al., 2011).因此这些方法在低信噪比情况下压制随机噪声的同时会损失一部分有效信号或者产生假象,导致压制噪声后剖面的保真度降低.
经验模态分解(Huang,1996) 是近年发展起来的一种处理非线性非平稳信号的新方法,它是一种多尺度且自适应的分解算法.该算法从对地震资料的简单分析(Huang et al., 1998;Battista et al., 2007) 到地震波场的分离去噪(宋海斌等,2010;Ma et al., 2015)、以及地震属性分析(Wu and Huang, 2009;Mijovic et al., 2010),在地震勘探领域形成了一套独特的方法体系,并且在地震数据处理上有自适应的优势.传统EMD去噪(李月等,2013) 通常认为尺度小的前二个IMF分量是由高频随机噪声引起(尺度大的IMF分量为原始信号),将其直接舍掉,然后利用剩余的IMF重构原始信号;然而,EMD方法本身存在模态混叠,会导致分解出的IMF失真.不仅噪声压制不干净,并且在低频段部分,随机噪声的分量含有有效波的信息,使得噪声衰减后损失部分有效信号.
Hausdorff分数维(Nath and Dewangan, 2002) 的抗噪性具有很好的理论基础,根据分形理论(常旭和刘伊克,2002;De Michelis et al., 2015) 可知,地震记录中有效信号和噪声具有不同的维数,同时EMD变换可将地震记录分解成不同的尺度, 各尺度的地震包络具有很好的分形自相似性(朱卫星等,2011), 从广义分维的概念出发,计算出每一道地震记录的分数维(Gholamy et al., 2006),以求其瞬时分数维剖面(Huang et al., 2015),最后根据各采样点维数的差异压制噪声是可行的.
本文将EMD算法和分数维抗噪性相结合,提出一种新的地震资料随机噪声衰减方法.该方法首先通过EMD算法对地震信号进行多尺度分解,得到一系列不同分辨率的固有模态函数,对含有随机噪声的分量进行选择;然后应用Hausdorff分数维去识别噪声,对提取的含有噪声的IMF剖面做进一步的阈值处理;最后利用处理后的IMF分量重构信号,从而得到去噪后的剖面.该方法充分发挥了两者的优点,既较好地保留了信号的特征信息,且可靠性高、自适应能力强,也在更精细的尺度上对随机噪声进行压制.处理结果表明,本文方法能够有效压制地震信号中的随机噪声.
2 EMD方法和Hausdorff分数维计算原理 2.1 经验模态分解Huang(1996) 所介绍的EMD方法是一种处理非线性、非平稳信号的方法,它把信号分解为具有不同尺度的IMF分量,每个IMF分量代表一个振动模式,同时该算法对地震数据具有很好的自适应性.
对于给定的信号,首先找到信号的极大值和极小值,通过三次样条拟合对所有的极值点进行插值,从而求得信号的上下包络曲线Xmax(t)和Xmin(t);然后计算上包络和下包络曲线在每一个极值点上的平均值,从而获得平均值曲线m1(t).设分析信号为X(t),则
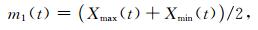
|
(1) |
再用X(t)减掉m1(t)得到h1(t),即
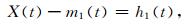
|
(2) |
对于不同的信号,h1(t)可能是一个IMF分量,也可能不是.通常来说,该分量并不完全满足IMF所需的条件,此时把h1(t)看作一个新的信号,重复上述步骤,即得:
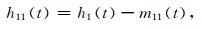
|
(3) |
式中,m11(t)是h1(t)的上、下包络线的均值.若h11(t)不是IMF分量,则继续上面的步骤,重复上面的方法k次,可以得到第k次循环的数据h1k(t):
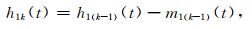
|
(4) |
h1k(t)满足筛选终止条件的要求,则h1k(t)为第一阶IMF,记为c1(t),即
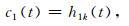
|
(5) |
从原信号中减去c1(t)得到剩余信号,即残差r1(t):
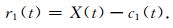
|
(6) |
这里,第一个被分离出来的固有模态函数,也是尺度最小的分量;然后,把r1(t)作为一个新的原序列,按照以上的步骤,依次提取出第二、第三、…、直至第n个固有模态函数;最后,得到的rn(t)是单调的函数,不能再被分解了.通过这样我们得到了原始序列X(t):
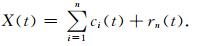
|
(7) |
EMD分解过程其实是一个“筛选”的过程,在消除模态波形叠加影响的情况下,有利于波形轮廓对称性.该分解方法从特征时间尺度来说,首先分离出来的是信号中特征尺度最小的固有模态分量;然后是特征时间尺度较大的固有模态分量;最后分离出来的是特征时间尺度最大的固有模态分量,因此我们可以把EMD方法看成是一个高通滤波器(贾瑞生等,2015),能对复杂的波场进行分离处理.同时这种EMD分解方法是自适应的.为应用EMD算法分离去噪提供了理论可行性.
2.2 Hausdorff维数的计算方法Hausdorff维数的计算方法原理如下:在给定的时窗内(地震信号序列上一定数量的采样点个数),运用结合法(Hybird Method)的“步长”R(Liao et al., 2010),来近似求取所在时窗内的地震时间序列的长度.也就是说计算得到的曲线长度为步数与步长的乘积;然后变换步长R的大小,又可以求出该时窗内的曲线长度L.通过一系列的步长R,我们可以求出该时窗内一系列相对应的曲线长度L,根据上述的地震时间序列分形模式,就有如下关系式:
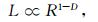
|
(8) |
其中L为时窗内的曲线长度,R为步长,D为分数维.我们根据一系列的步长曲线长度,通过最小二乘法等方法可以拟合出一条直线(M-R曲线),其斜率K与分数维的关系是
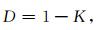
|
(9) |
其中,
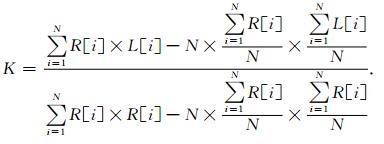
|
(10) |
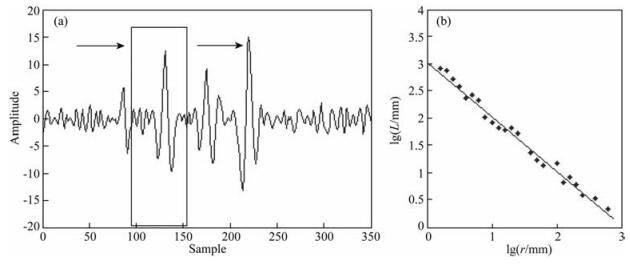
式中,R[i]为时窗内变化步长(取其对数)所得到的一系列值,L[i]为时窗内对应步长计算所得到的曲线长度(取其对数).求解得到斜率K,就能得到该时窗内的Hausdorff维数,经过试验我们将其维数值放在时窗内中间采样点位置.继续移动工作窗的位置,每次移动一个采样(如图 1a所示),以此类推,可以求取整条地震道曲线的瞬时分数维维数曲线.M-R曲线(如图 1b所示)的斜率小于等于零,因此,根据分数维的变换特征判别地震波的初至走时,地震记录的维数被定义在1和2之间.上述过程如图 1所示(常旭,2002).在分数维计算的过程中,分数维是频率、振幅及波长的综合特征体现(Srivastava and Sen, 2009),利用EMD分解将地震记录分解成不同尺度的IMF分量,这些分量的地震包络具有很好的分形自相似性, 使得噪声与有效波的综合特征在特定的IMF分量上存在区别, 故此种方法在噪声识别方面有一定优势.
|
图 1 分数维的求取过程(常旭,2002) Fig. 1 Process of resolving fractal dimensions (Chang, 2002) |
假设含噪信号d由无噪信号s和噪声信号n组成,首先应用EMD算法,将目标信号分解得到不同特征的IMF分量,其中包括含有部分噪声的信号sn,有效信号
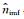
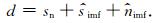
|
(11) |
我们可以利用IMF分量具有很好分形自相似性的特点,通过公式(10) 对含有噪声的部分进行Hausdorff维数计算,得到信号的瞬时分数维值k(sn).基于有效波和噪声的分数维差异,进行相应的阈值处理,则含有噪声的sn可分解为:
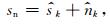
|
(12) |
式中,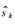
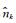
最后对两部分的有效信号进行重构,得到压制噪声后的有效信号:
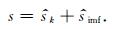
|
(13) |
EMD分解为地震资料随机噪声压制提供了理论基础,去噪过程实质是一个波场分离的过程,从(7) 式中可知,整个地震数据可分解成不同分辨率的信号,随机噪声成分一定存在于有限个的IMF分量中.由于与有效波频带接近部分存在模态混叠比较严重的情况,导致某些有效波IMF分量存在噪声成分.因此达不到理想的去噪效果.而Hausdorff维数正好充分利用了固有模态函数IMF对瞬时维数的适应性,以及对噪声的识别能力.在EMD分解的基础上,IMF分量满足分形理论的自相似性.因此对含有噪声的IMF分量进行相应的维数阈值滤波处理.重构信号后即得到最终的去噪结果.
EMD与Hausdorff维数联合去噪算法步骤如下:
(1) 应用EMD将目标信号分解为IMF集,分析其频谱.由于大部分随机噪声表现为高频噪声,因此IMF集可分为三类:第一类为较大尺度的只含有有效波成分的IMF分量;第二类为较小尺度的噪声部分;第三类为同时含有有效波和随机噪声的IMF分量.接下来针对第三类IMF分量进行维数滤波处理.
(2) 通过仿真信号实验对Hausdorff瞬时维数进行抗噪性分析.得出有效波和随机噪声的维数差异.然后针对第三类IMF分量应用Hausdorff维数算法进行处理,选取合适的时窗大小、初始步长以及递增量,计算出每个分量Hausdorff瞬时维数.总体来说,时窗大小通常要小于信号周期,一般要小于其周期的一半,才能够较为精细地显示维数差异,初始步长的选取一般为时窗大小的十分之一较为合适;而步长递增量的选取比较开放,最大可以达到时窗大小的两倍(李信富等,2007).
(3) 根据仿真信号实验结果,随机噪声维数基本在1~1.05之间,而有效波的维数要大于1.05且小于2,此外,为了增大有效波和噪声的维数差异,我们会对数据的振幅做加强处理.因此在第一步的基础上,基于随机噪声和有效信号的维数差异,将每个IMF分量上分数维值小于等于1.05的采样点提取出来,从而分离出残留的噪声.实际数据中为了排除其他噪声对维数的影响,需要先对数据进行相应的预处理.
(4) 利用经过维数滤波处理的IMF分量和第一次选择后的有效波IMF分量进行重构,即可得到去噪后的结果.
3 仿真信号实验为了验证EMD分解和Hausdorff维数联合去噪算法的有效性,同时为了充分反映该方法分离信号和噪声的能力, 首先选择不同噪声水平的模拟数据对有效波和随机噪声分数维差异进行测试.
下面选取模拟地震数据道的部分数据段进行试验,对其分别加20%、60%的随机噪声,并对加噪数据计算其瞬时分数维.通过测试,选取时窗为20个采样点,初始步长为三倍的平均距离,递增量为五倍的平均距离比较适合.
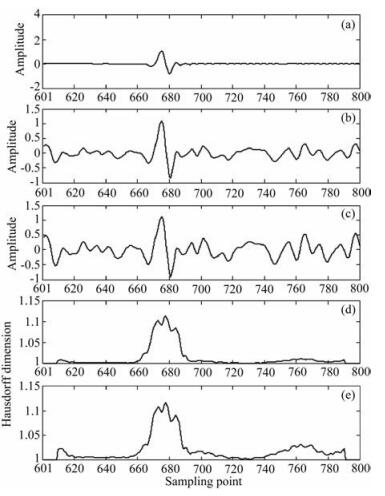
通过上述加噪处理,有效信号到达之前是随机噪声的成分,这个阶段,其分数维值很低,接近于1;当有效信号出现后,即有效信号混叠有随机噪声,分数维值突然增大.从图 2来看,我们分别加入20%和60%的噪声,有效信号部分和随机噪声部分的维数值有非常明显的差别,但噪声的大小对维数影响极小.从而可以说明,Hausdorff瞬时维数的抗噪性较好,因此通过Hausdorff瞬时维数可以有效地识别出噪声和有效波.
|
图 2 Hausdorff瞬时维数计算结果 (a)原始地震道数据;(b)加20%的噪声;(c)加20%噪声的Hausdorff瞬时维数;(d)加60%的噪声; (e)加60%噪声的Hausdorff瞬时维数. Fig. 2 Calculation results of Hausdorff instantaneous dimensions (a) Original seismic trace data; (b) Data with 20% noise added; (c) Hausdorff instantaneous dimension with 20% noise; (d) Data with 60% noise added; (e) Hausdorff instantaneous dimension with 60% noise added. |
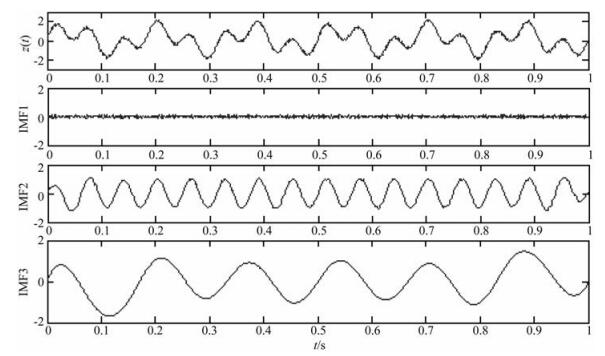
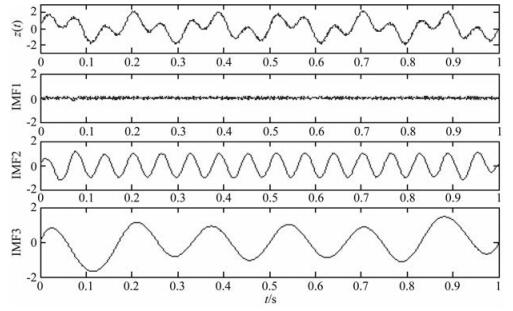
接下来对由简单信号合成的复杂信号进行EMD和分数维联合分解,同时和单独进行EMD分解进行比较.合成信号z(t)由x(t)=sin(12×π×t),y(t)= sin(32×π×t),noise=0.2×rand(1, 1000) 组成.分解结果如图 3和图 4所示.从图中可以看出,两种方法对多尺度信号z(t)中的三个分量都能比较清晰地分解出来,而且分解得到的IMF分量是按频率尺度从高到低依次分解出的.但是从二种方法分解得到的IMF2分量上看,基于分数维约束的方法得到的分量更干净,每个分量的波形更平滑.传统的EMD方法因为本身算法的缺陷导致模态混叠问题的存在,在IMF2分量上存在随机噪声的信息,波形呈现出锯齿状.结果表明,利用EMD分解和Hausdorff瞬时维数联合分解去噪,可以有效地对信号进行分离,从而验证了该方法的理论可行性.
|
图 3 传统的EMD方法分解结果 Fig. 3 Decomposition results by the traditional EMD method |
|
图 4 传统EMD方法和分数维联合分解结果 Fig. 4 Joint decomposition results by the traditional EMD method and fractal dimension |
为了进一步探讨该方法在地震资料处理中的应用,首先对理论模型进行去噪实验.本文选取主频为20 Hz的Ricker子波,采用射线追踪方法构建一个含有道数为256道,每道512个采样点的含有断层的复杂结构合成地震数据,并在记录中加入随机噪声,然后分别用EMD分解算法和基于EMD的分数维算法进行去噪处理.
图 5a是模拟的地震记录,图 5b为加入随机噪声的地震剖面.对比图 5a和图 5b可见,加入噪声后的记录信噪比降低,断点不清晰,层的信息变得模糊,地下真实层位的信息被随机噪声掩盖了.

|
图 5 传统EMD方法去噪和联合去噪对比结果 (a)模型地震数据;(b)加噪声后的数据;(c)传统EMD去噪后的数据;(d)传统EMD去噪后的噪声部分;(e)联合去噪后的数据;(f)联合去噪后的噪声部分. Fig. 5 Comparison of results by conventional EMD denoising and joint denoising a) Seismic data of model; (b) Data with noise added; (c) Data after denoising by conventional EMD; (d) Noise section after denoising by conventional EMD; (e) Data after joint denoising; (f) Noise section after joint denoising. |
我们首先对加噪的地震记录进行EMD分解,得到不同的IMF分量的记录,经过数据的分析重构分别得到去随机噪声后的剖面和噪声剖面,如图 5c和图 5d所示,从图中能清楚地看到,压制随机噪声后的剖面还存在比较强的随机噪声;对含有噪声的剖面做进一步的分数维分析,从仿真数据的分析来看,模型数据与抗噪性实验所用数据相似.因此选取同样的时窗和步长进行计算.随机噪声的分数维值基本分布在1附近,我们基于有效波和噪声的分数维差别,进行相应的阈值处理,得到最终压制随机噪声的地震记录,如图 5e所示.图 5f是去除的随机噪声.对比图 5c和图 5e可见,基于EMD的分数维算法压制随机噪声的效果优于单纯的EMD算法压制效果,图中断层构造得到恢复,信噪比有了提高;此外,对比噪声部分图 5d和图 5f,传统方法压制后的噪声成分含有少量的有效波,而本文方法却很好地对有效波进行了保护.因此本文的联合算法更加完善.同时能够消除EMD算法模态混叠的问题.
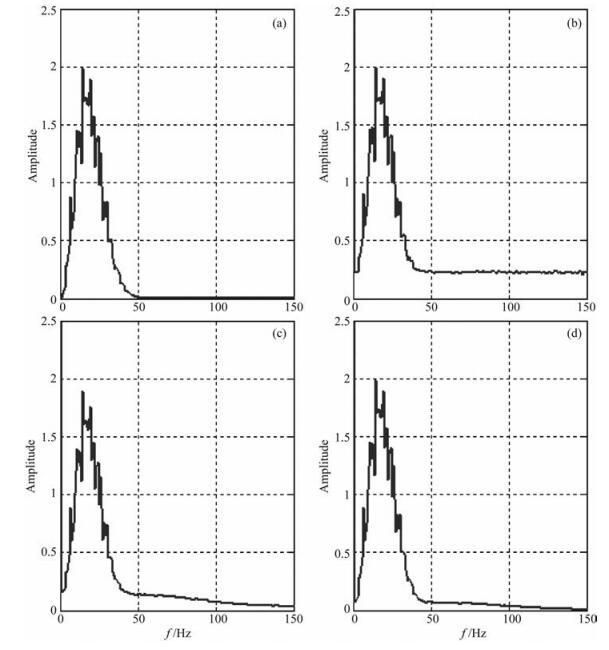
为了更加准确地反映两种方法的差异,我们对加噪数据和去噪后的数据进行频谱分析,得到图 6所示的频谱图,图 6a是原始模型数据的频谱图,图 6b是加随机噪声后的频谱图,从图中可以看出形态有较大的改变.图 6c是传统的EMD方法去噪的结果,图 6d是EMD和分数维联合压制噪声的结果.对于传统的EMD方法,当随机噪声处在其与有效波频率不交叉的范围内时,噪声可以得到较好的衰减,但对于与有效波重合的地带,噪声衰减达不到理想的效果.而且从频谱的形态来看,有效波的成分也受到了一些损伤.这是由算法本身分解过程中存在模态混叠和边际效应所引起的.而本文研究的基于EMD的分数维去噪方法,既利用了EMD分解的自适应的特点,也基于噪声和有效波分数维差异进行更加精确的噪声压制.从图 6c可以看出,频谱形状与原来基本一致,有效的反射信号没有损失,且噪声得到更好的压制,因此更加有利于对地震资料进行高分辨率处理.同时验证了该方法在地震去噪方面的可行性.
|
图 6 两种方法的频谱分析对比 (a)模型数据的频谱;(b)加噪后数据的频谱;(c)传统EMD方法去噪后的频谱;(d)联合去噪后的频谱. Fig. 6 Comparison of spectra between the two methods (a) Spectrum of model data; (b) Spectrum of data with noise added; (c) Spectrum of data after denoising by the conventional EMD; (d) Spectrum of data after joint denoising. |
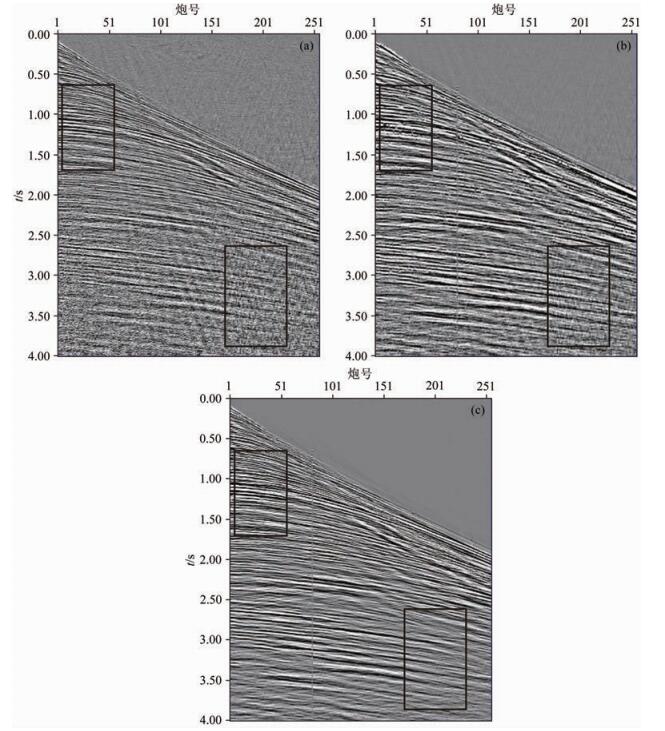
为了充分验证基于EMD的分数维去噪方法在实际地震资料中的应用效果,本文选取了某海域的二维地震资料进行算法测试,对资料的叠前和叠后数据进行噪声衰减处理,并与传统EMD分解算法处理效果进行对比.图 7a是原始的单炮记录.首先利用EMD自适应分解方法对整个原始剖面数据进行分频处理,得到不同尺度的IMF剖面,这里由于实际数据的信噪比相对较低,EMD分解过程中会有比较严重的端点效应,因此采用镜像延拓(李月等,2013) 方法对边界进行处理,分析其信噪比的大小,对含有随机噪声的信噪比相对较低的分量挑选处理,并分别进行更严格的阈值处理,分离出随机噪声,通过数据重构得到传统EMD方法压制随机噪声的结果,如图 7b所示.本文方法是在EMD分解后的IMF分量基础上做分数维的计算,通过有效信号与随机噪声的维数差异对噪声进行识别.由于实际数据波场复杂,为避免其他位置的数据影响,在计算过程中基本采用二个层位段的时窗大小;同时为了增大维数的差异,对振幅进行加强处理;再通过相应的维数阈值处理,对选择的IMF分量进行滤波压制,重构两部分的有效数据得到去噪后的剖面,如图 7c所示.
|
图 7 叠前地震数据传统EMD方法和联合去噪结果对比 (a)原始叠前地震数据;(b)传统EMD方法去噪结果;(c)联合去噪后结果. Fig. 7 Comparison of denoising results by traditional methods and joint denoising on prestack seismic data (a) Original prestack seismic data; (b) Traditional EMD denoising; (c) Joint denoising. |
对比单炮处理结果,两种方法均可实现随机噪声的有效压制,有效信号的同相轴得到呈现,但传统的EMD方法去噪的结果会伤害有效波的成分,同相轴出现畸变(如图 7矩形框所示),同时会残留少量的随机干扰.而本文的方法在压制随机噪声的时候,能很好对有效信号进行保护.
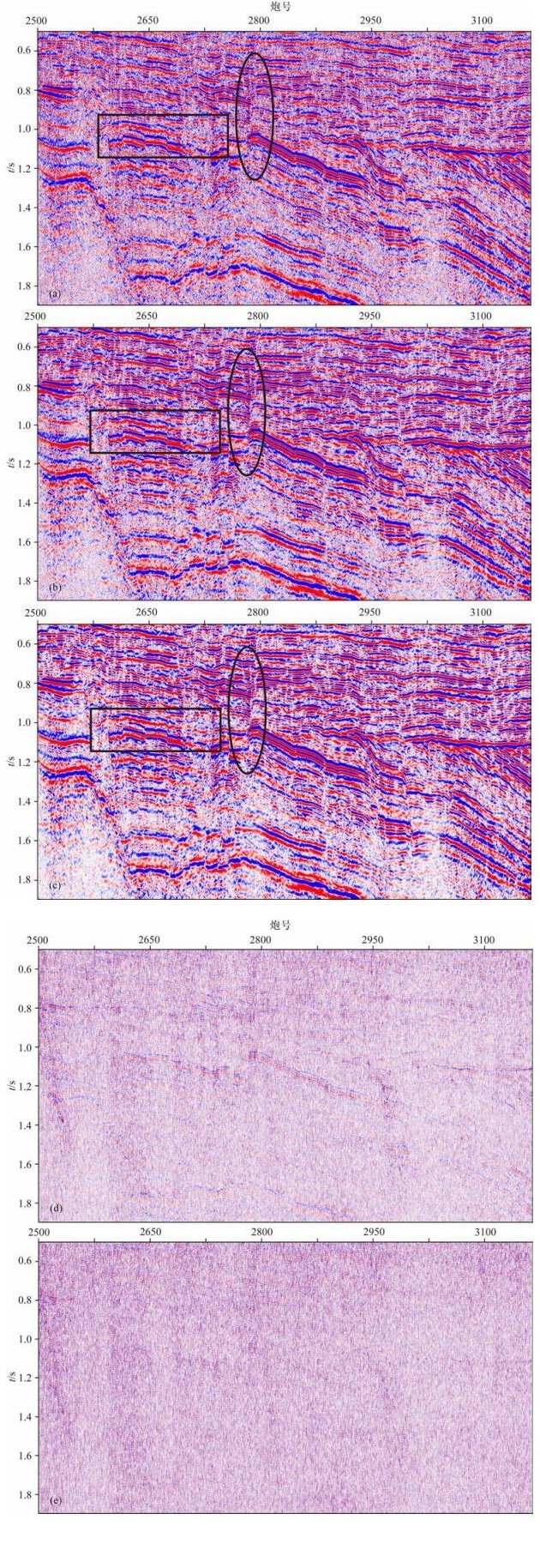
图 8a是原始的地震叠加数据.该区有较强的随机噪声,剖面信噪比较低,断点位置不够清晰,小断层不易识别,同时噪声使得同相轴的连续性受到一定程度的破坏,在某些部位有杂乱反射区域,不利于横向的追踪.分别应用基于EMD的分数维压制方法和传统的EMD方法对比处理,得到结果如图 8b和图 8c,两种方法原始剖面中的随机噪声均得到了一定压制,剖面信噪比也得到明显提高.但本文的方法比传统的EMD去噪方法处理后同相轴变得更加清晰,连续性有了明显增强,断点位置、波组特征更加清楚(如图 8方形黑框所示区域),次级断层更加清晰(如图 8椭圆黑框所示区域);同时相对能量较弱的层位也有了体现,一些大角度的相干噪声也得到相应压制,杂乱反射区的信息也得到恢复,使得剖面质量得到了全面提高.图 8d和图 8f分别是两种方法压制噪声后的残差,从图中对比可以看出,传统的EMD方法由于其算法有模态混叠的缺陷,使得某些部分的有效信息有所伤害,去除的噪声剖面中混有有效波的成分.而本文的方法刚好能弥补传统EMD方法的不足,使得整个处理过程中能保持有效波的完整性.
|
图 8 叠后地震数据传统EMD方法和联合去噪结果对比 (a)原始地震数据;(b)传统EMD方法去噪结果:(c)联合去噪后结果;(d)传统EMD方法去噪后残差;(e)联合去噪后残差. Fig. 8 Comparison of denoising results by traditional methods and joint denoising on stacked seismic data (a) Original seismic data; (b) Traditional EMD denoising; (c) Joint denoising; (d) Residuals after traditional EMD method denoising; (e) Residual after joint denoising. |
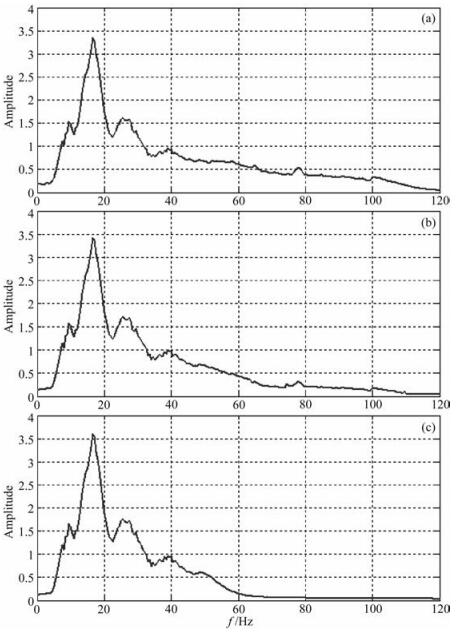
对比原始地震数据和两种滤波方法的处理结果,对其进行频谱分析,图 9a、9b、9c分别是对应方法处理前后的振幅谱.从图中可见,两种压噪方法高频处的随机噪声幅度均低于处理前,而且频谱的主要结构特征没有被破坏.然而基于EMD的分数维滤波算法,在随机噪声压制方面更加彻底,不仅表现在高频范围内,深部的低频部分的随机噪声也得到相应的衰减;同时压制后的频谱上的振幅在不同频段都有一定的提升,表明噪声压制后,整个剖面的信噪比得到了提高.以上结果表明,本文的联合算法与传统的EMD算法相比,能更加有效地压制随机噪声,同时保持有效频带的信息不被损失.
|
图 9 两种方法压制噪声后频谱对比结果 (a)原始叠后数据频谱;(b)传统EMD方法去噪后数据频谱;(c)联合去噪后数据频谱. Fig. 9 Comparison of spectra between the two methods (a) Spectrum of the original data; (b) Spectrum of data after conventional EMD denoising; (c) Spectrum of data after joint denoising. |
本文将EMD分解算法和Hausdorff维数计算方法相结合,既能充分利用两种方法的优势,同时又能针对彼此方法的缺陷起到改进的作用.对于EMD算法,其本身对非平稳地震信号有自适应分解特点,能得到不同尺度属性的IMF分量,但由于其模态混叠的问题,使得滤波分解过程不是很严格.而Hausdorff维数的约束很好地解决了这个问题.对于Hausdorff瞬时维数的计算,EMD分解得到的IMF分量,使得各个尺度的地震包络具有很好的分形自相似性, 有利于计算的准确性.因此本文提出一种新的基于EMD的分数维地震随机噪声衰减方法.通过对仿真信号、模拟地震数据和实际地震数据的实验,表明了本文方法的可行性,并且是有效的.同时,通过与传统EMD方法压制噪声结果的对比可见,本文的方法去噪效果更好,并能保持有效波信息的完整性.
| Battista B M, Knapp C, McGee T, et al. 2007. Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data. Geophysics, 72(2): H29-H37. DOI:10.1190/1.2437700 | |
| Chang X, Liu Y K. 2002. The generalized fractal dimension of seismic records and its applications. Chinese Journal of Geophysics (in Chinese), 45(6): 839-846. | |
| De Michelis P, Consolini G, Tozzi R. 2015. Magnetic field features fluctuation at Swarm's altitude:a fractal approach. Geophysics Research Letters, 42(9): 3100-3105. DOI:10.1002/2015GL063603 | |
| Gholamy S, Javaherian A, Ghods A. 2006. Automatic detection of wavelets interfering in seismic sections using fractal methods.//Proceedings of the 8th SEGJ International Symposium. Kyoto, Japan, 1-4. | |
| Huang N E. 1996. Computer implemented empirical mode decomposition method, apparatus, and article of manufacture. United States Patent 5983162. 1999-11-09. | |
| Huang N E, Zheng S, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 | |
| Huang Y P, Geng J H, Guo T L. 2015. New seismic attribute:fractal scaling exponent based on gray detrended fluctuation analysis. Applied Geophysics, 12(3): 343-352. DOI:10.1007/s11770-015-0509-x | |
| Jia R S, Zhao T B, Sun H M, et al. 2015. Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis. Chinese Journal of Geophysics, 58(3): 1013-1023. DOI:10.6038/cjg20150326 | |
| Li X F, Li X F, Wu Y. 2007. Fractal theory in seismology application. Progress in Geophysics, 22(2): 411-417. DOI:10.3969/j.issn.1004-2903.2007.02.011 | |
| Li Y, Peng J L, Ma H T, et al. 2013. Study of the influence of transition IMF on EMD do-noising and the improved algorithm. Chinese Journal of Geophysics, 56(2): 626-634. DOI:10.6.38/cjg20130226 | |
| Liao B Y, Chen C C, Sheu T W. 2010. Using a fractal analysis and polarization method for phase identification in three-component seismograms. Terrestrial Atmospheric and Oceanic Sciences, 21(5): 791-805. DOI:10.3319/TAO.2010.01.28.01(T) | |
| Lin H B, Li Y, Xu X C. 2011. Segmenting time-frequency peak Filtering method to attenuation of seismic random noise. Chinese Journal of Geophysics, 54(5): 1358-1366. DOI:10.3969/j.issn.0001-5733.2011.05.025 | |
| Liu C, Liu Y, Yang B J, et al. 2006. A 2D multistage median filter to reduce the random seismic noise. Geophysics, 71(5): V105-V110. DOI:10.1190/1.2236003 | |
| Liu C C, Chen X H, Du J, et al. 2012. Random noise attenuation using f-x regularized nonstationary auto regression. Geophysics, 77(2): V61-V69. DOI:10.1190/geo2011-0117.1 | |
| Liu G C, Chen X H, Li J Y, et al. 2011. Seismic noise attenuation using nonstationary polynomial fitting. Applied Geophysics, 8(1): 18-26. DOI:10.1007/s11770-010-0244-2 | |
| Liu S, Han L G. 2014. Study of seismic spectrum decomposition based on CEEMD. Global Geology, 17(2): 120-126. | |
| Liu Y, Fomel S, Liu C, et al. 2009. High-order seislet transform and its application of random noise attenuation. Chinese Journal of Geophysics, 52(8): 2142-2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 | |
| Lu W K. 2011. Seismic random noise suppression based on the discrete cosine transform. Oil Geophysical Prospecting, 46(2): 202-206. | |
| Lu Y H, Lu W K. 2009. Edge-preserving polynomial fitting method to suppress the random seismic noise. Geophysics, 74(4): V69-V73. DOI:10.1190/1.3129907 | |
| Ma Y Y, Li G F, Wang Y J, et al. 2015. Random noise attenuation by f-x spatial projection-based complex empirical mode decomposition predictive filtering. Applied Geophysics, 12(1): 47-54. DOI:10.1007/s11770-015-0467-3 | |
| Mijovic B, De Vos M, Gligorijevic I, et al. 2010. Source separation from single-channel recordings by combining empirical-mode decomposition and independent component analysis. IEEE Transactions on Biomedical Engineering, 57(9): 2188-2196. DOI:10.1109/TBME.2010.2051440 | |
| Nath S K, Dewangan P. 2002. Detection of seismic reflections from seismic attributes through fractal analysis. Geophysical Prospecting, 50(3): 341-360. DOI:10.1046/j.1365-2478.2002.00323.x | |
| Song H B, Bai Y, Dong C Z, et al. 2010. A preliminary study of application of empirical mode decomposition method in understanding the features of internal waves in the northeastern South Chinese Sea. Chinese Journal of Geophysics, 53(2): 393-400. DOI:10.3969/j.issn.0001-5733.2010.02.017 | |
| Srivastava R P, Sen M K. 2009. Fractal-based stochastic inversion of poststack seismic) data using very fast simulated annealing. Journal of Geophysics and Engineering, 6(4): 412-425. DOI:10.1088/1742-2132/6/4/009 | |
| Wang W, Gao J H, Chen W C, et al. 2012. Random seismic noise suppression via structure-the adaptive median filter. Chinese Journal of Geophysics, 55(5): 1732-1741. DOI:10.6038/j.issn.0001-5733.2012.05.030 | |
| Wu Z H, Huang N E. 2009. Ensemble empirical mode decomposition:a noise-assisted data analysis method. Advances in Adaptive Data Analysis, 1(1): 1-41. DOI:10.1142/S1793536909000047 | |
| Zhang Y, Cheng L Z. 2011. A new wavelet denoising method of seismic signals based on a recursive optimal thresholding. Acta Scientiarum Naturalium Universitatis Nankaiensis, 44(4): 67-71. | |
| Zhu W X, Yang S H, Xu W H, et al. 2011. The oil prediction algorithm based on the method of combining multi decomposition theory of wavelet transforms and amplitude spectrum fractal dimension. Progress in Geophysics, 26(5): 1748-1754. DOI:10.3969/j.issn.1004-2903.2011.05.029 | |
| 常旭, 刘伊克. 2002. 地震记录的广义分维及其应用. 地球物理学报, 45(6): 839–846. | |
| 贾瑞生, 赵同彬, 孙红梅, 等. 2015. 基于经验模态分解及独立成分分析的微震信号降噪方法. 地球物理学报, 58(3): 1013–1023. DOI:10.6038/cjg20150326 | |
| 李信富, 李小凡, 武晔. 2007. 分形理论在地震学中的应用研究. 地球物理学进展, 22(2): 411–417. DOI:10.3969/j.issn.1004-2903.2007.02.011 | |
| 李月, 彭蛟龙, 马海涛, 等. 2013. 过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法. 地球物理学报, 56(2): 626–634. DOI:10.6.38/cjg20130226 | |
| 林红波, 李月, 徐学纯. 2011. 压制地震勘探随机噪声的分段时频峰值滤波方法. 地球物理学报, 54(5): 1358–1366. DOI:10.3969/j.issn.0001-5733.2011.05.025 | |
| 刘洋, FomelS, 刘财, 等. 2009. 高阶seislet变换及其在随机噪声消除中的应用. 地球物理学报, 52(8): 2142–2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 | |
| 陆文凯. 2011. 基于离散余弦变换的地震随机噪声压制技术. 石油地球物理勘探, 46(2): 202–206. | |
| 宋海斌, 拜阳, 董崇志, 等. 2010. 南海东北部内波特征——经验模态分解方法应用初探. 地球物理学报, 53(2): 393–400. DOI:10.3969/j.issn.0001-5733.2010.02.017 | |
| 王伟, 高静怀, 陈文超, 等. 2012. 基于结构自适应中值滤波器的随机噪声衰减方法. 地球物理学报, 55(5): 1732–1741. DOI:10.6038/j.issn.0001-5733.2012.05.030 | |
| 张一, 成礼智. 2011. 一种基于递归最优阈值选择算法的小波地震信号的去噪方法. 南开大学学报(自然科学版), 44(4): 67–71. | |
| 朱卫星, 杨少虎, 徐文会, 等. 2011. 小波多尺度分解的振幅谱分维算法油气预测. 地球物理学进展, 26(5): 1748–1754. DOI:10.3969/j.issn.1004-2903.2011.05.029 | |
 2017, Vol. 60
2017, Vol. 60


