2. 黑龙江省普通高校科技创新团队"断层变形、封闭性及流体运移", 黑龙江大庆 163318
2. Science and Technology Innovation Team on Fault Deformation, Sealing and Fluid Migration, Heilongjiang Daqing 163318, China
叠前逆时偏移方法最早由Whitmore(1983)在SEG年会上提出,随后,Baysal等(1983)、Loewenthal和Mufti(1983)和McMechan(1983)将其运用到纵波资料的叠后偏移.该方法基于双程波动方程理论,对地震波的近似较少,理论上可对多种波场(一次反射波、多次波、棱柱波等)准确成像,而且无成像倾角限制.与单分量地震资料相比,多波多分量地震资料含有更为丰富的波场信息,对其进行弹性波逆时偏移(ERTM)能够形成多波成像数据,提供更为精确的地下构造信息,从而减少纵波勘探的盲区(Du et al., 2012;Duan and Sava, 2015;Gu et al., 2015).弹性波叠前逆时偏移是一种以矢量波理论为基础的深度域偏移方法,考虑了地震波在地下传播过程中的耦合特征,能够形成具有明确物理意义的成像剖面.近年来,随着计算机硬件技术的发展,以及GPU在油气勘探领域的成功应用(刘国峰等,2009;李博等,2010;刘红伟等,2010),地震成像的计算成本得以大幅度降低,具有矢量特征的多波多分量地震数据的弹性波逆时偏移成像也在油气勘探中彰显了更大的研究潜力和发展前景.
弹性波逆时偏移最初是由Sun和McMechan(1986)提出,随后Chang和McMechan(1987, 1994)利用激发时间成像条件实现了2D和3D的弹性波逆时偏移,但是,成像结果均受纵横波串扰(crosstalk)的影响,且物理意义不明确,只能用来描述构造,无法进行后续的解释.Yan和Sava(2008)提出把震源波场和检波点波场用旋度和散度算子分离为纵波和横波波场,然后再对分离的波场进行互相关成像,这种方法不仅保留了弹性波波场的矢量特征,也更加符合地震波在地下介质中的传播规律,避免了多分量之间成像所引发的多波串扰,使成像结果更具明确的物理意义.类似于声波逆时偏移,弹性波逆时偏移在互相关成像时,也需要传播时间相同但传播方向相反的震源波场和检波点波场.目前,有四种方法处理震源波场和检波点波场的不同传播方向问题:一是全波场存储,即完全保存震源或检波点在每个时刻的波场;二是检查点(checkpointing)存储(Symes,2007);三是随机边界存储(Clapp,2009);四是边界存储(Feng and Wang, 2012;王保利等,2012).全波场存储要求巨大的存储资源,在实际中不是可行方法.为了减低重算比,检查点存储方法也必须存储许多中间时刻波场.随机边界方法无需额外存储波场,但会在偏移结果中引入随机噪声,而且计算量也增加近乎1倍.上述的边界存储方法主要是针对声波方程逆时偏移开展的研究.与此同时,专家们也一直积极地寻求非互相关成像条件的逆时偏移成像方法,以降低数据存储空间,如激发振幅成像条件(Nguyen and McMechan, 2013,2015;Wang and McMechan, 2015;Wang et al., 2016),多激发时间成像条件(Jin et al., 2015),稀疏互相关成像条件(Nguyen and McMechan, 2015)等,实际上这些成像条件都是互相关成像条件的特殊情况(Chattopadhyay and McMechan, 2008).
对旋度和散度算子分离矢量波场的弹性波逆时偏移方法,其转换波成像受极性反转影响(Du et al., 2012;Duan and Sava, 2015;Gu et al., 2015;Li et al., 2016),当完成互相关成像的多炮数据叠加后,偏移结果不实.Du等(2012)利用震源波场和检波点波场的方向矢量计算出符号因子,进一步利用符号因子对PS和SP成像数据进行校正.代替使用检波点波场的方向矢量信息,Duan和Sava(2015)利用纵横波传播方向与界面法线方向关系,校正了PS和SP成像极性反转问题.Li等(2016)提出利用弹性波解耦方程组的极化方向矢量计算符号因子,进而校正PS和SP成像的极性.上述三种极性校正方法均在炮域完成,也有更为直接的在角度域完成的校正方法(Rosales and Rickett, 2001;Rosales et al., 2008),角度域方法相对准确,但是计算量较大.
本文在前人研究工作的基础上,针对各向同性介质的弹性波逆时偏移成像开展研究,利用散度、旋度算子将矢量波场分离为纵波和横波波场,纯波的互相关成像大大降低纵横波成像串扰.详细分析了分离的横波在纵波垂直入射位置两侧发生极性反转,从而导致转换波成像极性反转,由此提出一种在共炮域估算入射角度的极性校正方法.将降低存储成本的震源波场逆时重建策略用于弹性波逆时偏移成像中,利用少量弹性参数做震源波场重建,为弹性波逆时偏移的进一步实用化研究提供可选方案.
2 方法原理 2.1 波场分离的弹性波逆时偏移基于波场分离的弹性波逆时偏移包括三个步骤:(1) 构建震源波场和检波点波场;(2) 分离矢量波场;(3) 应用互相关成像条件.本文基于震源波场重建的弹性波逆时偏移算法流程如图 1所示,它包括震源波场的正传并保存R层边界内速度波场值(R为空间差分阶数的一半);利用边界内存储的波场和最后时刻所有弹性参数波场反传重建震源波场;在震源波场重建的同时,反传检波点波场;在相同时刻,利用Helmholtz分离震源和检波点矢量波场;对PP波以及PS波分别应用互相关成像条件.图中it表示时间变量,nt表示最大时刻.对弹性波正演、震源波场反传重建及检波点波场反传等成本较高的计算,均采用GPU加速.图中提及的矢量波场分离和极性校正详见后文.

|
图 1 弹性波逆时偏移流程 Fig. 1 Flow chart of elastic reverse time migration (ERTM) |
考虑各向同性介质,构建震源波场和检波点波场的一阶速度-应力方程为

|
(1) |
其中,vx和vz分别为质点在水平方向和垂直方向的振动速度,σxx和σzz分别为水平方向和垂直方向的正应力,τxz为切应力,ρ为介质的密度,λ和μ为介质的拉梅常数,t为时间变量.文中采用时间二阶,空间十二阶交错网格(Madariaga,1976;Virieux,1986)进行有限差分数值计算,采用PML吸收边界压制来自边界的反射,式(1) 所示的一阶速度-应力方程的离散形式为
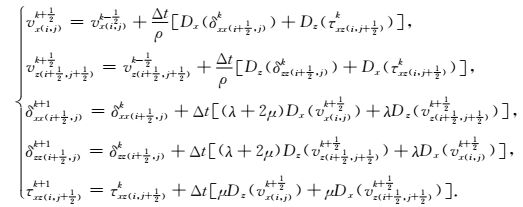
|
(2) |
其中,Δt为时间步长,k为时间变量,Dx和Dz为空间高阶差分算子,公式为

|
(3) |

|
(4) |
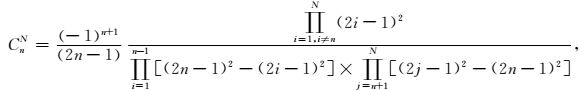
|
(5) |
其中:Δx和Δz分别表示沿x和z方向的空间网格大小,N等于空间差分阶数的一半,CnN为差分系数.
2.2 边界存储策略逆时重建震源波场类似于声波逆时偏移,应用互相关成像条件的弹性波逆时偏移也需要同一时刻的震源波场和检波点波场值,但是两波场的传播方向相反,因此最直接的方法就是存储两者之一所有时刻的波场值,另一波场传播时再把存储的波场提取出来做互相关,这样将会产生巨大的存储需求.因此,为了减少存储需求,本文发展了一种适用于弹性波逆时偏移的逆时重建震源波场方法,并采用GPU并行加速弹性波正演,利用了以计算换存储的思想.
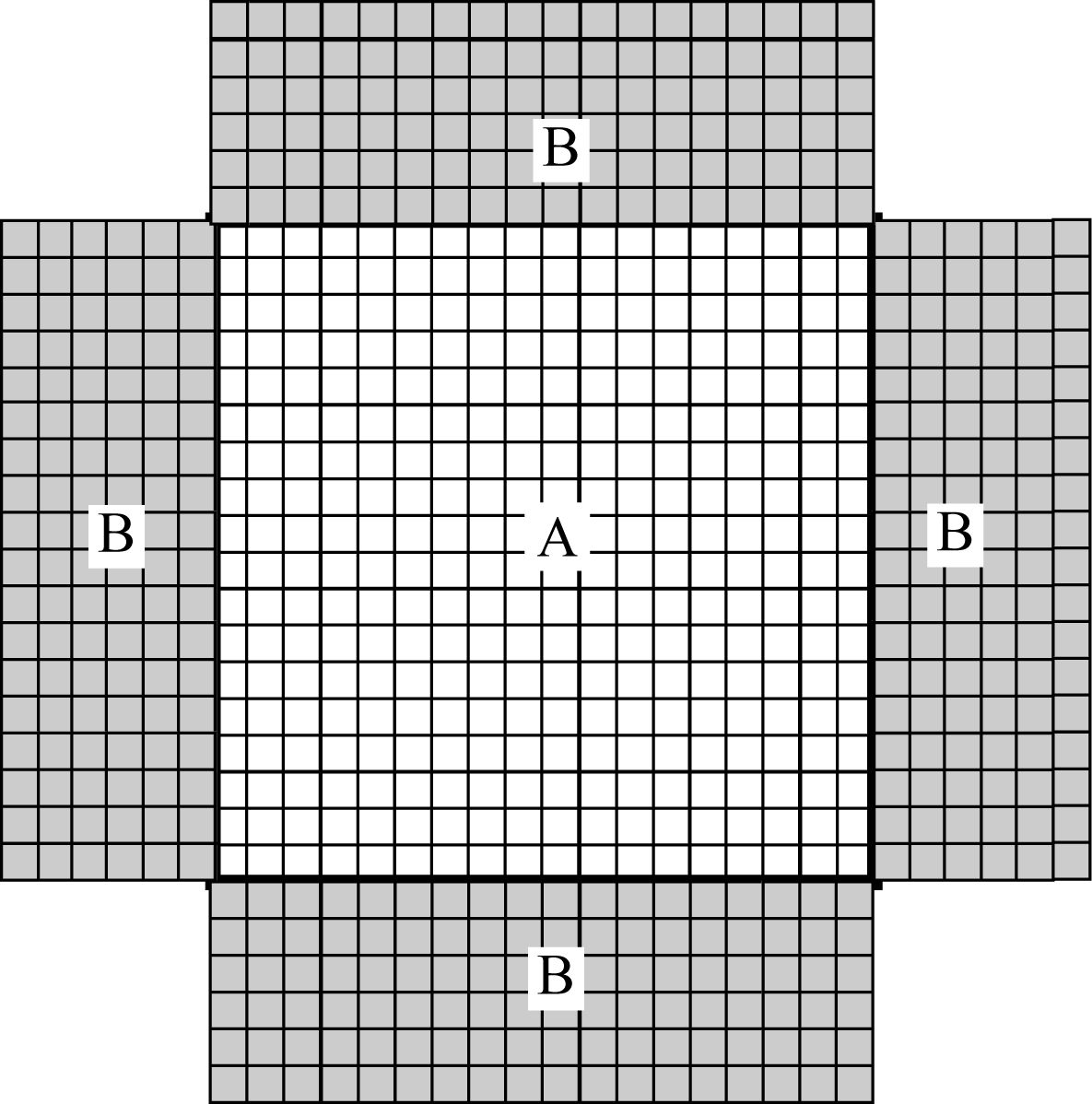
边界存储示意图如图 2所示,A为未加边界的原模型区域,B为一部分PML边界区域,它为震源波场正传过程中存储波场的边界区域,文中边界存储区域厚度为6层(空间差分阶数的一半,即图 1中R的值).Feng和Wang(2012)等提出在靠近A区域边界处,空间采用变阶数的差分格式,边界存储区域B的厚度可以减少到1层,可以进一步减少存储成本,但重建精度也随之降低.由于一阶速度-应力方程共有五个波场变量(vx, vz, δxx, δzz, τxz),在存储波场时,为了减少GPU显存的花费,文中选择存储两个分量的速度波场,因为应力和速度之间的递推关系,应力波场可以由速度波场重建出来,因此在正传过程中不需要存储B区域内的应力波场.综合图 1和图 2,逆时重建震源波场可以概括为:在给定的初始条件和加PML边界的速度模型情况下,进行弹性波正演,并存储B区域内所有时刻的速度波场,直到震源波场正传结束时,保存最大时刻(nt)的原模型区域A的全波场分量.当检波点波场逆时反传时,利用最大时刻的震源波场进行反传,在反传的每一个时刻,将B区域内的速度场用正传过程中保存的速度场更新,再利用更新后的速度场以及公式(2) 的逆时反传形式,重建出计算区域内应力场,然后根据应力和速度之间的关系,则可以实现速度和应力波场之间的递推,逆时重建出所有时刻的震源波场.
|
图 2 边界存储 Fig. 2 Schematic diagram of boundary storage |
为了验证边界存储方法逆时重建震源波场的有效性,设计了一个均匀各向同性弹性介质模型,模型的大小为200×200网格,两个方向的网格尺寸均为10 m,纵波速度为3000 m·s-1,横波速度为1734 m·s-1,密度为2000 kg·m-3,PML边界厚度为50个网格,时间采样间隔为1 ms,在模型中央放置纯纵波源,采用了主频为25 Hz的雷克子波作为激发震源.图 3a和3c分别是不同时刻(t=0.11 s,0.21 s,0.31 s和0.41 s)正传的水平和垂直速度分量波场;图 3b和3d分别是不同时刻(0.41 s,0.31 s,0.21 s和t=0.11 s)逆时反传的水平和垂直速度分量波场.观察可知,边界存储方法可较好地重建模型区域内的震源波场.进一步的单道数据分析如图 4和图 5所示,抽取了t=0.31 s,x=0.8 km位置的正传和反传弹性波波场,分别对比了水平分量和垂直分量,计算了它们之间的绝对误差,可以看出,单道分析的绝对误差较小,进一步验证了文中所述的边界存储方法逆时重建震源波场的有效性.接下来,我们以该模型为例,对比分析全波场存储和边界存储内存消耗,设波传播时间为5 s,波场数据类型为4字节浮点型,全波场(五个波场变量)存储需要消耗约3.73 G存储空间,而文中所用的边界存储策略仅消耗约183 M存储空间(计算方式为:4×(nx+nz)×nt×R×4byte,nx和nz分别表示沿x和z方向的网格点数,nt为总时间采样间隔),因此文中所述方法大幅度降低了弹性波逆时偏移的存储成本,为它的进一步实用化研究提供可选方案.

|
图 3 均匀各向同性介质的弹性波波场快照(t=0.11 s,0.21 s,0.31 s,0.41 s) (a)正传的水平分量波场;(b)逆时反传的水平分量波场;(c)正传的垂直分量波场;(d)逆时反传的垂直分量波场. Fig. 3 Snapshots of homogeneous isotropic medium at 0.11 s, 0.21 s, 0.31 s and 0.41 s (a) Forward-propagating horizontal component wavefields; (b) Backward-propagating horizontal component wavefields; (c) Forward-propagating vertical component wavefields; (d) Backward-propagating vertical component wavefields. |

|
图 4 正传及反传的水平分量弹性波波场(t=0.31 s)单道对比 (a)正传;(b)逆时反传;(c)绝对误差. Fig. 4 Single trace comparison of forward-propagating and backward-propagating horizontal component wavefield at 0.31 s (a) Forward-propagating; (b) Backward-propagating; (c) Absolute error. |

|
图 5 正传及反传的垂直分量弹性波波场(t=0.31 s)单道对比 (a)正传;(b)逆时反传;(c)绝对误差. Fig. 5 Single trace comparison of forward-propagating and backward-propagating vertical component wavefield at 0.31 s (a) Forward-propagating; (b) Backward-propagating; (c) Absolute error. |
为了减少矢量分量(如速度矢量分量)成像引发的串扰,使成像结果物理意义更加明确,需要在应用成像条件之前将震源和检波点速度矢量波场分离为纵、横波场.在各向同性介质中,根据Helmholtz分解理论,弹性波矢量场可以分解为一个无旋的标量纵波波场Up和一个无散的横波矢量场Us,即:
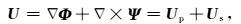
|
(6) |
其中,Φ和Ψ分别为标量和矢量势.对于各向同性弹性波波场,公式(6) 并不能直接实现波场分离,可以对延拓的弹性波矢量波场应用旋度散度算子进行分离.文中矢量波场U代表速度矢量波场,对其求散度和旋度,能够得到标量纵波分量P和矢量横波分量S为
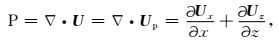
|
(7) |

|
(8) |
利用高阶有限差分算子对上两式离散,便可以在构建震源波场和检波点波场过程中实现纵、横波波场的分离.在2D各向同性介质中,S即代表SV波.图 6为均匀各向同性介质多分量波场快照(t=0.31 s)及波场分离结果,模拟时采用混合震源,其余参数与波场重建模拟参数相同,可以看出散度和旋度算子较好地分离了纵横波场.

|
图 6 多分量波场快照及波场分离结果 (a)水平分量;(b)垂直分量;(c) P波分量;(d) S波分量. Fig. 6 Snapshots of multi-component wavefields and separated P-and S-wavefields (a) Horizonal component; (b) Vertical component; (c) P-wave; (d) S-wave. |
对于震源和检波点波场中分离的纵波分量和横波分量,文中使用震源归一化互相关成像条件(9) 和(10).公式为

|
(9) |

|
(10) |
其中,IPP表示PP成像,IPS表示PS成像,SFP表示震源波场中分离的纵波分量,RFP表示检波点波场中分离的纵波分量,RFS表示检波点波场分离的横波分量,(x, z)代表空间位置,nt为总采样时间间隔数,因此应用公式(9) 和(10) 能得到纯波成像数据.
2.5 转换波成像极性反转基于波场分离的弹性波逆时偏移面临着一个严重的问题,即利用Helmholtz分解定理提取纵波和横波分量时,分离的横波分量发生极性反转,而分离的纵波分量为标量,在直接使用互相关成像条件计算IPS时,PS成像就发生了极性反转,当多炮偏移成像叠加之后,极性的反转导致虚假的同相轴信息,因此对转换波成像IPS的极性校正显得尤为重要.
下面先分析利用旋度算子分离矢量波场,进而分析转换波成像发生极性反转的原因.在2D各向同性介质中,可在波数域研究旋度算子分离弹性波波场的本质特征,式(8) 在波数域中可以表示为(Du et al., 2012):

|
(11) |
其中,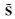

|
图 7 S波的极性反转 Fig. 7 Schematic diagram of polarity reversal of S-waves |
值得说明的是,文中仅研究IPP和IPS成像,对于ISP成像,由于SP波发生极性反转,因此它也发生类似IPS成像的极性反转情况,校正方法此处不做详细讨论.对于ISS成像则不会发生极性反转,这是因为震源和检波点波场中分离的S波分量互相关时,自动补偿了S波分量的极性反转.
3 极性校正从上面的分析看出,在2D各向同性介质中,IPS成像极性反转发生在纵波垂直入射的位置两侧,若能够计算出每个成像时刻每个成像点的纵波入射角度,再将负的入射角度(或正入射角度)的成像值乘以-1,那么IPS成像的极性反转能够校正.因此,校正IPS极性的震源归一化互相关成像条件可以改写为
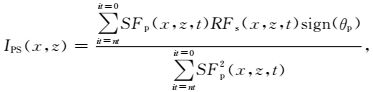
|
(12) |
其中,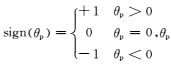
基于方向矢量的方法能够高效地估算波的传播方向(角度),在逆时偏移的角度域共成像点道集(ADCIGS)提取中得到广泛应用(Zhang and McMechan, 2011a,b;Wang and McMechan, 2015).对2D各向同性介质,纵波的极化方向和传播方向平行,对纵波波场作用梯度算子可获得传播方向,即:

|
(13) |
其中,(nx, nz)为纵波传播方向,∇为梯度算子.因此,纵波的传播角度αp为

|
(14) |
瞬时波数可用于估算界面法线方向.考虑2D弹性波逆时偏移PP成像IPP(x, z),为了计算偏移剖面的法线方向,首先分别计算偏移剖面沿x或z方向的希尔伯特变换,公式为

|
(15) |

|
(16) |
公式(15) —(16) 中,Hx和Hz分别代表沿x和z方向的希尔伯特变换Q(x, z)代表IPP(x, z)沿x或z方向的希尔伯特变换.
因此,PP成像IPP(x, z)的复地震信号c(x, z)可以表示为

|
(17) |
其中,a(x, z)是复信号的瞬时振幅,φ(x, z)是复信号的瞬时相位,i代表虚数单位.瞬时相位φ(x, z)的梯度就给出了空间位置的瞬时波数方向,即界面法线方向(Zhang and McMechan, 2011a,b).公式为

|
(18) |
其中,kx和kz分别为波数k的水平和垂直分量,它们表示界面的法线方向,real表示复数的实部.因此成像剖面的局部倾角可以表示为

|
(19) |
从上面计算得到纵波的传播角度αp和界面的局部倾角β,根据两者之差即可以得到纵波的入射角度θp为

|
(20) |
将上式代入公式(12),可校正IPS成像的极性,进而解决成像的极性反转问题.
4 模型测试为了验证文中所述基于波场分离的弹性波逆时偏移方法和极性校正方法的有效性,文中测试了地堑模型和Marmousi2模型.
4.1 地堑模型
设计地堑模型,如图 8a所示,纵波和横波速度满足关系VS=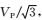

|
图 8 地堑模型参数及单炮成像结果 (a)地堑模型;(b) PP成像;(c) PS成像;(d)校正极性后的PS成像. Fig. 8 Graben model parameters and single-shot imaging results (a) Graben model; (b) PP imaging; (c) PS imaging without polarity reversal correction; (d) PS imaging with polarity reversal correction. |
将基于波场分离的弹性波逆时偏移方法和极性校正方法应用于该地堑模型,成像结果如图 8所示,图 8b、8c和8d分别为PP成像,PS成像和极性校正后的PS成像.由于应用散度算子分离得到的纵波为标量,因此PP成像不会发生极性反转,剖面成像清晰,同相轴自然连续.未做极性校正的PS成像,如图 8c所示,在纵波垂直入射位置(对应于图 8a中的A、B、C点)附近能量消失,同相轴断开,垂直入射点两侧同相轴极性相反.利用前述的极性校正方法,对转换波成像进行校正,PS成像结果如图 8d所示,校正后的三个点A、B和C两端的同相轴极性一致,提高了转换波成像精度.由于相同频率的纵波波长比横波波长长,因此PS成像比PP成像的分辨率更高.
4.2 Marmousi2模型
进一步借助国际通用的Marmousi2模型(Martin et al., 2006)测试所述方法的有效性,该模型构造极为复杂,具有多个密集薄互层,浅部有陡倾角断层,深部有不整合面以及刺穿盐丘结构,横向速度变化大,地层倾角不断变化.Marmousi2的纵波速度模型如图 9a所示,横波速度按VS=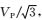

|
图 9 Marmousi2速度模型及不同类型的叠加成像剖面 (a) Marmousi2纵波速度模型;(b) PP成像剖面;(c)未校正极性的PS成像剖面;(d)校正极性后的PS成像剖面. Fig. 9 P-wave velocity and different types of stacked imaging profiles for Marmousi2 model (a) P-wave velocity for Marmousi2 model; (b) PP image; (c) PS image without polarity reversal correction; (d) PS image with polarity reversal correction. |
从成像剖面看出,PP成像能够对背斜和断层清晰成像,同相轴连续无错段,如图 9b所示.而未进行极性校正的PS成像可见同相轴不连续,如图 9c箭头所示,多炮成像叠加剖面严重受损,成像精度大幅度下降.为了改善PS成像质量,利用了文中所述的极性校正方法,校正后的成像剖面如图 9d所示,可见背斜和断层构造成像清晰,同相轴连续,而且可获得比PP成像分辨率更高的效果.值得说明的是,文中在模拟时使用了爆炸震源,横波是由纵波转换而来,能量相对较弱,因此这里未对SS和SP的成像做深入讨论.
将图 9b所示的框内区域与图 9c和9d的相应区域进行局部放大显示,如图 10a,10b和10c所示.对比发现,图 10a所示的PP成像的振幅和相位保持很好,同相轴连续,成像精度较高.图 10b所示的未校正极性的PS成像效果变差,同相轴错段,能量不聚焦,伴有随机噪声出现,这是因为在PS成像中,叠加了极性相反的同相轴,导致最终成像结果遭到破坏.校正极性后的PS成像,如图 10c所示,其振幅和相位保持很好,同相轴连续,成像清晰,较图 10a所示的PP成像,分辨率有明显提高.

|
图 10 图 9的局部放大 (a) 图 9b的局部放大显示;(b) 图 9c的局部放大显示;(c) 图 9d的局部放大显示. Fig. 10 Partial enlargement of Fig. 9 (a) Partial zoom-in of Fig. 9b; (b) Partial zoom-in of Fig. 9c; (c) Partial zoom-in of Fig. 9d. |
为测试所述偏移算法及极性校正方法的抗噪性,对所观测的地震记录加入Gaussian随机噪声(sn=5),含噪声的两分量地震记录(第85炮激发)如图 11所示.图 12a、12b和12c分别给出了利用文中方法计算的PP成像、PS成像以及校正极性后的PS成像结果.研究发现,PP成像仍然能够对背斜和断层清晰成像,同相轴连续无错段,除层间含少量随机噪声外,整体成像效果与未加入噪声测试的PP成像(图 10b)一致;未进行极性校正的PS成像的同相轴不连续,多炮成像叠加剖面严重受损,随机噪声同时也淹没了有效同相轴,成像精度大幅度下降;校正极性后的PS成像同相轴连续,但是层间的随机噪声较PP成像更多,这是由于观测记录中的横波是由纵波转换而来,能量较弱,所以PS成像更易受噪声的影响,但是,背斜和断层构造仍能够清晰成像.在噪声适度的情况下,文中所述的偏移和极性校正方法,具有良好的抗噪性.

|
图 11 含高斯噪声(sn=5) 的第85炮地震记录 (a)水平分量;(b)垂直分量. Fig. 11 Seismograms bearing Gaussian noise (sn=5) of the 85th shot (a) Horizontal velocity component; (b) Vertical velocity component. |

|
图 12 含高斯噪声的地震记录偏移结果 (a) PP成像剖面;(b)未校正极性的PS成像剖面;(c)校正极性后的PS成像剖面. Fig. 12 Results of seismic migration with Gaussian noise for the Marmousi2 model (a) PP image; (b) PS image without polarity reversal correction; (c) PS image with polarity reversal correction. |
本文提出了一种基于波场分离的弹性波逆时偏移成像的可行方法,在应用互相关成像条件的情况下,采用边界存储方法逆时重建震源波场,仅保存PML边界内若干层的速度分量,再逆时重建震源波场相关的所有分量,大大降低了弹性波逆时偏移存储成本,为弹性波逆时偏移的实用化研究开辟了新的思路.本文详细分析了转换波成像发生极性反转的原因,源于施加旋度算子分离横波时发生的极性反转,对此提出一种共炮域估算入射角度进而校正转换波成像的极性,极大地提高了转换波成像精度.文中所提出的弹性波逆时偏移形成的纯波成像剖面,能够对复杂地下构造准确成像,相比于纵波成像,极性校正后的成像数据提高了分辨率.
| Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics, 48(11): 1514-1524. DOI:10.1190/1.1441434 | |
| Chang W F, McMechan G A. 1987. Elastic reverse-time migration. Geophysics, 52(10): 1365-1375. DOI:10.1190/1.1442249 | |
| Chang W F, McMechan G A. 1994. 3-D elastic prestack, reverse-time depth migration. Geophysics, 59(4): 597-609. DOI:10.1190/1.1443620 | |
| Chattopadhyay S, McMechan G A. 2008. Imaging conditions for prestack reverse-time migration. Geophysics, 73(3). DOI:10.1190/1.2903822 | |
| Clapp R G. 2009. Reverse time migration with random boundaries.//79th Annual International Meeting, SEG. Expanded Abstracts, 2809-2813. | |
| Du Q Z, Zhu Y T, Ba J. 2012. Polarity reversal correction for elastic reverse time migration. Geophysics, 77(2): S31-S41. DOI:10.1190/geo2011-0348.1 | |
| Duan Y T, Sava P. 2015. Scalar imaging condition for elastic reverse time migration. Geophysics, 80(4): S127-S136. DOI:10.1190/geo2014-0453.1 | |
| Feng B, Wang H Z. 2012. Reverse time migration with source wavefield reconstruction strategy. J. Geophys. Eng., 9(1): 69-74. DOI:10.1088/1742-2132/9/1/008 | |
| Gu B L, Li Z Y, Ma X N, et al. 2015. Multi-component elastic reverse time migration based on the P-and S-wave separated velocity-stress equations. Journal of Applied Geophysics, 112: 62-78. DOI:10.1016/j.jappgeo.2014.11.008 | |
| Jin H, McMechan G A, Nguyen B. 2015. Improving input/output performance in 2D and 3D angle-domain common-image gathers from reverse time migration. Geophysics, 80(2): S65-S77. DOI:10.1190/GEO2014-0209.1 | |
| Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys., 53(12): 2938-2943. DOI:10.3969/j.issn.0001-5733.2010.12.017 | |
| Li Z Y, Ma X N, Fu C, et al. 2016. Wavefield separation and polarity reversal correction in elastic reverse time migration. Journal of Applied Geophysics, 127: 56-67. DOI:10.1016/j.jappgeo.2016.02.012 | |
| Liu G F, Liu H, Li B, et al. 2009. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese J. Geophys., 52(12): 3101-3108. DOI:10.3969/j.issn.0001-5733.2009.12.019 | |
| Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys., 53(7): 1725-1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 | |
| Loewenthal D, Mufti I R. 1983. Reversed time migration in spatial frequency domain. Geophysics, 48(5): 627-635. DOI:10.1190/1.1441493 | |
| Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. | |
| Martin G S, Wiley R, Marfurt K J. 2006. Marmousi2:An elastic upgrade for Marmousi. The Leading Edge, 25(2): 156-166. DOI:10.1190/1.2172306 | |
| McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420. DOI:10.1111/j.1365-2478.1983.tb01060.x | |
| Nguyen B D, McMechan G A. 2013. Excitation amplitude imaging condition for prestack reverse-time migration. Geophysics, 78(1): S37-S46. DOI:10.1190/GEO2012-0079.1 | |
| Nguyen B D, McMechan G A. 2015. Five ways to avoid storing source wavefield snapshots in 2D elastic prestack reverse time migration. Geophysics, 80(1): S1-S8. DOI:10.1190/geo2014-0014.1 | |
| Rosales D, Rickett J. 2001. PS-wave polarity reversal in angle domain common-image gathers.//71st Annual International Meeting, SEG. Expanded Abstracts, 1843-1846. | |
| Rosales D A, Fomel S, Biondi B, et al. 2008. Wave-equation angle-domain common-image gathers for converted waves. Geophysics, 73(1): S17-S26. DOI:10.1190/1.2821193 | |
| Sun R, McMechan G A. 1986. Pre-stack reverse-time migration for elastic waves with application to synthetic offset vertical seismic profiles. Proc. IEEE, 74(3): 457-465. DOI:10.1109/PROC.1986.13486 | |
| Symes W W. 2007. Reverse time migration with optimal checkpointing. Geophysics, 72(5). DOI:10.1190/1.2742686 | |
| Virieux J. 1986. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. DOI:10.1190/1.1442147 | |
| Wang B L, Gao J H, Chen W C, et al. 2012. Efficient boundary storage strategies for seismic reverse time migration. Chinese J. Geophys., 55(7): 2412-2421. DOI:10.6038/j.issn.0001-5733.2012.07.025 | |
| Wang W L, McMechan G A. 2015. Vector-based elastic reverse time migration. Geophysics, 80(6): S245-S258. DOI:10.1190/geo2014-0620.1 | |
| Wang W L, McMechan G A, Tang C, et al. 2016. Up/down and P/S decompositions of elastic wavefields using complex seismic traces with applications to calculating Poynting vectors and angle-domain common-image gathers from reverse time migrations. Geophysics, 81(4): S181-S194. DOI:10.1190/geo2015-0456.1 | |
| Whitmore N D. 1983. Iterative depth migration by backward time propagation.//53rd Annual International Meeting, SEG. Expanded Abstracts, 827-830. | |
| Yan J, Sava P. 2008. Isotropic angle-domain elastic reverse-time migration. Geophysics, 73(6): S229-S239. DOI:10.1190/1.2981241 | |
| Zhang Q S, McMechan G A. 2011a. Direct vector-field method to obtain angle-domain common-image gathers from isotropic acoustic and elastic reverse time migration. Geophysics, 76(5): WB135-WB149. DOI:10.1190/geo2010-0314.1 | |
| Zhang Q S, McMechan G A. 2011b. Common-image gathers in the incident phase-angle domain from reverse time migration in 2D elastic VTI media. Geophysics, 76(6): S197-S206. DOI:10.1190/geo2011-0015.1 | |
| 李博, 刘红伟, 刘国峰, 等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报, 53(12): 2938–2943. DOI:10.3969/j.issn.0001-5733.2010.12.017 | |
| 刘国峰, 刘洪, 李博, 等. 2009. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报, 52(12): 3101–3108. DOI:10.3969/j.issn.0001-5733.2009.12.019 | |
| 刘红伟, 李博, 刘洪, 等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725–1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 | |
| 王保利, 高静怀, 陈文超, 等. 2012. 地震叠前逆时偏移的有效边界存储策略. 地球物理学报, 55(7): 2412–2421. DOI:10.6038/j.issn.0001-5733.2012.07.025 | |
 2017, Vol. 60
2017, Vol. 60


