2. 大地测量与地球动力学国家重点实验室, 武汉 430077;
3. 中国石油集团东方地球物理勘探公司, 河北涿州 072751
2. State Key Laboratory of Geodesy and Earth's Dynamics, Wuhan 430077, China;
3. Bureau of Geophysical Prospecting INC, CNPC, Hebei Zhuozhou 072751, China
由于受勘探成本、采集条件等因素的影响,地震数据在采集过程中,不可避免地会出现空道和坏道.这些地震道的剔除会导致地震数据的缺失,而缺失的地震波场会降低数据信噪比,对偏移成像产生较大影响(陈必远和马在田,1994).针对这一问题,Larner等(1981)就地震道插值方法进行了初步探讨,提出了最大相干倾角的插值方法.经过三十多年的发展,国内外众多学者对这一问题进行了系统研究,提出了一系列地震数据重建方法.这些方法主要可以归结为三大类:基于滤波的重建方法(Claerbout and Nichols, 1991; Spitz,1991;Gulunay and Chambers, 1997)、基于波动方程的重建方法(Ronen,1987;Canning and Gardner, 1996;Biondi et al., 1998)、基于函数变换的重建方法(Thorson and Claerbout, 1985;Duijndam et al., 1999;Ge et al., 2015).在这三类方法中,基于变换域的Radon变换方法,因充分考虑了地震同相轴的走时特征和物理意义,受到众多学者的关注. Radon变换最早是在时间-空间域进行处理,通过Radon正变换扫描地震波场中的同相轴,再经过Radon反变换填补缺失的地震信号(Thorson and Claerbout, 1985). Trad针对Radon变换在时间-空间域的重建精度、解的稳定性等问题进行改进,发展为高分辨率时变Radon变换(Trad,2001;Trad et al., 2002, 2003).但即使经过改进,时间-空间域的Radon变换仍需要对大矩阵求逆,不仅计算量巨大,而且解的稳定性比较差. Hampson(1986)将Radon变换由时间-空间域转换到频率-空间域进行处理,并利用抛物线来近似同相轴,得到了频域抛物Radon变换.频域抛物Radon变换可以在频率域解耦,对每一个频率单独进行正反变换,减小了计算量;并且频域抛物Radon变换可以只选择在有效地震信号的频带范围内进行重建,剔除了高频噪声,从而在重建的同时也起到一定的去噪作用.频域抛物Radon变换因独特的优势而备受学者的青睐,经过不断发展形成了一套系统的方法理论. Sacchi和Ulrych(1995)提出高分辨率抛物Radon变换地震重建方法,该方法结合最大熵原则利用抛物Radon变换稀疏性提高解的精度. Kabir和Verschuur(1995)提出了迭代抛物Radon变换重建方法,该方法通过多次迭代对近偏移距数据有较好的重建效果. Schonewille和Duijndam(2001)对抛物Radon变换的参数采样、计算效率和稳定性等方面进行深入剖析,给出了更加稳定的采样和计算方法. 刘喜武等(2004)详细分析了高分辨率Radon变换的性质和应用效果,并利用稀疏约束预条件共轭梯度法获得了改进后的高分辨率Radon变换. 王维红等(2007)提出了加权抛物Radon变换,该方法引入变化的权系数,减少迭代次数,节省了计算时间. Abbad等(2011)提出一种改进的抛物Radon变换的方法,该方法消除了变换算子对频率的依赖,显著提高了计算效率. 霍志周等(2013)利用预条件共轭梯度法解算反演矩阵,该方法加快了迭代速度,改进了共轭梯度算法的收敛性.以上研究主要针对2D地震数据展开,基于3D Radon变换的地震数据重建研究仍停留在方法原理阶段(Donati and Martin, 1995;Zhang et al., 2013),在3D实际地震资料应用处理方面还有较大缺口.
随着相关研究的不断深入,频域2D抛物Radon变换理论体系逐渐趋于完善,方法存在的诸多问题逐渐得到解决.但Radon变换对振幅变化信息不敏感,针对含有AVO特性的地震数据,重建无法有效地保留波场AVO信息(Sacchi and Ulrych, 1995),而地震数据的AVO特性对偏移成像有重要意义(Gray,2014).为解决3D保幅重建问题,唐欢欢和毛伟建(2014)以及Tang等(2016)利用正交多项式拟合含有AVO特征的地震信息,将正交多项式与频域抛物Radon变换相结合,发展为具有良好保幅效果的3D高阶抛物Radon变换;但该方法使正变换系数矩阵扩大j×j倍(j为正交多项式的阶数),计算量增加,生产成本提高.
为提高3D高阶抛物Radon变换的计算效率,本文引入Abbad在f-λ域处理2D抛物Radon变换算子的思想,提出一种3D快速高阶抛物Radon变换重建地震波场的计算方法.该方法引入新变量λx=qxf和λy=qyf,通过对qxf和qyf的整体采样,消除变换算子L(λx)、L(λy)对频率的依赖,在解算不同频率的正变换系数矩阵M(f)时,变换算子L(λx)、L(λy)均相同,因此变换算子的求逆过程只需要进行一次,显著提高计算效率.本文通过对理论模型和实际地震资料的测试,在数据的重建效果、计算效率方面均取得满意的结果.
2 方法原理 2.1 3D高阶抛物Radon变换原理传统3D抛物Radon正变换表达式为:
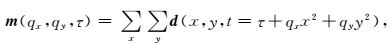
|
(1) |
其反变换为
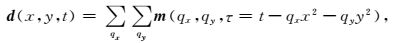
|
(2) |
式中,d(x, y, t)为t-x-y域中的地震数据体,m(qx, qy, τ)为地震数据在τ-qx-qy域中的表达形式,qx和qy为曲率变换参数.
传统3D抛物Radon变换的物理意义是沿着不同曲率的同相轴进行叠加运算,并没有考虑振幅随偏移距的变化.因此,针对含有AVO特征的地震数据,在利用传统抛物Radon变换进行重建时,重建数据的振幅会有较大误差. Johansen等(1995)利用正交多项式来描述地震数据的AVO信息,其正交多项式拟合可表达为
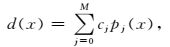
|
(3) |
其中,j表示正交多项式的阶数,M表示其最高阶数,cj表示第j阶正交多项式系数.地震数据振幅的变化信息都包含在系数cj中. pj(x)表示第j阶正交多项式基函数,满足pi(x)pj(x)=δij,δij为脉冲函数.pj(x)的求取方法为(唐欢欢和毛伟建,2014):
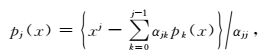
|
(4) |
系数的求取方法为
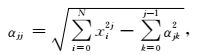
|
(5) |
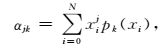
|
(6) |
通过(4)、(5)、(6) 式,可以构造任意偏移距的正交多项式,给定α00=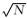
针对(3) 式,利用最小二乘方法可以得到系数的表达式为
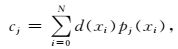
|
(7) |
其中,N表示偏移距方向检波点个数.同相轴振幅随偏移距的变化信息,一般可以用前三阶系数c(t, 0)、c(t, 1) 和c(t, 2) 准确描述,因此对应的正交多项式基函数取到第2阶即可.将公式(1) 和公式(7) 相比可以发现, 抛物Radon变换是沿着同相轴进行叠加,Johansen提出的方法是以基函数为准则进行叠加,二者具有一致性. 唐欢欢和毛伟建(2014)以及Tang等(2016)将正交多项式的思想引入到3D抛物Radon变换中,发展为具有良好保幅效果的3D高阶抛物Radon变换. 3D高阶抛物Radon变换的正变换表达式为
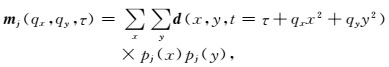
|
(8) |
其反变换表达式为
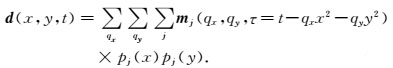
|
(9) |
高阶抛物Radon变换将传统抛物Radon变换的一个τ-qx-qy剖面分成了能够描述AVO信息的j个剖面(j表示正交多项式的阶数).对公式(9) 作Fourier变换,得到频率域3D高阶抛物Radon反变换公式为
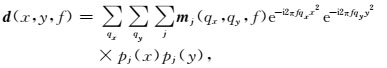
|
(10) |
(10) 式可重写为
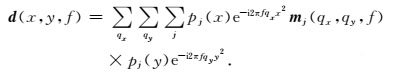
|
(11) |
对每一频率f, 将(11) 式写成矩阵形式为
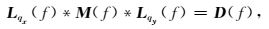
|
(12) |
式中,Lqx=p(x)e-i2πfqxx2, Lqy=p(y)e-i2πfqyy2, M(f)为频率域f-qx-qy数据矩阵,D(f)为频率域f-x-y数据矩阵.利用最小二乘求解正变换系数矩阵M(f)的表达式为
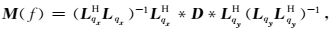
|
(13) |
式中,LqxH为Lqx的共轭转置矩阵,LHqy为Lqy的共轭转置矩阵.
2.2 3D快速高阶抛物Radon变换原理为消除3D高阶抛物Radon变换算子Lqx(f)和Lqy(f)对频率的依赖,引入了新变量λx=qxf和λy=qyf.针对每一个频率f,(11) 式可变为
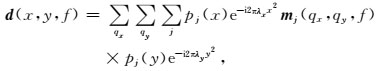
|
(14) |
将(14) 式写为矩阵形式为
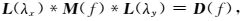
|
(15) |
式中L(λx)=p(x)e-i2πλxx2,L(λy)=p(y)e-i2πλyy2.
类比离散Fourier变换,λx与x2、λy与y2分别构成傅里叶变换因子,由奈奎斯特采样定理(Whittaker,1915; Nyquist,2002),可得出3D快速高阶抛物Radon变换参数λx和λy的采样准则为(Schonewille and Duijndam, 2001;Abbad et al., 2011):
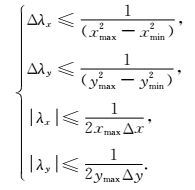
|
(16) |
一般情况下,λxmax和λymax的值均取上界.由(16) 式确定的采样准则可以看出,快速高阶抛物Radon变换算子L(λx)=p(x)e-i2πλxx2、L(λy)=p(y)e-i2πλyy2的参数λx和λy采样只与偏移距有关,使变换算子L(λx)和L(λy)消除了对频率的依赖;当频率不同时,抛物Radon变换算子L(λx)和L(λy)均相同.
标准高阶算法和快速高阶算法在进行地震数据重建时均需求解重建频带内每一个频率的正变换系数矩阵M(f)对于标准高阶算法,其抛物Radon变换算子Lqx(f)和Lqy(f)是随频率而变化的,利用(13) 式在求解不同频率下的正变换系数矩阵M(f)时均要重新计算(LqxHLqx)-1和(LqyLqyH)-1的值,而这两部分的计算时间是整个重建过程最为耗时的部分.对于快速高阶算法,不同频率的抛物Radon变换算子L(λx)和L(λy)均相同,在求解不同频率下的正变换系数矩阵M(f)时(LλxHLλx)-1和(LλyLλyH)-1的值不需要重新计算,节省了重建过程最为耗时的部分,可以提高算法计算效率.
3D快速高阶抛物Radon变换只是在计算上采取了一种灵活的处理方式,实际物理意义仍由标准高阶抛物Radon变换来体现.标准高阶抛物Radon变换曲率参数qx和qy的扫描范围是事先设定并对所有频率是相同的,而快速高阶抛物Radon变换的参数λx=qxf和λy=qyf所包含的曲率qx和qy是随频率变化的,对低频信号,λx和λy的采样拓宽了曲率qx和qy的范围,同相轴扫描范围更广(Abbad et al., 2011).
3 方法应用实例3D快速高阶抛物Radon变换对缺失地震数据进行重建的原理是利用抛物Radon变换在正变换中的能量聚焦并通过反变换过程来填补空道数据.该过程在将重建道置入缺失道时,传统的方法是在时间域执行此操作,并经多次正反迭代后得到满足重建条件的缺失道信息.而Abma和Kabir(2006)、Gao等(2010, 2013)的研究表明,对于时间方向不存在缺失采样的地震数据,可以将重建迭代过程由时间域转移到频率域,避免每次迭代都对时间t做正反傅里叶变换.该方法只需要在重建开始前作一次正FFT和重建结束后作一次反FFT,压缩计算成本.本文采用在频率域将重建道置入缺失道的方法,其频率切片的迭代过程主要包括四步:(1) 对频率切片进行抛物Radon正变换;(2) 对正变换后得到的Radon域数据进行抛物Radon反变换;(3) 将频域已知道信息置入重建数据;(4) 判断是否满足重建条件,不满足则返回第一步.第四步中重建条件一般为误差限或最大迭代次数,误差限的设定方法为(Gao et al., 2013):
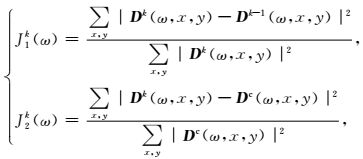
|
(17) |
其中,Jk(ω)表示误差限,Dk(ω, x, y)表示第k次迭代重建后的缺失道数据,Dc(ω, x, y)表示缺失道所对应的原数据.在实际情况中并不知道缺失道所对应的原数据,可以用J1k(ω)做误差限,J2k(ω)一般作为实验数据做重建测试时的误差评估参数.重建流程如图 1所示.
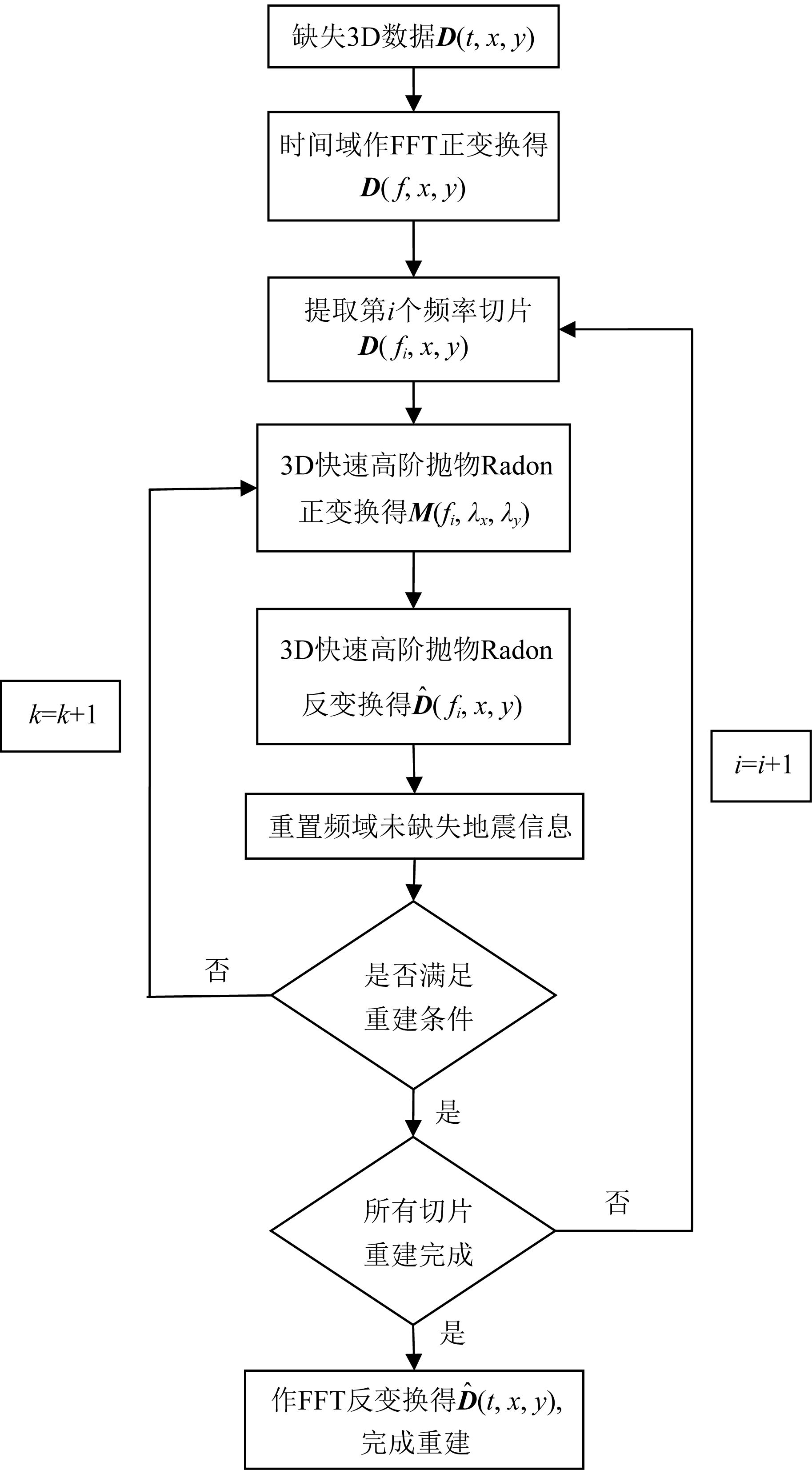
|
图 1 3D快速高阶抛物Radon变换重建流程 Fig. 1 Flow chart of the 3D FHOPRT reconstruction method |
为测试3D高阶抛物Radon变换的保幅性,现合成含有四种不同类型同相轴的三维AVO地震记录.记录沿测线方向(X方向)有128道,道间距10 m;沿垂直测线方向(Y方向)有64道,道间距20 m,时间采样个数为512,时间采样间隔为2 ms.
我们分别利用3D传统抛物Radon变换(3D Parabolic Radon Transform, 3D PRT)和3D高阶抛物Radon变换(3D High order parabolic Radon Transform, 3D HOPRT)对3D AVO合成地震数据进行一次正反变换. 图 2给出了3D传统抛物Radon变换和3D高阶抛物Radon变换沿Y方向第1条测线变换后结果的比较. 图 2a为3D传统抛物Radon变换方法做变换后的结果,图 2b为3D高阶抛物Radon变换方法的结果,图 2c和图 2d分别为传统方法和高阶方法变换数据与原始数据作差得到的误差剖面;由图 2可以看出,对于AVO地震数据,传统方法进行一次正反变换后与原始数据存在较大误差,而由高阶方法进行正反变换后的误差较小,由此可以看出高阶算法具备良好的保幅变换效果.一般情况下,正交多项式的阶数取2时即可确保变换具有良好的保幅效果,但当正交多项式阶数取2时,高阶抛物Radon变换正变换系数矩阵M(f)是传统抛物Radon变换的3×3倍, 计算量很大.

|
图 2 3D PRT和3D HOPRT方法保幅性比较 (a) 3D PRT方法变换后数据;(b) 3D HOPRT方法变换后数据;(c) 3D PRT方法误差剖面;(d) 3D HOPRT方法误差剖面. Fig. 2 Comparison of 3D PRT and 3D HOPRT for amplitude preserved transform (a) Recovered data of 3D PRT; (b) Recovered data of 3D HOPRT; (c) Errors of 3D PRT; (d) Errors of 3D HOPRT. |
为测试3D快速高阶抛物Radon变换的重建精度,现将上述合成地震数据随机缺失50%,图 3为3D地震数据缺道平面图,该图为X-Y平面, 震源在原点位置, 图中符号“·”表示未缺失地震道,符号“×”表示缺失地震道.

|
图 3 3D合成地震数据缺失平面 Fig. 3 Planar diagram of missed 3D synthetic seismic data |
我们分别利用3D快速高阶抛物Radon变换(3D Fast High Order Parabolic Radon Transform,3D FHOPRT)和3D高阶抛物Radon变换(3D High Order Parabolic Radon Transform,3D HOPRT)方法对上述合成地震数据进行重建.重建在频率为0~50 Hz的频带范围内进行,根据采样准则(16) 式,重建过程中参数λx和λy的采样个数均为100.一般情况下λx和λy采样个数在100~300之间即可取得满意的重建效果.
两种算法的重建过程均发生5次迭代,J25(ω) < 0.02.现分别在Y方向和X方向选取测线Y1和测线X5进行分析.重建结果如图 4、图 5所示;图 4c为Y1剖面重建效果,由图 4c可以看出利用3D FHOPRT重建后的波场连续性良好.图 4d为随机选取的缺失道第100道的详细重建效果;图 5c为X5剖面重建效果,图 5d为随机选取的缺失道第27道详细重建效果.由图 4d和图 5d可以看出,3D快速高阶抛物Radon变换与3D高阶抛物Radon变换重建精度一致,其相位、振幅信息均重建良好,确保了3D快速高阶抛物Radon变换较高的重建精度.

|
图 4 Y1地震剖面缺失重建 (a)原始数据;(b)缺失数据;(c) 3D FHORPT方法重建数据;(d) 3D FHOPRT方法与3D HOPRT方法重建第100道对比. Fig. 4 Reconstruction of seismic profile Y1 (a) Original data; (b) Missing data; (c) Recovered profile Y1 from 3D FHORPT; (d) Comparison of the 100th trace. |
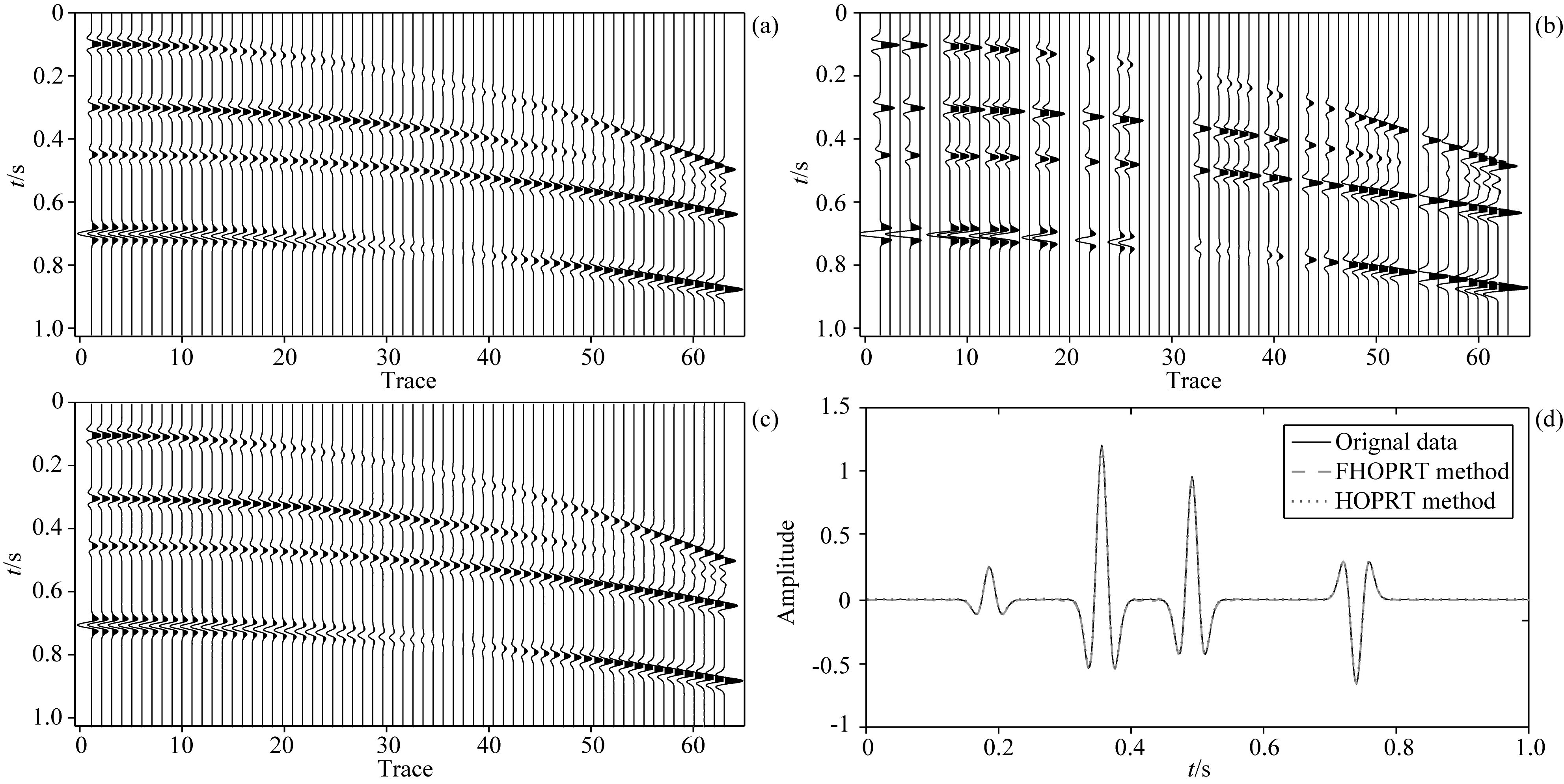
|
图 5 X5地震剖面缺失重建 (a)原始数据;(b)缺失剖面;(c) 3D FHORPT方法重建数据;(d) 3D FHOPRT方法与3D HOPRT方法重建第27道对比. Fig. 5 Reconstruction of profile X5 (a) Original data; (b) Missing data; (c) Recovered profile X5 from 3D FHORPT; (d) Comparison of the 27th trace. |
为检验该方法的实际应用效果,现分别利用3D快速高阶抛物Radon变换和3D高阶抛物Radon变换对实际地震资料进行重建.实际地震资料在X方向有113道,道间距100 m,Y方向有39道,道间距200 m,时间采样个数为1000,时间采样间隔均为8 ms,该数据含有较强的高频噪声,将该实际地震数据随机缺失50%,缺失情况如图 6所示.

|
图 6 3D实际地震数据缺失平面 Fig. 6 Planar diagram of real missed 3D seismic data |
实际地震数据重建在频率为0~50 Hz的频带范围内进行,根据采样准则(16) 式,重建过程中参数λx和λy的采样个数均为200. 3D FHOPRT和3D HOPRT两种算法的重建过程均发生20次迭代,J120(ω) < 0.02.现分别选取测线Y20和测线X57进行分析. 图 7和图 8给出了3D FHOPRT方法和3D HOPRT方法的重建结果. 图 7为测线Y20的重建效果,图 7e为Y20第70道重建效果;图 8为测线X57的重建效果,图 8e为X57第18道重建效果.由图 7和图 8可以看出,3D快速高阶算法与3D高阶算法对该地震资料进行重建均取得了良好的保幅效果.

|
图 7 Y20地震剖面缺失重建 (a)原始数据;(b)缺失数据;(c) 3D FHORPT方法重建数据;(d) 3D HORPT方法重建数据;(e) 3D FHOPRT方法与3D HOPRT方法重建第70道对比. Fig. 7 Reconstruction of missed seismic profile Y20 (a) Original data; (b) Missing data; (c) Recovered profile Y20 from 3D FHORPT;(d) Recovered profile Y20 from 3D HORPT; (e) Comparison of the 70th trace. |

|
图 8 X57地震剖面缺失重建 (a)原始数据;(b)缺失数据;(c) 3D FHORPT方法重建数据;(d) 3D HOPRT方法重建数据;(e) 3D FHOPRT方法与3D HOPRT方法重建第18道对比. Fig. 8 Reconstruction of missed seismic profile X57 (a) Original data; (b) Missing data; (c) Recovered profile X57 from 3D FHORPT;(d) Recovered profile X56 from 3D HORPT; (e) Comparison of the 18th trace. |
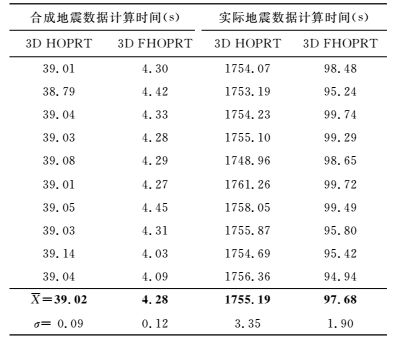
为检测3D快速高阶抛物Radon变换的计算效率,表 1给出了3D FHOPRT和3D HOPRT对上述合成地震数据和实际地震资料发生一次迭代的重建计算时间对比结果,重建在相同计算机环境下重复实验10次. 表 2为合成地震数据和实际地震数据重建时的实验参数. 表 3为程序运行时的计算机环境.由表 1可以看出,对该合成地震数据,3D FHOPRT方法相对于3D HOPRT计算效率提高了7倍以上;对该实际地震资料,3D FHOPRT方法相对于3D HOPRT计算效率提高了16倍以上.
|
|
表 1 3D FHOPRT和3D HOPRT方法计算效率对比 Table 1 Comparison of computational efficiency of 3D FHOPRT and 3D HOPRT |
|
|
表 2 合成地震数据和实际地震数据的实验参数 Table 2 Experimental parameters of real seismic data and synthetic seismic data |
|
|
表 3 计算机环境 Table 3 Computer environment |
快速算法节省计算时间的多少主要取决于频率切片个数和变换算子矩阵大小.频率切片个数与重建选取的频带范围有关,频带范围越宽,频率切片越多.变换算子矩阵大小与参数采样个数有关,采样个数越多,变换算子矩阵越大.对不同频率切片个数和参数采样个数的情况,快速高阶算法相对于标准高阶算法提高的计算效率不同.下面详细分析频率切片个数和参数采样个数对计算效率的影响.
4.1 频率切片个数对计算效率的影响地震数据重建的计算过程包含了变换算子求逆和一系列其他运算,快速高阶算法只是节省了不同频率的变换算子求逆时间,其他运算仍然需要进行.频域抛物Radon变换进行地震数据重建都是按照单个频率独立计算的,快速算法所能提高的计算效率可表示为
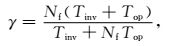
|
(18) |
式中,γ为3D HOPRT方法与3D FHOPRT方法计算时间的比值. Nf为频率切片个数,Tinv为单个频率切片进行重建时的变换算子求逆时间,Top为单个频率进行重建时的其他运算时间.由公式(18) 可以看出随着频率切片个数Nf的增加,分母项Tinv+NfTop的值逐渐趋于NfTop,当Nf→+∞,分母项中的Tinv可忽略不计,此时(18) 式变为
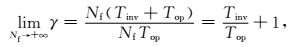
|
(19) |
Tinv和Top大小不变,当频带范围逐渐加宽,由(18)、(19) 式可以看出,快速高阶算法相对于标准高阶算法提高计算效率逐渐增大并最终会趋于稳定.
为了检测频率切片个数对计算效率的影响,对上述合成地震数据,设定参数采样个数不变,比较不同频率切片个数情况下3D快速高阶算法和3D标准高阶算法发生一次迭代的重建计算时间.表 4给出了频率切片个数从22依次至93的计算时间结果,该时间为10次重复实验的平均值.由3D FHOPRT和3D HOPRT计算时间的对比可知,随着频率切片个数的增加,快速高阶算法相对于标准高阶算法提高的计算效率从4倍以上增大到9倍以上,并最终趋于稳定.
|
|
表 4 频率切片个数对计算效率的影响 Table 4 Influence of the number of frequency slices on computational efficiency |
当参数采样个数增加时,变换算子矩阵增大;变换算子矩阵的增大会影响Tinv和Top的值.设参数采样个数为n时,单个频率下变换算子求逆时间为Tinvn,其他运算时间为Topn,并设Tinvn=kTopn,则(18) 式变为
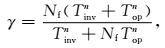
|
(20) |
(20) 式中分子分母均除Tinvn后变为
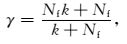
|
(21) |
一般情况下k大于1,且随着变换算子的增大,k还会逐渐增加.公式(21) 是关于k的增函数,当k增大时,快速高阶算法相对于标准高阶算法所能提高的计算效率就越高.
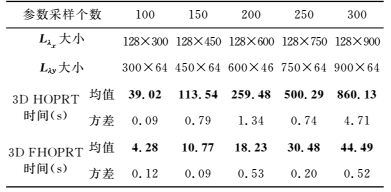
为检测变换算子矩阵大小对计算效率的影响.对上述合成地震数据,设定重建频带范围为0~50 Hz不变, 比较不同参数采样个数情况下3D快速高阶算法和3D标准高阶算法发生一次迭代的重建计算时间. 表 5给出了参数采样个数从100依次加密至300的计算时间结果,该时间为10次重复试验的平均值.由表 5可以看出,快速算法提高的计算效率从7倍以上增大到17倍以上.对参数采样密集的地震数据,其参数采样个数多,变换算子矩阵较大,快速高阶算法相对于标准高阶算法节省的计算时间越多.
|
|
表 5 3D变换算子矩阵大小对计算效率的影响 Table 5 Influence of operator matrix size on computational efficiency |
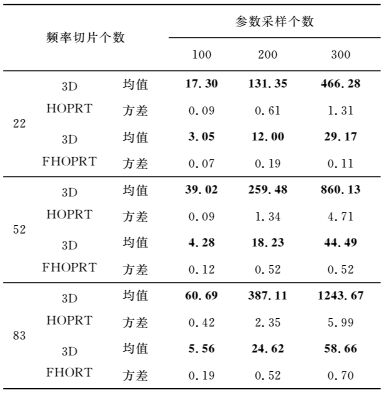
为了分析频率切片个数和变换算子大小对计算时间的联合影响,表 6给出了该合成地震数据在不同频率切片个数和不同变换算子大小的情况下,利用3D快速高阶抛物Radon变换和3D标准高阶抛物Radon变换发生一次迭代的重建计算时间,该时间为10次重复实验的平均值.由表 6可以看出该地震数据在参数采样个数为100、频率切片个数为22的情况下,利用快速高阶算法计算效率提高了4倍以上;参数采样个数为300、频率切片个数为83的的情况下,利用快速高阶算法计算效率提高了20倍以上.比较表 6中不同参数采样个数和频率切片个数情况下3D HOPRT与3D FHOPRT计算时间的比值可以发现,参数采样个数和频率切片越多,快速算法相对于标准算法提高的计算效率越高.
|
|
表 6 频率切片个数和变换算子大小对计算效率的联合影 Table 6 Joint influence of frequency slice numbers and operator matrix size on calculation efficiency |
本文针对3D AVO地震资料,提出了3D快速高阶抛物Radon变换重建地震波场的计算方法.该方法引入新变量λx=qxf和λy=qyf,通过对qxf和qyf的整体采样,消除了3D高阶抛物Radon变换算子对频率的依赖,在保证数据重建效果的基础上显著提高了计算效率.通过理论模型和实际地震资料的测试分析得到以下结论:
(1) 利用3D快速高阶抛物Radon变换对地震数据重建具有良好的保幅重建效果,重建精度与3D标准高阶抛物Radon变换一致,重建后的相位、振幅信息均良好.
(2) 3D快速高阶算法的计算效率与频率切片个数和参数采样个数成正比.利用该方法对实际地震资料进行重建,计算效率明显提升.
本文对理论模型和实际地震资料的试算均得到了良好的重建效果,使得3D快速高阶Radon变换方法在工业界的应用具有可行性.本文在解算正变换系数矩阵M(f)时采用了传统的最小二乘方法,通过构建3D Radon变换的稀疏高分辨率重建模型可以进一步提高解的精度和分辨率,这将是下一步研究方向.
致谢感谢高建军老师为本文提出的建设性意见,感谢审稿专家提出的宝贵建议.
| Abma R, Kabir N. 2006. 3D interpolation of irregular data with a POCS algorithm. Geophysics, 71(6): E91-E97. DOI:10.1190/1.2356088 | |
| Abbad B, Ursin B, Porsani M J. 2011. A fast, modified parabolic Radon transform. Geophysics, 76(1): V11-V24. DOI:10.1190/1.3532079 | |
| Biondi B, Fomel S, Chemingui N. 1998. Azimuth moveout for 3-D prestack imaging. Geophysics, 63(2): 574-588. DOI:10.1190/1.1444357 | |
| Canning A, Gardner G H F. 1996. Regularizing 3-D data sets with DMO. Geophysics, 61(4): 1103-1114. DOI:10.1190/1.1444031 | |
| Chen B Y, Ma Z T. 1994. New technic for 3D prestack migration. Chinese J. Geophys., 37(3): 400-407. | |
| Claerbout J F, Nichols D. 1991. Interpolation beyond aliasing by (t, x)-domain PEFs.//53rd EAEG Meeting. EAGE. | |
| Donati M S, Martin N W. 1995. Seismic reconstruction using a 3D tau-p transform. CREWES Research Report-Volume 7:11-1-11-16. | |
| Duijndam A J W, Schonewille M A, Hindriks C O H. 1999. Reconstruction of band-limited signals, irregularly sampled along one spatial direction. Geophysics, 64(2): 524-538. DOI:10.1190/1.1444559 | |
| Gao J J, Chen X H, Li J Y, et al. 2010. Irregular seismic data reconstruction based on exponential threshold model of POCS method. Applied Geophysics, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 | |
| Gao J J, Stanton A, Naghizadeh M, et al. 2013. Convergence improvement and noise attenuation considerations for beyond alias projection onto convex sets reconstruction. Geophysical Prospecting, 61(S1): 138-151. | |
| Ge Z J, Li J Y, Pan S L, et al. 2015. A fast-convergence POCS seismic denoising and reconstruction method. Applied Geophysics, 12(2): 169-178. DOI:10.1007/s11770-015-0485-1 | |
| Gray S H. 2014. Seismic imaging and inversion:What are we doing, how are we doing, and where are we going?//SEG Technical Program Expanded Abstracts. SEG, 4416-4420. | |
| Gulunay N, Chambers R E. 1997. Generalized f-k domain trace interpolation.//SEG Technical Program Expanded Abstracts. SEG, 1100-1103. | |
| Hampson D. 1986. Inverse velocity stacking for multiple elimination. Journal of the Canadian Society of Exploration Geophysicists, 22(1): 44-45. | |
| Hou Z Z, Xiong D, Zhang J F. 2014. Application of the preconditioned conjugate gradient method to reconstruction of seismic data. Chinese J. Geophys., 56(4): 1321-1330. DOI:10.6038/cjg20130426 | |
| Johansen T A, Bruland L, Lutro J. 1995. Tracking the amplitude versus offset (AVO) by using orthogonal polynomials. Geophysical Prospecting, 43(2): 245-261. DOI:10.1111/gpr.1995.43.issue-2 | |
| Kabir M M N, Verschuur D J. 1995. Restoration of missing offsets by parabolic Radon transform. Geophysical Prospecting, 43(3): 347-368. DOI:10.1111/gpr.1995.43.issue-3 | |
| Larner K, Gibson B, Rothman D. 1981. Trace interpolation and the design of seismic surveys. Geophysics, 46(4): 407-415. | |
| Liu X W, Liu H, Li Y M. 2004. High resolution radon transform and its application in seismic signal processing. Progress in Geophysics, 19(1): 8-15. DOI:10.3969/j.issn.1004-2903.2004.01.002 | |
| Nyquist H. 2002. Certain topics in telegraph transmission theory. Proceedings of the IEEE, 90(2): 280-305. DOI:10.1109/5.989875 | |
| Ronen J. 1987. Wave-equation trace interpolation. Geophysics, 52(7): 973-984. DOI:10.1190/1.1442366 | |
| Sacchi M D, Ulrych T J. 1995. High-resolution velocity gathers and offset space reconstruction. Geophysics, 60(4): 1169-1177. DOI:10.1190/1.1443845 | |
| Schonewille M A, Duijndam A J W. 2001. Parabolic Radon transform, sampling and efficiency. Geophysics, 66(2): 667-678. DOI:10.1190/1.1444957 | |
| Spitz S. 1991. Seismic trace interpolation in the F-X domain. Geophysics, 56(6): 785-794. DOI:10.1190/1.1443096 | |
| Tang H H, Mao W J. 2014. Amplitude preserved seismic data reconstruction by 3D high-order parabolic Radon transform. Chinese J. Geophys., 57(9): 2918-2927. DOI:10.6038/cjg20140917 | |
| Tang H H, Xu Q R, Mao W J. 2016. Applications of 3D multiple frequency high-order parabolic radon transform in amplitude preserved data regularization.//78th EAGE Conference and Exhibition. Vienna, Austria:EAGE. | |
| Thorson J R, Claerbout J F. 1985. Velocity-stack and slant-stack stochastic inversion. Geophysics, 50(12): 2727-2741. DOI:10.1190/1.1441893 | |
| Trad D. 2001. Implementations and applications of the sparse Radon transform[Ph. D. thesis]. Vancouver, Canada:The University of British Columbia. | |
| Trad D, Ulrych T, Sacchi M. 2003. Latest views of the sparse Radon transform. Geophysics, 68(1): 386-399. DOI:10.1190/1.1543224 | |
| Trad D O, Ulrych T J, Sacchi M D. 2002. Accurate interpolation with high-resolution time-variant Radon transforms. Geophysics, 67(2): 644-656. DOI:10.1190/1.1468626 | |
| Wang W H, Pei J Y, Zhang J F. 2007. Prestack seismic data reconstruction using weighted parabolic Radon transform. Chinese J. Geophys., 50(3): 851-859. DOI:10.3321/j.issn:0001-5733.2007.03.026 | |
| Whittaker E T. 1915. On the functions which are represented by the expansions of the interpolation theory. Proc. Roy. Soc. Edinburgh, 35: 181-194. DOI:10.1017/S0370164600017806 | |
| Zhang P, Zhang Y Q, Lu W K. 2013. A new 3D high resolution tau-p transform.//75th EAGE Conference and Exhibition. EAGE. | |
| 陈必远, 马在田. 1994. 三维叠前偏移新技术. 地球物理学报, 37(3): 400–407. | |
| 霍志周, 熊登, 张剑锋. 2013. 预条件共轭梯度法在地震数据重建方法中的应用. 地球物理学报, 56(4): 1321–1330. DOI:10.6038/cjg20130426 | |
| 刘喜武, 刘洪, 李幼铭. 2004. 高分辨率Radon变换方法及其在地震信号处理中的应用. 地球物理学进展, 19(1): 8–15. DOI:10.3969/j.issn.1004-2903.2004.01.002 | |
| 唐欢欢, 毛伟建. 2014. 3D高阶抛物Radon变换地震数据保幅重建. 地球物理学报, 57(9): 2918–2927. DOI:10.6038/cjg20140917 | |
| 王维红, 裴江云, 张剑锋. 2007. 加权抛物Radon变换叠前地震数据重建. 地球物理学报, 50(3): 851–859. DOI:10.3321/j.issn:0001-5733.2007.03.026 | |
 2017, Vol. 60
2017, Vol. 60