2. 中国地震局地球物理研究所, 北京 100081;
3. 广东省地震局, 广州 510000
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China;
3. Earthquake Administration of Guangdong Province, Guangzhou 510000, China
K指数最早由Bartels等(1939)提出,后由IAGA观测规范所采纳,是目前最为通用的地磁活动性指数之一.K指数以3小时为一时段,用0、1、…、9分10级来表示地球变化磁场受外源场影响的程度,是磁层电离层电流体系引起磁场扰动程度的客观监测指标.K值大小由各个时段的纯干扰变化幅度决定,纯干扰变化幅度就是消除了太阳静日变化和太阴日变化之后的纯属地磁扰动的幅度(徐文耀, 2003, 2009).
磁层电离层电流体系对地球磁场的影响存在经度效应(也称为地方时效应),为了得到全球性的地磁活动指标,从全球地磁台网选择13个台站,用它们的K指数分别求出每个台站的标准化指数KS,然后用这些KS指数的平均值确定一种新指数,称为行星性(或国际)3小时磁情指数,记作Kp.Kp取值范围为0~9,共28级:00、0+、1-、1、1+…9-、90.需要注意的是:这13个台站全部是位于地磁纬度44°N到60°S之间的高纬地磁观测天文台(徐文耀, 2003, 2009),而且主要分布在欧洲和北美.虽然Kp比K更具有全球意义,但Kp毕竟是从13个高纬地磁台站的K指数平均得到,并不能完全消除纬度影响.K指数作为区域性地磁场扰动程度的一个指标仍然具有重要意义,K指数已成为地磁台站的常规产出内容之一.
一个单一的K指数,描述世界时(UT)3小时段单一观测点的地磁活动特征,其值是根据扣除了当天非K变化(Sq,Cr)后水平分量的变化幅度来确定的.K指数共分10个级别,每3小时的K指数是0~9中的一个数字,对应于所测到的两个水平分量H、D(或者X、Y)变化幅度中较大的一个(Bartels, 1957; 程安龙,1998;徐文耀, 2003, 2005, 2009).K指数测量的关键在于,如何识别出所谓的非K变化、也即在磁静日情况下地磁分量“本该”呈现出的SR光滑变化曲线.
在地磁三分量观测均为模拟图纸的时代,台站工作者根据Mayaud提出的估计非K变化的规则,从模拟地磁图上估计SR(规则日变化)曲线,人工测量K指数.虽然人工方法一定程度上依赖于台站工作者个人主观因素,但实践证明一致性尚好,不同工作者测定结果的最大差别不会超过一个单位(Menvielle et al., 1995).
随着地磁台站工作的数字化和自动化,使用计算机软件生成K指数已势在必行.Menvielle等(1995)对12种计算K指数的方法进行了统计分析对比后指出:“在计算机自动计算K指数和人工量算K指数之间所做的一些比较显示,只有FMI和ASm两种自动计算方法与人工量算有很好的一致性.最好的FMI方法和传统的人工方法得到的K值之间几乎没有任何的跳跃(低K(K=0) 除外)”.然而,国际上关于K指数的自动计算方法并没有达成共识,目前所有向International Real-time Magnetic Observatory Network (下文简称:INTERMAGNET)上传数据的台站仍然使用各自的计算方法生成并上报K指数.
计算K指数的思路是:先用台站观测的分钟值数据分别计算两个水平分量(H、D或者X、Y)的规则日变化SR,然后用分钟值数据减去SR得到两者的残差,最后用每3小时两个水平分量中的残差较大者来确定K值大小.因此,不同K指数计算方法的根本区别在于规则日变化SR的确定方法不同,其他过程完全一致.
单个台站的K指数具有明显的日变化,地方子夜时段相对稳定,而正午前后扰动较大.该日变化也呈现出明显的季节和纬向差异.在Kp指数的计算过程中,已经应用Bartels等(1949)提出的标准化算法,剔除了K指数的日变化.该标准化算法大致为:应用指定的13个台站1943~1948的K指数推算出每个台站的标准化表,标准化表与0~9每个K值出现的时段相关(Kp指数网站, http://www.gfz-potsdam.de/Kp-index/).其他台站K值因为没有可用的标准化表,从而无法去除日变化.
自2000年起,中国地磁台网经过“九五”、“十五”两次改造,大约于2007年底开始全面进入数字化观测时代,K指数人工量算已不再可能,中国地磁台网亟需一套成熟可靠的数字化K指数自动计算方法及软件.国家地磁台网中心于2007年正式引入FMI方法来计算K指数,在使用过程中发现FMI方法存在一些不足之处.本文对这些不足之处进行了说明,并提出了相应的改进措施,将计算结果分别与原FMI方法、Kp指数以及INTERMAGNET年度光盘中台站用其他方法(Asm、LRNS、USGS)计算的K值进行一致性比较,以检验改进措施的有效性.
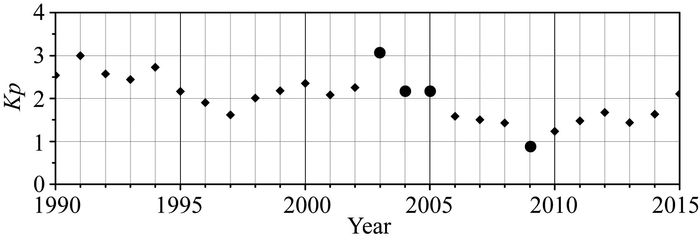
2 选用资料和研究方法 2.1 选用资料本文选用的资料时间段为2003—2005年,2009年共4年时间,图 1为1990—2015年期间的Kp指数历年均值,2003年Kp指数年均值最高,2009年最低,2004—2005年大概处于中间水平.选用资料的时间段包含了一个磁场扰动最强的年份,一个最弱的年份,两个处于中间水平的年份,以此保证K值在0~9之间有足够的样本数.
|
图 1 1990—2015年期间Kp指数历年均值 Fig. 1 Annual Kp indices from 1990 to 2015 |
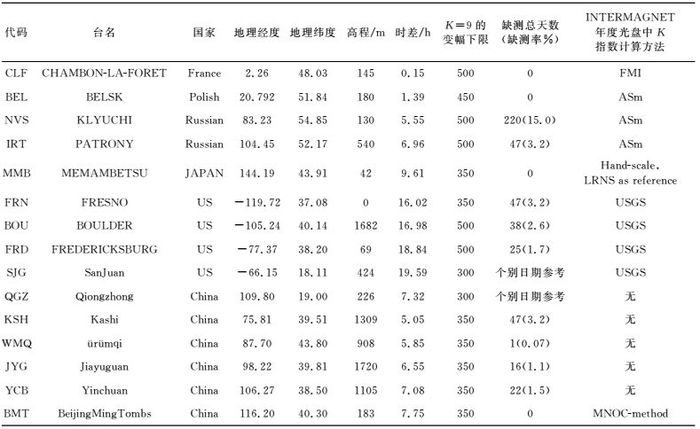
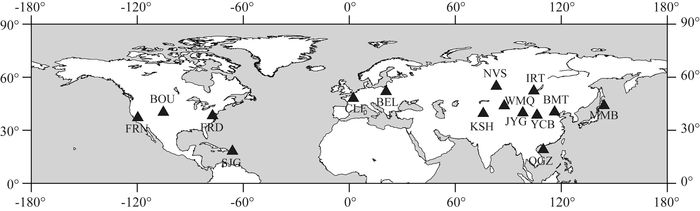
表 1为本文中选用台站的基本信息,图 2为选用台站空间分布图.由于部分台站在这个时间段内缺测较多或者数据质量不好,或者上传给INTERMAGNET的K值很差,为了增强比对效果,本文选择40°N附近数据质量较好的地磁台站进行对比分析(SJG和QGZ两个台站处于中低纬度,仅用于个别日期判定).
|
|
表 1 本文中引用选用地磁台站的基本信息 Table 1 List of the geomagnetic observatories selected in this paper |
|
图 2 本文中选用地磁台站的空间分布图 Fig. 2 Location of the geomagnetic observatories selected in this paper |
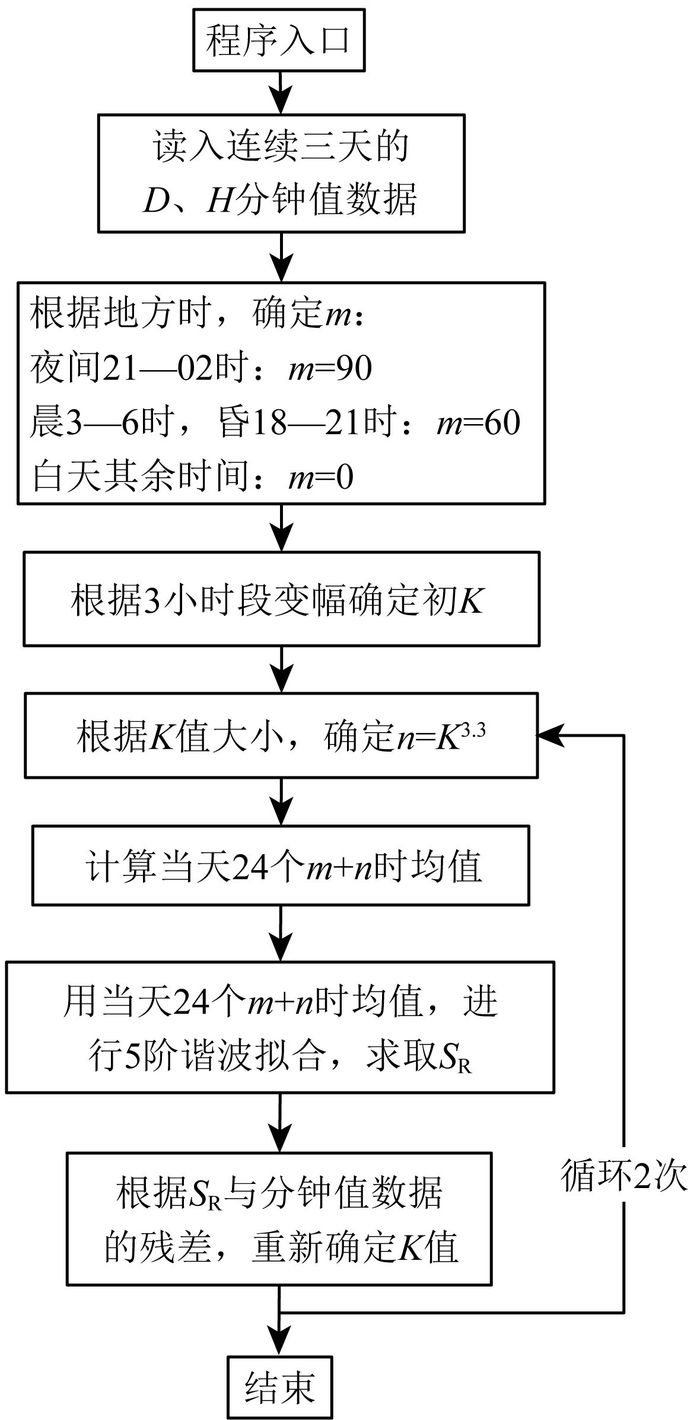
FMI方法由Finnish Meteorological Institute (芬兰气象研究所, FMI)研制.图 3为FMI方法(V1.0) 的计算流程,详细解释如下:
|
图 3 原FMI方法计算流程 Fig. 3 Flow path of the FMI method |
用来生成一天Sq曲线的24个值,都是每一世界时及其两端各m+n分钟之内所有分钟值资料的平均值HR.数据窗口的大小随m和n的大小变化而滑动.m与地方时有关,每3个小时取一个相同的值:白天为0分,黎明3—6时和傍晚18—21时为60分,而午夜为90 min.n取决于地磁活动性,定义为n=(取整)K3.3min (Bitterly, 2000; 杨马陵,2004).
具体计算步骤为:① 直接根据三小时段变幅确定n所用的初K值.② 用一个5次协和函数拟合所得到的HR值,得到SR曲线,继而得到新的K值.③ 用所得到的新K值重新确定n,再用5次协和函数拟合新的HR值得到最后的SR曲线,从而得到最后的K指数值(SR拟合时所用到的5次协和函数,实际是观测数据中包括的从大到小前5个周期,这5个周期依次为24、12、8、6、4.8 h).
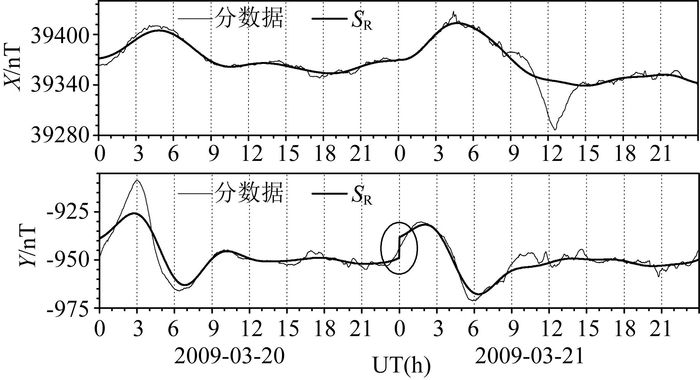
2.3 原FMI方法的不足之处对FMI方法计算的K值与Kp指数进行比较后发现,两者在中国区域内出现“不同台站之间K1~K8两头离散、K值整体高出Kp约0.5个单位”的现象.图 4为2009年40°N附近5个中国地磁台(自东向西均匀分布)的K指数年均值,从图中可很明显地看出上述现象.进一步检查后发现还存在“个别日期SR计算错误、相邻日期SR频繁出现跨天台阶”现象,图 5为QGZ台站2009年3月20—21日连续两天的SR图形,SR(Y)在3月20日明显计算错误,3月21日出现跨天台阶(图中圆圈处).

|
图 4 FMI方法计算K指数年均值(2009年) Fig. 4 Annual K indices of 2009 derived with the FMI method |
|
图 5 2009年3月20—21日QGZ台X、Y分均值数据和FMI方法计算出的SR对比(图中圆圈处为跨天台阶) Fig. 5 Comparison between the X, Y minutely averages and the SR derived with the FMI method at QGZ on march 20—21, 2009 (The circle indicates the step between the SR on march 20 and that on march 21) |
针对FMI方法计算K值在中国区域内出现的若干问题,在对其计算思路做详细研究后提出了四项改进措施,依次标记为L、S0、30、H105,原FMI方法标记为UT24.例如:UT24L表示在原方法上进行了L改进,UT30H105S0L表示进行了L、S0、30、H105共四处改进.具体的改进方法及原因如下:
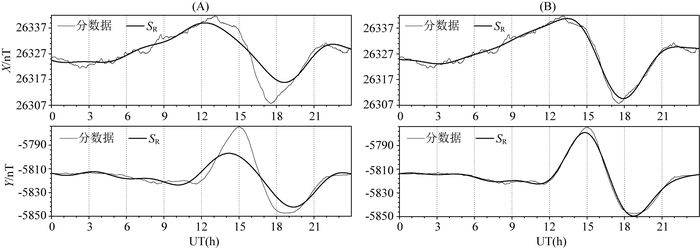
(1) 改进循环次数(L):K值计算时的循环次数原方法为2次,改进为10次(含初K循环),如果当前计算K值与上一次完全一样时提前退出循环.此处改进是为了解决“个别日期的SR计算错误”现象,因为原方法中的初K值由三小时变幅确定,往往初K值很高,偶尔会出现2次循环后仍未计算出正确的SR就提前结束,从而导致SR计算错误.图 6A中原FMI方法(UT24) 的SR(X)和SR(Y)明显计算错误,图 6B增加L改进后循环至第8次才退出,SR(X)和SR(Y)正确.
|
图 6 2009年1月7日SJG台X、Y分均值数据和分别用UT24方法(A)以及UT24L方法(B)计算出的SR对比 Fig. 6 Comparison between the X, Y minutely averages and the derived SR with the UT24 method (A) and the UT24L method (B) at SJG on Jan. 7, 2009 |
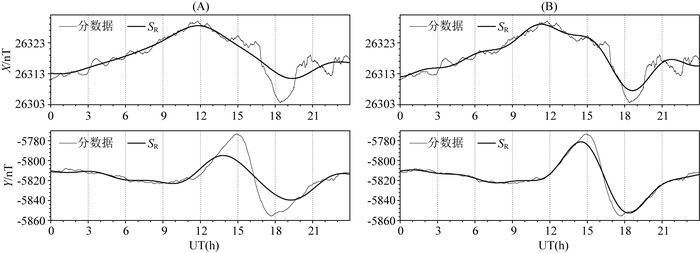
(2) 改进初K计算方法(S0):原方法根据3小时段变幅来确定初K,改进为由24个时均值进行SR拟合,然后根据残差来确定初K.通过此处改进,试图让初K值更为接近真实K值,尽可能避免“个别日期的SR计算错误”现象.图 7A为L改进(UT24L)后的结果,Y分量循环至第3次时因为当前K值与上一次K值完全相同导致循环过程提前终止,但SR(Y)计算结果却明显错误,图 7B增加S0改进后SR(Y)正常.
|
图 7 2009年1月15日SJG台X、Y分均值数据和分别用UT24L方法(A)以及UT24S0L方法(B)计算出的SR对比 Fig. 7 Comparison between the X, Y minutely averages and the derived SR with the UT24L method (A) and the UT24S0L method (B) at SJG on Jan. 15, 2009 |
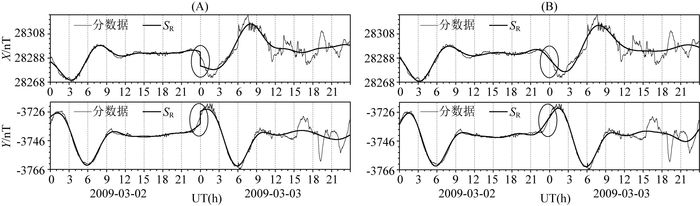
(3) 改进SR拟合时参与的时均值个数(30):进行SR值拟合时,原方法为24个m+n时均值参与拟合,改进为30个时均值(前一天后三个时均值+当天24个m+n时均值+下一天前三个时均值)参与拟合.因为原方法中当天的24个m+n时均值在进行SR拟合时没有考虑前后两天的曲线走势,以此来解决“K1~K8两头离散或翘起、相邻日期SR频繁出现跨天台阶”现象.图 8A为L、S0两种改进(UT24S0L)后X、Y分量SR出现跨天台阶现象(图中圆圈处),图 8B增加30改进后跨天台阶现象基本消失(图中圆圈处).
|
图 8 2009年3月2—3日BMT台X、Y分均值数据和分别用UT24S0L方法(A)以及UT30S0L方法(B)计算出的SR对比(图中圆圈处为跨天台阶) Fig. 8 Comparison between the X, Y minutely averages and the derived SR with the UT24S0L method (a) and the UT30S0L method (B) at BMT on March 2—3, 2009 (The circles indicate the steps between the SR on march 2 and that on march 3) |
(4) 改进非扰日期的SR谐波拟合阶数(H105):原方法为5阶,非扰日期时改进为10阶(周期依次为24、12、8、6、4.8、4、3.4、3、2.7、2.4 h).非扰日期界定方法:首先以拟合阶数为10循环计算K值,如果8个K值全部小于5,该日期视为非扰日期,否则视为扰动日期.判定为扰动日期后,该日期的拟合阶数仍按照5阶进行计算,这是因为磁场扰动越大时,正确的SR曲线也应该趋近于静日变化形态,此时不宜再增加拟合阶数以致SR出现更多波动.
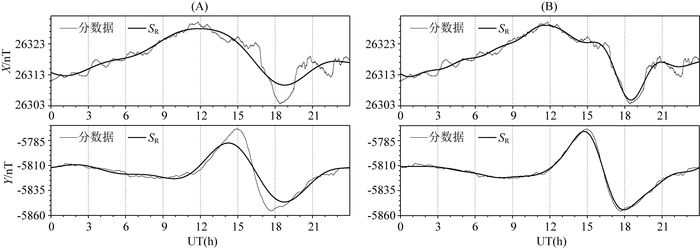
此处改进通过增加非扰日期的谐波拟合阶数,使SR和观测值的拟合度更高,此时计算K值将会减小,以此来解决“K值整体高出Kp约0.5个单位”现象.图 9A为L、S0、30三种改进(UT30S0L)后,SR(Y)与原始分钟值相差较大,图 9B增加H105改进后SR(Y)拟合效果明显更好.
|
图 9 2009年1月15日SJG台X、Y分均值数据和分别用UT30S0L方法(A)以及UT30H105S0L方法(B)计算出的SR对比 Fig. 9 Comparison between the X, Y minutely averages and the derived SR with the UT30S0L method (A) and the UT30H105S0L method (B) at SJG on Jan. 15, 2009 |
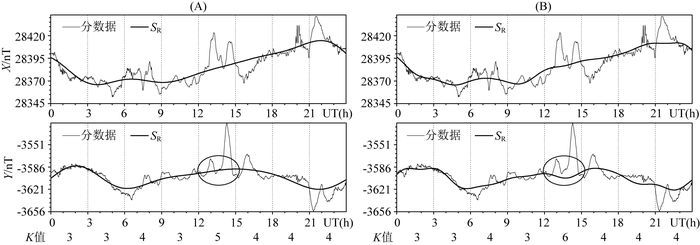
图 10为L、S0、30三种改进(UT30S0L)基础上SR谐波拟合5阶与10阶在磁扰日的对比,图 10B为10阶,明显比5阶(图 10A)增加了一些短周期波动,尤其是第5个3小时段(图中圆圈处),计算K值由5变为6.显然,在磁扰日5阶谐波要更为合理一些.
|
图 10 2003年3月17日BMT台X、Y分均值数据和用UT30S0L方法5阶谐波拟合(A)以及10阶谐波拟合(B)计算出的SR对比 Fig. 10 Comparison between the X, Y minutely averages and the derived SR with the 5 order harmonic fitting UT30S0L method (A) and the 10 order harmonic fitting UT30S0L method (B) at BMT on March 17, 2003 |
选定8个40°N附近的国际地磁台站CLF、BEL、NVS、IRT、MMB、FRN、BOU和FRD,从INTERMAGNET年度光盘中导入2003—2005年,2009年这4年期间的分钟值观测数据和K指数,然后分别用改进前的FMI方法(UT24) 和改进后的FMI方法(UT30H105S0L)计算K指数,INTERMAGNET年度光盘中各台站用其他方法计算的K值标记为“UTVcd”.
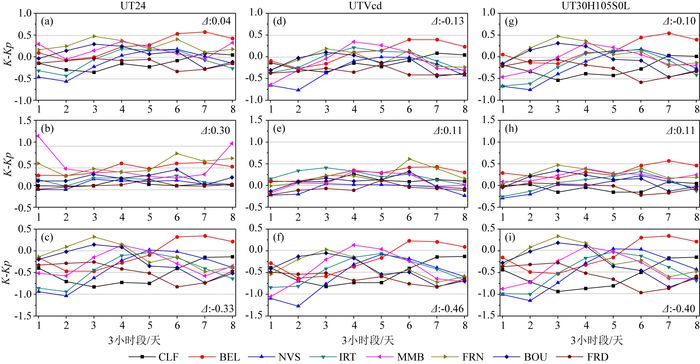
图 11为这三种方法的通、静、扰日K-Kp差值结果.图中K-Kp两者的差值在每个台站的地方子夜时段相差较小,正午时段相差较大,这是因为Kp已经使用标准化算法去除了K指数日变化,而计算K指数无法去除日变化所致.UT24在磁静日(图 11b)出现“不同台站之间K1~K8两头离散”现象,日本的MMB台表现最为明显,UTVcd和UT30H105S0L计算结果明显改善.从Δ数值大小来看,UTVcd和UT30H105S0L在通、静、扰日(图 11(d, e, f, g, h, i))均非常接近,说明改进后的FMI方法和国际其他方法(Asm、LRNS、USGS)计算的K值更为接近.
|
图 11 用UT24(a, b, c)、UTVcd (d, e, f)和UT30H105S0L (g, h, i)三种方法计算的国际8台K-Kp通日(a, d, g,)、静日(b, e, h)、扰日(c, f, i)差值(Δ为K-Kp总平均值) Fig. 11 Difference between K and Kp of 8 abroad observatories on the all, quietest and disturbed days respectively. The K indices are derived with UT24, UTVcd and UT30H105S0L methods respectively (The Δ indicates the average K-Kp) |
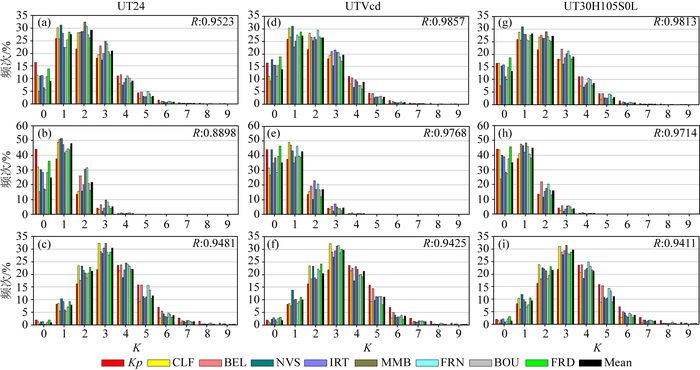
图 12为上述三种方法的通、静、扰日K值频次分布图.UT24在通日(图 12a)相对于Kp的“0低2高”现象非常明显,UTVcd和UT30H105S0L明显改善.UTVcd、UT30H105S0L在通日和静日(图 12(d, e, g, h))的R值明显高于UT24,说明这两种方法在通日和静日与Kp更为接近;它们之间的R值相差很小,说明这两种方法之间也很接近.三种方法在磁扰日(图 12(c, f, i)的R值相差很小,说明它们在磁扰日的K值非常接近.
|
图 12 用UT24(a, b, c)、UTVcd (d, e, f)和UT30H105S0L (g, h, i)三种方法计算的国际8台通日(a, d, g)、静日(b, e, h)、扰日(c, f, i)K值频次分布图 R值为8个台站的频次均值与Kp频次的相关系数. Fig. 12 K frequency of 8 abroad observatories on the all, quietest and disturbed days respectively The K indices are derived with UT24, UTVcd and UT30H105S0L methods respectively. The R indicates the correlation coefficients between the average K frequency of 8 international observatories and the Kp frequency. |
选定5个40°N附近的中国台站KSH、WMQ、JYG、YCB和BMT,导入2003—2005年,2009年这4年的分钟值观测数据,分别用改进前的FMI方法(UT24) 和改进后的FMI方法(UT30H105S0L)计算K指数.
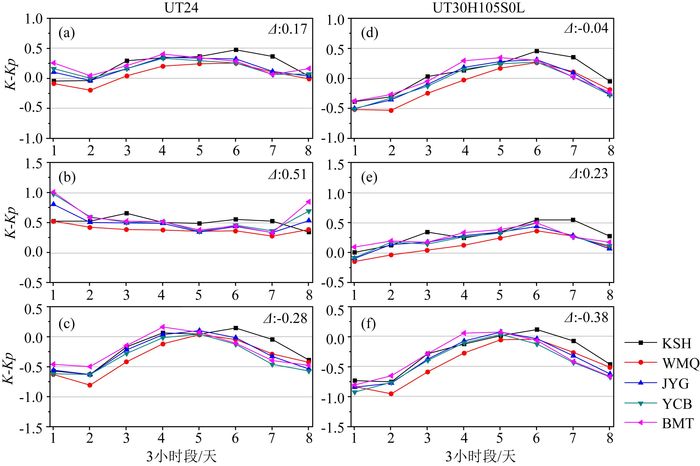
图 13为这两种方法的通、静、扰日K-Kp差值结果.图中K-Kp差值在地方子夜时段相差较小,正午时段相差较大.5个台站的经度相差范围大约40°(时差约2.7 h),自东向西有明显的相位差(图 13(c, d, f)),但因为经度相差不大,5个台站之间的K-Kp差值有很好的一致性.UT24在磁静日(图 13b)表现出“不同台站之间K1~K8两头离散”现象,自西向东愈加明显,K值高出Kp约0.5个单位,UT30H105S0L计算结果明显改善.
|
图 13 用UT24(a, b, c)和UT30H105S0L (d, e, f)两种方法计算的中国国内5台站K-Kp通日(a, d)、静日(b, e)、扰日(c, f)差值 (Δ为K-Kp总平均值) Fig. 13 Difference between K and Kp of 5 observatories of China on the all, quietest and disturbed days respectively. The K indices are derived with UT24 and UT30H105S0L methods respectively (The Δ indicates the average K-Kp) |
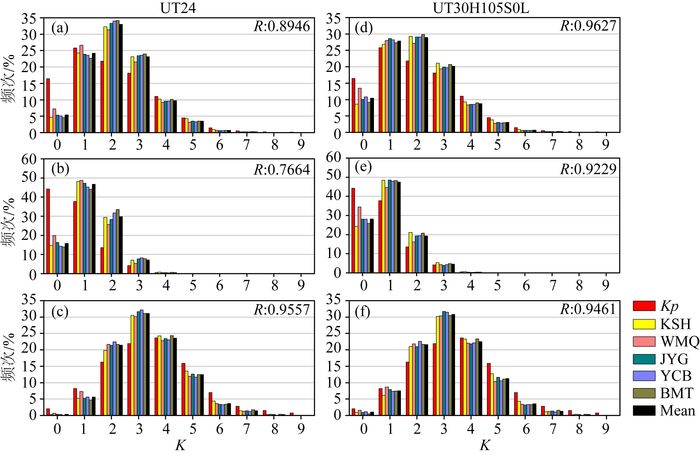
图 14为上述两种方法的通、静、扰日K值频次分布图.UT24在通日(图 14a)相对于Kp的“0低2高”现象非常明显,UT30H105S0L已有明显改善但并未消除.UT30H105S0L在通日和静日(图 14d, e)的R值明显高出UT24很多,说明它在通日和静日与Kp更为接近;两种方法在磁扰日(图 14c, f)的R值相差很小,说明它们在磁扰日期的K值非常接近.
|
图 14 用UT24(a, b, c)和UT30H105S0L (d, e, f)两种方法计算的中国国内5台站通日(a, d)、静日(b, e)、扰日(c, f)K值频次分布图 R值为5个台站的频次均值与Kp频次的相关系数. Fig. 14 K frequency of 5 observatories of China on the all, quietest and disturbed days respectively. The K indices are derived with UT24 and UT30H105S0L methods respectively. The R indicates the correlation coefficients between the average K frequency of 5 observatories of China and the Kp frequency. |
太阳静日变化Sq主要由1~4次谐波组成,它们的周期分别是24、12、8、6 h,其振幅依次减小(徐文耀,2009).赵旭东等(2014)选取1~8次谐波来表示磁静日的变化,通过将快速傅里叶(FFT)变化的拟合结果与台站观测结果进行对比,8次谐波能较好地反映太阳静日变化.8次及更高次的谐波系数幅度非常小且稳定,基本上趋近于0(赵旭东,2014).改进后的FMI方法将原方法中的5阶调整为:非扰日期时使用10阶,可使SR中增加一些较小周期成份,使其SR和原始观测值的拟合度更高;扰动日期时仍用5阶不变,因为磁场扰动越大时,正确的SR曲线应该越趋近于静日变化的形态,此时不宜再增加拟合阶数以致SR出现更多波动.
FMI方法的K值频次分布相对于Kp的“0低2高”现象,与IAGA磁情工作组在1991年的分析结果一致:FMI方法总是在K=2为最高的单峰分布,并且在K=0的频次总是远远低于其他方法(Menvielle et al., 1995).改进后的FMI方法有明显好转,但仍未彻底消除此现象.
针对FMI方法在磁静日(图 11b,图 13b)出现的“不同台站之间K1~K8两头离散”现象,日本的MMB台最为明显,中国地区次之,而欧美的台站却不明显.该现象通过改进SR拟合时参与的时均值个数,考虑前后两天的曲线走势后基本消失.图 15(a, b, c)为8个国际台站的地方时(LT)数据曲线,可以看出LT6h-18h通常为地磁日变化最大时段,LT12时大概是这个时间段的中心位置.图 15d为台站在LT时间轴上对应的UT00时间.中国的JYG、YCB、BMT,以及其他国际台站(IRT、MMB、FRN、BOU)的UT00时间正好处于日变化最大时间段内,FMI原方法由于未考虑前后两天的曲线走势导致UT00时的SR曲线失真,应该对这些台站UT00时段的计算K值影响最大,而其他欧美台站因为UT00时间大多对应于磁场平静时段,所以受到影响较小.也就是说台站UT00时间距离其LT12h越近,其UT00时段计算K值受到的影响应该越大,距离越远受到的影响应该越小,这应该是上述“K1~K8两头离散现象,日本的MMB台最为明显,中国地区次之,而欧美的台站却不明显”的根本原因.

|
图 15 2009年1月12日8个国际台站的X、Y、Z分量的地方时数据曲线(a, b, c)和各台站在LT时间轴上对应的UT=00的时间点(d) Fig. 15 X, Y, Z variation of 8 abroad observatories on local time on Jan. 12, 2009 (a, b, c) and the indications of UT=00 for each observatory (d) |
单台K指数具有明显的日变化,从而造成K-Kp的差值出现与地方时相关的拱形形态:地方子夜时段相差较小,正午时段相差较大.这是因为Kp指数已经通过标准化消除了日变化,而单台计算K指数无法消除日变化所致,因此也会造成两者比较时出现一定的偏差.但目前除了Kp指数外再无法找到比它更为合适的能够描述全球地磁场活动程度的标准化指数.因此,针对不同台站的K指数,如何能寻找到一种更为科学的标准化算法,让每个台站通过该标准化算法剔除K值日变化后再去比较,这是我们下一步工作的重点.
4.2 结论通过对FMI方法计算的K值与Kp指数进行比较后发现,两者在中国区域内出现“不同台站之间K1~K8两头离散、K值整体高出Kp约0.5个单位、个别日期SR计算错误、相邻日期SR频繁出现跨天台阶”现象.为改善这些现象,我们对FMI方法计算思路进行详细研究后提出了四项改进措施,并对改进前后的效果进行了比对.通过改进循环次数和初K计算方法,改善了“个别日期SR计算错误”现象;通过增加SR拟合时参与的时均值个数,改善了“K1~K8两头离散或翘起、相邻日期SR频繁出现跨天台阶”现象;通过增加非扰日期的SR谐波拟合阶数,改善了“K值整体高出Kp约0.5个单位”现象.
为检验改进后的FMI方法,基于40°N附近的8个国际地磁台站和5个中国地磁台站4年的分钟值观测数据,利用改进前的FMI方法(UT24) 和改进后的FMI方法(UT30H105S0L)计算K指数,并与INTERMAGNET年度光盘中相应台站用其他方法计算的K值(UTVcd)进行对比分析.分析结果表明:
(1) FMI原方法K-Kp差值出现的“不同台站之间K1~K8两头离散,相邻日期SR频繁出现跨天台阶”现象,是由于当天的24个m+n时均值在进行SR拟合时未考虑前后两天的曲线走势,导致UT00时的SR曲线失真,改进后的FMI方法在考虑前后两天的曲线走势后,此现象基本消失.K1~K8两头离散现象,日本的MMB台最明显,中国地区次之,而欧美的台站却不明显.这是因为就UT00时的SR曲线失真而言,如果台站的UT00时间距离其LT12h越近,其计算K值受到的影响越大,距离越远受到的影响越小.
(2) 在通日和静日,UTVcd和UT30H105S0L两种方法与Kp更为接近,而且这两种方法之间也非常接近.在磁扰日,三种方法相差很小.
从对比结果可看出,改进后的FMI方法与Kp指数和国际其他K指数计算方法(Asm、LRNS、USGS)的结果更为接近,并且在通日和静日都明显优于原方法.
致谢本文中用到的地磁台站数据来自INTERMAGNET地磁台网和中国地震局地球物理研究所国家地磁台网中心,国际地磁静扰日列表来自日本京都世界地磁数据中心,在此表示诚挚的谢意.
| Bartels J, He ck, N H, Johnston H F. 1939. The three-hour-range index measuring geomagnetic activity. Journal of Geophysical Research, 44(4): 411-454. DOI:10.1029/TE044i004p00411 | |
| Bartels J.1949.The standardized index Ks and the planetary index Kp. IATME Bulletin 12b, 97. | |
| Bitterly M, Menvielle M, Bitterly J, et al. 2000. A comparison between computer derived (FMI method) and hand scaled K indices at Portaux Francais and Port Alfred French Observatories. | |
| Cheng A L, Zhou J P, Huang W B, et al. 1998. Analysis of measured K indices in geomagnetic observatory network of China. Seismological and Geomagnetic Observation and Research, 19(2): 48-55. | |
| Menvielle M, Papitashvili N, Häkkinen L, et al. 1995. Computer production of K indexes:review and comparison of methods. Journal of Geophysical Research, 123(3): 866-886. DOI:10.1111/gji.1995.123.issue-3 | |
| Xu W Y. 2003. Geomagnetism. Beijing: Seismological Press. | |
| Xu W Y. 2005. Improvement of scaling and evaluating of K index. Northwestern Seismological Journal, 27(S1): 36-41. | |
| Xu W Y. 2009. Physics of Electromagnetic Phenomena of the Earth. Hefei: University of Science and Technology China Press. | |
| Yang M L, Liu C M, Ye D H, et al. 2004. Preliminary study of computing K indices with FMI method. Seismological and Geomagnetic Observation and Research, 25(2): 55-61. | |
| Zhao X D, Yang D M, He Y F, et al. 2014. The study of Sq equivalent current during the solar cycle. Chinese J. Geophys., 57(11): 3777-3788. DOI:10.6038/cjg20141131 | |
| 程安龙, 周锦屏, 黄蔚北, 等. 1998. 中国地磁台网的K指数测量结果分析. 地震地磁观测与研究, 19(2): 48–55. | |
| 徐文耀. 2003. 地磁学. 北京: 地震出版社. | |
| 徐文耀. 2005. 地磁活动K指数值量算和确定方法的改进. 西北地震学报, 27(S1): 36–41. | |
| 徐文耀. 2009. 地球电磁现象物理学. 合肥: 中国科学技术大学出版社. | |
| 杨马陵, 刘昌谋, 叶东华, 等. 2004. FMI方法计算地磁K指数的初步研究. 地震地磁观测与研究, 25(2): 55–61. | |
| 赵旭东, 杨冬梅, 何宇飞, 等. 2014. Sq等效电流在太阳活动周中的分析研究. 地球物理学报, 57(11): 3777–3788. DOI:10.6038/cjg20141131 | |
 2017, Vol. 60
2017, Vol. 60