2. 中国石油集团测井有限公司, 西安 710077
2. China Petroleum Logging Co., Ltd, Xi'an 710077, China
自21世纪初Baker Hughes公司成功研制出第一台三维感应测井仪器3DEX以来,有关三维感应测井响应的数值模拟、资料处理以及井下仪器的改进等已成为非常重要的研究课题 (Rabinovich et al., 2007).目前,三维有限差法 (沈金松,2003;Davydycheva et al., 2009;杨守文等,2009) 和三维有限体积法 (Hou et al., 2006;张烨等, 2012;王浩森等, 2016) 等数值方法、2.5维数值模式匹配算法 (Wang et al., 2012; 汪宏年等,2012) 以及解析方法 (Liu and Chew, 1992; Wang et al., 2008a, 2009; 魏宝君等,2009; 姚东华等,2010) 均已成为解决不同情况下三维感应测井数值模拟问题的重要方法.在仪器研制方面,目前在石油工业界已经出现了4种不同类型的三维感应测井仪器,例如Baker Hughes公司3DEX (Zhdanov et al., 2001)、Schlumberger公司的RT Scanner (Davydycheva et al., 2009)、Halliberton公司的3D-Induction Xaminer (Hou et al., 2013) 以及中国石油集团测井有限公司的TDIT (朱天竹等,2017).其中,中国石油集团测井有限公司 (CPL) 研制的三维感应测井仪器由3个相互正交的发射器、4个源距相对较短的轴向接收器和4个源距相对较长的三分量接收器组成,通过3个不同工作频率以及不同源距的单轴与三轴接收器可以同时提供96条视电导率曲线.从理论上说,利用这些测井曲线能够提取地层横向与纵向电导率、层厚以及地层倾角等信息,可以有效解决各向异性储层的评价问题.
然而,由于共面线圈系受井眼环境影响很大以及视电导率值与地层电导率间存在着较强的非线性关系,导致三维感应资料处理仍然面临诸多困难 (Wang et al, 2008b; Wang, 2011; 洪德成等,2013; Yang et al., 2014;周建美等, 2014).数值模拟结果以及井场实际测井资料均证明,多分量阵列感应测井资料不仅与地层厚度、地层横向与纵向电导率以及地层倾角与方位角等相关,而且整个测井响应同样受到井眼半径、泥浆电导率、仪器偏心距与仪器自旋角等因素的影响.在测井过程中仪器往往会发生偏心与自旋,然而,人们过去对偏心问题比较重视却往往忽略了仪器自旋对测井响应的影响.最近,我们在对多分量感应的实测资料进行处理时发现,同一仪器在同一口井中进行连续两次测量所得到的多分量视电导率曲线有时会存在较大差异.按照常规测井质量评价方法,这样的曲线应该是不合格的 (重复性差).在排除了仪器的稳定性和测量误差的原因后,基本可以断定曲线重复性差是由于仪器在下井作业过程中的偏心和自旋造成的.因此,必须分析研究仪器在偏心和自旋情况下的响应特征,解决测井曲线重复性差的问题.
本文拟利用2.5维数值模式匹配算法建立一套仪器偏心与旋转情况下TDIT测井响应的数值模拟方法,并通过数值模拟结果,对仪器偏心无自旋角、仪器偏心且存在自旋角两种情况下TIDI的响应进行对比分析,总结自旋角对TDIT响应产生影响的规律,为TDIT实测资料自旋角校正预处理和反演提供理论基础.
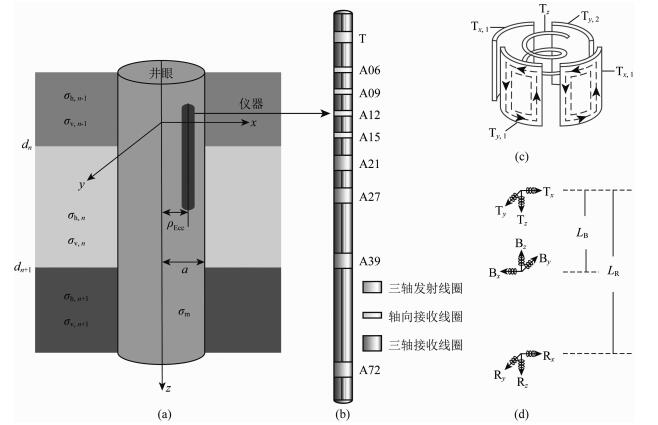
2 理论图 1a是包含井眼的水平层状非均质TI地层模型与仪器偏心示意图,其中,井眼半径和泥浆电导率分别为a和σm,地层n-1和地层n间的界面深度为dn,地层n中横向与纵向电导率分别为σh, n和σv, n,仪器偏心距为ρEcc.为简单起见,这里忽略了芯棒和侵入带的存在.图 1b是三维感应测井仪器 (TDIT) 线圈系结构示意图,整个仪器包含一个三轴发射线圈、4个短源距的轴向接收线圈 (A06、A09、A12、A15)、4个长源距的三轴接收线圈系 (A21、A27、A39、A72).图 1c是三轴发射 (三轴接收类似) 线圈系的结构示意图,其中,x和y方向的共面发射与接收线圈由对称分布在仪器芯棒两边的两个大小相同的线圈组合在一起形成的 (图 1c),其目的是便于共面线圈系的安装并保证仪器居中情况下x和y方向的两个共面电磁响应相同.在进行多分量阵列感应电磁数值模拟时,当井眼与周围地层电导率反差较大时,如果仅仅用一个位于仪器芯棒中心的x和y方向的单一磁偶极子近似模拟图 1c所示的组合型共面线圈系的电磁响应,往往会产生较大的误差.为了取得高精度的多分量电磁响应结果,必须考虑到线圈系的这种实际分布对测井响应的影响.z方向线圈则是将导线直接缠绕在仪器芯棒上形成轴向线圈.为降低直藕信号影响,在发射线圈和每对接收线圈之间加装一组屏蔽线圈系,且屏蔽线圈缠绕方向与主接收线圈相反,LR和LB分别代表接收线圈系和屏蔽线圈系到发射线圈系的距离 (图 1d).仪器采用3个不同的工作频率依次进行测量,其低、中、高频分别为26.254、52.512、105.024 kHz.
|
图 1 包含井眼的水平层状地层模型及TDIT结构 (a) 包含井眼的水平层状地层模型;(b) TDIT结构;(c) 三轴向线圈系结构;(d) 三轴向收发模块. Fig. 1 Schematic diagram of TDIT in horizontally layered TI formation with a borehole (a) Horizontally layered TI formation with borehole; (b) Schematic diagram of TDIT tool; (c) Structure of triaxial coil array; (d) Transmitter and receiver system of triaxial coil array. |
本节将在利用2.5维模式匹配算法给出水平层状非均质各向异性地层中磁流源并矢Green函数的半解析解的基础上,根据线圈系的真实结构,应用叠加原理与旋转矩阵进一步给出仪器偏心以及存在自旋角情况下多分量阵列感应测井响应的计算方法.
2.1 直井偏心水平层状非均质TI地层中并矢Green函数的计算在忽略仪器芯棒影响的情况下,图 1a中电导率的空间分布是轴对称的且具有如下的解析表达式为 (Wang et al., 2012):
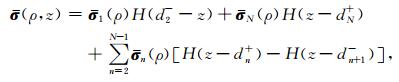
|
(1) |
其中,
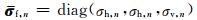

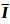
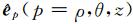
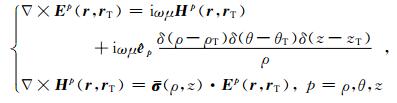
|
(2) |
其中,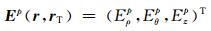
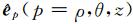

由于电导率空间分布的轴对称性,方程 (2) 是典型的2.5维电磁正演问题,利用Fourier级数展开式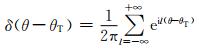
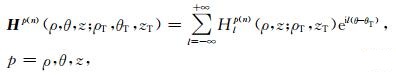
|
(3) |
其中:
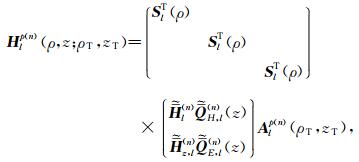
|
(4) |
它是用数值模式匹配算法得到的地层n中磁场的第l阶谐变分量;
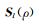
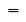
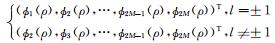
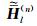
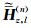
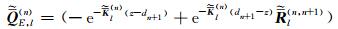
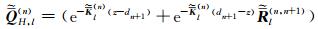
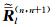
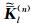
将方程 (3) 中柱坐标系下3个单位正交发射源磁场转化到直角坐标系中,可以得到直角坐标系下磁流源磁场并矢Green函数为

|
(5) |
该式右端磁场强度的第一个下标代表接收线圈的法向方向,第二个下标代表发射线圈的法向方向.
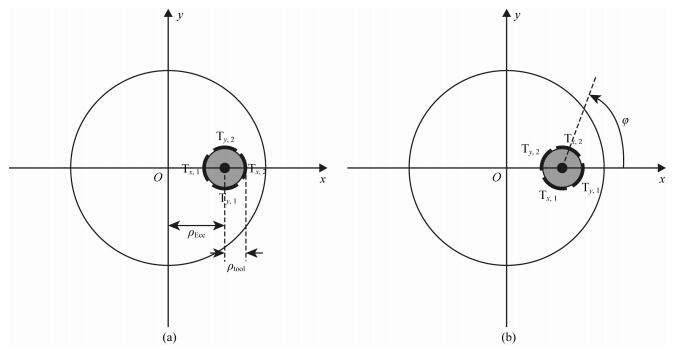
2.2 偏心与自旋角不为零情况下三维感应测井响应的计算三维感应测井仪器在井下测量过程中,不可避免的会发生偏心和自旋,不仅改变了仪器在井中的位置还影响了三轴线圈系的指向.图 2是仪器偏心情况下出现的两种可能的情况:仪器偏心但自旋角为零 (图 2a)、仪器偏心且自旋角不为零 (图 2b),其中,ρEcc和ρtool分别是仪器偏心距和仪器芯棒半径,仪器自旋角用φ表示.在图 2中建立了一个平面坐标系Oxy,其中,x轴位于井轴和仪器轴的垂直连线且坐标原点位于井轴,y轴也垂直于井轴,而z轴与井轴平行且垂直向下.当仪器偏心且自旋时,3个正交发射线圈的方向可以分别表示为Tx=(cosφ sinφ 0)T、Ty=(-sinφ cosφ 0)T和Tz=(0 0 1)T.由于三分量接收线圈与发射线圈是平行的,3个正交接收线圈方向为Rx=Tx、Ry=Ty和Rz=Tz.此外,由于x和y方向的共面发射与接收线圈对称贴附在半径为ρtool的仪器芯棒两边,因此,x方向的两个发射线圈位置为rTx, 1=(ρEcc-ρtoolcosφ, -ρtoolsinφ, zT) 和RTx, 2=(ρEcc+ρtoolcosφ, ρtoolsinφ, zT),y方向的两个发射线圈位置为rTy, 1=(ρEcc-ρtoolsinφ, -ρtoolcosφ, zT) 和rTy, 2=(ρEcc-ρtoolsinφ, ρtoolcosφ, zT).同样地,x方向的两个接收线圈位置为rRx, 1=(ρEcc-ρtoolcosφ, -ρtoolsinφ, zR) 和rRx, 2=(ρEcc+ρtoolcosφ, ρtoolsinφ, zR),y方向的两个接收线圈位置为rRy, 1=(ρEcc+ρtoolsinφ, -ρtoolcosφ, zR) 和rRy, 2=(ρEcc-ρtoolsinφ, ρtoolcosφ, zR),其中,zT和zR分别是发射与接收线圈所在的深度位置.在数值模拟过程中,为了尽可能减少Green函数的计算次数以便提高数值模拟效率,z方向发射线圈分别用与x、y方向的共面发射线圈位置相同的4个垂直方向磁流源近似,即z方向发射线圈的位置为rTz, α=rTx, α, rTz, α+2=rTy, α, α=1, 2;同样地,z方向接收线圈假定与x、y方向的4个共面接收线圈位置相同,这时z方向接收线圈的位置为rRz, α=rRx, α, rRz, α+2=rRy, α, α=1, 2.
|
图 2 井下仪器偏心与自旋情况下发射线圈位置与方向 (a) 自旋角φ=0;(b) 自旋角φ≠0. Fig. 2 Schematic diagram of position and directions for transmitting coils at the condition of eccentricity and spin (a) Spin angle φ=0; (b) Spin angle φ≠0. |
根据线圈系的这种真实分布情况下,利用叠加原理以及方程 (5) 给出的磁流源并矢Green函数的半解析表达式,可以给出发射线圈Tp(p=x, y, z)在接收线圈Rq(q=x, y, z) 上的磁场强度计算公式为
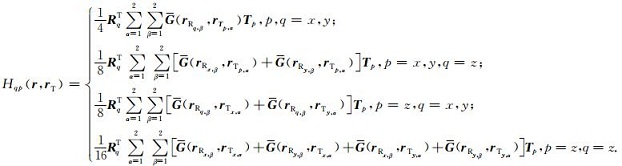
|
(6) |
从公式 (6) 可以看出,只需要利用4个不同发射位置rTx, 1、rTx, 2、rTy, 1和rTy, 2上并矢Green函数在4个不同接收位置rRx, 1、rRx, 2、rRy, 1和rRy, 2上的值就能够计算出多分量发射与接收线圈上磁场强度的9个分量,有效提高了计算效率.TDIT收发线圈系统由一个三分量发射线圈、一个三分量屏蔽线圈和主接收线圈组成 (如图 1d),因此,根据复合线圈系结构计算出复合线圈系上的磁场张量,并结合不同分量的仪器常数得到视电导率张量为 (朱天竹等,2017):
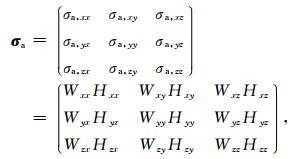
|
(7) |
其中,Wpq和Hpq(p、q=x、y、z) 分别为TDIT的仪器系数和合成磁场张量.
3 数值结果本节首先通过对比三层模型上2.5维模式匹配算法与三维有限体积算法的数值结果,检验2.5维模式匹配算法的有效性与计算效率;然后,通过一个包含井眼的7层水平层状各向异性地层模型,考察仪器偏心且自旋角φ=0°和φ=30°两种情况下三维感应测井的完整96条测井曲线,通过对比分析,了解仪器在偏心且不同自旋角情况下,不同源距的各个测井分量的响应特征与变化规律.
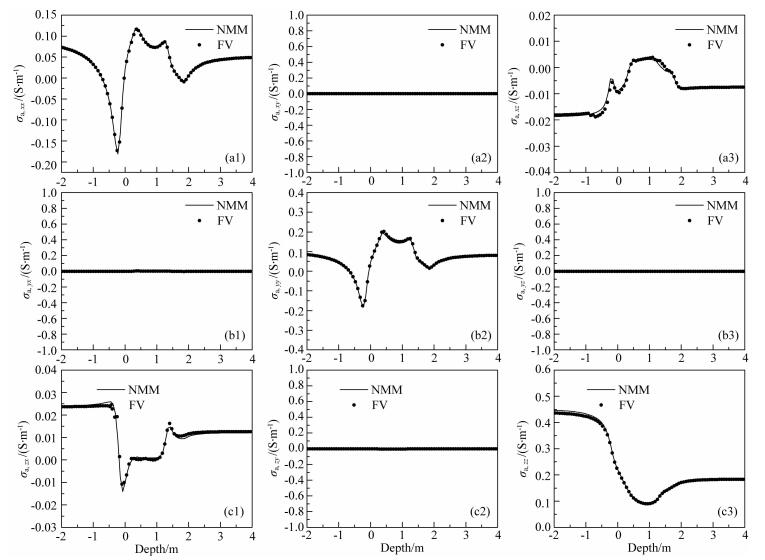
3.1 结果验证为了考察直井偏心情况下模式匹配算法的计算精度,选择一个包含井眼的三层水平层状TI地层模型,其井眼半径为0.1 m,井眼泥浆电阻率为0.5 Ωm,仪器沿x方向偏心且偏心距为0.05 m,并假定仪器自旋角为零,井眼外为三层水平分层TI地层,其横向电阻率分别为2.0、20.0、5.0 Ωm,纵向电阻率分别为6.0、80.0、12.0 Ωm,中间层厚度为2 m.TDIT采用3个不同频率、4个短源距轴向接收系统和4个长源距三轴向接收系统,可以同时采集96条不同阵列、不同频率和不同分量的测井曲线.因为计算不同阵列、不同频率的视电导率张量的核心算法类似,为了清楚起见,我们仅挑选出低频情况下阵列A21中的9个分量进行比较.图 3是仪器在偏心情况下,分别利用有限体积 (FV) 和2.5D数值模式匹配算法 (2.5D NMM) 计算的视电导率9分量的对比结果.从图中可以看出,两种方法计算的视电导率各分量均吻合得非常好,证明了利用NMM计算多分量阵列感应测井响应的有效性.利用FV同时计算上述地层模型中96条测井曲线大约需要13 h,而利用NMM算法只需2 h,说明NMM算法具有较高的计算效率.此外,从图 3中可以看出,当仪器沿x轴发生偏移且自旋角为零时,主分量σa, xx、σa, yy、σa, zz和交叉分量σa, xz、σa, zx对地层模型具有明显的响应,而剩下的4个交叉分量σa, xy、σa, yx和σa, yz、σa, zy恒为零.
|
图 3 模式匹配法 (NMM) 和有限体积法 (FV) 的计算结果对比 Fig. 3 Comparison of methods NMM and FV |
为了更系统的对TDIT 96条测井曲线进行综合分析,选取一个7层地层模型,其井眼半径为0.1 m,井眼泥浆为电阻率为100.0 Ωm的高阻泥浆.井眼外地层为水平层状TI地层,其横向电阻率分别为2.0、10.0、1.0、22.0、3.0、0.3、3.0 Ωm,纵向电阻率分别为2.0、40.0、2.0、80.0、12.0、1.5、3.0 Ωm,中间层厚分别为0.9、1.5、1.5、2.0、0.6 m.为了考察仪器偏心时,自旋角对测井响应的影响,分别计算了自旋角φ=0°和自旋角φ=30°时TDIT96条测井曲线,假定偏心距ρEcc=0.05 m.
图 4是该模型在自旋角φ=0°时,TDIT的96条测井曲线.其中,图 4a1—a3是TDIT短源距收发线圈 (A06—A15) 的响应曲线,图例A06_H和A06_M分别代表高频和中频情况下阵列线圈A06的测井响应,其余图例类似.由于阵列线圈A06—A15的源距较小,因此响应曲线均具有较高的纵向分辨率.余下的图 4b1—d3中9幅子图,分别代表长源距三分量线圈系 (A21—A72) 的测井响应,图例A21_M和A21_L分别代表中频和低频情况下阵列线圈A21的测井响应,其余图例类似.9幅图分别对应公式 (7) 中视电导率张量的各个分量.从图中可以看出,除了视电导率分量σa, xx、σa, yy、σa, zz、σa, xz和σa, zx,其余4个视电导率分量σa, xy、σa, yx、σa, yz和σa, zy恒为零.

|
图 4 TDIT 96条测井曲线 (ρEcc=0.05 m, φ=0°) Fig. 4 96 logging curves of TDIT (ρEcc=0.05 m, φ=0°) |
图 5是在相同地层模型下自旋角φ=30°时TDIT的96条测井曲线.与图 4相比,测井响应曲线更加复杂,视电导率各分量全部不为零.同一个测井仪器在同样的地层模型中,仅仅由于仪器自身的自旋,其测井曲线发生了较大变化,给测井数据带来较大的不确定性.因此,为了更准确的得到地层模型参数,在对测井资料反演前,必须根据测井资料计算仪器自旋角,对测井资料进行自旋角校正.此外,由于A72阵列源距较大,其响应对层边界的响应不够灵敏,如果让A72阵列的测井响应参与反演,势必会给地层模型参数的反演带来较大的不确定度.因此,将来的反演将主要考虑A21、A27、A39阵列线圈的测井响应.

|
图 5 TDIT 96条测井曲线 (ρEcc=0.05 m, φ=30°) Fig. 5 96 logging curves of TDIT (ρEcc=0.05 m, φ=30°) |
本文利用模式匹配算法建立了水平层状非均质各向异性地层中仪器偏心且存在自旋角情况下,三维感应测井仪器响应的数值模拟方法,该算法能够提供96条不同阵列、不同频率、不同分量的视电导率曲线.数值结果表明,仪器偏心情况下,自旋角对TDIT响应的影响很大.当仪器偏心且自旋角为零时,每组阵列的张量视电导率的9个分量中只有3个主分量和两个次主分量不为零;而当仪器偏心且自旋角不为零时,每组阵列的张量视电导率的9个分量均不为零.由于仪器在井下测量时,自旋角是不可控的,在不同采样点处,其方位角可能完全随机,所以,自旋角的存在给资料的解释和处理增加了难度,如何从测量资料中提取出自旋角角并进行自旋角校正,对于简化资料的处理是非常重要的.
| Davydycheva S, Homan D, Minerbo G. 2009. Triaxial induction tool with electrode sleeve: FD modeling in 3D geometries. J. Appl. Geophys., 67(1): 98-108. DOI:10.1016/j.jappgeo.2008.10.001 | |
| Hong D C, Xiao J Q, Zhang G Y, et al. 2013. Fast inverse the relative dip using cross-component in highly deviated well. Chinese J. Geophys., 56(7): 2494-2501. DOI:10.6038/cjg20130735 | |
| Hou J S, Mallan R K, Torres-Verdín C. 2006. Finite-difference simulation of borehole EM measurements in 3D anisotropic media using coupled scalar-vector potentials. Geophysics, 71(5): G225-G233. DOI:10.1190/1.2245467 | |
| Hou J S, Sanmartin L, Wu D G, et al. 2013. A new multi-frequency triaxial array induction tool for enhancing evaluation of anisotropic formations and its field testing.//SPWLA 54th Annual Logging Symposium. New Orleans: Society of Petrophysicists & Well Log Analysts. | |
| Liu Q H, Chew W C. 1992. Diffraction of nonaxisymmetric waves in cylindrically layered media by horizontal discontinuities. Radio Sci., 27(5): 569-581. DOI:10.1029/92RS00910 | |
| Rabinovich M, Corley B, Georgi D, et al. 2007. Multi-component induction logging: 10 years after.//SPWLA 48th Annual Logging Symposium. Austin, Texas: Society of Petrophysicists & Well Log Analysts. | |
| Shen J S. 2003. Modeling of 3-D electromagnetic responses in frequency domain by using staggered-grid finite difference method. Chinese J. Geophys., 46(2): 281-288. | |
| Wang G L, Torres-Verdín C, Gianzero S. 2009. Fast simulation of triaxial borehole induction measurements acquired in axially symmetrical and transversely isotropic media. Geophysics, 74(6): E233-E249. DOI:10.1190/1.3261745 | |
| Wang H N. 2011. Adaptive regularization iterative inversion of array multicomponent induction well logging datum in a horizontally stratified inhomogeneous TI formation. IEEE Trans. Geosci. Remote Sens., 49(11): 4483-4492. DOI:10.1109/TGRS.2011.2142187 | |
| Wang H N, Hu P, Tao H G, et al. 2012. Fast algorithm of responses of array multicomponent induction logging tool in horizontally stratified inhomogeneous TI Media. Chinese J. Geophys., 55(2): 717-726. DOI:10.6038/j.issn.0001-5733.2012.02.036 | |
| Wang H N, So P, Yang S W, et al. 2008a. Numerical modeling of multicomponent induction well-logging tools in the cylindrically stratified anisotropic media. IEEE Trans. Geosci. Remote Sens., 46(4): 1134-1147. DOI:10.1109/TGRS.2008.915748 | |
| Wang H N, Tao H G, Yao J J, et al. 2008b. Fast multiparameter reconstruction of multicomponent induction well-logging datum in a deviated well in a horizontally stratified anisotropic formation. IEEE Trans. Geosci. Remote Sens., 46(5): 1525-1534. DOI:10.1109/TGRS.2008.916080 | |
| Wang H N, Tao H G, Yao J J, et al. 2012. Efficient and reliable simulation of multicomponent induction logging response in horizontally stratified inhomogeneous TI formations by numerical mode matching method. IEEE Trans. Geosci. Remote Sens., 50(9): 3383-3395. DOI:10.1109/TGRS.2012.2183135 | |
| Wang H S, Yang S W, Bai Y, et al. 2016. Three-dimensional finite volume simulation of the response of azimuth electromagnetic wave resistivity while drilling in inhomogeneous anisotropic formation. Acta Phys. Sin., 65(7): 079101. DOI:10.7498/aps.65.079101 | |
| Wei B J, Wang T T, Wang Y. 2009. Computing the response of multi-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Green's function. Chinese J. Geophys., 52(11): 2920-2928. DOI:10.3969/j.issn.0001-5733.2009.11.028 | |
| Yang S W, Wang H N, Chen G B, et al. 2009. The 3-D finite difference time domain (FDTD) algorithm of response of multi-component electromagnetic well logging tool in a deviated and layered anisotropic formation. Chinese J. Geophy., 52(3): 833-841. | |
| Yang S W, Wang J X, Zhou J M, et al. 2014. An efficient algorithm of both Fréchet derivative and inversion of MCIL data in a deviated well in a horizontally layered TI formation based on TLM modeling. IEEE Trans. Geosci. Remote Sens., 52(11): 6911-6922. DOI:10.1109/TGRS.2014.2305669 | |
| Yao D H, Wang H N, Yang S W, et al. 2010. Study on the responses of multi-component induction logging tool in layered orthorhombic anisotropy formations by using propagator matrix method. Chinese J. Geophys., 53(12): 3026-3037. DOI:10.3969/j.issn.0001-5733.2010.12.028 | |
| Zhang Y, Wang H N, Tao H G, et al. 2012. Finite volume algorithm to simulate 3D responses of multi-component induction tools in inhomogeneous anisotropic formation based on coupled scalar-vector potentials. Chinese J. Geophys., 55(6): 2141-2152. DOI:10.6038/j.issn.0001-5733.2012.06.036 | |
| Zhdanov M, Kennedy D, Peksen E. 2001. Foundations of tensor induction well-logging. Petrophysics, 42(6): 588-610. | |
| Zhou J M, Zhang Y, Wang H N, et al. 2014. Efficient simulation of three-dimensional marine controlled-source electromagnetic response in anisotropic formation by means of coupled potential finite volume method. Acta Phys. Sin., 63(15): 159101. DOI:10.7498/aps.63.159101 | |
| Zhu T Z, Yang S W, Bai Y, et al. 2017. Efficient and high-precision establishment of borehole correction database for multicomponent array induction logging in vertical boreholes by a 2. 5D NMM algorithm.Chinese J. Geophys. (in Chinese), 60(3): 1221-1233. DOI:10.6038/cjg20170332 | |
| 洪德成, 肖加奇, 张国艳, 等. 2013. 大斜度井中利用交叉分量快速反演井斜角. 地球物理学报, 56(7): 2494–2501. DOI:10.6038/cjg20130735 | |
| 沈金松. 2003. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报, 46(2): 281–288. | |
| 汪宏年, 胡平, 陶宏根, 等. 2012. 水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算. 地球物理学报, 55(2): 717–726. DOI:10.6038/j.issn.0001-5733.2012.02.036 | |
| 王浩森, 杨守文, 白彦, 等. 2016. 非均质各向异性地层中方位随钻电磁测井响应三维有限体积法数值模拟算法. 物理学报, 65(7): 079101. DOI:10.7498/aps.65.079101 | |
| 魏宝君, 王甜甜, 王颖. 2009. 用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应. 地球物理学报, 52(11): 2920–2928. DOI:10.3969/j.issn.0001-5733.2009.11.028 | |
| 杨守文, 汪宏年, 陈桂波, 等. 2009. 倾斜各向异性地层中多分量电磁波测井响应三维时域有限差分 (FDTD) 算法. 地球物理学报, 52(3): 833–841. | |
| 姚东华, 汪宏年, 杨守文, 等. 2010. 用传播矩阵法研究层状正交各向异性地层中多分量感应测井响应. 地球物理学报, 53(12): 3026–3037. DOI:10.3969/j.issn:0001-5733.2010.12.028 | |
| 张烨, 汪宏年, 陶宏根, 等. 2012. 基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应. 地球物理学报, 55(6): 2141–2152. DOI:10.6038/j.issn.0001-5733.2012.06.036 | |
| 周建美, 张烨, 汪宏年, 等. 2014. 耦合势有限体积法高效模拟各向异性地层中海洋可控源的三维电磁响应. 物理学报, 63(15): 159101. DOI:10.7498/aps.63.159101 | |
| 朱天竹, 杨守文, 白彦, 等. 2017. 利用2.5维数值模式匹配算法高效高精度建立垂直井眼中多分量阵列感应井眼校正库. 地球物理学报, 60(3): 1221–1233. DOI:10.6038/cjg20170332 | |
 2017, Vol. 60
2017, Vol. 60

