2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
岩石破坏导致的各类地质灾害,如岩爆、崩滑与强震等,常造成巨大的人员伤亡和财产损失.对地质灾害的准确预测,是防灾减灾的关键,也是学者们长期研究的热点和难点问题.尽管诸多学者在岩爆 (Wang and Park, 2001;Alexeev et al., 2004;何满潮等,2007)、崩滑 (Crosta and Agliardi, 2003;黄润秋,2007;Mufundirwa et al., 2010) 与强震 (Das and Aki, 1977;茂木清夫,1986;马瑾等,1996) 等预测研究中已做出了巨大努力,但对世界上许多灾难性地质灾害屡屡预测失败的现实表明,脱离物理机制的经验或统计方法难以对其做出可靠的预测预报.
诸多岩体失稳致灾的演化方式是蠕变破坏或准蠕变破坏,即在长期缓慢的构造应力加载或环境因素作用下,岩体内微裂隙丛集导致宏观破裂的过程,大地震孕育过程是典型实例.我们近6年的研究表明 (秦四清等, 2010a, 2010b;Xue et al., 2014a, 2014b;秦四清等, 2016a, 2016b, 2016c;吴晓娲等,2016),掌握岩石变形破坏过程中体积膨胀点至峰值强度点之间加速破裂行为的演化规律,是实现地质灾害物理预测的关键.目前用于描述蠕变加速阶段的模型,如岩石复合流变模型 (邓荣贵等,2001)、分数阶导数蠕变模型 (Zhou et al., 2013) 与考虑初始损伤和蠕变损伤的岩石蠕变全过程本构模型 (王其虎等,2016) 等,或存在原理上的缺陷,或表达复杂难以应用,都无法准确描述该阶段的力学行为.
崩滑与大地震等地质灾害的演化过程虽高度复杂,但遵循统一的失稳机制,即大尺度岩石的宏观破裂,均由较小尺度的局部破裂逐渐累积形成,即损伤累积导致突变.许多研究 (Aviles et al., 1987;Hirata,1987;谢和平,1996) 表明,不同尺度的岩石破裂呈现统计自相似行为,即局部破裂的形态、过程和信息都是整体缩小的体现.
分形几何的奠基人Mandelbrot (1983)指出,自然界无特征尺度的几何对象通常都具有自相似性.岩石受载产生的裂纹系最基本特征是具有无特征尺度的层次结构 (郑捷,1992),即自相似性.例如,岩石的断口形态 (倪玉山等,1992;谢和平,1996) 和破裂系 (李彪等,1993) 等都具有分形结构.Aviles等 (1987)和Hirata (1989)研究了地表断裂带的自相似性,讨论了分形的区域差异;Aki (1981)和King (1983)认为Gutenberg-Richter幂律中的b值是表征地震活动性分维的指标;张智等 (1987)、Lei等 (2003)和Kong等 (2016)指出,岩石声发射与天然地震序列具有自相似特征;Smalley等 (1987)与安镇文等 (1989)认为地震活动的时空分布类似于广义Cantor集,具有统计意义上的尺度不变性和自相似性.无疑,前人的研究奠定了破裂分形的认识基础,但大部分工作是统计检验某些现象符合幂律分布以及探寻分维的物理意义,聚焦于几何自相似而忽略了物理自相似.必须强调,岩石破裂失稳演化是物理过程,打开地质灾害物理预测大门的钥匙是研究岩石破裂的物理自相似特征.
如上所述,前人主要聚焦于岩石破裂的几何自相似研究且已取得诸多进展,但在物理自相似研究方面则亟需深入.重整化群理论 (Wilson,1979) 的实质是通过改变研究对象的粗视化程度,以凸显其内部某种物理量不变特征,进而揭示其规律,是研究物理自相似现象的重要工具.Allègre等 (1982)利用重整化群理论研究了岩石破裂的尺度律,指出其在地震预测中具有潜在应用前景;Madden (1983)利用重整化群理论研究了含有随机分布裂纹结晶岩的电导率与破坏临界行为;Smalley等 (1985)构建了断层中凹凸体破裂过程的重整化群模型,解释了断层的黏滑行为并给出了临界滑动条件.然而,这些研究仅限于解释岩石破裂过程中某些物理量的变化特征以及某些观测现象,并未发现岩石破裂失稳的一般性规律.秦四清等 (2010a, 2010b) 采用重整化群理论和损伤理论相结合的研究方法,建立了孕震断层或斜坡滑动面中锁固段体积膨胀点与峰值强度点的力学联系,发现每个锁固段宏观破裂点与加速破裂起点的应变比,有着依赖于锁固段个数的指数律关系,且指数函数的底数为常数1.48.然而,该常数是否为物理自相似常数,在崩滑和地震预测等领域是否具有普适性仍需进一步探索.
本文从等效应力概念出发,基于统计强度理论、断裂力学与分形几何,建立Weibull形状参数m与裂纹尺度分维的定量关系,进而探讨应变比常数1.48的物理内涵,并通过实例分析阐明以此构建的多锁固段脆性破裂理论对不同尺度岩石破裂失稳的预测能力.此外,本文导出了b值与m值关系的表达式,以定量解释b值的物理意义.
2 m值与分维Df的关系岩石内部不同尺度的缺陷 (裂纹) 具有随机分布特点,岩石 (岩样) 宏观破坏常源自于其内部一条或几条主控裂纹的失稳扩展,因此采用经典统计强度理论常涉及的最弱环模型,描述受载时其导致的宏观力学行为是“对症下药”.Weibull (1951)提出的统计强度理论以最弱环模型为基础,认为材料强度由其最弱环的强度决定,即最弱环一旦破坏,就会引发整个链条发生连锁反应式的破坏.考虑由Ns个 (Ns足够大) 环组成的链,在应力为σ时每个环断裂的概率为F(σ),若最弱环的断裂导致整条链的断裂,则其断裂概率可近似表达为
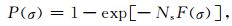
|
(1) |
若将环视为裂纹,则P(σ) 表示应力为σ时含有Ns条裂纹材料的断裂概率.
在单轴、等双轴和等三轴应力作用下,采用双参数Weibull分布函数 (Weibull, 1939, 1951),则式 (1) 可写为
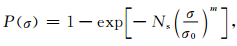
|
(2) |
式中,σ0为尺度参数,是微元体 (环) 平均应力的测度;m为形状参数,其不仅与介质的均匀性有关,而且还与介质所处的环境条件 (如应力水平、温度、加载速率等) 以及破坏模式有关,本质上可反映岩石破坏脆性程度.m值越大,岩石破坏的脆性程度越大.
本文规定应力符号受压为正,受拉为负.对岩样含多裂纹的情况,本文作如下假设:(1) 仅考虑主控裂纹对岩石断裂的作用,忽略其他小裂纹的影响.(2) 当裂纹较短且间距较大时,可忽略其间的相互作用.(3) 当两条裂纹相距较近时,若其间距满足合并规则 (汪微微,2009),将两条裂纹合并为一条大尺寸裂纹处理;反之,仍按单条裂纹处理.如此,多数情况下可不考虑复杂的裂纹干涉效应,以使本文关注的m-Df关系问题可解,且便于洞察b值的本质涵义.需指出的是,采用Weibull分布研究脆性材料损伤破坏行为时,亦需做与上述类似的假设,即不考虑裂纹的扩展、串接乃至贯通导致的局部应力场改变,也不考虑裂纹之间的相互作用.尽管如此,但试验结果和理论对比分析 (曹文贵和张升,2005;张明等,2010;曹瑞琅等,2013) 表明,采用Weibull分布能较好地描述岩石宏观破裂行为,具有广泛的适用性.
在远场三轴不等应力作用下,设沿某平面裂纹 (如Griffith型裂纹) 面作用有正应力σn和剪应力τn,当沿该裂纹面法线方向无限远处的应力σef与 (σn,τn) 产生的力学效应等效时,称σef为等效应力.当裂纹受拉张开时,等效应力 (Batdorf,1978;彭图让和张泽华,1989) 可表达为

|
(3) |
对平面裂纹,系数ρ仅与选用的断裂判据有关.当采用正应力判据时,ρ=0.当裂纹沿原方向扩展且采用最大能量释放率 (MG) 判据 (Zhao,1987) 时,ρ=1.当裂纹沿能量释放率最大的方向扩展时,考虑到:(1) MG判据的表达式较为复杂,不便使用;(2)Zhao (1990)提出的椭圆规律断裂 (ER) 判据在量值上相当接近MG判据,且本文不关注裂纹扩展方向.因此,我们采用ER判据,此时有ρ=(KⅠc/KⅡc)2,KⅠc和KⅡc分别为Ⅰ型和Ⅱ型裂纹断裂韧性,是材料常数.
当裂纹面受压闭合时,设其间的摩擦系数为f且为一常量,则等效应力 (朱乃龙和饶云刚,2006) 可表达为
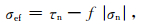
|
(4) |
当σef≤0时,取σef=0.显然,若闭合裂纹扩展需满足σef>0的条件.
参考Batdorf (1978)和Matsuo (1981)对多轴Weibull分布函数的研究,任意三轴应力状态下微元体的破坏概率可采用
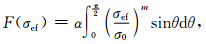
|
(5) |
式中,α为常数,θ为裂纹面法向与最大主应力方向夹角,σ0可视为用等效应力表示的尺度参数.
当裂纹张开时,根据线弹性断裂力学 (李世愚等,2015),裂纹尖端处的应力强度因子可表达为
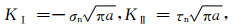
|
(6) |
式中,a为裂纹尺度.当裂纹开始扩展时,根据ER判据有
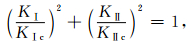
|
(7) |
结合式 (3)、(6) 和 (7),得到
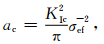
|
(8) |
式中,ac为裂纹扩展的临界尺度 (Griffith型裂纹半长).
地壳岩石一般处于多向压缩状态,在较小压力作用下即使先存张开型裂纹也能闭合.由于裂纹闭合,裂纹面两侧介质相互不可入,裂纹面的位移只有相互剪切错动,σn不会引起裂纹尖端的应力奇异性,故此应视为纯Ⅱ型剪切裂纹.根据上述分析和式 (4),裂纹闭合时裂纹尖端处的应力强度因子可表达为
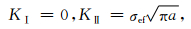
|
(9) |
当裂纹开始扩展时,式 (9) 代入式 (7) 或直接利用Ⅱ型裂纹断裂韧性判据得到
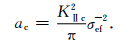
|
(10) |
为便于表达,将式 (8) 和 (10) 统一写为
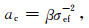
|
(11) |
式中,β为比例常数.
鉴于裂纹分布具有分形特征,F(σef) 也可表达为裂纹尺度a的分形函数,高峰等 (2004)给出裂纹尺度的概率密度分布函数为
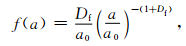
|
(12) |
式中,a0为裂纹特征尺度,Df为裂纹分布分维.
设裂纹的尺度分布与方位分布相互独立 (高峰等,2004),其概率密度函数分别为f(a) 和g(θ),则在等效应力作用下某条裂纹扩展导致的微元体破坏概率为

|
(13) |
式 (12) 代入式 (13) 得
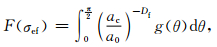
|
(14) |
当裂纹或张开或闭合时,式 (11) 代入式 (14) 得
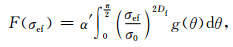
|
(15) |
式中,α′为比例系数.
对裂纹方位分布,除常采用均匀分布和正态分布外,亦可采用其他合理的分布函数.因应力作用下裂纹扩展导致岩石损伤破坏,显然式 (5) 和 (15) 是等效破坏概率事件.比较该两式知,令g(θ)=Asinθ(A为常数) 合理,则式 (15) 可变为
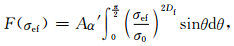
|
(16) |
对比式 (5) 和 (16),只有当
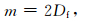
|
(17) |
该两式才可能完全等效.式 (17) 适用于描述岩样在任意三轴应力状态下的力学行为,可视为m与Df关系的一般解.在单轴拉应力条件下,高峰等 (1993)曾得到与式 (17) 相同的表达式,但从其公式推导过程看,隐含着裂纹面与拉应力方向垂直的假设,故只能视为一个特解.
许江等 (1986)对单轴应力状态下砂岩微观断裂全过程的试验表明,随应力增加,与轴向应力方向成较小夹角的微裂纹数目增加速率,远大于与轴向应力方向成较大夹角的微裂纹数目增加速率.这与正弦分布预示的结果基本一致,亦说明裂纹方位分布采用正弦分布优于均匀分布和正态分布.
显然,在三轴压缩下,随围压增大,m值应减小,Df值亦应减小,这与杨永明等 (2014)采用CT扫描技术观测三轴压缩下砂岩裂纹扩展得到的结果 (图 1) 一致,表明式 (17) 合理.
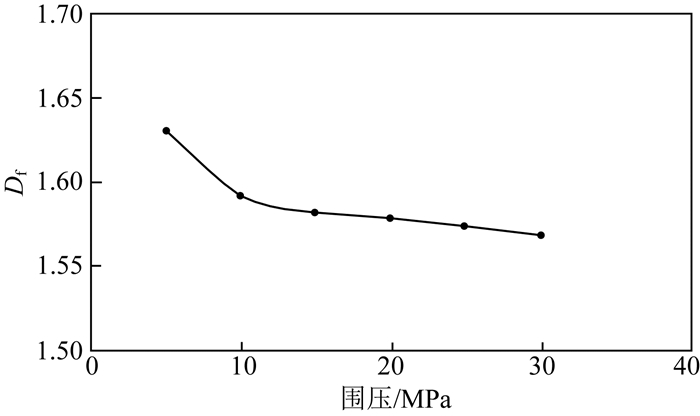
|
图 1 砂岩破坏裂纹分维Df与围压的关系 (杨永明等,2014) Fig. 1 Relationship between fractal dimension Df of fractured cracks and confined pressure for sandstone (Yang et al., 2014) |
在加速破裂阶段,不同尺度岩石的力学行为遵循相同的演化规律,称之为物理自相似.秦四清等 (2010b)以岩石的非均匀性为楔入点,基于重整化群理论和损伤理论,导出了岩石变形破坏峰值强度点与体积膨胀点应变比 (位移比) 的表达式,即

|
(18) |
式中,εf和εc分别为岩石峰值强度点和体积膨胀点对应的沿滑面或断层面剪切应变值.显然,该应变比值仅与m值有关,与其他因素无关.
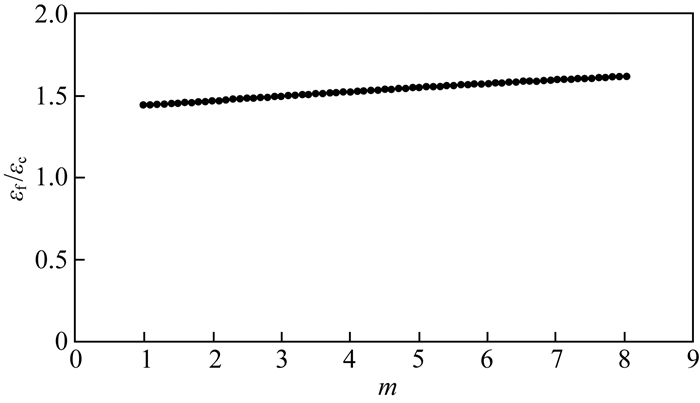
为确定m值的取值范围,诸多学者进行了大量研究.例如,Wang等 (2010)给出了单轴压缩条件下煤岩的m值为1.4~2.1;曹文贵和张升 (2005)假定微元体破坏符合Mohr-Coulomb准则,通过拟合不同围压 (0~40 MPa) 的大理岩三轴试验曲线,得到m值的范围为1.0684~3.6920;曹瑞琅等 (2013)假定微元体破坏符合Hoek-Brown屈服准则,当围压在0~20 MPa区间内,得到花岗岩m值的范围为7.281~15.538.由试验结果可看出,不同学者给出的岩石m值变化范围相差较大,其原因可能是:(1) 计算m值时,采用不同的本构模型和破坏准则会得到不同的结果;(2) 基于试验曲线拟合确定m值,采用不同拟合方法得到的结果不同;(3) 基于理论公式计算,需确定弹性模量、泊松比等参数,而这些参数难以准确获得.因此,m值的合理取值范围仍存争议,是一个亟需解决的问题.
将式 (17) 代入式 (18) 得到

|
(19) |
可看出岩石峰值强度点与体积膨胀点应变比仅与分维Df有关,其比值是一个物理意义明确且具有自相似属性的参数.因Df值应小于3.0,故m值的上限应小于6.0;再者,对具有应变弱化性质的介质,通常认为m≥1.0.因此,m值的理论取值范围应为[1.0,6.0).王士民等 (2006)的研究表明,当m=5.0时,岩样破裂行为更加趋于均质材料的性质,故m∈[1.0,5.0) 更为合理.考虑到地质体所处实际环境条件,不能忽视围压、温度和加载速率等因素对m值的影响.曹瑞琅等 (2013)指出,随着围压增大,花岗岩m值减小;贾延等 (2010)通过高围压与变温环境下大理岩损伤试验,指出m值随温度增大而减小,且在150~500 ℃间变化较平稳;Nakamura等 (2007)对玄武岩不同加载速率 (0.035~14 mm·min-1) 的拉伸试验表明,m值随加载速率增大而增大,但并非呈现单调线性增长趋势;杨仕教等 (2005)对石灰岩的单轴压缩试验亦表明,随加载速率增大,峰后曲线形态变陡,意味着m值增大.必须指出,崩滑与大地震的孕育演化是一个长期过程,其加载速率极其缓慢,故m值应较小.结合上述前人研究结果,当应用式 (18) 预测地质体失稳时,我们推测m∈[1.0,4.0]合理,其优势区间为[1.5,3.0].从图 2看出,应变比对m值的变化不敏感.m值在[1.0,4.0]或[1.5,3.0]区间,应变比的平均值约为1.48,则式 (18) 可简化为
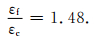
|
(20) |
|
图 2 εf/εc与m的关系 Fig. 2 Relation between εf/εc and m |
由式 (19) 知,应变比值仅与分维Df有关,故“1.48”是一个物理自相似常数.若用阿拉伯数字和常用数学常数表示,则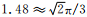
Smalley等 (1987)、Hirata (1987)与郑捷 (1992)的研究表明,地震和岩石破裂现象在时间集聚特征、空间分布、震级大小统计规律和破裂表面的几何形态等诸方面均具有明显的分形结构,即自相似性存在于各级尺度岩石破裂过程中,具有普适性质.因此,可认为“1.48”是描述岩石加速破裂规律的普适物理自相似常数.该常数的存在,避免了准确测定深部岩石物理力学参数的困难,使得对地质灾害尤其是大地震的预测成为可能.
4 多锁固段脆性破裂理论不同尺度的岩体失稳主要受控于先存弱面中未贯通区域.为此,诸多学者提出了不同的断续结构破坏模型.在工程岩体尺度上,连续介质常被若干条状或线状缝隙间隔为岩桥,其破坏模式可分为拉张、剪切与拉剪混合三类 (Shen et al., 1995;Morgan et al., 2013;Huang et al., 2016).在地震断层尺度上,某些学者认为失稳源于断层 (带) 中非均质高强度部分的破坏与摩擦滑动,分别提出了障碍体模型 (Das and Aki, 1977)、凹凸体模型 (Wyss et al., 1981) 与坚固体模型 (梅世蓉,1995) 等,用于解释地震多物理场前兆、地表破裂形态、地震时空序列、位移与应力变化等,在基础理论、试验和数值模拟等方面均取得诸多进展 (Dobrovolsky et al., 1979;Das and Kostrov, 1983;Zhang et al., 1986;刘庭金和唐春安,2002).遗憾的是,上述研究均未涉及岩石加速破裂导致突变失稳这一共性特征,只能用于定性解释某些观测现象.
秦四清等 (2010b)在式 (20) 的基础上,导出了多锁固段 (图 3) 发生宏观破裂的临界应变 (位移) 准则为
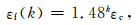
|
(21) |
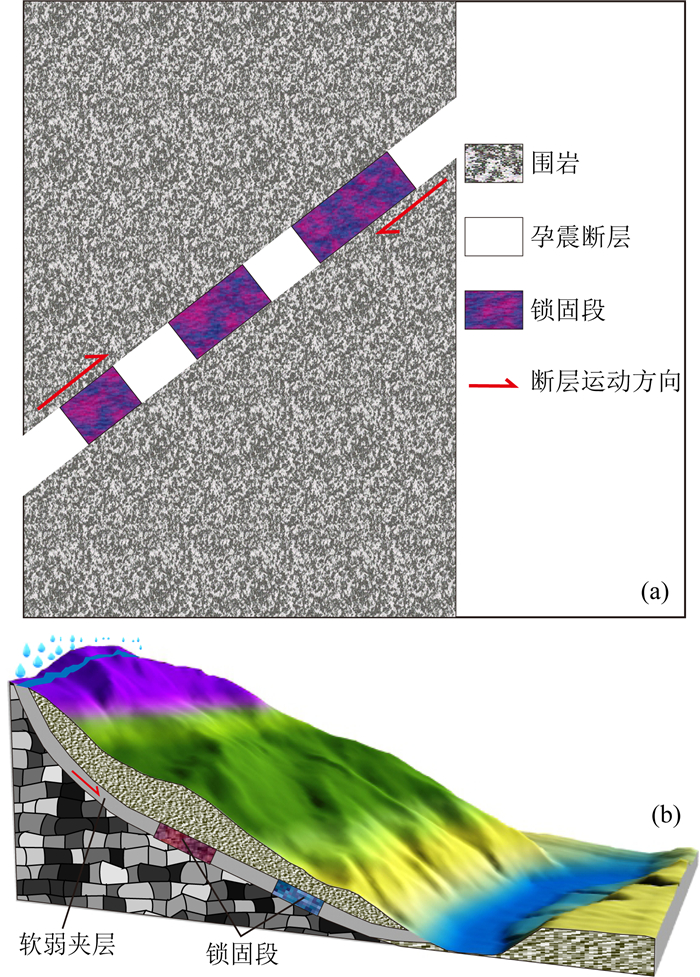
|
图 3 多锁固段概念模型 (a) 断层面上的多锁固段;(b) 斜坡滑动面上的多锁固段. Fig. 3 A conceptual model of multiple locked patches (a) Multiple locked patches along a seismogenic fault; (b) Multiple locked patches along a slip surface of slope. |
式中,k为锁固段个数.由于沿断层面深部滑移应变ε难以测量,应寻求某种易测的替代物理量.对某一地震区,假设地震效率为一常量,则可认为累积Benioff应变 (CBS) 是ε的一个测度 (Benioff,1951),因此式 (21) 可写为
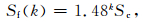
|
(22) |
式中,Sc为第1个锁固段体积膨胀起点对应的CBS (Cumulative Benioff Strain) 值,Sf(k) 为第k个锁固段峰值强度点对应的CBS值.秦四清等 (2016a, 2016b, 2016c) 对全球62个地震区标志性地震事件孕育规律的分析表明,上述假设合理.式 (21) 或 (22) 是我们提出的多锁固段脆性破裂理论体系中最重要的定量力学关系.基于此,可根据锁固段体积膨胀起点对应的应变值,提前给出锁固段发生宏观破裂对应的临界应变值,结合实时监测信息可进行预测.运用该理论,对诸多崩滑实例 (秦四清等,2010a) 和全球62个地震区历史大地震的回溯性验证效果良好 (秦四清等, 2016a, 2016b, 2016c),对某些地震区的中长期前瞻性预测得到证实 (秦四清和薛雷,2011;秦四清等, 2012, 2013, 2014a, 2014b, 2014c, 2014d).
需指出的是,上述预测方法属于“点对点”预测,而非过程预测,若能对两点间演化过程有所了解,则能更为有效地把握锁固段加速破坏的演化趋势.大地震的能量积累载体——锁固段,其空间尺度大,当被某些中小尺度断层围限,常形成次级结构,可称之为次级锁固段 (图 4).由上述分析知,不同层次锁固段的破裂特征应具有自相似性,其加速破裂规律应统一遵循式 (21) 或 (22).如此,可对锁固段宏观破裂前发生的中间过程事件 (preshock) 进行预测.
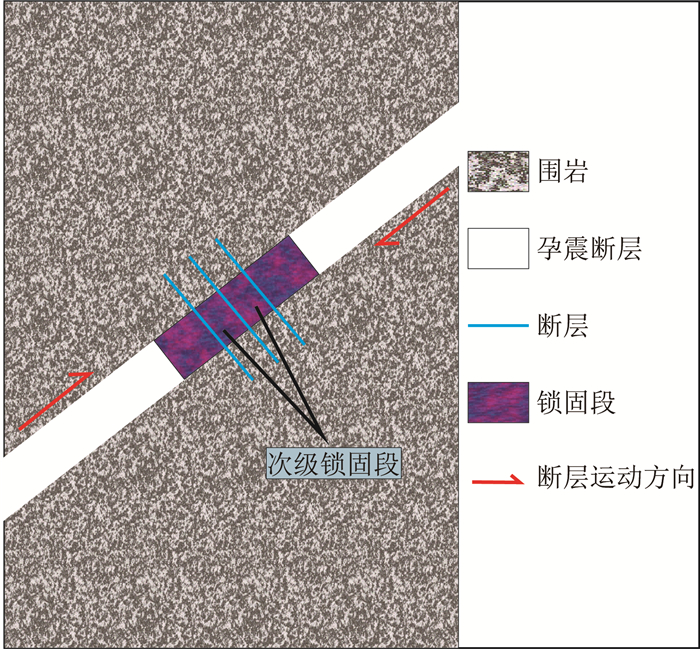
|
图 4 锁固段分层次结构示意图 Fig. 4 Schematic illustration of the hierarchical structure of locked patch |
以下,我们给出4个不同尺度岩石破裂失稳实例,说明多锁固段脆性破裂理论的预测能力.
5.1 砂岩蠕变失稳Tan和Kang (1980)用扭转流变仪对尺寸为280 mm×86 mm的圆柱形砂岩样加载,给出了阶梯荷载下砂岩的蠕变试验结果.该试样可视为单锁固段模型,根据锁固段在体积膨胀点的位移uc,利用式 (21) 可预测其在宏观破裂点的位移uf.从图 5看出,预测值接近砂岩失稳临界位移值.
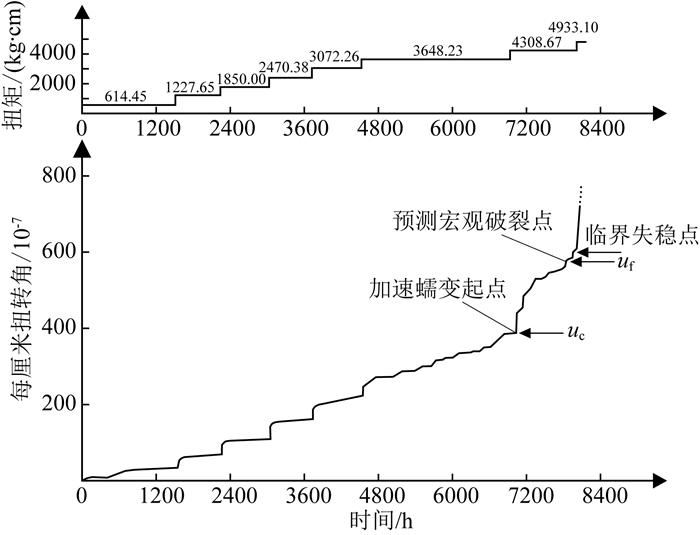
|
图 5 砂岩在阶梯荷载下的蠕变曲线 (据Tan和Kang (1980)修改) Fig. 5 Creep curve of sandstone under step load (modified after Tan and Kang (1980)) |
1980年6月3日,湖北盐池河发生了体积约1.5×106m3的岩崩,导致284人死亡和近1亿元经济损失 (黄润秋,2007).孙玉科和姚宝魁 (1983)通过地质调查,认为该崩塌体的稳定性受单锁固段控制.根据锁固段在体积膨胀点的位移uc,利用式 (21) 可预测其在宏观破裂点的位移uf.从图 6看出,预测值十分接近岩崩的临界位移值 (最后一次观测值),对应于实际破坏前1d.
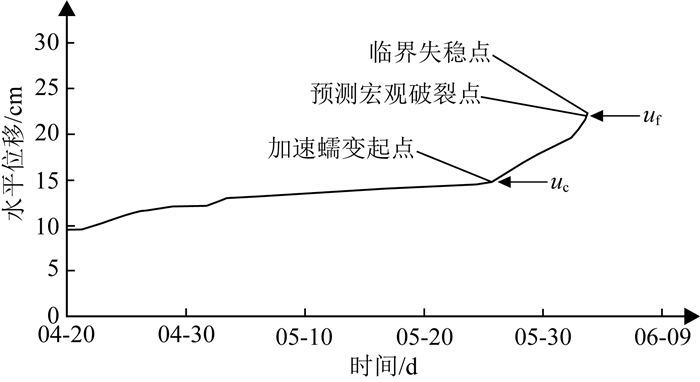
|
图 6 盐池河山崩4号裂缝1980年水平位移观测记录 (据孙玉科和姚宝魁 (1983)修改) Fig. 6 Cumulative horizontal displacement observed at crack No.4 of the Yanchihe avalanche in 1980(modified after Sun and Yao (1983)) |
1976年7月28日 (按UTC为27日),河北唐山发生MS7.8地震,造成24.25万人死亡,70.86万人受伤,直接经济损失达132.75亿元 (温玉婷等,2010).唐山地震区 (图 7中编号27) 当前周期曾发生5次标志性地震事件 (秦四清等,2016b),即1597年10月6日渤海MS7.5地震、1668年7月25日郯城MS8.0地震、1679年9月2日三河—平谷MS7.8地震、1888年6月13日渤海湾MS7.8地震与1976年7月27日唐山MS7.8地震.从图 8看出,误差修正 (秦四清等,2010c) 后标志性地震事件的孕育规律遵循式 (22).
|
图 7 中国及其周边地震区划分图 (秦四清等, 2016b, 2016d) Fig. 7 Division map of seismic zones in China and its adjacent areas (Qin et al., 2016b, 2016d) |
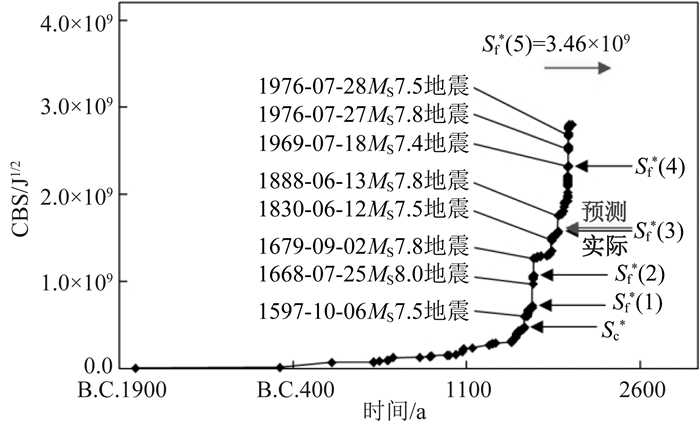
|
图 8 唐山地震区公元前1767—2015-11-21之间CBS值与时间关系 数据分析时选取MS≥5.0地震事件;误差修正已被考虑. Fig. 8 Temporal distribution of CBS in the period from B.C. 1767 to 21 November 2015 for the Tangshan seismic zone The earthquake events with MS≥5.0 are selected for data analysis. The error correction is also considered. |
伊斯兰堡—加德满都地震区 (图 7中编号60) 当前周期曾发生5次标志性地震事件 (秦四清等,2016b),即1669年6月4日巴基斯坦拉瓦尔品第MK8.0地震、1803年9月1日印度库马翁MS8.1地震、1833年8月26日尼泊尔加德满都北部MS8.0地震、1897年6月12日印度阿萨姆邦MS8.5地震与1950年8月15日中国西藏察隅MW8.6地震.从图 9a看出,误差修正 (秦四清等,2010c) 后标志性地震事件的孕育规律遵循式 (22).
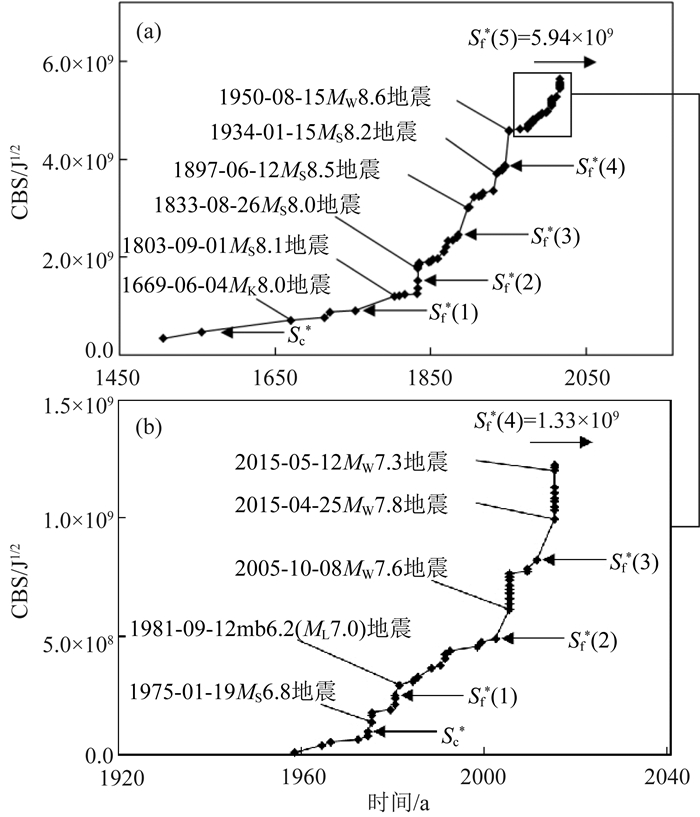
|
图 9 伊斯兰堡—加德满都地震区CBS值与时间关系 (a) 1505-06-06—2016-02-18之间CBS值与时间关系 (数据分析时选取ML≥6.4地震事件;误差修正已被考虑);(b) 1958-12-28—2016-02-18之间CBS值与时间关系 (数据分析时选取ML≥6.1地震事件;误差修正已被考虑). Fig. 9 Temporal distribution of CBS for the Islamabad-Kathmandu seismic zone (a) Temporal distribution of CBS in the period from 6 June 1505 to 18 February 2016 (The earthquake events with ML≥6.4 are selected for data analysis. The error correction is also considered); (b) Temporal distribution of CBS in the period from 28 December 1958 to 18 February 2016 (The earthquake events with ML≥6.1 are selected for data analysis. The error correction is also considered). |
截取该区自1958年12月28日至2016年2月18日之间数据,基于式 (22) 可建立误差修正 (秦四清等,2010c) 后次级锁固段破裂导致的标志性preshock事件之间的力学联系.从图 9b看出,根据1975年1月19日克什米尔MS6.8地震前的CBS值,可较准确地连续预测到1981年9月12日克什米尔mb6.2(约相当于ML7.0) 地震、2005年10月8日巴基斯坦穆扎法拉巴德MW7.6地震与2015年4月25日尼泊尔MW7.8地震的临界CBS值.
对该地震区的分析表明,锁固段和次级锁固段的加速破裂规律均满足式 (22),即整体与局部地震序列遵循相同演化规律,展现出显著的物理自相似行为.
对上述实例的分析表明,不同尺度岩石加速破裂失稳具有物理自相似性特征,其演化规律可用式 (21) 或 (22) 描述.
6 b值的物理意义由式 (12) 可导出岩样中尺度不小于a的裂纹数目为
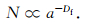
|
(23) |
由上述分析知,加载时不同尺度岩石的破裂行为相似,可以类比.如把岩样视为一个地震区或该区的某个锁固段,岩样中的某条裂纹视为一次地震事件产生的地震断层,裂纹尺度a视为等效地震破裂尺度r,则式 (23) 可写为

|
(24) |
式中,N为破裂尺度不小于r的地震事件总数.
Gutenber和Richer (1954)提出的地震震级M-频度N统计关系可表达为
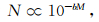
|
(25) |
式中,b为常数.关于b值的物理意义,尚存争议,如Mogi (1962)认为b值取决于介质的非均匀性,但Scholz (1968)认为b值及其变化由岩石所处的应力状态决定.为此,我们将建立b值与m值关系,以揭示b值的内涵.
Kanamori和Anderson (1975)给出一次地震的地震矩M0与震级M的关系为
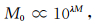
|
(26) |
式中,λ为依赖于震源相对持续时间和记录系统常量的参数.他们的研究还表明 (27) 式是一个很好的近似关系,即
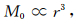
|
(27) |
结合式 (25)、(26) 与 (27) 得到
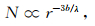
|
(28) |
比较式 (24) 和 (28) 得到
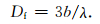
|
(29) |
(29) 式说明,b值与地震破裂尺度 (地震活动性) 分维有关.在λ取值方面,Main等 (1989)指出受拉岩石断裂取λ=3.0合理,Kanamori和Anderson (1975)认为对大多数地震取λ=1.5合理.然而,Dubois和Novaili (1989)通过对板块俯冲带震源深度为100~700 km的地震活动性分析,得到λ=2.4.在地震活动性分析中,常用λ=1.5,则式 (29) 可写为
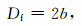
|
(30) |
式 (17) 代入式 (30) 得到
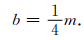
|
(31) |
(31) 式说明,b值仅与Weibull形状参数m有关,是反映岩石破坏脆性程度的参数,其与岩石破裂 (地震) 过程无关.再者,对特定地震区的某一锁固段而言,当锁固段被加载至体积膨胀点和峰值强度点之间,在长期相对稳定的围压与温度等环境条件下,m值与b值均可视为定值.因此,不能把b值作为预测地震的指标.
从分维变化角度考虑,当岩样被加载至体积膨胀点与峰值强度点之间,采用盒维数法计算分维时,由于裂纹的丛集效应,随应力增大含有裂纹的盒子数略有增多或近似不变,故分维值呈现略有增长或近似不变的趋势,这与尹小涛等 (2008)采用CT扫描观测砂岩破裂过程得到的结果 (图 10) 一致.这再次说明,b值对应力变化不敏感,将其应用于地震预测预报缺乏依据.
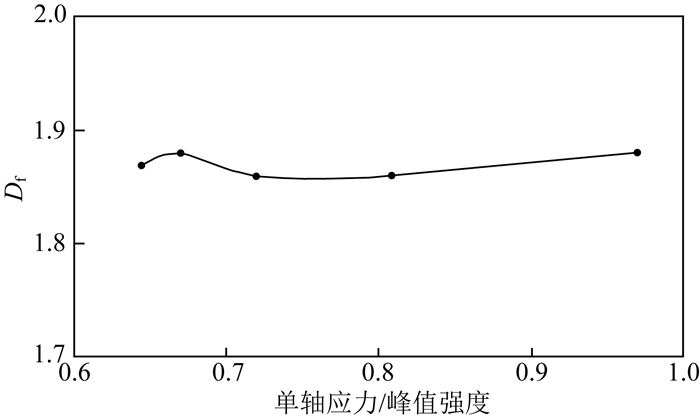
|
图 10 单轴压缩下砂岩裂纹分布分维Df与应力关系 (尹小涛等,2008) Fig. 10 Relation between fractal dimension Df of crack distribution and stress for sandstone subjected to uniaxial compression (Yin et al., 2008) |
诸多学者 (Smith,1981;马鸿庆,1982;Molchan and Dmitrieva, 1990) 指出,某些大震发生前的b值呈显著降低趋势,我们对其分析结果的可靠性持怀疑态度,因为b值计算主要依赖于时空范围的选择,在不能正确划定地震区和确定当前孕育周期开始时间与标志性地震事件的情况下,选择不同时空范围的数据进行统计分析,会得到不同甚至截然相反的结果.
以唐山地震区为例,说明标志性地震事件发生前b值的变化特征.取公元前1767年为统计时间起点t0,统计区间为 (t0,ti)(i=1,2,3,…),依据震级-频度公式 (25) 可计算 (t0,ti) 区间对应的bi值.从图 11看出,b值变化呈现与图 10类似的特征.简言之,每次标志性地震事件发生前,b值均呈缓慢增长的稳态特征,但震时下降,其中1668年郯城MS8.0地震发生时下降最明显,1679年三河—平谷MS7.8地震发生时次之.这表明唐山地震区各标志性地震事件发生前,b值变化未呈现可判识的显著“涨落”行为,难以用其预测大地震.
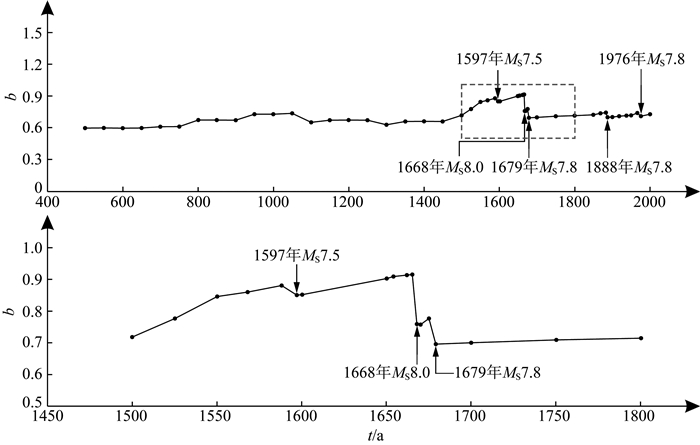
|
图 11 唐山地震区b值与时间关系 数据分析时选取MS≥5.0地震事件. Fig. 11 Relationship between b-value and time for the Tangshan seismic zone The earthquake events with MS≥5.0 are selected for data analysis. |
如上所述,分形对象具有自相似的层次结构,适当放大或缩小对象的几何尺寸,某些参量或性质保持不变,因此与等比数列有着自然的密切联系 (Shriki and Nutov, 2016),如Cantor三分集、Koch曲线、Sierpinski垫片和地毯等分形对象的生成过程,均可由等比数列描述.由于第k+1个锁固段的体积膨胀点应变等于第k个锁固段的峰值强度点应变,故式 (21) 亦可表达为
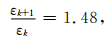
|
(32) |
式中,εk和εk+1分别为第k个锁固段体积膨胀点和峰值强度点的应变值.显然,式 (32) 是一个公比为1.48的等比数列.这再次说明,多锁固段脆性破裂理论以自相似性为基石,具有普适性,是预测岩石蠕变破坏或准蠕变破坏导致失稳的利器.
为进一步探讨常数1.48与已知数学常数的内在联系,可按如下规则构造广义Cantor三分集 (戴振祥,2001):第一步将区间[0,1]分成3份,设其第1和第3个区间的长度为ω(0 < ω < 0.5),第2个区间长度为1-2ω,去掉中间的一个开区间 (ω,1-ω);第二步将剩下的两个小闭区间[0,ω]和[1-ω,1]分别按同样的比例分成3份,并各去掉中间的开区间.如此下去,最后得到的集合即为广义Cantor三分集,其分维为
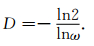
|
(33) |
令ω=1-1.48-1,易知其满足0 < ω < 0.5,将其代入式 (33) 得D≈0.616,可看出该值十分接近0.618.由此看来,常数1.48与黄金分割数0.618可能有潜在的关联.尽管这种关联性的内涵目前尚不清楚,仍需进一步探索,但这意味着某些自然对象的复杂演化过程蕴含简单的共性规律.
8 结论(1) 导出了岩石在三轴压缩下Weibull分布m值与裂纹分布分维Df关系的表达式,指出岩石峰值强度点与体积膨胀点应变比仅与m或Df有关.
(2) 对岩石蠕变或准蠕变破坏,合理的m值范围为[1.0,4.0],在该范围内应变比近似为常数1.48.
(3)“1.48”是描述不同尺度岩石加速破裂失稳规律的一个物理自相似常数,该常数的存在,避免了准确测定深部岩石物理力学参数的困难,使得对地质灾害尤其是大地震的预测成为可能.
(4) 实例分析表明,多锁固段脆性破裂理论在崩滑和大地震预测领域,具有良好的应用前景.
(5) 描述地震活动性的b值仅与Weibull形状参数m有关,是反映岩石破坏脆性程度的参数,其与岩石破裂 (地震) 过程无关,不能作为预测地震的指标.
| Aki K. 1981. A probabilistic synthesis of precursory phenomena.//Simpson D W, Richards P G eds. Earthquake Prediction: An International Review. Washington, D C: AGU, 566-574. | |
| Alexeev A D, Revva V N, Alyshev N A, et al. 2004. True triaxial loading apparatus and its application to coal outburst prediction. Int. J. Coal. Geol., 58(4): 245-250. DOI:10.1016/j.coal.2003.09.007 | |
| Allègre C J, Le Mouel J L, Provost A. 1982. Scaling rules in rock fracture and possible implications for earthquake prediction. Nature, 297(5861): 47-49. DOI:10.1038/297047a0 | |
| An Z W, Wang L Y, Zhu C Z. 1989. The characteristics of fractal dimension in the temporal-spatial distribution of earthquakes befor and after the occurrence of a large earthquake. Acta Seismologica Sinica, 11(3): 251-258. | |
| Aviles C A, Scholz C H, Boatwright J. 1987. Fractal analysis applied to characteristic segments of the San Andreas fault. J. Geophys. Res., 92(B1): 331-344. DOI:10.1029/JB092iB01p00331 | |
| Batdorf S B. 1978. Fundamentals of the statistical theory of fracture.//Bradt R C, Hasselman D P H, Lange F F eds. Proceedings of the International Symposium on Fracture Mechanics of Ceramics. New York: Plenum Press, 1-30. | |
| Benioff H. 1951. Earthquakes and rock creep (Part Ⅰ: Creep characteristics of rocks and the origin of aftershocks). Bull. Seismol. Soc. Am., 41(1): 31-62. | |
| Cao R L, He S H, Wei J, et al. 2013. Study of modified statistical damage softening constitutive model for rock considering residual strength. Rock and Soil Mechanics, 34(6): 1652-1660. DOI:10.16285/j.rsm.2013.06.018 | |
| Cao W G, Zhang S. 2005. Study on the statistical analysis of rock damage based on Mohr-Coulomb criterion. Journal of Hunan University (Natural Sciences), 32(1): 43-47. | |
| Crosta G B, Agliardi F. 2003. Failure forecast for large rock slides by surface displacement measurements. Can. Geotech. J., 40(1): 176-191. DOI:10.1139/T02-085 | |
| Dai Z X. 2001. Hausdoroff dimension of generalized Cantor sets. Journal of Zhejiang Normal University (Natural Sciences), 24(2): 143-145. | |
| Das S, Aki K. 1977. Fault plane with barriers: a versatile earthquake model. J. Geophys. Res., 82(36): 5658-5670. DOI:10.1029/JB082i036p05658 | |
| Das S, Kostrov B V. 1983. Breaking of a single asperity: rupture process and seismic radiation. J. Geophys. Res., 88(B5): 4277-4288. DOI:10.1029/JB088iB05p04277 | |
| Deng R G, Zhou D P, Zhang Z Y, et al. 2001. A new rheological model for rocks. Chinese Journal of Rock Mechanics and Engineering, 20(6): 780-784. | |
| Dobrovolsky I P, Zubkov S I, Miachkin V I. 1979. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys., 117(5): 1025-1044. DOI:10.1007/BF00876083 | |
| Dubois J, Novaili L. 1989. Quantification of the fracturing of the slab using a fractal approach. Earth Planet. Sci. Lett., 94(1-2): 97-108. DOI:10.1016/0012-821X(89)90086-1 | |
| Gao F, Xie H P, Zhao P. 1993. Fractal properties of Weibull modulus and rock strength. Chinese Science Bulletin, 38(15): 1435-1438. | |
| Gao F, Zhong W P, Li L Y, et al. 2004. Fractal and statistical analysis of strength of jointed rocks. Chinese Journal of Rock Mechanics and Engineering, 23(21): 3608-3612. | |
| Gutenberg B, Richter C F. Seismicity of the Earth and Associated Phenomena. Princeton: Princeton University Press, 1954: 245. | |
| He M C, Miao J L, Li D J, et al. 2007. Experimental study on rockburst processes of granite specimen at great depth. Chinese Journal of Rock Mechanics and Engineering, 26(5): 865-876. | |
| Hirata T. 1987. Omori's power law aftershock sequences of microfracturing in rock fracture experiment. J. Geophys. Res., 92(B7): 6215-6221. DOI:10.1029/JB092iB07p06215 | |
| Hirata T. 1989. Fractal dimension of fault systems in Japan: fractal structure in rock fracture geometry at various scales. Pure Appl. Geophys., 131(1-2): 157-170. DOI:10.1007/BF00874485 | |
| Huang D, Gu D M, Yang C, et al. 2016. Investigation on mechanical behaviors of sandstone with two preexisting flaws under triaxial compression. Rock Mech. Rock Eng., 49(2): 375-399. DOI:10.1007/s00603-015-0757-3 | |
| Huang R Q. 2007. Large-scale landslides and their sliding mechanisms in China since the 20th century. Chinese Journal of Rock Mechanics and Engineering, 26(3): 433-454. | |
| Jia Y, Kang Y M, Wang D, et al. 2010. Research on critical damage for rock subjected to high confining pressure and temperature-change. Journal of Sichuan University (Engineering Science Edition), 42(6): 79-84. | |
| Kanamori H, Anderson D L. 1975. Theoretical basis of some empirical relations in seismology. Bull. Seismol. Soc. Am., 65(5): 1073-1095. | |
| King G. 1983. The accommodation of large strains in the upper lithosphere of the earth and other solids by self-similar fault systems: the geometrical origin of b-value. Pure Appl. Geophys., 121(5-6): 761-815. DOI:10.1007/BF02590182 | |
| Kong X G, Wang E Y, Hu S B, et al. 2016. Fractal characteristics and acoustic emission of coal containing methane in triaxial compression failure. J. Appl. Geophys., 124: 139-147. DOI:10.1016/j.jappgeo.2015.11.018 | |
| Lei X L, Kusunose K, Satoh T, et al. 2003. The hierarchical rupture process of a fault: an experimental study. Phys. Earth Planet. Inter., 137(1-4): 213-228. DOI:10.1016/S0031-9201(03)00016-5 | |
| Li B, Ma S L, Zhang L. 1993. Fractal dimension of main fractures of marble under different experimental conditions. Seismology and Geology, 15(2): 157-163. | |
| Li S Y, He M T, Yin X C. Rock Fracture Mechanics. Beijing: Science Press, 2015: 537. | |
| Liu T J, Tang C A. 2002. Numerical test on influence of weak & hard touching on fracture model of specimen with inclusion. Journal of Seismological Research, 25(1): 53-57. | |
| Ma H Q. 1982. The spatial distribution of the b-values before large and moderate earthquakes. Acta Seismologica Sinica, 25(2): 163-171. | |
| Ma J, Ma S L, Liu L Q, et al. 1996. Geometrical texture of faults evolution of physical field and instability characteristics. Acta Seismologica Sinica, 18(2): 200-207. | |
| Madden T R. 1983. Microcrack connectivity in rocks: a renormalization group approach to the critical phenomena of conduction and failure in crystalline rocks. J. Geophys. Res., 88(B1): 585-592. DOI:10.1029/JB088iB01p00585 | |
| Main I G, Meredith P G, Jones C. 1989. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Int., 96(1): 131-138. DOI:10.1111/gji.1989.96.issue-1 | |
| Mandelbrot B B. 1983. The Fractal Geometry of Nature. New York: W. H. Freeman and Company, 466. | |
| Matsuo Y. 1981. Statistical fracture theory for multiaxial stress states using Weibull's three-parameter function. Eng. Fract. Mech., 14(3): 527-538. DOI:10.1016/0013-7944(81)90040-0 | |
| Mei S R. 1995. On the physical model of earthquake precursor fields and the mechanism of precursors' time and space distribution (Ⅰ)—origin and evidences of the strong body earthquake-generating model. Acta Seismologica Sinica, 17(3): 273-282. | |
| Mogi K. 1962. Study of elastic shocks caused by the fracture of heterogeneous materials and its relations to earthquake phenomena. Bull. Earthq. Res. Inst., 40(1): 125-173. | |
| Mogi K. Earthquake Prediction in Japan. Beijing: Seismological Press, 1986: 326. | |
| Molchan G M, Dmitrieva O E. 1990. Dynamics of the magnitude-frequency relation for foreshocks. Phys. Earth Planet. Inter., 61(1-2): 99-112. DOI:10.1016/0031-9201(90)90098-I | |
| Morgan S P, Johnson C A, Einstein H H. 2013. Cracking processes in Barre granite: fracture process zones and crack coalescence. Int. J. Fract., 180(2): 177-204. DOI:10.1007/s10704-013-9810-y | |
| Mufundirwa A, Fujii Y, Kodama J. 2010. A new practical method for prediction of geomechanical failure-time. Int. J. Rock Mech. Min. Sci., 47(7): 1079-1090. DOI:10.1016/j.ijrmms.2010.07.001 | |
| Nakamura A M, Michel P, Setoh M. 2007. Weibull parameters of Yakuno basalt targets used in documented high-velocity impact experiments. J. Geophys. Res., 112: E02001. DOI:10.1029/2006JE002757 | |
| Ni Y S, Kuang Z B, Yang Y Q. 1992. Fractal study of the fracture surface of grantite caused by triaxial compression. Chinese Journal of Rock Mechanics and Engineering, 11(3): 295-303. | |
| Peng T R, Zhang Z H. 1989. Distributed functions of fracture size and their applications in fatigue statistical analysis. Journal of Shandong Institute of Building Materials, 3(3): 1-10. | |
| Qin S Q, Wang Y Y, Ma P. 2010a. Exponential laws of critical displacement evolution for landslides and avalanches. Chinese Journal of Rock Mechanics and Engineering, 29(5): 873-880. | |
| Qin S Q, Xu X W, Hu P, et al. 2010b. Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction. Chinese J. Geophys., 53(4): 1001-1014. DOI:10.3969/j.issn.0001-5733.2010.04.025 | |
| Qin S Q, Xue L, Huang X, et al. 2010c. A forward prediction of strong earthquakes in the Tibet region. Progress in Geophys., 25(6): 1879-1886. DOI:10.3969/j.issn.1004-2903.2010.06.001 | |
| Qin S Q, Xue L. 2011. A summary of prediction for the Yingjiang MS5.8 earthquake in Yunnan and the Burma MS7.2 earthquake as well as the analysis on the earthquake situation after the earthquake. Progress in Geophys., 26(2): 462-468. DOI:10.3969/j.issn.1004-2903.2011.02.010 | |
| Qin S Q, Xue L, Li G L, et al. 2012. The verification of prospective prediction for the Zhaotong earthquakes on 7 September 2012. Progress in Geophys., 27(5): 1837-1840. DOI:10.6038/j.issn.1004-2903.2012.05.001 | |
| Qin S Q, Xue L, Li G L, et al. 2013. The verification of prospective prediction for the Minxian-Zhangxian MS6.6 earthquake in Gansu province and an analysis on the future earthquake situation. Progress in Geophys., 28(4): 1860-1868. DOI:10.6038/pg20130427 | |
| Qin S Q, Xue L, Li P, et al. 2014a. A review of prospective prediction for the Jinggu MS6.6 earthquake in Yunnan province and an analysis on future earthquake situation. Progress in Geophys., 29(5): 2479-2482. DOI:10.6038/pg20140574 | |
| Qin S Q, Xue L, Li G L, et al. 2014b. The verification of prospective prediction for the Lushan MS7.0 earthquake on 20 April 2013 and an analysis on future earthquake situation. Progress in Geophys., 29(1): 141-147. DOI:10.6038/pg20140118 | |
| Qin S Q, Xue L, Li P, et al. 2014c. A review of prospective prediction for the Yutian 7.3 earthquake in Xinjiang province and an analysis on future earthquake situation. Chinese J. Geophys., 57(2): 679-684. DOI:10.6038/cjg20140231 | |
| Qin S Q, Li P, Xue L, et al. 2014d. The definition of seismogenic period of strong earthquakes for some seismic zones in southwest China. Progress in Geophys., 29(4): 1526-1540. DOI:10.6038/pg20140407 | |
| Qin S Q, Li P, Yang B C, et al. 2016a. The identification of mainshock events for main seismic zones in seismic belts of the Circum-Pacific, ocean ridge and continental rift. Progress in Geophys., 31(2): 574-588. DOI:10.6038/pg20160209 | |
| Qin S Q, Yang B C, Wu X W, et al. 2016b. The identification of mainshock events for some seismic zones in mainland China (Ⅱ). Progress in Geophys., 31(1): 115-142. DOI:10.6038/pg20160114 | |
| Qin S Q, Yang B C, Xue L, et al. 2016c. The identification of mainshock events for main seismic zones in the Eurasian seismic belt. Progress in Geophys., 31(2): 559-573. DOI:10.6038/pg20160208 | |
| Qin S Q, Yang B C, Xue L, et al. 2016d. Revision method of earthquake magnitude. Progress in Geophys., 31(3): 965-972. DOI:10.6038/pg20160305 | |
| Scholz C H. 1968. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am., 58(1): 399-415. | |
| Shen B T, Stephansson O, Einstein H H, et al. 1995. Coalescence of fractures under shear stresses in experiments. J. Geophys. Res., 100(B4): 5975-5990. DOI:10.1029/95JB00040 | |
| Shriki A, Nutov L. 2016. Fractals in the mathematics classroom: the case of infinite geometric series. Learning and Teaching Mathematics, 2016(20): 38-42. | |
| Smalley R F Jr, Turcotte D L, Solla S A. 1985. A renormalization group approach to the stick-slip behavior of faults. J. Geophys. Res., 90(B2): 1894-1900. DOI:10.1029/JB090iB02p01894 | |
| Smalley R F Jr, Chatelain J L, Turcotte D L, et al. 1987. A fractal approach to the clustering of earthquakes: applications to the seismicity of the New Hebrides. Bull. Seismol. Soc. Am., 77(4): 1368-1381. | |
| Smith W D. 1981. The b-value as an earthquake precursor. Nature, 289(5794): 136-139. DOI:10.1038/289136a0 | |
| Sun Y K, Yao B K. 1983. Mechanism research on the collapse of Yanchihe mining area. Hydrogeology and Engineering Geology(1): 1-7. | |
| Tan T K, Kang W F. 1980. Locked in stresses, creep and dilatancy of rocks, and constitutive equations. Rock Mechanics, 13(1): 5-22. DOI:10.1007/BF01257895 | |
| Wang E Y, He X Q, Wei J P, et al. 2010. The coupling model of stress and electricity of EME of coal or rock. J. Min. Sci., 46(4): 367-374. DOI:10.1007/s10913-010-0046-1 | |
| Wang J A, Park H D. 2001. Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunnelling and Underground Space Technology, 16(1): 49-57. DOI:10.1016/S0886-7798(01)00030-X | |
| Wang Q H, Ye Y C, Liu Y Z, et al. 2016. A creep constitutive model of rock considering initial damage and creep damage. Rock and Soil Mechanics, 37(S1): 57-62. DOI:10.16285/j.rsm.2016.S1.007 | |
| Wang S M, Zhu H H, Feng X T, et al. 2006. Influence of heterogeneity on macroscopical crack form of the brittle rock. Rock and Soil Mechanics, 27(2): 224-227. | |
| Wang W W. 2009. Study on the interaction and merging condition of multiple [Master's thesis] (in Chinese). Nanjing: Nanjing University of Technology. | |
| Weibull W. 1939. A Statistical Theory of the Strength of Materials. Stockholm: Generalstabens Litografiska Anstalts Föerlag. | |
| Weibull W. 1951. A statistical distribution function of wide applicability. J. Appl. Mech., 18(3): 293-297. | |
| Wen Y T, Li N, Li X Q, et al. 2010. Contrast of disaster losses resulted from the Wenchuan and Tangshan earthquakes and rescue actions in these two events. Journal of Catastrophology, 25(2): 68-72. | |
| Wilson K G. 1979. Problems in physics with many scales of length. Sci. Am., 241(2): 158-179. DOI:10.1038/scientificamerican0879-158 | |
| Wu X W, Qin S Q, Xue L, et al. 2016. Physical mechanism of major earthquakes by earthquake cases. Chinese J. Geophys., 59(10): 3696-3710. DOI:10.6038/cjg20161016 | |
| Wyss M, Johnston A C, Klein F W. 1981. Multiple asperity model for earthquake prediction. Nature, 289(5795): 231-234. DOI:10.1038/289231a0 | |
| Xie H P. Fractal-Rock Mechanics. Beijing: Science Press, 1996: 369. | |
| Xu J, Li H, Xian X F, et al. 1986. Meso-mechanical experiment of microfracture progress of sandstone under uniaxial stress condition. Mechanics in Engineering(4): 16-20. | |
| Xue L, Qin S Q, Li P, et al. 2014a. New quantitative displacement criteria for slope deformation process: From the onset of the accelerating creep to brittle rupture and final failure. Eng. Geol., 182: 79-87. DOI:10.1016/j.enggeo.2014.08.007 | |
| Xue L, Qin S Q, Sun Q, et al. 2014b. A quantitative criterion to describe the deformation process of rock sample subjected to uniaxial compression: From criticality to final failure. Physica A, 410: 470-482. DOI:10.1016/j.physa.2014.05.062 | |
| Yang S J, Zeng S, Wang H L. 2005. Experimental analysis on mechanical effects of loading rates on limestone. Chinese Journal of Geotechnical Engineering, 27(7): 786-788. | |
| Yang Y M, Ju Y, Mao L T. 2014. Growth distribution laws and characterization methods of cracks of compact sandstone subjected to triaxial stress. Chinese Journal of Geotechnical Engineering, 36(5): 864-872. DOI:10.11779/CJGE201405008 | |
| Yin X T, Wang S L, Dang F N, et al. 2008. Study on fractal characteristics of sandstone damage-fracture under ct test condition. Chinese Journal of Rock Mechanics and Engineering, 27(S1): 2721-2726. | |
| Zhang M, Lu Y J, Yang Q. 2010. Failure probability and strength size effect of quasi-brittle materials. Chinese Journal of Rock Mechanics and Engineering, 29(9): 1782-1789. | |
| Zhang Z, Wu K T, Geng N G, et al. 1986. An experimental study of barriers on earthquake fault plane under triaxial compression. Journal of Seismological Research, 9(6): 733-740. | |
| Zhang Z, Wu K T, Jiao Y B. 1987. The changes of b value on samples contained barriers during rupture process. Earthquake Research in China, 3(1): 70-78. | |
| Zhao Y S. 1987. Griffith's criterion for mixed mode crack propagation. Eng. Fract. Mech., 26(5): 683-689. DOI:10.1016/0013-7944(87)90133-0 | |
| Zhao Y S. 1990. Elliptic rule criterion for mixed-mode crack-propagation. Eng. Fract. Mech., 37(2): 283-292. DOI:10.1016/0013-7944(90)90041-E | |
| Zheng J. 1992. Nonlinear scientific methods applied to rock rupture and earthquake phenomena. Progress in Geophys., 7(1): 20-35. | |
| Zhou H W, Wang C P, Mishnaevsky L, et al. 2013. A fractional derivative approach to full creep regions in salt rock. Mechanics of Time-Dependent Materials, 17(3): 413-425. DOI:10.1007/s11043-012-9193-x | |
| Zhu N L, Rao Y G. 2006. Study on constitutive model for quasi-rock materials based on statistical fracture theory. Chinese Journal of Rock Mechanics and Engineering, 25(S2): 3939-3944. | |
| 安镇文, 王琳瑛, 朱传镇. 1989. 大震前后地震活动的时空分维特征. 地震学报, 11(3): 251–258. | |
| 曹瑞琅, 贺少辉, 韦京, 等. 2013. 基于残余强度修正的岩石损伤软化统计本构模型研究. 岩土力学, 34(6): 1652–1660. DOI:10.16285/j.rsm.2013.06.018 | |
| 曹文贵, 张升. 2005. 基于Mohr-Coulomb准则的岩石损伤统计分析方法研究. 湖南大学学报 (自然科学版), 32(1): 43–47. | |
| 戴振祥. 2001. 一类广义Cantor集的Hausdorff维数. 浙江师大学报 (自然科学版), 24(2): 143–145. | |
| 邓荣贵, 周德培, 张倬元, 等. 2001. 一种新的岩石流变模型. 岩石力学与工程学报, 20(6): 780–784. | |
| 高峰, 谢和平, 赵鹏. 1993. Weibull模量和岩石强度的分形性质. 科学通报, 38(15): 1435–1438. DOI:10.3321/j.issn:0023-074X.1993.15.016 | |
| 高峰, 钟卫平, 黎立云, 等. 2004. 节理岩体强度的分形统计分析. 岩石力学与工程学报, 23(21): 3608–3612. DOI:10.3321/j.issn:1000-6915.2004.21.009 | |
| 何满潮, 苗金丽, 李德建, 等. 2007. 深部花岗岩试样岩爆过程实验研究. 岩石力学与工程学报, 26(5): 865–876. | |
| 黄润秋. 2007. 20世纪以来中国的大型滑坡及其发生机制. 岩石力学与工程学报, 26(3): 433–454. | |
| 贾延, 康亚明, 王东, 等. 2010. 高围压与变温环境下大理岩的临界损伤度研究. 四川大学学报 (工程科学版), 42(6): 79–84. | |
| 李彪, 马胜利, 张流. 1993. 不同实验条件下大理岩主破裂的分数维. 地震地质, 15(2): 157–163. | |
| 李世愚, 和泰名, 尹祥础. 岩石断裂力学. 北京: 科学出版社, 2015: 537. | |
| 刘庭金, 唐春安. 2002. 软硬接触对含包体试样破裂模式影响的数值试验. 地震研究, 25(1): 53–57. | |
| 马鸿庆. 1982. 大、中地震前b值的区域分布. 地球物理学报, 25(2): 163–171. | |
| 马瑾, 马胜利, 刘力强, 等. 1996. 断层几何结构与物理场的演化及失稳特征. 地震学报, 18(2): 200–207. | |
| 茂木清夫. 日本的地震预报. 北京: 地震出版社, 1986: 326. | |
| 梅世蓉. 1995. 地震前兆场物理模式与前兆时空分布机制研究 (一)——坚固体孕震模式的由来与证据. 地震学报, 17(3): 273–282. | |
| 倪玉山, 匡震邦, 杨英群. 1992. 常规三轴压缩下花岗岩断裂表面的分形研究. 岩石力学与工程学报, 11(3): 295–303. | |
| 彭图让, 张泽华. 1989. 裂纹尺寸分布函数及其在疲劳统计分析中的应用. 山东建材学院学报, 3(3): 1–10. | |
| 秦四清, 王媛媛, 马平. 2010a. 崩滑灾害临界位移演化的指数律. 岩石力学与工程学报, 29(5): 873–880. | |
| 秦四清, 徐锡伟, 胡平, 等. 2010b. 孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索. 地球物理学报, 53(4): 1001–1014. DOI:10.3969/j.issn.0001-5733.2010.04.025 | |
| 秦四清, 薛雷, 黄鑫, 等. 2010c. 西藏地区未来强震预测. 地球物理学进展, 25(6): 1879–1886. DOI:10.3969/j.issn.1004-2903.2010.06.001 | |
| 秦四清, 薛雷. 2011. 云南盈江MS5.8级地震和缅甸MS7.2级地震预测总结及震后趋势分析. 地球物理学进展, 26(2): 462–468. DOI:10.3969/j.issn.1004-2903.2011.02.010 | |
| 秦四清, 薛雷, 李国梁, 等. 2012. 云南昭通"9·7地震"的前瞻性预测验证. 地球物理学进展, 27(5): 1837–1840. DOI:10.6038/j.issn.1004-2903.2012.05.001 | |
| 秦四清, 薛雷, 李国梁, 等. 2013. 甘肃岷县漳县6.6级地震的前瞻性预测验证及震后趋势分析. 地球物理学进展, 28(4): 1860–1868. DOI:10.6038/pg20130427 | |
| 秦四清, 薛雷, 李培, 等. 2014a. 云南景谷MS6.6级地震前瞻性预测回顾及其震后趋势分析. 地球物理学进展, 29(5): 2479–2482. DOI:10.6038/pg20140574 | |
| 秦四清, 薛雷, 李国梁, 等. 2014b. 四川省芦山"4·20"7.0级地震的前瞻性预测验证及震后趋势分析. 地球物理学进展, 29(1): 141–147. DOI:10.6038/pg20140118 | |
| 秦四清, 薛雷, 李培, 等. 2014c. 新疆于田7.3级地震前瞻性预测回顾及其震后趋势分析. 地球物理学报, 57(2): 679–684. DOI:10.6038/cjg20140231 | |
| 秦四清, 李培, 薛雷, 等. 2014d. 中国西南地区某些地震区强震孕育周期界定. 地球物理学进展, 29(4): 1526–1540. DOI:10.6038/pg20140407 | |
| 秦四清, 李培, 杨百存, 等. 2016a. 环太平洋、大洋海岭与大陆裂谷地震带主要地震区主震事件判识. 地球物理学进展, 31(2): 574–588. DOI:10.6038/pg20160209 | |
| 秦四清, 杨百存, 吴晓娲, 等. 2016b. 中国大陆某些地震区主震事件判识 (Ⅱ). 地球物理学进展, 31(1): 115–142. DOI:10.6038/pg20160114 | |
| 秦四清, 杨百存, 薛雷, 等. 2016c. 欧亚地震带主要地震区主震事件判识. 地球物理学进展, 31(2): 559–573. DOI:10.6038/pg20160208 | |
| 秦四清, 杨百存, 薛雷, 等. 2016d. 地震震级修订方法. 地球物理学进展, 31(3): 965–972. DOI:10.6038/pg20160305 | |
| 孙玉科, 姚宝魁. 1983. 盐池河磷矿山体崩坍破坏机制的研究. 水文地质工程地质(1): 1–7. | |
| 王其虎, 叶义成, 刘艳章, 等. 2016. 考虑初始损伤和蠕变损伤的岩石蠕变全过程本构模型. 岩土力学, 37(S1): 57–62. DOI:10.16285/j.rsm.2016.S1.007 | |
| 王士民, 朱合华, 冯夏庭, 等. 2006. 细观非均匀性对脆性岩石材料宏观破坏形式的影响. 岩土力学, 27(2): 224–227. | |
| 汪微微. 2009. 多裂纹相互作用及其合并条件的研究[硕士论文]. 南京: 南京工业大学. | |
| 温玉婷, 李宁, 刘雪琴, 等. 2010. 汶川地震与唐山地震损失与救助之对比. 灾害学, 25(2): 68–72. | |
| 吴晓娲, 秦四清, 薛雷, 等. 2016. 基于震例探讨大地震的物理机制. 地球物理学报, 59(10): 3696–3710. DOI:10.6038/cjg20161016 | |
| 谢和平. 分形-岩石力学导论. 北京: 科学出版社, 1996: 369. | |
| 许江, 李贺, 鲜学福, 等. 1986. 对单轴应力状态下砂岩微观断裂发展全过程的实验研究. 力学与实践(4): 16–20. | |
| 杨仕教, 曾晟, 王和龙. 2005. 加载速率对石灰岩力学效应的试验研究. 岩土工程学报, 27(7): 786–788. | |
| 杨永明, 鞠杨, 毛灵涛. 2014. 三轴应力下致密砂岩裂纹展布规律及表征方法. 岩土工程学报, 36(5): 864–872. DOI:10.11779/CJGE201405008 | |
| 尹小涛, 王水林, 党发宁, 等. 2008. CT实验条件下砂岩破裂分形特性研究. 岩石力学与工程学报, 27(S1): 2721–2726. | |
| 张明, 卢裕杰, 杨强. 2010. 准脆性材料的破坏概率与强度尺寸效应. 岩石力学与工程学报, 29(9): 1782–1789. | |
| 张智, 吴开统, 焦远碧. 1987. 含有障碍体的岩石样品破裂发展过程中的b值变化. 中国地震, 3(1): 70–78. | |
| 郑捷. 1992. 研究地震和岩石破裂现象的非线性科学方法. 地球物理学进展, 7(1): 20–35. | |
| 朱乃龙, 饶云刚. 2006. 基于统计断裂理论的岩石类材料本构模型的研究. 岩石力学与工程学报, 25(S2): 3939–3944. | |
 2017, Vol. 60
2017, Vol. 60


