地球物理学报  2017, Vol. 60 Issue (4): 1389-1397   PDF    
引用本文
曲中党, 贺日政, 张训华, 等. 2017. 时频域相位滤波在远震接收函数噪声压制中的应用. 地球物理学报, 60(4): 1389-1397, doi: 10.6038/cjg20170413.  
QU Z D, HE R Z, ZHANG X H, et al. 2017. The time-frequency domain phase filter and its application in noise suppression of teleseismic receiver functions. Chinese J. Geophys. (in Chinese), 60(4): 1389-1397, doi: 10.6038/cjg20170413.  
时频域相位滤波在远震接收函数噪声压制中的应用
曲中党1,2,3, 贺日政2 , 张训华3, 吴蔚2     
1. 中国海洋大学, 海洋地球科学学院, 青岛 266100;
2. 中国地质科学院地质研究所, 国土资源部深部探测与地球动力学重点实验室, 北京 100037;
3. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266000
收稿日期 2016-03-06, 2017-02-22 收修定稿
基金项目: 国家自然基金项目（41574086，41274095，41430213，41590863），国家重点基础研究发展计划项目（2013CB429701，2016YFC0600301），中国地质调查局项目（12120115027101），国土资源部公益行业基金项目（201011013，201011044）资助
作者简介: 曲中党, 男, 1991年生, 博士研究生, 海洋地球物理学专业, 主要从事地震学研究.E-mail:quzhongdang@163.com
通讯作者: 贺日政, 男, 1973年生, 博士, 研究员, 主要从事青藏高原深部结构与构造研究.E-mail:herizheng@cags.ac.cn
摘要: 宽频带地震观测数据中有效信号和干扰噪声经常发生混频效应，常规的频率域滤波方法很难将二者分离.地震波信号属于时变非平稳信号，时频分析方法能够同时得到地震波信号随着时间和频率变化的振幅和相位特征，S变换是其中较为高效的时频分析工具之一.本文以S变换为例，提出了基于相位叠加的时频域相位滤波方法.与传统叠加方法相比，相位叠加方法对强振幅不敏感，对波形一致性相当敏感，更加利于有效弱信号信息的检测.时频域相位滤波方法滤除与有效信号不相干的背景噪声，保留了相位一致的有效信号成分，显著提高了信噪比.运用理论合成的远震接收函数数据和实际的宽频带地震观测数据检验结果显示该方法较传统的带通滤波方法相比，即使在信噪较低且混频严重条件下，时频域相位滤波方法的滤波效果依然很明显，有助于识别能量较弱的有效信号.
关键词: 时频域      S变换      相位叠加      相位滤波      远震接收函数     
The time-frequency domain phase filter and its application in noise suppression of teleseismic receiver functions
QU Zhong-Dang1,2,3, HE Ri-Zheng2, ZHANG Xun-Hua3, WU Wei2     
1. College of Marine Geosciences, Ocean University of China, Qingdao 266100, China;
2. Key Laboratory of Earth Probe and Geodynamics Institute of Geology, Chinese Academy of Geological Sciences, Beijing 100037, China;
3. Function Laboratory for Marine Mineral Resource Geology and Exploration, Qingdao National Oceanography Laboratory, Qingdao 266000, China
Abstract: In broadband seismology, the signals and ambient noises are usually frequency mixed, so it is hard to extract the signals from the ambient noises by the conventional filter algorithms. Due to the frequency mixing of seismic noise and the non-stationarity of the recorded signal, tools that can effectively take into account the frequency-time variation of the seismic recordings are more suitable for fulfilling this task. The S-transform is an invertible time-frequency spectral localization technique that combines elements of wavelet transforms and short-time Fourier transforms. The time-frequency resolution of S-transform is related to the width of Gaussian window, which has high frequency resolution at low frequency section and high time resolution at high frequency section. The obvious advantage of using the S-transform is that it is convenient not only to denoise but also to directly invert from time-frequency domain to the time domain. Taking the S transform as an example, this paper proposes a new method of phase filter based on phase stack. Phase direction of the coherent signals in the complex plane is consistent, rather that of ambient noises is tanglesome. Compared with the conventional stack method of seismic data, the phase stack of seismic data will get statistical phase of those signals, which is more sensitive to waveform similarity, less to strong amplitude. Phase filter of phase stack in the time-frequency domain easily recognizes ambient noises and also extract coherent signals. So, the method can obviously improve S/N ratio of seismic data. The results of the synthetic benchmark showed that the method performs better than conventional band-pass filter, also very well even if the signal has much lower S/N ratio. Of course, as the increasing of noise levels, the reconstructed signal still has serious noise, especially when the signal and the most energetic part of the noise share the same frequencies and phases. In these cases, the signal after phase filter by the method we presented can estimate reliably the first arrivals of direct P, Ps converted by Moho discontinuity and PpPs multiple. The application of a combination of de-noising with time-frequency phase filtering on real data shows the method is potentially useful to extract lower amplitude converted waves from seismograms, and to obviously improve S/N ratio of seismic data. Therefore, the method presented in this paper can be used for weak signal recognition or arrival-time picking of broadband seismic data. Also, the phase filter method can be widely used in reflection seismic exploration data processing.
Key words: The time-frequency domain      S transform      Phase stack      Phase filter      Teleseismic receiver function     
1 引言

最近十多年来科学家们充分利用了宽频带地震观测中的地震噪声开展结构探测研究 (Shapiro and Campillo, 2004; Yao et al., 2008; Yang et al., 2008), 但是在传统方法研究中 (如体波/面波层析成像, 接收函数方法) 背景噪声仍是影响地震震相识别和处理解释最为主要的因素 (Kafka and Weidner, 1979; Banka and Crossley, 1999), 噪声源包括微震、地电场、磁场、风速、气压、温度、台站架设方式、台基的非线性干扰等 (尹昕忠等, 2013).固定台站远离噪声源, 从而固定台站数据背景噪声较低, 信噪比较高. 20世纪90年代, 针对特殊对象 (如火山喷发) 或应急性观测 (如灾难性地震后余震观测), 兴起了宽频地震流动观测技术, 受到研究区范围的限制, 在有限观测周期内开展致密的台站观测, 尽管采取多种规避噪声源的措施, 但仍难以避免 (刘旭宙等, 2014).因此, 流动观测数据信噪比相对较低, 如何压制宽频带地震数据中的噪声一直是地震学研究的重点.

常规滤波方法是基于傅里叶变换的频率域内开展不同方式的带通滤波 (Douglas, 1997).这种常规的傅里叶变换是一种全局变换, 适合于时间域或频率域内平稳信号分析, 但不能同时保留时间和频率信息, 所以也无法有效检测非平稳时变信号的频率随时间的变化特征, 更无法得到非平稳信号的某些局部特征.事实上, 由于地下介质的不均匀性和地层的吸收衰减等因素, 地震信号往往是一种非平稳信号, 其频率的局部特性具有非常重要的研究意义 (许丰, 2013; 郑成龙和王宝善, 2015).为此, 许多研究者在傅里叶变换的基础上提出了很多的时频分析方法, 如:短时傅里叶变换 (Gabor, 1946)、小波变换 (Grossmann et al., 1985)、S变换 (Stockwell et al., 1996)、广义S变换 (Pinnegar and Mansinha, 2003a, 2003b) 等, 将一维时间信号转换到二维时间-频率域后就可以同时得到信号在时间域和频率域的变化结果.其中, S变换结合了小波变换和短时傅里叶变换的优点, 在低频区有较高的频率分辨率, 在高频区有较高的时间分辨率, 便于分析信号的局部特征, 提高了对非平稳时变信号的分析能力 (Stockwell et al., 1996; Stockwell, 1999; 陈学华等, 2008).本文以S变换时频分析方法为例, 通过有效信号和噪声信号在相位信息上的差异来设计滤波器, 噪声压制效果明显, 地震信号的信噪比得到显著的提高.

2 时频域相位滤波方法

时频滤波去噪方法通常是将单道地震信号变换到时间-频率域内, 根据有效信号和干扰信号在时频平面上能量分布的差异, 并结合阈值方法设计合适的滤波器, 将干扰区域充零, 然后将滤波后的时频谱反变换到时间域 (陈雨红等, 2006; 赵淑红和朱光明, 2007; 赵淑红和王璇, 2007; Parolai, 2009; 郑成龙和王宝善, 2015; 曲中党等, 2015).当有效信号和噪声信号不易通过时频平面中能量分布的差异来区分时 (即混频现象), 将干扰区充零的做法将不再适用.

本文以S变换时频分析方法为例, 提出的基于相位叠加的时频域相位滤波方法是通过地震波数据之间横向相位的叠加来识别出有效信号的主相位, 然后滤除与所统计的主相位信息不相符的噪声.识别有效信号的主相位借鉴了Schimmel等 (1997, 2011) 的相位互相关方法, 消弱相位中不相干成分.相位滤波后的地震信号通过S变换反变换到时间域, 最终实现滤除与有效信号混频的干扰噪声.

2.1 S变换时频分析方法

S变换是由美国地球物理学家Stockwell等提出的一种类似于短时傅里叶变换 (Gabor, 1946) 的时频谱表示方法, 函数h(t) 的S变换定义为 (Stockwell et al., 1996):

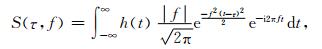
(1)

其中, t表示时间, f表示频率, τ是控制高斯窗在t轴的位置的参数.其时窗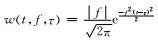的宽度随频率呈反向变化 (曲中党等, 2015).由于时窗越宽, 所得到的时频分析谱时间分辨率越低, 频率分辨率越高; 时窗越窄, 所得到的时频分析谱时间分辨率越高, 频率分辨率越低.所以S变换在低频段的时窗较宽, 从而获得较高的频率分辨率; 而高频段的时窗较窄, 故可获得很高的时间分辨率 (Pinnegar and Mansinha, 2003b; Parolai, 2009; 李振春等, 2010; 曲中党等, 2015).

S变换也可以由h(t) 的傅里叶频谱H(f) 表示 (Stockwell, 1999):

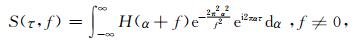
(2)

该过程充分利用了快速傅里叶变换的高效性和卷积定理 (Stockwell et al., 1996).

S变换表示的是局部的频谱特征, 将其在时间方向积分可以容易地得到傅里叶频谱 (Stockwell et al., 1996):

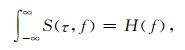
(3)

因此, h(t) 也可以由S(τ, f) 准确的反变换得到:

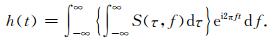
(4)

2.2 相位叠加

目前, 大多数的信号检测工具是通过有效信号和噪声在不同属性 (例如, 极性、相干性、瞬时频率) 上的差异和在不同的域 (如:时间域、频率域、慢度域、波数域, 或者它们之间的相互组合) 表现方式的差异来区分有效信号和噪声 (Schimmel and Gallart, 2007).然而, 宽频带地震数据中有效信号和噪声之间并没有非常明显的区别, 所以, 在任何域都很难建立一个客观的评判标准来区分噪声和有效信号.

通常我们通过统计叠加的方式来确定有效信号, 线性叠加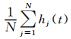是最常用的一种方式, hj(t) 代表所用于统计的地震数据, j=1, 2, 3…, N.然而, 当某道噪声信号较强时, 会使得统计叠加的信号偏向噪声的振幅和相位, 不利于有效信号的识别.但是, 连贯一致的有效信号在相同时刻的相位信息应该是一致的 (Schimmel et al., 2011), 相位信息与振幅强度无关, 因此, 本文借鉴Schimmel等 (1997)提出的无关振幅的相位叠加方式来确定有效信号的相位信息.

相位叠加公式为

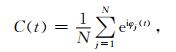
(5)

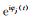
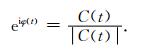
C(t) 是N道信号hj(t) 在t时刻相位φj(t) 的e指数函数的叠加平均.该公式的计算不依赖于振幅信息, 不受信号振幅能量大小的影响. C(t) 利用了有效信号和噪声信号相位复叠加相互干扰的优势.有效信号在复平面内都有相同的方向, 通过相位复叠加可以获得有效信号相位信息.对噪声信号来说, 由于其在复平面内方向的不确定性, 相位复叠加会使得噪声之间相互削弱抵消.因此, 有效信号的相位函数φ(t) 的e指数函数为

(6)

结合S变换时频分析方法 (公式2), 信号hj(t) 在S变换时频域Sj(τ, f) 的相位叠加公式为

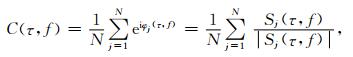
(7)

其时频域相位函数φ(τ, f) 的e指数函数为

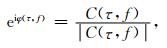
(8)

φ(τ, f) 即为在现有理论基础上所认为的有效信号在时频域的相位信息.

2.3 时频域相位滤波

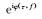
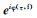
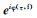
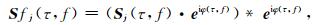
在复平面上, 复数与从原点指向点z=x+yi的平面向量一一对应, 复数z能用向量z来表示.因此, 通过2.2节, 我们已经获得的有效信号在S变换时频域的相位信息能用向量来表示, 该向量的辐角即为φ(τ, f); 同理, 各地震信号hj(t) 的S变换Sj(τ, f) 也可以用向量Sj(τ, f) 来表示.向量Sj(τ, f) 在方向的投影即为有效信号成分, 仅保留投影后的有效信号成分.基于此理论我们提出了基于S变换的时频域相位滤波公式:

(9)

·表示两个向量之间的数量积, *表示标量和向量之间的数乘, Sfj(τ, f) 是滤波之后信号在S变换域的表现形式, 其仍然是一个复数矩阵, 通过S反变换 (公式4) 即可得到滤波后的信号在时间域的表现形式.

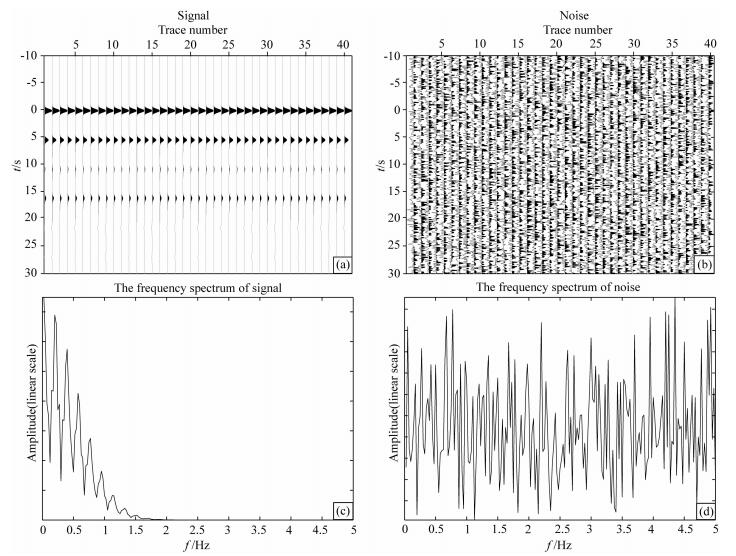
3 理论合成数据的检测

利用地壳厚度为40 km, 壳内P波速度VP=6.0 km·s-1, 壳内S波速度VS=3.5 km·s-1, 地幔P波速度VP=8.0 km·s-1, 地幔S波速度VS=4.7 km·s-1的简单速度模型, 利用Randall的高效算法 (Randall, 1989), 生成了高斯参数为2.5的理论接收函数 (图 1a). 0 s处为直达P波, 5.5 s处为一级结构间断面 (Moho面) 的Ps转换震相, 16.2 s为Moho面的PpPs转换震相, 它们在接收函数的后期处理和解释中起着至关重要的作用, 是我们重点识别和处理的震相.在理论接收函数 (即有效信号) 中, 加入了高斯白噪 (图 1b).有效信号和高斯白噪声的频谱分析图 (图 1c、d) 可以看出, 有效信号的能量集中在2 Hz以下, 而噪声信号的能量则均匀分布在0~5 Hz之间, 因此, 在展示时频域相位滤波方法的去噪效果之前, 有必要对加了高斯白噪声之后的理论数据做低通滤波.

图 1 (a) 简单速度模型的理论接收函数; (b) 高斯白噪声; (c) 图 (a) 有效信号的频谱分析图; (d) 图 (b) 噪声的频谱分析图 Fig. 1 (a) Synthetic receiver function of simple velocity model; (b) White Gaussian Noise; (c) The frequency spectrum of signal in Fig.(a); (d) The frequency spectrum of noise in Fig.(b)

为定量描述各步骤的滤波效果，采用能量叠加方法来评估各数据的信噪比 (张军华等, 2009):

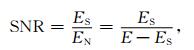
(10)

其中, SNR代表信噪比; E代表地震数据的总能量; ES代表有效信号总能量; EN代表噪声信号的总能量.

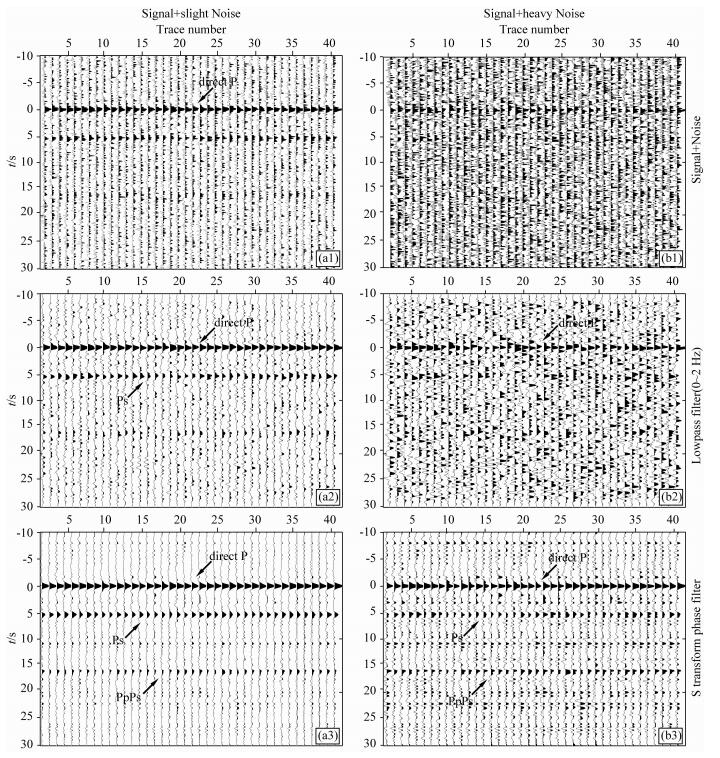
图 2(a1) 是加了高斯白噪声之后的理论数据, SNR=0.376, 0 s处的直达P波和5.5 s处的Ps转换波仍可辨别, 但PpPs转换波已无法辨别.利用巴特沃斯低通滤波器滤除2 Hz以上的高频噪声之后 (图 2a2, SNR=1.395), 直达P波和Ps转换波更加清晰, PpPs转换波隐约可见.在低通滤波的基础之上运用S变换时频域相位滤波方法处理之后 (图 2a3, SNR=4.631), 直达P波和Ps转换波更加清晰, 波形更加平滑, 同时16.2 s处PpPs转换波也清晰可见.由此可见, S变换时频域相位滤波方法可以有效滤除噪声, 提高信噪比.

图 2 (a1) 有效信号和噪声的叠加, SNR=0.376; (a2) 图a1的低通 (0~2 Hz) 滤波结果, SNR=1.395; (a3) 图a2的时频域相位滤波结果, SNR=4.631; (b1) 与图a1相同, 但是加入了振幅能量更大的噪声, SNR=0.042; (b2) 图b1的低通 (0~2 Hz) 滤波结果, SNR=0.137; (b3) 图b2的时频域相位滤波结果, SNR=0.384. Fig. 2 (a1) The combine of signal and noise, SNR=0.376; (a2) shows lowpass (0~2 Hz) filter output of the data from (a1), SNR=1.395; (a3) shows phase filter in time-frequency domain output of the data from (a2), SNR=4.631; (b1) Same as (a1), but with large noise contamination, SNR=0.042; (b2) shows lowpass (0~2 Hz) filter output of the data from (b1), SNR=0.137; (b3) shows phase filter in time-frequency domain output of the data from (b2), SNR=0.384.

图 2(b1、b2、b3) 展示了与图 2(a1、a2、a3) 相同的处理过程, 只是图 2(b1) 中加入了更强的高斯噪声, 使得原始数据中直达P波都很难辨别, SNR=0.042.在实际数据处理中, 一般信噪比如此低的数据都直接舍弃不用, 本文为展示时频域滤波方法的滤波效果, 仍对图 2中的(b1) 的数据进行处理.经过低通滤波之后 (图 2(b2), SNR=0.137), 可以识别出直达P波, 但Ps转换波和PpPs转换波仍然无法识别.再利用S变换时频域相位滤波方法处理之后 (图 2(b3), SNR=0.384), 直达P波、Ps转换波和PpPs转换波都可以清晰的识别, 但是, 在20 s之后, 几乎不存在有效信号 (图 1a), 运用相位叠加方法统计得到的参考相位是噪声信号的相位信息，在这种情况下使用时频域相位滤波方法, 无法有效滤除噪声, 出现了几个虚假波形, 该部分的波形信息不可靠.但从整体而言, 时频域相位滤波方法的滤波效果仍然是十分明显的, 有效压制了通带范围内的混频干扰噪声.

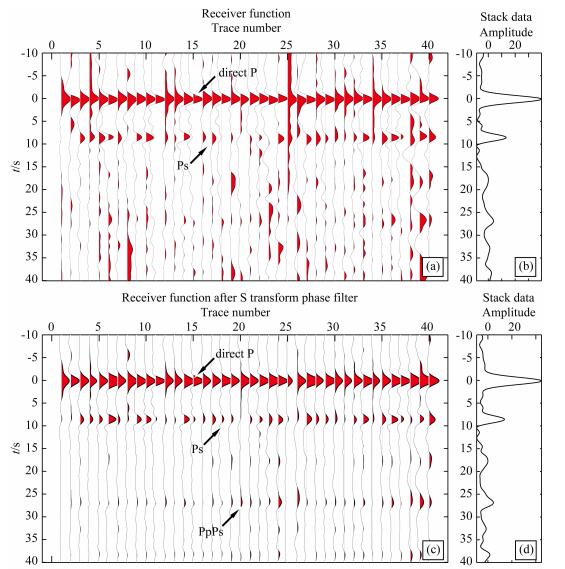
4 实际观测数据的滤波效果

本文选取西藏羌塘实测宽频带地震台站所观测到的地震事件数据 (邹长桥等, 2013; 刘国成等, 2014) 为例, 展示时频域相位滤波方法去噪效果.首先, 对原始数据低通滤波处理, 滤除1 Hz以上的高频噪声; 之后对数据做去均值、去线性趋势、去仪器响应等初步处理, 挑取Z分量P波初至起跳较为明显的数据，将水平分量N、E旋转至R、T方向, 利用频率域反卷积算法, 用Z分量反卷积R分量, 得到高斯参数为1.0的R分量的P波接收函数, 再次从中挑取一级结构间断面Ps转换震相相对明显的数据 (图 3a) 用于后期处理. 图 3a中0 s处直达P波和8.5 s处的Ps震相已经可以分辨, 但是由于噪声的干扰, 波形信息一致连贯性较差, 观察不到PpPs转换波, 不利于后续分析处理 (如H-K扫描等).在图 3a的叠加数据 (图 3b) 中, 10 s之后的几个波组波形较宽, 起跳不明显, 不利于区分.利用基于S变换的时频域相位滤波对其做进一步处理之后 (图 3c), 直达P波之前的噪声得到明显的压制, 直达P波和8.5 s处的Ps转换波起跳更加明显, 波形更加连贯一致, 同时可以清晰的识别出26.5 s处一级结构间断面的PpPs转换波. 图 3c的叠加数据 (图 3d) 与图 3b相比, 直达P波的振幅更大, 能量更强, 10 s之后的各个波组波形进一步锐化, 起跳更加明显, 分辨率进一步提高.从图 3的滤波效果对比中可以看出时频域相位滤波方法去噪效果明显.与相位加权叠加方法 (Schimmel and Gallart, 2007; 沈旭章和周蕙兰, 2009; Schimmel et al., 2011; 司少坤等, 2012) 相比, 本文提出的时频域相位滤波方法几乎不改变有效信号的绝对振幅信息，更适合于远震接收函数地震数据的分析处理.

图 3 (a) R分量P波接收函数; (b) 图a的叠加数据; (c) 图a的时频域相位滤波结果; (d) 图c的叠加数据 Fig. 3 (a) The receiver function of P wave in R component; (b) The stack data of (a); (c) shows phase filter in time-frequency domain output of the data from (a); (d) The stack data of (c)
5 结论

运用相位线性叠加方式识别出有效信号的相位信息, 然后利用S变换在时频域滤除与有效信号相位不相符的噪声成分.相位叠加方法基于有效信号的相位在波形中是相对稳定的理论基础 (Schimmel et al., 2011; Schimmel and Paulssen, 1997), 有效的避免了拟合大振幅噪声数据而忽视波形中弱能量相干信号的情况.时频域相位滤波充分利用了有效信号和噪声信号在相位上的差异, 滤波效果明显, 有效的压制了混频干扰噪声, 提高了信噪比, 即使在数据量较少的情况下, 依然能够检测出有效弱能量信号.但当有效信号和噪声信号在能量上悬殊太大时, 该方法的滤波效果也是有限的.因此, 为了地震数据后期处理的准确性, 最根本的做法仍然是在野外数据采集时尽最大可能采集高信噪比的原始资料.时频域相位滤波方法对地震波到时的拾取和信号识别等意义重大, 同样适用于共中心点道集的石油地震勘探数据的滤波去噪.

致谢

感谢中国地质科学院地质研究所岩石圈中心张洪双博士在宽频带地震数据处理过程中的指导与帮助, 也感谢本中心的其他成员分享他们宝贵的写作经验.文中的数据处理和成图是通过Matlab、SAC和CorelDRAW软件来完成的.

参考文献
Banka D, Crossley D. 1999. Noise levels of superconducting gravimeters at seismic frequencies. Geophysical Journal International, 139(1): 87-97. DOI:10.1046/j.1365-246X.1999.00913.x
Chen X H, He Z H, Huang D J. 2008. Generalized S transform and its time-frequency filtering. Signal Processing, 24(1): 28-31.
Chen Y H, Yang C C, Cao Q F, et al. 2006. The comparison of some time-frequency analysis methods. Progress in Geophysics , 21(4): 1180-1185. DOI:10.3969/j.issn.1004-2903.2006.04.019
Douglas A. 1997. Bandpass filtering to reduce noise on seismograms:Is there a better way. Bulletin of the Seismological Society of America, 87(3): 770-777.
Gabor D. 1946. Theory of communication. Part 1:The analysis of information. Journal of the Institution of Electrical Engineers-Part Ⅲ:Radio and Communication Engineering, 93(26): 429-441. DOI:10.1049/ji-3-2.1946.0074
Grossmann A, Morlet J, Paul T. 1985. Transforms associated to square integrable group representations. I. General results. Journal of Mathematical Physics, 26(10): 2473-2479. DOI:10.1063/1.526761
Kafka A L, Weidner D J. 1979. The focal mechanisms and depths of small earthquakes as determined from Rayleigh-wave radiation patterns. Bulletin of the Seismological Society of America, 69(5): 1379-1390.
Li Z C, Diao R, Han W G, et al. 2010. Review on linear time-frequency analysis methods. Progress in Exploration Geophysics , 33(4): 239-246.
Liu G C, Shang X F, He R Z, et al. 2014. Topography of Moho beneath the central Qiangtang in North Tibet and its geodynamic implication. Chinese J. Geophys. , 57(7): 2043-2053. DOI:10.6038/cjg20140702
Liu X Z, Shen X Z, Li Q S, et al. 2014. An analysis of the tele-seismic waveforms and ambient noise of temporary broadband seismic array on the Northeastern margin of the Tibetan Plateau. Acta Geoscientica Sinica , 35(6): 759-768. DOI:10.3975/cagsb.2014.06.12
Parolai S. 2009. De-noising of seismograms using the S transform. Bulletin of the Seismological Society of America, 99(1): 226-234. DOI:10.1785/0120080001
Pinnegar C R, Mansinha L. 2003a. Time-local spectral analysis for non-stationary time series:The S-transform for noisy signals. Fluctuation and Noise Letters, 3(3): L357-L364. DOI:10.1142/S0219477503001439
Pinnegar C R, Mansinha L. 2003b. The S-transform with windows of arbitrary and varying shape. Geophysics, 68(1): 381-385. DOI:10.1190/1.1543223
Qu Z D, Wu W, He R Z, et al. 2015. Soft threshold filter based on S transform and its application to data processing of deep seismic reflection. Chinese J. Geophys. , 58(9): 3157-3168. DOI:10.6038/cjg20150912
Randall G E. 1989. Efficient calculation of differential seismograms for lithospheric receiver functions. Geophysical Journal International, 99(3): 469-481. DOI:10.1111/gji.1989.99.issue-3
Schimmel M, Paulssen H. 1997. Noise reduction and detection of weak, coherent signals through phase-weighted stacks. Geophysical Journal International, 130(2): 497-505. DOI:10.1111/gji.1997.130.issue-2
Schimmel M, Gallart J. 2007. Frequency-dependent phase coherence for noise suppression in seismic array data. Journal of Geophysical Research, 112(B4). DOI:10.1029/2006JB004680
Schimmel M, Stutzmann E, Gallart J. 2011. Using instantaneous phase coherence for signal extraction from ambient noise data at a local to a global scale. Geophysical Journal International, 184(1): 494-506. DOI:10.1111/j.1365-246X.2010.04861.x
Shapiro N M, Campillo M. 2004. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophysical Research Letters, 31(7). DOI:10.1029/2004GL019491
Shen X Z, Zhou H L. 2009. The low-velocity layer at the depth of 620 km beneath Northeast China. Chinese Science Bulletin, 54(17): 3067-3075. DOI:10.1007/s11434-008-0559-z
Si S K, Tian X B, Zhang H S, et al. 2013. Prevalent thickening and local thinning of the mantle transition zone beneath the Baikal rift zone and its dynamic implications. Science China Earth Sciences, 56(1): 31-42. DOI:10.1007/s11430-012-4547-4
Stockwell R G, Mansinha L, Lowe R P. 1996. Localization of the complex spectrum:The S transform. IEEE Transactions on Signal Processing, 44(4): 998-1001. DOI:10.1109/78.492555
Stockwell R G. 1999. S-transform analysis of gravity wave activity from a small scale network of airglow imagers[Ph. D. thesis]. Ontario:University of Western Ontario.
Xu F. Application of Greenspline interpolator and S-transform to processing gravity and seismic data[Master's thesis] . Beijing: China University of Geosciences (Beijing), 2013.
Yang Y J, Ritzwoller M H, Lin F C, et al. 2008. Structure of the crust and uppermost mantle beneath the western United States revealed by ambient noise and earthquake tomography. Journal of Geophysical Research, 113(B12). DOI:10.1029/2008JB005833
Yao H J, Beghein C, Van Der Hilst R D. 2008. Surface wave array tomography in SE Tibet from ambient seismic noise and two-station analysis-Ⅱ. Crustal and upper-mantle structure. Geophysical Journal International, 173(1): 205-219. DOI:10.1111/j.1365-246X.2007.03696.x
Yin X Z, Chen J H, Li S C, et al. 2013. The research on self-noise measurement method of moveable broadband seismometer. Seismology and Geology , 35(3): 576-583. DOI:10.3969/j.issn.0253-4967.2013.03.011
Zhang J H, Zang S T, Zhou Z X, et al. 2009. Quantitative computation and comparison of S/Nratio in seismic data. Oil Geophysical Prospecting , 44(4): 481-486.
Zhao S H, Wang X. 2007. Comparison between the time-frequency filtering of S transform method and other filter method. Northwestern Seismological Journal , 29(3): 224-229. DOI:10.3969/j.issn.1000-0844.2007.03.005
Zhao S H, Zhu G M. 2007. Time-frequency filtering to denoise by S transform. Oil Geophysical Prospecting , 42(4): 402-406.
Zheng C L, Wang B S. 2015. Application of S transform in seismic data processing. Progress in Geophysics , 30(4): 1580-1591. DOI:10.6038/pg20150412
Zou C Q, He R Z, Gao R, et al. 2012. Deep structure of the central uplift belt in the Qiangtang terrane Tibetan Plateaufrom teleseismic P-wave tomography. Chinese Science Bulletin , 57(28-29): 2729-2739. DOI:10.1360/972011-2430
陈学华, 贺振华, 黄德济. 2008. 广义S变换及其时频滤波. 信号处理, 24(1): 28–31.
陈雨红, 杨长春, 曹齐放, 等. 2006. 几种时频分析方法比较. 地球物理学进展, 21(4): 1180–1185. DOI:10.3969/j.issn.1004-2903.2006.04.019
李振春, 刁瑞, 韩文功, 等. 2010. 线性时频分析方法综述. 勘探地球物理进展, 33(4): 239–246.
刘国成, 尚学峰, 贺日政, 等. 2014. 藏北羌塘盆地中部莫霍面形态及其动力学成因. 地球物理学报, 57(7): 2043–2053. DOI:10.6038/cjg20140702
刘旭宙, 沈旭章, 李秋生, 等. 2014. 青藏高原东北缘宽频带地震台阵远震记录波形及背景噪声分析. 地球学报, 35(6): 759–768. DOI:10.3975/cagsb.2014.06.12
曲中党, 吴蔚, 贺日政, 等. 2015. 基于S变换的软阈值滤波在深地震反射数据处理中的应用. 地球物理学报, 58(9): 3157–3168. DOI:10.6038/cjg20150912
沈旭章, 周蕙兰. 2009. 接收函数CCP-PWS偏移方法探测中国东北地区620 km深处低速层. 科学通报, 54(2): 215–223.
司少坤, 田小波, 张洪双, 等. 2012. 贝加尔裂谷区地幔过渡带大范围增厚与局部减薄现象及其动力学意义. 中国科学:地球科学, 44(11): 1647–1659.
许丰. 2013. 格林函数样条插值和S变换在重、震数据处理中的应用[硕士论文]. 北京: 中国地质大学 (北京).
尹昕忠, 陈九辉, 李顺成, 等. 2013. 流动宽频带地震计自噪声测试研究. 地震地质, 35(3): 576–583. DOI:10.3969/j.issn.0253-4967.2013.03.011
张军华, 藏胜涛, 周振晓, 等. 2009. 地震资料信噪比定量计算及方法比较. 石油地球物理勘探, 44(4): 481–486.
赵淑红, 王璇. 2007. S变换时频滤波与其它滤波方法的比较. 西北地震学报, 29(3): 224–229. DOI:10.3969/j.issn.1000-0844.2007.03.005
赵淑红, 朱光明. 2007. S变换时频滤波去噪方法. 石油地球物理勘探, 42(4): 402–406.
郑成龙, 王宝善. 2015. S变换在地震资料处理中的应用及展望. 地球物理学进展, 30(4): 1580–1591. DOI:10.6038/pg20150412
邹长桥, 贺日政, 高锐, 等. 2012. 远震P波层析成像研究羌塘中央隆起带深部结构. 科学通报, 57(28-29): 2729–2739. DOI:10.1360/972011-2430