高精度静电悬浮加速度计是重力卫星的核心载荷(Touboul et al., 1999, 2004, 2012)，其功能是测量卫星所受的非保守力引起的加速度(Tapley et al., 2007).由于加速度计在卫星上的安装位置与卫星质心位置之间不可避免地存在一定偏差，卫星姿态旋转将引入离心加速度.加速度计自身无法区分卫星受到的非保守力和姿态旋转引入的扰动加速度，为使测量输出主要反映非保守力，必须保证加速度计检验质量与卫星质心的相对位置控制在一定的范围内，从而使旋转引入的扰动加速度不影响到非保守力测量精度.卫星在轨期间，由于推进剂的消耗，卫星质心会相对于卫星框架发生变化，而加速度计和卫星框架之间是近似刚性连接，因此加速度计检验质量与卫星质心在轨实际位置会随时间发生变化，这就需要在卫星整个寿命周期内定期测量二者的质心位置偏差，并利用质心调节机构进行在轨调节，将二者偏差控制在一定范围内(Wang, 2003; Flury et al., 2008; Case et al., 2010).对于GRACE卫星而言，使用加速度计与星敏感器测量数据联合估计加速度计与卫星质心的位置偏差，然后通过移动已知质量块在轨调节卫星的质心，使之控制在所需范围内.GRACE卫星质心位置偏差控制要求为不超过0.1 mm，质心位置估计精度要求优于0.05 mm.Wang (2003)详述了GRACE的质心标定原理和过程，国内在此领域的研究主要集中在使用模拟数据进行标定算法的研究(郑伟等，2009；辛宁等，2013).

本文利用国内某试验卫星首次搭载的我国自主研制的静电悬浮加速度计的数据，对加速度计相对卫星质心位置的估计进行了研究.利用加速度计测量输入是偏离质心带来的旋转耦合加速度这一特性，结合加速度计数据以及卫星的姿态运动数据对加速度计测量值的正确性与精度进行了检验，同时利用上述数据对加速度计与卫星质心位置偏差进行了估计.本文首先简介静电悬浮加速度计的工作原理、在轨测量数据以及本次试验卫星搭载的加速度计基本配置，接下来描述卫星的姿态运动特征与测量数据的预处理流程，最后给出加速度计与卫星质心之间位置偏差的最小二乘法估计原理与估计结果，并对计算误差进行分析.

高精度静电悬浮加速度计核心单元包含一块可自由运动的检验质量、包围检验质量的电容极板(检验质量、电容极板构成敏感探头)以及外围的电容传感与静电反馈控制电路(Josselin et al., 1999；白彦峥等，2010；Hu et al., 2014).静电悬浮加速度计由六路原理相同的传感、控制与反馈电路组成，同时测量同一个检验质量的三个平动加速度与三个角加速度.

加速度计主要测量值为三个平动自由度的加速度矢量a_in^SC，加速度计输出此矢量在加速度计坐标系三个方向的分量，其包含卫星平台所受的非保守加速度a_ng^SC以及平台姿态旋转附加加速度a_Rot^SC, 公式为

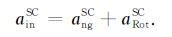
(1)

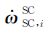
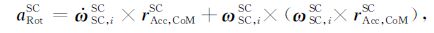
为明确各矢量意义，文中具有三个上下标的矢量的意义为：x_{a, b}^c表示a相对于b的x矢量在c坐标系中的表达.如ω_{SC, i}^SC为SC (航天器)相对于i (地心惯性坐标系，J2000坐标系)的角速度在SC (航天器)坐标系中的表达.旋转附加加速度a_Rot^SC如(2)式所示，包含两项：第一项为切向附加加速度，与卫星的角加速度有关；第二项为向心加速度，与卫星的角速度ω_{SC, i}^SC相关(Wang，2003；Milani and Gronchi, 2009；祝竺等，2010).公式为

(2)

其中r_{Acc, CoM}^SC为在航天器(SC)坐标系中卫星平台质心指向加速度计检验质量质心处的位移矢量，这里约定加速度计坐标系与卫星本体坐标系三轴方向一致.两个坐标系的转换矩阵R_SC^Acc=I为单位对角阵，则有a_Rot^Acc=R_SC^Acca_Rot^SC=a_Rot^SC，将(2)式展开写成矩阵形式为：

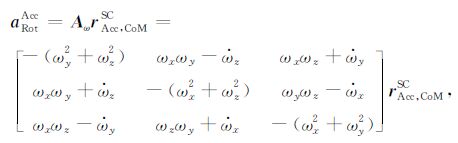
(3)

其中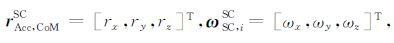

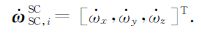
在有关部门资助下，华中科技大学自主研制的静电悬浮加速度计飞行样机于2013年搭载我国某试验卫星，首次进行了在轨飞行试验，成功验证了其在轨工作性能.加速度计检验质量质心距卫星质心的偏差在发射前的测量估算值r_{Acc, CoM}^SC约为{0.0025, 0.1200, -0.0064}m (精度约为1 mm).搭载的静电悬浮加速度计(高灵敏轴)量程设计约为10^-3 m·s^-2，分辨率在0.1 Hz为3×10^-8 m·s^-2/Hz^1/2.根据该卫星轨道高度，卫星所受的主要非保守力是太阳光压，大气阻尼力可忽略.根据卫星的外形估算其所受的太阳光压量级|a_{ng, solar}| < 10^-7m·s^-2，而姿态机动过程带来的旋转加速度a_Rot^SC远大于非保守力加速度，峰峰值可达10^-5 m·s^-2，因此可认为卫星姿态机动的过程中加速度计主要输入为卫星旋转带来的扰动加速度.

本次搭载试验卫星姿态控制系统的传感器包含星敏感器和陀螺仪，分别用于测量卫星相对于惯性坐标系的姿态角度q_SCⁱ和角速度ω_{SC, i}^SC.卫星姿态运动工作模式包括周期巡航与定点指向两种模式.周期巡航状态下卫星以轨道周期做姿态运动，定点指向模式指的是卫星在特定的时间内(一般持续数分钟)进行姿态机动，以实现对地定点指向，便于数据传输，一段时间之后再转回正常巡航模式.在此过程中卫星的角速度与角加速度呈现较大的变化，使得加速度计的测量值变化也比较大，为加速度计在轨质心估计提供很好机会.

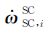
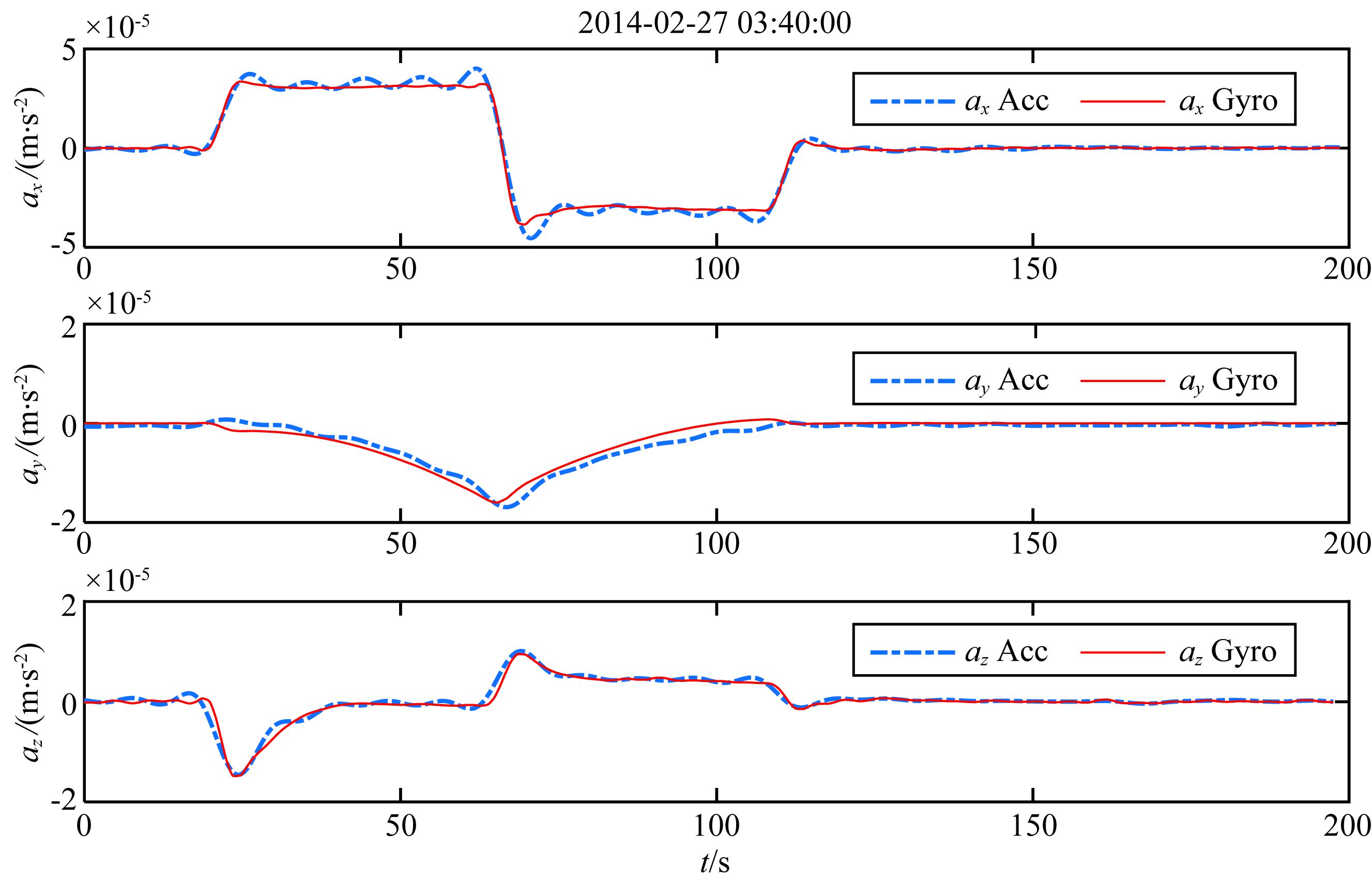
加速度计原始数据(L0级数据)包含三个平动自由度和三个转动自由度的反馈电压信号，频率为4 Hz，本文只取三个平动自由度反馈电压V_fed=[V_x, V_y, V_z]来进行分析，使用公式a_out=H_aV_fed(H_a为地面标定得到的反馈执行机灵敏度系数)转换后得到原始的加速度L1级数据.L1级数据经过野值剔除、偏值纠正、时间码修正、插值与降采样滤波后得到有效加速度信号，最终的处理结果为采样率1 Hz的三轴平动加速度信号.陀螺仪原始数据为0.5 Hz角速度信号，经时间码调整、插值、数值微分与滤波处理后得到与加速度计时间码严格对应的1 Hz的三轴角速度ω_{SC, i}^SC与角加速度信号.为使两者反映同样的频域信息，两个仪器信号处理过程中选用的滤波器的截止频率一致，取0.1 Hz.

选取一次姿态机动时刻的陀螺仪数据并代入(3)式计算姿态旋转引起的加速度a_Rot^SC，将其与同一时段的加速度计数据进行对比可得图 1，图中实线为根据陀螺角速度计算得到的加速度曲线，虚线为加速度计测量值，由图可见加速度计测量和陀螺仪估算加速度有较好的吻合，可直接验证加速度计在轨工作状态正常.图 1中Z轴的两条曲线吻合最好，X轴输入加速度上升下降时刻(图中70 s与110 s附近)出现小幅度抖动，主要是由加速度计测量到的卫星本体的高频结构振动，而陀螺仪受到测量频带及其内部的滤波器带宽限制，无法测量到这些高频振动.

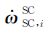
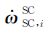
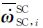
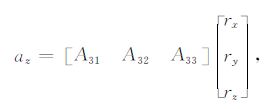
由2.2和2.3节可知，在卫星姿态机动过程中，加速度计测量变化主要来自于转动引入的加速度a_Acc^SC=A_ωr_{Acc, CoM}^SC，其中A_ω为ω_{SC, i}^SC与的非线性组合，加速度计距离卫星质心位置拟合是一个非线性拟合问题.为简化拟合过程，使用ω_{SC, i}^SC与的测量值ω_{SC, i}^SC与计算，组合得到矩阵A_ω的测量值A_ω，将此矩阵的时间序列作为新的姿态运动测量值代入拟合，从而将非线性拟合转化为线性拟合.矩阵方程a_Acc^SC=A_ωr_{Acc, CoM}^SC共有三行，意味着加速度计存在三个方向的测量：a_Acc^SC=[a_x, a_y, a_z]，每个方向的测量都可以单独进行质心位置拟合，例如对于Z方向有：

(4)

其中令，为Z轴加速度的测量序列，根据角速度和角加速度测量的时间序列计算得到的加速度为：

图 1

Fig. 1

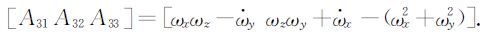
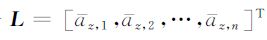
图 1 卫星姿态机动时加速度计测量值(蓝色虚线)与姿态测量数据计算出的加速度(红色实线)对比 Fig. 1 Comparison of accelerometer measurement with acceleration derived by gyroscope during satellite attitude maneuver

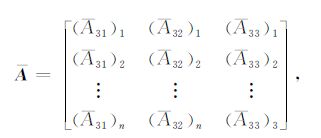
(5)

(4)式的观测方程为L=Ar_{Acc, CoM}^SC+ε，这里ε为观测噪声，则r_{Acc, CoM}^SC的最小二乘估计(沈云中和陶本藻, 2012)为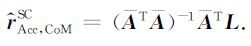

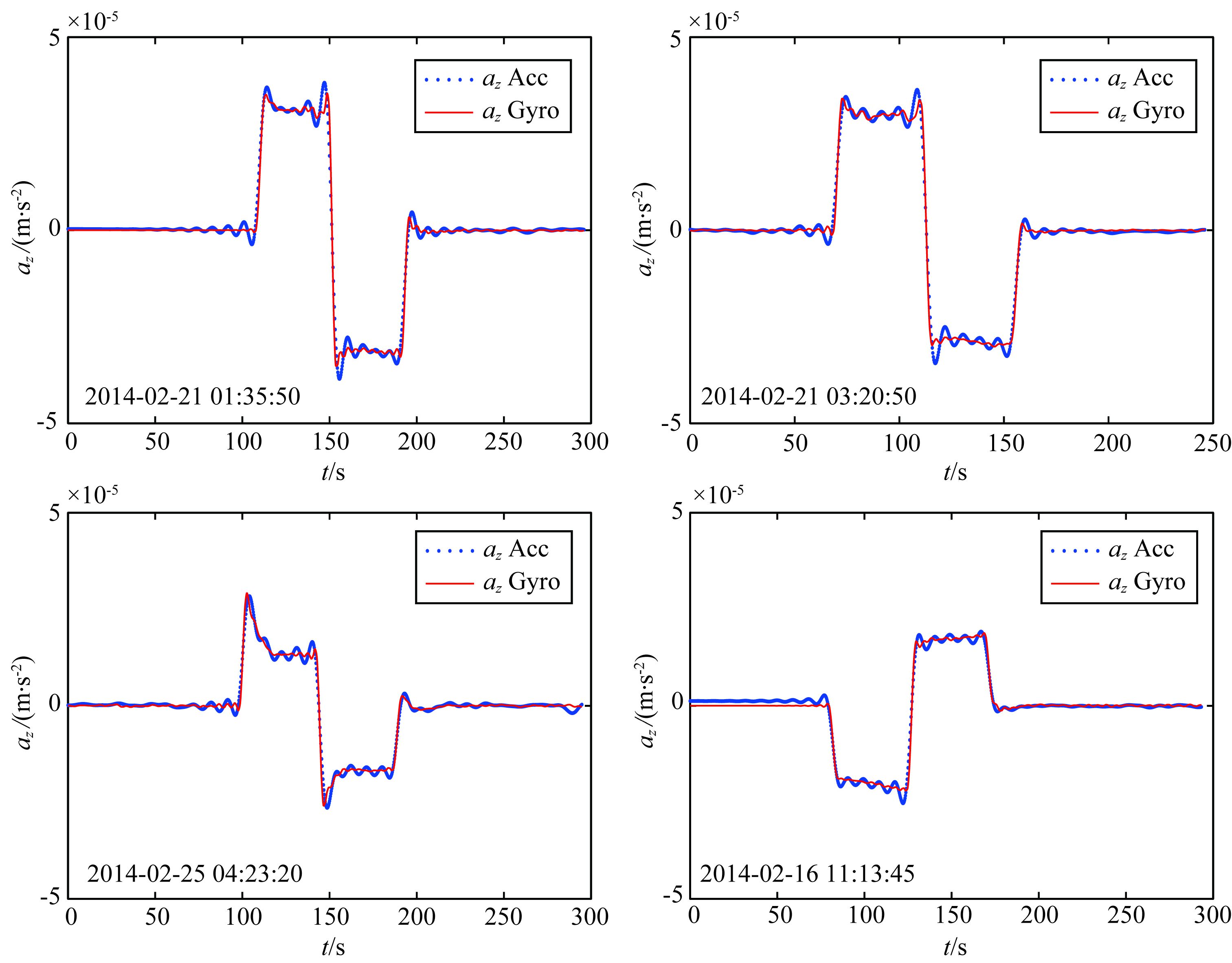
加速度计三个测量轴中Y、Z轴是高灵敏轴，其分辨率比X轴高，且Z轴方向姿态机动引入加速度明显大于Y轴的引入加速度.因此，可选择使用Z轴的加速度分量a_z进行质心估计，以获得更佳精度.根据3.1节所述的拟合方法，选取四个典型机动区间数据，每段时长约300 s，对加速度计距离质心位置进行了拟合，结果如表 1所示.表 1中的结果表明，四次拟合结果的标准差小于1 cm，其中Y方向标准差最小，约为0.36 cm.加速度计检验质量质心距卫星质心的坐标差在发射前估算值为r_{Acc, CoM}^SC={0.0025, 0.1200, -0.0064}m，其估算精度约为1 mm.拟合结果与模型估计值符合较好.四次拟合的曲线如图 2所示，其中虚线为加速度计测量，实线为陀螺仪数据拟合曲线.

表 1(Table 1)

表 1 机动拟合加速度计距离卫星质心的偏差值 Table 1 CoM calibration using Z axis acceleration during typical attitude maneuver 机动时间 拟合结果/m rx ry rz 1 -0.0054 0.1202 0.0025 2 0.0096 0.1197 -0.0025 3 0.0037 0.1177 -0.0009 4 -0.0008 0.1260 -0.0081 平均 0.0018 0.1209 -0.0022 标准差 0.0064 0.0036 0.0044

表 1 机动拟合加速度计距离卫星质心的偏差值 Table 1 CoM calibration using Z axis acceleration during typical attitude maneuver

图 2

Fig. 2

图 2 Z轴加速度计测量值与陀螺仪数据拟合所得Z轴加速度比较 Fig. 2 Comparison of CoM calibration using Z axis acceleration during typical attitude maneuver

使用最小二乘法同时估计卫星质心位置三个自由度坐标，各待估计参数互相耦合，无法给出误差传递的独立表达式.且当前数据中不仅包含仪器误差还包含平台的未知扰动，因此难以通过仪器精度评定质心拟合精度.对未来的重力卫星，为简化分析并给出质心测量精度的定性表达式，以分析r_x的测量误差δr_x为例，假设另两个参数r_y、r_z为已知固定值.由方程(4)可得：

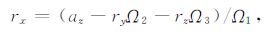
(6)

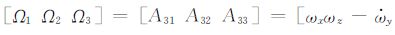
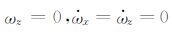
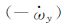
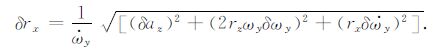
其中.进一步简化，假设卫星只绕Y轴做平面转动，另外两个方向锁定，则ω_x=，(6)式化简为r_x=(a_z+r_zω_y²)/.根据误差传递原则，可得此情况下r_x测量误差传递为

(7)

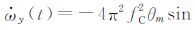
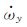
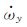
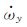
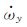
针对重力卫星质心估计，可设计专门的姿态机动方式以获取更好的估计效果.用于r_x测量的运动模式设计为围绕Y轴做往复转动，转动角度与时间关系为θ_y(t)=θ_msin (2πf_Ct)，角速度ω_y(t)=2πf_Cθ_mcos (2πf_Ct)，角加速度sin (2πf_Ct).假设往复运动频率f_C=10 mHz，范围θ_m=10°.对于重力卫星GRACE而言，其静电悬浮加速度计精度为δa_z=1×10^-10m·s^-2(噪声谱密度3×10^-10m·s^-2·Hz^-1/2在0.1 Hz内的积分)，星敏感器精度为δθ=1×10^-5rad (约2角秒)，仪器采样频率为1 Hz.由星敏感器测量的角度数据可获得的角速度与角加速度精度为δω_y=1×10^-5rad·s^-1，=1×10^-5rad·s^-2.另保守假设质心偏差最大值|r_{Acc, CoM}^Sc|≤3×10^-4m，为允许偏差最大值的三倍.由(7)式可知，越大则估计精度越高，选取在最大值附近一段范围，其数值范围为6.2×10^-4≤(t)≤6.9×10^-4，此时有-4.76×10^-3≤ω_y(t)≤4.76×10^-3，将此数据代入(7)式，可得测量精度为(δr_x)_min≈4.6×10^-6m，满足未来的重力卫星任务中将质心位置的估计精度提高到5×10^-5m的需要.分别设定加速度计与星敏感器的测量噪声为零，可计算两个仪器噪声对估计精度的独立贡献.经分析表明在此精度下加速度噪声的贡献小于10^-6m，90%以上的噪声仍然由星敏感器贡献.加速度计的噪声即使变差一个量级，达1×10^-9m·s^-2，星敏感器保持2角秒分辨率，质心测量精度仍可达5×10^-6m.实际应用中，卫星质心位置以月为单位缓慢漂移，可认为在质心测量时保持不变，那么使用一段较长时间的数据(如几个轨道周期)进行最小二乘估计可极大减小估计误差.同时，上述计算中使用的质心估计运动模式为保守设计，在实际任务中，保持往复运动幅度不变情况下，角加速度与f_C²成正比，根据(7)式可知，使用更高频率的摆动幅度可有效改进质心估计精度.同时对于r_y、r_z可设计相应的角度摆动模式，在不同的时间段，逐个估计r_x、r_y和r_z，从而最大可能地降低三个自由度之间的耦合与估计精度的相互影响.因此，基于本文所用的方法原理，用于重力卫星加速度计相对卫星质心的位置标定，可以满足其标定精度要求.

使用星载静电悬浮加速度计的测量数据和陀螺仪姿态数据比对表明，首次搭载的静电悬浮加速度计在卫星姿态机动时能够准确测得姿态机动引入的加速度.使用上述两项数据对加速度计与卫星质心的距离进行了标定，可获得mm级精度的初步结果，对未来重力卫星质心标定具有重要的参考意义.精度分析的结果表明，未来重力卫星在加速度计测量水平提高至1×10^-10 m·s^-2，以及使用精度达到2角秒的星敏感器的基础上，使用本文提供的方法进行质心标定，精度可达4.6×10^-6 m，可满足重力卫星的需求，同时可以设计更好的姿态机动策略来提高质心估计的精度.

感谢卫星用户及卫星研制方航天东方红卫星有限公司提供了有关数据.