2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
可控源音频大地电磁法 (Controlled-Source Audio-Frequency Magnetotellurics,CSAMT) 是20世纪70年代提出的一种人工源电磁法,该方法采用两端接地的长偶源为场源,在距离发射源3~5倍趋肤深度以远的一定区域内接收电磁信号,获得卡尼亚视电阻率信息.由于CSAMT方法信号强度大、工作效率高,在油气、金属矿、地热与地下水资源勘探及工程勘察等领域中有着广泛应用 (Bartel and Jacobson, 1987;Kawasaki et al., 1986;Wannamaker,1997;吴璐苹等,1996;底青云等,2005).目前,CSAMT法反演解释多采用一维、二维技术,对三维电性目标体的解释结果可能会带来误差,为获得精确的地下介质电性信息,需发展三维正反演技术.正演是反演的基础,因此,开展三维数值模拟研究尤为必要.
目前常用的三维电磁法数值模拟手段包括积分方程法 (Hohmann,1975;SanFilipo and Hohmann, 1985;Zhdanov and Fang, 1996;Wannamaker,1991),有限差分法 (Mackie et al., 1994;Newman and Alumbaugh, 1995) 和有限元法 (Wannamaker et al., 1986;Unsworth et al., 1993).积分方程法和有限差分法主要采用结构化网格剖分,而有限元法对网格剖分的要求较灵活,能更有效地处理三维复杂问题.纵观已有的文献资料 (王若等, 2007, 2014;张继锋等,2009;徐志峰和吴小平,2010),CSAMT法三维有限元数值模拟多是将计算区域进行结构化网格单元 (六面体单元) 剖分,这种网格模拟复杂地质模型 (如地形起伏,倾斜界面等) 时,在电性边界处会产生较大的几何离散误差,并最终影响视电阻率数值解的精度.为此,本文开展非结构化网格有限元数值模拟研究.
电磁法非结构化网格有限元数值模拟研究是新兴的研究热点,Rücker等 (2006)首次将非结构化网格应用到直流电阻率法有限元数值模拟研究中.已有的研究主要集中在直流电阻率法 (Liu et al., 2008;任政勇和汤井田,2009;Wang et al., 2013),大地电磁法 (Key and Weiss, 2006;Li and Pek, 2008) 和海洋有源电磁法 (Li and Key, 2007;蔡红柱等,2015;杨军等,2015)3个方面,关于CSAMT方法的非结构化数值模拟成果较少.本文采用节点有限元法,实现了三维CSAMT数值模拟,采用Tetgen软件进行非结构化网格剖分,有利于进一步开展自适应有限元数值模拟算法的研究.
为解决有限元数值模拟计算范围过大及源的奇异性问题,本文将电磁场分为背景场和异常场分别计算,从Maxwell方程组出发,推导了三维异常电场满足的偏微分方程,并加入散度条件对电场进行约束,实现了三维非结构化网格剖分有限元数值模拟算法,通过单元高斯加权平均计算得到异常磁场值,进而得到卡尼亚视电阻率 (Cagniard, 1953).
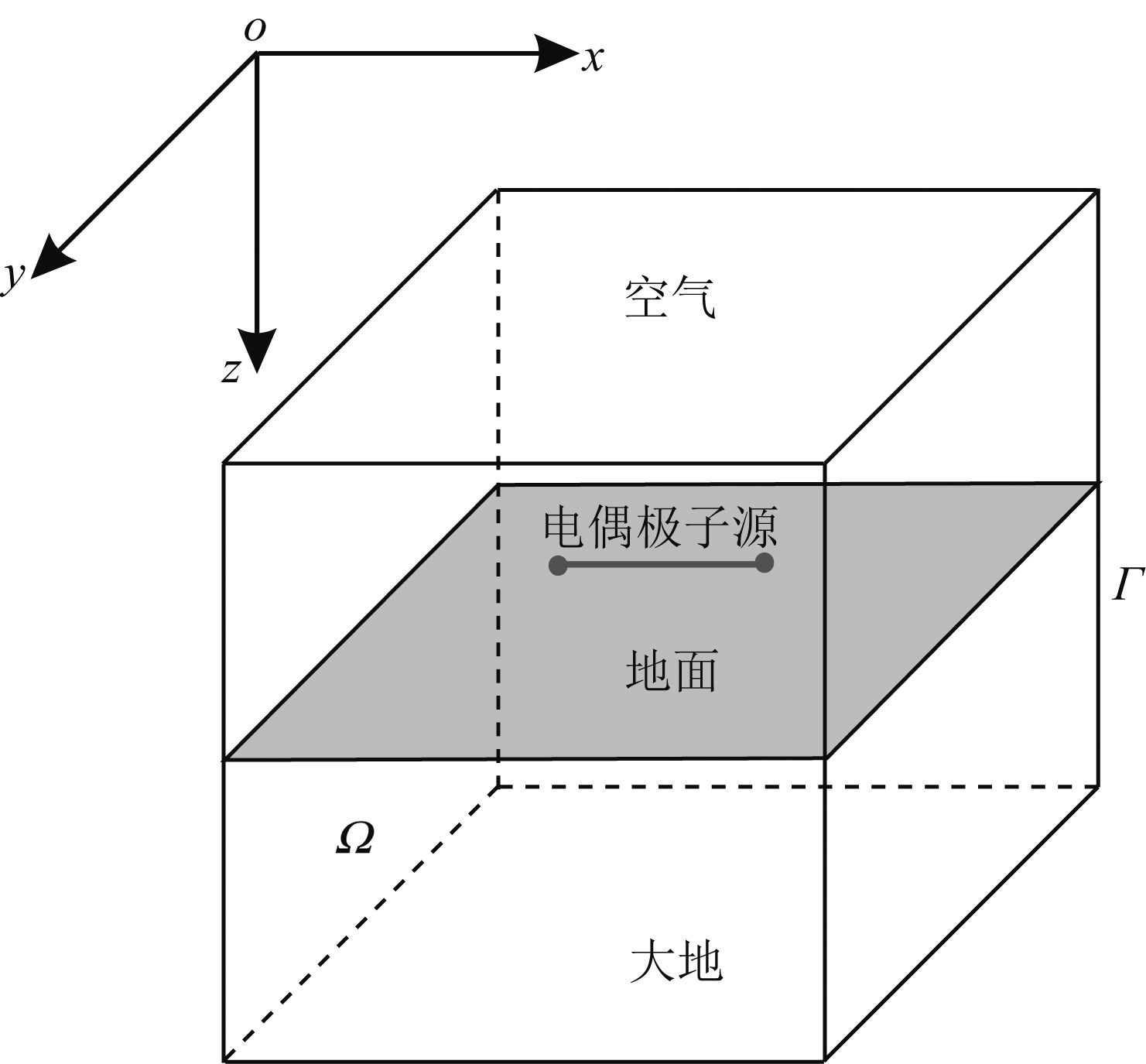
2 电场方程 2.1 异常电场边值问题对于三维电磁场数值模拟,研究区域包括空气层和地层的广大区域,如图 1所示.假设x向是电偶源方向,z轴垂直向下方向为正.
|
图 1 研究区域示意图 Fig. 1 Diagrammatic sketch of research area |
假定电磁场时间因子为e-iωt,在准静态近似下,电偶源激发的频率域电场E,磁场H满足的控制方程如下:
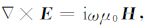
|
(1a) |
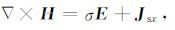
|
(1b) |
其中,μ0是自由空间磁导率,ω是角频率,σ是地下介质的电导率,Jsx是x向电偶极子源电流密度.
对 (1a) 式两端同时取旋度,并将 (1b) 式代入得到:
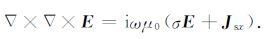
|
(2) |
在电偶源激励下,任何介质感应的电磁场均满足 (2) 式.若将均匀半空间或水平层状介质 (电导率记为σ0) 感应的电场记为Ep,即背景电场,则Ep满足:
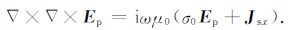
|
(3) |
在背景介质中,加入三维异常体,构成三维地质模型 (电导率记为σ),在同一水平电偶源激励下,感应的总电场Et满足:
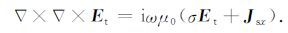
|
(4) |
记三维异常体在该水平电偶源激励下感应的电场为Es,显然异常电场Es是总电场Et与背景电场Ep之差,将 (4) 式减去 (3) 式,可得:
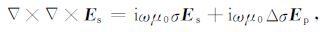
|
(5) |
其中,Es=Et-Ep,为异常电场,Δσ=σ-σ0,为异常体电导率与背景介质电导率之差.(5) 式中的背景电场Ep可由汉克尔变换算法求出 (Key,2009).考虑到计算区域比异常体区域大得多,且异常电场较弱,可近似认为在计算区域的外边界处,异常电场为零.因此,异常电场Es满足的边值问题如 (6) 式,其中Γ是研究区域的外边界.
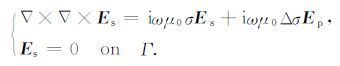
|
(6) |
根据电磁场传播规律,在有源区域,电场应满足 (7) 式,在无源区域,电场应满足 (8) 式,称为散度条件.
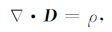
|
(7) |
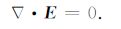
|
(8) |
然而在电磁场节点有限元数值模拟中,离散计算区域时只要求插值函数连续,而对其导数未作任何要求,这种条件下获得的电场解有时是错误的,即存在伪解情况 (金建铭,1982).
因此,在电磁场求解过程中需要加入散度条件,对电场进行约束,以消除伪解.由于异常电场是在无源区域内,将 (8) 式代入 (6) 式,并写成标量形式,则异常电场满足的边值问题可写为:
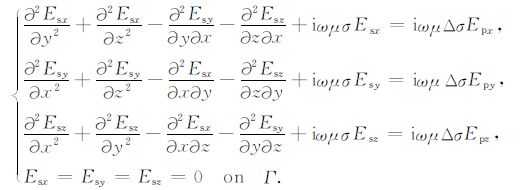
|
(9) |
采用有限元方法求解 (9) 式所描述的边值问题时,需要对研究区域进行剖分.相对于结构化网格剖分,非结构化网格在模拟复杂模型时更有优势.目前,已经有许多成熟算法能自动生成非结构化网格 (Shephard and Georges, 1991;Möller and Hansbo, 1995;Shewchuk,2002),但就精度、质量与可靠性的数学理论而言,约束Delaunay三角化算法 (Constraint Delaunay Triangulation, CDT) 效果最好.该算法生成的单元边长均匀性较好,可方便地对已经生成的网格单元进行加点和减点操作,且保证新生成的网格单元尽量饱满.
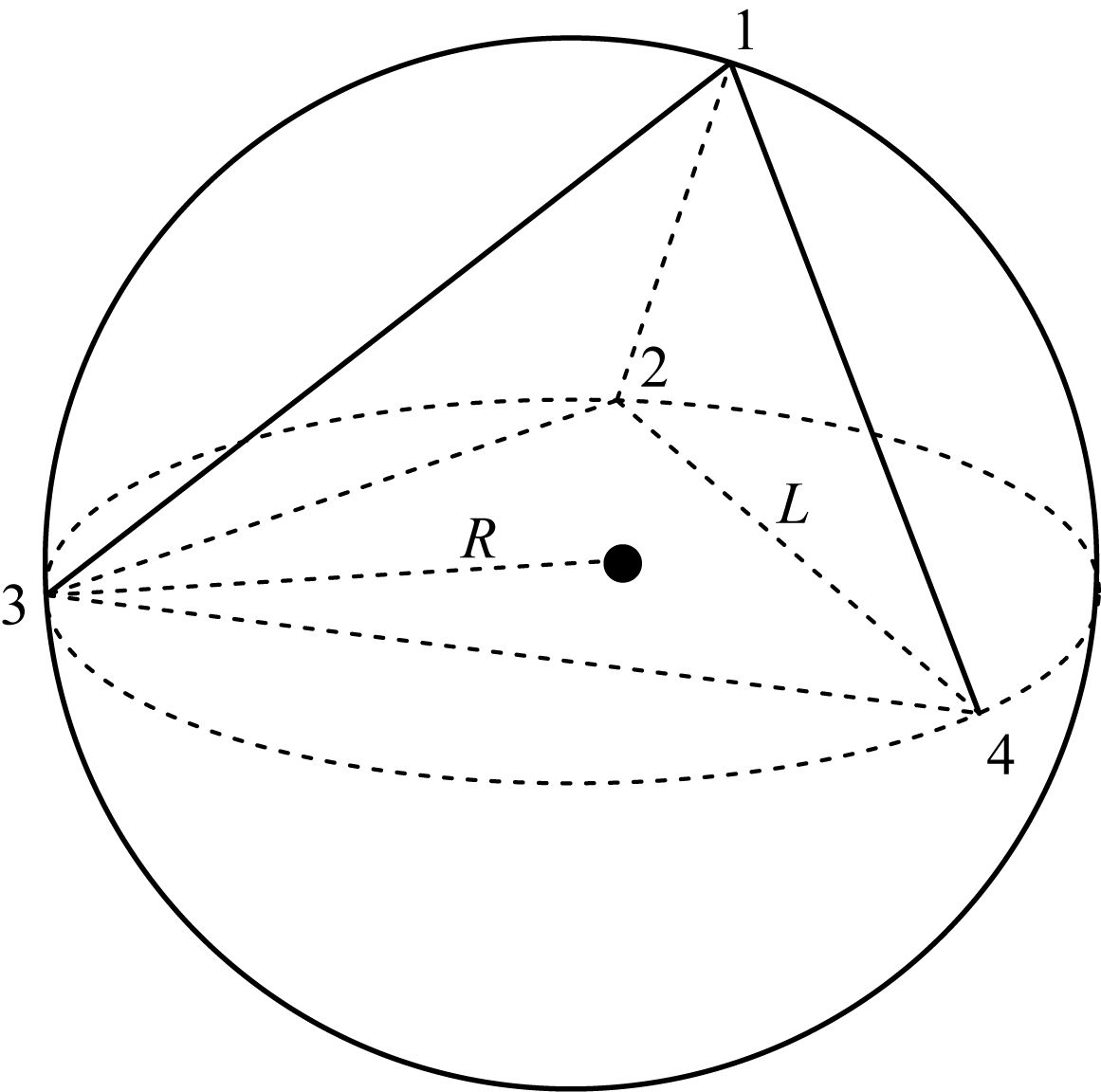
本文使用Tetgen软件对三维地质模型进行网格剖分 (Si,2015).Tetgen软件采用CDT算法,并通过参数Q控制所生成四面体单元的质量.如图 2所示,Q是指四面体的外接球半径R与四面体最短边L之比,即Q=R/L.一般情况下,Q越小,四面体质量越好,反之,质量越差.但太小的Q值会大大增加四面体数量,降低计算效率.Q默认值是2,在生成四面体单元时,若要得到质量较高的剖分单元,需指定Q值,一般取1~1.4.
|
图 2 四面体网格单元示意图 Fig. 2 Sketch of tetrahedron grid cell |
针对Tetgen软件剖分得到的四面体单元 (图 2),其节点i(i=1, 2, 3, 4) 上的一次形函数可表示为:
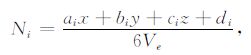
|
(10) |
式中,Ve为四面体单元的体积,根据形函数的性质可唯一地求出 (10) 式中的系数ai, bi, ci, di(详见附录).将四个节点上的形函数写成矢量有:
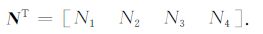
|
(11) |
同样,将四个节点上的异常电场三分量写成矢量有:
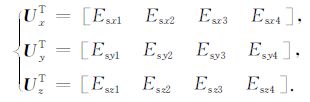
|
(12) |
由此,该单元中任一点处的异常电场三分量可表示为:
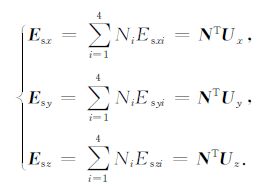
|
(13) |
针对某一四面体单元,将 (13) 式代入 (9) 式中,边值问题离散为:
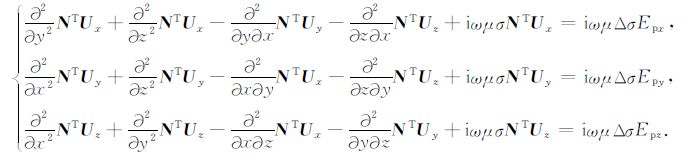
|
(14) |
利用伽里金有限元法,在 (14) 式两端同时乘以形函数,并在单元上积分有:
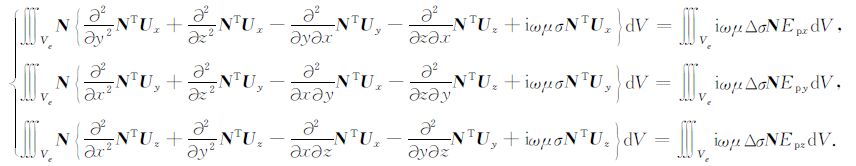
|
(15) |
利用高斯定理,将 (15) 式进行降阶处理,加入边界条件,可写成如下矩阵形式:
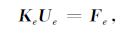
|
(16) |
其中,
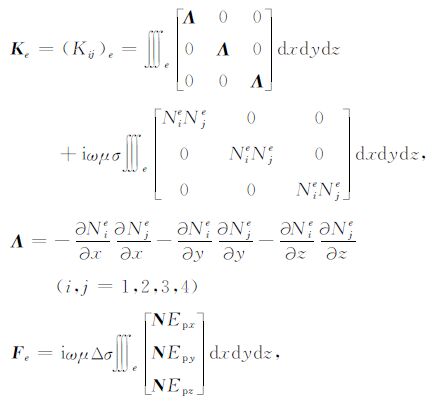
|
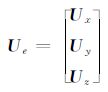
在计算区域内,将所有四面体单元的有限元方程,根据节点间的拓扑关系合成总体有限元方程:
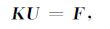
|
(17) |
K是总体刚度矩阵,反映网格节点之间的拓扑关系;F是质量矩阵,反映源的作用;U是所有节点上的待求电场矢量.通常,K是一大型稀疏矩阵,本文使用行压缩 (Compressed Sparse Row) 即CSR存储模式,只存储K中非零元素的值及其位置,大大减小了存储空间.使用Intel mkl函数库中的Pardiso解算器进行 (17) 式的求解,得到所有网格节点上的异常电场三分量.
4 视电阻率求解根据 (1a) 式,可由异常电场计算得到对应节点上异常磁场值.针对x向电偶极源,其产生的y向异常磁场计算公式为:
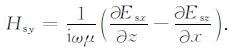
|
(18) |
对一个四面体单元,节点上的异常电场Esx和Esz的导数计算如下:
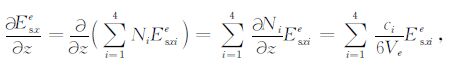
|
(19) |
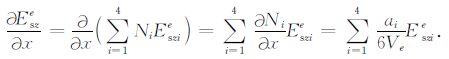
|
(20) |
对于结构化网格单元,若某个节点有n个相关单元,那么该节点电场值的导数是这n个相关单元导数的平均值,然而在非结构化网格单元中,每个单元对该节点的贡献并不相同,按照平均值计算会产生一定误差 (蔡红柱等,2015).为此,本文采用高斯加权函数对各单元的贡献进行约束,使中心点较近的单元赋予更高的权重,以获得较精确的计算结果,异常磁场的求解公式见 (21) 式.
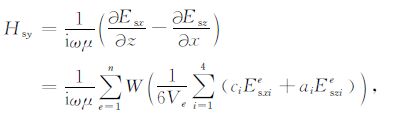
|
(21) |
式中,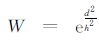
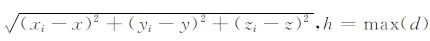
根据 (21) 式计算出异常磁场后,将异常电磁场加上背景电磁场,获得总电磁场.进而根据 (22) 式求得x向水平电偶极源激发下某点的卡尼亚视电阻率:
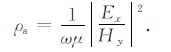
|
(22) |
根据以上理论,编制了异常场的有限元数值模拟程序及背景场计算程序.通过层状介质模型和典型三维异常体模型验证了算法的可靠性和有效性.
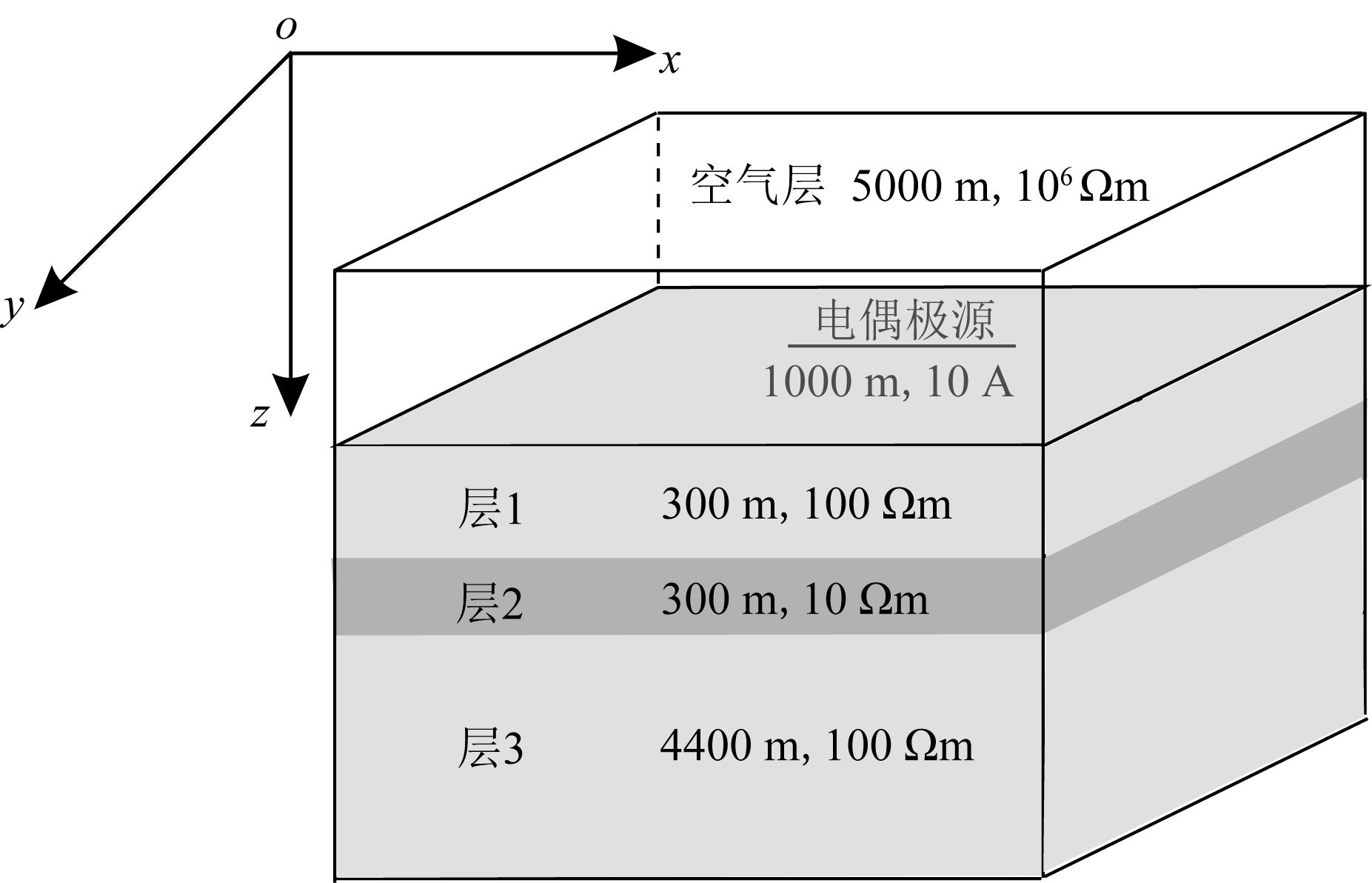
5.1 程序正确性验证设计如图 3所示的三层水平层状介质,计算区域Ω={-5 km≤x, y, z≤5 km},坐标原点位于计算区域的中心,发射源位于y轴-3000 m处.采用本文的有限元算法和Utah大学的三维积分方程算法计算了2-2~213Hz范围内16个频点的电磁响应,通过结果对比验证有限元算法的正确性.使用这两种方法进行模拟时,均将模型中的第二层视为异常体.针对图 3所示的模型,有限元数值模拟中生成的四面体单元数为17358个,网格节点数为2891个,方程自由度为8673.在CPU主频为3.40 GHz,内存为8 GB的个人PC机上,运行时间约1 min.
|
图 3 三层水平层状介质示意图 Fig. 3 Sketch of three-layer horizontal model |
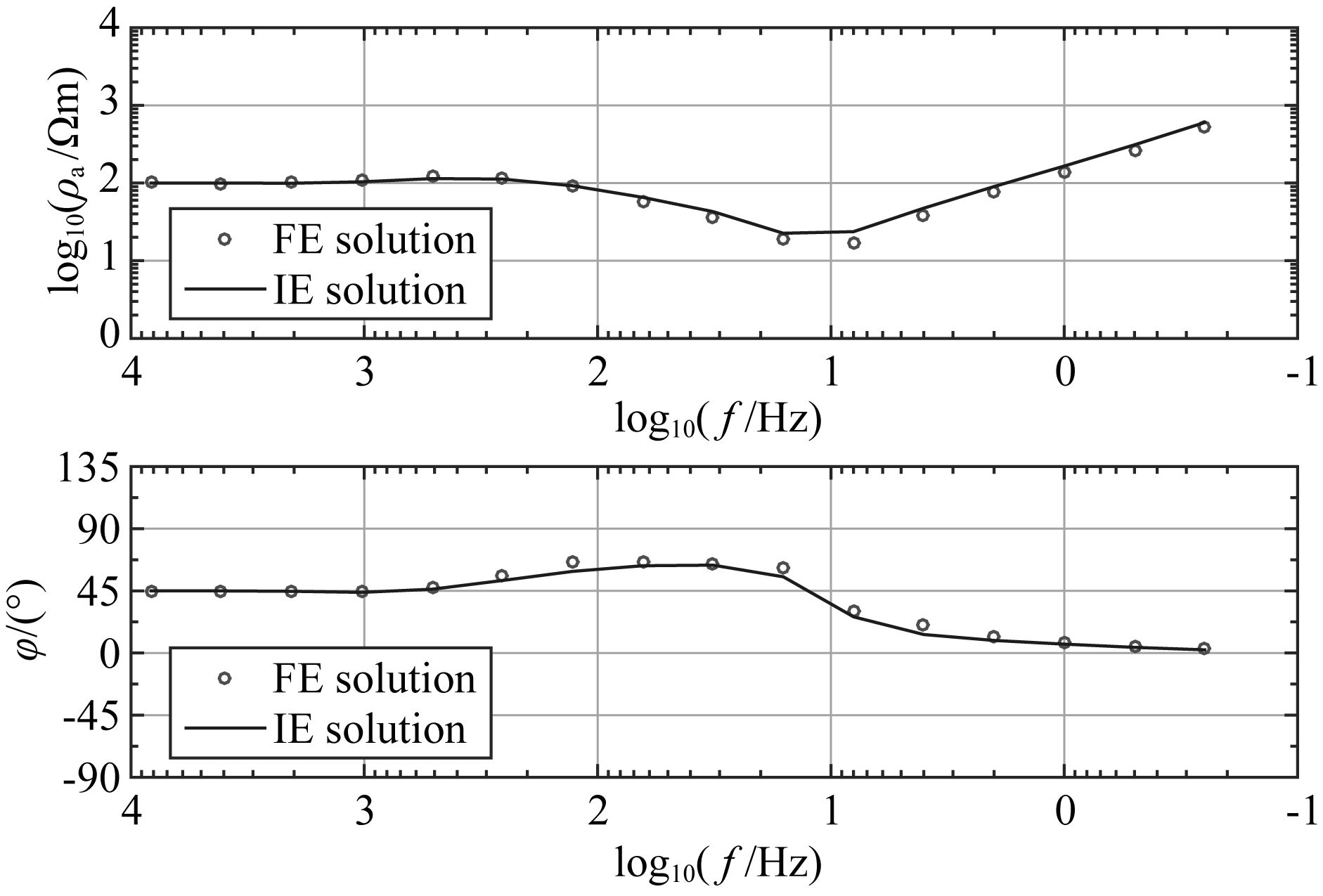
图 4给出了某一测点上两种方法计算视电阻率和阻抗相位的对比曲线.从图 4可以看出两种方法计算的曲线形态一致,经统计,两者百分比误差小于3%,说明有限元程序基本正确,可用于三维模型的CSAMT数值模拟.
|
图 4 三层介质模型某点视电阻率和阻抗相位对比曲线 Fig. 4 Comparison curves of apparent resistivity and impedance phase at one point in a three-layer model |
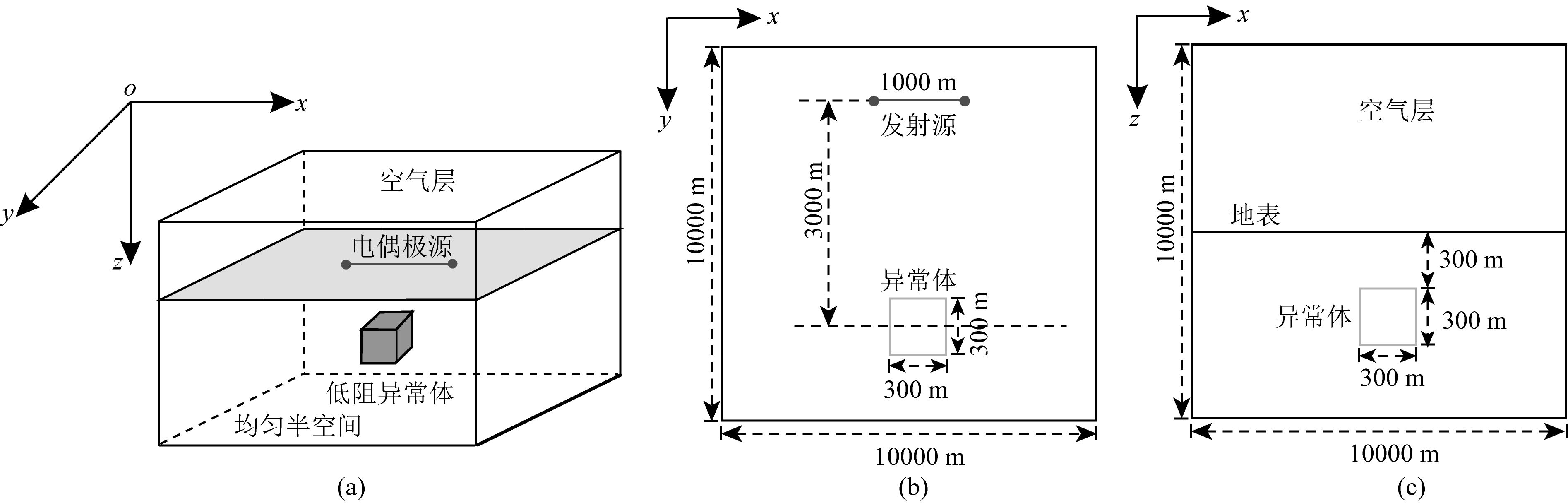
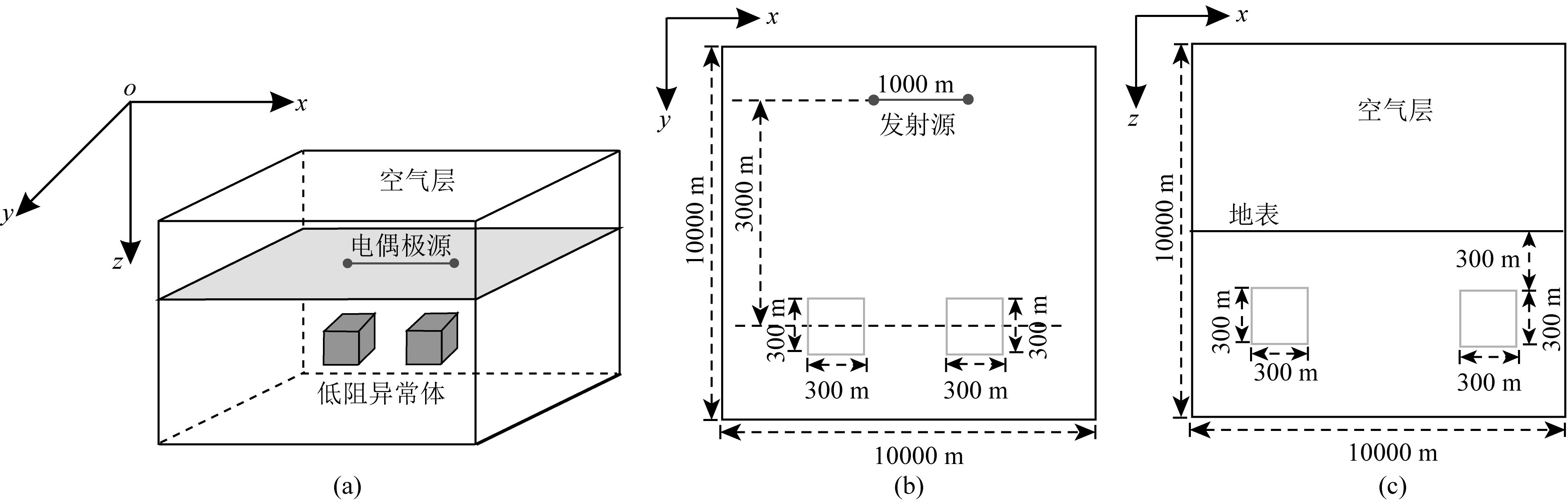
设计如图 5所示的单个三维低阻异常体模型,进行电磁响应分析.图 5中,以低阻异常体中心在地面的投影为坐标原点,z轴垂直向下为正;x,y向范围、z向空气层参数与图 3所示的层状介质模型相同;异常体长、宽、高和顶部埋深均是300 m,电阻率是10 Ωm.
|
图 5 单个三维低阻异常体模型 (a) 三维示意图; (b) 平面图; (c) 剖面图. Fig. 5 Model of single low-resistivity anomaly body (a) 3D view; (b) Planar view; (c) Section view. |
发射源位于y轴-3000 m处,偶极长度为1000 m,发射电流为1 A.接收区域设计5条测线,测线方向沿x向,测线y向坐标范围为-400~400 m,线距200 m;每条测线有60个测点,坐标范围为-900~900 m,点距30 m.
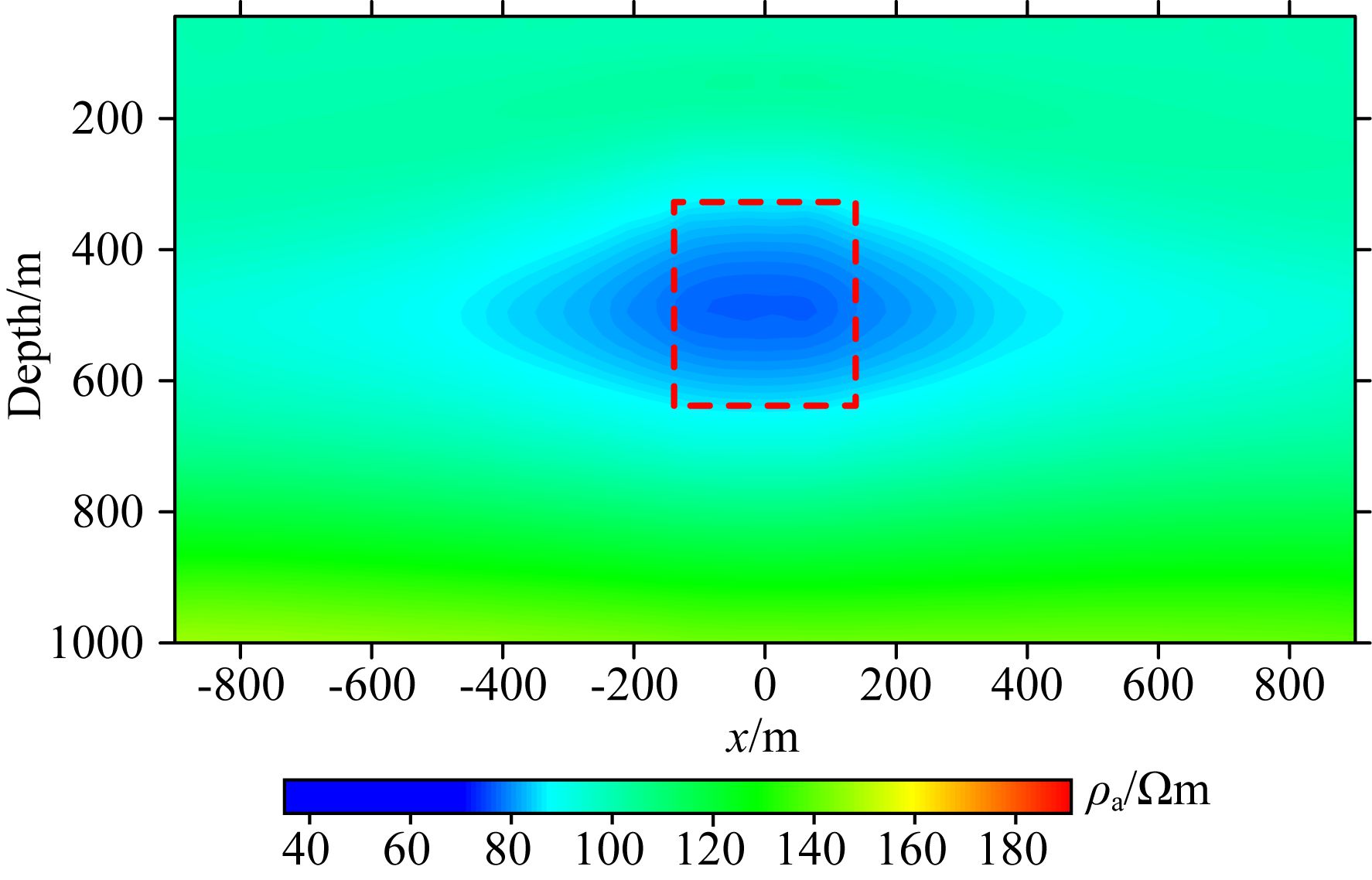
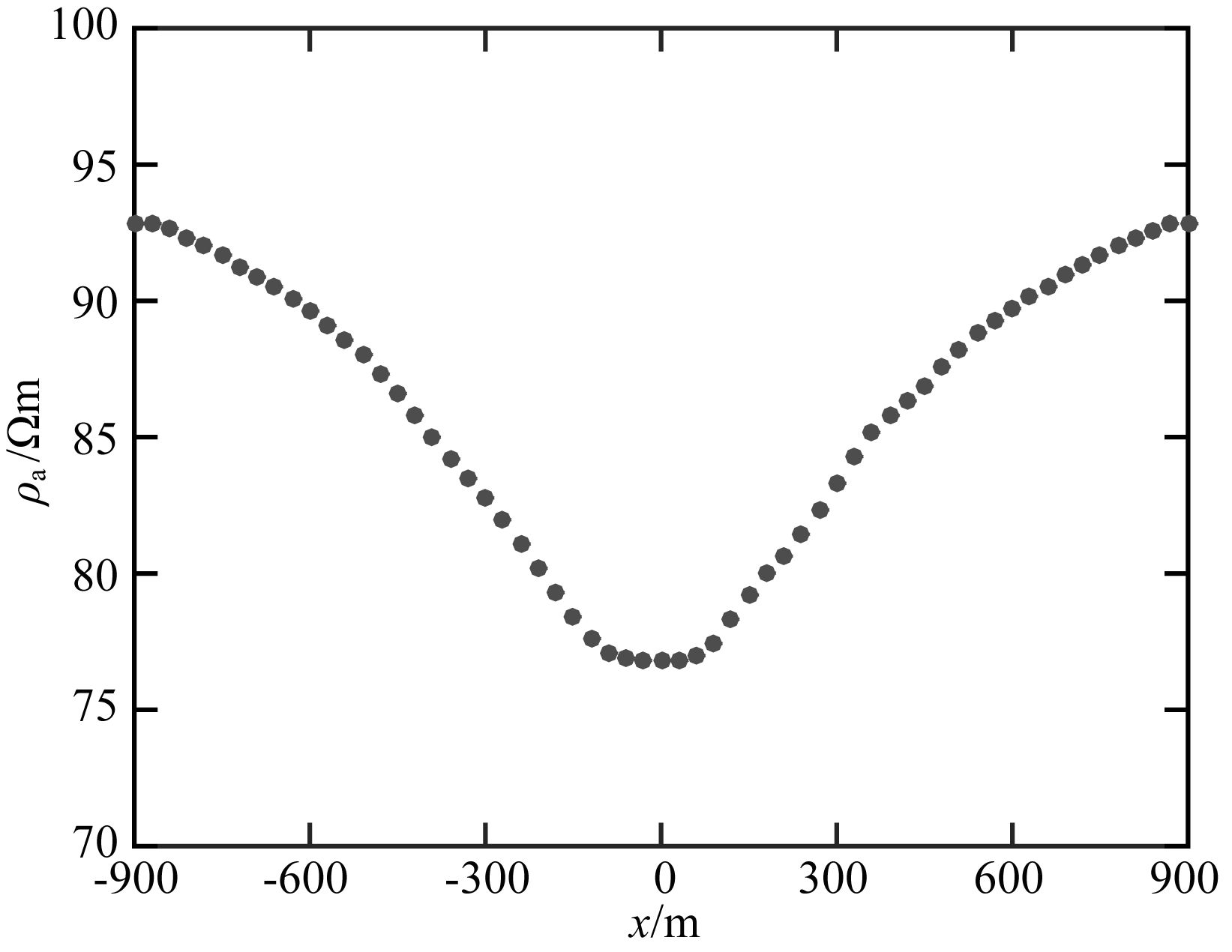
图 6是y=0 m测线的视电阻率-深度拟断面图,横轴为测点坐标,纵轴为视深度,视深度根据趋肤深度公式得到,红色虚线方框为低阻异常体范围.图 7是64 Hz时y=0 m剖面上视电阻率-测点曲线.从图 6可以看出低阻区域与低阻异常体吻合较好,尤其对异常体的埋深和厚度反映较好.从图 7可以看出,主剖面上低阻异常体的横向位置和宽度也得到较好的反映.
|
图 6 y=0 m视电阻率拟断面图 Fig. 6 Apparent resistivity pseudo-section diagram |
|
图 7 y=0 m剖面视电阻率-测点曲线 Fig. 7 Apparent resistivity-measurement site curve in profile y=0 m |
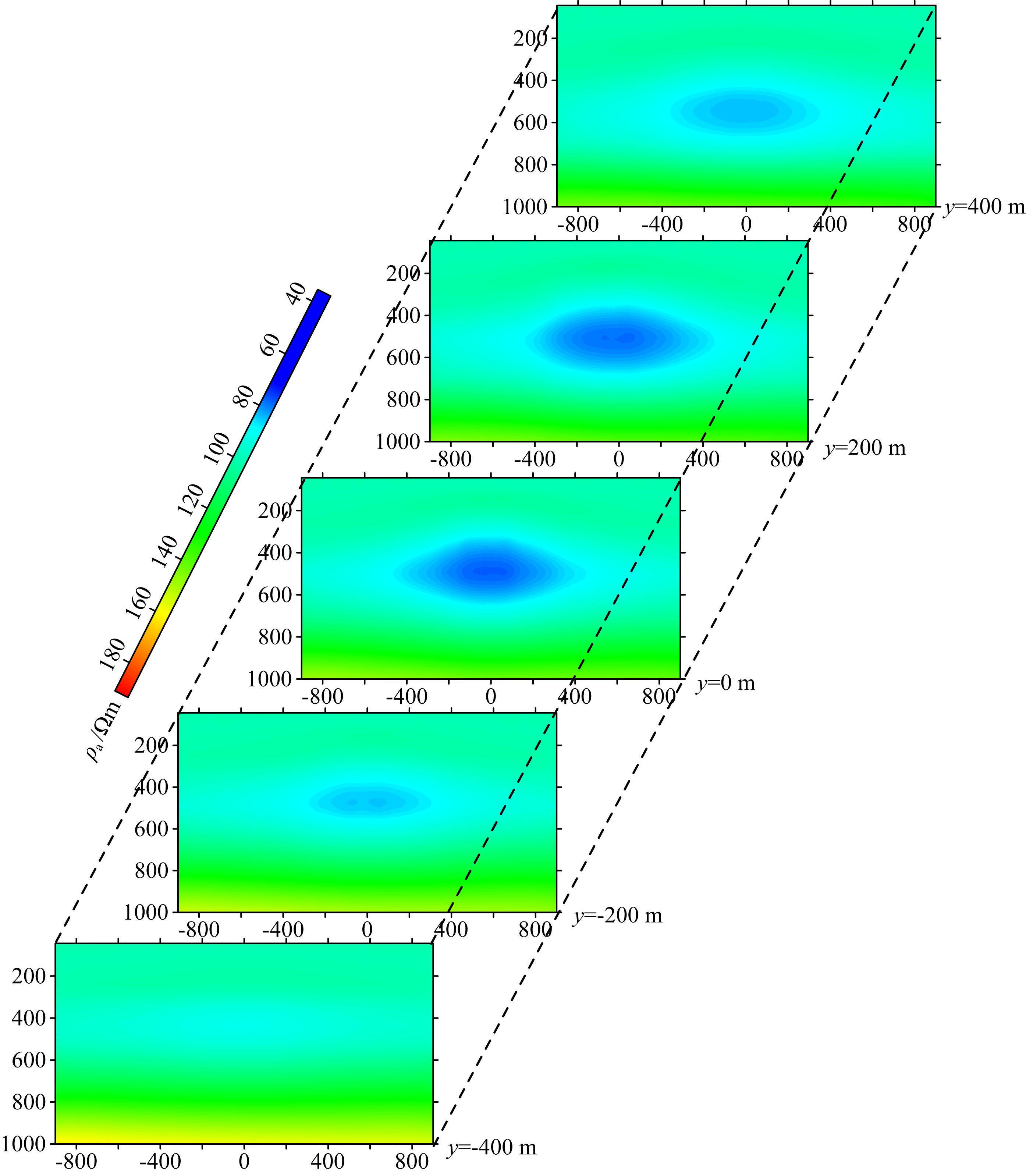
为分析异常体在不同测线上的响应以及收发距对电磁响应的影响,图 8给出了5条测线的视电阻率拟断面图,其中y=0 m为主测线,其他4条测线称为旁测线,和图 6一样,图中横轴是测点坐标,纵轴是视深度.可以看出,主测线上对异常体的视电阻率幅值、位置及范围反映比旁测线灵敏;剖面距离异常体越远,异常体的反映越不明显;距离发射源远的旁测线要比距离发射源近的旁测线对异常体的反映明显,且异常响应范围更大,低阻区域中心位置越深,这与有源电磁法中的阴影效应相符 (陈明生和闫述,2005).
|
图 8 单个低阻异常体模型不同断面视电阻率切片图 Fig. 8 Different slices of single low-resistivity anomaly body |
设计如图 9所示的三维双低阻异常体模型.计算区域、发射源、接收区域与坐标系参数与图 5所示的单个低阻异常体模型相同.图 9中背景介质的电阻率为100 Ωm,两个低阻异常体的电阻率均为10 Ωm,低阻异常体的长、宽、高和顶层埋深均为300 m,两个低阻异常体中心点的距离为900 m.第一个低阻异常体中心点坐标为 (-450 m,0 m,450 m),第二个低阻异常体中心点坐标为 (450 m,0 m,450 m).
|
图 9 双低阻异常体模型 (a) 三维示意图;(b) 平面图;(c) 剖面图. Fig. 9 Model of double low-resistivity anomaly bodies (a) 3D view; (b) Planar view; (c) Section view. |
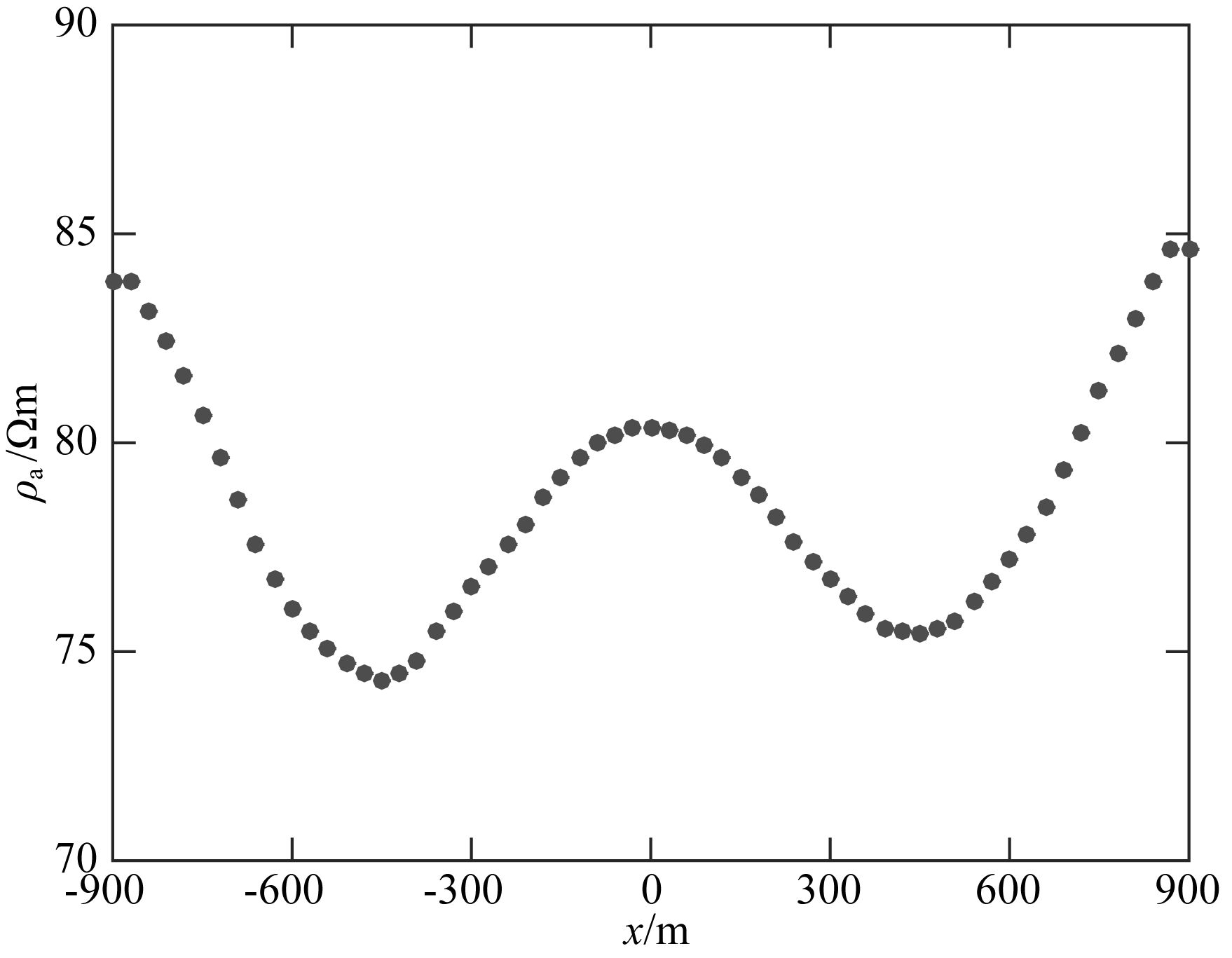
图 10是64 Hz时y=0 m剖面上的视电阻率-测点曲线.可以明显看出存在两个低阻异常响应,第一个低阻异常位于-600~-300 m,第二个低阻异常位于300~600 m,这和设计模型中两个低阻异常体的位置和宽度完全相符.
|
图 10 y=0 m剖面视电阻率-测点曲线 Fig. 10 Apparent resistivity-measurement site curve in profile y=0 m |
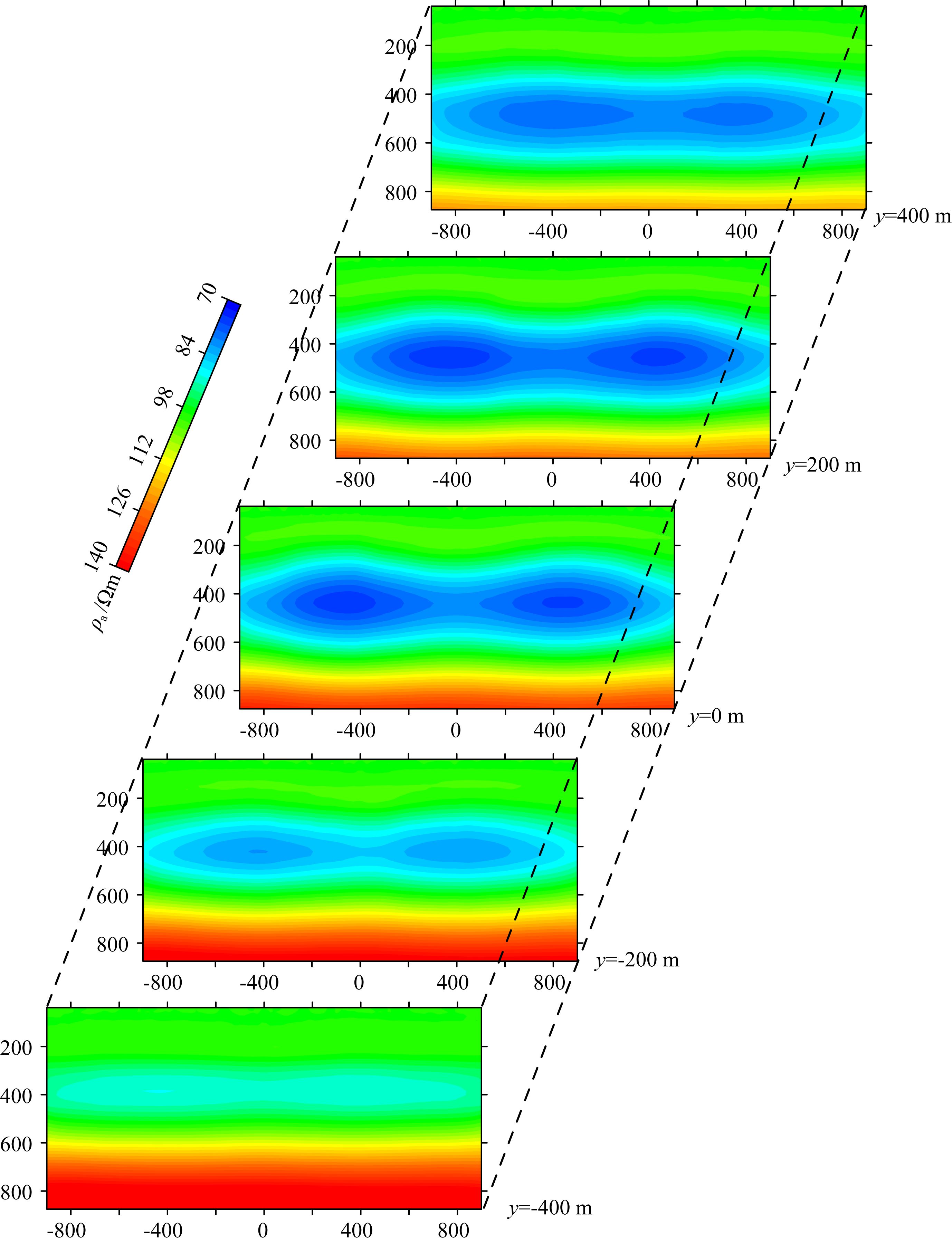
图 11为5条测线的视电阻率拟断面图.从该图可以看出,在y=0 m主剖面上,两个低阻异常体响应反映明显,图中的低阻区域与低阻异常体埋深和纵向范围吻合很好.在距离发射源远的旁测线上,两个低阻异常体也有一定响应,且测线距离发射源越远,低阻区域范围越小,中心位置深度越深,这是有源电磁法的阴影效应所致.而测线距离发射源越近,深部的高阻反映越明显,这是有源电磁法的近场效应所致.
|
图 11 双低阻异常体模型不同断面视电阻率切片图 Fig. 11 Different slices of double low-resistivity anomaly bodies |
本文从Maxwell方程出发,推导了异常电场满足的有限元方程,通过加入散度条件对电场进行约束,发展了基于非结构化网格的三维有限元数值模拟技术,避开了源的奇异性问题,减小了计算区域.针对非结构化网格单元,采用高斯加权平均方法获得了精度较高的异常磁场.针对层状介质模型,本文的有限元程序与Utah大学积分方程程序的计算结果误差控制在3%以内.进一步对三维单个低阻异常体和双低阻异常体模型进行了电磁响应分析,视电阻率拟断面图中以及主测线上的低阻区域与低阻异常体的位置和范围吻合很好,低阻异常体反映明显,表明本文算法正确可靠,所编制程序可适用于三维地质模型的CSAMT方法正反演研究.
附录 形函数的系数求解不失一般性,设在三维研究区域内,场值是一阶连续的.则四面体内任一点的场值u可写成如下形式:
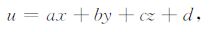
|
(A1) |
假定四面体单元的四个节点分别用i, j, k, m表示,则这4个节点上的场值可表达为:
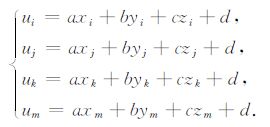
|
(A2) |
上述式子中a, b, c, d为未知系数,可唯一地用各节点上场值及坐标表示.以系数a为例,表示如下:
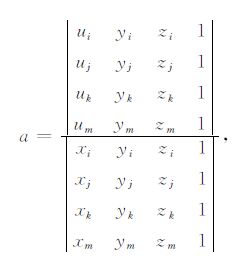
|
(A3) |
显然,(A3) 式中的分母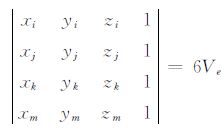
其中Ve为该四面体的体积.根据行列式的性质,可将 (A3) 式进一步写为:
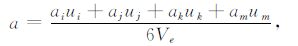
|
(A4) |
其中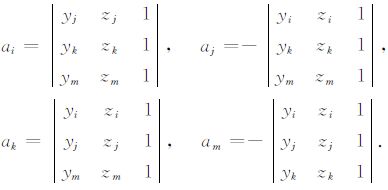
同理,
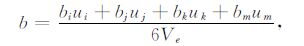
|
(A5) |
其中,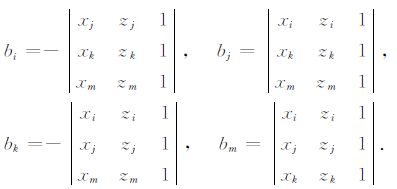
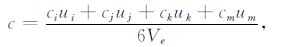
|
(A6) |
其中,
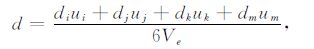
|
(A7) |
其中,
感谢王妙月研究员和涂小磊博士提供的建议和帮助.感谢审稿专家和编辑提出的宝贵意见.
| Bartel L C, Jacobson R D. 1987. Results of a controlled-source audiofrequency magnetotelluric survey at the Puhimau thermal area, Kilauea Volcano, Hawaii. Geophysics, 52(5): 665-677. DOI:10.1190/1.1442334 | |
| Cagniard L. 1953. Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics, 18(3): 605-635. DOI:10.1190/1.1437915 | |
| Cai H Z, Xiong B, Zhdanov M. 2015. Three-dimensional marine controlled-source electromagnetic modelling in anisotropic medium using finite element method. Chinese J. Geophys. (in Chinese), 58(8): 2839-2850. DOI:10.6038/cjg20150818 | |
| Chen M S, Yan S. 2005. Analytical study on field zones, record rules, shadow and source overprint effects in CSAMT exploration. Chinese J. Geophys. (in Chinese), 48(4): 951-958. | |
| Di Q Y, Wu F Q, Wang G J, et al. 2005. Geophysical exploration over long deep tunnel for west route of south-to-north water transfer project. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 24(20): 3631-3638. | |
| Hohmann G W. 1975. Three-dimensional induced polarization and electromagnetic modeling. Geophysics, 40(2): 309-324. DOI:10.1190/1.1440527 | |
| Jin J M. Finite Element Method of Electromagnetic Field (in Chinese).Xi'an: Xi'an Electronic University Press, 1982. | |
| Kawasaki K, Okada K, Kubota R. 1986. Geophysical Surveys in the Hishikari mine area. Shigen-Chishitsu (in Japanese), 36: 131-147. | |
| Key K, Weiss C. 2006. Adaptive finite-element modeling using unstructured grids:the 2D magnetotelluric example. Geophysics, 71(6): G291-G299. DOI:10.1190/1.2348091 | |
| Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. DOI:10.1190/1.3058434 | |
| Li Y G, Key K. 2007. 2D marine controlled-source electromagnetic modeling:Part I-An adaptive finite element algorithm. Geophysics, 72(2): WA51-WA62. DOI:10.1190/1.2432262 | |
| Li Y G, Pek J. 2008. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media. Geophysical Journal International, 175(3): 942-954. DOI:10.1111/gji.2008.175.issue-3 | |
| Liu C S, Ren Z Y, Tang J T, et al. 2008. Three-dimensional magnetotellurics modeling using edgebased finite-element unstructured meshes. Applied Geophysics, 5(3): 170-180. DOI:10.1007/s11770-008-0024-4 | |
| Mackie R L, Smith T J, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite difference equations:The magnetotelluric example. Radio Sci., 29(5): 923-935. | |
| Möller P, Hansbo P. 1995. On advancing front mesh generation in three dimensions. Int. J. Numer. Meth. Eng, 38(21): 3551-3569. DOI:10.1002/(ISSN)1097-0207 | |
| Newman G A, Alumbaugh D L. 1995. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophysical Prospecting, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 | |
| Ren Z Y, Tang J T. 2009. Finite element modeling of 3-D DC resistivity using locally refined unstructured meshes. Chinese J. Geophys. (in Chinese), 52(10): 2627-2634. DOI:10.3969/j.issn.0001-5733.2009.10.023 | |
| Rücker C, Günther T, Spitzer K. 2006. Three dimensional modelling and inversion of DC resistivity data incorporating topography I. Modelling. Geophysical Journal International, 166(2): 495-505. DOI:10.1111/gji.2006.166.issue-2 | |
| SanFilipo W A, Hohmann G W. 1985. Integral equation solution for the transient electromagnetic response of a three-dimensional body in a conductive half-space. Geophysics, 50(5): 798-809. DOI:10.1190/1.1441954 | |
| Shephard M S, Georges M K. 1991. Automatic three dimensional mesh generation by the finite Octree technique. Int. J. Numer. Meth. Eng., 32(4): 709-749. DOI:10.1002/(ISSN)1097-0207 | |
| Shewchuk J R. 2002. Delaunay refinement algorithms for triangular mesh generation. Computational Geometry:Theory and Application, 22(1-3): 21-74. DOI:10.1016/S0925-7721(01)00047-5 | |
| Si H. 2015. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Trans. Math. Software, 41(2):Article No. 11. | |
| Unsworth M J, Travis B J, Chave A D. 1993. Electromagnetic induction by a finite electric dipole source over a 2-D earth. Geophysics, 58(2): 198-214. DOI:10.1190/1.1443406 | |
| Wang R, Wang M Y, Lu Y L. 2007. Preliminary study on 3D3C CSAMT method modeling using finite element method. Progress in Geophysics (in Chinese), 22(2): 579-585. | |
| Wang R, Wang M Y, Di Q Y, et al. 2014. 3D1C CSAMT modeling using finite element method. Progress in Geophysics (in Chinese), 29(2): 839-845. DOI:10.6038/pg20140249 | |
| Wang W, Wu X P, Spitzer K. 2013. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids. Geophysical Journal International, 193(2): 734-746. DOI:10.1093/gji/ggs124 | |
| Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements. Geophysics, 51(11): 2131-2144. DOI:10.1190/1.1442065 | |
| Wannamaker P E. 1991. Advances in three-dimensional magnetotelluric modeling using integral equations. Geophysics, 56(11): 1716-1728. DOI:10.1190/1.1442984 | |
| Wannamaker P E. 1997. Tensor CSAMT survey over the Sulphur Springs thermal area, Valles Caldera, New Mexico, United States of America, Part I:Implications for structure of the western Caldera. Geophysics, 62(2): 451-465. DOI:10.1190/1.1444156 | |
| Wu L P, Shi K F, Li Y H, et al. 1996. Application of CSAMT to the search for groundwater. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese), 39(5): 712-717. | |
| Xu Z F, Wu X P. 2010. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method. Chinese J. Geophys. (in Chinese), 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 | |
| Yang J, Liu Y, Wu X P. 2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids. Chinese J. Geophys. (in Chinese), 58(8): 2827-2838. DOI:10.6038/cjg20150817 | |
| Zhang J F, Tang J T, Yu Y, et al. 2009. Three dimensional controlled source electromagnetic numerical simulation based on electric field vector wave equation using finite element method. Chinese J. Geophys. (in Chinese), 52(12): 3132-3141. DOI:10.3969/j.issn.0001-5733.2009.12.023 | |
| Zhdanov M S, Fang S. 1996. Quasi-linear approximation in 3-D electromagnetic modeling. Geophysics, 61(3): 646-655. DOI:10.1190/1.1443994 | |
| 蔡红柱, 熊彬, ZhdanovM. 2015. 电导率各向异性的海洋电磁三维有限单元法正演. 地球物理学报, 58(8): 2839–2850. DOI:10.6038/cjg20150818 | |
| 陈明生, 闫述. 2005. CSAMT勘探中场区、记录规则、阴影及场源复印效应的解析研究. 地球物理学报, 48(4): 951–958. | |
| 底青云, 伍法权, 王光杰, 等. 2005. 地球物理综合勘探技术在南水北调西线工程深埋长隧洞勘察中的应用. 岩石力学与工程学报, 24(20): 3631–3638. | |
| 金建铭. 电磁场有限单元法.西安: 西安电子科技大学出版社, 1982. | |
| 任政勇, 汤井田. 2009. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟. 地球物理学报, 52(10): 2627–2634. DOI:10.3969/j.issn.0001-5733.2009.10.023 | |
| 王若, 王妙月, 卢元林. 2007. 三维三分量CSAMT法有限元正演模拟研究初探. 地球物理学进展, 22(2): 579–585. | |
| 王若, 王妙月, 底青云, 等. 2014. CSAMT三维单分量有限元正演. 地球物理学进展, 29(2): 839–845. DOI:10.6038/pg20140249 | |
| 吴璐苹, 石昆法, 李荫槐, 等. 1996. 可控源音频大地电磁法在地下水勘查中的应用研究. 地球物理学报, 39(5): 712–717. | |
| 徐志峰, 吴小平. 2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931–1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 | |
| 杨军, 刘颖, 吴小平. 2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827–2838. DOI:10.6038/cjg20150817 | |
| 张继锋, 汤井田, 喻言, 等. 2009. 基于电场矢量波动方程的三维可控源电磁法有限单元法数值模拟. 地球物理学报, 52(12): 3132–3141. DOI:10.3969/j.issn.0001-5733.2009.12.023 | |
 2017, Vol. 60
2017, Vol. 60


