2. 西北核技术研究所, 西安 710024
2. Northwest Institute of nuclear technology, Xi'an 710024, China
在瞬变电磁数值模拟方法中,频域方法发展时间长,技术方法成熟,较为常见,其缺点是计算量大,频带窄.时域方法可以直观全面地展示电磁波在复杂介质中的传播过程,通过时频变换可以得到宽频信息,理论简单容易理解、适用性强等优点,在多个领域都得到广泛应用.时域方法主要包括有限差分法(FDTD)、有限元法(FETD)、时域伪谱方法(PSTD)、多分辨率分析法(MRTD)和积分方程法(TDIE)等,其中FDTD法应用范围最广.近年来,随着计算机硬件和数值计算方法的快速发展,不断出现一些性能优良的FDTD算法,如交替隐式时域有限差分法(ADI-FDTD)、有限体积法(FVTD)、高阶有限差分法等.
在时域瞬变电磁正演方面,Oristaglio和Hohmann (1984)以DuFort-Frankel有限差分法为基础对二维介质开展了瞬变电磁数值模拟,在地空边界采用向上延拓的方法,避免了场在空气中的步进求解.Wang和Hohmann (1993)对麦克斯韦方程组采用DuFort-Frankel显式有限差分法进行离散,用均匀半空间浅层电磁场的解析解作为初始值,对回线源瞬变电磁场进行了三维数值模拟.吴广耀在Wang和Hhomann的基础上开发研制了瞬变电磁三维有限差分数值模拟计算系统.闫述等(2002)通过时域电场的齐次扩散方程,在时间域对负阶跃脉冲激发的二维瞬态场进行了数值分析.王华军(2001)根据电磁场迭加原理导出了中心回线法瞬变电磁二次场的2.5维计算公式,采用有限元方法进行正演计算.宋维琪和仝兆歧(2000)实现了水平电偶极子激发的三维地电介质时域电磁场的有限差分计算.谭捍东等(2003)采用了解大型系数矩阵方程组的双共轭梯度稳定解法,实现了三维交错有限差分数值模拟算法.徐凯军和李桐林(2004)、孙怀凤等(2013)将Maxwell方程在似稳态条件下转换为扩散方程,引入虚拟位移电流项构建显式时域有限差分方程,对不同关断时间下的地质模型进行了正演计算.岳建华等(2007)用三维磁偶极源来模拟了二维均匀介质和层状介质中方形和薄板低阻体的全空间响应特征.邢涛等(2008)利用有限差分法完成大定源瞬变电磁法三维正演模拟程序的开发.肖明顺(2008)通过拉普拉斯变换和走向方向的傅立叶变换将时间域三维电磁场问题转化为拉氏和傅氏域的二维问题,开展了地形影响条件下的2.5维有限元数值模拟研究.陈丹丹(2008)从均匀半空间表面垂直磁偶极子的频率域电场表达式出发计算电磁场初始值,利用拉氏变换和数字汉克尔变换求取贝塞尔函数积分等方法,求出了阶跃响应的时间域电场解析解,对均匀半空间模型、低阻体或高阻体模型进行模拟计算.李建慧等(2013)基于电场异常场Helmholtz方程实现了交错网格有限差分法和有限体积法对回线源瞬变电磁法的三维正演.总体上讲,上述方法的不足主要表现(1)频域方法计算场源时要求近地表介质是均匀的,这与实际地质环境有一定差距;(2)扩散方程的时间步长大,计算速度快,但是对高阻介质容易造成计算发散;(3)采用狄利克雷边界条件导致空间较大,计算耗时较长.
2 瞬变电磁场理论及有限差分方程 2.1 Maxwell控制方程时域有限差分法采用三维交错网格来离散计算模型(Yee,1966),电场分量定义在网格单元各棱边中点,方向平行棱边,磁场定义在网格单元各面中心,方向平行各面法线,这种空间分布符合法拉第定律和安培定律.模型介质的电导率和介电常数分布与电场分量相同,磁导率分布与磁场分量相同.构造有限差分算法的出发点是麦克斯韦方程组,在无磁性介质中,麦克斯韦时域微分方程为
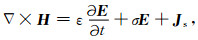
|
(1) |
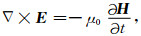
|
(2) |
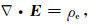
|
(3) |
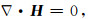
|
(4) |
式中H为磁场强度(A·m-1),E为电场强度(V·m-1),ε为介质介电常数(F/m),σ为介质电导率(S),μ0为真空磁导率(H/m),Js为源电流密度(A·m-2),ρe为电荷密度(C·m-3),在无源区域Js=0,ρe=0.
由于FDTD的更新方程满足散度方程,进行差分离散时只需要考虑(1)、(2)两个旋度方程即可.在直角坐标系中,对两个旋度方程用差分代替微分,利用Yee剖分网格对麦克斯韦方程离散为差分方程组,经整理后可得Ex、Hx迭代方程为
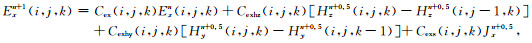
|
(5) |
其中,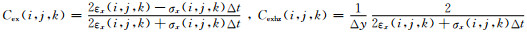
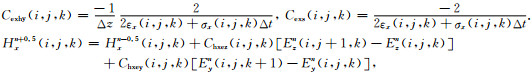
|
(6) |
其中,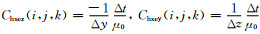
其他场量的更新方程略去.需要注意的是,(5)-(6)式中,电场E和磁场H的空间坐标(i, j, k)均是场量数组的空间坐标,由于电场和磁场数组各自单独定义,统一到同一个YEE坐标系下相差半个网格,因此Ex(i, j, k)的实际坐标是Ex(i+1/2, j, k),Hx(i, j, k)的实际坐标是Hx(i, j+1/2, k+1/2),其他场量类似.为了公式简洁,文中场量的空间位置均采用数组坐标形式.
2.2 CPML吸收边界条件在瞬变电磁法数值模拟中,模型的地下边界通常采用采用Dirichlet边界条件,即在足够远的边界处,电磁场的各个分量近似为零.在大地介质的电阻率较高的干旱地区以及低频工作条件下,Dirichlet边界条件常常导致计算空间很大,计算时间耗时过长.卷积完善匹配层(Convolutions Perfectly Matched Layer,CPML)吸收边界方法可以将大的计算空间截断为比较小的计算空间,CPML层可以迅速吸收电磁波,数值反射极小,而且与背景介质的电性参数无关,适合多种复杂介质.建立地空模型时将CPML设置为向模型内部收缩,可以保证空气层和大地的介质参数与相邻的CPML参数一致.
在无磁性介质中,基于伸缩坐标下的无源修正Maxwell频域方程为(Chew and Weedon, 1994)
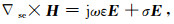
|
(7) |
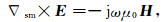
|
(8) |
其中算子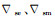
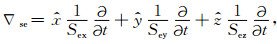
|
(9) |
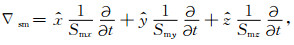
|
(10) |
其中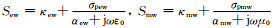
将(7)式的频域方程变换到时域,差分离散后电场分量Ex的更新方程为
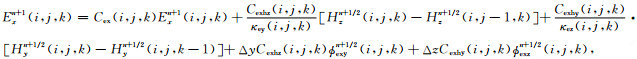
|
(11) |
其中:
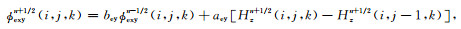
|
(12) |
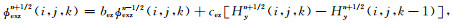
|
(13) |
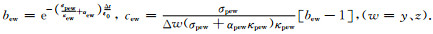
|
(14) |
在瞬变电磁法工作原理中,发射电磁场一部分向空中逸散,一部分向地下传播,直接使用麦克斯韦方程离散的差分数值计算需要处理无耗的空气和有耗的大地两种边界.在离散差分网格中,电场定义在网格棱边中点上,磁场定义在网格面元中心,电场和磁场在空间上相差半个网格,比例伸缩因子Sew、Smw的参数取值也因此相差半个网格,并不严格满足Sew=Smw的无反射条件,这使得电磁波在CPML各层分界面上有反射.
假定分界面1和分界面2的比例因子分别为S1e、S1m和S2e、S2m,则垂直入射的电磁波在相邻两层介质分界面的反射系数r12为
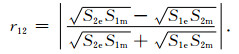
|
(15) |
(15)式表明反射系数与α、k、σp的分布以及频率有关,与入射角度无关,由于反射系数在w=x, y, z三个方向都相同,因此后文中均省去w下标.在时域瞬变电磁法三维有限差分正演计算中,主要考虑空气介质(电阻大于1013Ω)和大地介质(电阻低于104Ω),在频率低于106 Hz的似稳态条件下的吸收效率.
在不满足无反射条件时,α取值远小于ωε0时对衰减的影响可以忽略不计(ω为场源的最大频率),σp和k都在d层CPML上满足各自的离散函数分布,并且电场比例伸缩因子Se的参数σpe、ke和磁场比例伸缩因子Sm的参数σpm、km相差半个网格,假设k的分布函数为g,σp的分布函数为f,将磁场比例因子参数κm、σpm利用一阶泰勒公式在电场节点ke、σpe处展开,并设:
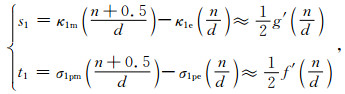
|
(16) |
带入(15),当s1、t1分布为常数或者同分布,化简可得:
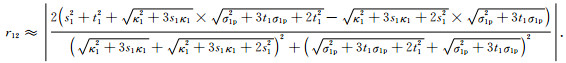
|
(17) |
在无耗介质和似稳态条件下,参数k对电磁波的衰减不敏感,s1、t1越小则反射系数越小,因此在CPML各层上取恒定常量k=1,此时s1=0;为减小t1,将d层厚度的CPML的参数分布(Roden and Gedney, 2000)修改为
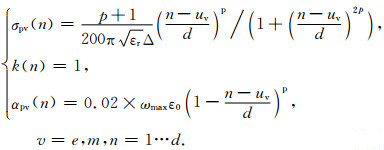
|
(18) |
在计算电导率σpe时ue=0.75,在计算磁导率σpm时um=0.25,p参数取2~4,Δ为网格的大小.数值模拟结果表明,(18)式的参数分布适合吸收低频电磁波,反射误差很小.
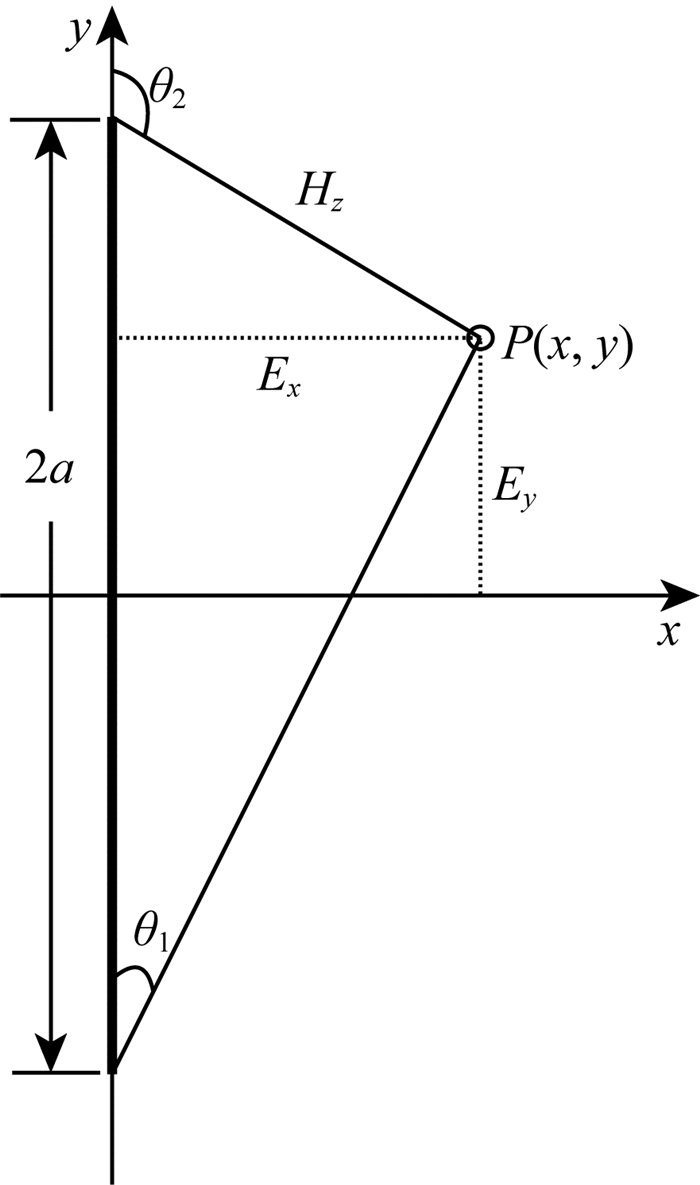
2.3 有限长有源细导线模型在瞬变电磁数值模拟中,发射线框为近场激励源,既可以是电压源也可以是电流源.在电压源模型中,电流在各个网格节点上用电压差和导线电阻的比值来计算,与实际应用相比有诸多不便,因此场源使用电流源模型作为激励源.在(1)式中,Js是相邻4个磁场分量所围面积中的电流密度,由于导线的横截面积远远小于磁场网格面积,电流赋值在源所在的网格节点上时,附近相邻单元的磁场不能直接用Maxwell方程计算.对于有限长度的直导线,如图 1所示,导线长度为L=2a,P(x, y)点的电场分量Ex和磁场分量Hz可表示为
|
图 1 有限长导线的电场Ex和磁场Hz Fig. 1 Electric field Ex and magnetic field Hz produced by a finite length conductor |
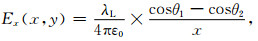
|
(19) |
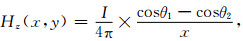
|
(20) |
当导线长度趋于无限长时,θ1→0,θ2→π,此时距离导线x处的Ex、Hz按照1/x的规律变化;而对于有限长细导线,径向电场Ex和径向磁场Hz的规律变化与无线长细导线模型并不完全相同.
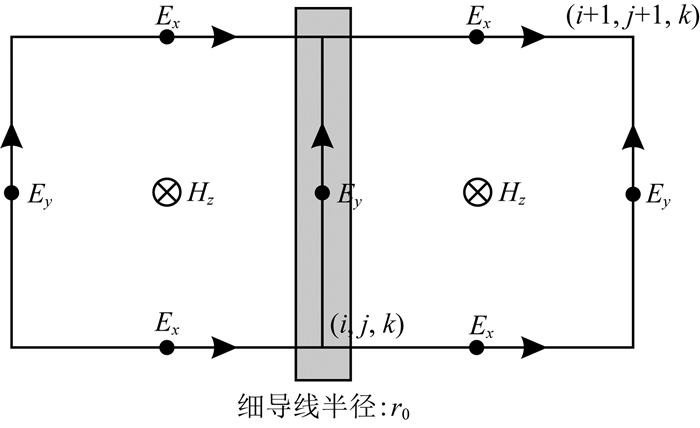
在有限长细导线模型中,如图 2所示,x、y方向的网格大小为Δx、Δy,场源所在的相邻网格,距离x处的Ex、Hz场量可以表示为
|
图 2 细导线临近网格的Hz分量 Fig. 2 Hz magnetic field component of a thin conducting wire near the grid |
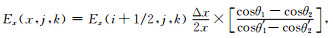
|
(21) |
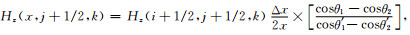
|
(22) |
θ′ 1和θ′ 2为网格中心点与导线两端的夹角.
图 2右侧网格环路根据法拉第电磁感应定律:
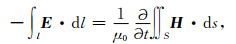
|
(23) |
整理可得:
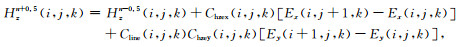
|
(24) |
其中:
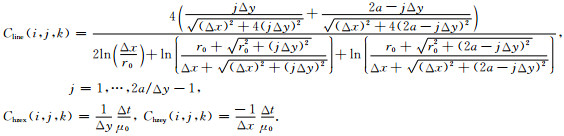
|
(25) |
Hx计算方法和Hz相同,而Hy可以在垂直导线的网格平面内利用(23)式推导出,如图 3,在忽略导线横截面积的情况下,第一象限的Hy更新方程为
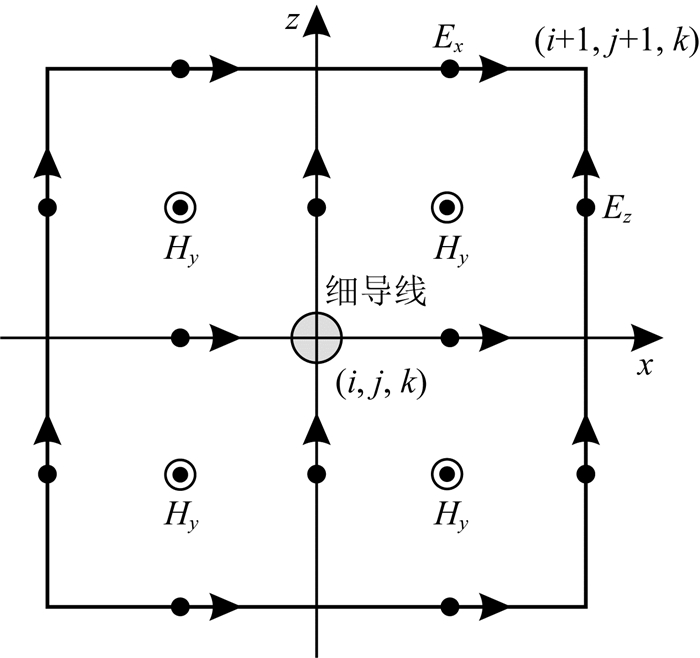
|
图 3 细导线临近网格的Hy分量 Fig. 3 Magnetic field Hy of a thin conducting wire near the grid |
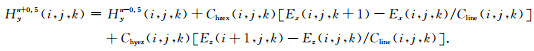
|
(26) |
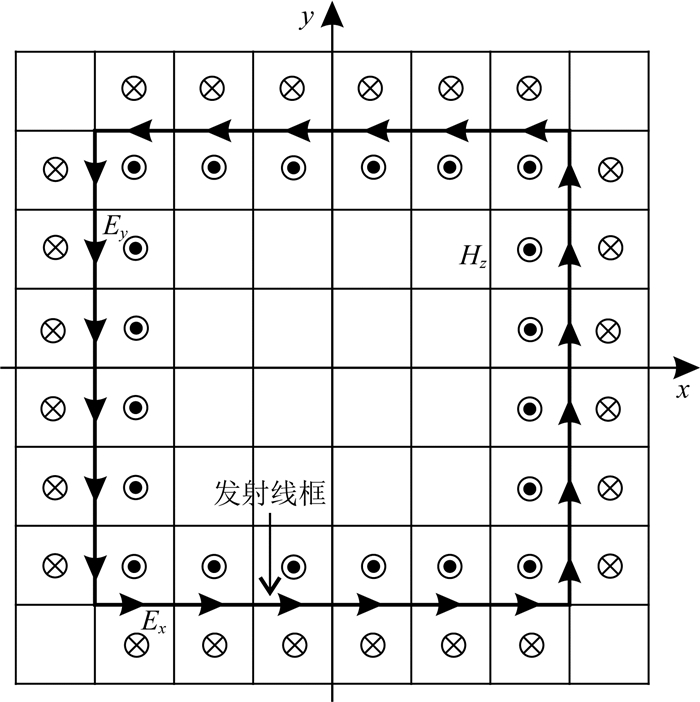
细导线模型仅需要对与导线相邻网格的磁场Hx、Hy和Hz重新计算,电流可以直接赋值在导线所在的网格节点上,这是因为在导线内部没有径向电场分量,只有平行导线方向的电场分量.对于矩形发射线框,电场分量的赋值与磁场分量的更新分布见图 4.在矩形线框的内角点处,磁场既与水平方向也与垂直方向的电场相关,Hx、Hy和Hz三个磁场分量在内角点都要利用(23)式重新计算,限于篇幅,此处不再累述.
|
图 4 矩形线框的电场分布与磁场Hz的更新区域 Fig. 4 Electric field distribution of a rectangular wire frame and updated region of Hz |
在瞬变电磁法勘探中,发射线框通恒定电流,在电流关断的瞬间激发地下感应涡流,电流波形近似上升沿和下降沿很窄的梯形.细导线模型不仅可以避免近地表介质必须是均匀的限制,也不受地形起伏的影响,如果地形能够离散成精确的三维网格模型,只需要在导线所在的网格上赋予对应的电场分量即可.时间步长采用CFL稳定条件,公式为
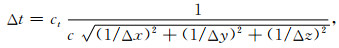
|
(27) |
式中Ct的取值范围0.5~0.9,取值应随着近地表介质的电阻率的降低而变小.
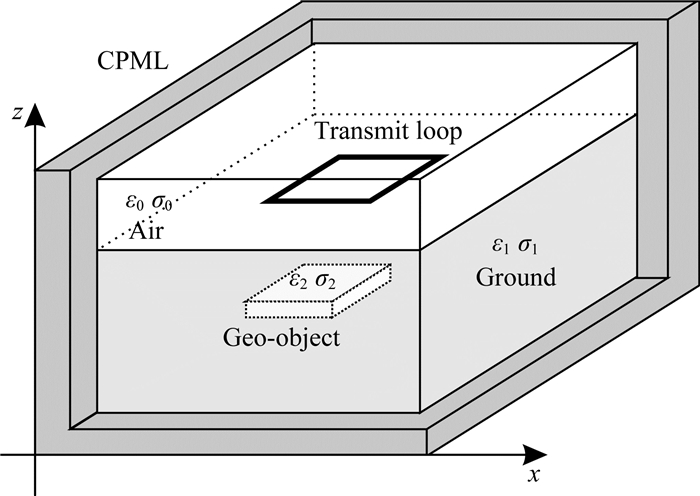
3 正演算法与数值模拟结果 3.1 算法优化时域瞬变电磁三维正演的计算效率是影响其实用性的制约因素之一,正演算法需要迭代时间和三维空间循环,其中空间又分为计算域、CPML区域和场源三个区域,见图 5.在不同的区域采用不同的处理方法,需要使用较多的判断条件,在迭代次数很大的情况下,也会影响计算效率.通过分析Maxwell方程在不同区域更新方程的差异可以看出,三种方程的计算方法本质相同,只是在不同区域,场分量的系数不同,因此将空间循环改为矩阵运算,四重循环的三维正演就可以转换为只有时间迭代的一重循环.矩阵优化一方面可以大大减少判断条件,另一方面也可以充分利用CPU的SIMD指令集对数据进行流水线处理,可以成倍提高计算速度.
|
图 5 计算模型的组成部分 Fig. 5 Composition of the calculation model |
以计算Ex为例,场量Ex、Hz、Hy和系数矩阵Cex、Cexhy、Cexhz大小定义均为整个空间(计算域和CPML区域).在(11)式中,根据模型定义的电性参数空间分布和时间步长,计算出系数矩阵Cex、Cexhy和Cexhz,将系数矩阵两侧的CPML区域数值保留作为卷积函数的系数矩阵.在y方向,根据Key的分布修改Cexhz系数矩阵两侧CPML区域的的数值,z方向根据Kez的分布修改Cexhy系数矩阵的两侧CPML区域的数值,这些矩阵初始化完成后,在时间循环内,一次矩阵运算就可以完成整个模型的Ex计算,然后再用卷积函数更新y、z方向的CPML区域即可.磁场的更新和电场一样,只不过在场源加载的时间范围内,还需要用有限长细导线模型对场源临近的磁场分量单独计算,这些网格的数量很少,源加载的时间步长也很短,对计算耗时的影响极小.
3.2 空间消耗和时间效率在使用多重循环方式进行三维正演时,空间消耗主要是6个电磁场分量和电性参数分布的空间大小,单值系数和一维CPML卷积系数占用的空间可以忽略不计.使用矩阵优化方法三维正演除了6个场分量占用的空间外,还需要定义18个(无磁性介质可以减少到15个)与场分量同样大小的系数矩阵和24个d层厚度的CPML卷积函数及卷积函数的系数矩阵,需要较大的内存空间.为了对比,分别建立5种不同大小的非磁性均匀介质模型,其中CPML厚度为8个网格,电磁场分量都采用双精度数值,在cpu为Intel I7、内存8 GB的电脑上迭代计算1000步,两种计算方法的耗时比较见表 1.
|
|
表 1 两种方法的计算效率对比 Table 1 Comparison of efficiency of two methods |
多重循环方式的计算时间远远多于矩阵方式,一个主要原因是,电磁场6个分量的大小均不相同,比如计算空间大小为m×n×p个网格,Hx分量需要在y方向和z方向外扩一个网格,大小变为m×(n+1)×(p+1),用于计算Ey和Ez的边界;而Ex分量需要在x方向外扩一个网格,同时在y方向和z方向都是从第二个网格开始计算,其他分量类似.在差分计算时,很难在一个多重循环中计算大小不同的所有分量,因此每个分量的差分计算和更新吸收边界,都需要多重循环单独计算,迭代次数很多,平均耗时是矩阵方式的2.9倍.
两种计算方法的存储空间消耗,除去软件运行环境占用的资源外,都与计算的节点数量成正比.矩阵方式的存储空间除了电磁场分量和系数矩阵外,还有48个吸收边界数组.当网格节点数较少时,吸收边界在全部节点数中的比例相对较大,随着节点数的增加,吸收边界所占的比例逐渐降低.例如在模型1中,矩阵方式的空间消耗是多重循环方式的5.8倍,随着节点数的增加,空间消耗降低到多重循环方式的4.3倍.
当计算复杂模型、磁性或者非均匀介质时,多重循环方式的算法实现复杂度和存储空间会迅速增加,矩阵优化方式不用判断复杂模型的边界,不需要改变算法,只要各个地质体模型的电磁参数空间分布已知即可,也适用于并行计算.
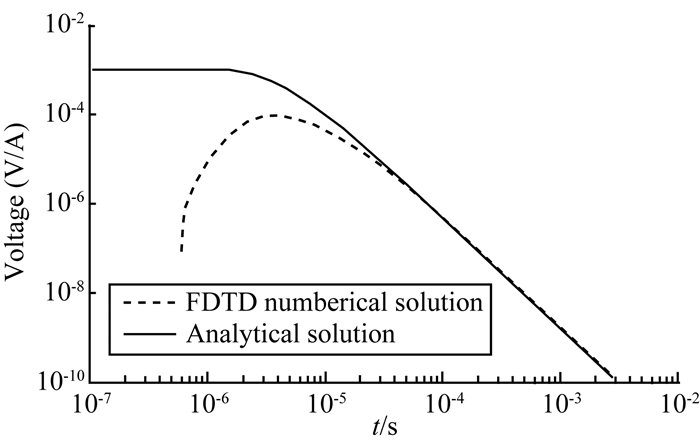
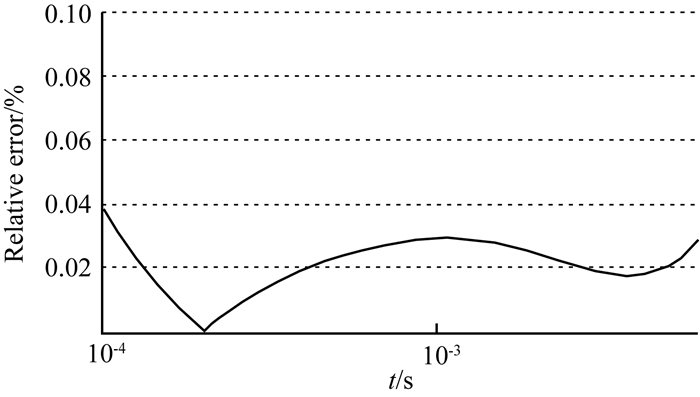
3.3 均匀大地介质的数值解和解析解对比以100 Ωm的均匀半空间为对比模型,发射线圈采用110 m×110 m的方形回线,接收线圈1 m2,激发电流1 A,线性下降沿宽度均为2 μs,计算时长5 ms.模型大小156×156×92的均匀网格剖分,网格间距10 m.图 6给出了均匀半空间解析解与三维时域有限差分的归一化感应电动势衰减曲线对比,同白登海和Meju (2001)、杨海燕和岳建华(2008)等得出结果是一致的.图 7为关断时间为2 μs的相对误差,需要说明的是解析解是电流垂直关断条件下的频域表达式经傅里叶逆变换得到的,在时域计算中,电流从恒定值降低为零的关断时间总是存在的,时域响应和频域解析解在早期存在较大差异,考虑大定源中心回线法在实际测量时,有效时间道均晚于10-4s,因此误差对比的起始时间晚于10-4s.此外,随着关断时间增大时,电流低频成分比关断时间小的更占优,计算时需增加CPML厚度.
|
图 6 关断时间为2 μs的FDTD计算结果和解析解对比 Fig. 6 Comparison of FDTD calculation results and analytical solutions (ramp time 2 μs) |
|
图 7 FDTD计算结果与解析解的相对误差 Fig. 7 Relative errors between calculated results and analytical solution of FDTD |
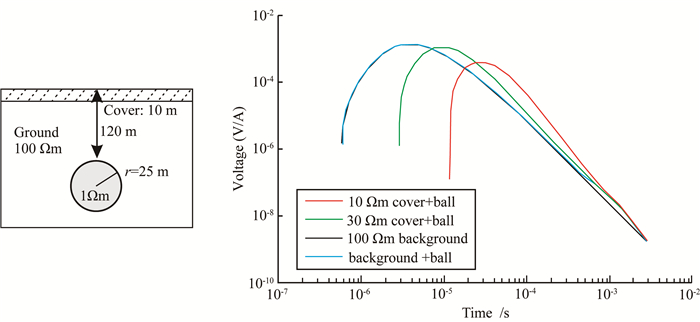
为研究近地表低阻覆盖层对深部探测能力的屏蔽作用,在100 Ωm的均匀大地介质中,建立直径50 m电阻率1 Ωm的低阻球体,球体顶部埋深120 m.然后地表覆盖一层厚度10 m,电阻率30 Ωm的相对低阻层,然后改变覆盖层的电阻率为10 Ωm,发射关断时间1 μs,发射线框大小为90 m×90 m,线框中心与球心在地表的投影重合,计算响应曲线见图 8.没有覆盖层时,球体响应和背景响应相比异常响应特征明显,在1.2×10-3s时差异最大.由于覆盖层的影响,球体响应曲线与KH型地层类似,但是晚期响应幅值要小很多.可见近地表覆盖层电阻越低,反演球体的轮廓边界和埋深不确定范围变大,球体阻值上升,与背景电阻的差异变小,对结果的偏离程度越大.
|
图 8 近地表低阻覆盖层模型和对探测的影响 Fig. 8 Low resistivity coverage model and its influence on TEM detection |
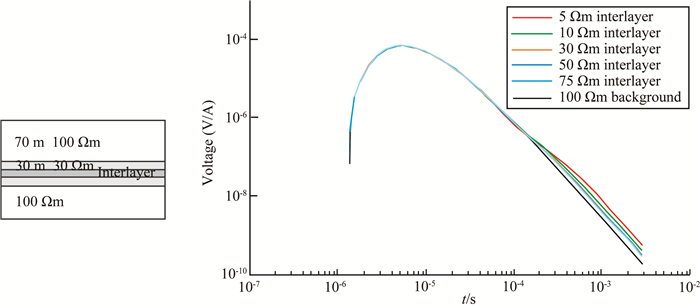
在干旱地区的冲洪积扇上,地层多为砂岩泥岩交互的情况,为了给工程施工和探查地下水提供准确的依据,开展了薄层的分辨能力研究.建立H型地层模型:第一层厚度70 m,电阻率100 Ωm,第二层厚度30 m,电阻30 Ωm,底层电阻率100 Ωm.在第二层中加入10 m厚度的夹层,依次将夹层电阻率改为5 Ωm、10 Ωm、50 Ωm和75 Ωm,计算得到响应见图 9.
|
图 9 H地层中的夹层模型和夹层不同电阻率的响应曲线 Fig. 9 Interlayer model and responses with different electrical parameters |
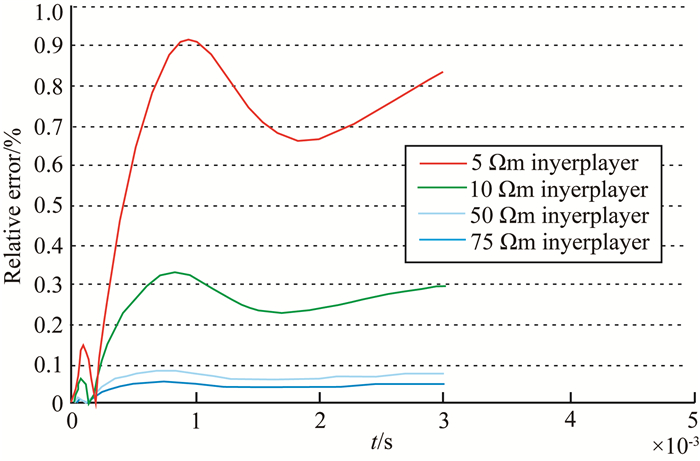
判断夹层是否可以识别出来的,可以从有无夹层的响应的差别上进行判断.图 10显示了没有夹层时(三层地层)的电磁响应与有夹层时(五层地层)的响应,在全时间道上(3 ms)的相对偏差.在地面瞬变电磁法技术规程中规定,有位差的测量精度误差在10%~15%之内,超出这个范围的可以认为是模型的不同电性差异造成的,而不是测量误差造成的.根据计算结果,可以认为对于10 m厚度的夹层,当夹层的电阻低于相邻层电阻的1/3时是可以识别出来的,而高于相邻层电阻时则不能分辨出夹层.将H型地层的第一层厚度增加到120 m,其他参数不变,也有相同的结果.
|
图 10 不同电阻率的夹层与无夹层瞬变电磁响应的相对偏差 Fig. 10 Relative deviations of the TEM response of the interlayer with different resistivity |
采用瞬变电磁法进行矿产勘察和工程物探时,经常会遇到地形起伏的工作环境,了解地形对测量结果的影响,可以避开不利的环境因素.分别建立山谷(图 11a)、山丘(图 11b)和断崖(图 11c)地形,其中背景介质100 Ωm,山谷深度、山区高度和断崖高度都是70 m.山谷地形和山丘地形的发射线圈位于谷底和山顶的正中间,断崖地形的发射线圈右侧距离崖边10 m.

|
图 11 山谷地形、山丘地形和断崖地形模型 Fig. 11 Terrain models of valley, hill and cliff |
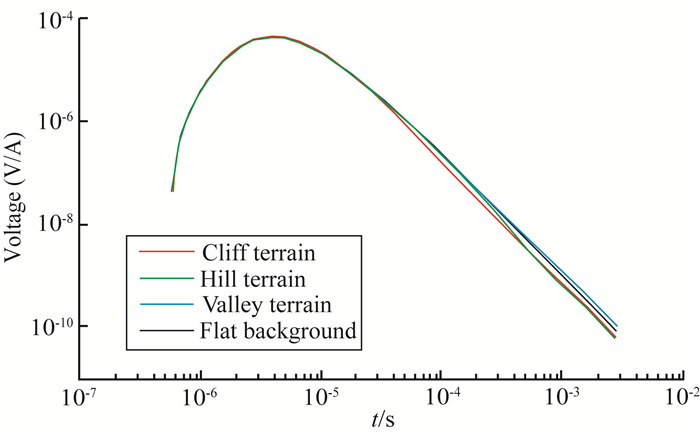
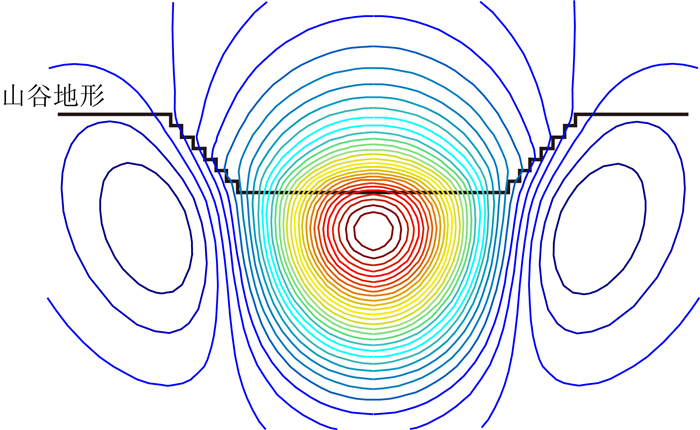
对比背景为100 Ωm的平坦地形,在山谷底部的瞬变电磁响应衰减变慢,并且在10-4s到10-3s之间的响应出现震荡现象,见图 12.原因是山谷两侧的高地会在场源作用下激发出微弱涡流,与山谷底部的涡流相互影响引起磁场产生畸变,见图 13,造成震荡.计算结果表明,当背景电阻降低时,震荡的幅度会变小,但是衰减会更慢.山谷地形的这种震荡对测量结果的影响较大,实际工作中应该避免在山谷地形中进行瞬变电磁勘测.山丘地形在10-4s后衰减速度变快,断崖地形在2×10-5s后衰减速度变快,反演时会造成浅部的电阻值偏高.
|
图 12 不同的地形瞬变电磁响应 Fig. 12 TEM response of valley, hill and cliff terrain |
|
图 13 5×10-5s时山谷地形的垂直剖面磁场等值线 Fig. 13 Vertical magnetic field contours of valley terrain at 5×10-5second |
在时域瞬变电磁有限差分三维正演方法中,场源采用有限长细导线模型,将电流直接加入Maxwell有源差分方程,避免了复杂的时频域转换计算,以及近地表介质必须是均匀的限制.引入空气层后,可以对不同地形影响下的异常响应进行模拟计算,在边界采用CPML边界吸收条件,改进了CPML的参数分布,能够有效吸收低频电磁波,反射误差满足精度要求.对时间空间的四重循环迭代计算优化为矩阵运算,提高了计算速度.对层状地层和地形模型进行了正演计算,并且和解析解进行对比验证了计算方法的正确性.目前开展的研究工作还需要进一步完善,加入空气层后,可以模拟任意地形的电磁场响应,但是准确的地形剖分占用存储空间很大.由于空气层为无耗介质,在地表电阻率较低时,为了满足CFL稳定条件、避免磁场在地空分界面的震荡现象,时间步长较小,迭代次数多,总体计算耗时依然较大.下一步的研究工作开展有限差分的并行算法研究,提高计算速度.
| Bai D H, Meju M. 2001. The effect of two types of turn-off current on tem responses and the correction techniques. Seismology and Geology (in Chinese), 23(2): 245-251. | |
| Chen D D. 2008. Study of three-dimensional forward of TEM[Master thesis] (in Chinese). Beijing:China University of Geosciences. | |
| Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified Maxwell's equations with stretched coordinates. Microwave and Optical Technology Letters, 7(13): 590-604. | |
| Ge D B, Yan Y B. Finite-Difference Time-Domain Method for Electromagnetic Waves (third edition)(in Chinese).Xi'an: Xidian University Press, 2011. | |
| Li J H, Hu X Y, Zeng S H, et al. 2013. Three-dimensional forward calculation for loop source transient electromagnetic method based on electric field Helmholtz equation. Chinese Journal of Geophysics (in Chinese), 56(12): 4256-4267. DOI:10.6038/cjg20131228 | |
| Oristaglio M L, Hohmann G W. 1984. Diffusion of electromagnetic fields into a two-dimensional earth:A finite-difference approach. Geophysics, 49(7): 870-894. DOI:10.1190/1.1441733 | |
| Roden J A, Gedney S D. 2000. Convolution PML (CPML):an efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters, 27(5): 334-339. DOI:10.1002/(ISSN)1098-2760 | |
| Song W Q, Tong Z Q. 2000. Forward finite differential calculation for 3-D transient electromagnetic field. Oil Geophysical Prospecting (in Chinese), 35(6): 751-756. | |
| Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time. Chinese J. Geophys. (in Chinese), 56(3): 1049-1064. DOI:10.6038/cjg20130333 | |
| Tan H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered grid finite difference method. Chinese J. Geophys. (in Chinese), 46(5): 705-711. | |
| Wang H J. 2001. Study on 2.5-D forward and inversion for Transient electromagnetic with central loop[Ph. D. thesis] (in Chinese). Wuhan:China University of Geosciences. | |
| Wang T, Hohmann G W. 1993. A finite-difference time-domain solution for three-dimensional electromagnetic modeling. Geophysics, 58(6): 797-809. DOI:10.1190/1.1443465 | |
| Xiao M S. 2008. Study on 2.5D numerical modeling for transient electromagnetic method by finite element method with topography[Master thesis] (in Chinese). Beijing:China University of Geosciences. | |
| Xing T, Liu S C, Li J H, et al. 2008. Program exploitation on 3D forward of large fixed loop TEM. Chinese Journal of Engineering Geophysics (in Chinese), 5(6): 664-669. | |
| Xu K J, Li T L. 2004. A finite-difference time-domain solution for transient electromagnetic fields. Global Geology (in Chinese), 23(3): 301-305. | |
| Yan S, Chen M S, Fu J M. 2002. Direct time-domain numerical analysis of transient electromagnetic fields. Chinese J. Geophys. (in Chinese), 45(2): 275-284. | |
| Yang H Y, Yue J H. 2008. Research on response calculation and correction technique of turn-off current in the transient electromagnetic method. Progress in Geophysics (in Chinese), 23(6): 1947-1952. | |
| Yee K S. 1966. Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media. IEEE Transactions on Antennas and Propagation, 14(3): 302-307. DOI:10.1109/TAP.1966.1138693 | |
| Yue J H, Yang H Y, Hu B. 2007. 3D finite difference time domain numerical simulation for TEM in-mine. Progress in Geophysics (in Chinese), 22(6): 1904-1909. | |
| 白登海, MejuM. 2001. 瞬变电磁法中两种关断电流对响应函数的影响及其应对策略. 地震地质, 23(2): 245–251. | |
| 陈丹丹. 2008.瞬变电磁法三维正演研究[硕士论文].北京:中国地质大学. | |
| 葛德彪, 闫玉波. 电磁波时域有限差分方法(第三版).西安: 西安电子科技大学出版社, 2011. | |
| 李建慧, 胡祥云, 曾思红, 等. 2013. 基于电场Helmholtz方程的回线源瞬变电磁法三维正演. 地球物理学报, 56(12): 4256–4267. DOI:10.6038/cjg20131228 | |
| 宋维琪, 仝兆歧. 2000. 3D瞬变电磁场的有限差分正演计算. 石油地球物理勘探, 35(6): 751–756. | |
| 孙怀凤, 李貅, 李术才, 等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049–1064. DOI:10.6038/cjg20130333 | |
| 谭捍东, 余钦范, BookerJ, 等. 2003. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 46(5): 705–711. | |
| 王华军. 2001.中心回线瞬变电磁2.5维正反演方法研究[博士论文].武汉:中国地质大学. | |
| 肖明顺. 2008.带地形的瞬变电磁2.5维有限元数值模拟研究[硕士论文].北京:中国地质大学. | |
| 邢涛, 刘树才, 李建慧, 等. 2008. 大定源瞬变电磁法三维正演程序开发. 工程地球物理学报, 5(6): 664–669. | |
| 徐凯军, 李桐林. 2004. 时域瞬变场电磁场有限差分法. 世界地质, 23(3): 301–305. | |
| 闫述, 陈明生, 傅君眉. 2002. 瞬变电磁场的直接时域数值分析. 地球物理学报, 45(2): 275–284. | |
| 杨海燕, 岳建华. 2008. 瞬变电磁法中关断电流的响应计算与校正方法研究. 地球物理学进展, 23(6): 1947–1952. | |
| 岳建华, 杨海燕, 胡搏. 2007. 矿井瞬变电磁法三维时域有限差分数值模拟. 地球物理学进展, 22(6): 1904–1909. | |
 2017, Vol. 60
2017, Vol. 60


