2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
借鉴地震资料处理方法中逆时偏移的原理,人们首先提出的电磁偏移方法与地震偏移方法类似(Zhdanov and Frenkel, 1983),能够快速地将观测数据转换为地下构造界面,在偏移场的计算上采用了类似地震勘探方法中Kirchhoff积分的Stratton-Chu积分,并借助格林函数计算.Lee等(1987)详细地阐述了该方法的理论, 利用Claerbout单程有限差分方程实现了MT资料的偏移,并对理论和实际模型进行了模拟计算, 得到了较好的结果.原苏联学者在电磁法中确立了正则偏移和解析延拓偏移两种方法,并对俄罗斯科拉半岛瞬变测深法实测数据资料进行了偏移处理,得到了较好的结果.Zhdanov和Booker (1993)确定了电磁偏移方法应用于实际中的几个重要问题:数据密度、一次场与二次场分离以及正确的偏移场计算,并系统阐述了电阻率偏移成像方法,其中利用了反射函数的方法获取地下电阻率成像(Zhdanov et al., 1994, 1995a, 1995b).紧接着,电磁偏移方法与传统反演方法的联系在理论上得到证明,说明电磁偏移(基于反演成像)是一种近似的反演过程,它是反演的第一步迭代过程.之后,一种预处理时域电磁偏移成像方法被提出(Zhdanov and Traynin, 1996; Zhdanov and Li, 1997, 1998; Zhdanov et al., 2001),通过引入一种特殊格式的偏移电阻率权矩阵,达到了提高电磁偏移成像有效性的结果.Furukawa和Zhdanov (2007)对二维时域电磁偏移成像方法做了理论上的研究,其中将计算偏移场的方法称为积分变换法(区别于有限差分方法),并利用反演方法中的Newton方法进行成像.
在国内,王家映等(1985)提出了大地电磁拟地震解释法,之后又提出的垂直时距曲线法, 可以比较成功地求取电磁波的平均速度(刘晓山,1986).20世纪90年代,国内开展了一系列电磁数据偏移初步探索(魏胜和王家映,1993;陈乐寿等,1993;李吉松和朴化荣,1994).于鹏等(2001)提出一种改进的有限差分法进行大地电磁场偏移成像,通过保留波数对水平方向的一阶导数项,使差分方程精度和成像分辨率得到了提高.继而,在改进的有限差分法大地电磁场偏移成像技术基础上,研究了全频段偏移成像技术,丰富了成像信息,提高了分辨率,并推进到适用于复杂地电模型和实际资料处理解释阶段(于鹏等,2005).姚伟华和李貅(2013)开始在航空瞬变电磁数据处理中应用瞬变电磁拟地震偏移成像技术.
电磁偏移成像方法,由Zhdanov等人提出到经过后来30余年的发展,其理论及方法不断丰富,但仍有许多关键问题需要进一步探索和分析.其中计算偏移场的积分变换方法,应用于实际资料处理时,首先必须离散化,得到合理的数值滤波器.至今国内外学者对数值滤波器的构建、滤波器参数选择、以及如何应用数值滤波器缺乏深入的分析和探讨,而这些因素直接影响偏移成像效果.本文基于偏移场满足的微分方程,详细推导并构建了电磁数据偏移数值滤波器.为了合理选择数值滤波器参数,找到了一个满足偏移方程的测试场.通过偏移场和偏移数值滤波器处理结果比较,分析了偏移滤波器参数的影响,确定了数值滤波器参数选择原则.考虑到实际应用的可行性,本文在计算偏移电导率时,引入背景场求取反射函数.最后,在数值试验中,依据所提出的参数选择原则,构建了偏移数值滤波器.相比国内外简单模型的处理结果,本文构建了多种典型复杂地电模型,对数值偏移滤波器进行检验.
2 电磁偏移基础理论
当频率小于105 Hz时,对大地介质有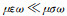
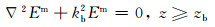
|
(1) |
边界条件:
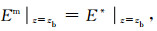
|
(2) |
式中Em表示电磁偏移场,
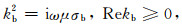
|
(3) |
其中,zb,E*,σb分别表示观测面位置、观测场共轭、以及背景电导率.
定义偏移场的空间频率谱:
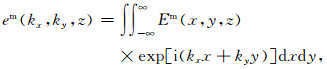
|
(4) |
式中kx, ky为空间频率.
在空间频率域中,偏移场满足:
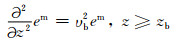
|
(5) |
上述方程的一般解如下:
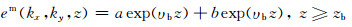
|
(6) |
式中υb=(kx2+ky2-iωυσb)1/2为空间频率域中的波数.考虑到偏移场下行特征,不难得到:
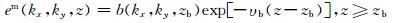
|
(7) |
对空间频率域中的偏移场做逆傅里叶变换,可得空间域偏移场的解:
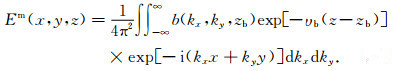
|
(8) |
由边界条件:
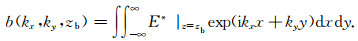
|
(9) |
利用卷积定律:
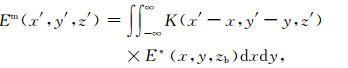
|
(10) |
其中K(x′, y′, z′)是偏移运算的卷积核函数:

|
(11) |
根据表格积分
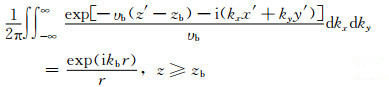
|
(12) |
其中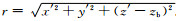
因此,卷积核函数可以表示为:
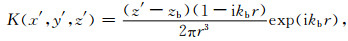
|
(13) |
式中波数kb=2π(1+i)/λb,其中λb是均匀半空间的波长.
偏移场可以表示为:
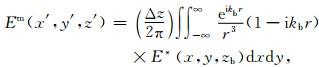
|
(14) |
其中Δz=z′-zb.
3 数值滤波器构建及参数分析 3.1 数值滤波器构建设x′=0,y′=0, 采样间隔x=nΔx,y=lΔy.其中Δx、Δy分别为水平x向和y向采样步长,即x向和y向两个邻近测点间的距离.
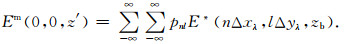
|
(15) |
由(15)式,数值滤波器系数:

|
(16) |
式中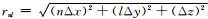
实际工作中,在x和y方向仅有有限个采样数(2N+1)和(2L+1).偏移场实际数值计算公式变为:

|
(17) |
因此有限个数据采样点的电磁偏移场实际上就是在x和y方向有限个采样数据(2N+1)和(2L+1)的线性组合.
数值滤波器窗口如图 1所示,数值滤波器在x和y方向的尺度分别为:
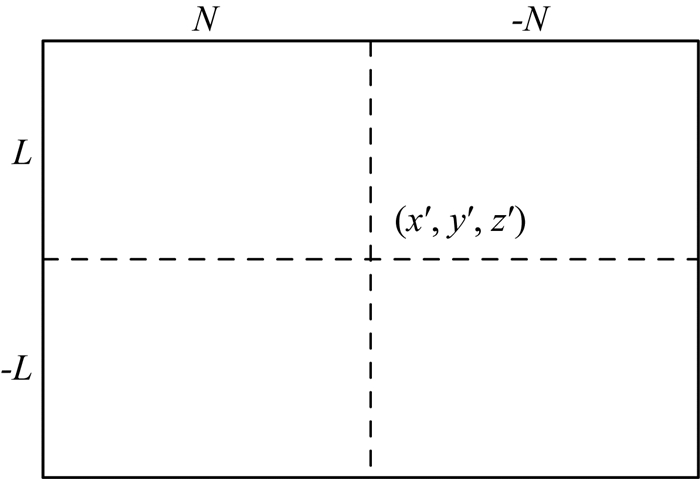
|
图 1 滤波器窗口 Fig. 1 Filter window |
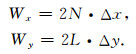
|
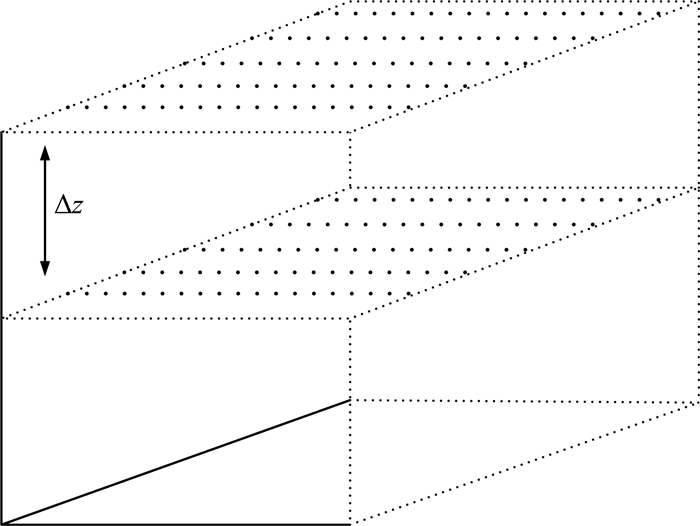
实际电磁偏移场计算过程如图 2所示.
|
图 2 实测数据面与偏移场面 Fig. 2 Measured surface and migration surface |
图 2上层数据点为观测面上的电磁数据采集点,下层数据点为某一偏移深度Δz处由偏移滤波器处理上层实际电磁数据得到.
3.2 数值滤波器参数分析在应用偏移滤波器之前,需对数值滤波器进行参数分析,其目的:(1)分析偏移变换中滤波器参数对偏移效果的影响;(2)确定数值滤波器参数选择原则.
基于偏移场控制方程,可以找到满足方程的测试场:
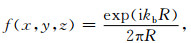
|
(18) |
式中: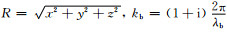
根据上述测试场公式,可以给出地表观测平面上的场分布,同时可以算出地下任意位置的场分布.利用偏移数值滤波器对观测位置场分布进行偏移处理,得到地下场分布.如果数值滤波器构造合理,利用数值滤波器得到的地下场分布应该与测试场计算的场分布一致.
本文选择场的周期为10 s,均匀背景电导率分布1 S·m-1.这种情况下,场的波长为:
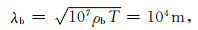
|
(19) |
水平采样步长先分别取:Δx=100 m,Δy=100 m.垂直偏移距离取z-zb=50 m,Δz=50 m.垂直偏移距是指利用偏移滤波器由某平面上的已知值求其下另一平面上偏移场时,两个平面间的距离.
观测区域范围为20 km×20 km:-10 km≤x≤10 km, -10 km≤y≤10 km.
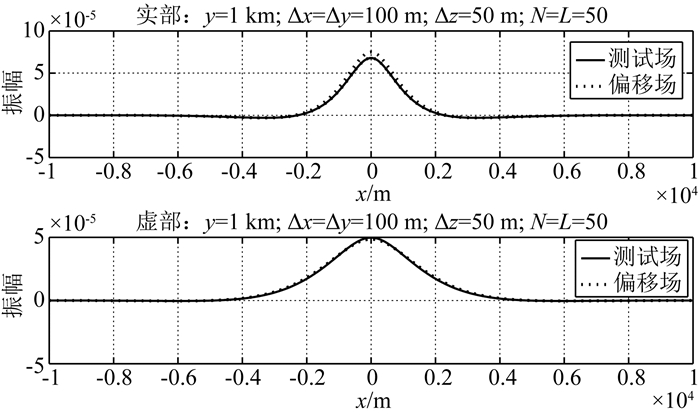
3.2.1 水平采样步长利用数值滤波器,对观测面上的测试场进行偏移,垂直偏移距离为50 m.为了比较方便,取观测面上一根测线y=1 km作比较,偏移成像的深度为100 m.图 3给出了地下50 m处场的实部和虚部.可以看到,测试场和偏移场的虚部几乎完全一样.但是,很明显,在位置x=0 km附近,两个场实部差异较大.其原因是对于设定的数值试验,选择滤波器的参数不合理.
|
图 3 滤波器水平采样步长100 m Fig. 3 Filter horizontal spacing 100 meters |
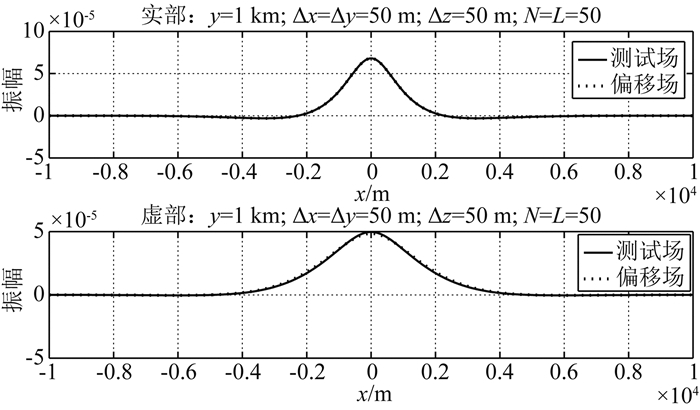
把滤波器水平步长从100 m减小到50 m,保持其他参数不变,测试场和偏移场实部虚部如图 4所示.这种情况下,看不到测试场和偏移场实部虚部之间的任何差别.结果说明,减小水平采样步长可以显著改善偏移成像结果.
|
图 4 滤波器水平采样步长50 m Fig. 4 Filter horizontal spacing 50 meters |
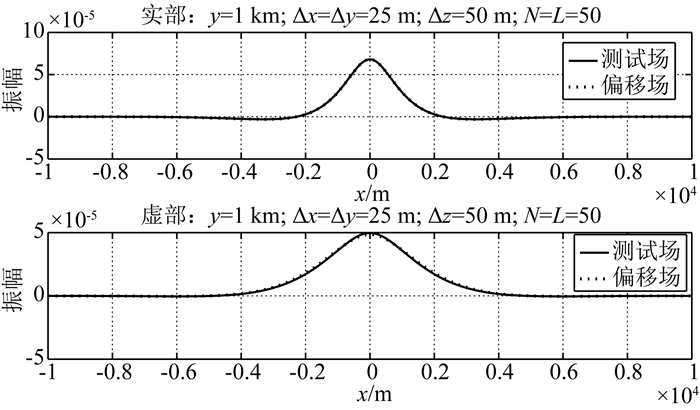
把滤波器水平步长继续减小,从50 m减小到25 m,保持其他参数不变,测试场和偏移场实部虚部如图 5所示.这时,仍然看不到测试场和偏移场实部虚部之间的任何差别.结果说明,当水平采样步长减小到一定程度,即可得到合理的偏移效果.如果继续减小水平步长,对偏移成像结果的影响不大.
|
图 5 滤波器水平采样步长25 m Fig. 5 Filter horizontal spacing 25 meters |
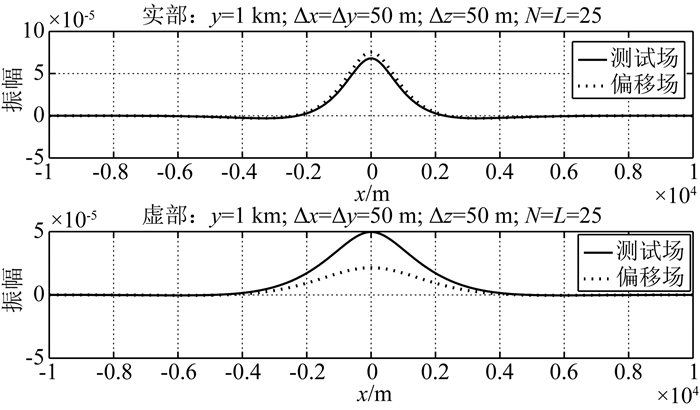
保持两个方向水平采样间隔均为50 m,垂直偏移距50 m,把两个方向窗口尺寸由50减小为25.测试场和偏移场实部虚部如图 6所示,相比之前的窗口尺寸,滤波器实部和虚部均出现明显差异.结果说明,对于一定的水平采样间隔和垂直偏移距,需通过试验确定合理的窗口尺度,过小的窗口无法得到有效的偏移效果.
|
图 6 滤波器窗口尺度25 Fig. 6 Filter window size 25 |
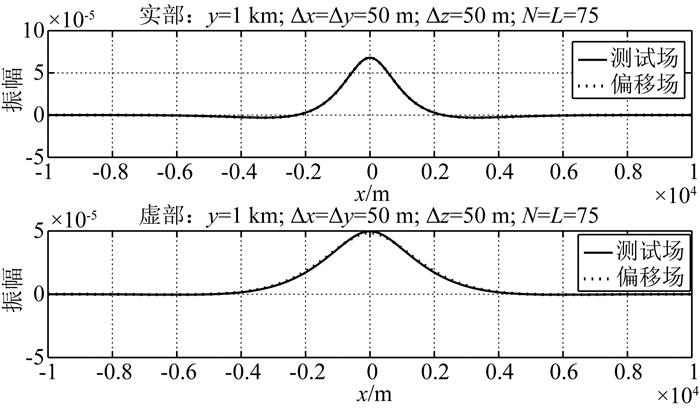
保持两个方向水平采样间隔均为50 m,垂直偏移距50 m,把两个方向窗口尺寸由50增加到75,测试场和偏移场实部虚部如图 7所示.相比之前的窗口尺寸,滤波器实部和虚部均无明显差异.说明,当滤波器窗口尺度增大到一定程度,继续增大窗口尺度对最终的偏移效果影响不大.
|
图 7 滤波器窗口尺度75 Fig. 7 Filter window size 75 |
取两个方向水平采样间隔为50 m,保持两个方向窗口尺寸为50,垂直偏移距由50 m变化为25 m.测试场和偏移场实部虚部如图 8所示,测试场和偏移场的实部出现明显差异.结果表明,垂直偏移距对偏移效果影响明显,为了保证偏移效果,两个方向的水平采样间隔不能大于垂直偏移距离.

|
图 8 滤波器参数 Fig. 8 Filter parameters |
针对频率域电磁观测数据,利用偏移数值滤波器求出相应的偏移场,然后求出背景场,计算反射系数,叠加反射系数,得到偏移电磁场的分布.为了得到偏移电阻率分布,考虑到实际应用可行性,定义反射函数如下:
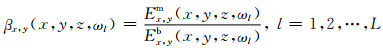
|
(20) |
式中Ex, yb(x, y, z, ωl)表示观测面上的背景场:
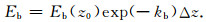
|
(21) |
定义偏移电导率如下:
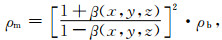
|
(22) |
其中ρb=1/σb.
偏移电导率成像处理流程如图 9.
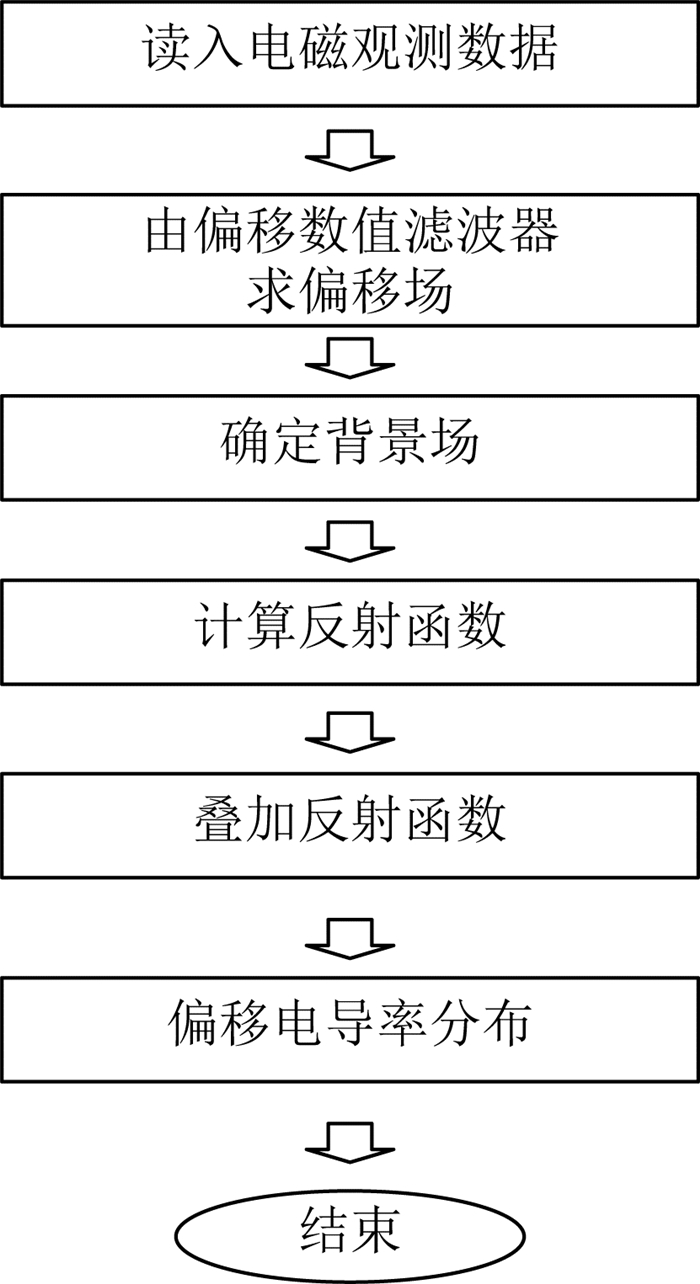
|
图 9 偏移电导率计算流程图 Fig. 9 Flow chart of migration conductivity |
根据成像处理流程,对全空间各种低阻和高阻模型,收发距从近场直至上千公里不同地电模型进行偏移成像处理,得到一系列的地电模型,下面仅展示三个典型地电模型数值试验结果.以下三个数值试验中,偏移滤波器的参数设置为:两个方向的水平步长均为50 m,垂直偏移距为50 m,滤波器两个方向的窗口大小均为50.
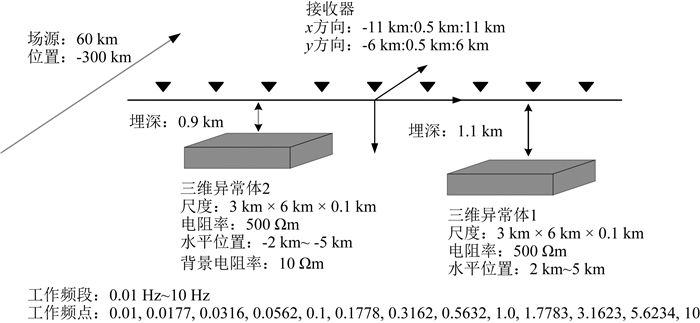
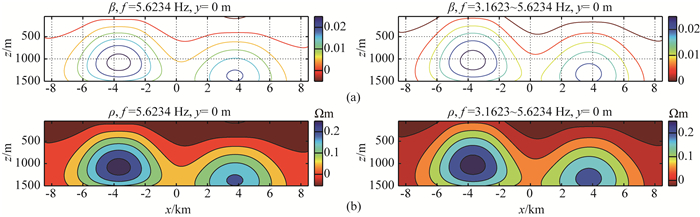
图 10所示的地电模型,人工源距测区中心水平距离300 km.地下均匀半空间背景模型中,有两个三维高阻异常体,顶面埋深各为0.9 km和1.1 km,背景电阻率为10 Ωm.利用数值滤波器偏移地表测点处的电磁场,得到地下偏移电阻率分布,抽取中心一条测线偏移成像结果如图 11所示.偏移成像结果合理反映了地下两个高阻体的水平位置和垂直埋深,以及电阻率相对高低.试验显示,如果频率选择合适,只需较少频率资料,就能够利用数值偏移滤波器得到合理的地下电阻率分布结果.实测资料处理中,可以利用实测资料一维反演结果确定背景场,也可以用电磁场分解技术确定背景场(Wang and Zhdanov, 2010).
|
图 10 两个三维异常体模型 Fig. 10 The model including two 3D targets |
|
图 11 两个三维异常体模型的偏移成像结果 (a)反射函数分布; (b)偏移电阻率分布. Fig. 11 Migration imaging of the model including two 3D targets |
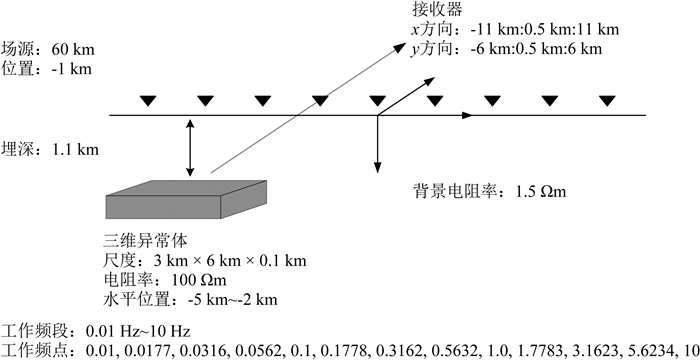
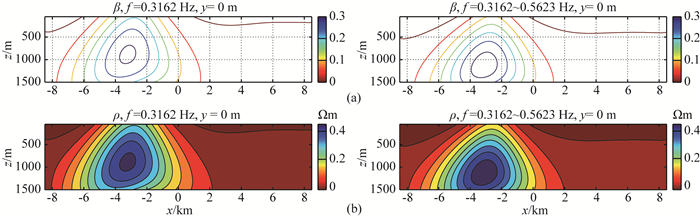
图 12所示的地电模型中,人工源位于测区内距测区中心测点非常近.地下均匀半空间背景模型中,有一个三维高阻异常体,顶面埋深为1.1 km,背景电阻率为1.5 Ωm.利用数值滤波器对地表测点处的电磁场进行偏移,得到地下偏移电阻率分布,其中测区中心一条测线偏移成像结果如图 13所示.结果证明,即使在近场情况下,偏移成像结果依然能够给出合理的地下三维高阻体的水平位置和垂直埋深,以及电阻率相对高低.试验结果显示,两个频点资料的偏移效果能更准确反映异常体垂直埋深.
|
图 12 近场一个三维异常体模型 Fig. 12 The model including one 3D target for near-field |
|
图 13 近场三维异常体模型的三维偏移成像结果 (a)反射函数分布; (b)偏移电阻率分布. Fig. 13 3D migration imaging of the model including one 3D target for near-field |
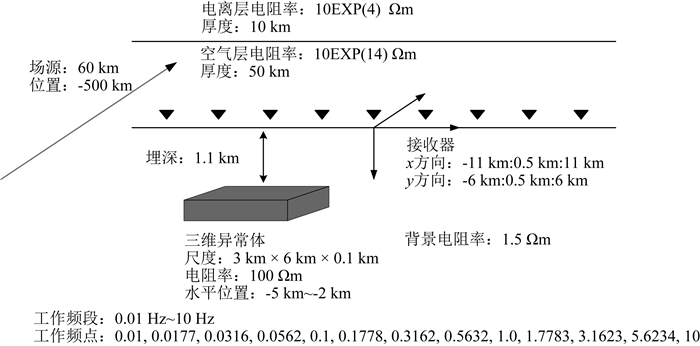
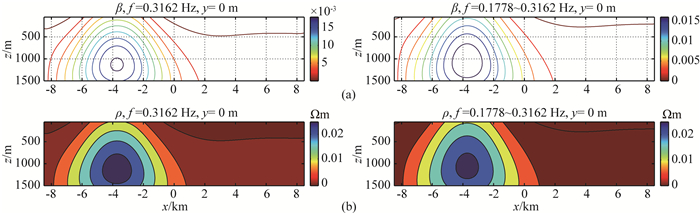
图 14所示的地电模型,人工源距测区中心水平距离500 km.这时,由于收发距远,数值试验中地电模型考虑了电离层.地下均匀半空间背景模型中,有一个三维异常体,顶面埋深为1.1 km,背景电阻率为1.5 Ωm.利用数值滤波器偏移地表测点处的电磁场,得到地下偏移电阻率分布,中心测线偏移成像结果如图 15所示.偏移成像结果显示出了地下异常体合理的水平位置,垂直埋深稍有差异,其中两个频点资料偏移结果更接近真实垂向位置.
|
图 14 电离层地电模型 Fig. 14 The geo-electromagnetical model including ionosphere |
|
图 15 电离层地电模型的三维偏移成像结果 (a)反射函数分布; (b)偏移电阻率分布. Fig. 15 3D migration imaging of the geo-electromagnetical model including ionosphere |
数值试验结果表明,依据本文提出的滤波器参数选择原则构建的滤波器,偏移成像过程稳定,偏移结果能合理反映模型中异常体的空间位置和电阻率相对高低.数值试验证实电磁偏移成像是一种快速、可靠、稳定的电磁资料解释技术.
5 结论基于电磁偏移理论,推导了电磁偏移场解析式,对电磁偏移理论滤波器做离散化处理,实现了电磁偏移场计算数值滤波器.为了合理应用电磁偏移技术,引入偏移测试场,对比测试场和数值滤波器偏移场,研究了滤波器滤波窗口尺度、垂直偏移步长、水平采样间距之间的关系对数值滤波器偏移效果的影响,确定了滤波器最优参数选择原则.
数值模型试验中,首先建立不同收发距典型复杂三维不同地电模型.利用偏移成像技术处理数值模拟数据,得到了合理的地下勘探体位置.数值试验偏移成像结果证明了本研究确定的偏移滤波器选择原则,同时证明电磁偏移成像技术是一种可靠稳定的电磁资料解释技术.在本文研究成果基础上,可以进一步研究能提高偏移成像精度的迭代偏移成像.
致谢本文部分基础性工作得到了美国犹他大学Zhdanov教授的帮助和支持,作者表示诚挚感谢.
| Chen L S, Wang G E, Chen J P, et al. 1993. A MT imaging technique. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 36(3): 337-346. | |
| Furukawa T, Zhdanov M S. 2007. Two-dimensional time-domain electromagnetic migration using integral transformation.//SEG Technical Program Expanded Abstracts 2007. SEG, 584-588. | |
| Lee S, McMechan G A, Aiken C L V. 1987. Phase-field imaging:The electromagnetic equivalent of seismic migration. Geophysics, 52(5): 678-693. DOI:10.1190/1.1442335 | |
| Li J S, Piao H R. 1994. Research on phase shift migration of magnetotelluric data. Oil Geophysical Prospecting (in Chinese), 29(2): 189-198, 212. | |
| Liu X S, Yang L, Fang S, et al. 1986. A new magnetotelluric inversion method & vertical Time-distance curve method. Oil Geophysical Prospecting (in Chinese), 22(4): 453-455. | |
| Wang J Y, Oldenburg D, Levy S. 1985. The magnetotelluric interpretation simulating seismic method. Oil Geophysical Prospecting (in Chinese), 20(1): 66-79. | |
| Wang S M, Zhdanov M S. 2010. Removal of the airwave effect on MCSEM data by separation of the main part of the anomalous field.//SEG Technical Program Expanded Abstracts. SEG, 732-736. | |
| Wei S, Wang J Y. 1993. Migration of 2-D magnetotelluric data. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 36(2): 256-262. | |
| Yu P, Wang J L, Wu J S. 2001. Multi-parameter migration imaging of magnetotelluric data using finite difference method. Chinese Journal of Geophysics (in Chinese), 44(4): 552-562. | |
| Yu P, Wang J L, Wu J S. 2005. Magnetotelluric sounding whole frequency bands migration imaging versus inversion technique. Journal of Tongji University (in Chinese), 33(4): 540-544. | |
| Zhdanov M S, Booker J R. 1993. Underground imaging by electromagnetic migration.//SEG Technical Program Expanded Abstracts. SEG, 355-357. | |
| Zhdanov M S, Frenkel M A. 1983. Electromagnetic migration.//Hjelt S E. The Development of the Deep Geoelectric Model of the Baltic Shield, Part 2. Oulu:Univ. of Oulu, 37-58. | |
| Zhdanov M S, Traynin P, Portniaguine O. 1994. Migration and analytic continuation in geoelectric imaging.//SEG Technical Program Expanded Abstracts. SEG, 357-360. | |
| Zhdanov M S, Traynin P N, Portniaguine O. 1995a. Resistivity imaging by time domain electromagnetic migration (TDEMM). Exploration Geophysics, 26(3): 186-194. DOI:10.1071/EG995186 | |
| Zhdanov M S, Traynin P, Portniaguine O, et al. 1995b. Time domain electromagnetic migration in INEL RWMC Cold Test Pit characterization.//Symposium on the Application of Geophysics to Engineering and Environmental Problems. SEG, 919-924. | |
| Zhdanov M S, Traynin P. 1996. Inversion versus migration in two-dimensional geoelectrical problems.//SEG Technical Program Expanded Abstracts. SEG, 253-256. | |
| Zhdanov M S, Li W D. 1997. 2-D finite-difference time domain electromagnetic migration.//SEG Technical Program Expanded Abstracts. SEG, 370-373. | |
| Zhdanov M S, Li W S. 1998. Preconditioned time domain electromagnetic migration.//SEG Technical Program Expanded Abstracts. SEG, 461-464. | |
| Zhdanov M S, Pavlov D, Ellis R. 2001. Fast imaging of TDEM data by 2.5-D finite difference electromagnetic migration.//SEG Technical Program Expanded Abstracts. SEG, 1447-1450. | |
| 陈乐寿, 王光锷, 陈久平, 等. 1993. 一种大地电磁成像技术. 地球物理学报, 36(3): 337–346. | |
| 李吉松, 朴化荣. 1994. MT法电磁相位移偏移研究. 石油地球物理勘探, (2):189-198(2): 189–198, 212. | |
| 刘晓山, 杨菱, 方胜, 等. 1986. 一种全新的大地电磁反演法--垂直时距曲线法. 石油地球物理勘探, 22(4): 453–455. | |
| 王家映, OldenburgD, LevyS. 1985. 大地电磁测深的拟地震解释法. 石油地球物理勘探(1): 66–79. | |
| 魏胜, 王家映. 1993. 二维大地电磁资料的偏移. 地球物理学报(2): 256–263. | |
| 姚伟华, 李貅. 2013.航空瞬变电磁偏移成像方法应用.//中国地球物理2013-24分会场论文集. | |
| 于鹏, 王家林, 吴健生. 2001. 有限差分法大地电磁多参数偏移成像. 地球物理学报, 44(4): 552–562. | |
| 于鹏, 王家林, 吴健生. 2005. 大地电磁全频段偏移成像结合反演技术. 同济大学学报(自然科学版), 33(4): 540–544. | |
 2017, Vol. 60
2017, Vol. 60


