线性构造通常形成于断裂发育、块体或物性边界等区域,反映了块体的相互作用、构造变形和物性的空间分布差异,其探测与识别为地学研究的重要目标之一.很多情况下,线性构造表现为地下岩层的密度、电阻率、弹性性质等物理特征的不连续变化,因此可采用相应的地球物理方法进行探测.大地电磁法是一种重要的电磁测深方法,长期以来,主要依赖反演得到的电性结构进行地质和地球物理解释推断.大地电磁反演结果存在较强的不确定性,且由于软硬件平台、观测资料等方面的限制,目前二维反演依然是大地电磁法的主流解释技术.二维反演假定整条剖面具有相同的构造走向方位,因而其结果除了二维模型的假设与真实大地有较大的差异以外,还无法给出不同剖面位置、不同深度的构造走向方位及构造之间接触转换关系等信息,而这些信息往往与大地构造变形演化过程有着密切的联系.因此,单纯的大地电磁二维反演结果在解释线性构造几何特征方面具有较大的局限性.
大地电磁观测的数据响应是一个随频率变化的阻抗张量.依据阻抗张量分解技术(Bahr, 1988, 1991;Groom et al., 1989, 1991;Caldwell et al., 2004;Bibby et al., 2005;蔡军涛等,2010),我们可以获得观测点附近对应频率的电性主轴方位、构造维性、区域阻抗等参数.可以想见,如果大地岩体的线性构造表现为岩石电性的差异,则其几何特征可以利用电性主轴方位和维性因子来判别描述.由于在利用阻抗张量分解确定电性主轴方位时受到构造维性和观测噪声等因素的影响,传统的确定性分析方法无法有效地对线性构造进行判别分析.在本研究系列(四)(陈小斌等,2014)中,提出了基于阻抗张量分解的多测点-多频点统计成像分析方法(以下简称为阻抗张量成像).该方法在考虑多种影响因素的前提下,利用玫瑰图、统计分布云图等可视化技术,可有效给出电性主轴方位和维性分布的频率-空间的统计分布图像,因而有可能为探测大地线性构造的几何特征提供新的技术手段.不过,该文只是提出并实现了阻抗张量成像,重点在于阐述该方法的基本原理、实现和验证,没有具体论述其在线性构造探测方面的应用,甚至对其所可能具备的这一重要应用没有认识.
本文对大地电磁阻抗张量成像在大地线性构造探测中的应用展开了具体研究.我们设计了多个理论模型和选择了多条实测剖面进行了该问题的相关分析讨论.限于篇幅,本文选择其中的“立交桥”三维理论模型和一条穿越郯庐断裂带南段的大地电磁实测剖面为例,展示该方法在探测大地线性构造中的有效性、实用性.由于阻抗张量成像分析中所提供的图像组合较多,信息较为丰富,其数据处理与分析较为繁杂,本文通过理论模型和实测数据的处理分析,归纳了其基本步骤与一个较为规范的分析过程.
2 理论模型分析:线性构造识别的基本过程线性构造的主要几何特征包括走向、倾角和空间分布范围等,其中走向是一个关键性的参数.对于二维模型而言,假定构造的走向是已知的,而对于实测数据和三维复杂模型而言,走向是未知的.走向的识别往往是断裂、块体边界存在与否的直接证据,也是推断相邻构造空间接触关系和变形演化过程的重要参考信息.因而走向的确定及相关的分析讨论是线性构造探测中一个重要的议题,对于掩埋于地下深处的隐伏构造尤为重要.利用阻抗张量成像识别线性构造,可为主观性较强的地学构造推断提供有力的观测证据.
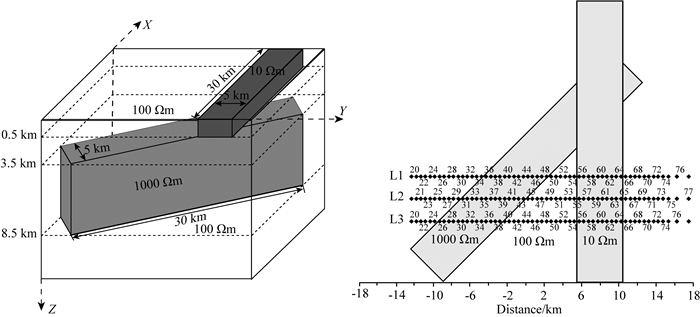
2.1 模型设计和正演计算为研究阻抗张量分解成像方法在探测复杂模型的线性构造识别中的应用,本文设计了典型的三维“立交桥”模型(见图 1),浅部低阻异常体(电阻率为10 Ωm)构造走向为0°,深部高阻异常体(电阻率为1000 Ωm)走向为45°.采用Mackie等的三维有限差分正演程序(Mackie et al., 2001)获得了该模型的三维正演响应,然后在MT-Pioneer软件系统(陈小斌等,2004)上,基于共轭阻抗张量分解(蔡军涛等,2010)进行了多测点-多频点的统计成像分析.
|
图 1 “立交桥”模型(左)及平面视图(右) 右图中给出了本文后续所要分析的剖面L1、L2、L3位置及测点分布情况,其中L1、L2、L3的剖面间距为3 km.三维正演计算网格为88×98×64,覆盖了左图的整个模型范围,并在四个水平方向分别往外延伸至190 km、垂直方向延伸到800 km以消除边界的影响,计算频率范围为0.0001~1000 Hz,共计40个频点数据. Fig. 1 An "Overpass" model (left) and its plan view (right) The right image shows the locations of profile L1, L2, L3 and the distribution of sites, where L1, L2 and L3 are 3 km apart. The three-dimensional modeling grid is 88×98×64, covering the entire model range, extending out to 190 km in four horizontal directions and 800 km in vertical direction to eliminate the influence of the boundary, and the calculation frequency band is 0.0001~1000 Hz, a total of 40 frequencies. |
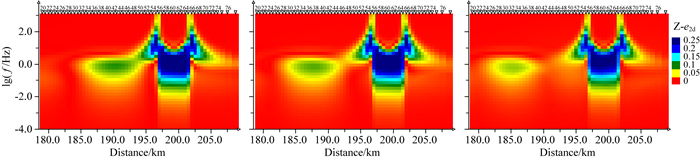
图 2给出了该三维“立交桥”模型上三条剖面(位置见图 1)的二维有效因子e2d(陈小斌等,2014)的分布情况.由图可见存在两个二维性较强的区域,分别对应于模型的低阻和高阻异常体,可视为线性构造发育的部位.图 2显示,由L1至L3,两个线性构造区的距离越来越大,表明两个三维异常体的距离越来越远,与模型中对应剖面的位置完全一致.仔细分析二维有效因子的分布,可以看出,浅部高导异常体的影响频率范围很宽,由最高频1000 Hz一直到0.01 Hz附近,而深部高阻体的影响范围较窄,在数赫兹到数秒之间.这一现象表明,在频率域定性分析深度域的问题时,不能简单地根据频率的高低来确定深度,还要充分考虑模型电阻率值的大小.
|
图 2 “立交桥”模型L1剖面(左)、L2剖面(中)、L3(右)剖面的二维有效因子e2d的分布图 Fig. 2 Distribution of 2D effective factor e2d of L1 profile (left), L2 profile (middle), L3profile (right) of "overpass" model |
从图 2中线性构造区的形状来看,依据最高频的二维有效因子可以很好地确定低阻异常体两侧边界.此时,异常体内部的二维有效因子很小,对于高频而言,可视为一维结构.随着频率的降低,二维有效因子的显著区慢慢扩展,最终重合在一起往下延伸,在频率域形成鼎状的线性构造响应区.而高阻异常体由于埋深较深,其所在的频率范围,整体呈碗状.这些特征与大地电磁的分辨率随着频率的降低快速下降是一致的.这意味着在AMT这样的高频工程探测中,利用二维有效因子确定浅部断裂的横向分布具有较好的分辨能力和应用价值.
图 3给出了三条剖面的最佳主轴方位的统计成像结果,结果显示,三条剖面上都存在两个最佳主轴方位,分别分布在0°和45°附近,与真实模型的设计一致.统计玫瑰图显示0°更为显著;频率分布云图表明0°的主轴始于较高的频率,且影响频带较宽,类似于浅部高导体的特征,45°的主轴始于相对较低的频率,表明其顶部存在一定的埋深;测点分布云图则清楚地显示两个不同主轴方位的线性构造在剖面上的空间分布位置不同.三条剖面结果的对比分析表明,从L1剖面至L3剖面,两个线性构造之间的距离越来越大,且相对而言45°构造的显示越来越强,0°构造的显示越来越弱.这种现象可用高阻阻挡和高导集流效应来解释:当两个异常体距离较近时,有更多的电流沿着高导体流动,故高导体显示更强,而高阻体显示更弱;当两个异常体距离较远时,二者之间的相互影响越来越小,高导体里的电流相对减少,高阻体内的电流相对增多,故使得高导体的识别相对变弱,而高阻体的识别相对变强.

|
图 3 “立交桥”模型L1剖面(上)、L2剖面(中)、L3剖面(下)多测点-多频点最佳主轴方位的统计玫瑰图(左)、频率分布云图(中)和测点分布云图(右),统计中进行了维性加权 Fig. 3 Statistical images of geo-electrical strikes for L1 profile (upper), L2 profile (middle), L3 profile (lower) with all sites-all frequencies data calculated with dimensional weighting by using of CCZ method. From left to right, the graphs are respectively rose diagram, site-based cloud diagram and frequency-based cloud diagram |
根据图 3,我们还可以看出,利用多条邻近剖面的测点分布云图,可以排除令人头疼的阻抗最佳主轴的90°的模糊性.在测点分布云图上,如果某个相近的方位在多条相邻剖面的某些特定区段连续出现,则可以确定电性主轴的走向方位是与这些特定区段的连接线的展布方位相近,从而去掉另一个相差90°的主轴方位.例如模型中的45°走向的高阻体,在单条剖面上分析,其走向也可能是135°.假设其在L1剖面上为135°,那么其出现在L2、L3剖面上时,对应的测点号将会越来越大.而图 3中,其出现的测点号越来越向小号.由此可以唯一确定该处线性构造的走向角为45°而非135°.
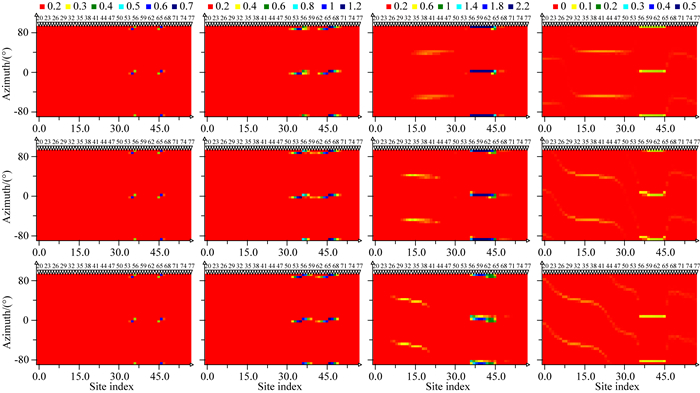
2.3 分频段统计成像从以上分析中可以看到,利用最佳主轴统计成像技术,可以较好地分辨出模型中两个线性构造的走向(或倾向)方位特征、频率和空间分布特征.利用多条相邻剖面,还可以消除线性构造走向和倾向方位的模糊性.为了进一步揭示主轴方位随频率变化的具体细节,依据频率分布云图(图 3)所显示的各主要主轴方位的频率分布范围,分不同频段分别进行统计成像,结果见图 4所示.由图 4可得以下认识.
|
图 4 “立交桥”模型L1剖面(上)、L2剖面(中)、L3剖面(下)分频段统计的测点分布云图 自左至右频率范围依次为:40~100 Hz、3.5~40 Hz、0.005~3.5 Hz、0.0001~0.005 Hz,统计中进行了维性加权. Fig. 4 Site-based cloud diagram for L1 profile (upper), L2 profile (middle), L3 profile (lower) of "overpassed" model with different frequency bands calculated with dimensional weighting by using CCZ method From left to right, the frequency bands are respectively 40~100 Hz、3.5~40 Hz、0.005~3.5 Hz、0.0001~0.005 Hz. |
(1)1000~40 Hz频段:电性主轴方位主要为0°,从测点分布云图上可以准确定位0°主轴方位的异常体的边界,左侧在测点55附近之间,右侧在测点65附近,与三条剖面在模型中跨越浅部低阻异常体的位置完全一致.该频段没有发现埋深较大的走向为45°的高阻异常体构造;
(2)3.5~40 Hz频段:统计频次依然主要集中于高导异常体边界附近,但向各自两侧有所扩展.该频段也没有出现埋深较大的走向为45°的高阻异常体构造的响应;
(3)0.005~3.5 Hz频段:剖面左侧出现了45°的统计显示,且由L1剖面至L3剖面,其显示位置依次往左偏移,分别位于L1剖面的测点36~47之间、L2剖面的测点30~44之间、L3剖面的测点26~40之间,可见L2剖面、L3剖面中45°高阻异常体位置与真实模型(位置见图 1)吻合得很好,L1剖面由于附近三维性较强,位置有所偏差.右侧0°的统计频次依然非常显著.此时,浅部的高导异常体的主轴统计频次已连接在一起,呈现为整体性的线性构造指示区,但其两侧的边界依然比较清晰;
(4)0.0001~0.005 Hz频段:虽然依然可以看到两个异常体的统计响应,但频次值已经很小,在实际资料中很容易被各种噪声所淹没.
根据以上分析可知,利用阻抗张量成像技术(包括二维有效因子成像和最佳主轴统计成像)可以较好地识别三维“立交桥”模型的线性构造.利用二维有效因子可以确定线性构造发育的频率-空间分布位置,利用最佳主轴统计成像则可进一步确定各线性构造的走(倾)向方位问题.尤其是,利用多条剖面,可以勾勒出同一线性构造的空间延伸方位,从而可以解决数据分析过程中的走向和倾向之间所存在的90°的模糊性.
需要注意的是,这项技术对于高导线性构造的识别非常敏感,但由于高导体的趋肤深度较小,即使其埋深浅,其所影响的频率范围也可能会很低,因而在由频率分析线性构造的深度时一定要非常小心.
2.4 识别线性构造的基本步骤通过上述案例的研究,可以发现,利用阻抗张量成像法探测识别线性构造大致可分为以下三个基本步骤.
首先,进行全剖面的构造维性分析,主要依据二维有效因子成像确定线性构造(二维性强)的频率-剖面距分布情况;
其次,进行全剖面的线性构造方位分析,利用电性主轴方位统计成像,确定剖面上主要的几个线性构造走(倾)向方位值及其频率分布范围、测点分布范围,并与二维性分析结果进行对比,分析其对应性;
第三,在上述两个步骤的基础上,进行不同测点范围、频段范围的分解分析,进一步确定不同剖面位置、不同频段范围的线性构造显示情况及其几何方位分布特征.
按照上述三个步骤,可以使我们在反演以前,对剖面上的线性构造发育情况有个基本的了解.其分析结果不仅为后续的地质解释提供了直接的构造发育信息,而且为二维反演结果的可靠性分析提供了参考依据:反演结果所给出的构造框架应该与这个分析结果有着对应的一致性.
3 实测算例:郯庐断裂带南段大地线性构造的识别为进一步展示阻抗张量成像技术在探测线性构造中的应用效果,以下研究一个实测算例.事实上,在本文成文之前,该方法已在多个项目中应用,并取得了较好的效果.本文的研究是在已有实际资料应用的推动之下开展起来的.
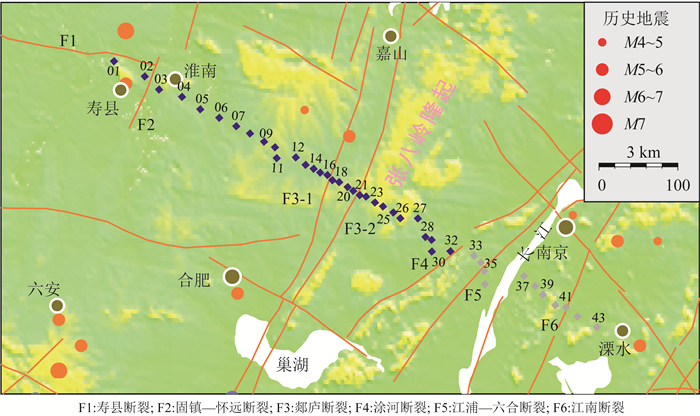
3.1 剖面展布情况以下以郯庐断裂带南段的一条大地电磁野外实测剖面为例进行讨论.该剖面数据来源于中国地震局华北震情跟踪项目.剖面西起安徽省中部六安市寿县,横跨郯庐带南段、张八岭隆起等重要构造区,止于南京市溧水县,呈北西-南东向展布,全长约255 km,共计43个测点.由于干扰的原因,编号大于32的测点数据质量较差,尤其是低频段,故这些测点数据在本文研究中未参与分析.剖面测点分布见图 5所示,小号点为西北侧,大号点为东南侧.图 5还给出了测区活动断裂及中强以上历史地震的分布情况.
|
图 5 大地电磁实测剖面测点分布图 图中菱形点为大地电磁测点,蓝色测点为本文所采用,灰色测点未采用;红色圆点为历史地震;粗实线为活动断裂. Fig. 5 Distribution of MT surveying profile and sites The rhombic points are the MT sites, the blue sites are used in this paper, the gray sites are not used, the red dots are the historical earthquakes, and the thick solid lines are the active faults. |
按照上述总结的基本步骤,首先对该剖面数据进行构造维性分析.基于共轭阻抗法的维性成像结果见图 6.由图可知,该剖面低频段( < 0.1 Hz)三维性较强,中、高频部分二维性较好.其中,剖面的偏右侧、约0.1~320 Hz范围内,存在二维有效因子明显偏大的线性构造指示区.根据二维有效因子分布的特点,对比前面理论模型算例的研究,推测该线性构造发育区为一出露于地表的二维异常体,异常体两侧边界分别为测点21和测点26附近;另又依据视电阻率拟断面图(图 7),可知该异常体为出露于地表的高阻体.
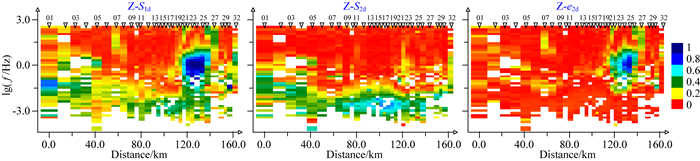
|
图 6 基于共轭阻抗法(CCZ)的构造维性成像 自左至右分别为阻抗一维偏离度(Z-S1d)、二维偏离度(Z-S2d),二维有效因子(Z-e2d),图中空白区域表示张量分解中被删除的飞点数据. Fig. 6 The cloud maps of dimensionality based on CCZ method From left to right, the maps are 1D skew, 2D skew and 2D effective factor, respectively. Data in the blank blocks is deleted. |
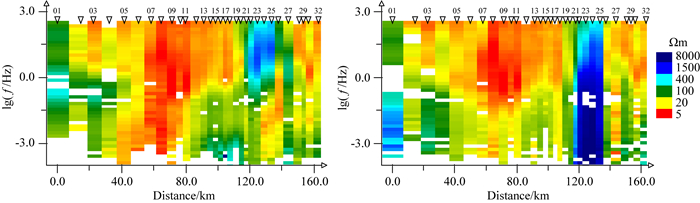
|
图 7 沿剖面的视电阻率拟断面图 左为TE模式; 右为TM模式,空白表示质量不好而被删除的数据. Fig. 7 Maps of resistivity alone the MT profile The left is for TE mode; The right is for TM mode. The blanks are the deleted data for their poor quality. |
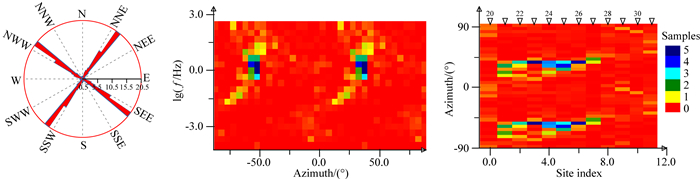
其次,进行沿剖面的电性主轴统计成像分析.图 8展示了该剖面所有测点和频点电性主轴统计成像结果.如果忽略90°的模糊性问题(以下讨论均遵循此原则,即当我们说NE多少度时,同时也意味着其也可能是NW的共轭方向),玫瑰图显示剖面电性主轴方位集中于NE35°左右;频率分布云图显示该电性主轴主要分布于0.2~20 Hz频段,其高频段(>20 Hz)有北北东向的次级线性构造指示区, 低频段( < 0.2 Hz)则没有显著的主轴方位;测点分布云图则展示该剖面在电性主轴方位存在两个差异显著的分区:西北侧电性主轴不明显,仅7号测点处存在一定的集中;东南侧主要为上述线性构造的发育范围,该线性构造区沿剖面展布范围约30 km.
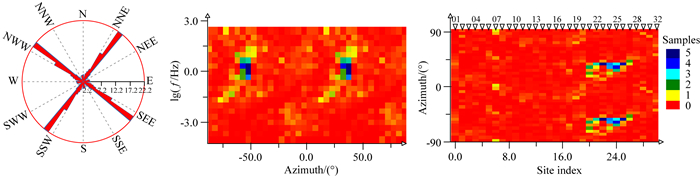
|
图 8 电性主轴统计成像结果 由左至右依次为统计玫瑰图、频率分布云图、测点分布云图,统计过程施加了二维性加权. Fig. 8 tatistical images of geo-electrical strikes for all sites-all frequencies data calculated with dimensional weighting by using of CCZ method. From left to right, the graphs are respectively rose diagram, frequency-based cloud diagram and site-based cloud diagram. |
通过以上分析可以发现,由于剖面上两个分区的电性主轴统计分布差异很大,可能存在一个分区被另一个分区压制的现象,因而需要将二者分开,分别进行多测点-多频点的电性主轴统计成像分析.此外,在成像分析过程中,发现低频段( < 0.015 Hz)全剖面具有较为一致的电性主轴特征,故最后在该频段又进行了全剖面统计成像分析.
3.3 剖面西北段的统计成像图 9给出了剖面西北段(测点01-19)电性主轴统计成像结果.从统计玫瑰图上可以看出,存在北北东、北东和北东东3个比较显著的主轴方位.从频率分布云图大致可分出4个特征较为一致的频段:高频段(60~320 Hz)、中高频段(3~60 Hz)、中低频段(0.015~3 Hz)和低频段( < 0.015 Hz),中低频段稍显显著.从测点分布云图上则可以看出,测点07和18较其他测点的电性主轴更为集中,表明这两个测点附近可能发育线性构造.
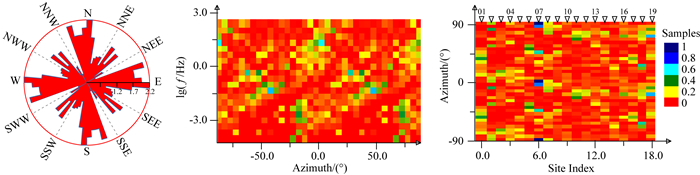
|
图 9 剖面西北段电性主轴统计成像结果 由左至右依次为统计玫瑰图、频率分布云图、测点分布云图,统计过程施加了二维性加权. Fig. 9 Statistical images of geo-electrical strikes of the NW parts of the profile for all sites, all frequencies data calculated with dimensional weighting by using of CCZ method From left to right, the graphs are respectively rose diagram, frequency-based cloud diagram and site-based cloud diagram. |
图 10给出了该段剖面(测点01-19)前4个频段的统计成像结果,可以得到以下认识.
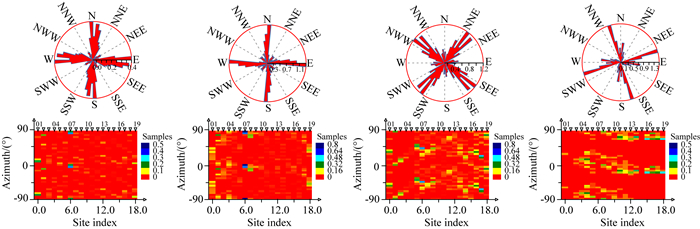
|
图 10 剖面西北段电性主轴分频段统计成像结果 上为统计玫瑰图,下为测点分布云图,自左至右频率范围依次为:60~320 Hz、3~60 Hz、0.015~3 Hz、0.0001~0.015 Hz,统计过程施加了二维性加权. Fig. 10 Statistical images of geo-electrical strikes of the NW parts of the profile calculated with dimensional weighting by using of CCZ method The uppers are rose diagrams and the lowers are site-based cloud diagram. From left to right, the frequency bands are respectively 60~320 Hz、3~60 Hz、0.015~3 Hz、0.0001~0.015 Hz. |
(1)高频段(60~320 Hz):测点07处的近南北-东西向电性主轴最为显著,其次是测点01号点处的北北东向电性主轴,测点02处的北东向和测点19处的近南北-东西向电性主轴方位也有所显示;
(2)中高频段(3~60 Hz):测点07处的近南北-东西向电性主轴变得更加显著,并向测点08处扩展,衍生出北东东向方位,同时,测点02处的电性主轴也变得比高频时更为显著,但方位为北东东向,此外,测点01和19处也存在电性主轴集中现象,但不是很显著;
(3)中低频段(0.015~3 Hz):主轴方位较高频段和中高频段有较大的变化,电性主轴主要集中于北北东和北东方向:北北东向主轴主要分布在测点15-18附近,尤以测点18最为显著,而北东向主轴主要分布在测点01、测点04-09之间,测点01处延续了中高频段的主轴方位,而测点04-09处的主轴方位与中高频段的差异很大,因而在此处形成比较典型的立交桥结构;
(4)低频段(0.0001~0.015 Hz):北东东向的电性主轴非常显著,与中低频段存有30°左右的夹角,形成深一层的立交桥结构.测点分布云图显示:北东东向的电性主轴在测点04以东均有分布,其中,测点08以东呈现较为单一的NE75°方位;测点04-07之间,则出现近南北、北北东、北东东等多个方位;测点01主要呈现为北北东、北东向方位,与中低频变化不大.
通过以上成像分析,我们在剖面西北段上识别出数个线性构造指示区,同时还揭示其深部存在着立交桥构造模式.我们所推测的线性构造区有以下5个.
①测点07处的近南北-东西向构造非常显著,该线性构造分布在3~320 Hz范围内,根据图 7,测点07处的视电阻率10 Ωm左右,按照趋肤深度推测该断裂最大深度大致为1 km,浅部可能出露于地表,推测为沉积盖层里发育的断裂;沉积层以下,测点07附近出现过两次构造方位的改变,分别为中低频的北东向和低频的北东东向,虽然不能唯一确定其构造走向方位,但可以据此判定该区域由浅到深存在两层立交桥结构,推测其电性主轴方位的转换面对应于构造演化过程中的不整合面;
②测点01处存在延伸深度大且方位较为稳定的北东向(或南西向)线性构造,根据地质资料的对比,推测为南西向延伸的寿县断裂(F1),由于在低频段( < 0.015 Hz)该断裂依然有所显示,故其延伸深度可能超过40 km,属于较深的断裂;
③测点18处的线性构造出现在中低频段,在地表对应于郯庐带的一枝(F3-1),其北北东向主轴方位也与郯庐带的走向一致,按照平均电阻率50 Ωm计算,趋肤深度推测其延伸深度大致30 km,应在地壳以内;
④测点08-19之间的低频段存在显著的北东东(或北北西)向构造,按照趋肤深度计算,推测其为主要发育于上地幔顶部的线性构造;
⑤测点02、测点19等处还存在一些小的不太显著的线性构造发育.
3.4 剖面东南段的统计成像图 11给出了剖面东南段(测点20-32)的电性主轴统计成像结果.由于测点21-26之间的强二维构造体的存在,统计玫瑰图上北北东向构造非常显著,而其他方位的构造没法显示出来.然而,从频率分布云图和测点分布云图上还是可以看到一些变化,尽管这些变化在强二维体的同一色标体系下显得不明显.
|
图 11 剖面右半部电性主轴统计成像结果 由左至右依次为统计玫瑰图、频率分布云图、测点分布云图,统计过程施加了二维性加权. Fig. 11 Statistical images of geo-electrical strikes of the SE part of the profile for all sites-all frequencies data calculated with dimensional weighting by using of CCZ method From left to right, the graphs are respectively rose diagram, frequency-based cloud diagram and site-based cloud diagram. |
依据图 11中的频率分布云图,可以大致区分出5个电性主轴特征相对一致的频段,分别为140~320 Hz、14~140 Hz、0.14~14 Hz、0.015~0.14 Hz、0.0001~0.015 Hz.图 12给出了前4个频段的分频段统计成像结果,从图中可以看出以下特征:
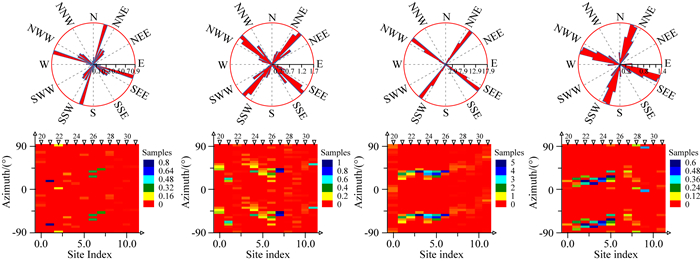
|
图 12 剖面东南段电性主轴分频段统计成像结果 上为统计玫瑰图,下为测点分布云图,自左至右频率范围依次为:140~320 Hz、14~140 Hz、0.14~14 Hz、0.015~0.14 Hz,统计过程施加了二维性加权. Fig. 12 Statistical images of geo-electrical strikes of the SE part of the profile calculated with dimensional weighting by using of CCZ method The uppers are rose diagrams and the lowers are site-based cloud diagram. From left to right, the frequency bands are respectively 140~320 Hz、14~140 Hz、0.14~14 Hz、0.015~0.14 Hz. |
(1)频段140~320 Hz:统计玫瑰图上显示存在NE20°和NE30°两个电性主轴方位,测点分布云图上显示NE20°电性主轴分布在测点21处,NE30°电性主轴分布在测点26处,构成强二维构造体在地表附近的出露边界;
(2)频段14~140 Hz:最显著的电性主轴方位是北东向,同时夹有北北东向方位,分布范围主要在测点20~27之间,显示为一系列北北东-北东向的线性构造,其中测点27最为显著,端部测点32处也存在电性主轴的集中;
(3)频段0.14~14 Hz:最显著的电性主轴方位为NE35°左右,在测点21-26之间,为强二维构造体的主要体现频段,此外测点20的南北-东西向、测点27-29的北东向、测点32的北东东向等电性主轴方位也有所显示,但不是很明显;
(4)频段0.015~0.14 Hz:主要电性主轴方位为NE10°-NE30°,分布于测点20-26之间,次要构造测点28、测点29之间的近南北-东西向构造.
通过以上成像分析,我们发现:在剖面东南段,最主要的线性构造为北北东(NE30°左右)走向的强二维高阻异常体,该二维构造体在测点21(对应于郯庐断裂带东枝F3-2)、测点26处可能出露于地表,从地质图上看,其范围和走向与张八岭隆起构造非常一致.该强二维构造体的主要响应频段为0.14~14 Hz,按照图 7给出的大致500 Ωm的电阻率计算,其底界深度应在30 km以浅,属于壳内构造.
3.5 全剖面低频段(0.0001~0.015 Hz)统计成像在成像分析过程中,我们发现在低频段(0.0001~0.015 Hz)剖面西北段与东南段有着较为一致的线性构造发育图像,故将此频段的电性主轴的统计成像结果绘制于图 13之中.剖面西北段低频段电性主轴的主要特征前面已经描述.剖面东南段:统计玫瑰图显示其主要电性主轴方位为北东东方位,杂有北北东、北东方位等;测点云图显示,较为稳定的北东东向电性主轴主要分布在测点26以西,为NE75°左右,该主轴方位在测点20处表现最为显著,且与剖面西北段的测点19的主轴方位相一致,不过,在测点22处,也存在较显著的NE35°左右的电性主轴方位;测点26以东,电性主轴也以北东东向为主,但较为散乱.
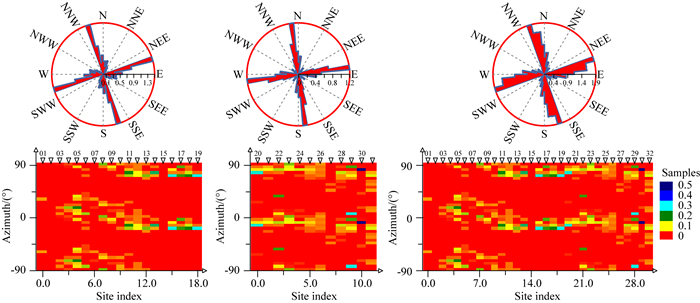
|
图 13 低频段(0.0001~0.015 Hz)电性主轴分频段统计图 上为统计玫瑰图,下为测点分布云图,自左至右依次为剖面西北段、剖面东南段、全剖面统计成像,统计过程施加了二维性加权. Fig. 13 Statistical images of geo-electrical strikes of the lowest frequency band (0.0001~0.015 Hz) calculated with dimensional weighting by using of CCZ method The uppers are rose diagrams and the lowers are site-based cloud diagram. From left to right, the graphs are respectively for the NW part of the profile, the SE part of the profile and the whole profile. |
从全剖面低频段成像结果上看,在测点10-32之间,总体上电性主轴方位集中于NE75°左右,其中横跨郯庐断裂带(F3)的测点16-测点21之间最为显著.此频段的主要电性主轴与频段0.015~0.14 Hz之间存在较大的夹角,故而其对应的岩层与上覆岩层之间形成立交桥构造.根据前面的深度估算,该北东东向的线性构造的顶部埋深大致为35 km,故其主体可能发育于上地幔顶部,显示了与上覆地壳岩层之间的不整合接触关系.
3.6 分析结果的归纳现对以上分析结果做简单的归纳.整条剖面的地壳结构存在西北段和东南段两个不同特征的分区.东南段地壳中存在走向为NE30°左右的高阻二维体,其西侧为郯庐断裂带东枝(F3-2),向东的横向延伸范围20 km左右,出露地表,深度在30 km以上,在地质构造上对应于张八岭隆起;西北段地壳中存在沉积盆地和结晶地壳之间的不整合接触:沉积盆地以东西-南北构造为主,而地壳中则以北北东-北西西构造为主.此外,我们还发现,地壳与地幔之间具有立交桥式的不整合接触关系,地壳以北北东向(NE30°左右)构造为主,而上地幔顶部则以北东东向(NE75°左右)构造为主,二者的电性主轴夹角大于40°,形成立交桥构造.北北东向的郯庐断裂带(F3)主要发育于地壳以内,电性主轴方位为NE20°左右.郯庐带下方地幔顶部,北东东向(NE75°左右)线性构造特征显著,为该剖面上地幔顶部线性构造发育最为集中的区段.
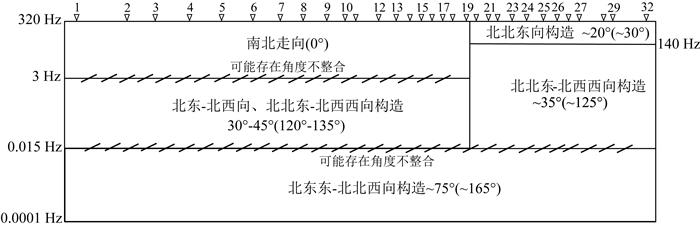
忽略分析过程中个别测点或局部区域独特的电性主轴分布情况,将整条剖面的主要电性主轴归纳于图 14中.该图不仅可为二维反演中电性主轴方位的选择提供依据,还可直观地分析剖面上纵横向的构造接触关系.
|
图 14 电性主轴分析综合结果图 忽略了个别测点和局部小区域独特的主轴分布.括号中的角度表示可能出现的电性主轴的共轭方位,需要根据其他资料确定其唯一性. Fig. 14 Integrated result of statistical analysis of geo-electrical strikes Very few sites and local peculiar azimuth of geo-electrical strike are ignored. The angle in parentheses indicates the possible conjugate azimuth of geo-electrical strike and their uniqueness need to be determined on the basis of other information. |
本文基于多测点-多频点大地电磁阻抗张量分解统计成像方法(简称大地电磁阻抗张量成像),通过对三维“立交桥”模型等理论模型以及横跨郯庐断裂带的一条实测剖面的分析研究,详细地展示了该项技术在大地线性构造判别中的应用过程,证明利用该项技术可以较好地识别存在电性差异的线性构造发育的几何特征、测点范围和频率范围;利用电性主轴方位在不同频段、不同剖面位置之间的变化,可以获得不同线性构造之间的纵横向转换信息,进而可推测大地构造的运动变形及其演化过程.本文研究结果证明,大地电磁阻抗张量成像的分析结果可将大地电磁观测响应与地质构造几何特征直接联系起来,为大地电磁资料的地质解释提供了独立于反演的新的技术手段.由于这一技术没有反演所固有的非唯一性,故其分析结果具有较好的确定性.
从本文分析中可以看出,郯庐断裂带南段壳幔之间的电性主轴存在较大的差异(壳幔间电性主轴夹角大于40°),我们也知道南非阿特拉斯山脉岩石圈也存在类似的立交桥构造,并在电性主轴的选择方面引起了较大争论(Jones et al., 2012;Anahnah et al., 2012),这意味着类似于这种立交桥构造在实际大地构造中较为常见.立交桥构造下大地电磁二维反演,电性主轴如何选择,在目前还未曾解决的一个问题.大地电磁阻抗张量成像技术能够给出电性主轴较为完整的频率-空间分布图像,使得在进行大地电磁二维反演时,在不同剖面位置、不同频段选择合理的电性主轴方位成为可能,因而为探寻立交桥构造的大地电磁二维反演的合理解决方案提供了技术基础依据.
然而,也要看到,由于大地电磁阻抗张量成像技术是在频率域进行的,故而在将统计成像结果转换到深度域时,比如确定线性构造的倾角和发育深度等,还存在困难.当前基于视电阻率值估算趋肤深度的方法存在较大的不确定性.如何将统计结果由频率域较好地转换到深度域,获得类似于地震深度偏移那样的成像结果,是这一技术亟待发展完善的研究方向.
| Anahnah F, Galindo-Zaldivar J, Chalouan A, et al. 2012. Reply to the comment by A. G. Jones et al. on "Deep resistivity cross section of the intraplate Atlas Mountains (NW Africa):New evidence of anomalous mantle and related Quaternary volcanism". Tectonics, 31(5). DOI:10.1029/2010TC003116 | |
| Bahr K. 1988. Interpretation of the magnetotelluric impedance tensor:regional induction and local telluric distortion. J. Geophys, 62: 119-127. | |
| Bahr K. 1991. Geological noise in magnetotelluric data:a classification of distortion types. Phys Earth Planet In, 66(1-2): 24-38. DOI:10.1016/0031-9201(91)90101-M | |
| Bibby H M, Caldwell T G, Brown C. 2005. Determinable and non-determinable parameters of galvanic distortion in magnetotellurics. Geophys J Int, 163(3): 915-930. DOI:10.1111/j.1365-246X.2005.02779.x | |
| Cai J T, Chen X B, Zhao G Z. 2010. Refined techniques for data processing and two-dimensional inversion in magnetotelluric Ⅰ:Tensor decomposition and dimensionality analysis. Chinese Journal of Geophysics (in Chinese), 53(10): 2516-2526. DOI:10.3969/j.issn.0001-5733.2010.10.025 | |
| Caldwell T G, Bibby H M, Brown C. 2004. The magnetotelluric phase tensor. Geophys J Int, 158(2): 457-469. DOI:10.1111/j.1365-246X.2004.02281.x | |
| Chen X B, Cai J T, Wang L F, et al. 2014. Refined techniques for data processing and two-dimensional inversion in magnetotelluric (Ⅳ):Statistical image method based on multi-site, multi-frequency tensor decomposition. Chinese Journal of Geophysics (in Chinese), 57(6): 1946-1957. DOI:10.6038/cjg20140625 | |
| Chen X B, Zhao G Z, Zhan Y. 2004. A visual integrated windows system for MT data process and interpretation. Oil Geophysical Prospecting (in Chinese), 39(Suppl.): 11-16. | |
| Groom R W, Bailey R C. 1989. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion. J. Geophys. Res., 94(B2): 1913-1925. DOI:10.1029/JB094iB02p01913 | |
| Groom R W, Bailey R C. 1991. Analytic investigations of the effects of near-surface three-dimensional galvanic scatterers on MT tensor decompositions. Geophysics, 56(4): 496-518. DOI:10.1190/1.1443066 | |
| Jones A G, Kiyan D, Fullea J, et al. 2012. Comment on "Deep resistivity cross section of the intraplate Atlas Mountains (NW Africa):New evidence of anomalous mantle and related Quaternary volcanism". Tectonics, 31(5). DOI:10.1029/2011TC003051 | |
| Mackie R L, Madden T R, Wannamaker P E. 1993. Three-dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions. Geophysics, 58(2): 215-226. DOI:10.1190/1.1443407 | |
| 蔡军涛, 陈小斌, 赵国泽. 2010. 大地电磁资料精细处理和二维反演解释技术研究(一)--阻抗张量分解与构造维性分析. 地球物理学报, 53(10): 2516–2526. DOI:10.3969/j.issn.0001-5733.2010.10.025 | |
| 陈小斌, 赵国泽, 詹艳. 2004. MT资料处理与解释的Windows可视化集成系统. 石油地球物理勘探, 39(Suppl.): 11–16. | |
| 陈小斌, 蔡军涛, 王立凤, 等. 2014. 大地电磁资料精细处理和二维反演解释技术研究(四)--阻抗张量分解的多测点-多频点统计成像分析. 地球物理学报, 57(6): 1946–1957. DOI:10.6038/cjg20140625 | |
 2017, Vol. 60
2017, Vol. 60

