由于次声频率低、衰减慢、传播距离远等优势,在地震、火山爆发、泥石流等灾害预报以及爆炸事件监测中发挥着重要作用.地震的发生存在诸多不确定性和复杂性,使得地震预报工作十分困难,准确的预报还很难实现(Chen, 2007).近些年来,研究者发现,很多地震发生前会产生异常次声波,这为地震的预报工作增加了一种可能的前兆信息.胡心康等(1980)初步探索了大气中一种压力波动与区域地震间的关系,发现该大气波周期为几十秒至500 s的次声波;吕君等(2012)在北京海淀区的一次小地震前4天监测到异常次声波信号;北京工业大学地震研究所长期关注地震预测研究,其中,李均之等(2006, 2007)分别在2001年昆仑山地震和2004年印尼地震前10天和前7天均观测到异常次声信号,2008年四川汶川地震以及2010年青海玉树地震时,该所也收到多种临震信息,如:次声波、磁三针、电离层等异常信号(陈维升等,2013a),并通过对2011年日本大地震的观测研究发现:大地震在震前几年就会出现前兆异常信息,尤其在震前几天会陆续出现临震前兆异常(陈维升等,2013b);Su和Tian (2001)通过对2000年阿富汗、印度尼西亚、日本等地震的分析,观测到在震前10天左右会产生前兆性次声波;Xia等(2011)研究了2002-2008年在北京观测到的地震前异常次声信号,结果表明85%的地震在震前1~15天会接收到次声信号.另外,火山爆发、泥石流等自然灾害发生时也会产生次声信号,Johnson等(2003, 2004)利用次声探测仪对5处活火山进行监测,并分析火山次声信号的产生机理及频谱特性;章书成和余南阳(2010)通过实验研究,成功地研制了泥石流次声警报器,该系统可以在泥石流来临之前观测到次声异常信号并进行预警;Arnold等(2014)研究发现泥石流会产生两个频段的声波,其中一个频段为低频声能,即次声.
次声还是监测大气层、浅地表爆炸的有效手段.自1996年以来,全面禁止核试验条约组织(CTBTO)计划在全球范围内建设60个次声台站,以监测全球范围内可能发生的核试验,目前,已建成48个,4个处于建设之中.无论是地震等自然灾害次声的监测,还是爆炸事件的次声监测,准确地获取次声信号慢度和方位角等参数,将有助于分析源信号的传播、定位以及源性质识别等工作.次声慢度和方位角的主要算法有最小二乘估计方法、基于互相关的估计方法(David, 2008)以及FK法等,其中应用最普遍的是FK法.FK法是一种台阵信号分析处理方法,广泛应用于地震波、次声等台阵信号处理.Capon (1969)最早描述分析了FK法,之后许多研究者对该方法进行了改进,主要有宽带FK法(Kvaerna and Doorbvos, 1986)、最大似然估计方法(Kvaerna and Ringdal, 1986)等.目前,最常用的FK法是Kvaerna和Doorbvos提出的宽带FK法(严峰等, 2006).但是,将宽带FK法应用于次声信号分析时,计算得出的慢度和方位角分辨率不高,伪峰较明显,严重影响了慢度和方位角的计算精度.
在通信、雷达、电子侦察、射电天文等领域对信号波达方向的研究由来已久,其中,子空间分解算法的提出具有里程碑式的意义(Schmidt, 1986; Roy and Kailath, 1989).该算法将接收数据的协方差矩阵分解出信号子空间和噪声子空间,利用信号和噪声之间的正交特性构造出高分辨率的空间谱峰,大大提高了算法的分辨能力,应用十分广泛(Paaso and Henna, 2013; Gupta and Kar, 2015; Kar and Palanisamy, 2012).然而,此类方法的研究主要针对波达方向一维估计,多维算法主要针对频率、时延、俯仰角等参数(许凌云等, 2011; 包志强等, 2006; 梁军利等, 2007),没有涉及慢度参数.有鉴于此,本文根据次声信号的时频特性,基于次声信号子空间和噪声子空间的不相关性,构建了次声信号慢度和方位角二维子空间计算模型,并在此基础上提出了一种高分辨率次声信号二维子空间算法.
多年来,课题组对次声信号的预处理、降噪、检测、分类识别等方面进行了广泛而深入的研究,取得了一定的研究成果,为本文的工作打下了坚实的基础.课题组开展的研究主要有:分析了影响次声台站的主要背景噪声源--风、温度、压强等气象要素,基于蒙古次声台站实测数据,对不同时间尺度下各气象要素与次声信号、各气象要素变化量与次声信号变化量的关系及影响规律进行了分析,提出了应用分布建模补偿法对气象要素引起的背景噪声信号进行消除(李妍等, 2015; Li et al., 2014; 李妍等, 2014; 李夕海等, 2015);研究了单阵元次声事件信号和多阵元事件次声信号的检测方法,提出了基于EMD分解和STA/LTA的联合检测方法、基于时频图区域能量比的检测方法、基于小波包分解和STA/LTA的联合检测方法,并进行了详细的理论分析、大量的仿真实验和实测数据验证实验(张万刚等, 2015a, 2015b);对地下爆破产生次声信号的机理进行了定性和定量分析,提取了次声信号时域、频域、倒谱域和时频域的特征,并通过实验对其识别效果进行了对比分析,验证了其有效性(姜楠等, 2013, 2014; 李夕海等, 2014).
2 二维子空间模型假设次声台阵是由M个阵元组成的任意阵,次声信号为远场窄带信号,中心频率为w0,以方位角θ和慢度p经过次声台阵,如图 1所示.
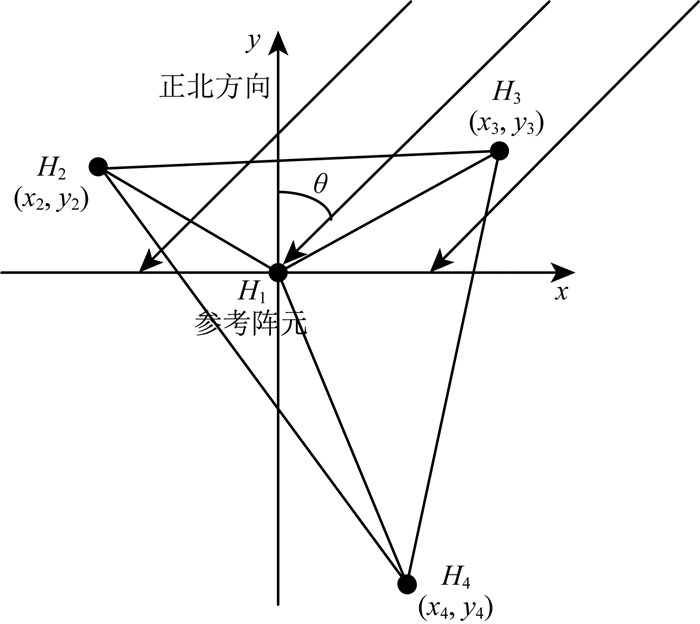
|
图 1 任意型次声阵接收信号模型 Fig. 1 The signal model of infrasound array in arbitrary geometry |
s(t)表示参考阵元H1接收到的信源信号,可表示为
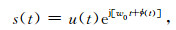
|
(1) |
其中u(t)表示信号幅度,ϕ(t)表示信号的相位.则第m个阵元接收的信源信号:
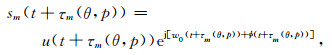
|
(2) |
式中τm(θ, p)为信号从第m个阵元传播到参考阵元的时间差,假设第m个阵元的坐标为(xm, ym),则:
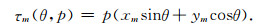
|
(3) |
对于远场窄带信号来说,同一时刻空间源信号在各阵元处的u(t)和ϕ(t)均保持不变,仅有因空间源信号到达各阵元的波程差而引起的相位变化,信号包络相对于信号随时间的相位变化来说是慢变化的.因此,可得出如下关系式:
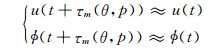
|
(4) |
由此可得:
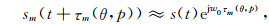
|
(5) |
则第m个阵元接收的观测信号为
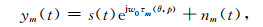
|
(6) |
其中nm(t)表示第m个阵元接收的噪声信号.将M个阵元在特定时刻接收的信号写成一个列向量,即:
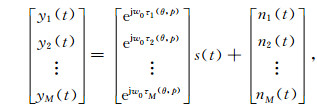
|
(7) |
写成矩阵形式为
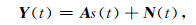
|
(8) |
其中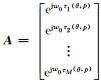
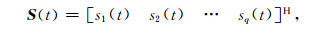
|
(9) |
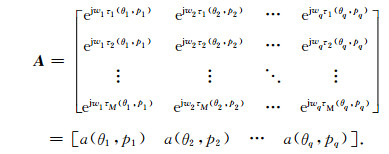
|
(10) |
其中,H为共轭转置.
3 子空间分解算法由公式(9)和(10)可知,任意型台阵接收远场窄带次声信号的模型可表示为
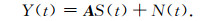
|
(11) |
假定信号和噪声是互不相关的,则阵列数据的协方差矩阵为
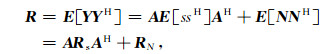
|
(12) |
即可将数据的协方差矩阵变成信号部分ARs A H和噪声部分R N,假设背景噪声为高斯白噪声,且功率为σ2,则有:
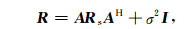
|
(13) |
对协方差矩阵进行特征分解R=EΛE H,其中E为特征矢量矩阵,对角阵Λ由特征值组成:
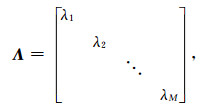
|
(14) |
将R的特征值按大小顺序排列,其中较大的特征值与信号有关,其数值大于σ2,较小的特征值与噪声有关,其数值理论上为σ2.对于数据中包含q个次声信号时,上式中特征值的大小关系为
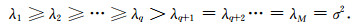
|
(15) |
信号的特征值对应的特征矢量构成信号子空间E s=[ e1 e2 … eq],噪声的特征值对应的特征矢量构成噪声子空间E n=[ eq+1 eq+2 …eM ].由于信号和噪声之间是不相关的,理想条件下信号子空间和噪声子空间是正交的,故可得:
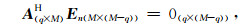
|
(16) |
此为矩阵形式,标量形式为
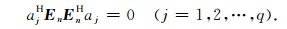
|
(17) |
从理论上讲,满足(17)式的慢度和方位角即为待求的慢度和方位角.在实际计算中,可将求解转化为搜索慢度和方位角以满足最小化要求,即
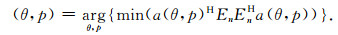
|
(18) |
在此最小化要求下,可通过构造慢度和方位角二维子空间谱函数,用搜索最大值代替搜索最小值,即
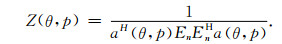
|
(19) |
在慢度和方位角二维空间中,对函数进行谱峰搜索,峰值对应的(θ1, p1),(θ2, p2),…,(θq, pq)即为q个次声信号慢度和方位角的估计.
4 仿真实验及结果分析 4.1 窄带信号分析仿真实验采用国际上惯用的高斯调制正弦信号作为仿真次声信号,高斯调制正弦波公式为
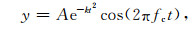
|
(20) |
其中,
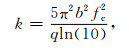
|
(21) |
A是振幅,b是归一化带宽,q是衰减因子,fc是中心频率(Hz).
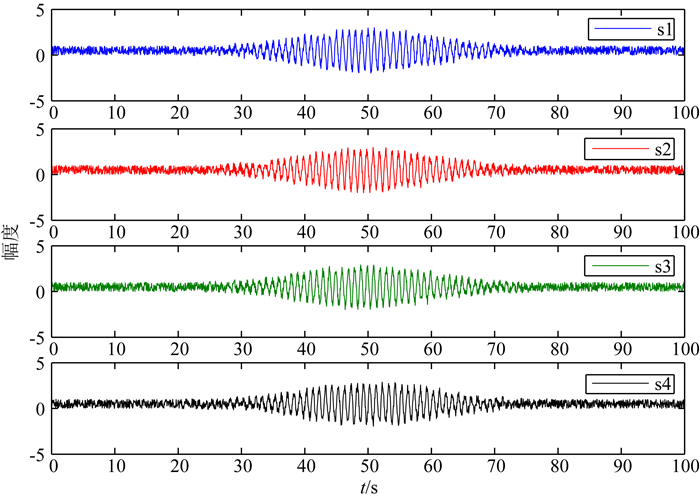
根据IMS关注的可疑核爆频率范围一般为0.02~4 Hz,仿真信号的频率设为2 Hz.一般情况下,次声监测台站距离次声源较远,因此,次声信号相对于台阵为远场信号,并假设该次声信号以340 m·s-1的速度、50°的方位角经大气传播到国际次声台站IS55.IS55中心四个阵元的分布如图 2所示.图 3所示为IS55中心四个阵元接收的仿真次声信号,采样频率为20 Hz,采样点数为2000点,并添加了10 dB的高斯白噪声.
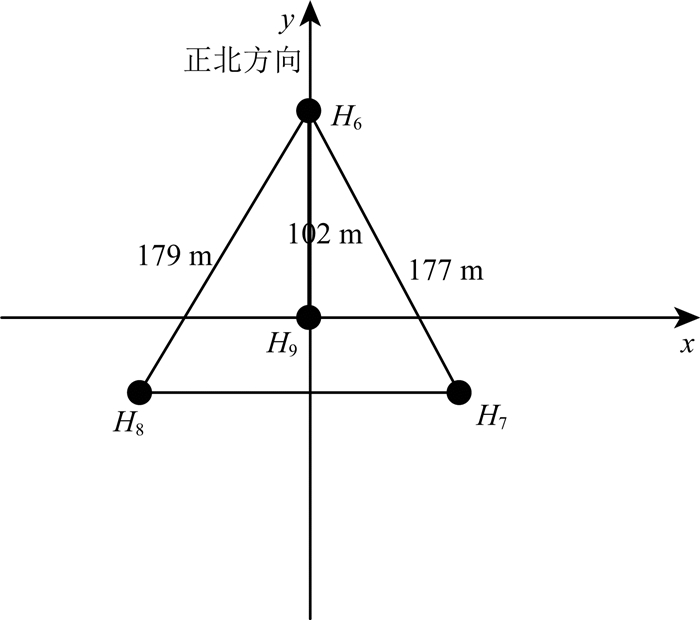
|
图 2 IS55中心四个阵元的分布图 Fig. 2 The distribution of the elements in IS55 |
|
图 3 四个阵元接收到的含噪信号 Fig. 3 The simulated signals received by the four elements |
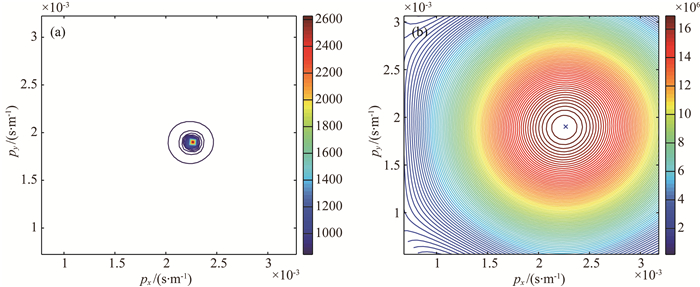
利用子空间模型法与原始FK法对上述数据进行分析处理,计算结果如图 4所示.从图 4的对比中可以看出,子空间模型法的分辨率明显高于原始FK法.为进一步对比两种算法的性能,分别计算慢度和方位角的均值、方差以及均方根误差(Root mean square error,RMSE),RMSE的定义为
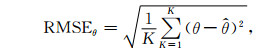
|
(22) |
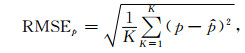
|
(23) |
|
图 4 两种方法对窄带信号处理结果对比 (a)子空间模型法分析结果;(b) FK法分析结果. Fig. 4 Comparison results of the two methods with anarrowband signal (a) Computed result with subspace model algorithm; (b) Computed result with FK method. |
其中,K表示实验次数,θ表示真实次声方位角,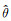
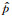
|
|
表 1 10 dB的条件下两种算法计算结果性能对比 Table 1 The results of the two methods when SNR=10 dB |
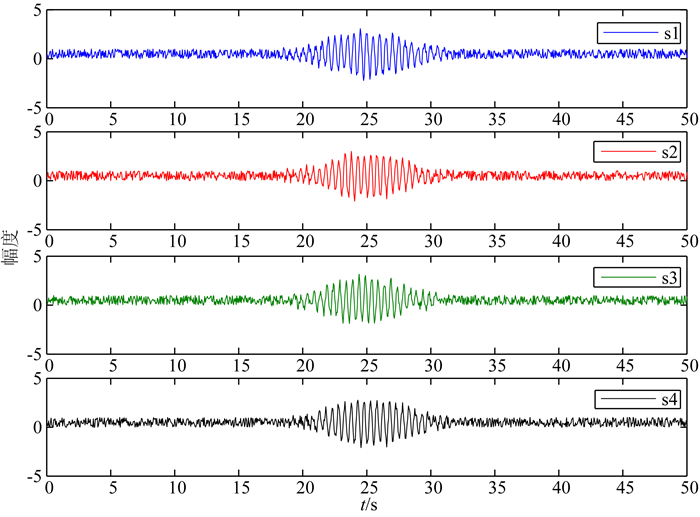
由于台阵接收的次声信号往往是宽带信号,因此,为进一步验证算法的有效性,采用中心频率为2 Hz、带宽2 Hz的高斯调制正弦信号模拟次声信号,速度340 m·s-1,方位角50°,并添加10 dB的高斯白噪声,信号波形如图 5所示.
|
图 5 四个阵元接收到的宽带仿真信号 Fig. 5 The simulated broadband signals received by four elements |
处理宽带次声信号,首先是将接收数据从时域转换到频域,在频域上把宽带信号分割成J个窄带,然后用上述窄带处理方法处理每个窄带信号,得到各窄带的谱函数,最后对这些空间谱进行叠加平均,得到宽带信号的谱函数.每个频率点的数据协方差矩阵可表示为
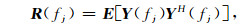
|
(24) |
对每个频率点的R(fj)做特征分解,得到噪声子空间为E n(fj),同样根据信号子空间和噪声子空间的正交性,构造宽带信号慢度和方位角二维子空间谱函数:
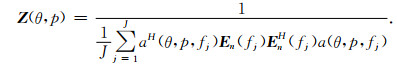
|
(25) |
两种方法的计算结果如图 6所示.从图 6的结果可以看出:对于宽带信号,子空间模型法分辨率仍然明显优于原始FK法.为进一步验证算法的有效性,在10 dB的条件下,同样重复做了20次实验,对比速度和方位角的均值、方差以及RMSE,结果如表 2所示.表 2的结果表明子空间模型法的均值、方差以及RMSE仍然优于FK法,反应子空间模型法计算精度更高,稳定性更好.
|
图 6 两种方法对宽带信号处理结果对比 (a)子空间模型法分析结果;(b) FK法分析结果. Fig. 6 Comparison results of the two methods with a broadband signal (a) Computed result with subspace model algorithm; (b) Computed result with FK method. |
|
|
表 2 10 dB的条件下两种算法计算结果性能对比 Table 2 The results of the two methods when SNR=10 dB |
次声台阵在接收数据的时候,常常会遇到这样的情况:背景噪声源产生的次声信号持续时间较长,而感兴趣的次声源产生的信号持续时间较短,并与背景噪声源混合.如果两种声源的带宽接近,则很难在时频域内进行分离,此时可以在空间域内,利用信号慢度和方位角的不同进行分离.因此,用两个宽带信号模拟次声信号,对比分析子空间模型法和FK法的分辨能力,两个宽带信号分别为:
(1)中心频率为2 Hz、带宽2 Hz的高斯调制正弦信号,速度340 m·s-1,方位角50°,并添加10 dB的高斯白噪声;
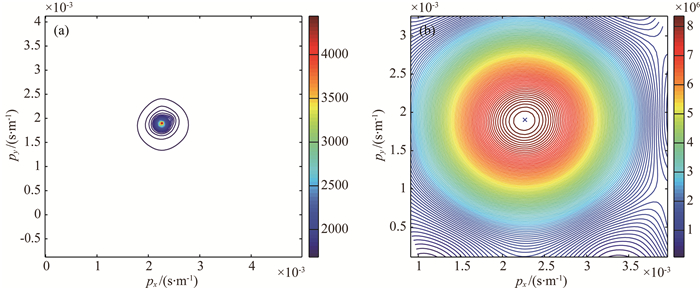
(2)2~4 Hz的线性调频信号,速度340 m·s-1,方位角60°.线性调频信号表达式为
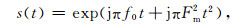
|
(26) |
其中,f0为调频起始频率,Fm为调频斜率.
合成信号的波形如图 7所示,两种方法的对比分析结果如图 8所示,其中,子空间模型法可以有效分开两个信号,得到两个信号的速度分别为339.1 m·s-1和340.7 m·s-1,方位角为59.8°和49.9°,而FK法无法对两个信号进行有效分离,只能得到一个信号,其速度为342.5 m·s-1,方位角为56.8°,说明子空间模型法在分析多个信号时性能更优.
|
图 7 四个阵元接收到的两个宽带信号的合成信号 Fig. 7 The combined signals with two broadband signals received by four elements |
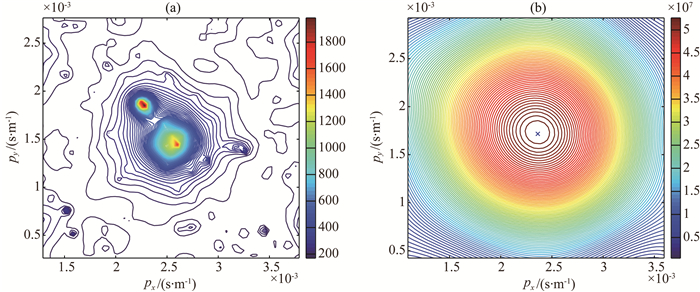
|
图 8 两种方法对两个宽带信号合成后的处理结果对比 (a)子空间模型法分析结果;(b) FK法分析结果. Fig. 8 Comparison results of the two methods with a combined signal with two broadband signals (a) Computed result with subspace model algorithm; (b) Computed result with FK method. |
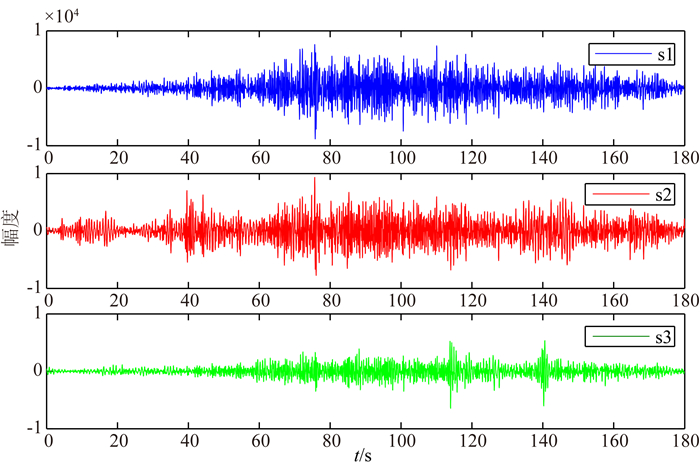
实际数据为嫦娥1号运载火箭发射时产生的次声信号,时间为2007年10月24日18时,地点为四川省西昌卫星发射中心.探测阵位于西昌黄联镇附近,距离发射点约70 km,为三阵元小孔径次声阵,孔径约50 m,接收到火箭发射时的次声信号波形如图 9所示.利用本文提出的方法以及FK法对数据进行分析处理,计算结果如图 10所示,其中由子空间模型法得出的信号速度为331.95 m·s-1,方位角为348.4°,而由FK法得出的信号速度为326.26 m·s-1,方位角为18.9°.根据探测阵与发射点的经纬度计算得出的方位角为351.3°,而且探测阵与发射点之间的距离并不远,可以看出,FK法计算的方位角与实际方位角相差较大,而由子空间模型法计算得出的方位角较准确,更符合实际情况.对于子空间模型法存在的误差,分析造成的原因为两方面:一是背景环境风速的影响,使得次声在传播的过程中方向有所改变;二是阵元附近噪声较明显,信噪比不高.
|
图 9 探测阵三阵元接收到的次声信号 Fig. 9 The actual signals received by the three elements |
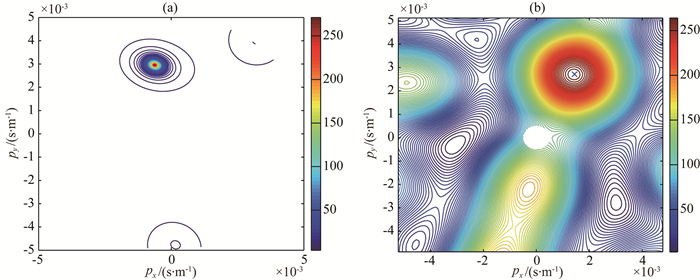
|
图 10 两种方法对实际次声信号处理结果对比 (a)子空间模型法分析结果;(b) FK法分析结果.图中心空白圆圈为无数据区,不影响分析研究结果. Fig. 10 Comparison results of the two methods with a real signal (a) Computed result with subspace model algorithm; (b) Computed result with FK method. The blank circle in the center of the figure represent no data, and it doesn′t affect the results of the studies. |
对于自然灾害预警以及人为爆炸事件定性,次声信号的观测与分析正发挥着越来越重要的作用.本文针对现有的次声慢度和方位角算法-FK法存在计算精度和分辨率不高的问题,基于次声信号子空间和噪声子空间的不相关性,构建了次声慢度和方位角二维子空间模型,并提出了一种基于次声信号二维子空间模型的慢度和方位角算法.利用国际上惯用的高斯调制正弦信号模拟次声信号,以实际次声台站IS55为背景,首先研究了窄带信号情况下子空间模型法算法的性能,对比分析了子空间模型法与FK法计算得出的慢度和方位角的均值、方差以及RMSE,结果表明子空间模型法性能明显优于FK法;然后,将该算法推广到宽带次声信号,并研究了对于时频域混叠的两个宽带次声信号,利用子空间模型法能够有效分离两个信号,而FK法无法实现有效分离;最后,对实际次声信号进行分析处理,通过对比,表明由本文提出的方法计算得出的方位角更准确,更符合实际情况.
| Arnold K, Johannes H, Emma S, et al. 2014. lnfrasound produced by debris flow:propagation and frequency content evolution. Natural Hazards, 70(3): 1713-1733. DOI:10.1007/s11069-011-9741-8 | |
| Bao Z Q, Wu S J, Zhang L R. 2006. A novel algorithm for joint source-number detection and DOA estimation. Acta Electronica Sinica(in Chinese), 34(12): 2170-2173. | |
| Brown D J, Whitaker R, Kennett B L N, et al. 2008. Automatic infrasonic signal detection using the Hough transform. Journal of Geophysical Research, 113: D17105. DOI:10.1029/2008JD009822 | |
| Capon J. 1969. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278 | |
| Chen W S, Li J Z, Liu Y C, et al. 2013a. Abnormal signals before Wenchuan and Yushu earthquakes. Journal of Beijing University of Technology(in Chinese), 39(10): 1505-1508. | |
| Chen W S, Li J Z, Xia Y Q, et al. 2013b. Early prediction of great earthquake and tsunami in Japan and impending signals. Journal of Beijing University of Technology(in Chinese), 39(8): 1206-1209. | |
| Chen Y T. 2007. Earthquake prediction:Progress, difficulties and prospect. Seismological and Geomagnetic Observation and Research, 28(2): 1-24. | |
| David J B, et al. 2008. Automatic infrasonic signal detection using the Hough transform. Journal of Geophysical Research, 113: D17105. DOI:10.1029/2008JD009822 | |
| Gupta P, Kar S P. 2015. MUSIC and improved MUSIC algorithm to estimate direction of arrival.//2015 International Conference on Communications and Signal Processing (ICCSP). Melmaruvathur:IEEE, 757-761. | |
| Hu X K, Shi J R, Ren J G. 1980. Preliminary study of the relation between a kind of pressure waves in the atmosphere and earthquakes. Acta Geophysica Sinica(in Chinese), 23(4): 450-458. | |
| Jiang N, Zhang Y, Meng L. 2013. Overview of early warning in major natural disasters based on infrasound.//Geophysical Series of National Security (9):Disaster prevention and national security (in Chinese), 180-185. | |
| Jiang N, Li X H, Yan S K, et al. 2014. Feature extraction of infrasound signals based on component ratio of IMF.//Geophysical Series of National Security (10):Geophysical Environment and National Security (in Chinese), 305-311. | |
| Johnson J B. 2003. Generation and propagation of infrasonic airwaves from volcanic explosions. Journal of Volcanology and Geothermal Research, 121(1-2): 1-14. DOI:10.1016/S0377-0273(02)00408-0 | |
| Johnson J B, Aster R C, Kyle P R. 2004. Volcanic eruptions observed with infrasound. Geophysical Research Letters, 31(14): L14604. DOI:10.1029/2004GL020020 | |
| Kar S P, Palanisamy P. 2012. Novel 2-D real-valued sinusoidal signal frequencies estimation approach based on modified ESPRIT and propagator method.//2012 IEEE International Conference on Advanced Communication Control and Computing Technologies (ICACCCT). Ramanathapuram:IEEE, 321-326. | |
| Kogelnig A, Hübl J, Suriñach E, et al. 2014. lnfrasound produced by debris flow:propagation and frequency content evolution. Natural Hazards, 70(3): 1713-1733. DOI:10.1007/s11069-011-9741-8 | |
| Kværna T, Doornbos D J. 1986. An integrated approach to slowness analysis with arrays and three-component stations. NORSAR Scientific Report:Semiannual Technical Summary No. 2-1985/1986, NORSAR, Kjeller, Norway, 60-69. | |
| Kværna T, Ringdal F. 1986. Stability of various F-K estimation techniques. NORSAR Scientific Report:Semiannual Technical Summary No. 1-1986/1987, NORSAR, Kjeller, Norway, 29-40. | |
| Li J Z, Chen W S, Xia Y Q, et al. 2006. The precursors of Ms8. 1 earthquake occurred in west of mountain gap of Kunlun, China. Progress in Geophysics(in Chinese), 21(2): 340-344. | |
| Li J Z, Chen W S, Xia Y Q. 2007. Imminent very strong infrasonic wave precursor received before the earthquake of magnitude M=9.0, 26th Dec. 2004 of Indonesia. Progress in Geophysics(in Chinese), 21(4): 1061-1063. | |
| Li X H, Zhang Y, Meng L, et al. 2015. The analysis of the effect of array parameter on infrasound noise reduction system performance. Acta Acustica(in Chinese), 40(3): 370-380. | |
| Li Y, Li X H, Meng L. 2014. Analysis of the characteristics of the background ambient noise origin of infrasound station. Advanced Materials Research, 1044-1045: 1061-1065. DOI:10.4028/www.scientific.net/AMR.1044-1045 | |
| Li Y, Li X H, Jiang L, et al. 2014. Survey on infrasound station background noise modeling technology.//Geophysical Series of National Security (10):Geophysical Environment and National Security (in Chinese), 312-318. | |
| Li X H, Zhang Y, Meng L, et al. 2015. The analysis of the effect of array parameter on infrasound noise reduction system performance. Acta Acustica(in Chinese), 40(3): 370-380. | |
| Liang J L, Yang S Y, Zhang J Y. 2007. A new frequency and 2-D DOA estimation algorithm. Chinese Journal of Radio Science(in Chinese), 22(6): 1008-1013. | |
| Lü J, Guo Q, Feng H N, et al. 2012. Anomalous infrasonic waves before an small earthquake in Beijing. Chinese J. Geophys.(in Chinese), 55(10): 3379-3385. DOI:10.6038/j.issn.0001-5733.2012.10.020 | |
| Paaso H, Mämmelä A, Patron D, et al. 2013. Modified MUSIC algorithm for DOA estimation using CRLH leaky-wave antennas.//8th International Conference on Cognitive Radio Oriented Wireless Networks. Washington, DC:IEEE, 166-171. | |
| Roy R, Kailath T. 1989. ESPRIT-Estimation of signal parameters via rotational invariance techniques. IEEE Transactions on Acoustics, Speech, and Signal Processing, 37(7): 984-995. DOI:10.1109/29.32276 | |
| Schmidt R. 1986. Multiple emitter location and signal parameter estimation. IEEE Transactions on Antennas and Propagation, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 | |
| Su F, Tian W. 2001. Measure and study of precursory infrasonic waves of strong earthquakes in May 2000. Low Frequency Noise, Vibration and Active Control, 20(3): 177-191. DOI:10.1260/0263092011493127 | |
| Xia Y Q, Liu J Y T, Cui X Y, et al. 2011. Abnormal infrasound signals before 92 M≥7.0 worldwide earthquakes during 2002-2008. Journal of Asian Earth Sciences, 41(4-5): 434-441. DOI:10.1016/j.jseaes.2010.04.015 | |
| Xu L Y, Zhang X F, Xu Z Z. 2011. Joint 2D angle and frequency estimation based on uniform square array. Journal of Applied Sciences(in Chinese), 29(2): 187-194. | |
| Yan F, Jin P, Fan G C. 2006. Comparison between two estimation methods of azimuth, slowness of seismic signal in frequency and time domains on seismic array. Northwestern Seismological Journal(in Chinese), 28(4): 327-330. | |
| Zhang S C, Yu N Y. 2010. Early warning system to debris flow. Journal of Mountain Science(in Chinese), 28(3): 379-384. | |
| Zhang W G, Li X H, Meng L. 2015a. Infrasonic signals integrity detection based on wavelet packet and STA/LTA. Nuclear Electronics and Detection technology(in Chinese), 35(9): 853-856. | |
| Zhang W G, Li X H, Meng L. 2015b. Spike processing of infrasound station data based on STA/LTA and polynomial fitting.//Geophysical Series of National Security (11):the Application of Geophysical Front (in Chinese), 209-213. | |
| 包志强, 吴顺君, 张林让. 2006. 一种信源个数与波达方向联合估计的新算法. 电子学报, 34(12): 2170–2173. | |
| 陈维升, 李均之, 刘程艳, 等. 2013a. 汶川和玉树地震前兆异常信息. 北京工业大学学报, 39(10): 1505–1508. | |
| 陈维升, 李均之, 夏雅琴, 等. 2013b. 日本大地震及海啸的早期预测及临震信号. 北京工业大学学报, 39(8): 1206–1209. | |
| 胡心康, 石金瑞, 任建国. 1980. 大气中一种压力波动与地震关系的初步探索. 地球物理学报, 23(4): 450–458. | |
| 姜楠, 张勇, 孟亮. 2013.基于次声的自然灾害预警概述.//国家安全地球物理丛书(九):防灾减灾与国家安全, 西安:地图出版社, 180-185. | |
| 姜楠, 李夕海, 闫双卡等. 2014.基于IMF分量比的次声信号特征提取.//国家安全地球物理丛书(十):地球物理环境与国家安全, 305-311. | |
| 李均之, 陈维升, 夏雅琴, 等. 2006. 昆仑山口西MS8.1级地震前兆. 地球物理学进展, 21(2): 340–344. | |
| 李均之, 陈维升, 夏雅琴. 2007. 在2004年12月26日印尼9级地震前收到特大临震信息. 地球物理学进展, 21(4): 1061–1063. | |
| 李夕海, 姜楠, 孟亮. 2014. 禁核试后美国核试验相关技术问题研究综述. 第二炮兵工程大学学报, 28(3): 87–91. | |
| 李夕海, 张勇, 孟亮, 等. 2015. 降噪阵列参数对次声降噪系统性能的影响分析. 声学学报, 40(3): 370–380. | |
| 李妍, 李夕海, 姜楠等. 2014.次声台站背景噪声建模技术现状与展望.//国家安全地球物理丛书(十):地球物理环境与国家安全, 312-318. | |
| 李妍, 李夕海, 孟亮. 2015. 次声台站环境背景噪声源特性分析. 科学技术与工程, 15(2): 245–249. | |
| 梁军利, 杨树元, 张军英. 2007. 一种信号频率及二维到达角联合估计新方法. 电波科学学报, 22(6): 1008–1013. | |
| 吕君, 郭泉, 冯浩楠, 等. 2012. 北京地震前的异常次声波. 地球物理学报, 55(10): 3379–3385. DOI:10.6038/j.issn.0001-5733.2012.10.020 | |
| 许凌云, 张小飞, 许宗泽. 2011. 平面阵列下的二维角度和频率联合估计. 应用科学学报, 29(2): 187–194. | |
| 严锋, 靳平, 范广超. 2006. 地震台阵上信号方位角和慢度的时、频域估计方法比较. 西北地震学报, 28(4): 327–330. | |
| 章书成, 余南阳. 2010. 泥石流早期警报系统. 山地学报, 28(3): 379–384. | |
| 张万刚, 李夕海, 孟亮. 2015a. 基于小波包分解及STA/LTA法的次声事件信号检测. 核电子学与探测技术, 35(9): 853–856. | |
| 张万刚, 李夕海, 孟亮. 2015b.基于STA/LTA及多项式拟合的次声台站数据野值处理方法.//国家安全地球物理丛书(十一):地球物理应用前沿, 209-213. | |
 2017, Vol. 60
2017, Vol. 60


